Structure and Dynamics of the Actin Filament

Abstract

We used all-atom molecular dynamics simulations to investigate the structure and properties of the actin filament, starting with either the recent Oda model or the older Holmes model. Simulations of monomeric and polymerized actin show that polymerization changes the nucleotide-binding cleft, bringing together the Q137 side chain and bound ATP in a way that may enhance ATP hydrolysis rate in the filament. Simulations with different bound nucleotides and conformations of the DNase I binding loop show that the persistence length of the filament depends only on the loop conformation. The computational modeling reveals how bound phalloidin stiffens actin filaments and inhibits the release of the γ-phosphate from ADP-P_i actin.

Introduction

The protein actin is highly conserved, abundant in eukaryotic cells, and known to play a role in a wide range of cellular functions. Actin is chiefly found in two forms: monomeric (or globular) actin and its polymerized counterpart, filamentous actin. The dynamic equilibrium between the forms is controlled by a variety of factors within the cell.¹ Actin filaments are a central structural feature of all muscle tissue,² and controlled polymerization of branched networks of actin filaments produce force for cell motility.³

The structural and dynamical properties of actin monomers and filaments depend, at least in part, on the state of the bound nucleotide.^4–7 Both forms of actin strongly bind ATP or ADP, but polymerized actin hydrolyzes its bound ATP about 40,000-fold faster⁸ than monomeric actin,⁹ but the mechanism is a major unsolved challenge.¹⁰ It is assumed that changes in the nucleotide-binding cleft increase the ATPase activity of polymerized actin. Previous molecular dynamics (MD) studies of actin and Arps showed that the conformation of nucleotide-binding cleft depends on the bound nucleotide in monomeric actin and Arps^11–13 and actin trimers.¹² However these findings do not address the means by which polymerization changes the rate of ATP hydrolysis. Experimental data^14,15 showed that residue Q137 is important in ATP hydrolysis, and Oda et al. hypothesized that flattening of the actin molecule moves residue Q137 closer to the bound ATP.¹⁶ Crystal structures of monomeric actin^5,6 show that Q137 coordinates a water molecule that might attack the bound ATP.

Several dozen crystal structures of actin monomers have been determined since the first crystal structure of ATP-actin bound to DNase I¹⁷, but currently no high-resolution crystal structures of filamentous actin are available. The parameters of the actin helix were originally established by x-ray diffraction of whole muscle^18,19 and electron microscopy.^20–22 The first model of filamentous actin built with a crystal structure of the subunit is now commonly known as the Holmes model.²³ Recently Oda et al.¹⁶ obtained higher-resolution fiber diffraction data from filamentous actin stabilized by phalloidin and aligned with a superconducting magnet. Their refined model has the same helical arrangement of the actin subunits, but the actin subunit itself is flatter in the filament than is any crystal structure of monomeric actin. In the Oda model filament the two halves of the protein (c.f., Fig. 1) are rotated about 20° so that all four subdomains are close to lying in a plane. Oda et al. and previous workers²⁴ have observed this flattening of the actin subunit in 3D reconstructions of filaments from electron micrographs. These models suggest that flattening of the actin subunit is a main conformational change associated with actin polymerization, and that this change underlies the higher ATPase activity of filamentous actin.^16,25

Figure 1.

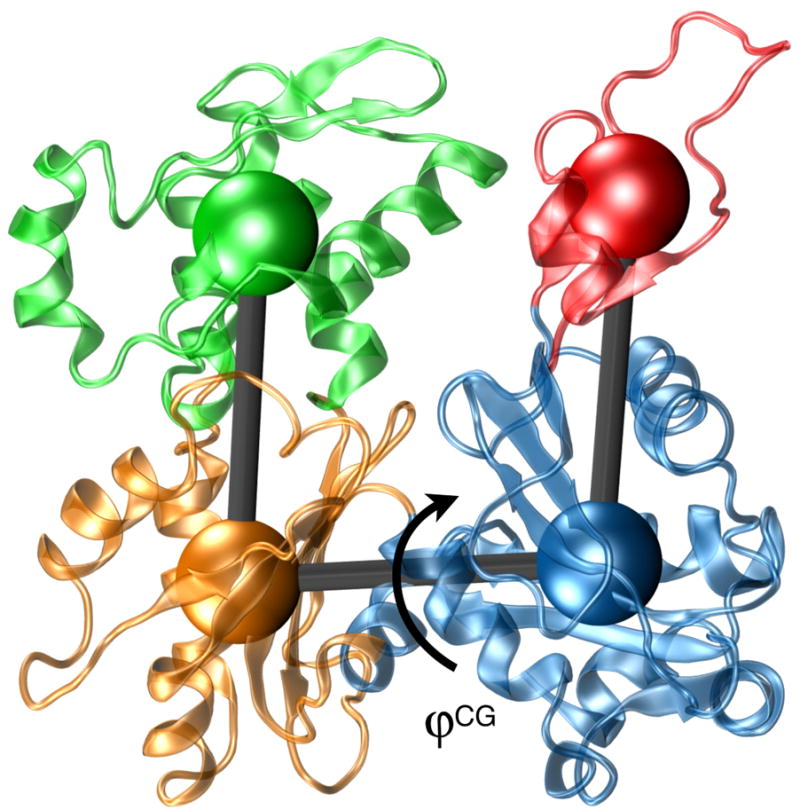
Actin subunit from the Oda et al.¹⁶ filament model in atomistic (cartoon) and coarse-grained (CG) representation. The four subdomains shown are: S1 (blue) residues 1-32, 70-144 and 338-375; S2 (red) residues 33-69; S3 (orange) residues 145-180 and 270-337; and S4 (green) residues 181-269. The cartoon representation of the protein is from PDB entry 2ZWH, and the “flatness” order parameter used for analysis is labeled.

The conformation of the DB loop in actin filaments is unsettled. The observation that the DB loop of some⁶ but not all⁹ crystals of ADP-bound actin form a well-defined α-helix led to the idea that DB loop folds into a helix in conjunction with ATP hydrolysis and phosphate release. The Oda model is based on a form of monomeric actin with an unstructured DNase-I binding loop (DB loop),^5,17 but Oda et al. proposed that an extension of the helical DB loop into the neighboring actin subunit in filaments could also explain the observed diffraction patterns.¹⁶ This is an intriguing possibility given the evidence that release of the inorganic phosphate subsequent to ATP hydrolysis within filamentous actin softens the filament^4,26 as well as increases the susceptibility to attack by severing proteins.²⁷ Additionally, computational studies²⁶ have drawn comparisons between the ATP-bound (DB loop unstructured) and ADP-bound (DB loop folded) forms of filamentous actin. A recent computational study of monomeric and trimeric actin demonstrated that folding of the DB loop in ADP-actin is thermodynamically favorable.¹²

Motivated by the unanswered questions concerning the structure and properties of actin filaments, we present a large scale all-atom MD study of the Oda and Holmes filament models with variations in both the bound nucleotide and the conformation of the DB loop. Previous MD simulations of actin and actin related proteins (Arps)^{11–13,26,28,29} explored the structure and dynamics of actin on timescales ranging from a few ns to 100 ns. Actin and Arp simulations based on purely classical MD methods investigated the short timescale properties of the actin monomer or filament, especially the conformation of the DB loop and properties of the nucleotide-binding cleft. Although MD simulations are limited to short time scales, they offer a complementary perspective to experimental techniques, inasmuch as they are fully atomistic in character and therefore permit sampling and observation of all atomic degrees of freedom in the system.

We performed MD simulations in an explicitly solvated aqueous environment of nine different actin filaments based on either the Holmes or Oda models with bound ATP or ADP and either folded or unfolded DB loops, including an additional simulation with bound phalloidin to further replicate the experimental conditions under which the filament models were obtained. We investigated the equilibrium dynamics of each of these filaments with an emphasis on understanding how polymerization stimulates the ATP hydrolysis rate and how the bound nucleotide influences the structure of the DB loop and macroscopic filament properties. The simulations give the persistence length of each filament for comparison with experimental measurements. We also performed a 50 ns simulation of ATP-bound monomeric for comparison with filamentous actin. The total amount of MD simulation performed in this study is over 0.5 μs for the actin filament.

Results

This section summarizes the findings obtained from our MD simulations. Properties reported were calculated from the last 20 ns of each simulation with data collected once the system had equilibrated. The criteria used to establish whether a particular filament simulation had equilibrated are discussed in the methods section. For reference, Table S1 in the Supplementary Material summarizes each of the systems investigated in this study. We systematically varied the filament model, bound nucleotide and the initial conformation of the DB loop. For brevity the results of these eight simulations are presented in shorthand notation to describe each system. For example, H/ATP/unfold refers to the simulation of a Holmes actin filament with bound ATP and the DB loop initially in the unfolded configuration.

Filament and Monomer Structure

The simulations were performed in the isobaric-isothermal (constant NPT) ensemble, and therefore required adjustment of the unit cell dimensions to maintain a constant pressure. As in previous NPT simulations with longitudinal periodicity²⁶ the filament crossover length fluctuates at the beginning but levels out to an approximately constant value, which we report as equilibrium filament lengths in Table 1. The experimentally measured crossover length of the Oda and Holmes filaments is 358 Å, whereas the crossover lengths reported in Table 1 range from 354 to 373 Å. Both of our simulations of ADP Oda filaments have a crossover of 357 Å, in very good agreement with the Oda model with ADP-actin subunits. The equilibrium crossover lengths of all the Oda filaments are smaller than the corresponding Holmes filaments.

Table 1.

Structural properties of actin filaments investigated by molecular dynamics.

Filament Model	Bound Nucleotide	DNase-I Loop1	Crossover Length2 (Å)	Filament RMSD3 (Å)
Oda	ATP	unfolded	362(±4)	5.7(±0.5)
	ATP	folded	354(±5)	6.9(±0.3)
	ADP	unfolded	357(±4)	5.6(±0.4)
	ADP	folded	357(±3)	6.4(±0.6)
Holmes	ATP	unfolded	364(±2)	8.3(±1.0)
	ATP	folded	363(±6)	10.5(±0.4)
	ADP	unfolded	373(±2)	7.1(±0.4)
	ADP	folded	366(±5)	8.2(±0.4)
Oda + phalloidin	ATP	unfolded	362(±1)	5.0(±0.2)

¹Refers to the initial conformation of the DNase-I binding loop. Further details are provided in the methods section.

²The crossover length is calculated by averaging the unit cell length over the last 20 ns of each simulation. Simulations were performed of one filament crossover distance (13 actin subunits) with periodicity along the longitudinal axis of the filament.

³The RMSD (of 4875 C^α atoms) is calculated with respect to the initial structure and using the last 20 ns of each data set as described in the methods section.

Our simulations of Oda filaments were more stable than simulations of Holmes models based on the root-mean-square deviations (RMSD), reported in Table 1 as ensemble average RMSD of all 4875 C^α atoms in an actin 13-mer calculated with respect to the starting structure. This suggests that the higher-resolution Oda model more accurately captures the subunit interactions that ultimately give rise to stable filament dynamics. The significantly larger filament RMSD values for the Holmes model simulations also indicate that the individual subunits must undergo some conformational shifts within the respect to the filament superstructure prior to equilibration. The RMSD of filaments were significantly higher than individual actin monomers or actin related proteins Arp2 and Arp3. The RMSD determined from MD simulations of actin or Arp2/Arp3 were reported to range from 2–2.5 Å.^{11–13,26,28} However, because of the supramolecular nature of the actin filament, i.e., the actin subunits are only constrained to each other by non-covalent bonds, it is not surprising that the RMSD of the entire actin 13-mer was higher than actin monomers, especially considering the fluctuations in filament crossover length.

For control purposes we performed simulations of actin filaments with bound ATP and a folded DB loop region. As detailed below in the discussion of the filament stiffness, the purpose of this control simulation was not to simulate a known experimental state of actin, but to test a hypothesis regarding the connection between the state of the nucleotide, the DB loop conformation, and the filament stiffness. In the ATP/(DB fold) Oda filament model simulation we found that the DB loop unfolded in the individual actin subunits during simulations of the state. In contrast, the folded DB loop in the ADP filament simulations was much more stable, in agreement with recent folding simulations that showed a thermodynamic driving force for a folded DB loop within actin trimers based on the Oda filament model.¹² The observed unfolding in the ATP/fold filament occurred slowly with respect to the simulation timescale and by the end of the simulation most of the DB loops were partially or fully unfolded. This is consistent with previous work that showed unfolding of the DB loop during simulation of ATP-actin monomers²⁸ and that the ATP-actin trimers are thermodynamically unfavorable for folding of the DB loop region.¹² Additionally, these studies were performed with the CHARMM22/27 and AMBER99SB (respectively) force fields. Consistent results for the ATP-actin (DB fold state) have now been obtained from three separate studies and two different force fields. Finally, these observations are consistent with the absence of experimental evidence folded DB loops in ATP-actin.

We characterized the flatness actin molecules with a four subunit coarse-grained (CG) representation of actin (Fig. 1).^13,17,30 The model consists of four actin subdomains, which provide an intuitive means to understand actin’s global shape and structure. The 4-site CG model is completely specified with six internal coordinates, typically chosen to be three bonds, two bending angles and a single dihedral. The flatness of subunits within a filament depends on the dihedral angle, which we chose as an order parameter to monitor in the atomistic MD simulations. The 4-site CG model accurately captures the flattening reported in the Oda model: the dihedral angles of crystallized monomeric actin range from 156 to 159° (obtained from PDB entries 1J6Z⁶ and 1NWK⁵, respectively; whereas the dihedral angle for the Oda actin filament model is 176° (PDB 2ZWH¹⁶). An angle of 180° corresponds to a completely planar (flat) monomer in the CG model.

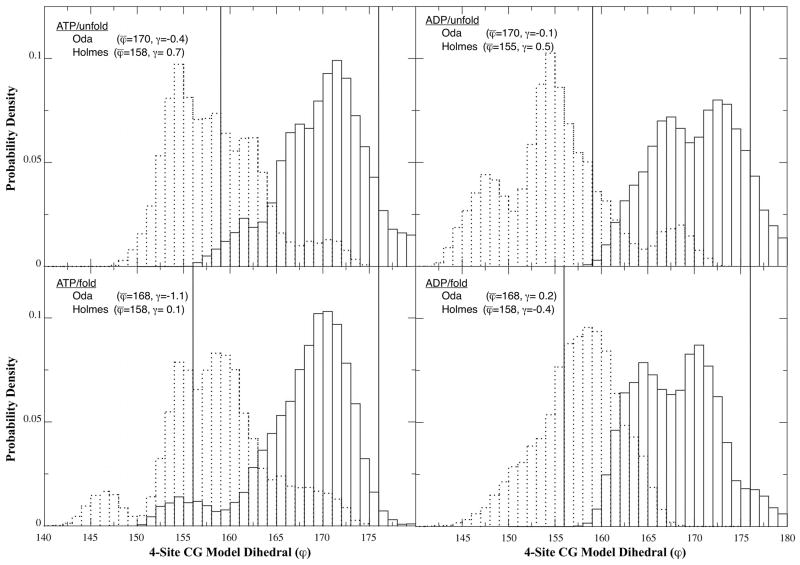
We used the CG structures produced by our atomistic MD simulations to calculate probability densities for dihedral angles of the actin subunits in filaments based on the Oda and Holmes models with bound ATP or ADP and unfolded or folded DB loops (Fig. 2). Each panel of the figure also shows the starting angles and the sample mean and skewness (γ), or third moment of the distribution defined as:

$$\gamma =\frac{\frac{1}{N}{\displaystyle \sum _{i=1}^N}{({\varphi }_i-\langle \varphi \rangle )}^3}{{\left(\frac{1}{N}{\displaystyle \sum _{i=1}^N}{({\varphi }_i-\langle \varphi \rangle )}^2\right)}^{3/2}}$$ (1)

where N is the total number of dihedral angles (ϕ), e.g. the number of trajectory snapshots times 13. The skewness measures the asymmetry of a distribution – a distribution that is positively skewed appears to lean to the left and have a longer tail to the right, and vice versa.

Figure 2.

Probability distributions for dihedral angle in the four-site CG model. Each panel contains the distributions for the Oda (solid) and Holmes (dashed) models for the four different nucleotide/DB loop pairs. The width of the bars is 1 deg, and the initial value for each model is labeled with a vertical line. The sample mean and skewness are listed in each panel.

For both ATP and ADP filaments with folded or unfolded DB loops the means of the distributions of dihedral angles are similar to the starting filament model, 169° for the Oda model and 157° for the Holmes model. Given enough simulation time the two models presumably would converge to the same dihedral angle, however such large-scale rearrangement is not generally observed in MD simulations. However, it is illustrative to describe the overall tendencies of the “flatness” order parameters with respect to the initial and mean values. The Oda ADP models had the narrowest distribution of dihedral angles from 156°–180° with a skew away from the mean and initial dihedral values toward a less flat conformation. All of the other systems had larger ranges of dihedral angles. Under all four conditions the simulations of Oda filaments were less flat than the initial model. While the Holmes filaments maintained an average dihedral angle approximately equal to the starting value, the simulations skewed the distributions toward flatter dihedral angles in both Holmes filaments with unfolded DB loops and in the other direction with folded DB loops. Both of the ATP/fold simulations show dihedral angle distributions that are bimodal. The heights of the two peaks in each distribution are constant for the entire 20 ns period over which the data were collected indicating that these data are equilibrated on the timescale of the simulations performed in this paper. Additionally we performed the same dihedral angle analysis of the ATP/unfold+phalloidin simulation. A comparison between the two filaments (with and without phalloidin) is shown in Supplementary Fig. S1. The phalloidin angle distribution is narrower, symmetric, and also more closely centered on the starting value from the Oda et al. structure. This is not surprising given the well-known stabilizing effect that phalloidin has on actin filaments. Additionally, since the Oda model was derived using actin filaments with bound phalloidin, it is possible that the phalloidin-free filament systems simulated in this work may eventually undergo conformational changes on significantly longer timescales (e.g. microsecond or longer) as they approach their equilibrium states.

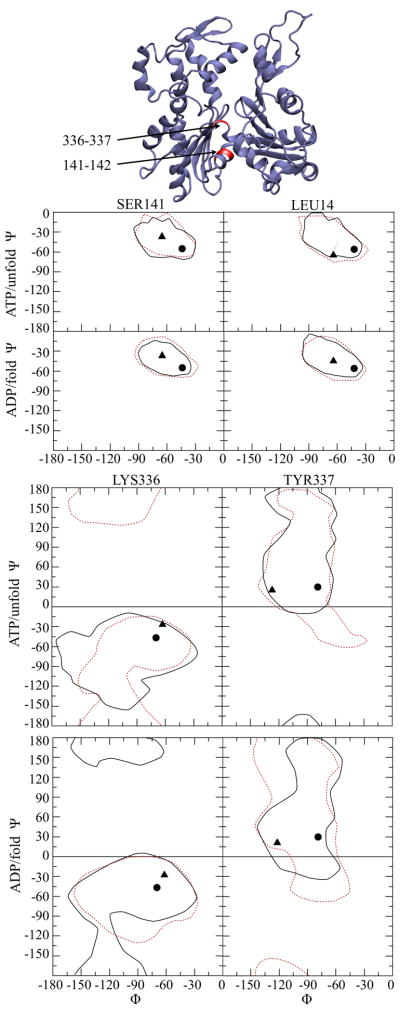
We investigated the dynamical properties of the backbone dihedral angles between residues 141-142 and 336-337 (the so-called “hinge-region” of actin) that Oda et al. used to explain the domain rotation that flattened the subunit in their model.¹⁶ We examined the distributions of these backbone dihedral angles for each subunit in the ADP/fold and ATP/unfold filament systems and used Ramachandran plots of these angles to display the distributions for the ATP/unfold and ADP/fold systems (Fig. 3). For residues 141-2, the data are very similar for all systems. The Oda and Holmes models differ in their initial φ values, but the ensemble data overlap nearly completely on the 50–100 ns timescale. The backbone angles for residues 336-337 show the few observed differences between the two systems more clearly. In both residues 336 and 337 the observed range of φ angles has nearly complete overlap for both filament models. In contrast the ψ angles have broader distributions and regions that do not overlap. It is interesting to see, especially in the case of residue 337 that the Oda and Holmes φ values almost form boundaries of the range of observed values. The ensemble of backbone angles for these residues has a very high standard deviation, and it was therefore not possible to obtain a meaningful correlation between the flatness order parameter we developed and the configuration of residue 141-142 / 336-337. However, qualitatively, there is a link between the observation that the subunits within the Oda filaments generally became “less flat” and the backbone dihedral distributions for the residues that are linked to the subunit flattening overlap significantly with those from the classical Holmes model.

Figure 3.

Ramachandran plots for residues 141-142 and 336-337 in actin filaments derived from NPT MD simulations. The initial values for the Oda and Holmes filaments are represented by circle and triangles, respectively. The regions encompassing the values observed during MD simulation are marked with a dashed line (Oda) or solid line (Holmes). The lines are drawn with a contour level that encloses 100% of the observed backbone angles for the specific residues that are indicated. The Oda actin subunit is shown at the top with the residues of interest labeled in red.

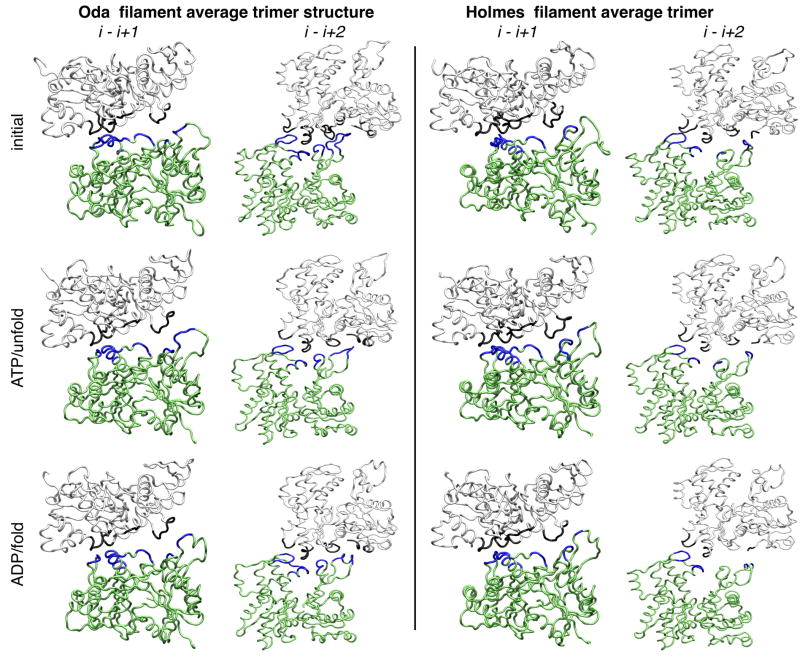
To better understand how the different filament models and bound nucleotide influence the actin-actin contacts we calculated the average actin trimer structure from each filament simulation using the last 20 ns of each simulation. Trimers contain the fundamental contacts common to all actin filaments, designated as the (i − i+1) contacts along the short-pitch helix, and the (i − i+2) contacts along the long-pitch helix. To calculate the average actin trimer from a given simulation each actin 13-mer was decomposed into eight separate trimers, e.g., A1-A2-A3, A2-A3-A4, and the average C^α position for each trimer was then calculated (Fig. 4). Residues in adjacent subunits were designated as “in contact” if their C atoms were closer than 10 Å (Table S2).

Figure 4.

Inter-subunit contact architecture of Oda and Holmes actin filaments derived from MD simulations. The average C^α position is depicted as a tube model to illustrate the cross-strand (i −i+1) and intra-strand (i −i+2) contacts. The initial structure is compared to the ATP/unfold and ADP/fold simulations. Contacts are shown in blue (subunit i) or black (subunits i+1 and i+2), and a contact is defined as two C^α atoms being less than 10 Å apart. Table S2 details the specific residues in contact for all of the models investigated.

The MD simulations reduced the contacts between subunits along both the short-pitch and long-pitch helices compared with the initial Oda model. It is interesting to note that the folded and unfolded DB loops had roughly the same number of contacts, consistent with the work of Oda et al., who noted that both DB loop conformations fit the observed fiber diffraction data.¹⁶ It is also noteworthy that the MD simulations shifted the DB loop from an out of contact position in the Holmes model into contact with the next subunit along the short-pitch helix, but these contacts are not as extensive as those created by “flattening” in the original Oda model or after the simulations.

Properties of Nucleotide-Binding Cleft

Our MD simulations show the time evolution of all the atomic degrees of freedom in the system and allow observations of the dynamics of the nucleotide-binding cleft (although limited to the timescales accessible by MD). Table 2 lists structural parameters that describe the behavior of the gamma phosphate group in simulations with bound ATP and the whole filaments for comparison with monomeric actin. The table lists average distances or bond lengths obtained over the last 20 ns of each simulation.

Table 2.

Geometric parameters that characterize the nucleotide-binding pocket in actin subunits from MD simulations.

Filament Model	Bound Nucleotide	DNase-I Loop1	B12 (Å)	B22 (Å)	B32 (Å)	B42 (Å)
Oda	ATP	unfolded	4.6(±0.2)	5.7(±0.4)	4.5(±0.4)	4.0(±0.5)
	ADP	unfolded				3.6(±0.5)
	ADP	folded				5.8(±1.5)
Holmes	ATP	unfolded	5.8(±0.3)	4.9(±0.3)	3.8(±0.4)	3.3(±0.8)
	ADP	unfolded				2.6(±0.6)
	ADP	folded				3.3(±0.8)
G-actin	ATP	unfolded	6.1(±.4)	3.4(±.1)	5.2(±.2)	3.0(±1.0)
Oda3 (initial structure)	ADP	unfolded	5.1		4.3
Monomeric actin3 (initial structure)	ATP	unfolded	7.1		3.9
Oda	ATP phalloidin	unfolded	4.7(±0.2)	4.2(±0.7)	5.7(± 0.4)	4.0(±0.8)

¹Refers to the initial conformation of the DNase-I binding loop. Further details are provided in the methods section.

²Definition of geometrical parameters: B1: distance between Q137 C^δ side chain atom and P^γ atom of bound ATP, B2: Distance between P^γ atom of bound ATP and O atom of closest coordinating water molecule, B3: Distance between P^γ atom of bound ATP and C^α atom of G156, B4: Distance between O atom in Q137 side chain and H atom of closest coordinating water molecule.

³The initial Oda structure properties were taken from PDB entry 2ZWH. The initial G-actin structure was taken from PDB entry 1NWK and prepared as described in the text.

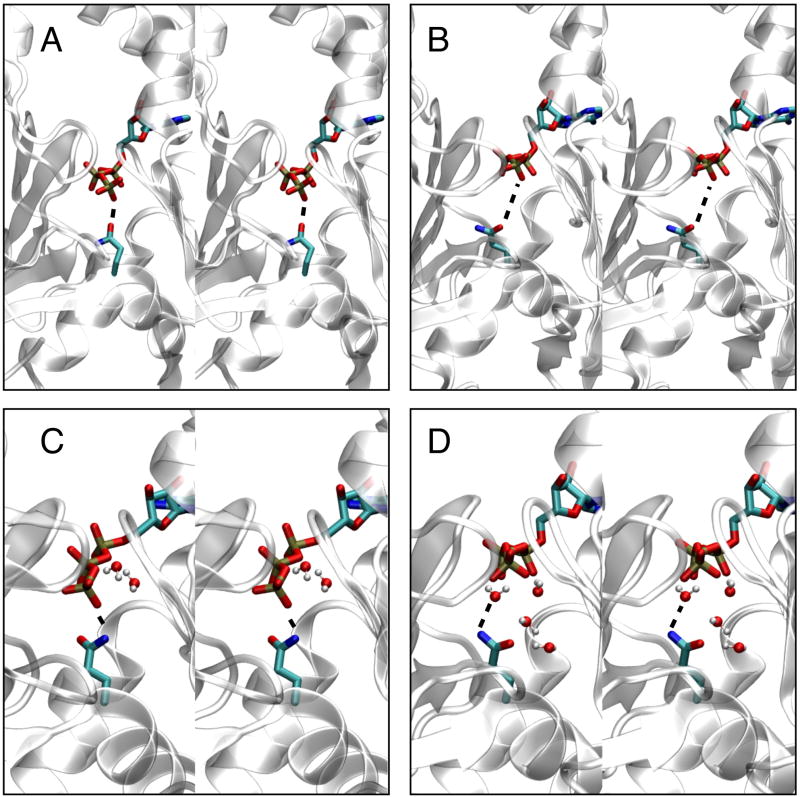
The average distance between the C^δ atom of Q137 and the P^γ of the bound ATP is 1.2 Å shorter in simulations of the Oda model than in simulations of the Holmes model. The actual coordination occurs through a non-bonded interaction between an O atom of the γ-PO₃ of ATP and one of the hydrogen atoms on the NH₂ group bound to the C^δ atom of Q137 side chain (Fig. 5). The slight reorientation of the “hinge region” including residues 137 – 146 flattens the actin subunit in the Oda model and allows orientation of the Q137 side chain anchored to the P^γ group, whereas the Holmes model does not. We also observed that γ-PO₃ group moves somewhat further away from the protein backbone in simulations of Oda models than Holmes models (item B3 in Table 2). The observed variances for B3 are higher than those for B1, making the magnitude of the difference difficult to discern.

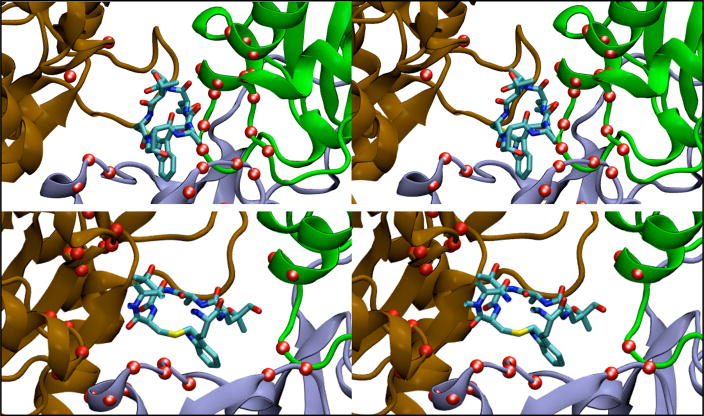
Figure 5.

Coordination of Q137 side chain with gamma phosphate group of bound ATP in actin filament simulations shown in stereo view. The protein is drawn with a cartoon representation, and the Q137 side chain and bound ATP molecule are shown in licorice format. Panels A and B show the initial configuration for the Oda and Holmes filament models, respectively. Panels C and D show a representative structure for the Oda and Holmes models, respectively. The distance between the NH₂ group and an O atom on the terminal PO₃ group of ATP is illustrated with a dashed line. Water molecules within 2.5 Å of the ATP molecule or Q137 side chain are shown.

Water coordinated differently with the γ-phosphate group of ATP and the side chain of Q137 in simulations based on Oda and Holmes models (items B2 and B4 in Table 2). Water shows a stronger tendency (shorter distance) to coordinate with one of the oxygen atoms of the γ-phosphate group of ATP (item B2) in the Holmes model compared to the Oda model. Water also coordinated more strongly (with a shorter distance) to the Q137 side chain in simulations of the Holmes model than the Oda model (distance B4 in Table 2).

Simulation of ATP-bound monomeric actin for 50 ns showed that the γ-phosphate of ATP is separated further from both the protein backbone and the Q137 side chain than in filaments. The γ-phosphate is less constrained by the protein but more likely to coordinate with water in the nucleotide-binding cleft of the monomer than in any of the filament models.

Persistence Length of Actin Filaments

We used the greatly increased computing power available since the original estimates persistence lengths of actin filaments from MD simulations²⁶ to re-examine the hypothesis that the stiffness of filaments depends on the DB loop conformation (Table 3). As in the previous work, the values obtained from MD simulations based both the Holmes and Oda models (in the ADP/folded and ATP/unfolded conformations) agreed well with experimentally measured^4,31 persistence lengths (using ADP-BeFe₃⁻ actin to stand in for short lived ATP-actin). Persistence lengths were almost two-fold higher with an unfolded DB loop than with a helical DB loop. The control studies with opposite DB loop conformations (ADP/unfold and ATP/fold) supported the hypothesis the conformation of the DB loop has a stronger influence on persistence length than the bound nucleotide. The table includes two values for the simulations of the Oda model with ATP and folded DB loop. During the simulation the DB helix unfolded and the stiffness increased. Simulation of the Oda model of ATP actin filaments and including the bound phalloidin ligands gave a persistence length very similar to experiment^4,31 and somewhat larger than obtained experimentally with ADP-BeF₃⁻. We note that phalloidin was included in the experimental preparation of the actin gels used in fiber diffraction experiments but not explicitly included in the model calculations of the Holmes and Oda models as discussed²³.

Table 3.

Comparison of experimental and calculated persistence lengths for actin filaments. All persistence lengths are given in units of μm.

Filament1	Lp (μm)
ATP unfolded
Experiment2	13.5
Oda	15.9(±0.3)
Holmes	14(±0.3)
ADP folded
Experiment3	9.1(±0.3)
Oda	8.7(±0.1)
Holmes	8.2(±0.1)
ADP unfolded
Holmes	14.8(±0.3)
Oda	17.2(±0.4)
ATP folded
Oda4	13.6(±0.1)
Oda4	8.6(±0.1)
Holmes	7(±0.05)
ATP unfold + phalloidin
Experiment2	18(±1)
Oda	20.5(±0.4)

¹The filament model is described by whether it is a model or experimental determination of the persistence length, the state of the bound nucleotide and the initial conformation of the DNase-I loop. Further details on model preparation are provided in the methods section. The configuration of the DNase-I loop was not determined via experiment, but inferred based on previous experiments and simulations as well as the present work.

²Experimental values from Isambert et al.⁴ with ADP-BeFe₃⁻ or ATP + phalloidin.

³Experimental value and error obtained via averaging results from Isambert et al.⁴ and McCullough et al.³¹

⁴The larger Oda value is obtained from the last 20 ns of NPT simulation when the DB loop regions became unfolded. The smaller value is from an earlier point in the simulation when equilibration had not yet been achieved (see Methods section), but the DB loop region was still folded.

Simulations of Filaments With Bound Phalloidin

Simulation an Oda model of an ATP-actin filament with bound phalloidin showed that the orientation of the phalloidin shifts from the initial position proposed by Lorenz et al.³² to a new equilibrium site with a large increase contacts between phalloidin and the (i − i+1) subunit along the short-pitch helix in the region of residues 69—78 on the adjacent subunit (Fig. 6). This region contains the evolutionary conserved residue 73 (3-methylhistidine)⁵ that is close to the nucleotide binding pocket and was previously shown to coordinate the P_i group upon ATP hydrolysis.¹² The number of cross-strand contacts between phalloidin and the (i − i+1) actin subunits increases from an initial value of 2 to 6.9(±0.4) for the entire subunit and from 2 to 4.4(±0.4) when only considering the important range of residues 69 – 78. A phalloidin – actin contact is defined when the two C^α atoms are located within 10.0 Å of each other. This increase in contacts between the helix strands points to a quantitative mechanism by which phalloidin stiffens the actin filament. In principle this observed correlation between the cross-strand contact architecture and the phalloidin binding site could be further explored using a non-equilibrium technique such as umbrella sampling, metadynamics, or steered MD; however, this would be a very computationally challenging calculation and is beyond the scope of the present work.

Figure 6.

Effect of bound phalloidin on contact architecture in actin filament simulations. The ribbon diagrams show subunits i (blue), i+1 (brown) and i+2 (green) and of phalloidin (licorice representation). Red spheres show the positions of all C^α atoms within 10.0 Å of the bound phalloidin. The two panels show stereo views for initial (top) and representative configuration (bottom) that illustrate how bound phalloidin increases the inter-strand (i − i+1) contacts in actin filaments.

Simulation of the Oda model with bound ATP, bound phalloidin and an unfolded DB loop gave persistence length close to the experimental value.⁴ It is interesting that the RMSD for the filament with phalloidin is the lowest of all the filaments investigated, so phalloidin even stabilizes filaments on the 50 ns time scale. The nucleotide-binding cleft of subunits in filaments with bound phalloidin was very similar to ATP-actin filaments without phalloidin.

Discussion

Our extensive MD simulations of actin filaments based on both the Holmes²³ and Oda¹⁶ filament models with ADP or ATP and two conformations of the DNase I binding loop have provided valuable insights into the means by which actin polymerization enhances ATP hydrolysis, and ATP hydrolysis in the actin subunit influences the structure and dynamics of filaments. Our simulations of actin with bound phalloidin address the means by which phalloidin stiffens actin filaments and suppresses ATP hydrolysis and/or release of the inorganic phosphate (Pi) after hydrolysis. The simulations performed in this work represent the most extensive sampling via MD simulation to date of the actin filament. Simulations on the 50 to 100 ns timescale such as those presented herein are useful for characterizing the local equilibrium of biomolecular assemblies, but cannot provide quantitative information regarding the equilibrium properties of rare events (e.g., certain protein conformational changes) that occur on significantly longer timescales (i.e., microsecond or longer).

The Oda filament model offered a potential explanation for how flattening of the actin subunit might enhance the rate of ATP hydrolysis by four orders of magnitude by locating the Q137 side chain closer to the γ-phosphate group of ATP. Actin residue Q137 is critical for ATP hydrolysis¹⁵, fiber diffraction methods do not currently have sufficient resolution to locate side chain atoms. Our simulations confirmed that flattening of the actin subunits during polymerization moves the Q137 side chain close to the γ-phosphate group of ATP. Residue Q137 is part of the hinge region that participates in flattening, which moves its side chain upward toward the nucleotide-binding pocket. This repositioning results in a pronounced increase in the coordination between the side chain and the γ-phosphate group, offering improved stabilization (and susceptibility to hydrolysis) of the triphosphate group compared with its position in actin monomers and in subunits in the Holmes filament model. Our simulations of ATP-bound monomeric actin confirmed this difference in the nucleotide-binding pockets of monomeric and filamentous actin.

Our simulations also address the relationship between the conformation of the DNase I loop and the stiffness of the actin filament. Previous simulations²⁶ showed that Holmes filaments with ADP/folded and ATP/unfolded subunits have persistence lengths in good agreement with those measured by experiment, leading to the hypothesis that that the conformation of the DB loop is a dominant factor in defining rigidity and filament related properties. Our recalculation of the Chu and Voth data and additional control studies of both the Oda and Holmes filament models in the ATP/folded and ADP/unfolded configurations support this hypothesis. Additionally, recent simulations¹² show that folding of the DNase I loop into an alpha helical conformation is thermodynamically favorable in actin trimers, especially within the Oda filament model. Taken together, this data points to a mechanism where i) polymerization flattens the actin subunits, promoting ATP hydrolysis, ii) dissociation of γ-phosphate induces changes in the DNase I loop, and iii) changes in the DNase I loop cause softening of the filament, i.e., reduction of its persistence length.

Our simulations of actin with bound phalloidin³² agree with experimentally measured effects of phalloidin on actin filaments. Phalloidin reoriented into a more favorable position and increased the (i − i+1) inter-strand contacts between subunits along the short-pitch helix, which explains how phalloidin stiffens and stabilizes filaments.⁴ Future studies from our group will use MD simulations to investigate the mechanism of P_i release and explore the atomistic deals of how phalloidin interferes with this process.

Methods

The coordinates for filamentous actin were based on the Oda¹⁶ or Holmes²³ models. Oda filaments were generated with either the DB loop in a folded or unfolded conformation. The initial unfolded conformation used was published by Oda et al. in PDB entry 2ZWH.¹⁶ The initial folded conformation was built by taking the folded DB loop from PDB entry 1J6Z⁶, splicing it into the 2ZWH structure, and relaxing the structure with an energy minimization routine. The initial coordinates for the filaments were obtained in an identical manner to a previously published study²⁶ from our group. Phalloidin binding site coordinates were obtained from the published data by Lorenz et al.³² The filament was placed in a box of explicit TIP3P water molecules³³ with a minimum distance of 15 Å between the protein and the border of the periodic boundary conditions. The charge of the system was neutralized via random placement of counter-ions (KCl) using the VMD autoionize plugin³⁴ The size of each system is detailed in Table S1 of the Supplementary Material.

All MD calculations were performed using NAMD.³⁵ The CHARM22/27³⁶ force field was used in conjunction with the particle mesh Ewald sum method³⁷ for calculating electrostatic interactions. All intramolecular hydrogen bonds were constrained using the SHAKE³⁸ algorithm allowing for an integration timestep of 2 fs. After heating the system to 310 K, a 100 ps equilibration was performed in the canonical ensemble by velocity rescaling. Following this, the simulations were continued in the isobaric-isothermal (constant NPT) ensemble (310 K, 1.01325 bar) through the use of Langevin dynamics and the Langevin piston method via its implementation in NAMD.^39,40 The damping coefficient used for Langevin dynamics was 0.5 ps⁻¹ and the Langevin piston was controlled using a piston period decay of 2 ps. Each simulation was continued for at least 50 ns, or until the unit cell length had equilibrated and sufficient equilibrated sampling of the NPT ensemble was achieved. The strategy we employed was to run the NPT simulation until the box length along the filament axis stabilized (normally 30 ns), and then continued for an additional 20 ns “production phase.” The exact length of each simulation is provided in Table S1. Unless otherwise noted, results reported from MD simulations are based on the last 20 ns of each trajectory. The unit cell length was the slowest property to equilibrate in the simulations performed in this work. By comparison, the filament RMSD (< 10 ns), system pressure (< 1 ns), and total energy (< 10 ns) equilibrated far faster. Analysis of MD calculations and creation of all protein figures was performed using Visual Molecular Dynamics (VMD).³⁴ Error estimation was performed with a standard block-averaging technique.^41,42 For average values of a property of a single actin subunit, that were derived from filament simulations, e.g., water coordination, the error for that property for each subunit was estimated via block-averaging, and the subsequent 13 error estimates were averaged to obtain an overall average error estimate.