Transverse acoustic trapping using a Gaussian focused ultrasound

Abstract

The optical tweezer has become a popular device to manipulate particles in nanometer scales, and to study the underlying principles of many cellular or molecular interactions. Theoretical analysis was previously carried out at the authors’ laboratory, to show that similar acoustic trapping of microparticles may be possible with a single beam ultrasound. This paper experimentally presents the transverse trapping of 125 μm lipid droplets under an acoustically transparent mylar film, which is an intermediate step toward achieving acoustic tweezers in 3D. Despite the lack of axial trapping capability in the current experimental arrangement, it was found that a 30 MHz focused beam could be used to laterally direct the droplets towards the focus. The spatial range within which acoustic traps may guide droplet motion was in the range of hundreds of micrometers, much greater than that of optical traps. This suggests that this acoustic device may offer an alternative for manipulating microparticles in a wider spatial range.

INTRODUCTION

Particle manipulation with precision has been crucial in studying biomechanical properties of various cells and molecules. In the early 1970s, Ashkin discovered that counteracting light beams could displace micron-sized dielectric spheres in either air or water (Ashkin 1970; Ashkin and Dziedzic 1971). Later Ashkin and his colleagues developed the first optical tweezer, also known as the single beam gradient optical trap, in which a tightly focused laser beam was used to trap dielectric spheres around its focus (Ashkin et al. 1986). When an incident light beam impinges on a sphere, the momentum transfer of optical energy from incident photons results in optical forces applied to the sphere. The forces can be classified into two categories: The scattering forces pointing in the direction of the beam propagation, and the gradient forces pointing towards the center of the beam. In particular, the gradient force is a restoring force that pulls the sphere towards the center of the trap. It was found that stable optical traps could be formed, when the gradient force overcame the scattering force (Ashkin 1997). Since the intensity gradient or trap strength increases as the focal spot size decreases, microscope objectives of high numerical apertures, greater than 1, have been chosen to produce strong focused beams. Optical tweezers typically output forces on the order of pico-Newtons, and such forces were large enough to displace small particles up to hundreds of nanometers in the trap.

Despite the precision and wide range of biological applications offered by optical tweezers, there are two common drawbacks that must be considered for practical purposes (Neuman and Nagy 2008). First, optical tweezers are vulnerable to optical perturbations that may distort energy distribution near the focus, and thus compromise its overall performance. The use of high-resolution optical tweezers, therefore, has been limited to optically purified samples or media, although in vivo trappings of lipid vesicles within eukaryotic cells (Gross 2003) and organelles within yeast cells have been carried out (Sacconi 2005). Second, the high energy of focused lasers has often induced local heating and photodamage, and adversely affected sensitive measurements of forces and displacements. Oxygen-mediated photodamages, in particular, could be reduced by either substituting oxygen with inert gases or removing it with enzymatic scavenging systems (Neuman 1999). Since these approaches described above require extra preparation prior to experiments, it would be rather cumbersome to implement them.

In acoustics, much effort, both in theory and experiment, have been devoted to controlling particle movements by employing various types of waves, such as standing waves and Bessel beams (Woodside et al. 1997; Marston 2006 and 2009; Liu and Hu 2009). Among them, Wu (1991) demonstrated that latex spheres or frog eggs could be trapped by two opposing sound beams at 3.5 MHz. The use of two transducers was necessary, because relatively broad beams could not produce the required sharp intensity gradient for single beam acoustic trapping. Recent advances in ultrasonic transducer technology (Snook et al. 2002; Cannata et al. 2008), on the other hand, enabled us to propose that the acoustic trapping of micron-sized particles or acoustic tweezer, might be feasible. A critical recognition was that in order for acoustic trapping to occur, a high frequency ultrasound (≥ 20 MHz) beam must be focused to a spot that is smaller than the particle size.

Principle of acoustic trapping

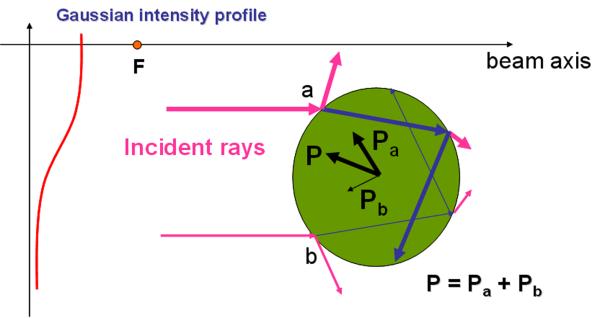
A sphere scatters an ultrasonic beam that has a Gaussian intensity distribution, as shown in Fig. 1. As the incident rays are bent, the difference between the incident and exiting rays imparts an equal and opposite momentum change to the sphere. Note that the attenuation of beam energy in the media was not considered here. As a result, the sphere experiences the acoustic radiation forces from all such rays, and the net force moves it towards the focus. Attenuation in effect was not considered.

Fig.1.

Illustration of ray interaction with a sphere. An ultrasonic transducer having a Gaussian beam profile is focused at F (a dot on the beam axis), and produces two representative rays denoted as a and b, along with its scattered rays around the sphere. Note that the thicker arrow indicates a ray carrying the higher energy. As the incident rays propagate through the sphere, due to the momentum transfer, the outgoing rays induce the pressures of P_a (a thick arrow) and P_b (a thin arrow), respectively. Because P_a is higher than P_b, the net pressure P will direct the sphere towards the focus F.

Preliminary studies analytically demonstrated that the single beam acoustic trapping could be achieved under specific conditions (Lee et al. 2005; Lee and Shung 2006). First, the acoustic impedance mismatch of particles and propagation media should be minimized to reduce reflections or scattering force components. In particular, the acoustic impedance of particles must be lower than that of the media. Since the impedance of lipids or fat, 1.3 MRayls, is lower than water’s, 1.5 MRayls (Schwan 1969), lipid droplets were selected as target particles to be trapped. Unlike solid elastic spheres whose resonances are important in the force analysis (Marston 2007), the droplet resonance was considered negligible. Second, the particle size must be greater than the ultrasonic wavelength to satisfy the ray acoustics regime. Third, for stable trapping, strongly focused beams must be used to form the steep intensity gradient around its focus.

In case of optical tweezers, these conditions will not preclude the applications to particles smaller than the wavelength or with the acoustic impedance larger or very different from the surrounding medium. The optical trapping of particles smaller than the wavelength has been shown to be possible (Svoboda et al. 1994). A solution to overcome the latter problem has been to coat the particle or carrier with different substance, to allow the interaction between the coated substance and the target particles to become more effective.

An experimental study was undertaken based on those conditions mentioned above. The transducer used was a highly focused custom made 30 MHz single element transducer. The lipid spheres of precise diameter were prepared by authors at University of California at Irvine with MEMS technology.

MATERIALS AND METHODS

Fabrication of ultrasonic transducer

A 30 MHz lithium niobate (LiNbO₃) single element transducer was designed and fabricated. Double matching layers and a backing medium were used for acoustic matching. Its aperture size and proper thickness of acoustic stacks, such as lithium niobate (LiNbO₃) single crystal, silver epoxy 1^st matching layer, and parylene 2^nd matching layer, were optimized by a KLM modeling software (PiezoCAD, Sonic Concepts, USA). A 36° rotated Y-cut lithium niobate plate (Boston Piezo-Optics, USA) was lapped to its designed thickness of 77 μm, and electroplated with 1500 Å chrome / gold (Cr / Au) layer on both sides, by an NSC-3000 automatic sputter coater (Nano-Master, USA). The silver epoxy matching layer, made from a mixture of Insulcast 501 epoxy (American Safety Technologies, USA) and 2-3 μm silver particles (Aldrich Chemical Co., USA), was cast and cured over the lithium niobate plates. After curing, the matching layer was lapped down to the desired thickness, 12 μm. The lapped lithium niobate / 1^st matching stacks were mechanically diced into square pieces, with the size that would encompass a circular aperture. A conductive silver epoxy (E-Solder 3022, Von Roll Isola Inc., USA) backing layer was then cast and centrifuged onto the back side of the electroplated lithium niobate. After curing, the acoustic stack was turned down to the designed diameter, 4 mm, and was concentrically placed in the brass housing. The gap between the stack and housing was filled in by an insulating epoxy (Epo-Tek 301, Epoxy Technologies, USA). The stack was press-focused (Cannata et al. 2003) at 3 mm to obtain an f# of 0.75. Hence the convergence angle of acoustic beams was formed to be 84° at the focus. Note that the measured beam width was approximately 37 μm at 30 MHz as shown in Fig. 4, and its more complete list is given in Table 1. The transducer surface was then sputtered with Cr / Au electrodes, to make ground connection between the stack and the brass housing. A 14 μm parylene layer was deposited using a PDS 2010 Labcoater (SCS, USA). The finished transducer element was connected to an SMA connector. To predict generated forces by the transducer, acoustic peak pressures, as in Table 2, were measured within its bandwidth, by a calibrated PVDF needle hydrophone (HPM04/01, Precision Acoustics, UK).

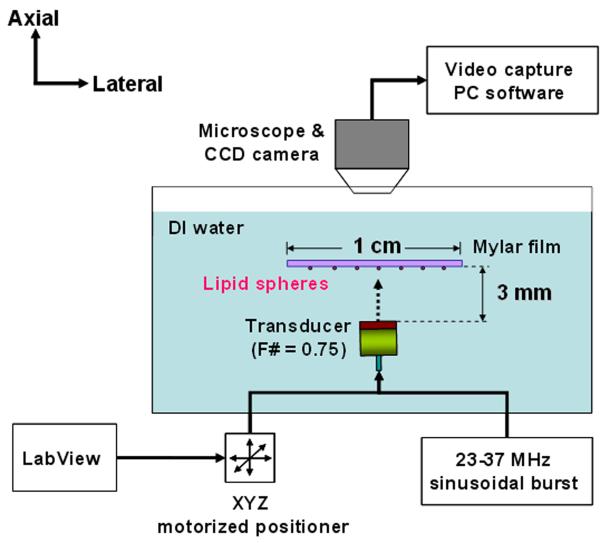
Fig. 4.

Experimental configuration of acoustic trapping. Burst waveforms for the transducer were generated from a function generator (AFG3251, Tektronix, USA) and then amplified by a 50dB power amplifier (325LA, ENI, USA) to achieve desirable voltage amplitudes. Pulse echo tests were carried out prior to the experiment, to make sure that the transducer aperture was in parallel with the mylar film.

Table 1.

Lateral beam widths of applied peak-to-peak voltages

Beam width (μm)		Frequency (MHz)
		23	24	27	30	33	36	37
Voltage (Vpp)	22	39.1	41.0	38.2	36.9	35.5	34.3	31.2
	32	38.5	40.5	37.5	36.0	35.0	36.5	31.8
	41	41.9	39.2	37.8	37.6	34.9	34.0	32.2

Table 2.

Measured zero-to-peak pressures at the focus

Zero-to-peak pressure (MPa)		Frequency (MHz)
		23	24	27	30	33	36	37
Voltage (Vpp)	22	0.9	1.2	1.8	2.2	2.0	1.3	1.1
	32	1.3	1.7	2.5	3.2	2.9	1.8	1.6
	41	1.6	2.1	3.3	3.7	3.8	2.3	2.0

Synthesis of lipid droplets

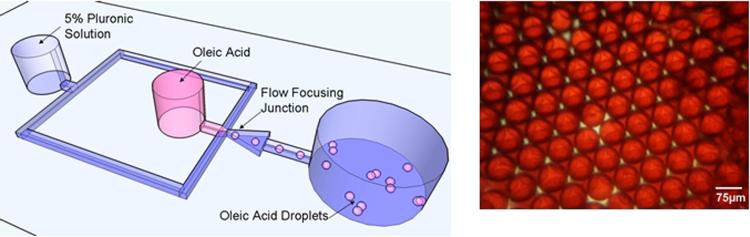
Oleic acid (Fisher Scientific, USA) lipid droplets were synthesized using droplet-based microfluidic devices, a robust method of forming monodispersed droplets and particles in the nanometer to micrometer size range (Teh et al. 2008). Microfluidic devices were fabricated in poly(dimethyl) siloxane (PDMS) using conventional soft lithography techniques (Whitesides et al. 2001). A hydrophilic surface treatment was applied to render the channel surfaces hydrophilic (Kozlov et al. 2003). As PDMS is inherently hydrophobic and the continuous phase used for the droplet generation is water, the hydrophilic surface treatment ensures complete wetting of the walls by the aqueous solution.

The aqueous phase consists of a 5 wt% mixture of Pluronic F-68 (Sigma Aldrich, USA) and ultra pure water (Millipore, USA). Pluronic F-68 stabilizes oleic acid droplets during storage and transport. As shown in Fig. 4a, the two liquid phases meet at the shear junction and oleic acid is sheared into droplets by the aqueous phase. The flow-focusing nozzle geometry creates a local shear maximum that ensures repeatable break up of the fluid stream (Tan et al. 2006). The droplets were formed at a rate of approximately 50 droplets/second and had a monodispersed size distribution as shown in Fig. 4b. The droplet size can be controlled by changing the relative flow rates of the solutions. The greater the oleic acid flow rate, the larger the droplet. Oleic acid and aqueous flow rates of 0.5 to 1 μl/min were applied to form oleic acid droplets of 75-300 μm in diameter. The average droplet diameter used for the experiment was 126 ± 5.6 μm. The resultant droplets tended to float because the density of oleic acid, 900 kg/m³, is known to be less than that of the water.

Experimental procedure

The maximum displacement, a value that indicates how far a trapped droplet could be held or attracted from the center of the transducer, was measured in order to analyze the trapping behavior. The experimental arrangement is illustrated in Fig. 6. The transducer was translated perpendicularly to the beam axis, and driven by sinusoidal bursts. The pulse repetition period was 5 ms, and its duty cycle was 3.3 %. The transducer was mounted on a three-axis motorized positioner (LMG26 T50MM, OptoSigma, USA). Control commands using a customized LabView interface were sent to the positioner through RS-232C ports. The positioner was moved by programmed increments that could be varied from 1 μm to 10 μm. Lipid droplets were then loaded below an acoustically transparent mylar film in the deionized water. A droplet near the focus became trapped by tuning the frequency and voltage applied to the transducer. Shortly after the droplet settled, the transducer was turned off and the position of the trap was translated by a programmed distance. The transducer was then turned on, to see if the droplet was directed towards the center of the trap and trapped once again. If so, the distance was further increased and the above procedure was repeated, until the droplet could no longer be attracted. The final distance was then identified as the maximum displacement. To measure the displacements for various excitation conditions, the frequency of the transducer was varied from 23 to 37 MHz, and its peak-to-peak voltages were applied at 22, 32, and 41 V_pp. Droplet motions were recorded via a CCD camera (Infinity X, Lumenera, USA) combined with a stereomicroscope (SMZ1500, Nikon, Japan). The film acted against the buoyancy of the lipid droplets, while maintaining the droplets within the field of view of the microscope.

RESULTS

Measurement of maximum displacement of trapped droplet

Given an excitation condition, the longest lateral range within which a droplet could be attracted towards the trap center was represented by the maximum or zero-to-peak displacement. It was observed that a droplet was drawn into the trap, as long as it was placed within a certain transverse distance from the focus (or maximum displacement), a value that is a function of excitation voltages and frequencies of the transducer. The measured maximum displacements were summarized in Table 3. Each measurement was repeated 10 times to calculate its average displacements at a given condition. Note that within the bandwidth of the transducer, the measured displacements in acoustic traps were in the range of hundreds of micrometers, much longer than those in optical cases.

Table 3.

Measured average maximum (zero-to-peak) displacements of trapped droplets. The standard deviations were given in parenthesis.

Average maximum displacement (μm)		Frequency (MHz)
		23	24	27	30	33	36	37
Voltage (Vpp)	22	246.0	306.5	339.0	353.5	343.5	313.5	247.5
		(±5.2)	(±5.3)	(±6.1)	(±4.7)	(±4.7)	(±4.1)	(±4.2)
	32	291.0	357.0	405.0	428.5	411.0	355.0	304.5
		(±8.1)	(±4.2)	(±6.2)	(±4.1)	(±4.6)	(±6.7)	(±6.9)
	41	327.0	381.0	430.5	457.5	448.0	404.5	349.5
		(±6.7)	(±7.0)	(±5.5)	(±5.4)	(±5.4)	(±6.4)	(±6.4)

The displacements were increased as the higher voltages were applied throughout the frequency range. Typically at 30 MHz, the average maximum displacement of the trapped droplet led to 353.5 μm with 22 V_pp, while it was 457.5 μm with 41 V_pp. At each voltage, the displacement also reached its maximum value at 30 MHz, which was consistent with peak pressure measurements in Table 2. No trapped droplets were detected at 42 MHz. In order to determine if it was possible to produce any trappings in this case, a much higher driving voltage was used, for instance, 95 V_pp, which did not produce any visible droplet movement. Physical damages of the droplets, caused by either cavitation or extreme temperature increase, were not observed throughout the experiment given the low mechanical (MI) and thermal (TI) indexes (AIUM 1992) produced by the ultrasound beam which are as low as 0.7 and 1.5 at 30 MHz. These measures have frequently been used to assess bioeffects induced by acoustic energy.

Droplet motion within acoustic trap

After the transducer was laterally translated, the once trapped droplet followed the motion of transducer with some lag, displayed as an asynchronous time delay between the transducer and droplet motion (Refer to the supplementary video). The lag depended on the relative distance of the droplet from the transducer, the farther the distance, the longer the lag. This observation indicated that the trapped droplet tended to restore to its original position (or the center of the trap), when located within the region of the maximum displacement. The droplet in a trap, therefore, could be thought as if it were attached to the center of the trap by a spring with a certain stiffness constant.

DISCUSSION

It is reasonable to expect that higher pressure, within its range currently used, would induce stronger trapping. As referred from Tables 2 and 3, the results at the given frequencies demonstrated that higher excitation voltages generated longer maximum displacements. It was also shown that by tuning frequencies at a certain voltage level, the transverse distance through which droplets were pulled back into the trap could be varied. The displacements at 30 MHz, in particular, were greater than any others, since that is the resonance frequency of our transducer.

In order to relate the focusing strength to the maximum displacement of trapped droplets, pressure gradients were obtained by dividing peak pressures by half beam widths, and the results are shown in Table 4. Note that the larger gradients represent the more focused beams. The gradients were increased as higher pressures were applied at each frequency. For example, 64.3 MPa/mm with 41 V_pp, nearly twice as much as 33.1 MPa/mm with 22 V_pp, was obtained at 33 MHz. Under the same conditions, the measured zero-to-peak pressures were 3.8 and 2.0 MPa, and their corresponding displacements were 448.0 and 343.5 μm, respectively. Therefore this indicates that wider trapping ranges can be achieved by increasing the applied pressures at a fixed beam width.

Table 4.

Measured pressure gradients around the focus

Pressure gradient (MPa/mm)		Frequency (MHz)
		23	24	27	30	33	36	37
Voltage (Vpp)	22	13.4	17.0	28.1	35.5	33.1	22.1	21.0
	32	19.0	24.1	39.4	52.6	47.7	29.4	28.5
	41	22.7	31.3	51.1	57.6	64.3	40.0	36.5

As far as the mylar layer is concerned, it was used to restrain droplet motions in the axial direction, and its effect on the trapping was not investigated here. Note that cover slips have also been used in a similar manner in many optical tweezers (Tam 2004). It has been reported that phase aberrations at the cover-to-water interface might affect the trapping performances (Reihani 2006), and such problems could be resolved by pre-distorting the beam profile with additional lens (Born 1999). The presence of a cover slip could also results in erroneous measurements of forces, when the fluid viscosity close to the cover differs from the trap center. This has often been corrected by factors derived by Brenner (1964). For a complete characterization of acoustic lateral trapping, hence, the effect of a membrane on it will be studied in the near future.

CONCLUSION

The experimental results demonstrated that a single beam ultrasound could transversely trap a lipid droplet in the presence of a mylar membrane. The results further showed that the use of a Gaussian intensity focused beam, with a large pressure gradient, enabled the droplet to be directed towards the focus within a range in the order of hundreds of micrometers. The transverse trapping characteristic, as in optical tweezers, could be described as if the droplet were attached to a Hookeian spring. The results therefore indicated that the acoustic trapping technique reported in this paper can be useful in that it is capable of handling larger cells, and providing longer trapping ranges than optical tweezers.

Summary.

Single beam ultrasound was used to experimentally demonstrate transverse acoustic trapping of micron-sized lipid droplets underneath an acoustically transparent mylar film.

Supplementary Material

01

Supplementary video 1: Trapped droplet motion A droplet of 150 μm at the center is trapped by 30 MHz bursts. The gold-colored background shows the transducer aperture. Once it is displaced slightly off the trap, the droplet experiences some restoring forces as if attached to a spring, and is directed towards the focus.

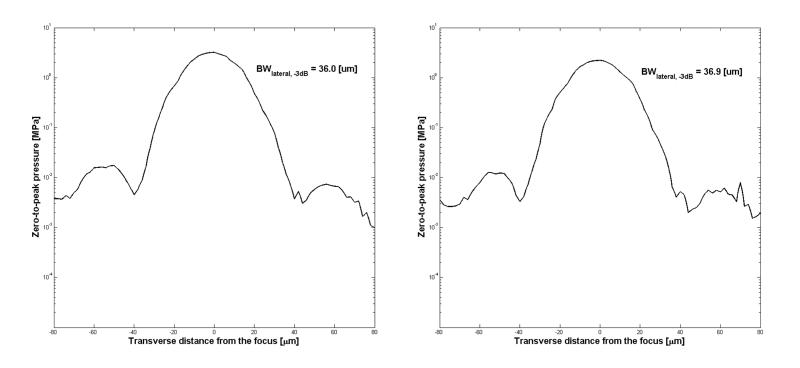
Fig. 2.

Lateral beam profiles of LiNbO₃ transducer. The 3dB beam width is denoted by BW_lateral,-3dB, and measures how tightly the beam is focused. The ordinate is drawn in log scale and represents the pressure in MPa, while the abscissa shows the lateral or transverse distance from the beam focus. (a, left) The measured beam width was 36.0 μm when driven at 30 MHz and 32 V_pp, (b, right) whereas it was 36.9 μm at 22 V_pp.

Fig. 3.

(a, left) Depiction of oleic acid droplet formation device. The microfluidic device has two inlet ports, one for the aqueous continuous phase and the other for the dispersed phase (oleic acid). The two phases meet at the shearing junction where oleic acid is sheared into droplets by the aqueous phase. At the outlet, the droplets are collected and stored inside glass vials. (b, right) Monodispersed population of oleic acid droplets. Oil Red (Dupont, USA) dye was added to aid in visualization.