Toward Clinical Application of Manganese-enhanced MRI of Retinal Function

Abstract

Purpose

The application of Manganese-Enhanced MRI (MEMRI) to measure retinal function in humans is unclear. To begin to address this gap, we tested the hypothesis that an FDA-approved manganese-based MRI contrast agent, Teslascan, is useful for measuring functional intraretinal ionic regulation.

Methods

Anesthetized dark- or light-adapted male healthy Sprague Dawley rats were infused for 30 min with 10 μmol/kg of Teslascan (clinically relevant dose; n=5), 100 μmol/kg Teslascan (n=5), or saline (n=5). Four hours post administration, high resolution MEMRI data were collected. Intraretinal signal intensities and enhancements were measured. Modelling was performed to estimate apparent retinal transfer constant K_i and to determine optimal data acquisition parameters.

Results

In light-adapted rats, intraretinal enhancements responded in a dose-response manner. In addition, in the outer retina the effect of light-adaptation was to reduce significantly Mn²⁺ uptake and K_i compared to dark-adaptation. A non-significant change was also observed in the inner retina. Modelling shows Mn²⁺ plasma concentration reaching a plateau after about 2 hours. Apparent K_i values for the clinically-relevant dose are 3-6 10^-3 min^-1, decreasing to 0.5-0.6 10^-3 min^-1 at the higher dose. Intraretinal signal is almost linear with K_i. Optimal TR for a spin echo sequence is 0.4-1.4s.

Conclusion

First time evidence is presented that a clinically-relevant dose and route of Teslascan can be used to measure intraretinal function. The potential for future clinical application of MEMRI in a broad range of retinopathies is high.

1. Introduction

At present, there are no widely used, non-invasive surrogate markers that reliably and analytically measure focal retinal damage before it is clinically evident, predict disease progression, or therapeutic effectiveness in patients with, for example, diabetic retinopathy or visual cycle defects associated with age-related macular degeneration or retinitis pigmentosa. Clinical detection and staging of such conditions is based upon funduscopic evaluation together with fluorescein angiography and optical coherence tomography (OCT). However, these techniques only detect disease in its later stages, when irreversible structural damage has occurred, and the likelihood of permanent visual dysfunction is increased. Furthermore, they are not established for predicting therapeutic efficacy. Consequently, it is critical to develop biomarkers for retinal anomalies that occur in the earliest stages of the disease and that can address these substantial surveillance gaps. Clearly, the application of such techniques in phase II clinical trials, for example, would facilitate more rapid development of therapeutic approaches and more effective intervention.

Retinal processing of visual information depends critically on proper regulation of ions [1]. For example, photoreceptor cells function at particularly high metabolic rates in order to generate a depolarizing dark current (i.e., the constant influx of ions such as calcium in dark adapted photoreceptors with an associated efflux, and generation of guanosine triphosphate leading to cyclic guanosine monophosphate production). In light adaptation, the influx of calcium is attenuated relative to that in the dark due to the graded potential of these cells and closure of ion channels. In addition, ionic control is important in the cell cycle and in neuronal development, and ionic activity has been used as an index of viability in proliferating cells [2] [3] [4]. Notably, abnormal regulation of ions can produce, for example, retinal acidosis associated with retinal neovascularization or increased intracellular calcium levels as an apoptic trigger in neurodegenerative diseases. Thus, a metric of retinal ion regulation would be expected to be useful as a surrogate marker of intraretinal health.

Recently, in pre-clinical models, we developed and applied non-invasive high resolution manganese-enhanced magnetic resonance imaging (MEMRI) with systemically administered MnCl₂ as a novel approach to measure the intraretinal regulation of ions such as calcium[5]. Manganese (Mn²⁺) is an ion analog of calcium, accumulates as a function of membrane integrity and activation in neurons and other cells, and is retained for long periods of time[5] [6] [7] [8] [9] [10]. In every model of retinopathy examined to-date we could evaluate drug treatment efficacy based on correction of abnormal MEMRI responses [5] [6] [8]. These results provide strong motivation for performing MEMRI clinically. Yet, MnCl₂ is not approved for human application and so the clinical application of MEMRI remains unclear.

In this study, we begin to address this issue by evaluating the usefulness of a clinically-relevant manganese-based contrast agent, Teslascan (MnDPDP[11] [12]), in a simple animal model. In addition, we apply a powerful modelling approach that may help optimize data collection parameters in future human studies, as well as obtaining values of apparent Mn²⁺ transfer constant for the retina [13] [14] [15] [16] [17].

2. Materials and Methods

The animals were treated in accordance with the ‘Principles of laboratory animal care’ (NIH publication no. 85-23, revised 1985; http://grants1.nih.gov/grants/olaw/references/phspol.htm), as well as the Association for Research in Vision and Ophthalmology (ARVO) Statement on Animals in Vision research.

Groups

Different groups of male Sprague-Dawley rats (Hilltop Lab Animals, Inc., PA) were studied using a previously described light and dark adaptation procedure [5]. All rats were maintained in darkness for 16 - 20 hours prior to Teslascan injection. Procedures (e.g., weighing, infusion, anesthetic administration, and MRI exam) were done under dim red light or darkness. Each rat was infused IV for 30 min with a clinically-relevant dose of Teslascan (10 μmol/kg = 0.01 mmol/kg; n = 4 (continued dark adaptation), n = 5 (subsequent light adaptation) - see table 1 below), saline (volume equivalent sample; n = 5), or a high dose of Teslascan (100 μmol/kg; n = 5). The recommended clinical dose is 5-10 μmol/kg dose [11] [17].

Table 1.

Signal, enhancement and effective or apparent K_i for 2 doses, 2 tissues (see also figures 4 and 5)

a) Clinically-relevant dose (10 μmol/kg)
	n	signal saline mean (sem)	signal Teslascan mean (sem)	enhancement (%)	apparent Ki 10-3 min-1
inner retina LA1	5	39.8 (0.97)	52.7 (0.90)	32.3	3.2
inner retina DA2	4		56.4 (1.2)	41.73	4.3
outer retina LA	5	34.4 (0.84)	45.4 (0.92)	32.0	3.2
outer retina DA	4		53.6 (0.98)*	55.83	5.7

b) High dose (100 μmol/kg)
	n	signal saline4	signal Teslascan	enhancement (%)	apparent Ki 10-3 min-1
inner retina LA	5	39.8	60.7 (1.01)	52.5	0.53
outer retina LA	5	34.4	54.3 (0.92)	57.8	0.59

¹light adapted

²dark adapted

³using LA signal saline values

⁴same data as for clinically-relevant dose

^*significant increase in outer retina DA signal compared to LA signal (p<0.05)

High resolution MRI

Following the infusion, rats were maintained in either dark or room light conditions for another 3.5 - 4 hours. Immediately before the MRI experiment, rats were anesthetized using urethane (36% solution, i.p., 0.083 ml / 20 g animal weight, prepared fresh daily, Aldrich, Milwaukee, WI) and xylazine (1-8 mg/kg, IP). Core temperatures were maintained using a recirculating heated water blanket. MRI data were acquired on a 4.7 T Bruker Avance system using a two-turn transmit/receive surface coil (1.0 cm diameter) placed over the left eye. A single transverse slice through the center of the eye (based on sagittal localizer images collected using the same adiabatic pulse sequence as above) was obtained for each rat. Transverse images were then acquired using an adiabatic spin-echo imaging sequence (repetition time TR 350 s, echo time TE 16.7 ms, number of acquisitions NA 16, sweep width 61728 Hz, matrix size, 512 × 512, slice thickness 620 μm, pixel size 23.4 × 23.4 × 620 μm³, field of view 12 × 12 mm²) [18]. After the MEMRI exam, rats were humanely euthanized.

Data Analysis

Layer specific signal intensity

For quantitative analysis, signal intensities were first extracted from each rat image using the program NIH IMAGE and derived macros [19] and the results from that group compared with a generalized estimating equation approach (described below) [5]. Changes in receiver gain between animals were controlled for by setting the signal intensity of a fixed region of noise in each rat to a fixed value. Post-receptor (or inner retina IR) and receptor (or outer retina OR) signal intensity data (from distances ± 0.4 - 1 mm from the optic nerve) were extracted as follows. As we have previously discussed, the inner / outer retinal division is observable in light adapted retina (based on contrast generated by the differential amount of manganese taken up in inner and outer retina) but is not observable in dark adapted retinas [5]. Thus, we take advantage of the fact that the division between inner and outer retina and between retina and choroid occur as in normal retina (about 100 μm from the vitreal-retinal border (or about 4 pixels (23.4 × 4 = 96 μm) for inner retina, and then 3 pixels posterior to this region to sample the outer retina. To further ensure that we are measuring from inner and outer retina, the pixel values just anterior each of these divisions were designated as representative of inner or outer retinal values, respectively. Data were analyzed as previously described [5].

Statistical Analysis

Comparisons of MEMRI retinal signal intensities were performed using a generalized estimating equation (GEE) approach [5]. GEE performs a general linear regression analysis using all of the pixels in each subject and accounts for the with-in subject correlation between adjacent pixels. To the best of our knowledge an “ANOVA”-type GEE test is not available and instead exact P values from two-tailed comparisons are provided. When the P values are very low (e.g., P = 0.0001), the likelihood of false rejection of a true null in multiple comparisons is very small.

Mn²⁺ retention in retina

A separate study was carried out to test the modelling assumption (see below) that Mn²⁺ efflux from the retina can be ignored in the first few hours after injection. An intra peritoneal dose of 44 mg/kg of MnCl₂ solution was given and retinal signal intensity measured at times from 4 hr to 7 days after injection. For each time-point, n = 3 or 4.

3. Modelling

Transfer constant K_i

Inflow of dissociated free Mn²⁺ tracer into the retina is characterised by an input transfer constant K_i (units: min^-1):

$$F=\frac{d{C}_t}{dt}=K_i{C}_p\left(t\right)$$ Eq 1

The inflow F (units: mmol ml^-1 min^-1) is proportional to the plasma concentration C_p(t) (units mmol ml^-1 = mM), and independent of the concentration of tracer already in the retina (i.e. there is no backflow term[20]). Efflux (outflow) from the retina is ignored (this was shown to be realistic - see figure 6 below). C_t is the concentration in the retinal tissue. The contribution of IV tracer to C_t is ignored (see discussion). The quantity K_i inherently characterises a one-way flow into the retina It is very similar to the widely used K^trans [21]; the only difference is that K^trans usually characterises bidirectional diffusive flow across the capillary endothelium, in which tracer first leaks out of the blood plasma, then returns later on as the plasma concentration decreases.

Figure 6.

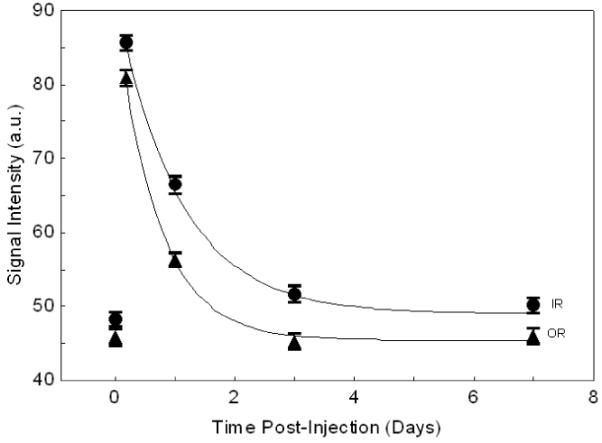
Mn²⁺ clearance from retina (IR=inner retina, OR=outer retina). Curves are fitted exponential decay; half-times are 19h (IR) and 11h (OR).

The plasma concentration in rats is well characterised by a single exponential decay [12]:

$$C_p\left(t\right)=Da{e}^{-mt}$$ Eq 2

D is the dose (mmole/kg), a is the initial plasma concentration for unit dose, and m is the decay rate (min^-1). Using the data of Hustvedt et al [12], for D=7 μM/kg bolus injection of ⁵⁴MnDPDP, C_p(0)= 0.185 mM, hence a=26.5 kg/l; also half life=24 min, hence m=0.0288 min^-1 (corresponding to an exponential decay time (1/m) of 35 min). (Using the reported value[12] for C_p(0) of 10.2 μg /ml Mn, and Mn mass is 54 g/mole, gives 0.185 mmole/litre)

The retinal concentration at a time t after injection is then:

$$C_t\left(t\right)=K_i{\int }_0^t{C}_p\left(t^{\prime }\right)d{t}^{\prime }=K_{i}D(a∕m)(1-e^{-m_{1}t})$$ Eq 3

and a long time after injection (t>5/m, i.e. after about 3 hrs), the tissue concentration reaches a plateau value that is proportional to K_i and D:

$$C_t\left(\infty \right)=K_{i}Da∕m$$ Eq 4

The value of retinal T₁ is reduced by the presence of Mn:

$$\frac{1}{T_1}=\frac{1}{T_{10}}+r_1{C}_t$$ Eq 5

T₁₀ is the value of T₁ before injection of Mn; a value of 1.6 s (measured in humans at 1.5T) was used[22]. r₁ is the relaxivity; a value of 8 s^-1 mM^-1 was used (measured in vitro at 1.4T and 23 °C) [23] (and see reference[24] page 72).

The signal enhancement for a spin echo sequence is then given by:

$$S_n=\frac{1-e^{-TR∕T_1}}{1-e^{-TR∕T_{10}}}$$ Eq 6

S_n is the normalised signal (i.e. S_n = 1 before injection of Mn). Thus for a given value of K_i, and knowing the dose D, the plasma constants a and m, T₁₀, r₁, TR and the time of imaging t, the retinal signal enhancement can be modelled, using eqs 3,5,6. Typical predicted enhancement curves are shown in figure 1. The plateau enhancement S_n(∞)(eqs 4-6) is highly linear with K_i (figure 2; for TR=350 ms).

Figure 1.

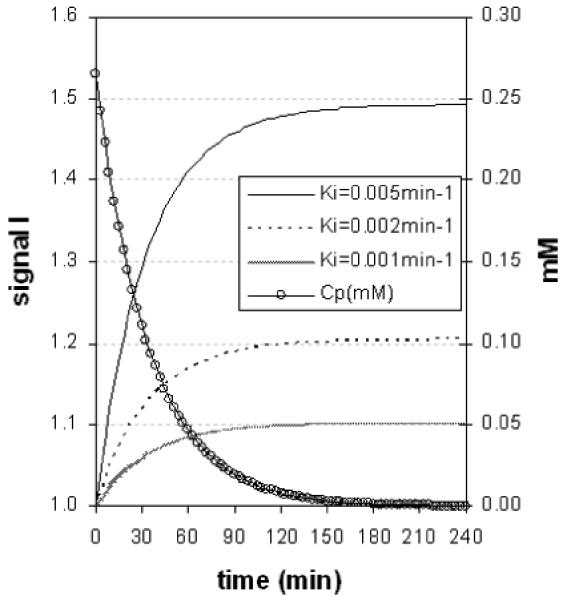
Modelled retinal enhancement curves (using eqs [2-4]). Parameter values: D=10 μmole/kg, T₁₀=1.7s, r₁=8 s^-1 mM^-1, TR=350 ms. After about 2 hours, plasma concentration (RH axis) has almost decayed to zero, and signal has almost reached a plateau.

figure 2.

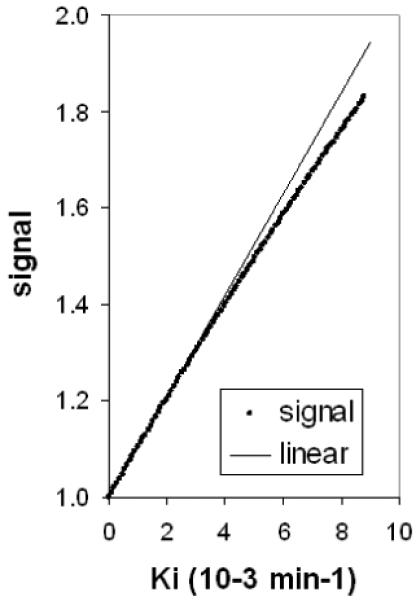
Almost linear dependence of plateau signal S_n (∞) on K_i. Parameter values: D=10 μmole/kg, T₁₀=1.7s, r₁=8 s^-1 mM^-, TR=350 ms.

Optimised acquisition - choosing TR

The spin echo acquisition can be optimised in terms of TR [25]. A long TR improves SNR by allowing more relaxation between 90° pulses, whilst a short TR improves SNR by giving more signal averaging. These two competing effects can be reconciled by choosing an optimum TR which maximised the SNR of the averaged image. Simple analysis of the equation for spin echo image intensity[25] shows that the minimum detectable Mn²⁺ concentration is:

$$C_{\min }=\left(\frac{3}{SN{R}_0{r}_1{e}^{-TR∕T_{10}}}\right){\left(\frac{N_{pe}}{T_{ex}TR}\right)}^{1∕2}$$ Eq 7

It is assumed that a signal change of 3 times the noise is needed to detect the effect of the added Mn. SNR₀ is the SNR of the relaxed sequence (TR»T₁₀, single average). N_pe is the number of phase encodes. T_ex is the total examination time (T_ex = N_av N_pe TR, where N_av is the number of averages). C_min has a broad minimum with respect to TR at TR=T₁₀/2 [25]; thus for T₁₀=1.6 s this would be at 800 ms. A typical optimisation curve is shown in figure 3.

Figure 3.

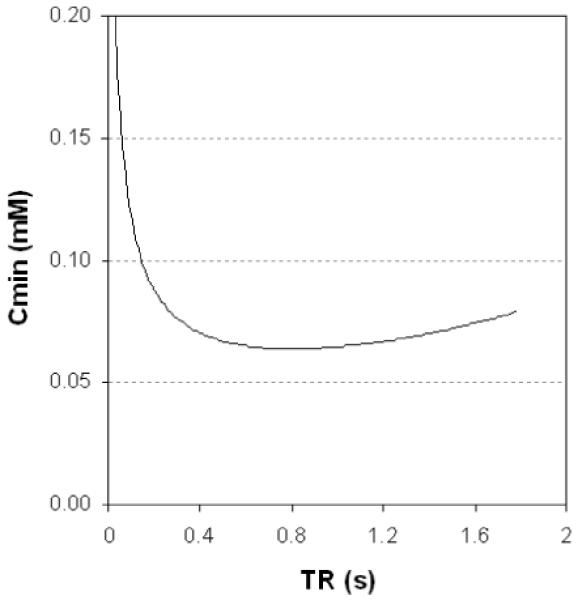
Minimum detectable Mn²⁺ concentration as a function of TR (from eq 7), for a spin echo sequence. T₁₀=1.6s, SNR₀=5, N_Pe=256, T_ex=20 min, r₁=8 s^-1 mM^-1. The optimum TR is 800 ms (i.e. 0.5 T₁₀ as previously found[25]), and at this TR N_av≈5. The curve is quite broad; TR can be in the range 0.4-1.4s without C_min rising more than 10% above its optimised value, and in the range 0.3-1.7s without rising 20% above its optimised value.

4. Results

Effect of dose

In light adapted rats, relative to baseline levels (i.e., animals not given Teslascan), the clinically-relevant dose (10 μmol/kg) of Teslascan increased IR and OR by 32% (P < 0.0001 in both cases), whilst the higher dose (100 μmol/kg) increased IR and OR by 52-58% (P < 0.0001 in both cases) (Figure 4).

Figure 4.

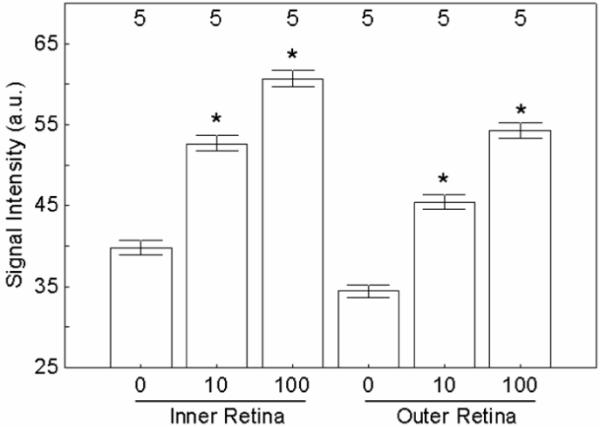
Summary of MEMRI changes in inner and outer retina of light-adapted rats following systemic Teslascan administration at different doses (0, 10 or 100 umol/kg). Significant comparisons to 0 dose are shown with a *. Error bars are SEM; numbers over bars are numbers of animals studied.

Light adaptation

With the clinically relevant dose, light and dark adapted retinas had similar (P = 0.13) inner retinal signal intensities, but different (P = 0.0018) outer retinal intensities (Figure 5). Thus the reduction in signal caused by light adaptation (compared to the value with dark-adaptation) was significant for the outer retina, but not quite significant for the inner retina.

Figure 5.

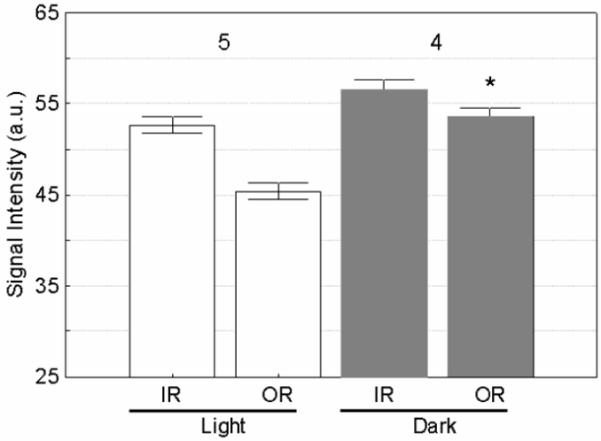
Summary of MEMRI changes in inner (IR) and outer retina (OR) as a function of light adaptation using Teslascan. Dark adapted OR signal is significantly raised compared to light adapted (shown with a *). Error bars are SEM; numbers over bars are numbers of animals studied.

Modelling

With the clinically relevant dose, values of K_i ranged from 3-6 10^-3 min^-1 (table 1). At the high dose, apparent K_i was reduced to 0.5-0.6 10^-3 min^-1.

Mn²⁺ efflux

Clearance of Mn²⁺ fitted a single exponential decay (figure 6), with half-times of 19h and 11h for inner and outer retina respectively.

5. Discussion

The results of this study show, for the first time, the feasibility of using systemically administered Teslascan to monitor intraretinal ion regulation changes associated with visual processing in vivo. Other laboratories have also found Teslascan useful for studying ion activity in the heart after a systemic injection and in optic nerve transport after an intravitreal injection [17] [26]. In this study, data were not collected optimally, per the model results, since our hardware setup maximized filling factor and thus signal-to-noise. This is not the situation in the clinic and more optimal acquisition parameters will be needed. Imaging 2-3 hours after injection seems to be optimal, in terms of allowing time for the retinal Mn²⁺ plateau to be reached (figure 1).

The proposed model is clearly a simplification of the actual Mn²⁺ transport process; however with only a single time point (which is a realistic assumption for potential clinical applications), more information cannot be extracted. A passive unsaturated transport mechanism has been assumed for retinal uptake (i.e. with uptake proportional to plasma concentration). In the well-understood case of passive transport of the imaging contrast agent Gd-DTPA through a defective blood-brain barrier[13] [21], transport can be bi-directional, and can be dominated by flow or permeability. However in this retinal model there is no backflow term and Mn²⁺ in the retina is effectively trapped for a long time (see eq 4 and figures 1 and 6). We have measured an apparent or effective transfer constant at a given dose and injection duration (analogous to the ‘apparent diffusion coefficient’). There is evidence of saturation of the transport mechanism at high dose (100 μmole/kg) - see table 1, giving a nonlinear response of Mn²⁺ retinal uptake to dose, and a reduction in apparent transfer constant. Even at the clinically-relevant dose (10 μmole/kg) there may be saturation, and a reduction in dose or plasma concentration may not degrade the contrast-to-noise ratio in the same proportion.

To build on these present initial findings, future studies could focus on the dependence of signal enhancement on time after injection and on size and duration of dose. Such data would allow the validity of the modelling to be evaluated, and better characterise the Mn²⁺ transport mechanism. Giving the Mn²⁺ dose over a long period of time (e.g. an infusion for 30 min, as in this study) may increase uptake compared with a bolus injection, since active transport mechanisms are less likely to saturate. Ignoring the contribution of intravenous Mn²⁺ to the tissue concentration (eq 1) is reasonable for several hours after injection, as retinal blood volume fraction is relatively small, and C_p is by then low (figure 1). A published human retinal T₁₀ value at 1.5T was used [22] (since no value at 4.7T was available); the true 4.7T value will be somewhat higher. The T₁₀ estimate is low by perhaps 30%; the model shows that increasing T₁₀ by 30% reduces the K_i estimates by about the same factor. Similarly, the relaxivity value r₁ is also an estimate and a true value at 4.7T and 37 °C would be valuable.

In this study the injection was given as a 30 min infusion, not a bolus. Given that the uptake is effectively complete after 3 hours (figure 1), then the bolus is a reasonable simplification. A more accurate modelling could replace the infusion with a bolus at a time half way through the infusion; alternatively the eq 8 could be modified to include a convolution to take account of the extended dose D.

Human studies will be constrained by a Mn²⁺ plasma concentration that is probably lower and shorter-lived than in rats[11]. The data of Toft et al (reference [11] figure 3c and d), for short injections of 5 and 10 μmol/kg, give initial plasma concentrations of 24 and 74 μM Mn²⁺, indicating a values (i.e. C_p(0)/D) of only 5-7 kg/l. Half lives are 18-20 min, indicating a faster m value of 0.035-0.038 min^-1. Both these factors would reduce the plateau retinal concentration (eq 4), to about 14-23% of the value in rat (assuming the human K_i values are similar to those in rat). However signal-to-noise ratio may be larger in human subjects (more spins per voxel), enabling lower concentrations of Mn²⁺ to be seen. The spin echo optimisation study (figure 3) indicates that contrast-to-noise ratio (or equivalently, the acquisition time) could be improved in clinical studies by using a longer TR value. Other T₁-weighted sequences (spoilt gradient echo and possibly MP-RAGE) would probably have advantages[25]. Active Mn²⁺ transport may still be effective at lower plasma concentrations (giving a higher effective K_i than we have reported). Probably as large a dose as possible should be given; with Gd-DTPA there is a precedent for giving more than the recommended clinical dose of 0.1 mmol/kg (up to three times this can be given when extra sensitivity is needed).

Humans dark adapt in about 30 min which is faster than that for the albino rats used in this study. One possible procedure for patient studies would be to compare manganese uptake in a dark adapted eye (patch light-tight for 30 min prior to Teslascan infusion) with that in the contra-unpatched eye (which would be light adapted). The time between the infusion and MRI examination would need to be optimized to minimize possible circulatory contamination and maximize retinal enhancement in patients. Images of patched and unpatched eyes could then be compared to assess retinal function. While a reasonable approach for optimization studies in controls and in some ocular diseases, this approach would not be applicable in diseases that occur asymmetrically.

The mechanism for production of free Mn²⁺ ions in plasma from Teslascan (Mn DPDP) is poorly understood, and the plasma concentration of free Mn is unknown. It is generally thought that Mn²⁺ is displaced from MnDPDP by Zn and Ca in plasma (transmetallation) [12] [27] [11], and subsequently bound to plasma proteins, principally albumin [27]. Although an ex vivo study failed to detect free Mn²⁺ ions [27], these must presumably be present for retinal uptake to be possible in our study. In our mathematical model we have assumed that all plasma Mn²⁺ is available for retinal uptake; the actual available concentration C_p(t) (eqn 2) could be lower depending on the equilibrium between free Mn²⁺and plasma-protein bound Mn²⁺; consequently our K_i values may be underestimates. Furthermore the uptake by the retina of Mn²⁺ ions is unlikely to be large enough to deplete the arterial plasma Mn²⁺ concentration (although there may be local depletion in capillaries if transport is flow limited[21]). The apparent dependence of K_i on dose (table 1) may in part be caused by a variable fraction of the plasma Mn being available for retinal uptake and more work is needed to understand the factors that regulate the above equilibrium. An explicit study of free Mn²⁺ concentration in plasma, including any dependence on disease, would be valuable, since accurate values of C_p(t) would then be available.

In conclusion, for the first time, the feasibility of using an FDA-approved manganese based contrast agent for functional retinal studies is demonstrated. The expected reduction in retinal activity with light adaptation has been measured. These data raise the possibility of performing experimental medicine studies with normal humans to validate the potential use of Teslascan as an image biomarker for ocular disease.