The Effect of Optical Zone Decentration on Lower- and Higher-Order Aberrations after Photorefractive Keratectomy in a Cat Model

Abstract

Purpose

To simulate the effects of decentration on lower- and higher-order aberrations (LOAs and HOAs) and optical quality, by using measured wavefront error (WFE) data from a cat photorefractive keratectomy (PRK) model.

Methods

WFE differences were obtained from five cats’ eyes 19 ± 7 weeks after spherical myopic PRK for −6 D (three eyes) and −10 D (two eyes). Ablation-centered WFEs were computed for a 9.0 mm pupil. A computer model was used to simulate decentration of a 6-mm subaperture in 100-μm steps over a circular area of 3000 μm diameter, relative to the measured WFE difference. Changes in LOA, HOA, and image quality (visual Strehl ratio based on the optical transfer function; VSOTF) were computed for simulated decentrations over 3.5 and 6.0 mm.

Results

Decentration resulted in undercorrection of sphere and induction of astigmatism; among the HOAs, decentration mainly induced coma. Decentration effects were distributed asymmetrically. Decentrations >1000 μm led to an undercor-rection of sphere and cylinder of >0.5 D. Computational simulation of LOA/HOA interaction did not alter threshold values. For image quality (decrease of best-corrected VSOTF by >0.2 log units), the corresponding thresholds were lower. The amount of spherical aberration induced by the centered treatment significantly influenced the decentration tolerance of LOAs and log best corrected VSOTF.

Conclusions

Modeling decentration with real WFE changes showed irregularities of decentration effects for rotationally symmetric treatments. The main aberrations induced by decentration were defocus, astigmatism, and coma. Treatments that induced more spherical aberration were less tolerant of decentration.

Correct alignment of the ablation to the visual axis of the eye is an essential requirement for optimal outcome in laser refractive surgery (LRS). Decentration of the ablation zone leads to incomplete refractive correction and induction of higher-order aberrations (HOAs), especially coma.^1–4 The expected benefit of less HOA induction in eye tracker–controlled treatments has been demonstrated.⁵ However, decentration still occurs as a result of misalignment of the tracking system,⁶ static registration errors due to surgeon offsets,⁷ and pupil center shifts as a function of dilation.⁸ In most cases, the magnitude of such misalignments is <500 μm.^1,7,9,10 A recent study showed that in uneventful wavefront-guided LASIK, coma induction occurred in a random fashion, independent of factors such as attempted correction and optical zone (OZ) diameter.¹¹ Thus, microdecentrations can be considered ubiquitous, random errors; however, their impact on optical quality is poorly understood.¹⁰ In contrast, gross decentrations of >500 μm are one of the most visually disturbing complications after LRS. Besides causing severe deterioration of visual quality, such complications are difficult to treat, and success is often limited.^12–18

Although several studies on decentration-induced aberrations after conventional^1,2,7 and wavefront-guided LRS^3,4,8,19 have been published, all assumed a perfect ablation and did not consider the inherent induction of HOA which occurs in real corneas as a result of wound healing and biomechanical effects.^20,21 The present study was conducted to investigate the effects of decentration of the laser ablation relative to the entrance pupil of the eye on LOA, HOA, and optical quality, in a cat photorefractive keratectomy (PRK) model. Although the optical effects of PRK for myopia, such as reduction of defocus, induction of coma, and positive spherical aberration are similar in cats and humans,^22,23 the greater corneal surface area and the naturally large scotopic pupil diameter (PD) of ~12 mm in cats allowed us to measure wavefront changes well beyond the ablation OZ. A simplified computational model was used to simulate decentration effects over a circular area of 3000 μm in diameter by calculating wavefront errors (WFEs) for systematically offset subapertures of 3.5 and 6.0 mm. Using this paradigm, we assessed (1) the nature and magnitude and spatial distribution of optical aberrations induced by different amounts of decentration, (2) the impact of such aberrations on theoretical optical quality, (3) whether residual refractive errors could be partially attributed to microdecentrations (≤500 μm), and (4) the impact of optical aberrations induced by laser refractive surgery on tolerance of decentration.

Materials and Methods

Subjects

Data were obtained from five eyes of five normal, male domestic short hair cats (Felis cattus), who underwent myopic PRK with an uncomplicated follow-up of at least 3 months and in which wavefront aberrations could be measured over a PD of 9 mm. Procedures were conducted according to the guidelines of the University of Rochester Committee on Animal Research (UCAR), the ARVO Statement for the Use of Animals in Ophthalmic and Vision Research, and the NIH Guide for the Care and Use of Laboratory Animals.

Photorefractive Keratectomy

Three cats’ eyes underwent PRK for −6 D, two with a programmed OZ of 6 mm and one with an 8-mm OZ; two eyes received a PRK for −10 D (6 mm OZ). The procedure has been described in detail elsewhere.²³ Briefly, all eyes received a conventional spherical ablation (Planoscan 4.14; Bausch & Lomb, Inc., Rochester, NY) performed by one of two surgeons (SM, JB) in animals under surgical anesthesia (Technolas 217 laser; Bausch & Lomb, Inc.). The ablation was centered on the pupil, which was constricted with 2 drops of pilocarpine 3% (Bausch & Lomb). After surgery, the cats received 2 drops of 0.3% tobramy-cin+0.1% dexamethasone 0.1% (Tobradex; Alcon, Fort Worth, TX) per eye, once a day, until the surface epithelium healed.

Wavefront Sensing

As described previously,^23,24 the cats were trained to fixate single spots of light presented on a computer monitor. Wavefront measurements were performed before surgery and 19±7 (12–24) weeks after surgery, with a custom-built Hartmann-Shack wavefront sensor. The wavefront sensor was aligned to the visual axis of one eye, while the other eye fixated a spot on the computer monitor.²⁴ At least 10 spot-array patterns were collected per imaging session per eye.

Calculation of Centered WFE Differences

From each single spot–array pattern, WFEs were calculated with a 2nd–10th-order Zernike polynomial expansion according to Vision Science and Its Application (VSIA) standards for reporting aberration data of the eye.²⁵ WFE changes were simulated in a multistep process. The first step included the determination of the center of the OZ. Because PRK was performed with the cat under general anesthesia and the ablation was registered to the pupil center, an alignment to the visual axis of the cat’s eye during surgery could not be ensured, and possible decentration effects had to be compensated for. Therefore, the centroiding area (analysis pupil) of 6-mm diameter was shifted manually in steps of 300 μm according to the distance between the lenslet centers to find the wavefront that yielded the most negative Z₂⁰ value (i.e., the maximum treatment effect. This was defined as the centered, postoperative wavefront (W_post[x, y]), which was then averaged from single measurements over a PD of 9 mm. In the second step, the horizontal and vertical offsets between the center of the OZ and the center of the original pupil were used to calculate preoperative WFEs (W_pre[x,y]), for the position that equaled the later treatment center. Like W_post(x, y), W_pre(x, y) was computed for a 9-mm PD. In a third step, the change in WFEs, ΔW(x, y), were obtained by subtracting the pre- from the postoperative Zernike coefficients. Thus, ΔW(x, y) reflected the treatment effect over a 9-mm PD, for a perfectly centered OZ, minimizing the potential influence of internal aberrations. The Zernike coefficient spectrum of each ΔW(x, y) (Table 1) was consistent with data obtained in humans after PRK.²²

Table 1.

Treatment Characteristics and WFE Changes for the Centered Treatment (ΔW[x, y]) over 6- and 9-mm PDs

				Centered Wavefront Error Change ΔW(x, y)
Eye	Treatment (D)	OZ (mm)	TTZ (mm)	PD (mm)	Sphere(D)	Cylinder (D)	Axis (°)	Total HOA RMS (μm)	Coma RMS (μm)	SA RMS (μm)	rHOA RMS (μm)
c1-005 OD	−6	8	11.1	9	+3.33	−0.58	172	2.412	1.019	1.838	1.184
				6	+4.71	−0.61	12	0.541	0.197	0.333	0.388
c2-001 OS	−6	6	9.1	9	+0.82	−0.37	91	1.790	0.516	1.585	0.650
				6	+2.17	−0.65	88	0.618	0.285	0.327	0.440
c2-006 OS	−6	6	9.1	9	+1.90	−0.11	79	1.155	0.324	0.991	0.496
				6	+2.56	−0.24	40	0.307	0.120	0.039	0.280
c5-005 OD	−10	6	9.1	9	+2.49	−0.28	29	2.182	0.414	2.108	0.381
				6	+4.11	−0.28	37	0.574	0.296	0.426	0.246
c5-026 OD	−10	6	9.1	9	+3.24	−0.45	174	2.983	0.423	2.924	0.409
				6	+5.29	−0.47	160	0.430	0.291	0.262	0.178

OZ, diameter of the programmed optical zone; TTZ, diameter of the total treatment zone; total HOA RMS, root mean square value of 3rd- to 10th-order aberrations; coma RMS, RMS value of 3rd- to 9th-order coma; SA RMS, RMS value of 4th- to 10th-order spherical aberration; rHOA RMS, residual RMS of all noncoma, nonspherical HOA.

Computer Modeling of Treatment Decentration

For each eye, decentration of a 6-mm subpupil relative to ΔW(x, y) was simulated by using custom software (MatLab 7.2; The MathWorks Inc., Natick, MA). Decentered WFE differences ΔW(x′, y′) were calculated for the size of the 6-mm subaperture along Cartesian decentrations Δx and Δy, where Δx and Δy were changed in steps of 100 μm, covering the entire 9-mm centroiding area and resulting in a maximum decentration range of 3000 μm over a circular region. Zernike polynomials for the 2nd to the 6th order were fitted to the data of each decentered wavefront ΔW(x′, y′) by using a singular value decomposition algorithm to calculate the pseudoinverse of the Zernike data to get the decentered subpupil Zernike coefficients. As a refinement of the manual determination of the centered position, the algorithm assigned the centered coordinates (Δx = 0, Δy = 0) to the ΔW(x′, y′) with the lowest Z₂⁰ value. For each eye, 709 WFEs, 1 centered and 708 decentered were calculated over a 6-mm PD.

Simulation of Decentered Treatment Effects and VSOTF Calculation

Theoretical optical quality was investigated by calculating the VSOTF metric (visual Strehl ratio based on the optical transfer function [OTF]). The VSOTF is the ratio of the contrast sensitivity–weighted OTF to the contrast sensitivity–weighted OTF of the diffraction-limited eye.^26,27 Because the preoperative WFEs W_pre(x, y) were decentered, calculating the VSOTF from preoperative HOA could lead to misinterpretation of optical quality due to over- or underestimation of HOA. Thus, we calculated a standard preoperative WFE, W_meanpre(x₀, y₀), from all eyes included in this study. For the calculation of W_meanpre(x₀, y₀), all preoperative, pupil-centered WFEs were averaged, resulting in a WFE representing the typical preoperative range of HOA (Table 2).^24,28 Simulated postoperative WFEs, W_post(x′, y′), were calculated by subtracting the W_meanpre(x₀, y₀) from each ΔW(x′, y′). This treatment simulation relative to a standard preoperative WFE allowed us to eliminate interindividual differences in preoperative optical quality and internal optics. Therefore, the independent variables in this experiment were the five different centered treatment effects ΔW(x, y) and their corresponding ΔW(x′, y′). A computer program (Visual Optics Laboratory, VOL-Pro 7.14; Sarver and Associates, Carbondale, IL) was used to calculate the VSOTF over an analysis PD of 3.5 and 6.0 mm. The VSOTF for a given WFE was calculated for the combination of LOA terms that provided the highest VSOTF simulating the optical quality with best spherocylindrical correction (BCVSOTF). Thus, for each simulated W_post(x′, y′), an LOA-derived refractive error based on 2nd-order terms and an “effective” refractive error based on the BCVSOTF were obtained. Differences between refractive errors were expressed as dioptric power vectors (M, J0, J45), where M corresponds to the spherical equivalent and J0 to the 0°/90° and J45 to the 45°/135° astigmatic components. The difference between the VSOTF- and 2nd-order–based power vectors could be considered a function of the interaction between HOA and LOA. Since “sphere” and “cylinder” are most commonly used in clinical settings, we displayed most of the results in terms of sphere and cylinder magnitude. To visualize decentration effects for single eyes, color maps plotting ΔLOA, ΔHOA, and Δlog BCVSOTF against horizontal and vertical decentration were created. For further statistical analysis, data for decentration along the 0°, 90°, 180°, and 270° meridians were averaged for each eye.

Table 2.

The Averaged Preoperative Mean WFE W_meanpre(x₀, y₀), Computed for 3.5- and 6-mm PDs

PD (mm)	Log BCVSOTF	Total HOA RMS (μm)	Coma RMS (μm)	SA RMS (μm)	rHOA RMS (μm)
3.5	−0.05	0.036	0.031	0.012	0.014
6.0	−0.38	0.185	0.145	0.078	0.083

For all calculations LOA were set to zero. BCVSOTF (visual Strehl ratio based on the optical transfer function, simulated for best correction); total HOA RMS, root mean square value of 3rd- to 6th-order aberrations; coma RMS, RMS of 3rd to 5th order coma; SA RMS, RMS of Z₄⁰ and Z₆⁰; rHOA RMS, residual RMS of all noncoma, nonspherical HOA.

Calculating Decentration Tolerance

Analysis of tolerance was performed by calculating the maximum permissible decentration that yielded a critical refraction or BCVSOTF difference. For sphere and cylinder, this threshold value was defined a priori as −0.5 D. For the optical quality metric BCVSOTF, we chose a critical decrease of 0.2 log units, which roughly equals a decrease of 2 logMAR steps.²⁷ For each parameter investigated, vectors r between the centered position (x, y) and each outmost coordinate below the criterion (threshold coordinates x′, y′) were calculated. The mean value, r̄, reflects the average maximum permissible decentration (in micrometers) that allows one to remain below the threshold criterion and equals the radius of a circle around the centered position. The standard deviation (SD) of r̄ and the coefficient of variation (CV) of r̄ served as metrics for regularity of decentration effects, where SD of r̄ reflects the absolute and CV of r̄ the relative irregularity. The smaller the SD and CV, the less variable were the decentration effects along different meridians (i.e., the more circle-shaped was the decentration pattern).

Statistical Analysis

All analyses were based on the difference values ΔW and Δ log BCV-SOTF, which reflected the treatment effects. Main outcome measures were the change of log BCVSOTF, the change of LOA, expressed in diopters, and the change of HOA as a function of decentration. All differences for the center position (x, y) were normalized to zero. Thus, values for decentered coordinates x′ and y′ reflect the deviation from the centered treatment effect. The difference between wavefront-and VSOTF-based refraction was considered an effect of interaction between LOA and HOA. Tolerance metrics were calculated as described earlier. HOAs were broken down into coma root mean square (RMS) (the RMS of all coma terms Z_n^±1), spherical aberration RMS (SA RMS, the RMS value of all coefficients Z_n⁰), and the RMS of the residual noncoma, nonspherical aberrations (rHOA, the RMS value of all remaining HOA Z_n^≥2).

The influence of the magnitude of HOA induction on decentration tolerance was assessed with linear regression analysis. The dependent variables were the mean vectors r̄ and their SD. To investigate the impact of HOAs on log BCVSOTF, we applied a multiple-regression model using HOAs as predictors and log BCVSOTF as dependent variables. The role of interaction on decentration tolerance was investigated by comparing r̄ and SD for 2nd-order sphere and cylinder with their VSOTF-based equivalents using a nonparametric test for matched pairs (Wilcoxon test). The same test was also applied to compare decentration tolerance for PDs of 3.5 and 6.0 mm. All statistical tests were performed with a commercial program (SPSS 11.0; SPSS Inc., Chicago, IL), assuming a significance level of P < 0.05 and using the Bonferroni adjustment for multiple tests.

Results

Change in Second-Order Aberrations

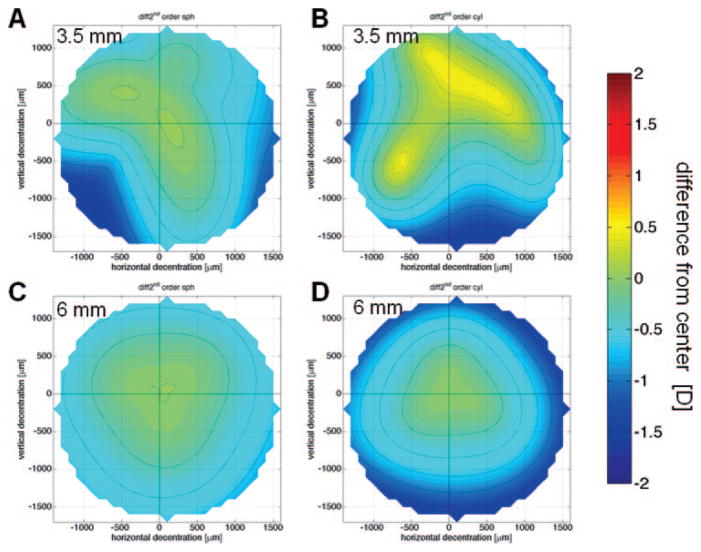
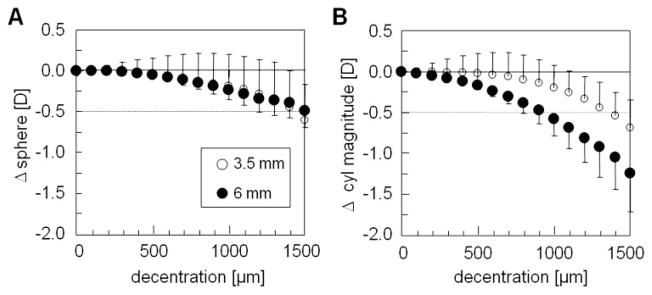
For all eyes examined, increasing decentration caused increasing undercorrection of 2nd-order sphere and induction of 2nd-order astigmatism. However, the pattern of decentration effects was triangular in shape rather than rotationally symmetric, as might have been predicted from the intended refractive correction (Fig. 1). These irregularities were more pronounced for 3.5-mm PDs which also showed reduction of cylinder magnitude with decentration (Figs. 1A, 1B). When averaging over all five eyes, decentrations of ≤1000 μm had a limited effect on sphere and cylinder magnitude, since the average undercorrection and cylinder induction were > −0.5 D (Fig. 2). In contrast, decentrations ≥1000 μm resulted in larger deviation from the central treatment effect. The mean induction of astigmatism was higher for 6- than for 3.5-mm PDs; however, the differences between the two PDs for decentrations ≥900 μm reached only local significance of P < 0.05, which was nonsignificant with the Bonferroni correction.

Figure 1.

Second-order refraction change decentration maps for the right eye of cat 5-005. (A) Change in sphere, 3.5-mm PD. (B) Change in cylinder magnitude, 3.5-mm PD. (C) Change in sphere, 6-mm PD. (D) Change in cylinder magnitude, 6-mm PD. The center (crosshair) is set to zero; dotted lines: 0.25-D steps.

Figure 2.

Mean effects of decentration on 2nd-order refraction change (averaged data from 0°, 90°, 180°, 270° meridians for the five eyes). (A) Change in sphere magnitude. (B) Change in cylinder magnitude. The center is set to zero. Dotted line: −0.5-D threshold.

Decentration Effects and the Interaction between HOAs and LOAs

VSOTF-based refraction data included interaction effects of LOA with HOA. Apart from a tendency of VSOTF-based M values to be more hyperopic at the centered position, there were no significant differences between 2nd-order and VSOTF-based power vectors (Table 3). Decentration effects were more irregular for VSOTF-based refraction data than for the corresponding wavefront-derived data, particularly for sphere measured over 6-mm PDs (local P < 0.05; Table 3). The effects of decentration on the VSOTF cylinder magnitude also showed high interindividual variability among the eyes.

Table 3.

Effects of Interaction between LOAs and HOAs on Treatment Effects as a Function of Decentration

		Difference between 2nd-Order and VSOTF-Based Refraction Change (D)
PD (mm)	Decentration (μm)	M	J0	J45
3.5	0	0.05 ± 0.11	−0.05 ± 0.07	−0.02 ± 0.06
	200	0.03 ± 0.26	−0.04 ± 0.09	−0.01 ± 0.07
	500	0.01 ± 0.37	−0.02 ± 0.08	0.03 ± 0.09
	1000	0.03 ± 0.39	−0.02 ± 0.13	0.04 ± 0.10
	1500	0.13 ± 0.43	−0.02 ± 0.11	0.02 ± 0.05
6.0	0	0.68 ± 0.31	−0.18 ± 0.14	0.03 ± 0.06
	200	0.61 ± 0.45	−0.16 ± 0.17	0.04 ± 0.08
	500	0.63 ± 0.28	−0.10 ± 0.23	0.00 ± 0.09
	1000	0.58 ± 0.53	−0.06 ± 0.13	−0.01 ± 0.12
	1500	0.560.65	−0.16 ± 0.37	0.01 ± 0.15

The data are averaged from the 0°, 90°, 180°, and 270° meridian and expressed as mean and SD of the difference between second-order and VSOTF-based dioptric power vectors M, J0, and J45. Differences were not statistically significant. VSOTF refraction, simulated endpoint of the subjective refraction based on the BCVSOTF; M, spherical equivalent; J0, 0°/90° astigmatic component; J45, 45°/135° astigmatic component.

Changes of HOAs and BCVSOTF

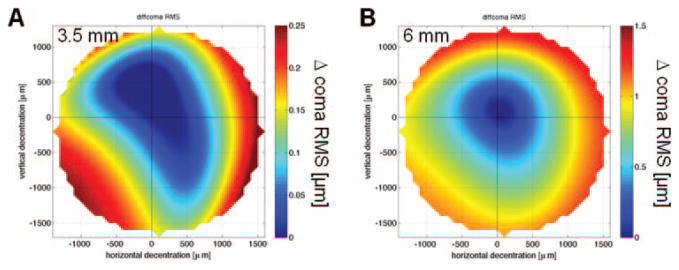
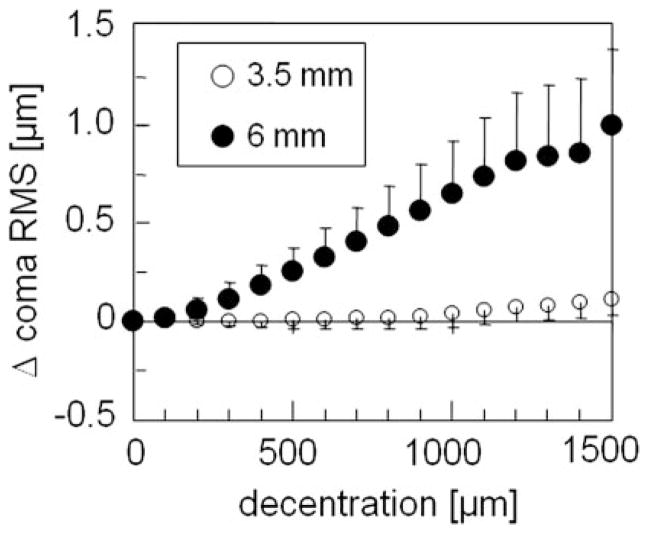
HOAs induced by decentration were dominated by coma (Table 4). As for 2nd-order aberrations, the decentration patterns for coma RMS were not rotationally symmetric, and displayed flatter slopes but higher irregularity for 3.5- than for 6-mm PDs (Fig. 3). We found a significant influence of the amount of decentration on the induction of coma RMS at a PD of 6 mm (adjusted R² = 0.51; B = 0.7 × 10⁻³, P < 0.001). At 3.5 mm, although much less pronounced (adjusted R² = 0.23, B = 0.08 × 10⁻³, P < 0.001), the same tendency was observed (Fig. 4). The induction of SA RMS and rHOA RMS was less influenced by decentration (no significant correlation), with irregular decentration patterns and high variability between individual eyes at the two PDs.

Table 4.

Change of VSOTF and Induction of Higher-Order Aberrations as a Function of Decentration

			HOA Induction
PD (mm)	Decentration (μm)	Δlog BCVSOTF	ΔComa RMS	ΔSA RMS	ΔrHOA RMS
3.5	0	0 ± 0	0 ± 0	0 ± 0	0 ± 0
	200	0 ± 0.04	0 ± 0.017	0 ± 0.006	0 ± 0.014
	500	−0.03 ± 0.09	0.004 ± 0.041	−0.001 ± 0.015	−0.001 ± 0.031
	1000	−0.12 ± 0.18	0.039 ± 0.069	0.011 ± 0.025	0.002 ± 0.044
	1500	−0.22 ± 0.21	0.112 ± 0.079	0.015 ± 0.034	0.003 ± 0.058
6.0	0	−0.14 ± 0.19	0.058 ± 0.039	0.270 ± 0.149	0.186 ± 0.042
	200	−0.18 ± 0.17	0.111 ± 0.080	0.275 ± 0.138	0.187 ± 0.041
	500	−0.24 ± 0.18	0.300 ± 0.147	0.295 ± 0.147	0.195 ± 0.047
	1000	−0.29 ± 0.20	0.660 ± 0.289	0.338 ± 0.184	0.223 ± 0.048
	1500	−0.29 ± 0.20	0.932 ± 0.403	0.317 ± 0.188	0.252 ± 0.042

The data are averaged from the 0°, 90°, 180°, and 270° meridian and expressed as mean and standard deviations. The values are normalized to the values for the centered position for a 3.5 mm pupil diameter (PD), i.e. each value reflects the difference to the value obtained from centered position over a 3.5 mm PD. Δx, horizontal decentration; Δy, vertical decentration. log BCVSOTF, visual Strehl ratio based on the optical transfer function, simulated for best correction; coma RMS, RMS of 3rd and 5th order coma terms; SA RMS, RMS of Z₄⁰ and Z₆⁰; rHOA RMS, residual RMS of all noncoma, nonspherical HOA.

Figure 3.

Decentration map for the change of coma RMS in the right eye of cat 5-005. (A) 3.5-mm PD; (B) 6-mm PD. The center (crosshair) is set to zero.

Figure 4.

Mean effects of decentration on the change of coma RMS (averaged data from 0°, 90°, 180°, and 270° meridians for the five eyes). The center is set to zero.

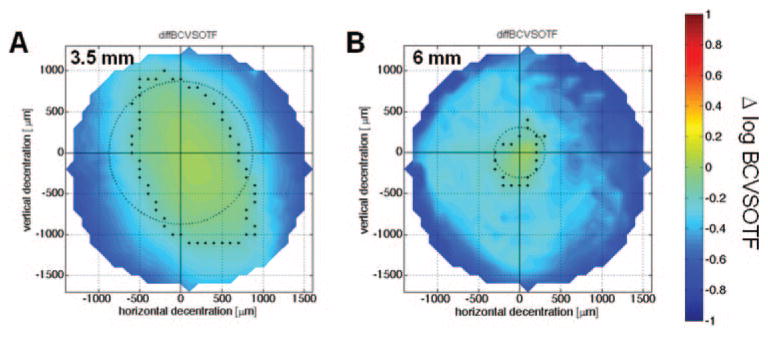
In all eyes, theoretical best-corrected optical quality expressed as BCVSOTF decreased by −0.41 ± 0.13 log units for 3.5-mm pupils and by −0.55 ± 0.19 log units for 6.0 mm pupils after a centered treatment. Decentration resulted in even higher decrease in log BCVSOTF (Figs. 5, 6). Furthermore, if Δlog BCVSOTF was computed for a 3.5-mm PD, the position that yielded the minimum decrease of BCVSOTF was located paracentrally in all eyes (Fig. 5A). The regression model revealed a significant influence of the HOAs on log BCVSOTF at both PDs (adjusted R² = 0.84 for 6-mm PD, R² = 0.81 for 3.5-mm PD) with the highest impact of coma RMS in both models.

Figure 5.

Decentration map for the change of image quality with best correction (Δ log BCVSOTF) for the right eye of cat 5-005. (A) 3.5-mm PD; (B) 6-mm PD. The center (cross-hair) is set to zero; the dots mark the outmost coordinates with a Δ log BCVSOTF > −0.2; the circle shows the mean tolerance r̄.

Figure 6.

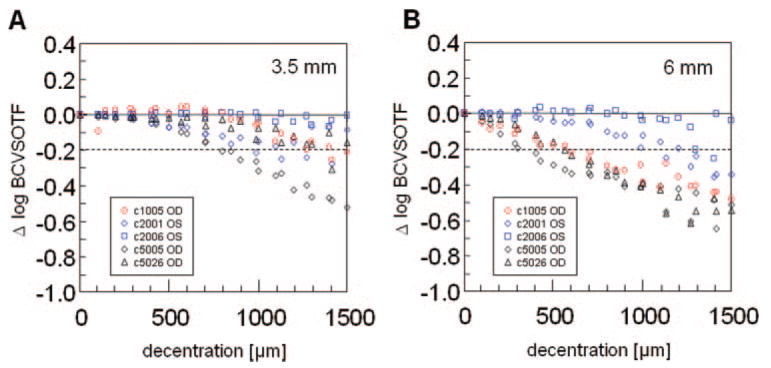
Mean effects of decentration on the change of log BCVSOTF (averaged data from 0°, 90°, 180°, and 270° meridians for the five eyes). The center is set to zero; dotted line: −0.2-log VSOTF threshold.

Analysis of Decentration Tolerance and Irregularity

Table 5 shows the mean vectors r̄ and their SDs. Both for wavefront-derived and for VSOTF-based sphere, the critical r̄ for an undercorrection of 0.5 D was greater than 1000 μm in all cases. The mean change of decentration tolerance due to interaction was 82 ± 232 μm for 6-mm PD and −92 ± 73 μm for 3.5-mm PD (both P > 0.05). For the 6-mm PD, r̄ of cylinder magnitude decreased by −160 ± 142 μm when interaction was simulated (P > 0.05). At the 3.5-mm PD, values remained almost constant (14 ± 153 μm; P > 0.05). While the r̄ of sphere and cylinder was similar at the two PDs, the data (Figs. 5, 6) suggested a higher decentration tolerance at the 3.5-mm PD with regard to log BCVSOTF. This was confirmed by analysis of r̄ (Table 5; local P < 0.05). Analysis of the SD and CV of r̄ showed that the 2nd-order sphere (6.0-mm PD) had more regular decentration patterns than did the other parameters (Table 5).

Table 5.

Analysis of Decentration Tolerance (Maximum Permissible Decentration to Maintain a Threshold Value)

		r̄ (μ m)		SD of r̄ (μm) (CV of r̄ [%])
Parameter	Threshold Value	3.5-mm PD	6-mm PD	3.5-mm PD	6-mm PD
Δ2nd-order sphere	−0.5 D	1255 ± 160	1313 ± 136	228 ± 60 (19 ± 7)	111 ± 47 (8 ± 3)
Δ2nd-order cylinder	−0.5 D	1304 ± 130	1008 ± 214	208 ± 64 (16 ± 6)	173 ± 102 (16 ± 8)
ΔVSOTF sphere	−0.5 D	1348 ± 104	1232 ± 314	204 ± 63 (15 ± 6)	246 ± 55 (20 ± 5)
ΔVSOTF cylinder	−0.5 D	1289 ± 201	1167 ± 271	226 ± 100 (19 ± 13)	207 ± 63 (20 ± 12)
Δlog BCVSOTF	−0.2	1219 ± 210	800 ± 512	248 ± 82 (21 ± 8)	143 ± 40 (21 ± 8)

The radius r̄ is the mean length of the vectors between the center and the locations with threshold values. The SD and CV of r̄ reflect the irregularity of the decentration behavior. All data are expressed as the mean and SD. PD, analysis pupil diameter. VSOTF sphere/cylinder, simulated endpoint of the subjective refraction based on the BCVSOTF.

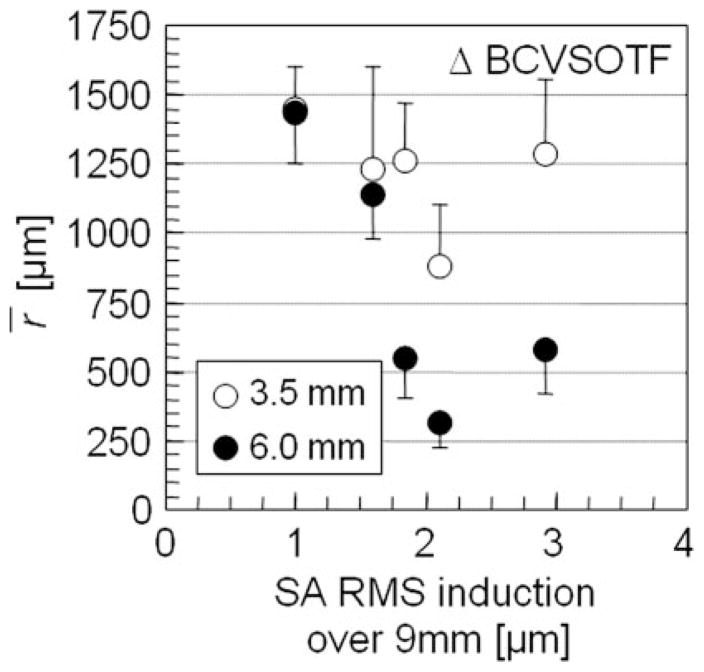
Linear regression analysis revealed that decentration tolerance r̄ was influenced significantly by spherical aberrations induced by the centered treatment. At 6-mm PD, 2nd-order sphere (R² = 0.87, B = −181; P < 0.05), 2nd-order cylinder (adjusted R² = 0.80, B = −278; P < 0.05), and the VSOTF sphere (R² = 0.80, B = −407; P < 0.05) were significantly influenced by ΔSA RMS but not by the amount of defocus or coma and rHOA RMS changes. Likewise, sphere and cylinder obtained over a 3.5-mm PD appeared not to be influenced by defocus change or HOA induction of the treatment. Steeper decrease of Δlog BCVSOTF with decentration was also associated with higher amounts of SA RMS induction by the treatment (Fig. 7), but this association did not reach statistical significance. In this series of eyes, we could not establish any correlation between the induced defocus or HOA and the irregularity index SD of r̄, neither for sphere and cylinder, nor for log BCVSOTF.

Figure 7.

Scatterplot showing the influence of spherical aberrations induced by the centered treatment on the decentration tolerance r̄ of image quality (Δ log BCVSOTF). Error bars: SD of r̄ for each eye indicating irregularity of the decentration pattern.

Discussion

Decentration Effects Followed an Irregular Pattern

The present experiments revealed that decentration effects were distributed asymmetrically, although the treatment involved only rotationally symmetric ablation patterns. This behavior affected all parameters investigated and was more pronounced at the smaller (3.5-mm) pupil size. The fact that only changes between post- and preoperative WFE (ΔW) were analyzed compensated for possible interference from internal aberrations. Thus, the observed asymmetry could be due only to the treatment itself. Aside from the induction of astigmatism, a considerable amount of nonrotational symmetric HOAs (e.g., trefoil and coma) were also induced (Table 1). For example, the triangular pattern in Figure 1 is likely to correlate with the presence of trefoil in the centered WFE difference ΔW(x, y). Because of the small sample size and the high variance among ΔW(x, y), we were not able to establish significant correlations between particular aberrations and asymmetry indices (SD and CV of r̄). However, high interindividual differences between attempted and achieved refractive corrections and the observed asymmetries in the centered ΔW(x, y) may be explained by individual differences in laser ablation rates,²³ local differences in laser energy, or irregularities in the biological response to PRK (i.e., wound healing and biomechanical changes in the cornea^21,23,29,30).

Decentration-Induced LOAs

As observed by others, ^1,2,14,31 there was undercorrection of the spherical refractive error and induction of astigmatism as a function of decentration in all eyes examined. However, to our knowledge, the present study is the first decentration model study that is based on real wavefront data. Because model studies in the literature have always assumed the Munnerlyn algorithm^1,2 or a perfect wavefront-guided ablation,^3,4,19 they probably underestimated the effects of HOA induced by the primary treatment. ^21,32 Unlike spherical aberrations that dominated ΔW(x, y), the amount of coma RMS and rHOA RMS induced by the treatment did not significantly influence decentration tolerance of sphere and cylinder. With calculation of a simulated endpoint of the subjective refraction based on the metric VSOTF, an investigation of interaction effects between LOA and HOA was possible. In particular, we asked whether induced HOA affected the endpoint of the subjective refraction and caused “residual refractive error.” All eyes showed a tendency toward hyperopic VSOTF sphere values over a 6-mm PD which could be explained by interaction with spherical aberration.³³ Furthermore, interindividual variability of interaction effects increased with decentration (Table 3, higher SDs for larger decentrations). Although cautious because of our small sample size, we believe that contrary to its effects on LOA induction, decentration did not consistently affect LOA/HOA interactions. However, VSOTF-based refraction results²⁷ may differ from subjective refraction, particularly with HOA-related image distortion. Our finding that only decentrations ≥1000 μm caused spherical and cylindrical undercorrection ≥0.5 D and larger suggests that ubiquitous microdecentrations^7,9,10 ≤500 μm are not a significant source of postoperative residual refractive errors.

HOA and Best-Corrected Optical Quality

Induction of HOAs, especially coma, is a key contributor to symptoms after LRS in humans.^{1,12–14,17,34,35} We noted that the induction of HOAs by decentration occurred in an irregular pattern that may have resulted from treatment-induced, non-rotationally symmetric aberrations. There was also a large difference in the induction of coma at 3.5- and 6-mm PDs. Although on average, the amount of spherical aberrations induced was not affected by decentration, the SDs increased with decentration, reflecting high interindividual differences. In all eyes examined, log BCVSOTF decreased asymmetrically as a function of decentration, displaying asymmetric decentration patterns. The obvious relationship between coma and log BCVSOTF in the decentration maps (Figs. 3, 4) was confirmed by regression analysis that revealed a highly significant, numerical impact of coma on log BCVSOTF at both 3.5- and 6-mm PDs. The large discrepancy between decentration tolerance at 3.5- and 6-mm PDs suggests that microdecentrations could be one cause of night vision disturbances in eyes that are asymptomatic under photopic conditions, particularly if center shifts between constricted and dilated pupil are involved.⁸ Indeed, significant amounts of coma have been reported in such symptomatic eyes.^34,35 Another potential reason for a high interindividual variability of symptoms is the compensation of corneal aberrations by the lens.³⁶ Further studies involving ray tracing models will be necessary to investigate the role of internal optics on decentration effects.

Conclusions

Anatomy, optics, function, and subjective perception are key levels in the concept of quality of vision after refractive surgical procedures.³⁷ The model described herein allowed us to investigate decentration tolerance as a novel dimension of the “optics” level in the quality of vision concept. Our calculations reduced possible biases resulting from aberrometer misalignments³⁸ or internal optics so that “pure” WFE changes could be investigated. Although these computations are laborious, an evaluation of decentration effects on novel treatment modalities (e.g., presbyopia-correcting laser profiles³⁹ or new multi-focal intraocular lenses) is now possible. As demonstrated in the context of image quality,³³ it appears logical that different aberrations should interact, affecting decentration tolerance. A limitation of our computational model, however, is that it simulates decentration by pupil shifts rather than by shifts of the treatment zone. Given that some of our treatments were decentered themselves, this could be a problem, especially if different portions of the central cornea yield significantly different biological responses.

Nevertheless, the computational model described in the present study is a powerful and versatile tool for the analysis of decentration effects on refractive outcome. Although based on a small sample of experimental eyes, it allowed us to reach conclusions of potential interest for refractive surgical practice: (1) Decentration of myopic treatments leads to consistent undercorrection of the defocus term and the induction of astigmatism. However, the decentration tolerance of sphere and cylinder (including simulated interaction effects) makes it unlikely that microdecentrations ≤500 μm are a significant cause of residual refractive errors in otherwise asymptomatic eyes. (2) In contrast to effects on LOAs, microdecentrations appear to be a source of HOA-related visual symptoms under mesopic conditions in a proportion of eyes that would be asymptomatic under photopic conditions. (3) Given the intra-and interindividual variability of effects in our model, it appears that only some eyes will experience symptoms in clinical practice. (4) Finally, our results suggest that minimizing the induction of spherical aberration by maximizing the functional optical zone of the cornea⁴⁰ using aspheric ablation pro-files^41,42 or large OZ diameters⁴³ could significantly increase decentration tolerance and by doing so, optimize refractive outcome.