Temporal Data Mining for the Assessment of the Costs Related to Diabetes Mellitus Pharmacological Treatment

Abstract

Diabetes care and chronic disease management represent data-intensive contexts which allow Local Healthcare Agencies (ASL) to collect a huge amount of information. Time is often an essential component of such information, given the strong importance of the temporal evolution of the considered disease and of its treatment. In this paper we show the application of a temporal data mining technique to extract temporal association rules over an integrated repository including both administrative and clinical data related to a sample of diabetic patients. We will show how the method can be used to highlight cases and conditions which lead to the highest pharmaceutical costs. Considering the perspective of a Regional Healthcare Agency, this method could be properly exploited to assess the overall standards and quality of care, while lowering costs.

1. Introduction

Italian local healthcare agencies (ASL) play the crucial role of monitoring health and healthcare expenditures of the Italian population. One of their main interests is to monitor the management of chronic diseases, which have an important socioeconomic impact on the national healthcare system. One of the most prevalent chronic diseases is Diabetes Mellitus (DM). The worldwide prevalence of DM for all age-groups is estimated to be 2.8% in 2000 and 4.4% in 2030¹, while in Italy it is around 4.5%². Worldwide, the annual direct healthcare costs of DM are estimated to be at least 153 billion dollars for the population in the range between 20 and 79 years¹. In Italy DM may cost around 5.17 million € per year, which is about the 6.65% of the total healthcare expenditure. The cost increases up to five times in case of micro and macro-vascular complications². Some Italian ASLs have therefore been implementing data warehouses to collect all the administrative and clinical information that allow to extract the disease patterns of chronic patients, and to support decision makers in improving the overall standards and quality of care, while lowering costs. Data Mining technologies seem particularly useful to perform this task. Rather interestingly, over the last fifteen years several methods and approaches have been devoted to the analysis of DM databases and data repositories. Data mining was used to deal with different tasks: analysis of blood glucose time series^3,4, prediction of metabolic control^5,6, prediction of vascular complications⁷, extraction of DM related risk factors⁸, risk assessment in diabetic foot care⁹, mortality prediction¹⁰, fraud detection and claim abuse¹¹, adverse-event analysis¹². Only in few cases administrative and clinical data have been jointly exploited to extract clinically useful patterns⁸ and there are no reports on the prediction of the most expensive disease patterns. Moreover, a very interesting feature of this data is the importance played by time in the development and treatment of the disease. In this paper we are interested in investigating the application of temporal data mining to highlight cases and conditions which lead to the highest pharmaceutical costs. In particular, our analysis will be focused on data related to a sample of patients suffering from DM which are collected in the central repository of the ASL of Pavia.

2. Methods

The frequent occurrence of relationships between clinical episodes and drug prescriptions can be conveniently mined in large databases through the exploitation of Temporal Association Rules (TARs) extraction techniques. The coupling of such rules with a cost synthesizing the expenditure related to a particular clinical scenario can be very useful for decision support and cost control purposes.

A TAR is defined as an association rule where the antecedent and the consequent are related by a temporal relationship. An example of such a rule could be Total Cholesterol >280 (very high) BEFORE Lipid modifying agents, which tells us that patients found to show a very high value for the total cholesterol will frequently undergo a following prescription of lipid modifying agents within a specific time lag (e.g. 1 year). Our mining algorithm is able to automatically extract such rules from data and it is based on an Apriori-like strategy which selects frequent rules based on thresholds on support and confidence. Herein the support is computed as the number of individuals satisfying a specific rule (in the case of the example the 2.6%), while the confidence represents the probability that a specific patient will experience the consequent given that the antecedent has occurred (here 62%). The algorithm to mine TARs will be detailed in Section 2.1.

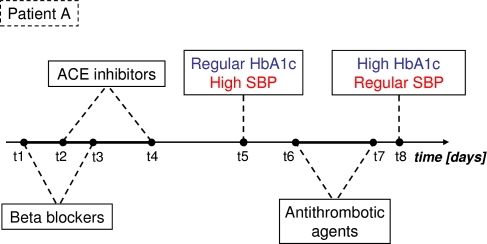
The data repository object of our study has two main features: first, it collects both clinical and administrative data which are by nature heterogeneous and, second, the data are strongly centred on the time dimension. To extract meaningful TARs from such data, the first interesting issue is the integration of both administrative and clinical data in order to obtain an uniform representation. On the one hand, healthcare administrative data are by nature represented by sequences of events. A sequence of events can be defined as a time ordered succession of episodes, where an episode formally identifies a single instance of a specific event. In more detail, each episode: i) represents a single occurrence of an event (e.g. the prescription of a specific drug); ii) is related to a subject (e.g. a specific patient) and iii) is characterized by its temporal coordinates within an observation period. On the other hand, clinical data are usually a set of time series of numeric values (e.g. the time series of blood glucose values). In order to get a representation of these data as temporal sequences of events (Figure 1), we pre-process them to obtain a discretization of the variables defined on the base of thresholds suggested by an expert clinician. For example the variable glycaemia was discretized as follows: “Glycaemia 65–100: regular”, “Glycaemia 100–125: Impaired Fasting Glucose”, “Glycaemia 126–180: high”, etc.

Figure 1.

Example of the integration of events coming from clinical outcomes and drug prescriptions through the uniform representation of temporal sequences.

As concerns administrative data, in the following we will exploit information related to drug prescriptions only. In this case the length of the time interval related to each episode is estimated on the basis of the days of Defined Daily Dose¹³ (DDD). This procedure could however be easily extended also to represent events like hospital admissions or lab tests. Each drug prescription can be associated to a cost, which is extracted from the Italian national pharmaceutical price list (AIFA – Italian National Pharmaceutical Agency¹⁴) which lists the reference prices associated to each drug available on the market.

Given that each rule is satisfied by a number of patients (y) and on a number of different episodes (x) corresponding to the number of boxes sold to the analyzed population, we can compute the average cost per patient (ACP) as follows:

$$\mathit{\text{ACP}}=[{\sum }_{i=1}^x\mathit{\text{cost}}(i)]/y$$

Knowing the confidence of the rule, which represents the probability that one patient will undergo the prescription of the drug given that he shows the clinical picture described in the antecedent, we can calculate the expected cost of a specific rule (EC) as follows:

$$\mathit{\text{EC}}=\mathit{\text{ACP}}\hspace{0.17em}*\hspace{0.17em}\mathit{\text{confidence}}$$

The quantity just defined represents the expenditure that will be related to a specific clinical condition in a period of time specified by the rule parameters.

2.1. The TARs extraction algorithm

In this section we will describe in more detail the rule mining algorithm used in this work. A central issue in this context is the temporal representation of the events¹⁵. The temporal nature of a single episode is strongly dependent on the choice of the temporal granularity, which we define as the maximum temporal resolution used for the representation of each sequence of events¹⁶. In our case, both the pharmaceutical archives and clinical databases store data with a resolution of one day, and as a result, the granularity was set to this value. Following this assumption, the analyzed temporal sequences include hybrid events, implying the presence of both interval-based and point-like events. Events like drug consumption, typically lasting a few days, can be represented as time intervals. Lab tests, performed in correspondence with a medical visit, can be represented simply as time points.

As already mentioned a TAR is defined as a relationship specified through a temporal operator which holds between an antecedent, consisting in a pattern of single or multiple cardinality, and a consequent, consisting in a pattern with single cardinality. Herein a pattern is defined as the occurrence of one or more contemporary events. The allowed temporal relationships are specified by Vilain¹⁷ and Allen’s¹⁸ operators, with the addition of the PRECEDES operator¹⁹. Besides the mentioned temporal operators, the exploited algorithm is provided with three temporal parameters (left shift, right shift and gap) which are used to properly control the mutual distance of the antecedent and the consequent of a rule²⁰. The rules extraction algorithm is designed following an Apriori-like strategy²¹, where the rule search and selection is performed on the basis of thresholds on support and confidence. The support is defined as:

$$\mathit{\text{support}}=\mathit{\text{NPR}}/\mathit{\text{NP}}$$

where NPR is the number of patients verifying the rule, and NP is the total number of patients included in the dataset.

The confidence is defined as:

$$\mathit{\text{confidence}}=\mathit{\text{NPR}}/\mathit{\text{NPA}}$$

where NPA is the number of patients verifying the pattern in the antecedent.

Moreover, the algorithm offers the additional opportunity to select specific rule templates, defining the event classes allowed for the antecedent and the consequent selection respectively. This feature helps to focus the search only on relationships between the members of the classes that the user wants to investigate, and may be particularly useful to present the resulting rules to the users (e.g. clinicians). As a representative example of the method, in this analysis we selected a specific rule template, where the antecedent selection was limited to events representing the discretized clinical variables, and the consequent selection was limited to events of drug prescriptions.

The methodology introduced in this section is then able to automatically highlight all the interesting relationships between the considered healthcare events. Compared to simple querying methods, this algorithm has the advantage to detect also unexpected associations not available into the already existing knowledge.

3. Results and discussion

In this section we present the application of the method to a dataset concerning a subgroup of diabetic patients living in the Pavia area. The analysis was focused on the integration of two databases, containing heterogeneous data. The first database contains clinical data collected by General Practitioners and transmitted to the ASL in order to monitor physiological variables to provide a feedback about the efficacy of the care delivery process. The second database is directly collected by the ASL and contains administrative healthcare data related to drug prescriptions.

The clinical dataset collects data on a selected sample of 1293 diabetic patients. In an observation period of three years (2006–2008) a total of 5715 inspections was recorded, each one characterized by the measurement of physiological parameters related to DM (Table 1).

Table 1.

List of the clinical variables considered for the diabetic patients. Variables assume continuous values within the range reported in square brackets.

Variable	Range	Unit
1. Body Mass Index (BMI)	[10–80]	Kg/m2
2. Systolic Blood Pressure	[60–240]	mmHg
3. Diastolic Blood Pressure	[30–150]	mmHg
4. Glycaemia	[50–500]	mg/dl
5. Glycated Haemoglobin (HbA1c)	[3–20]	%
6. Total Cholesterol	[80–500]	mg/dl
7. HDL Cholesterol	[10–120]	mg/dl
8. Triglycerides	[10–2000]	mg/dl
9. Cardio-Vascular Risk	[0–100]	%

In order to consider also the variable “age” in the analysis, the sample was further stratified into three age classes. The partition of the sample then resulted in the following distributions: 496 (38%) patients are aged in the range 45–65, 497 (39%) in the range 65–75, 300 (23%) are over 75 years old. In our sample the distribution of the most frequent pathologies concurrent to DM is as follows: 678 (52%) patients suffer from hypertension, 493 (38%) suffer from hypercholesterolemia, and 491 (38%) are affected by obesity.

The second dataset includes the administrative process data tracing all the drug prescriptions performed to the diabetic patients since 2006, excluding the over-the-counter drugs whose information is not collected. A drug prescription event is represented through the ATC¹³ (Anatomical Therapeutic Chemical) classification system. The ATC code intrinsically supports a hierarchical classification of the drugs and, according to our purposes, it was truncated to the 3^rd level (e.g. B01A: antithrombotic agents).

The mining step was then separately performed on the three partitions of the integrated databases according to age classes. The analysis was based on the selection of a specific rule template, where the antecedent selection was limited to events representing the discretized clinical variables, and the consequent selection was limited to events of drug prescriptions. The thresholds for minimum support and confidence were set to minsup=0.02 and minconf=0.3. The selection of a low support threshold (2% of the patients satisfying the rule) was oriented to a deep level analysis, in order to underline the most complex and interesting temporal behaviors that characterize very specific subgroup of patients. The value for the confidence threshold was chosen intentionally low in order to evaluate the wide range of possible drug prescriptions which characterize the healthcare delivery process. Since the target of the analysis was the investigation of precedence relationships between clinical patterns and subsequent drug prescriptions, we chose to use the BEFORE temporal operator. The gap parameter, which defines the maximum allowed distance between antecedent and consequent, was set to 365 days. The ultimate goal of our analysis is the estimation of the expected costs related to drug therapy, within a time window of one year, depending on the different combinations of measured physiological parameters.

A first evaluation of the extracted rules allows to detect the most expensive clinical “profiles”, as defined by the antecedent. The results related to the most expensive rules characterized by complex antecedents over the three different age classes are shown in Tables 2–4. The Total Expected Cost (TEC) of one specific antecedent is obtained as the sum of the ECs of each rule showing that particular antecedent.

Table 2.

Synthesis of the most expensive clinical profiles for the class 45–65 years.

Antecedent	#Rules	TEC(€)
-BMI 30–40 (obesity) -SBP 130–160 (mild hypertension) -HbA1c >7.9 (very high)	20	509
-TotChol 120–220 (regular) -HDLChol 40–80 (regular) -Trigl 170–350 (high)	18	478
-SPB 130–160 (mild hypertension) -HbA1c >7.9 (very high)	14	476

Table 4.

Synthesis of the most expensive clinical profiles for the class over-75 years.

Antecedent	#Rules	TEC(€)
-TotChol 120–220 (regular) -HDLChol <40 (low)	24	646
-HbA1c >7.9 (very high) -Trigl 170–350 (high)	11	611
-BMI 20–25 (regular) -HbA1c >7.9 (very high)	13	610

The results highlight that the profiles involving the greatest expected pharmaceutical expenditure are observed for the intermediate 65–75 class. This is explained by the comorbidity increasing with age, and considering that strong drug therapies are not justified for the over-75 class by a significant increase in the life expectancy. Moreover the measurement of an high value of glycated hemoglobin (>7.9) often characterizes the most expensive profiles across the three age classes.

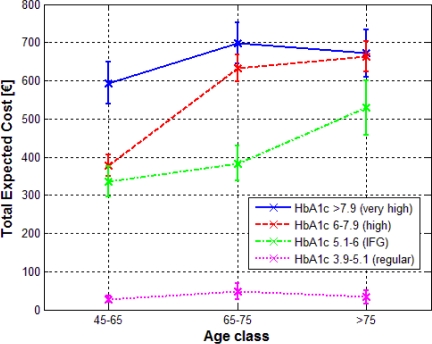
A second evaluation of the application allows to analyze the behavior of the TEC for different intervals of a clinical variable through the different age classes. As a representative example, we will consider the rules involving discretized glycated hemoglobin at the antecedent. Figure 2 represents the average values for the TEC at each level of the considered variable. Vertical lines represent the 95% confidence interval, calculated under the assumption of independency between the costs of each drug typology.

Figure 2.

Total expected cost for different intervals of the glycated hemoglobin (HbA1c) across the age classes. The plot represents the mean values and the 95% confidence interval.

The results highlight a similar behavior of the TEC for each class. The higher is the value of the measured glycated hemoglobin, the higher the expected pharmaceutical expenditures are. This feature then suggests a direct proportionality between the two variables, confirming in our population what was already shown by previous researches on the relationship between glycemic control and diabetes care charges22. Moreover it’s worth to underline the decreasing of the costs associated to “very high” values when shifting from the 65–75 class to over-75 class. This peculiar behavior also gives rise to a decreasing trend in the difference of the expected cost for “high” and “very high” values along the whole age dimension (p<0.05 only for the 45–65 class). Even for diabetic patients over 75 years old, the difference between the expected costs becomes negligible (664€ vs 671€). This behavior then suggests that for the oldest diabetic patients the highest values of glycated hemoglobin don’t have a strong impact on the prescribed drug therapy.

4. Conclusions

The analysis presented in this paper highlights the main potentials of the application of temporal association rules for the mining of healthcare databases. The applied algorithm allows to properly exploit the integration of different healthcare information sources, such as administrative data related to drug prescriptions and clinical data related to the most prevalent chronic pathologies, such as Diabetes Mellitus. The method allowed to highlight cases and conditions which lead to the highest expenditures related to pharmaceutical treatments. Considering the perspective of a Regional Healthcare Agency, this method could be properly exploited to assess the overall standards and quality of care, while lowering costs.

Table 3.

Synthesis of the most expensive clinical profiles for the class 65–75 years.

Antecedent	#Rules	TEC(€)
-BMI 25–30 (overweight) -Glycaemia > 180 (very high) -HbA1c >7.9 (very high)	18	804
-BMI 25–30 (overweight) -SBP 130–160 (mild hypertension) -Glycaemia > 180 (very high) -HbA1c >7.9 (very high)	17	758
-BMI 25–30 (overweight) -SBP 130–160 (mild hypertension) -HbA1c >7.9 (very high)	19	743