Abstract
Evolution at high mutation rates is expected to reduce population fitness deterministically by the accumulation of deleterious mutations. A high enough rate should even cause extinction (lethal mutagenesis), a principle motivating the clinical use of mutagenic drugs to treat viral infections. The impact of a high mutation rate on long-term viral fitness was tested here. A large population of the DNA bacteriophage T7 was grown with a mutagen, producing a genomic rate of 4 nonlethal mutations per generation, two to three orders of magnitude above the baseline rate. Fitness—viral growth rate in the mutagenic environment—was predicted to decline substantially; after 200 generations, fitness had increased, rejecting the model. A high mutation load was nonetheless evident from (i) many low- to moderate-frequency mutations in the population (averaging 245 per genome) and (ii) an 80% drop in average burst size. Twenty-eight mutations reached high frequency and were thus presumably adaptive, clustered mostly in DNA metabolism genes, chiefly DNA polymerase. Yet blocking DNA polymerase evolution failed to yield a fitness decrease after 100 generations. Although mutagenic drugs have caused viral extinction in vitro under some conditions, this study is the first to match theory and fitness evolution at a high mutation rate. Failure of the theory challenges the quantitative basis of lethal mutagenesis and highlights the potential for adaptive evolution at high mutation rates.
THE evolutionary consequences of a high mutation rate are mysterious. It is widely considered that mutations are essential for adaptation, but that the rate maximizing adaptation is far below what can be tolerated (e.g., Trobner and Piechocki 1984; Sniegowski 1997, 2001). In this “twilight zone” of higher-than-optimal mutation rates, the population experiences unique challenges. In one process, the “error catastrophe,” the best genotype is driven out of the population deterministically because the onslaught of viable, mutant genotypes simply overwhelms it (Eigen et al. 1988). With Muller's ratchet, a phenomenon of finite asexual populations, high mutation rates and genetic drift combine to cause loss of the wild-type genome, and the absence of recombination blocks its recreation (Muller 1964); fitness gradually decays as mutations continue their stochastic accumulation. Yet another high mutation rate process is the straightforward, deterministic decline in population fitness as deleterious mutations accumulate (Kimura and Maruyama 1966), leading to extinction if fecundity is too low to compensate (Maynard Smith 1978; Bull et al. 2007).
The problem with our understanding of evolution at a high mutation rate is that it is piecemeal. We do not yet know how to combine these different processes nor do we know their relative importance. For example, the fitness loss at a high mutation rate can be offset both by adaptation and by the error catastrophe, but for realistic models, there is no formal basis for predicting the magnitude of adaptation or even for recognizing an error catastrophe (Bull et al. 2005, 2007). Empirical studies are needed. Several studies of viruses have explored extinction through elevated mutation rate (lethal mutagenesis) (Domingo et al. 2001; Anderson et al. 2004; also see discussion), but they have not been tied to any quantitative model. The practical value of such work is that mutagenic drugs are sometimes used to treat viral infections, yet we do not know how the elevated mutation rate is affecting the virus.
Here we develop an empirical system to enforce viral evolution at a high mutation rate and test theory developed for lethal mutagenesis. A mutagen is applied to the culture in which the DNA bacteriophage T7 is grown, the mutation input per generation is measured on a genomewide scale, and the system is used to observe both molecular and fitness evolution. Comparison of data and theory provides new insights into the process that underlies lethal mutagenesis. However, existing theory must also be modified to address some empirical properties of the system.
Theory of fitness evolution at high mutation rate:
The objective is to develop a theory for data that are readily obtained. The most basic theory requires one population property (the deleterious mutation rate) to predict another population property (mean fitness), but other properties are not predicted. In experimental systems, mean fitness is easily measured, and the deleterious mutation rate can be estimated within bounds. A fully comprehensive model of evolution at a high mutation rate, one predicting full distributions of genotypes, could be developed if mutation rates and fitness effects were known for each individual mutation and for combinations of mutations, including recombination frequencies. However, the full spectrum of mutations and their fitness effects is too vast to allow those measurements in any biological system, so the only applicable theory describes just mean fitness.
If the fitness (e.g., viability) of the mutation-free genotype is assigned the value 1, the mean fitness of an infinite, asexual population at equilibrium is e−U, where U is the genomic deleterious mutation rate (discrete generations) (Kimura and Maruyama 1966). By itself, this result does not indicate whether a population will survive or not, but one simple modification extends the model to address lethal mutagenesis: fecundity. For an asexual population to survive, a minimal condition is that each parent must produce at least one surviving offspring. In the case of a virus, if each infection produces b viable progeny (in the absence of mutation), the inequality be−U < 1 ensures eventual extinction. When this inequality is met, the number of progeny in each generation starts out smaller than the number in the parent generation, so the population size declines (Bull et al. 2007).
This decline in fitness is not due to stochastic effects in small populations; extinction in this model formally requires a finite population, but the effect of deleterious mutations is treated deterministically. Finite population size can contribute to extinction at mutation rates below the threshold (e.g., from Muller's ratchet), but we limit ourselves to nearly infinite population sizes.
A useful property of the model is that the fitness effects of deleterious mutations and their individual rates need not be known, only the overall rate. Yet this elegance of the Kimura–Maruyama result starts to fade when considering empirical reality. The model considers only deleterious mutations, including lethals; neutral mutations are allowed but ignored, and beneficial mutations are not even allowed. Maximum fitness is assigned to the starting, mutation-free genotype, so any mutation that elevates fitness is excluded. Compensatory mutations that ameliorate the effect of deleterious mutations, and thus are beneficial only within mutated genomes, are also not allowed.
To consider a simple model with beneficial mutations, if the initial genotype does not have maximum possible fitness, but a fitness of W relative to the starting genotype is attainable by beneficial mutations (W > 1), then a modified equilibrium is simply We−U relative to a starting fitness of 1.0. In a virus whose initial fitness is b progeny, adaptive evolution could be accommodated in the model by increasing fecundity to B. The extent to which B exceeds b represents the extent to which the initial (wild-type) virus is poorly adapted to the mutagenic environment, which is unknown. Furthermore, this threshold relaxation omits compensatory mutations that ameliorate specific deleterious mutations and neglects any interference of deleterious mutations on the ascent of beneficial ones.
Two further empirical limitations of the Kimura–Maruyama model are evident. Following the onset of an increased mutation rate, the fitness equilibrium may require few or many generations to be approached closely and potentially could require more generations than would be experienced by any real population (Crow and Kimura 1970; Bull and Wilke 2008). The rate of approach depends on the details of the mutation rate and fitness effects, whereas the equilibrium mean fitness does not. We thus attempt to carry out experiments long enough to assume that fitness has neared equilibrium. Second, the Kimura–Maruyama model was developed explicitly for asexuals; the same equilibrium applies with free recombination and no epistasis, but not necessarily when either of these conditions is violated (Maynard Smith 1978; Kondrashov 1982, 1984; Keightley and Otto 2006).
In the Kimura–Maruyama model (Kimura and Maruyama 1966), fitness is measured per discrete generation as relative number of surviving offspring. In our viral study, fitness is measured as a growth rate, essentially the log of fitness in the Kimura–Maruyama model. This discrepancy can be resolved by deriving new results for growth rate, again assuming asexuality. Neglecting viral loss from death and other causes, a model of viral growth rate (r) is given by
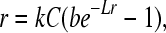 |
(1) |
where C is cell (host) density, k is the adsorption rate of virus to cells, b is burst size (average number of progeny per infected cell), and L is lysis time in minutes (Bull 2006). Cell density is assumed to be constant, and cells always outnumber virus (a condition that can be enforced experimentally). r is an exponential or geometric growth rate: at equilibrium, the number of virus at time t, Nt, as a function of initial density, N0, is given by Nt = ertN0. This model is tailored to the conditions used here, and a model for treatment of a mammalian infection would need to contend with spatial structure and the possibility that the viral population had reached a dynamic equilibrium in which exponential growth no longer applied (see also Steinmeyer and Wilke 2009).
With a deleterious, genomic mutation rate U per generation, the deterministic growth rate of the mutation-free class is simply
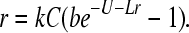 |
(2) |
By assumption, all mutation classes in the population are derived ultimately from the mutation-free class and, because all mutations in U are deleterious (neutral mutations are allowed but not counted), all mutants have slower growth rates than the mutation-free genotype. Back mutations and other forms of beneficial mutations are not allowed. It follows that the growth rate of the entire population at mutation–selection equilibrium is given by (2). This result is convenient because the average population growth rate can be understood from the growth rate of the mutation-free class. It is important to emphasize that the solution to (2) [and (1)] is an equilibrium that may require thousands of generations to be reached. Thus, if the solution is negative (r < 0), implying that the population will ultimately decline, the population may go extinct before attaining approximate equilibrium.
Equation 2 does not lend itself to an explicit solution, but it is easily solved numerically. Although the parameters in (2) are meant to apply across all mutation rates, the reality for any chemical mutagen or drug is that higher doses of mutagen will not only increase U but also directly reduce viral fitness, such as by reducing burst size. To address this issue, parameters should be estimated in the mutagenic environment. In turn, estimating parameters in the mutagenic environment creates the complication that lethal mutations kill progeny and reduce the apparent burst size (when burst size is determined by plaque counts). To overcome this latter problem, we partition the total deleterious mutation rate into the sum of the lethal rate (UX) and the nonlethal rate (Ud), U = UX + Ud, and rewrite Equation 2 as
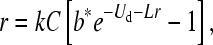 |
(3) |
where 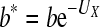 , the viable burst size. Now, the direct effect of mutagen on burst size is inseparable from the effects of lethal mutations.
, the viable burst size. Now, the direct effect of mutagen on burst size is inseparable from the effects of lethal mutations.
Population variation:
An important but subtle implication of the theory is that, when the mutation rate is high, the population will be genetically heterogeneous for deleterious mutations maintained at low to moderate frequencies (Haldane 1927; Crow and Kimura 1970; Eigen et al. 1988). Although every genome may contain many deleterious mutations, different genomes have different sets of deleterious mutations. Only a small proportion of the population may be of the best genotype, in which case, most individuals sampled will have lower fitness than that characterizing the population's growth (Rouzine et al. 2003, 2008). This heterogeneity has the effect of complicating one means of estimating population fitness. When fitness involves component life history parameters such as burst size and lysis time, a fitness calculation based on separate estimates of life history components appears to underestimate actual population fitness. We have observed this effect in unpublished simulations and suspect that it is a parallel to the principle that the average of a ratio is not the ratio of averages. The T7 system that we use here has the advantage that the intrinsic mutation rate of the virus is low. Thus the starting phage and isolates are genetically uniform and are not subject to this problem. Estimation of fitness directly (as population growth rate rather than from separate fitness components) avoids this problem as well.
METHODS
Strains:
IJ1133 [Escherichia coli K-12; F− lacX74 thi-1 (mcrC-mrr)102∷Tn10] was the host used for most adaptations and assays. IJ1133 with plasmid pAR2298 [containing T7 gene 5, cloned under control of the φ10 promoter in the BamHI site of pET1 (Studier 1991)] was used for propagation of the T7Δ5 phage. IJ1200 [K-12 galK150 (Am) cysI53 (Am) trp-49 (Am) adhC thi-1 supF ΔlacX74] with plasmid pT7-17, encoding the T7 tail fiber gene under lac promoter control in pUC18, was used for propagation of the T7Δ17 (tail-fiberless) phage.
T7+ (wild type) was the virus used for the primary adaptation. Its sequence [GenBank AY264774 (Bull et al. 2003)] is the same as that of the original T7 [GenBank V01146 (Dunn and Studier 1983] except for a 1-bp insertion following base 1896 in the nonessential gene 0.6. Alignments were done to V01146, and base positions in the genome use its reference sequence. T7Hi is a T7+ adapted to IJ1133 with a fitness of 47.9, described in Heineman and Bull (2007). T7Δ5 is T7+ deleted for T7 bases 14,156–16,747, with a linker (TTCCGGATCCGG) after base 14,155; it completely removes gene 5 (DNA polymerase) and parts of the nonessential genes 4.7 and 5.3, both of unknown function. T7Δ17 is T7+ deleted for T7 bases 34,552–36,285, with a linker (GAATTCGATATCAAGCTTCTCGAG) after base 34,551. The deletion completely removes gene 17 (tail fiber) and the φ17 promoter.
Growth conditions and fitness assays:
T7+ was evolved by serial transfer on cells in the presence of mutagen. Aliquots of cells were prepared from a large culture of exponentially growing cells, stored at −80°, and thawed shortly before use. Cells were added to 10 ml Luria–Bertani (LB) broth (10 g NaCl, 10 g Bacto Tryptone, 5 g Bacto yeast extract per liter) in a 125-ml flask, grown with aeration (200 rpm) at 37° for 45 min, at which point N-methyl-N′-nitro-N-nitrosoguanidine (NG) was added to 10 μg/ml, and the culture was incubated for another 15 min before phage addition. During passage, the minimum number of phage transferred was 105, and before transfer to the next flask, cultures were allowed to progress until most cells were lysed (a clearing of the culture), which typically required 60–80 min (130 min initially). The generation time was just under 20 min across the adaptation (see results), so a single culture spanned three to four generations. Most phage generations in each culture thus experienced low levels of coinfection, but the final generation was at high multiplicity, allowing recombination (Molineux 2005). Lysed cultures were stored, and the final culture from the passages on one day was used to seed the first culture when transfers were initiated on a subsequent day.
Three lines were created. Line 1, the primary focus of this study, was T7+ carried through 52 passages on IJ1133, or ∼200 generations. Line 2 was T7+ carried through a mere 4 transfers (15 generations) on IJ1133; this line was a replicate of the early evolution of line 1 but, in contrast to line 1, its lysates were not stored in media containing mutagen. It was used to estimate early fitness evolution in the mutagenic environment. The third line was T7Δ5 carried through 25 transfers (100 generations) on IJ1133(pAR2298).
Fitness is measured as the rate of population growth of a phage sample, represented as the number of doublings per hour. This metric provides an absolute measure that is comparable across phages with different generation times. Fitness is calculated as [log2(Nt/N0)]/t, where Nt is the number of phage at time t hours (N0 initially), corrected for dilutions over multiple transfers. The titer for the initial time point of the fitness assay was taken after 30–60 min of phage growth, to allow attainment of a stable “age of infection” distribution at the start of the assay. The final and initial titer time points were typically separated by at least 1 hr. Fitness was assayed under the same conditions used for adaptation (i.e., with mutagen), except that low numbers of phages were transferred (e.g., 103−104) and low phage densities (<107/ml) were maintained throughout the assay. The fitness assays thus matched the assumptions of the growth rate model in (2) and also matched growth conditions for all but the last generation in each flask.
Mutagen:
The mutagen NG acts directly on DNA by methylating oxygen and nitrogen atoms (Gordon et al. 1988, 1990). Following replication of the DNA, the net effect is a strong bias (>90%) for GC  AT transitions, but there is a further bias for particular sequences (Gordon et al. 1990). In theory, NG can act directly on genomes in virus particles, but storage of free virions for up to 5 days in media with NG failed to show an elevated mutation rate (data not shown).
AT transitions, but there is a further bias for particular sequences (Gordon et al. 1990). In theory, NG can act directly on genomes in virus particles, but storage of free virions for up to 5 days in media with NG failed to show an elevated mutation rate (data not shown).
Stocks of NG were dissolved in 100% ethanol at 4 mg/ml and stored at −80°. Fitness values of the same phage isolate were sometimes slightly but significantly affected by the particular NG stock, but the relative fitness differences were similar across different NG stocks. Fitness assays comparing different phages were therefore performed side-by-side with the same NG stock. Fitness assays of genetically heterogeneous stocks were reproducible only when transfer population sizes were at least 103.
Mutation-accumulation lines:
To provide estimates of genomic, viable mutation rates, two mutation-accumulation lines were created, each subjected to 10 single-plaque bottlenecks. In each cycle, phage were grown for a single mutagenic infection cycle and then plated in the absence of mutagen. Host cells were grown for 45 min and exposed to 10 μg/ml NG as described above. Approximately 105 phage were added, and 10 min later the culture was diluted 1:1000 with fresh LB broth containing 10 μg/ml NG, to halt subsequent infections. This culture was grown for 30 min to allow progeny release and plated on IJ1133 without mutagen. A random plaque was then used to found the next generation (tiny plaques that were unlikely to be successfully propagated were avoided once in each line). The outgrowth in a plaque spans approximately four generations and could have favored compensatory mutations or reversions, but because the mutation rate is low on the plate (no mutagen is present) and the number of generations small, we do not consider a serious bias to have been introduced. A study on evolutionary recovery of heavily mutated T7 lines showed that accumulation of compensatory mutations is slow even at large population sizes (Bull et al. 2003).
The 10th-generation plaque was suspended in broth without mutagen. To obtain large amounts of DNA of this genotype, a plate lysate was made to amplify phage while minimizing further evolution. Approximately 103−104 plaque-forming units were added to a single plate, enough to cause clearing of bacteria after a few generations, and the phage were recovered for DNA extraction. Although individual plaques no doubt acquired new mutations during growth on the plate, some of which might have been beneficial, it is unlikely that any mutations arising on the plate became common enough to be observed in a consensus sequence of the DNA pool from the entire plate.
Sequencing of the mutation-accumulation lines used ABI Big Dye mix (version 3.1) and an ABI 3100 sequencer; primers were spaced on the T7 genome at approximately every 500 bases (reads were typically 700 bases). ABI sequence files were aligned to the T7+ genome with Lasergene DNA Star version 8.0.2, and mutations were scored only if abundance of the wild-type base was <10% that of the mutant. Sequence was obtained from ∼85% of the genomes in each line; the calculation of mutations per genome per mutagenic generation was converted to a genome length of 39,937 bp (the genome length of T7+) and divided by 10 (the number of mutagenic generations).
One-step growth curves:
Life history parameters—burst size and lysis time—were measured by standard one-step growth curves. Assays were conducted with phage stocks <3 days old. Cells were grown as for fitness assays for 45 min in 10 ml LB broth, NG was added to 10 μg/ml, and cells were grown a further 15 min to a density of 2–10 × 107/ml. A total of 2 × 106 phage were added to the culture, incubated for 4 min, and then diluted separately by 10−3 and 10−6 into flasks containing LB broth with 10 μg/ml NG to curtail further infections. After an additional 5-min incubation, the culture was titered to obtain total phage density (NT). A portion was also centrifuged to titer free phages in the supernatant (Nf). The density of infected cells was obtained as CI = NT − Nf. The adsorption rate α was calculated from Nf = NTe−4Cα, where C is the cell concentration, with 4 being the adsorption time (minutes). Diluted cultures were plated at various times after phage addition. The burst was calculated as (N30 − Nf)/CI, where N30 was the phage density at 30 min. Average lysis time was considered to be the time at which phage density approximately equaled (N30 − Nf)/2.
Analysis of 454 sequences:
Three goals of sequencing mutated populations were to (i) estimate the input of mutations per generation in a large population sample, (ii) measure the frequency of mutations in the evolved populations, and (iii) have a low background error rate of base substitutions. The first two of these measurements present the same challenge: because most mutations are individually rare, sequences must be obtained from a large number of individual genomes rather than as an average or consensus. Thus sequences from a large number of phage genomes were needed. We used the “454” methodology for most sequencing (University of South Carolina Genomics Core facility, using an LR70). Intact genomic DNA was extracted from populations of interest and sent to the facility; all further processing occurred there.
To obtain DNA from evolved populations, a large sample of the population was used to make a lysate under the same conditions used for passaging (10 μg/ml NG). This lysate served as the source of virions for DNA extraction.
In one method to estimate the input of mutation per mutagenic generation, T7Δ17 was plaque purified and then briefly propagated in LB broth without mutagen on IJ1200 pT7-17, a host supplying the essential phage protein (gp17). The resulting phage were used to infect cells with the same conditions used for passaging (IJ1133 host with no plasmid and LB broth with 10 μg/ml NG media). Growth of T7Δ17 on IJ1133 without plasmid produces particles lacking tail fibers, thus preventing further infection. DNA for sequence analyses was isolated from the particles emerging after cell lysis.
This type of sequencing (454) returns reads of millions of individual strands. For most of the study, reads spanned ∼200 bases, so each read represents only a small portion of one genome. Thus, the characterization of a mutant population is by site rather than by complete, individual genomes. For a sample population, the raw SFF files obtained from the 454 sequencer were imported into DNAStar. Each sequence was trimmed using the automatic medium quality trim setting. Sequences were aligned to the T7+ sequence using the program's suggested parameters (pro assembler default settings except for the following: match space = 15, minimum sequence length = 40, maximum mismatched end bases = 0). When necessary, further manual alignment removed linker sequences and corrected alignments spanning large deletions. Aligned sequences were analyzed with a custom Python script, utilizing the extension module Biopython for text parsing (Cock et al. 2009). As the beginning and the end of individual reads are more prone to errors in base calling, ends were trimmed by 3 bases. This trimming threshold was chosen empirically: stepwise trimming up to 3 bases progressively decreased “anomalous” mutations (non GC 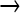 AT) more than the GC
AT) more than the GC 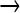 AT mutations expected of NG; further trimming was not applied as it decreased GC
AT mutations expected of NG; further trimming was not applied as it decreased GC 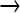 AT as much as other mutations.
AT as much as other mutations.
Mutation frequencies at a site were calculated simply as the number of reads with the mutation divided by the total number of reads at that site. In some cases, mutations were scored only if they fell within a certain frequency interval (e.g., <0.25), and genome positions were then excluded from consideration if the number of reads was insufficient to observe the threshold frequency (e.g., at least four reads are required to score a position for a possible frequency of ≤0.25).
The 454 sequencing protocol is known to experience a common type of error: the length of a homopolymeric tract (e.g., GGGGG) is commonly misread, leading to the erroneous interpretation of a base insertion or deletion (indel). As NG primarily causes base substitutions rather than indels (see above), we ignored short indels by setting the gap penalty to zero for the assembly in DNAStar and counting only base changes. Data presented below also support this neglect of indels.
The 454 data revealed a high incidence of mutations per phage genome, >250 for the endpoint population of the main mutagenic line. To test whether this incidence might be a sequencing artifact, an alternative sequencing method was applied for comparison to the 454 data. From the 200-generation population, 10 plaques were obtained (plated without mutagen) and each was subjected to PCR amplification of parts of the genome. The amplified DNA from each plaque was separately analyzed by dideoxy sequencing. Of 17,797 total bases sequenced from the 10 plaque isolates, 126 mutations were observed for an overall frequency of 7.08 × 10−3 (71 as singletons, 14 as doubles, 4 triples, and 3 mutations present in at least four samples). This corresponds to a rate of ∼280 mutations per genome, indicating that 454 sequencing did not inflate the mutation incidence. Additionally, the base change frequency spectrum obtained by dideoxy sequencing matched closely that observed by 454, with ∼90% being GC 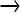 AT, as expected for NG (Gordon et al. 1988). As these sequences were necessarily obtained from viable genomes, the viability of the population with such a high incidence of mutation is not in question.
AT, as expected for NG (Gordon et al. 1988). As these sequences were necessarily obtained from viable genomes, the viability of the population with such a high incidence of mutation is not in question.
RESULTS
T7 was evolved by serial passage in cultures of cells at 10 μg/ml NG for a total of 52 passages (67 hr, or 200 generations). The minimum transfer size was 105. A previous study using frequent population bottlenecks with NG showed that T7 rapidly accumulates mutations and declines in fitness (Hillis et al. 1992; Bull et al. 2003). We therefore expected a substantial accumulation of deleterious mutations and consequent fitness decline, but little fixation of mutations because of the lack of bottlenecks.
The genome of T7 is dsDNA, so its intrinsic mutation rate is low [(Drake et al. 1998; Lynch 2007) amber revision frequencies are around 10−6, for example]. It is thus possible to start with a wild-type stock that is genetically uniform (T7+) that has not been previously exposed to a high mutation rate. Characterization of this initial population in the presence of mutagen yields the parameters that enable prediction of the course of fitness evolution and provides a baseline against which evolution is measured.
The initial, wild-type virus:
Life history parameters and fitness predictions:
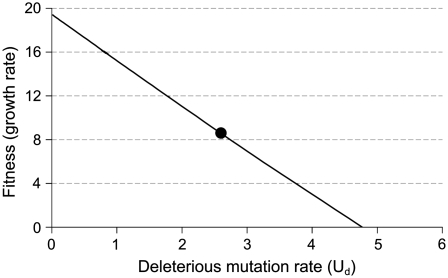
Predicting the fitness equilibrium of the wild-type virus subjected to high U requires separate measures of life history components of the initial phage rather than an overall measure of fitness because mutation is coupled to replication rather than to fitness per se (Bull et al. 2007). In the presence of 10 μg/ml NG, the viable burst of T7+ slightly exceeded 100 (118 ± 17.3). The adsorption rate was ∼2 × 10−9 (2.09 ± 0.04 × 10−9). Lysis time was difficult to quantify precisely because phage release spanned several minutes (no doubt due to the effect of NG on host and phage physiology), but half the final burst size was achieved in ∼18 min. At a cell density of 108/ml, the growth rate calculated from Equation 1 is 19.4 doublings/hr, in reasonable agreement with the direct measure of 18.3 ± 0.37, especially considering the neglect of lysis time variance in the calculations (Heineman and Bull 2007). This equivalence between observed and calculated fitness should apply if the impact of nonlethal, deleterious mutations is low during the first few generations. From these data, it is easy to estimate the long-term, equilibrium fitness for any deleterious mutation rate, Ud (Figure 1).
Figure 1.—
Predicted fitness equilibrium of wild-type T7 at different levels of deleterious mutation. This function is calculated for the parameters observed in the T7 mutagenic environment (10 μg/ml NG). Although there is a single value of Ud that applies in this environment, that value is estimated with uncertainty, so the graph shows the fitness equilibrium across a range of possible values of Ud. The solid circle gives the predicted fitness based on the estimated deleterious mutation rate of 2.6. This graph was calculated from Equation 3 for a viable burst size of 118, lysis time of 18 min, adsorption rate of 2.1 × 10−9, and cell density of 1 × 108/ml.
Mutation input:
The remaining parameter for the predicted fitness equilibrium of T7 is the deleterious genomic mutation rate, Ud. We estimated genomic mutation rates by two methods, both of which involved counting actual mutations in T7 genomes. In one method, wild-type T7 was propagated through 10 cycles of mutation accumulation (plaque-to-plaque transfers), with each plating preceded by a single, mutagenic infection cycle in liquid. The number of mutations per genome should then be ∼10-fold the nonlethal mutation rate, since genomes with lethals cannot form plaques, and the plates did not contain mutagen [the mutation rate for T7, a DNA virus, is expected to be low enough that 10 plaque-to-plaque transfers should not fix a single mutation (Drake et al. 1998; Lynch 2007)]. Estimates from two independent lines were 4.9 and 3.6 (average 4.3) mutations per genome per mutagenic generation. This value is about three orders of magnitude larger than the average value for DNA organisms and thus than the presumed T7 baseline (Drake et al. 1998).
The second method involved measuring the average number of mutations per genome in a population of T7 genomes subjected to a single infection cycle. This method used an otherwise wild-type phage genome that lacked a tail fiber gene, which produces normal particles when grown on a complementing host but emerges uninfective from a noncomplementing host because the virion lacks tail fibers (see methods). Since no selection for viability was applied after mutation, this measure includes lethal and nonlethal mutations. As mutagen-induced mutations are individually rare in the population, it is necessary to subtract the background incidence of errors due to the sequencing method, as estimated from nonmutated, control genomes. This background rate proved to be variable and of similar magnitude to the mutation input itself. Estimates of net mutation input from three separate trials yielded a mean of 6.2 total mutations per genome per generation (11.1 per genome in mutated genomes vs. 3.8 in the control; 7.7 vs. 3.4; and 13.3 vs. 7.2). The controls, consisting of DNA not exposed to mutagen, are affected by sequencing error, by the baseline mutation rate, and by any selectively favored mutations, so they provide an upper limit (perhaps too conservative) on the error rate. Even so, the two approaches yield comparable values; the lower mean from the mutation-accumulation lines (4.3) than of the populationwide estimate (6.2) is consistent with the inclusion of lethals in the latter. We use the former estimate because it is subject to less error and does not require an estimate of the lethal fraction of mutations.
The mutation-accumulation estimate of 4.3 viable mutations per genome per infection includes beneficial, neutral, and viable deleterious mutations, whereas only the latter enters into the fitness prediction from model (3). Studies of three viruses (two with RNA genomes, one with a ssDNA genome) give an average of 0.6 as the fraction of viable mutations that are deleterious: 0.48 for vesicular stomatitis virus, 0.61 for Qβ, and 0.7 for φX174 (Sanjuan et al. 2004; Domingo-Calap et al. 2009). Applying a proportion of 0.6 to the estimate of 4.3 viable mutations per generation in T7, the predicted deleterious rate is ∼2.6. The predicted equilibrium fitness of wild-type T7 in the mutagenic environment is 8.6 doublings/hr (Figure 1), just under half its initial value on this log scale. There is of course considerable variance in the estimate of 0.6 and reason to question whether it even applies to T7 (see discussion), so Figure 1 shows the predicted fitness across the range of possible deleterious mutation rates. However, we are unaware of studies using dsDNA viruses that have measured fitness effects of many individual, random mutations to provide the estimate we need. Note that if only 0.6 of viable mutations are deleterious, the total genomic mutation rate of viable mutations would need to be nearly 8 to cause extinction, neglecting any adaptation to the mutagenic environment (Figure 1).
The 200-generation population:
Fitness increases:
T7 was evolved for ∼200 mutagenic generations maintained at large population size. We therefore expected a substantial accumulation of deleterious mutations and consequent fitness decline, but little fixation of mutations. Whereas the initial fitness in the mutagenic environment was 18.3 ± 0.37, the final fitness was 21.9 ± 0.39, a significant increase of 3.6 [t(4) = 6.7, P ≈ 0.003]. The model of Equation 3 is not even qualitatively supported. Even if we overestimated the deleterious mutation rate, a lower rate is not compatible with a fitness increase. The main plausible explanation for the fitness increase is adaptive evolution, a process that lies outside the model.
Direct evidence that the wild type was not at its fitness maximum in the mutagenic environment is provided by fitness of a phage that had already been adapted to IJ1133 without NG (T7Hi of Heineman and Bull 2007). Its fitness in the mutagenic environment was 21.8 ± 0.52, indistinguishable from the fitness of the 200-generation adapted wild-type T7 line (21.9) and significantly higher than the 18.3 fitness of T7+ 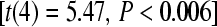 . This result establishes that wild-type T7 has the potential to evolve higher fitness in the NG environment even without exposure to the physiological effects of the mutagen.
. This result establishes that wild-type T7 has the potential to evolve higher fitness in the NG environment even without exposure to the physiological effects of the mutagen.
Average burst size declines:
The average burst size of the evolved population was 23.1 ± 2.8, one-fifth of its initial value. Lysis time (≈18 min) and adsorption rate (1.6 ± 0.2 × 10−9 ml/min) were largely unchanged from initial values, but the variance in lysis time was large enough to thwart accurate estimation of its mean (the data also do not allow a comparison of variances between initial and evolved populations). The main result is clearly the decline in average burst size, supporting a conclusion of a high load of deleterious mutations.
These two results—increased fitness and average burst reduction—appear to be contradictory, and we indeed went to great lengths to determine whether the estimate of burst size was biased or whether the sample of the evolved population was not representative. However, simulations revealed that it is possible to have a combination of mean lysis time and mean burst size maintained by deleterious mutation that is not representative of the population fitness (not shown). Thus, parameterizing Equation 3 with separate estimates of mean life history parameters from a heterogeneous population is not expected to yield the fitness value when estimated directly. At present, therefore, the low average burst size is not qualitatively at odds with the observation of an increased fitness, but a quantitative assessment of these data is needed, perhaps with further resolution of the lysis time mean and variance.
Mutations are plentiful:
Knowing the spectrum and frequency of mutations in the population is useful for understanding evolution at high mutation rates. Data on mutation abundance cannot be used to predict fitness without knowledge of fitness effects of individual mutations (Crow and Kimura 1970), but they can be used for other purposes. When a high overall mutation rate is imposed on a genome that historically experienced a low mutation rate, deleterious mutations are expected to accumulate at different sites in the genome, but individual deleterious mutations are expected to remain relatively rare in the population. Thus genomes may come to contain many mutations, but the identities of those differ between genomes, each genome carrying mutations that are found in only a small fraction of other genomes. Furthermore, the base changes of the deleterious mutations should reflect the mutational spectrum, which for NG is largely GC 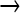 AT. In contrast to the evolutionary behavior of deleterious mutations, beneficial mutations are expected to reach high frequency and will not necessarily reflect the mutational bias of the mutagen.
AT. In contrast to the evolutionary behavior of deleterious mutations, beneficial mutations are expected to reach high frequency and will not necessarily reflect the mutational bias of the mutagen.
The endpoint population at 200 generations was sequenced with 95× coverage. At this coverage, >7500 sites in the genome were polymorphic. The average level of polymorphism, i.e., the average over all sites of 2pq (where p is the site mutation frequency and q the wild-type base frequency), was 0.0125, indicating that two randomly drawn genomes differ at one site in every 80 bases. Under full linkage equilibrium, the chance of two random genomes being identical is <10−210.
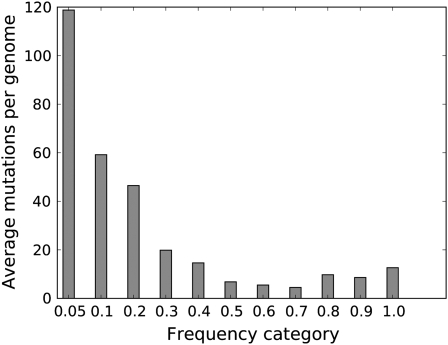
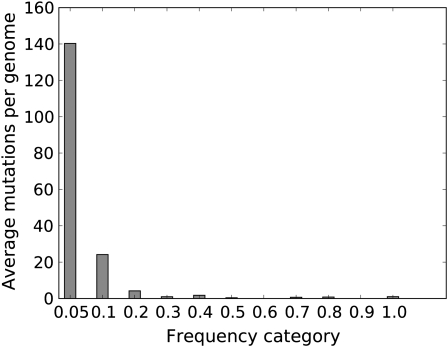
The high coverage enabled partitioning mutations according to their frequencies in the population (Figure 2). On average, genomes carried ∼120 mutations whose frequencies were ≤0.05 and another 60 mutations whose frequencies were between 0.05 and 0.10 (numbers are based on the observed genome size of 38,530, with a deletion in the phage early region). Furthermore, an average of nearly 40 mutations per genome were unique—seen in only one sequence of the sample. Scaling these numbers to a full T7+ genome (39.937 bases), the per-genome average number of mutations at frequency ≤0.25 is 245. For comparison, the average numbers of mutations whose frequencies were <0.25 observed in “control” DNA genomes, not subjected to mutagenesis, were 3.8, 3.4, and 7.2 per T7 equivalent, in different replicates.
Figure 2.—
Observed number of sites in the T7 genome with mutations at different frequencies (200 generations, 95× coverage of the genome). Sequences were obtained from only short regions (200 bases), so these calculations of per genome numbers of mutations are simply products of the mutation frequency at each site summed across all sites (they thus assume linkage equilibrium among different mutations). Numbers apply to the observed genome size of 38,530. Each bar indicates the number of mutations whose frequencies were less than or equal to the label, down to the frequency of the bar to its left.
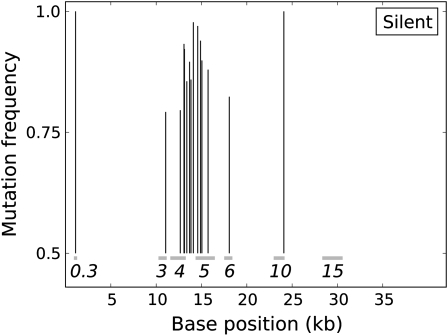
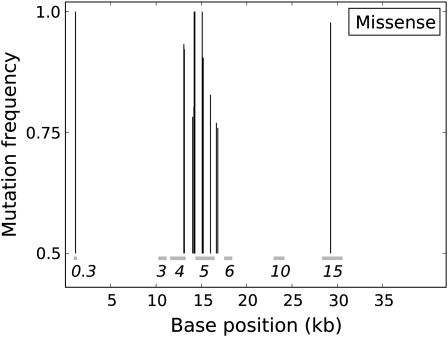
There was a progressive decline in numbers of nucleotide positions with higher mutation frequencies, up to a frequency of 0.5, beyond which mutation abundance began to increase. Fully 28 mutations in the population had frequencies of ≥0.75 (54 sites with mutation frequencies >0.5), those possibly representing adaptive changes or boosted to high frequency by virtue of being closely linked to adaptive changes (Figure 3). Of those at frequency ≥0.75, most were in the DNA polymerase (DNAP) gene 5 or in adjacent DNA metabolism genes (genes 3, 4, and 6). The association of adaptive changes with DNAP is not surprising, given that the mutagen alters nucleotide pools in the cell and interferes with genome replication, possibly in multiple ways (Gordon et al. 1988).
Figure 3.—
T7 genome positions of all mutations at frequencies of ≥0.75 (200 generations), distinguished by silent (top) and missense changes (bottom). Each mutation is represented by a vertical line, with the height representing the observed frequency. The position of the vertical line along the horizontal axis gives its genomic location, and horizontal bars indicate the locations of genes, identified by gene number. Genes 3, 4, 5, and 6 encode DNA metabolism genes of endonuclease, helicase/primase, DNA polymerase, and exonuclease, respectively. Genes 10 and 15 encode the major capsid protein and a virion internal core protein, respectively. The total number of high-frequency mutations is 28, with 23 in the cluster spanning genes 4–6 (inclusive). Some lines are too close together to be separable.
We observed 7642 sites in the genome with mutations whose frequencies in the population did not exceed 0.25; 90% were GC 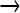 AT, the predominant type known for NG. For the 54 mutations in the high-frequency classes (≥0.5), 96% were GC
AT, the predominant type known for NG. For the 54 mutations in the high-frequency classes (≥0.5), 96% were GC 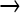 AT, not significantly different from the value for low-frequency mutations. This equivalence of mutation bias between presumably adaptive substitutions and deleterious mutations would not have been predicted, but is not implausible.
AT, not significantly different from the value for low-frequency mutations. This equivalence of mutation bias between presumably adaptive substitutions and deleterious mutations would not have been predicted, but is not implausible.
The T7 genome contains nearly 60 genes, but only about one-third of them, representing ∼70% of the genome length, are essential for growth in broth (Molineux 2005). Since the vast majority of mutations in the endpoint population have persisted for multiple generations and their frequencies were thus modified by selection, it is expected that (i) missense mutations will be less common than silent mutations and (ii) this bias will be strongest for essential genes. The observed number of missense and silent mutations in essential and nonessential genes was calculated for all mutations whose frequencies did not exceed 0.25.
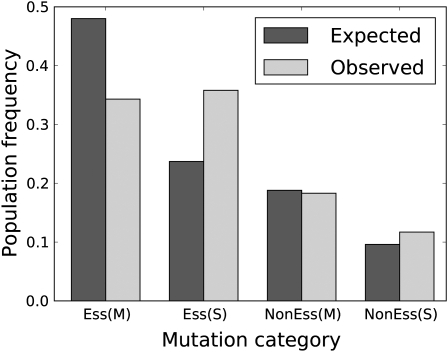
To generate a null expectation in the absence of selective differences among these categories, a simulation was conducted in which the observed mutation spectrum was applied across the T7 genome and adjusted for deletions, and the numbers of missense and silent changes were calculated for essential and nonessential genes; these numbers were then scaled so that the total expected mutations equaled the total observed mutations (Figure 4). Across the genome, observed missense changes in essential genes were indeed lower than expected by more than one-third. However, the paucity of missense changes in essential genes was almost fully compensated by silent changes in essential genes, so that the observed fraction of all mutations in essential genes (0.701) was nearly the expected fraction (0.717, corrected for the observed deletions of nonessential genes). This equivalence is not expected, because the difference should also be spread over nonessential genes. There also appears to be slightly greater selection against missense than silent changes in nonessential genes, but not nearly to the extent as in essential genes (many nonessential genes have important functions).
Figure 4.—
Expected and observed fractions of silent (S) and missense (M) mutations in essential (Ess) vs. nonessential (NonEss) genes at 200 generations. The expectations were generated by assigning the observed mutation spectrum throughout the genome and scaling the total number of expected mutations to equal the total observed. The total number of mutations is 7,642 and counts only those whose frequencies were ≤0.25. From left to right, expectations are 0.480, 0.237, 0.188, and 0.096.
Intermediate populations:
A fitness increase cannot occur if all mutations are deleterious, so some mutations in T7 must have been beneficial and risen to high frequency. To separate processes of adaptive evolution and deleterious mutation accumulation, we considered the theoretical result that beneficial mutations typically require hundreds or thousands of generations to reach high frequency [on the assumption that fitness effects are not large (Haldane 1927; Crow and Kimura 1970)], whereas the impact on mean fitness of highly deleterious and moderately deleterious mutations occurs rapidly. If much of the mutational load in this system is due to moderate-effect and large-effect deleterious mutations, the mutagenized line might have experienced a substantial decline in fitness early, before adaptation led to recovery at 200 generations. Fitness was measured at two additional times, 4 transfers (≈15 generations) and 21 transfers (≈80 generations). There was no significant difference in fitness between the wild-type ancestor and the population at 15 generations, but a slight and marginally significant decrease at 80 generations [1.2 doublings/hr lower than wild type, t(6) = 2.1, P ≈ 0.04, one-tailed]. This slight decline is consistent with our expectation of a (partial) temporal separation of adaptive and deleterious evolution, but the decline does not approach the magnitude expected at equilibrium in the absence of adaptation.
In addition, genomes were sequenced from the 80-generation population. The average load of mutations was 148 per full-sized genome (frequencies ≤0.25, an average of 175 per genome, when counting all mutations), moderately lower than the 245 observed at the endpoint (at only 6×, the coverage at 80 generations was too low to partition mutations into different frequency groups). Thus, while the endpoint population at 200 generations does not formally represent the equilibrium load, this comparison indicates that the number of mutations per genome was accumulating less than linearly with time.
The comparison of high-frequency changes between 80 and 200 generations is also interesting. At generation 200, 28 mutations had reached a frequency of ≥0.75. By generation 80, 5 mutations had reached a frequency of 0.75 (8 had reached 0.5), but only 2 of them were among the 28 at generation 200.
Blocking evolution of DNA polymerase does not lead to fitness decline:
The extreme clustering of apparently adaptive substitutions in and around the DNAP gene may indicate that much of the fitness gain during this adaptation could be prevented if evolution of the DNAP gene was blocked. A parallel, mutagenic passage was thus undertaken with T7Δ5, a T7 genome deleted in the region spanning the 3′ half of gene 4.7 through most of gene 5.3, thus preventing evolution in a contiguous set of genes containing 16 (57%) of the presumed adaptive substitutions in the 200-generation population (those at frequency ≥0.75). T7Δ5 is not viable on normal hosts but is readily propagated on hosts carrying the DNAP gene on a plasmid.
This passage was carried through 25 transfers (35 hr, ≈100 generations), under conditions otherwise the same as for the T7+ line. Because the phage must be complemented in trans (and the phage cannot acquire the DNAP gene by recombination with the plasmid), there is no expectation that it will have the same fitness as T7+, but a comparison between the starting and the evolved populations should reveal a fitness decrease if deletion of the polymerase gene blocks most of the adaptation to NG. Yet there was no significant change in fitness during growth in the mutagenic environment (11.7 ± 0.30 initially, and 12.5 ± 0.75 at 100 generations).
Furthermore, the sequence evolution of this phage is also broadly compatible with that of the T7+ line. The incidence of mutations at 100 generations (181 per full genome, ≤0.25) was less for the Δ5 line than for the T7+ line at 200 generations but greater than that of the T7+ line at 80 generations. The distribution of mutations by frequency category is clustered somewhat more at the low end for T7Δ5 at 100 generations than for T7+ at 200 generations (cf. Figure 5 and Figure 2), as expected because there was less time for mutations to ascend. The average polymorphism of T7Δ5 was about three-fourths that of the T7+ line at 200 generations (0.0093). Only three mutations exhibited frequencies >0.5, and one of those was the mutation in gene 10B that evolves in many T7 adaptations, which cannot be attributed to adaptation to a mutagenic environment. Overall, therefore, there is no basis for considering the two adaptations to be fundamentally different with respect to the accumulation of mutations or the fitness consequences of evolution at high mutation rate.
Figure 5.—
Observed number of sites in the T7Δ5 genome with mutations at different frequencies (100 generations, 152× coverage of the population). Approximately 28 mutations per genome were unique, seen in only one sequence, so the higher number of mutations in the 0.05 category compared to that in the 200-generation population of T7+ is not due to the higher coverage identifying more singletons. Numbers apply to the observed genome size of 37,337. Otherwise as in Figure 2.
The failure of this phage to decline in fitness seems contrary to the molecular evidence of adaptation of the T7+ line. The comparison is not so straightforward, however. First, the fitness of the initial T7Δ5 is considerably lower than that of T7+, so there may be ways the former could adapt that would not have been observed in the T7+ line. Second, the T7+ line showed only a modest increase in fitness from generation 80 to 200, yet it was that interval in which the DNA metabolism mutations rose to high frequencies. It is thus possible that the high-frequency mutations give a distorted view of adaptive changes in the T7+ line. Nonetheless, the result from T7Δ5 is unexpected and warrants further resolution.
DISCUSSION
This study provides the most comprehensive match to date of theoretical and empirical analyses of evolution at high mutation rates. After 200 generations in a mutagenic environment, the DNA virus T7 accumulated polymorphisms at >7500 sites in its genome, with a per genome average of nearly 250 low-frequency mutations (≤25% frequency). Despite this load, fitness increased from an initial 18.3 doublings/hr to 21.9, well above the predicted fitness equilibrium of 8.6 based on the estimated deleterious mutation rate of 2.6. The increase in fitness is in qualitative disagreement with the quantitative theory applied. The discrepancy likely reflects substantial adaptive evolution, a conclusion supported by the endpoint population containing 28 high-frequency mutations clustered mostly in DNA polymerase and other DNA metabolism genes.
Fitness did not evolve as expected, but other properties of the 200-generation, evolved population matched qualitative expectations: a high level of polymorphisms and a low average burst size (one-fifth of the initial one). Missense mutations in essential genes were underrepresented, relative to other mutations. These results support the view that the population experienced a sustained, high mutation rate (cf. Ojosnegros et al. 2008). Thus any explanation for the failed fitness predictions must be compatible with a high mutation rate. Adaptive evolution seems the most plausible explanation and is the only one to explain a fitness increase, but it is also possible that our equilibrium prediction of 8.6 doublings/hr is too low and thus that the discrepancy between observed and predicted is not as large as we report.
One possibility is that we overestimated the deleterious mutation rate, Ud, both because of error in the estimate of the total viable mutation rate and because the estimated fraction of nonlethal, deleterious mutations (0.6) from three other viruses may not apply to T7. Those three viruses all have genomes <12 kb and are single stranded, two have RNA genomes, and one has a ssDNA genome, but they are the only viruses for which direct estimates of this quantity have been given. The equilibrium with a deleterious mutation rate <2.6 is easily calculated, once the rate is known (Figure 1). A second possibility stems from recombination, which operated in the T7 population. Recombination can enhance fitness when deleterious mutations exhibit a certain type of epistasis (Kondrashov 1982, 1984) and can enhance fitness from stochastic effects of genetic backgrounds experienced by newly arising, beneficial mutations (Keightley and Otto 2006). Thus, the fitness effect of the genetic load with recombination may not be as extreme as predicted by Equation 3, which assumes asexuality. However, the quantitative effects of recombination are not easily predicted.
Although we were attempting to assess fitness evolution in a population surviving at a high mutation rate, the study is directly relevant to extinction by mutagenesis (Domingo et al. 2001; Anderson et al. 2004). We may consider how closely T7, in the mutagenic environment, approached the extinction threshold. In the absence of adaptive evolution and with a viable burst size, adsorption rate, and lysis time (118, 2.1 × 10−9 ml/min, 18 min), the model in (3) prescribes that a rate of 4.8 nonlethal, deleterious mutations per genome per generation would cause eventual extinction. The total viable genomic mutation rate measured was just under this threshold (4.3), so to achieve a deleterious rate that high requires elevating the total rate by the reciprocal of the deleterious fraction. With a deleterious fraction of 0.6, the elevation required is nearly twice what we achieved (8 mutations per generation); if the deleterious fraction is only 0.2, extinction requires 24 mutations per generation.
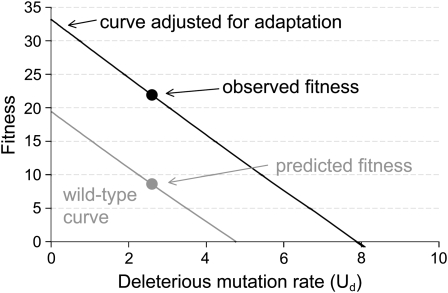
These calculations neglect adaptation of T7+ to the mutagenic environment. The observed fitness was 13.3 doublings/hr higher than predicted (21.9 instead of 8.6). If this “extra” fitness is attributed to adaptation, the extinction threshold should be recalculated: adjusting the burst size to achieve a fitness of 21.9 when the deleterious mutation rate is 2.6 (using the model underlying Figure 1), the extinction threshold increases to nearly 8 deleterious mutations per genome per generation instead of 4.8 (Figure 6). Furthermore, if only 60% of viable mutations are deleterious, extinction requires a total genomic mutation rate of nearly 13 total viable mutations per genome per generation, more than three times the rate we achieved. Given the uncertainty in the estimate of 0.6, there is a wide range of possibilities. Nonetheless, it is clear that (i) extinction would have required a substantial increase in mutation rate above what we achieved and (ii) adaptation elevated the threshold by nearly a factor of 2. If the deleterious fraction of mutations in large viral genomes proves to be ≪0.6, extinction through lethal mutagenesis might be effectively unattainable.
Figure 6.—
Predicted fitness equilibrium of wild-type T7 at different levels of deleterious mutation, showing both the prediction based on wild-type virus parameters (shaded lower line, from Figure 1) and the prediction based on the observed, evolved fitness at 200 generations (solid upper line). The upper line uses the lysis time and adsorption rate values estimated from wild type, as in the lower line, but uses a burst size that has been adjusted so that fitness matches the observed 21.9 when the deleterious mutation rate is 2.6. The shaded and solid circles show the predicted and observed fitnesses for a mutation rate of 2.6. The upper curve is merely parameterized with a hypothetical burst size that forces its fit to the observed fitness.
An inescapable conclusion from our study is that estimation of the parameters needed to fully quantify lethal mutagenesis is difficult. Even in our easily manipulated experimental system, estimates of one critical quantity (the proportion of deleterious viable mutations) had to be borrowed from unrelated model systems, and one property (the degree of adaptation) had to be observed post hoc. We succeeded in estimating life history parameters and total mutation input per generation, quantities central to the calculations, chiefly because of the uniform conditions afforded by the in vitro system. Attempts at lethal mutagenesis on patients will not have the luxuries enjoyed here, and efforts to fit theory to actual treatment will be seriously hampered. Thus, in addition to providing insight into the empirical issues underlying lethal mutagenesis, our study reveals the challenges that must be overcome to do so.
Many empirical studies of lethal mutagenesis have illustrated the basic essentials, that mutations accumulate and, in some cases, that in vitro populations can be driven to extinction (e.g., Domingo et al. 2001; Graci and Cameron 2002; Grande-Perez et al. 2002; Cases-Gonzalez et al. 2008; Martin et al. 2008; Ojosnegros et al. 2008). An early precedent for measuring viral viability and mutation level is that of Crotty et al. (2001). Our study has now achieved quantitative testing of predicted fitness evolution, with estimation of relevant parameters. Yet given the difficulties of making these measurements, we may ask whether there is a benefit to such quantitative efforts, especially when lethal mutagenesis can be made to work under some conditions.
The main relevance of quantitative studies is to treatments that do not clear the virus. One key issue in such failures is whether the initial mutagenic treatment, and even the continuation of treatment, impairs or enhances the virus. We have shown here that adaptation can occur despite a high mutation rate, yet the adapting genome also accumulates many deleterious mutations. If a high mutation rate accelerates adaptation, then the mutagen augments conflicting evolutionary processes—adaptive and degenerative evolution. In these cases, it is important and nontrivial to disentangle the opposing processes to reveal the net impact of the mutagen. More generally, a quantitative understanding of evolution at a high mutation rate is needed to know how to modify treatment to achieve clearance. Such studies may help identify types of viruses that are amenable to successful lethal mutagenesis.
Acknowledgments
We thank W. Studier for strains and Adam Stell for construction of the pT7-17 plasmid and the deletion phage T7Δ17. We thank Rafa Sanjuan, Marta Wayne, and Claus Wilke for useful comments on the manuscript and Claus Wilke for advice on the study. This work was funded by National Institutes of Health grants GM 57756 to J.J.B. and GM 32095 to I.J.M. J.J.B. also receives support from the Miescher Regents Professorship at the University of Texas.
References
- Anderson, J. P., R. Daifuku and L. A. Loeb, 2004. Viral error catastrophe by mutagenic nucleosides. Annu. Rev. Microbiol. 58 183–205. [DOI] [PubMed] [Google Scholar]
- Bull, J. J., 2006. Optimality models of phage life history and parallels in disease evolution. J. Theor. Biol. 241(4): 928–938. [DOI] [PubMed] [Google Scholar]
- Bull, J. J., and C. O. Wilke, 2008. Lethal mutagenesis of bacteria. Genetics 180 1061–1070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bull, J. J., M. R. Badgett, D. Rokyta and I. J. Molineux, 2003. Experimental evolution yields hundreds of mutations in a functional viral genome. J. Mol. Evol. 57(3): 241–248. [DOI] [PubMed] [Google Scholar]
- Bull, J. J., L. A. Meyers and M. Lachmann, 2005. Quasispecies made simple. PLoS Comput. Biol. 1 e61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bull, J. J., R. Sanjuan and C. O. Wilke, 2007. Theory of lethal mutagenesis for viruses. J. Virol. 81(6): 2930–2939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cases-Gonzalez, C., M. Arribas, E. Domingo and E. Lazaro, 2008. Beneficial effects of population bottlenecks in an RNA virus evolving at increased error rate. J. Mol. Biol. 384(5): 1120–1129. [DOI] [PubMed] [Google Scholar]
- Cock, P. J., T. Antao, J. T. Chang, B. A. Chapman, C. J. Cox et al., 2009. Biopython: freely available Python tools for computational molecular biology and bioinformatics. Bioinformatics 25(11): 1422–1423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crotty, S., C. E. Cameron and R. Andino, 2001. RNA virus error catastrophe: direct molecular test by using ribavirin. Proc. Natl. Acad. Sci. USA 98 6895–6900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crow, J. F., and M. Kimura, 1970. An Introduction to Population Genetics Theory. Harper & Row, New York/Evanston, IL/London.
- Domingo, E., C. K. Biebricher, M. Eigen and J. J. Holland, 2001. Quasispecies and RNA Virus Evolution: Principles and Consequences. Landes Bioscience, Georgetown, TX.
- Domingo-Calap, P., J. M. Cuevas and R. Sanjuan, 2009. The fitness effects of random mutations in single-stranded DNA and RNA bacteriophages. PLoS Genet. (in press). [DOI] [PMC free article] [PubMed]
- Drake, J. W., B. Charlesworth, D. Charlesworth and J. F. Crow, 1998. Rates of spontaneous mutation. Genetics 148 1667–1686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunn, J. J., and F. W. Studier, 1983. Complete nucleotide sequence of bacteriophage T7 DNA and the locations of T7 genetic elements. J. Mol. Biol. 166(4): 477–535. [DOI] [PubMed] [Google Scholar]
- Eigen, M., J. McCaskill and P. Schuster, 1988. Molecular quasi-species. J. Phys. Chem. 92 6881–6891. [Google Scholar]
- Gordon, A. J., P. A. Burns and B. W. Glickman, 1988. N-methyl-N′-nitro-N-nitrosoguanidine-induced mutation in a RecA strain of Escherichia coli. Mutat. Res. 201(1): 219–228. [DOI] [PubMed] [Google Scholar]
- Gordon, A. J., P. A. Burns and B. W. Glickman, 1990. N-methyl-N′-nitro-N-nitrosoguanidine induced DNA sequence alteration; non-random components in alkylation mutagenesis. Mutat. Res. 233(1–2): 95–103. [DOI] [PubMed] [Google Scholar]
- Graci, J. D., and C. E. Cameron, 2002. Quasispecies, error catastrophe, and the antiviral activity of ribavirin. Virology 298(2): 175–180. [DOI] [PubMed] [Google Scholar]
- Grande-Perez, A., S. Sierra, M. G. Castro, E. Domingo and P. R. Lowenstein, 2002. Molecular indetermination in the transition to error catastrophe: systematic elimination of lymphocytic choriomeningitis virus through mutagenesis does not correlate linearly with large increases in mutant spectrum complexity. Proc. Natl. Acad. Sci. USA 99 12938–12943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haldane, J. B. S., 1927. A mathematical theory of natural and artificial selection. Part V. Selection and mutation. Proc. Camb. Philos. Soc. 23 838–844. [Google Scholar]
- Heineman, R. H., and J. J. Bull, 2007. Testing optimality with experimental evolution: lysis time in a bacteriophage. Evolution 61 1695–1709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hillis, D. M., J. J. Bull, M. E. White, M. R. Badgett and I. J. Molineux, 1992. Experimental phylogenetics: generation of a known phylogeny. Science 255(5044): 589–592. [DOI] [PubMed] [Google Scholar]
- Keightley, P. D., and S. P. Otto, 2006. Interference among deleterious mutations favours sex and recombination in finite populations. Nature 443(7107): 89–92. [DOI] [PubMed] [Google Scholar]
- Kimura, M., and T. Maruyama, 1966. The mutational load with epistatic gene interactions in fitness. Genetics 54 1337–1351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kondrashov, A. S., 1982. Selection against harmful mutations in large sexual and asexual populations. Genet. Res. 40(3): 325–332. [DOI] [PubMed] [Google Scholar]
- Kondrashov, A. S., 1984. Deleterious mutations as an evolutionary factor. 1. The advantage of recombination. Genet. Res. 44(2): 199–217. [DOI] [PubMed] [Google Scholar]
- Lynch, M., 2007. The Origins of Genome Architecture. Sinauer Associates, Sunderland, MA.
- Martin, V., A. Grande-Perez and E. Domingo, 2008. No evidence of selection for mutational robustness during lethal mutagenesis of lymphocytic choriomeningitis virus. Virology 378(1): 185–192. [DOI] [PubMed] [Google Scholar]
- Maynard Smith, J., 1978. The Evolution of Sex. Cambridge University Press, Cambridge, UK.
- Molineux, I., 2005. The T7 group, pp. 277–301 in The Bacteriophages, edited by R. Calendar. Oxford University Press, London/New York/Oxford.
- Muller, H. J., 1964. The relation of recombination to mutational advance. Mutat. Res. 1 2–9. [DOI] [PubMed] [Google Scholar]
- Ojosnegros, S., R. Agudo, M. Sierra, C. Briones, S. Sierra et al., 2008. Topology of evolving, mutagenized viral populations: quasispecies expansion, compression, and operation of negative selection. BMC Evol. Biol. 8 207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouzine, I. M., J. Wakeley and J. M. Coffin, 2003. The solitary wave of asexual evolution. Proc. Natl. Acad. Sci. USA 100 587–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouzine, I. M., E. Brunet and C. O. Wilke, 2008. The traveling-wave approach to asexual evolution: Muller's ratchet and speed of adaptation. Theor. Popul. Biol. 73(1): 24–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanjuan, R., A. Moya and S. F. Elena, 2004. The distribution of fitness effects caused by single-nucleotide substitutions in an RNA virus. Proc. Natl. Acad. Sci. USA 101(22): 8396–8401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sniegowski, P., 1997. Evolution: setting the mutation rate. Curr. Biol. 7(8): R487–R488. [DOI] [PubMed] [Google Scholar]
- Sniegowski, P., 2001. Evolution: constantly avoiding mutation. Curr. Biol. 11(22): R929–R931. [DOI] [PubMed] [Google Scholar]
- Steinmeyer, S. H., and C. O. Wilke, 2009. Lethal mutagenesis in a structured environment. J. Theor. Biol. 261(1): 67–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Studier, F. W., 1991. Use of bacteriophage T7 lysozyme to improve an inducible T7 expression system. J. Mol. Biol. 219(1): 37–44. [DOI] [PubMed] [Google Scholar]
- Trobner, W., and R. Piechocki, 1984. Selection against hypermutability in Escherichia coli during long term evolution. Mol. Gen. Genet. 198(1): 177–178. [DOI] [PubMed] [Google Scholar]