Dynamic Principles of Gait and Their Clinical Implications

Abstract

A healthy gait pattern depends on an array of biomechanical features, orchestrated by the central nervous system for economy and stability. Injuries and other pathologies can alter these features and result in substantial gait deficits, often with detrimental consequences for energy expenditure and balance. An understanding of the role of biomechanics in the generation of healthy gait, therefore, can provide insight into these deficits. This article examines the basic principles of gait from the standpoint of dynamic walking, an approach that combines an inverted pendulum model of the stance leg with a pendulum model of the swing leg and its impact with the ground. The heel-strike at the end of each step has dynamic effects that can contribute to a periodic gait and its passive stability. Biomechanics, therefore, can account for much of the gait pattern, with additional motor inputs that are important for improving economy and stability. The dynamic walking approach can predict the consequences of disruptions to normal biomechanics, and the associated observations can help explain some aspects of impaired gait. This article reviews the basic principles of dynamic walking and the associated experimental evidence for healthy gait and then considers how the principles may be applied to clinical gait pathologies.

Although walking poses little challenge to individuals who are healthy, those with gait pathologies such as hemiparesis, spinal cord injury, or amputation can find it tiring and difficult. Pathological gait, for example, can require twice the metabolic energy of healthy gait.^1,2 It also can present neuromotor control challenges, such as to maintain balance or even to produce the gait pattern itself.^3,4 These issues are addressed, in part, with gait rehabilitation, where the course of treatment relies heavily on the expertise of the individual caregiver. This experience may require long practice to gain and, once gained, may be difficult to disseminate.⁵ Consistency and quality of rehabilitation might be enhanced by the application of fundamental principles supported by evidence. Here we examine some basic principles underlying the mechanics and control of gait, along with potential clinical ramifications.

A reasonable focus for gait rehabilitation—via therapy or assistive devices—is the recovery of mechanisms that reduce metabolic cost and increase stability. It is thus helpful to determine the mechanisms that underlie the metabolic cost and stability of healthy walking and to consider how they may be compromised by various pathologies. The purpose of this perspective is to review some of the important theoretical frameworks underlying healthy walking mechanics and how they might be applied to understand pathological gait. (To translate the principles presented here to walking in children with cerebral palsy, see Damiano et al⁶ in this issue.) We will focus on an approach termed dynamic walking, explaining some of its underlying principles, findings, and applications to clinical practice. (To compare and contrast dynamic walking with performance on elliptical training devices, refer to Burnfield et al.⁷) To put this approach in context, we begin by reviewing 2 historically important but contrasting paradigms—the “six determinants of gait” theory and the inverted pendulum model.

The “Six Determinants of Gait” Theory

One of the most influential and longest-standing theories of gait was that proposed by Saunders et al,⁸ often referred to as the “six determinants of gait.” The six determinants are kinematic features—for example, the rotation of the pelvis and the pattern of stance-phase knee motion—thought to contribute to economical locomotion. Underlying the kinematics are 2 hypothesized goals, the first concerning minimization of metabolic energy expenditure: “Fundamentally, locomotion is the translation of the center of gravity through space along a pathway requiring the least expenditure of energy.”8(p558) The second concept is that “minimizing the amount that the body's center of gravity is displaced from the line of progression is the major mechanism for reducing the muscular effort of walking, and consequently, saving energy.”9(p40)

For more than 40 years, the “six determinants of gait” theory was accepted nearly as fact.¹⁰ It was not until the late 1990s that researchers began to measure and quantify the kinematic features. The first kinematic feature to be examined was pelvic list—the frontal-plane tilt of the pelvis during single-limb support—which was found to have virtually no effect on the vertical excursion of the trunk.¹¹ The same team later examined stance-phase knee flexion, which was found not to contribute significantly to reduction of vertical displacement. This was followed by measurement of pelvic rotation about the vertical axis, which was found to have little effect on smoothing the body center of mass (COM) trajectory.¹² Reconsideration of all six determinants shows that some of the kinematic features do reduce COM displacement, but others appear to increase it.¹³ Although there may well be other aspects of the COM motion that are important to walking, there is little experimental evidence that humans seek to minimize its displacement.

Other studies also have examined the hypothesized link between COM displacement and metabolic energy expenditure. Three studies showed that walking with voluntarily reduced displacement causes energy expenditure to increase.^14–16 They also showed that the greater the reduction in displacement, the greater the energetic cost, with maximum reduction in displacement leading to a doubling or more of energy expenditure. The experimental evidence suggests that it is energetically costly to minimize vertical COM displacement.

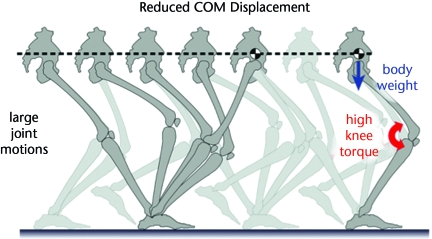
The high cost of low COM displacement can be explained by several contributions. Many of the joints must undergo greater excursions during single-limb support if the COM is to be kept on a level path (Fig. 1). This is most evident at the knee, which must flex and extend substantially through each single-limb–support phase, with the greatest flexion occurring at mid stance.¹⁷ One consequence of mid-stance knee flexion is the need for greater torque from knee extensors to support the body, with peaks more than 3 times higher than that of normal walking.¹⁶ Not only does this higher torque exact a high metabolic cost for producing muscle force, but it also acts through a greater angular displacement, resulting in 2 to 3 times as much work. This high cost of low COM displacement torque may explain why humans do not normally stand or walk with bent legs. Another disadvantage of bent-legged walking is that it requires greater angular excursions of the swing leg due to reduced ground clearance. Humans appear to compensate with a swing-leg trajectory with greater angular excursions, notably about the ankle and knee, and greater hip power during swing.¹⁶ The effects of reduced COM motion on additional stance and swing-leg motion and the torque required to support body weight, among other disadvantages, all appear to contribute to its high cost.

Figure 1.

The “six determinants of gait” theory^2,8 proposes that walking economy is enhanced by reducing displacement of the body center of mass (COM). One drawback of walking with a level path for the COM, however, is that the joints must undergo large motions. The knee also must be flexed at mid stance, so that substantial extension torque is needed to support body weight. The high torque and large joint motion lead to a more than doubling of knee joint work and metabolic energy expenditure compared with normal walking.

Center-of-mass displacement also can be reduced simply by taking shorter but faster steps.¹⁷ Such a strategy makes it possible to avoid both bending the legs and reducing the height of the hip relative to normal, but human experiments show that there also are substantial disadvantages. For example, walking at normal speed but with steps 40% shorter than normal results in more than doubling of the energy expenditure,¹⁴ a penalty similar to that of bent-legged walking. This increase in energy expediture may be attributed to the higher step frequency required to maintain normal speed with shorter steps, which means that the legs must be moved faster than normal, requiring more joint work. It appears that regardless of how COM displacement is reduced, there is a substantial energetic penalty.

These experiments expose several flaws in the “six determinants of gait” as a scientific theory. The theory was based on the interpretation of a descriptive set of observations, from which purpose and consequence were inferred but not tested. To be scientifically useful, a theory must be prescriptive and make predictions that then should be tested. If the theory survives a series of falsifying tests, it may gain credence. Only recently, however, has the “six determinants of gait” theory been subjected to the scrutiny required of the scientific method. Upon receiving that scrutiny, it has not prevailed.

One point of confusion stems from interpretation of the theory. Saunders et al claimed that energy is expended in the “elevation and depression of the center of gravity of the body”8(p553) and “an overall displacement of the center of gravity of the body through a sinusoidal path of low amplitude … requires the minimal expenditure of energy.”8(p554) More than a dozen textbooks have consistently interpreted this claim to mean that minimization or reduction of COM displacement is desirable.^18–32 Although there is no experimental support for this interpretation, it could be proposed that COM displacement should be reduced below its theoretical maximum and, equally importantly, increased above its theoretical minimum.

There are several conclusions to be drawn regarding the “six determinants of gait” theory. One conclusion is that they should more properly be called “kinematic features of gait.” Another conclusion is that they should have been proposed as a hypothesis rather than stated as fact. Finally, it would be preferable to make more specific, definitive, and quantitative predictions. For these and other reasons, Kirtley³³ considered the “six determinants of gait” theory to be discredited. It remains for other textbooks to follow this lead.

The Inverted Pendulum Model

Coexisting with the “six determinants of gait” theory is the inverted pendulum model of walking (Fig. 2). It states that the stance leg behaves like an inverted pendulum, allowing for economical gait. The advantage of a pendulum is that it conserves mechanical energy and thus requires no mechanical work to produce motion along an arc. Observations of mechanical energy exchange and leg-length change during single-limb support provide a strong indication of pendulum-like behavior.^34,35 The inverted pendulum model explains human gait far better than the “six determinants of gait” theory.

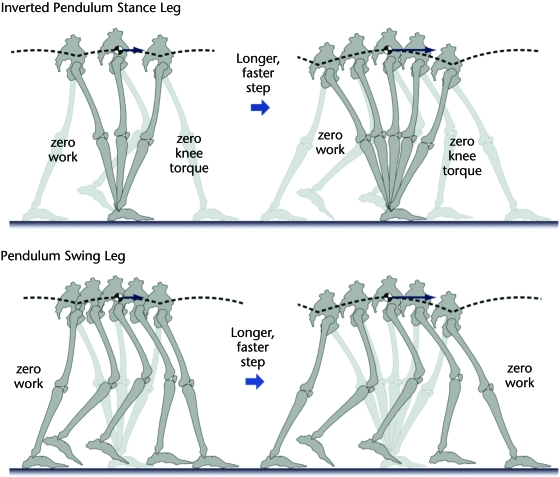
Figure 2.

The inverted pendulum analogy for the stance leg and its corollary for the swing leg. The stance leg appears to act like an inverted pendulum, which allows the body center of mass to move in an arc with conservation of mechanical energy. In principle, no mechanical work is needed to move or lift the body, and no knee torque is needed to support its weight. Longer and faster steps similarly require no effort. The swing leg also appears to move like a pendulum, whose ballistic motion theoretically requires no work. Mechanical energy conservation is unaffected by longer or faster steps

The inverted pendulum predicts exchange of mechanical energy. If an inverted pendulum is acting conservatively, any change in kinetic energy will be offset by an opposing change in gravitational potential energy, with no need for mechanical work performed by muscle. Fluctuations in these 2 types of energy verify that they do act in opposition to each other, with relatively little mechanical work performed by the stance leg during single-limb support.³⁴ Furthermore, the pattern of the energy exchange is very different during running, where the inverted pendulum mechanism is thought to be less dominant.³⁴

A less appreciated advantage of the inverted pendulum comes from the straight leg. It is possible for the leg to act as an inverted pendulum without being kept straight by keeping a fixed distance between the ground contact point and the hip. For example, the knee could be kept at a fixed angle, and the flexed leg could still behave as an inverted pendulum and benefit from conservation of mechanical energy.¹⁷ However, humans evidently choose to keep the stance leg relatively straight, presumably because doing so reduces the moment of body weight (a vertical force with line of action through the COM) about the knee and thus also reduces the muscle force needed to support body weight. A person may walk with the knees kept at a flexed and fixed angle and find it nearly as exhausting as walking with the COM on a level path. The force savings of the straightened knee, therefore, may be just as significant as the work savings.

A corollary to the inverted pendulum is the pendulum-like motion of the swing leg. The same conservation of mechanical energy applies, so that little work is needed to move the swing leg. Given an appropriate initial speed and position, the entire single-limb–support phase can be produced largely through the ballistic motion of 2 coupled pendulums representing the stance and swing legs.³⁶ This finding suggests that both the swing and stance legs may take advantage of pendulum dynamics during single-limb support.

Other considerations, however, reveal limitations to the pendulum model. It successfully explains differences in energy exchange between walking and running, but it does not quantitatively explain how they should vary as a function of walking speed. For example, as speed increases, there are changes in the kinetic and gravitational potential energy exchange³⁴ and the stance leg appears to behave less like a pendulum, but the pendulum analogy does not explain why this is the case. It gives no reason why longer and faster steps (up to the theoretical maximum walking speed) should require a different amount of mechanical work and force than shorter and slower steps. Taken literally, pendulum mechanics predict that a step requires no work or force whatsoever.¹⁷ Once walking has commenced, there is no reason why work must be performed to maintain the conservative motion. The pendulum analogy also does not apply to double-limb support, where a pendulum (inverted or otherwise) clearly cannot swing. Although the pendulum analogy is important for understanding how walking can be economical, it does not explain why walking costs energy at all. In that respect, the inverted pendulum model is incomplete.

Dynamic Walking

Building upon the pendulum analogy, the dynamic walking approach considers how passive dynamics alone can govern an entire gait cycle (Fig. 3). McGeer³⁷ extended the ballistic model of stance and swing-leg motion to include the heel-strike collision between the leading leg and the ground. Properly configured, this collision can produce conditions for a periodic walking gait, with no need for active control and no need for energy input except for that gained by descending a shallow ramp. McGeer³⁷ demonstrated both computational simulations and physical machines capable of passively stable locomotion. Subsequent robots have demonstrated walking on level ground,³⁸ also governed primarily by passive dynamics but with minimal active energy input. We use the term dynamic walking for locomotion generated primarily by the passive dynamics of the legs, whether or not active powering or active control also is applied.

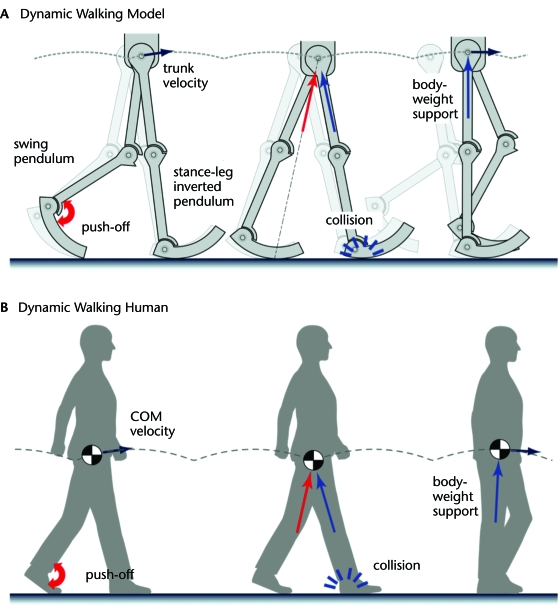
Figure 3.

Dynamic walking relies on passive leg dynamics to drive most or all of gait. (A) Dynamic walking uses the ballistic motions of the stance and swing legs behaving like pendulums, extended to a fully periodic motion. The collision of the leading leg with the ground redirects the body center of mass (COM) and initiates the subsequent step. (B) Dynamic walking also is thought to apply to humans, where passive dynamics allow much of gait to be produced with no work and body weight to be supported with little muscle force. Collision losses nevertheless must be offset by positive work, much of it at push-off.⁴²

The single-limb–support phase of dynamic walking resembles the inverted pendulum model (Fig. 3A). The original model of McGeer³⁷ incorporated rigid stance and swing legs with human-like mass distribution. Their ballistic motion was sufficient to produce an arced trajectory for the hip, with the COM velocity approximately perpendicular to the stance leg. Although the original machines lacked knees, additional machines with knees³⁹ have demonstrated that the principles of dynamic walking apply quite generally. Models with knees³⁹ use a passive knee extension stop to prevent the stance knee from hyperextending and maintain the stance leg in full extension. Body weight thus is supported passively, and the entire single-limb–support phase can be produced with no need for active control and no need to actively lift the COM against gravity.

A consequence of pendulum-like motion is that the transition to a new stance leg requires redirection of the COM velocity from one inverted pendulum arc to the next (Fig. 3B). This redirection occurs because the COM velocity is approximately perpendicular to the previous stance leg (trailing limb of double-limb support) and, therefore, directed forward and downward at the end of that step. The succeeding stance leg (leading limb of double-limb support) specifies a new arc for the COM, beginning with a forward and upward velocity. Although previous studies recognized that some form of redirection was necessary,⁴⁰ the dynamic walking approach explicitly modeled the redirection³⁷ as a collision and showed how it dissipates energy. The ground reaction force of the leading limb is oriented partially in opposition to the COM velocity and performs dissipative negative work on the COM as a result, which necessitates positive work to compensate for the dissipation. For a passive dynamic walking machine descending a ramp, the energy comes from gravitational potential energy. For level walking, energy may be supplied by pushing off at the ankle or powering the hip,^41,42 as demonstrated by dynamic walking robots.³⁸

This redirection of COM velocity also appears to be relevant to human walking. As with the pendulum analogy, humans may benefit from keeping the stance leg relatively straight by supporting body weight with relatively little knee torque and allowing the single-limb–support motion to occur with relatively little need for active muscle work.⁴² The negative work of the leading limb collision appears to be performed, in part, by active muscle, with an associated metabolic energy cost.^43,44 The positive work to restore energy appears to be performed almost entirely by active muscle, with a higher metabolic cost. The combined costs of using both limbs to redirect the COM are referred to as the step-to-step transition cost of human walking.

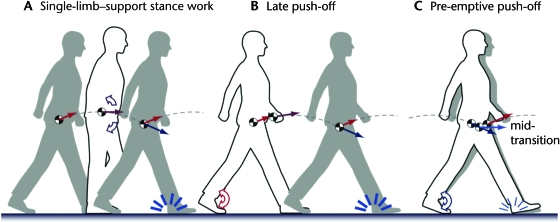
Much of the work performed during walking can be understood in terms of reducing step-to-step transition costs.⁴⁴ In principle, the positive work to restore collision losses can be performed at any time during a stride. For example, work can be performed during single-limb–support stance (Fig. 4A) by the hip muscles. As the hip extends, this torque will perform positive work that can compensate for the subsequent heel-strike collision. Another means of powering is to apply ankle push-off late in double-limb support (Fig. 4B), after the leading leg collision has occurred. A drawback of both of these methods, however, is that the heel-strike collision occurs at high velocity, resulting in a large amount of negative work. Negative work can be reduced, in an ideal dynamic walking model,⁴¹ by pushing off with the trailing limb in a brief pre-emptive impulse just before the leading-limb collision (Fig. 4C). Such a push-off reduces the collision velocity and, therefore, the amount of work that must be performed. If positive work is performed in another manner—for example, with single-limb–support hip torque—up to 4 times the energy can be lost in redirecting the COM velocity.⁴¹ If push-off work does not adequately compensate for the collision, additional work must be performed elsewhere in the stride to maintain steady walking speed, resulting in greater work overall. Of course, humans cannot perform work with ideal impulses, but they may still benefit by pushing off in a relatively short burst of work beginning just prior to the leading-limb collision. Empirical observations have shown that people who are healthy perform step-to-step transitions in this manner.⁴⁴ They perform positive mechanical work on the COM with the trailing leg, beginning just before and continuing throughout double-limb support. This work largely compensates for the negative work performed by the leading leg at most walking speeds.

Figure 4.

Alternative methods to perform positive work to offset collision losses. (A) Work can be performed during single-limb–support stance, for example, by leaning the torso forward. Hip extension torque then is needed to balance the torso, and this torque acts against the extending stance leg to perform positive work. (B) An alternative is to perform push-off about the ankle after heel-strike. Both (A) and (B) can restore work lost in collisions and successfully produce dynamic walking gaits, but higher economy can be achieved with another strategy. (C) Pre-emptive push-off refers to work commencing before the heel-strike collision. This work redirects the body center of mass velocity before the collision, so that the collision velocity (at mid-transition) is lower than in the other 2 cases. Pre-emptive push-off theoretically can reduce collision losses by three quarters and, therefore, reduce the amount of positive work needed to sustain steady gait.

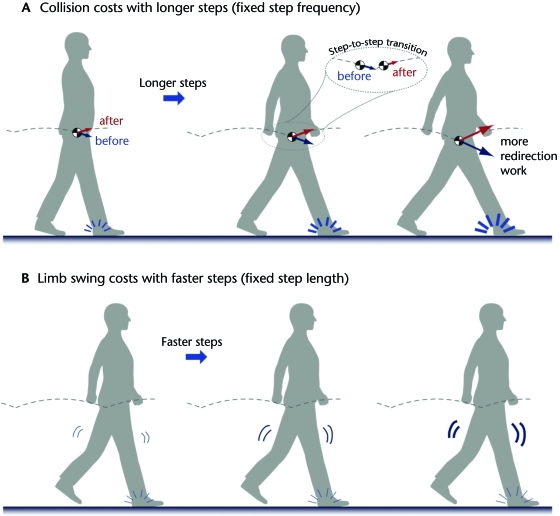
Another prediction of dynamic walking models is that step-to-step transition costs should increase with either longer or wider steps.⁴² Walking with longer steps while maintaining the same step frequency (Fig. 5A) requires the COM velocity to increase in magnitude and to undergo a greater directional change in the step-to-step transition.⁴⁴ Both magnitude and direction contribute to redirection work, with the rate of work increasing with the fourth power of step length. Walking with wider steps of the same length and frequency causes the COM velocity to undergo greater directional changes, with much less effect on magnitude.⁴³ The rate of work thus increases with the second power of step width. Experimental tests on humans support both of these predictions and show that the rate of metabolic energy expenditure increases with similar proportionalities, suggesting that the work performed to redirect COM velocity exacts a proportional metabolic cost.

Figure 5.

Two competing costs to human walking. (A) Dynamic walking predicts that step-to-step transition work—performed to redirect the body center of mass (COM) velocity between steps—increases with step length. At the end of a step and before the step-to-step transition, the COM velocity is directed downward (see inset). It must be redirected upward by the end of the transition for the next pendulum-like step. Keeping step frequency fixed, the work rate is predicted to increase with the fourth power of step length.⁴¹ Experimental measurements show that humans walking at increasing step lengths perform more work and expend more energy, both at rates roughly proportional to the prediction.⁴⁴ (B) Another possible contributor is the effort needed to move the legs back and forth relative to the body. Although pendulum-like motion requires no net work, both work and force may be used to induce faster leg motion. It may be economical to use energy to produce faster steps, if it reduces step-to-step transition costs.⁴⁸ Independent measurements of swinging a leg at increasing frequency but fixed amplitude show metabolic rate increasing with the fourth power of frequency.⁴⁶ The 2 competing costs of step-to-step transitions and forced leg motion appear to determine the preferred step length and frequency of normal human walking.⁴⁸

There also are complexities of the human step-to-step transition not captured by simple models.⁴² The models typically approximate the COM redirection as an instantaneous collision, but humans perform the negative work over a collision phase beginning at heel-strike and typically extending slightly beyond double-limb support. Joint power data show that much of the collision negative work may be attributed to the knee, which flexes while producing an extension torque. Some negative work also appears to be performed by other soft tissues, such as the heel pad, cartilage, viscera, and vertebral disks, but in an amount difficult to quantify. The collision is followed by a rebound phase, where the leg performs positive work to straighten the leg during the first half of single-limb support. The knee accounts for much of the rebound work, which may be due to both active muscle and elastic tendon. Toward the second half of single-limb support, the stance leg enters a second negative work region, referred to as the pre-load phase. This phase appears to be associated with storage of elastic energy in the Achilles tendon, to be released during the subsequent push-off phase. Push-off work typically commences before and continues through double-limb support and may supplement elastic energy with active muscle fiber work. This work compensates for much of the energy dissipated in the collision phase.

A second mechanism that people use to reduce step-to-step transition costs is to actively swing the leg back and forth (Fig. 5B). Dynamic walking models can walk faster simply by pushing off more, which results in longer steps. Greater push-off incurs a high cost for step-to-step transitions due to the step length dependence (discussed above). Walking speed, however, is the product of step length and step frequency, implying that another means to increase speed is to increase step frequency. Dynamic walking models show that elastic springs can passively speed leg swing, for example with biarticular springs about the hip and knee⁴⁵ or a single torsional spring about the hip for rigid-legged models.⁴¹ Such springs theoretically can reduce collision losses to zero by swinging the legs so fast that one leg contacts the ground directly after the next, forming a nearly continuous line of contact with the ground, like a rolling wheel. Of course, humans do not walk with infinitely fast and short steps. Even if elastic tendons were to aid leg motion, the muscles attached to those tendons also must produce active force, incurring an energetic cost. Human subject experiments have shown that isolated leg swinging, performed at roughly the same frequency and torque amplitude as during walking, costs substantial energy. The rate of metabolic energy expenditure increases approximately with the fourth power of swing frequency, suggesting a similarly high cost for the forced leg motion of walking.⁴⁶ This cost appears to be associated not only with active muscle work, but also with production of active muscle force.⁴⁷

The combined energetic costs of step-to-step transitions and forced leg motion appear to account for much of the cost of human walking. At a given speed, humans avoid long steps to reduce step-to-step transition costs, while also avoiding fast steps to reduce the cost of moving the legs back and forth. The trade-off between these 2 avoidance mechanisms appears to explain why humans walk faster by increasing step length and frequency in nearly equal proportion.⁴⁸ At a comfortable walking speed, roughly two thirds of the net metabolic cost is attributable to step-to-step transitions, and up to one third is attributable to forced leg motion. A similar trade-off may explain the selection of preferred step width in healthy human walking. Wider steps incur step-to-step transition costs that increase with the square of step width, whereas narrower steps appear to require forced lateral motion of the swing leg to avoid interference with the stance leg. The sum of these 2 costs is minimized when step width is narrow, but not so narrow as to require substantial lateral forcing of the swing leg to clear the stance leg.⁴³

A third means by which humans manage step-to-step transition costs is to use their feet like sections of wheels. In dynamic walking models, arc-shaped feet reduce negative collision work by reducing the directional change required of the COM. In theory, rigid feet with an arc radius equal to leg length will require no directional change and, therefore, no collision loss. Although such feet are impractical, arc-shaped feet with shorter radii and lengths still can reduce collision losses. Humans appear to take advantage of this feature: the human foot effectively rolls over the ground, with the center of pressure progressing on the ground like a wheel. Although the actions of the ankle and foot are quite complex,⁹ their effect on the center of pressure is quite simple, so that its progression resembles that of a wheel with a radius equal to 30% of leg length.^37,49,50 Experiments examining the effects of rigid foot curvature on human walking mechanics and energetics have demonstrated that a similar radius of curvature reduces COM redirection work and metabolic cost.⁵¹ The combined motion of the human ankle-foot system appears to benefit from effectively acting like a rigid, rolling foot.

Aside from human subject tests, these principles also have been applied to the design of dynamic walking machines and robots. The sagittal-plane motions of the original passive dynamic walking machines have been extended to included lateral motion,⁵² and both ankle and hip actuation have been incorporated for walking on level ground.³⁸ Other models and robots have been devised to include an upper body^53,54 and actuation of multiple joints^55,56 and have been found to display passive dynamic gaits with motion and stability similar to simpler models. These physical models have a variety of human-like and nonhuman features, but they all demonstrate that dynamic walking principles are based firmly in physics and have a degree of practical applicability.

Stability

Dynamic walking models provide a means to examine walking stability. One of their most important features is passive dynamic stability, where gait is stabilized from step to step with no need for direct control over limb motions. The term limit cycle stability refers to the tendency for a small perturbation to the periodic gait to be dissipated over subsequent steps. This tendency may be quantified with a small set of multipliers (also referred to as Floquet multipliers⁵⁷) that characterize the step-by-step amplification or reduction of perturbations in particular directions. A multiplier with magnitude of less than 1 indicates that a particular perturbation will decrease over each step. An arbitrary perturbation may be composed from combinations of these directions, so that general stability may be inferred from combinations of multipliers. If all multipliers have a magnitude of less than unity, the gait is considered stable to small perturbations. Passive stability makes it possible to walk with little or no active control, highlighting the role of dynamics in generating gait. It is helpful, therefore, to consider the features of the modeled dynamics that produce this step-to-step stability.

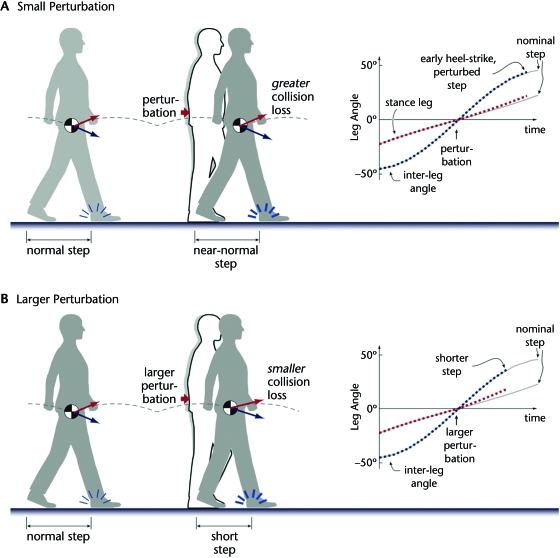
Passive dynamic stability typically is observed in the sagittal-plane motion of dynamic walking models. The most important feature contributing to stability is that collision losses increase with walking speed. As discussed previously, the loss per step increases in proportion to the square of walking speed and the square of step length.⁴¹ A feature of many dynamic walking gaits is that their step length is relatively insensitive to small fore-aft perturbations to the pelvis (Fig. 6A). This feature is indicated by the angle between the stance and swing legs, which increases slowly near the end of a step. The result is that a forward push will have little effect on step length, but will increase the COM velocity at the time of the next heel-strike. The velocity increase will cause the heel-strike collision to dissipate more than the nominal amount of energy, enough to counter the disturbance and stabilize the gait. This stability, however, is not retained for larger perturbations, which can cause substantially shorter steps (Fig. 6B). Shorter steps dissipate less energy, so the heel-strike collision may not be sufficient to gain passive stability. Fortunately, it appears that the range of recoverable perturbations is sufficient to make passive dynamic walking machines practical.³⁷

Figure 6.

Effect of (A) small and (B) larger perturbations on dynamic walking. A forward perturbation is applied at mid stance, causing the stance leg to move faster, resulting in a heel-strike collision that occurs both earlier and with higher speed. (A) Small perturbations have little effect on step length, so that the greater speed of collision results in more energy dissipation. The body center of mass (COM) velocity at the beginning of the next step is reduced and gradually returns to the nominal velocity over successive steps, contributing to passive dynamic stability. Inset shows the trajectory of stance leg angle (defined as positive in the clockwise direction relative to vertical) and inter-leg angle (defined as the angle between stance and swing legs) over a step. The inter-leg angle slows near end of swing, reducing sensitivity of step length to perturbations. (B) Larger perturbations cause a shortened step, which dissipates less energy. The COM velocity at the beginning of the next step is not reduced and increases with each step until the model falls. Inset shows how larger perturbations have relatively greater effect on step length, which is determined by the inter-leg angle at heel-strike.

Another instability can occur in the lateral direction (Fig. 7). A dynamic walking model with a degree of freedom in the ankle eversion/inversion direction—roughly corresponding to the subtalar ankle joint—is laterally unstable.⁵⁸ Its gait dynamics are similar to those of models constrained to the sagittal plane, including passive stability in that plane. However, even as perturbations have little effect on fore-aft motion, they cause the model to fall to the side relatively quickly. The amplification multiplier for this instability is great enough that even a very small perturbation can cause a fall within a few steps. The instability can be remedied somewhat in 3-dimensional models by removing the ankle degree of freedom and installing wide feet. Several dynamic walking robots produce stable gaits with such a configuration, but they are only able to reject small lateral direction perturbations. Humans bear closer resemblance to the models with unconstrained lateral motion and may have similar instability.

Figure 7.

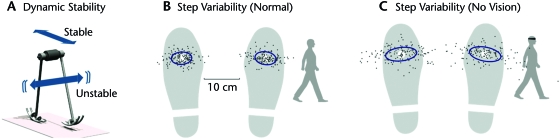
Dynamic stability and human gait variability. (A) Dynamic walking model is stable in the fore-aft direction, but unstable in the lateral direction. The instability can be controlled through active adjustments of lateral foot placement, using integrative sensing and control. (B) Measurements of normal human walking show more variability in step width than length. Individual footsteps for a representative person walking overground are shown as deviations from mean. Ellipses indicate ±1 standard deviation of variability across multiple subjects. (C) When humans walk with eyes closed, their step width variability increases substantially, with much less effect on step length variability. Humans appear to be more dependent on vision for lateral control of walking balance. Data are from Bauby and Kuo.⁵⁹

The solution to lateral instability is active feedback control. There are several ways to stabilize the model's gait, such as by moving the torso from side to side or producing active eversion/inversion torque at the ankle.⁵⁸ A particularly simple solution is to make lateral adjustments to foot placement through active hip abduction and adduction. These adjustments require little effort because the swing leg must be moved only a small amount over the relatively long duration of the swing phase. The amount of adjustment must be determined from feedback, sensing the body state (the positions and velocities of all body segments) at least once per step. Applied to humans, one possible implication of the hypothesized passive stability in the sagittal plane is that walking balance might be controlled largely through lateral foot placement, with little need for active fore-aft adjustments.⁵⁸ This control, in turn, implies a greater dependence on sensory information, integrated by the central nervous system (CNS) from multiple different sensory pathways, to drive lateral foot placement. In contrast, the sagittal-plane motions might be stabilized by passive dynamics, with lesser need for sensing and control. Perhaps the CNS takes advantage of this fore-aft stability, thereby reducing sensorimotor and attentional demand for balance. Dynamic walking models thus predict that the degree of active control needed for balance during walking should be direction dependent.

Direction dependence might be manifested in differences between fore-aft and lateral foot placement (Fig. 7). Whereas active control depends on sensory information that is necessarily imperfect, passive stability requires no control and no sensing. This difference leads to 2 predictions regarding human walking. First, the continual and imperfect adjustment of lateral foot placement would be expected to contribute to step width variability, whereas the hypothesized passive stability would be expected to cause step lengths to be less variable. Second, the dependence on sensory information implies that less information should render active control less precise, leading to greater step width variability without necessarily affecting step length variability. This hypothesis can be tested readily by removing vision. The greater uncertainty in sensing would be expected to result in greater step width variability, but not necessarily any change in step length variability.

These predictions are amenable to experimental testing. Overground⁵⁹ and treadmill⁶⁰ recordings of footsteps show that step width variability typically exceeds step length variability in normal walking, consistent with the hypothesized passive stability properties. When humans walk with their eyes closed, their step width variability increases substantially, by more than twice as much as step length variability.⁵⁹ The greater step width variability during normal walking and its increase with removal or perturbation of vision⁶¹ are both consistent with the hypothesis that humans actively perform integrative control of a lateral instability. The relatively low variability of step length is consistent with the hypothesis that passive dynamics contribute to fore-aft stability, reducing the need for integrative balance control.

Another experimental test is to manipulate lateral stability. Treadmill walking can be artificially stabilized through elastic cords extending laterally from the body and tensioned so that walking is essentially constrained to the sagittal plane. This external lateral stabilization causes adults who are healthy to walk with half the normal step width and about two thirds of the step width variability.⁶² These gait changes also are accompanied by a small (about 9%) but significant decrease in metabolic energy expenditure. Reductions in both step width and its variability may account for the reduced energy expenditure. The aggregate energy savings suggest that active control of balance requires some energy expenditure and that humans may benefit from passive dynamic stability in reducing the need for active control.

Clinical Implications

Energetics

Although humans who are healthy appear to accomplish economical step-to-step transitions across the full range of walking speeds, economy may be impaired in people with gait pathologies such as stroke, spinal cord injury, and amputation, due to the reduction in strength (force-generating capacity) and coordination of the affected leg or legs. As discussed above, dynamic walking models gain economy by beginning push-off immediately before heel-strike, thereby reducing the collision velocity.⁴¹ Impairing or otherwise reducing push-off would be expected to result in an increased contralateral collision, which would require compensation through a greater amount of positive work. This work can be performed at a different phase of the gait cycle or a different joint, but regardless of how and where it is performed, the overall work requirements theoretically are increased. The increased work may explain part of the energetic penalty of many forms of pathological gait.

In patients recovering from stroke, for example, mechanical work measurements suggest that the paretic leg performs much less push-off work and that both legs perform more total mechanical work than that performed by speed-matched individuals who are healthy.^63–65 This increase in work suggests that patients recovering from stroke experience an elevated metabolic cost because step-to-step transitions require more mechanical work and not because they perform work less efficiently. Indeed, it has been shown that the efficiency of step-to-step transition work in hemiparetic gait is equal to that of walkers who are healthy.⁶⁶ This finding is consistent with the efficiency of paretic leg work production estimated during cycle ergometry. Although the paretic leg of people with hemiparesis produces only a fraction of the work of their nonparetic leg or the legs of people who are healthy, it performs work with the same efficiency (about 20%⁶⁷), despite high levels of spasticity.

As with patients with stroke, people with reduced ankle mobility expend more energy to walk at the same speed as individuals without gait pathologies.² The energetic penalty increases with the degree of limb weakness, immobility, or loss. In some cases, such as ankle fusion, the energetic penalty is associated with reduction in ability to perform muscular work. The compensation for this loss apparently is less economical, or requires more mechanical work, than the unimpaired case. It is difficult to predict why an alternate recruitment pattern for the muscles might be less economical, but the theory of step-to-step transitions does explain why the amount of work might increase, because reduced push-off would be expected to cause increased collision work on the contralateral side.

Increased collision work theoretically can be countered by helping redirect the COM velocity with an appropriate foot bottom shape, which can greatly influence energy expenditure with a locked ankle. As mentioned above, shapes that are longer and have a higher radius of curvature can reduce the change in COM velocity for the step-to-step transition, thereby reducing work requirements.⁵¹ A walking boot with a fixed ankle and curved rocker bottom can have energy expenditure requirements essentially the same as for normal intact walking, when the weight of the boot is taken into account.⁶⁸ Recently, prosthetic feet have been designed with a curved foot bottom profile,⁶⁹ which may be energetically advantageous as well. Whether there is a net advantage depends on the decrease in collision due to foot bottom shape, relative to the possible increase in the contralateral collision due to reduced push-off. Although these questions remain unanswered, the dynamic walking approach provides a scientific framework for considering gait with impaired ankle function.

The concept of step-to-step transitions may help guide the design of rehabilitation strategies, rehabilitation devices, and assistive devices aimed at lowering metabolic cost and increasing patient mobility and stability. For assistive devices, it may be effective to assist push-off by electrically stimulating the paretic leg extensors in a manner similar to that currently used to correct drop foot.^70,71 The increased push-off may decrease the contralateral collision cost, decreasing the step-to-step transition cost. For rehabilitation strategies, the energetics of step-to-step transitions suggest that training should target not only the strength of paretic leg extensor muscles but also their ability to perform mechanical power with the appropriate timing.

The dynamic walking approach may provide insight regarding existing rehabilitation strategies. Partial body-weight support, which provides an upward force to the body during treadmill training, is an effective tool for both spinal cord and stroke rehabilitation.⁷² It is unlikely that this device reduces the energetic cost of limb swing because it applies external forces only to the torso. Its effect on step-to-step transition work also is likely to be modest, as COM redirection depends on body mass (which is not changed by the upward force) rather than body weight (which is changed). The upward force will reduce the COM velocity only slightly prior to the transition and help redirect it toward the post-transition velocity. It follows that experiments on subjects who are healthy have demonstrated that an upward force of three quarters of body weight reduces energy expenditure by less than a quarter.⁷³ Its main biomechanical effect may be to prevent the limbs from collapsing under body weight, while preserving the main contributions to the metabolic cost of walking.

Dynamic walking is applicable mainly to cases where the legs behave like pendulums. Many conditions (eg, crouch gait, toe walking, severe hemiplegic gait) may limit the degree to which the pendulum model is relevant. Such conditions may cause the COM to move in a path that results in unusual step-to-step transitions, for which collision models do not apply. For example, there may be negligible step-to-step transition costs when the COM moves in a level path, whereas the effort to support body weight increases drastically.¹⁴ Spasticity (hypertonicity or abnormal reflex activity) also may affect how the legs can move like pendulums and conserve mechanical energy. In these and other cases, step-to-step transition costs may not apply.

There may be cases in which the legs move with a great deal of co-contraction. It is difficult to quantitatively predict the energetic cost of co-contraction, but the qualitative prediction is that energy expenditure can be high even if little net work is performed about the joints. A challenge for many conditions affecting gait is that the kinematics, motor commands, and degree of co-contraction are not predictable. Computational models can make few quantitative predictions for such cases.

There are, nevertheless, general energetic principles that may apply to all pathological gait. Three general types of energetic cost appear to be relevant. The first is the step-to-step transition cost, which applies when the COM moves in an inverted pendulum arc. The combined costs of the negative collision work and the positive work to restore the energy dissipated may be substantial. Second is the cost of moving the legs back and forth relative to the body. When the legs are observed to swing like pendulums, there may be effort expended to force them to swing faster, with significant energetic cost. Finally, when body weight is supported on a bent leg, especially with knee flexion, substantial effort may be expended to counteract gravity. If the bent leg also undergoes flexion or extension motion, substantial work may be performed, at potentially very high energetic cost.

Stability

Balance is a limiting factor for the mobility of older adults, as well as those with vestibular, somatosensory, and other sensory deficits. The principles of dynamic walking may be helpful for addressing and understanding poor stability. If walking depends more critically on active control of lateral balance, but less for fore-aft control, there are several implications for impaired balance. One implication is that poorer sensing may adversely affect lateral balance, regardless of the modality. This adverse effect may result in increased step variability, perhaps accompanied by greater energy expenditure, which implies that the step width variability might serve as a useful quantifier of sensorimotor control of balance during walking.

One model of balance deficits considers active sensorimotor control in terms of noise-like imprecision. It proposes that some forms of sensory loss result in unpredictable errors that affect the repeatability of sensory measurements, thereby affecting variability without necessarily introducing systematic (and, therefore, predictable) distortions. It also assumes that motor output is subject to unpredictable errors that affect the precision with which control adjustments are made. All of these effects can be modeled as noise, affecting both sensors and motor commands. Such models are helpful for modeling variability of postural stability⁷⁴ and have been applied to stabilization of walking through lateral foot placement control.⁷⁵ In the latter case, sensorimotor noise can reproduce age-related trends in step width variability, even without systematic changes in the body. Assuming that the lateral foot placement is fully intact but operating on noisy information, the model predicts greater step variability—especially in the lateral direction—as the amount of noise increases.

There is some evidence to support these predictions. Older adults who are healthy walk with greater variability than younger adults, as assessed by a variety of measures, including step timing,⁷⁶ length, and width.⁶⁰ Among gait parameters, however, step width variability is the strongest discriminating factor,⁷⁷ agreeing well with the model prediction. Step width variability also appears to be related to variability of trunk motion in the frontal plane.⁷⁸ Therefore, it appears that one of the age-related factors affecting gait may be decreased sensorimotor precision, resulting in greater step variability, especially in the lateral direction.

Gait variability, however, is only one possible factor affecting mobility. Excessive step width variability has been linked to falling in older adults,⁷⁹ perhaps due to the detrimental effects of poor sensorimotor precision. Unusually low step width variability also has been linked to falls,^79,80 perhaps for different reasons. Dynamic walking models require that lateral foot placement be adjusted in proportion to errors in motion from the preceding step. A possible effect of poor sensory precision is to reduce the accuracy with which control adjustments are performed, also referred to as control sensitivity. This effect may be manifested in inaccurate foot placement adjustments, or even a failure to detect errors in motion altogether. Control sensitivity is a systematic rather than a random or unpredictable effect, and poor control sensitivity can lead to instability regardless of the noise-like effects. Computational models can hardly provide a full explanation for the cause of falls, but they do suggest how systematic and noise-like components both can be detrimental to walking balance.

This approach to lateral stability may suggest potential rehabilitation aids. Individuals with poor balance often rely on handrails or other supports during walking. A goal of balance rehabilitation is to decrease reliance on such aids, but there are few automatic or systematic means to control or quantify such reliance during walking exercises. It is possible that systematic scaling of balance assistance could be afforded by external lateral stabilization during treadmill walking.⁶² This external stabilization could aid lateral balance, perhaps in concert with other aids such as partial body-weight support that reduce the physical load but do not specifically address balance. The amount of external stabilization could be adjusted according to the degree of unsteadiness and gradually reduced during a rehabilitation program. The stabilizing forces also could be measured to assess the amount of dependence on the assistance. Understanding of lateral stability might be helpful for the design of these and other aids.

There are a few studies that demonstrate clinical applications of lateral stabilization. Older adults have been found to walk with reduced step width variability and energy expenditure when receiving external lateral stabilization,⁷⁵ and energy expenditure can even be reduced to levels similar to those for young adults.⁸¹ Patients with myelomeningocele have sensory deficits and difficulty controlling walking. The application of external lateral stabilization to these patients has been found to reduce their step width and increase step length, with a one-fourth decrease in heart rate.⁸²

It is important to note that the step-to-step stability considered here is concerned primarily with small or local deviations from the nominal gait. In rehabilitation, the overriding concern typically is a more global definition of stability, such as whether patients are susceptible to falling. The issue of global stability is far more complex than that of local, step-to-step stability. It is possible for an individual to have good local stability but still be sensitive to large perturbations or otherwise susceptible to falling. It also is possible for an individual to have poor local stability and yet high robustness to perturbations. The clinical relevance of step-to-step stability, therefore, is limited. We nevertheless propose that step-to-step stability serves as one useful indicator of walking balance and that good local stability contributes to economical gait.

Energy Minimization and the Determination of Gait

A number of studies assume that gait should minimize energy expenditure. As a general concept, it appears sensible for humans and other animals to conserve metabolic energy, historically a scarce resource. This is especially the case for locomotion, a costly and frequently performed task, as was stated explicitly as part of the “six determinants of gait” hypothesis as: “fundamentally locomotion is the translation of the center of gravity through space along a pathway requiring the least expenditure of energy.”8(p558) Although considerable experimental evidence would appear to support this statement, it is important to evaluate it with deeper consideration rather than treat it as scientific fact.

Much of the experimental evidence to date supports the energy minimization hypothesis for normal gait. For example, the comfortable walking speed typically is close to optimal.⁸³ At a given speed, humans are observed to walk at a combination of step length,⁸⁴ frequency,⁸⁵ and width⁴³ that minimizes energy expenditure. Deviations from the preferred values for these parameters cause energy expenditure to increase. There is no limit to ways in which walking otherwise could be altered, but to our knowledge, there are no elective changes that a person can make to his or her walking pattern that will decrease energy expenditure relative to the norm for a given speed.

Despite these observations, the minimization hypothesis (as stated by Saunders et al⁸) is incomplete as a scientific statement. Humans often locomote in a manner that does not minimize energy expenditure. They often walk very quickly or very slowly, and may occasionally even run—all examples of behaviors that expend more than a minimum of energy.⁸⁵ Some pedestrians can be observed to climb stairs in preference to an escalator or elevator that would clearly save their own energy. More generally, pedestrians in large cities have been observed to prefer walking speeds as much as twice as fast as those of pedestrians in small towns⁸⁶ and, therefore, to expend more energy to travel the same distance. They cannot all be using energy minimization as the only criterion for choosing their preferred walking pattern.

It is apparent, therefore, that locomotion can have multiple goals, as is recognized in the International Classification of Functioning, Disability and Health.⁸⁷ Even the speed of level walking is not necessarily energetically optimal because the need to travel within a specified amount of time may induce a person to hurry, even if that favors a faster-than-optimal speed. Such goals often are not explicitly clear. The faster walking speeds in large cities illustrate how implicit social and cultural cues also may play an important role. Even the apparently straightforward task of walking “normally” across a laboratory floor may entail implicit goals. These implicit goals may include unspoken social cues conveyed by the experimenter that could affect the preferred speed, the interpretation of “normal,” and even the quality of gait. Clinicians have remarked that the gait demonstrated by a patient in the clinic often is not representative of daily living. Energy minimization, therefore, should be considered an important contributing goal that competes and sometimes even conflicts with a variety of other possible interests. When gait is treated as the result of competing goals, some of them inexplicable, there is little room for definitive statements regarding energy minimization.

Although energy minimization may be one goal of gait, it remains to be determined how it applies to pathological gait. The hypothesis proposed by Saunders et al was that “pathological gait may be viewed as an attempt to preserve as low a level of energy consumption as possible by exaggerations of the motions at unaffected levels.”8(p558) Evidence is lacking to counter this proposal, but again implicit task goals may play a role. One possible implicit goal may be to appear healthy and avoid attention, for social and other reasons. For example, some patients may prefer to walk rather than to use a wheelchair, even if the wheelchair is more economical. Another issue in many clinical cases is symmetry. In the case where the body is symmetrical, it generally is expected that the dynamic walking gait, and perhaps the energetically optimal gait, also will be symmetrical. In pathological cases, however, there may be asymmetry in body biomechanics, such as differences in muscle strength, range of motion, or limb length, mass, or geometry. There also may be asymmetry in the neural command capacity, such as with the abnormal motor synergies that often accompany hemiplegia. In terms of passive dynamics, an asymmetric body generally will be expected to yield a passively asymmetric gait.³⁷ Some form of active control, therefore, would be needed to reduce the asymmetry. There is little reason to expect forced symmetry to improve upon economy. The desire for symmetry might be cosmetic and, in some cases, even contrary to the goal of economy.

Implicit task goals are difficult to identify, lessening the scientific utility of the energy minimization hypothesis. It nonetheless is instructive to consider an example where energy minimization may aid the design of experiments. Older adults have long been observed to expend more energy to walk than young adults moving at the same speed.² One possibility is that neuromechanical differences between the 2 age groups are small, and older adults select their gait because of implicit task goals rather than an inability to produce the optimal gait. Perhaps they prefer a wide step to enhance stability, with long-term benefits—for example, fewer falls—sufficient to justify greater short-term energy expenditure. It then is relevant to test whether there is a gait pattern more economical than the preferred one. Another possibility is that gait patterns change to remain energetically optimal. This possibility implies age-related changes in neuromotor control abilities or biomechanical properties that make it more economical to adopt a gait pattern different from that of a younger person. Perhaps the tendons have become stiffer, body mass distribution has changed, or sensor precision has degraded. These and a myriad of other changes might be optimized by an altered gait pattern. Although many such changes certainly do occur with age, it is unclear whether they indeed explain the gait pattern. These possibilities show how the energy minimization hypothesis can drive scientific inquiry, without need to be taken as scientific fact. The concept of optimization and the competition of multiple goals help to clarify possible hypotheses, drive new experiments, and further our understanding of the fundamental principles underlying walking and their application to clinical practice.

Limitations

We have reviewed how the principles of mechanics contribute to human walking. The dynamic behavior of the limbs is only one aspect of the overall walking pattern, and rehabilitation is necessarily concerned not with a single aspect but with the combined behavior of the CNS and the musculoskeletal system. It is challenging to incorporate other contributions into present quantitative models, because it is difficult to predict how neural control of muscular properties will adapt or compensate in response to injury or impairment. In some cases, the available theories are qualitative and difficult to make explicit and quantitative. In other cases, there may be quantitative theories that make predictions, but few methods of testing them experimentally. The intent of the present perspective is not to minimize the importance of neural control or musculoskeletal adaptations, but to highlight a few mechanical principles of walking that are amenable to experimental testing. A fortunate outcome of these experiments is the finding that the dynamics of the limbs play an important role in both determining the normal gait pattern, its overall energetic economy, and some aspects of step-to-step stability. We nevertheless consider the dynamic principles of gait not to offer a solution to rehabilitation, but rather to serve merely as a useful starting point for experimental inquiry.

Conclusion

We have reviewed the principles of gait, as examined with the dynamic walking approach. This approach begins with the dynamics of the limbs and shows how they may be sufficient to generate an economical and stable gait on their own. This approach then considers how motor inputs can best provide power and contribute to improved stability. The approach has utility in the design of experimental tests for healthy gait and may have implications for clinical gait. It is important to note that dynamic walking is only one of many possible approaches. Pathological gait almost certainly is best studied with a multimodal approach, integrating simple principles, clinical observations, and controlled experiments conducted to explicate the deficits. The examples here show how the dynamic walking approach might apply to the integrative study of gait pathologies. These examples may be viewed as starting points for new investigations, wherein experimental testing will be indispensible. Simple principles cannot explain all of the complexities of gait, but they may help to pose useful questions that must be answered to understand those complexities.