Abstract
Bed expansion behavior and sensitivity analysis for super-high-rate anaerobic bioreactor (SAB) were performed based on bed expansion ratio (E), maximum bed sludge content (V pmax), and maximum bed contact time between sludge and liquid (τ max). Bed expansion behavior models were established under bed unfluidization, fluidization, and transportation states. Under unfluidization state, E was 0, V pmax was 4 867 ml, and τ max was 844–3 800 s. Under fluidization state, E, V pmax, and τ max were 5.28%–255.69%, 1 368–4 559 ml, and 104–732 s, respectively. Under transportation state, washout of granular sludge occurred and destabilized the SAB. During stable running of SAB under fluidization state, E correlated positively with superficial gas and liquid velocities (u g and u l), while V pmax and τ max correlated negatively. For E and V pmax, the sensitivities of u g and u l were close to each other, while for τ max, the sensitivity of u l was greater than that of u g. The prediction from these models was a close match to the experimental data.
Keywords: Anaerobic bioreactor, Expansion behaviors, Bed expansion ratio, Fluidization state, Sensitivity analysis
1. Introduction
A range of high-rate anaerobic fluidized-bed (AFB) reactors such as upflow anaerobic sludge blanket (UASB), upflow-staged sludge bed (USSB), expanded granular sludge bed (EGSB), internal circulation (IC), and inverse anaerobic fluidized bed (IAFB) reactors, and two high-rate anammox reactors [sequencing batch reactor (SBR) and an upflow biofilter (UBF)] have been investigated (Lettinga et al., 1991; Lens et al., 1998; Chen et al., 2009; Pereboom and Vereijken, 1994; Sowmeyan and Swaminathan, 2008a; Jin et al., 2008). At the industrial scale, AFB reactor can bear very high loading rates, up to 40 g COD/(L·d) (Heijnen et al., 1989). Our preliminary laboratory scale studies revealed that the ability of AFB reactor was even greater than that. The organic loading rate (OLR) and volumetric biogas production (VBP) of the spiral automatic circulation (SPAC) reactor in our laboratory could reach up to 306 g COD/(L·d) and 131 L/(L·d) (Zheng et al., 2008; Chen et al., 2008), respectively. However, high OLR and VBP can result in high bed expansion ratio that changes not only bed sludge content but also contact time between sludge and liquid. A bed sludge content correlates positively with reaction rate, while it is opposite when it comes to bed contact time between sludge and the generation yield of reactants. The objective of this study was to investigate bed expansion behavior of super-high-rate anaerobic bioreactor (SAB) along with its relation with superficial liquid velocity and superficial gas velocity. Such investigation may be of some interest for further optimizing the operations and designs of such reactors.
2. Materials and methods
2.1. Bed expansion behavior model
Bed expansion behavior in reactors results from synergistic effect of superficial liquid velocity (u l, led by OLR) and superficial gas velocity (u g, led by VBP), which includes bed unfluidization, fluidization, and transportation states. The fluid superficial velocity (u) in bed can be obtained according to the vector relation: u=u l+u g. Generally, we consider u=u l+u g because directions of u, u l and u g are all up. When u is low, the drag force for granular sludge in the bed is less than its weight; therefore, the bed is under unfluidization state. When u is larger than minimum fluidization velocity (u mf), the drag force approaches to the weight. Consequently, the granular sludge begins to loosen, bed porosity increases, and the bed expands and comes into fluidization state. When u further increases to the minimum transportation velocity (u mt), the drag force for granular sludge in the bed is more than its weight, the bed enters transportation state, and washout of the granular sludge occurs. When SAB experiences three expansion states, its behavior can be expressed through its characteristics: bed expansion ratio (E), maximum bed sludge content (V pmax), and maximum bed contact time between sludge and liquid (τ max).
2.1.1. Bed expansion ratio
Bed expansion ratio E can be calculated using the following equation:
| E=(Hgls(ls)−Hu)/Hu×100%, | (1) |
where H gls(ls) represents the bed expansion height (mm) at gas-liquid-solid tri-phasic or liquid-solid bi-phasic condition; H u represents the sludge height (mm) under unfluidization state.
If the total sludge mass loaded into the reactor remains constant, Eq. (2) can be established:
| Hgls(ls)Aεs=HuA(1−ε0), | (2) |
where A is the cross-sectional area (mm2) of the reactor column, ε 0 is bed porosity in the beginning (dimensionless), and ε s is the granular sludge holdup (dimensionless). The bed expansion ratio can be transformed into Eq. (3) using Eqs. (1) and (2):
| E=(1−ε0−εs)/εs×100%. | (3) |
Thus, E for SAB is a function of ε 0 and ε s, which vary with OLR and VBP. So E under the tri-phasic state of SAB is different.
1. E for the unfluidization state
When superficial liquid velocity u l is less than the minimum superficial fluidization velocity u mf, the bed is under unfluidization state, where the sludge holdup keeps constant and the bed expansion ratio is zero. Based on statics equilibrium principles (Huang and Wu, 1996), u mf can be expressed under the liquid-solid bi-phasic condition as follows:
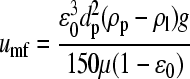 , ,
|
(4) |
where d p (mm) is particle diameter, ρ p (g/cm3) is particle density, ρ l (g/cm3) is liquid density, g (cm/s2) is acceleration of gravity, and μ [g/(cm·s)] is dynamic viscosity.
2. E for the fluidization state
When the superficial liquid velocity u l is between the minimum fluidization velocity u mf and the minimum transportation velocity u mt, the bed is under fluidization state. The following relationship holds among individual holdups:
| εg+εl+εs=1, | (5) |
in which ε g, the gas holdup (dimensionless), can be calculated using the correlation equation proposed by Chern et al. (1984) as follows:
| εg=0.098(ul/10)−0.98(ug/10)0.7. | (6) |
In the present study, large bioparticles (d p=Φ1.14 mm) were observed in the SAB. Thus, the generalized model was simplified by setting x=0 (ignoring the friction resistance caused by liquid wake) as a common assumption (Yu and Rittmann, 1997; Wu et al., 2006), as shown in the following equation:
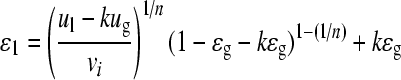 , ,
|
(7) |
where n is bed-expansion index (dimensionless) and k is mean volume ratio of wakes to bubbles (dimensionless). k can be calculated using the following equation:
| k=0.211(ul/10)1.293(ug/10)−0.739. | (8) |
vi (mm/s) represents terminal settling velocity of a particle (with diameter d p) in the reactor with equivalent diameter D:
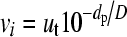 , ,
|
(9) |
where u t (mm/s) represents terminal settling velocity of a particle without wall effect.
If both u g and ε g are set at zero, Eq. (7) can be simplified to:
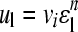 . .
|
(10) |
n of Eq. (10) and u t of Eq. (9) can be obtained by using the correlation equations proposed by Khan and Richardson (1987; 1989), as shown in the following equations:
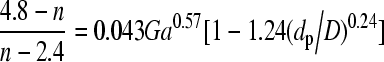 , ,
|
(11) |
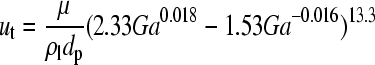 , ,
|
(12) |
where μ [g/(cm·s)] represents dynamic viscosity, and Ga represents Galileo number (dimensionless) and
| Ga=ρ1dp3(ρp−ρ1)g/μ2. |
Thus, k, n, and vi must be calculated first, followed by the calculation of ε g using Eq. (6) and the calculation of ε l using Eq. (7). Thereafter, the bed expansion ratio E can be calculated using Eqs. (3) and (5).
3. E for the transportation state
When superficial liquid velocity u l is larger than the minimum superficial transportation velocity u mt, the bed is under transportation state. u mt can be calculated theoretically under liquid-solid bi-phasic condition, as shown in the following equation:
| umt=(1−εs)ut. | (13) |
Thus, the bed-expansion ratio E can also be calculated using Eqs. (5)–(12) theoretically if the height of the bed is high enough because the transportation state is just a critical state of the fluidization state.
2.1.2. Maximum bed sludge content
If bed expansion ratio remains constant, sludge content is maximized when the effective volume of the bed is filled with granular sludge. Thus, the maximum bed sludge content V pmax can be expressed as follows:
| Vpmax=V0εs, | (14) |
where, V 0 (ml) represents the effective volume of the bed.
Thus, V pmax can be calculated using Eq. (14) and Eqs. (5)–(12).
2.1.3. Maximum bed contact time between sludge and liquid
If bed expansion ratio remains constant, the sludge content increases, and the maximum bed contact time between sludge and liquid τ max will become long. The τ max is maximum at the maximum sludge content. Under these conditions, τ max can be expressed in the following form:
| τmax=H0Aεl/ulA=H0εl/ul, | (15) |
where H 0 (mm) represents the height of the bed.
Thus, τ max can be calculated using Eq. (15) and Eqs. (5)–(12).
2.2. Experimental set-up
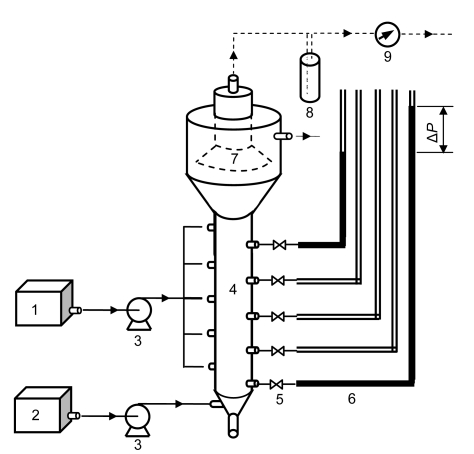
The schematic diagram of the experiment is presented in Fig. 1. The anaerobic bioreactor was fed with an aqueous solution of sulfuric acid (0.5%, w/w). Gas generation was performed by chemical reaction between sulfuric acid and saturated sodium bicarbonate. The bioreactor had five ports evenly distributed along the bed height to simulate biogas production, i.e., CO2 effervescence, of SAB. The bed was filled with anaerobic granular sludge to a height as per requirement of the experiment. Anaerobic granular sludge in SAB was adopted to simulate the working condition of processes.
Fig. 1.
Sketch of experimental apparatus
1: tank for saturated NaHCO3; 2: tank for H2SO4 (0.5%, w/w); 3: pump; 4: reactor; 5: valve; 6: L-type tube; 7: tri-phasic separator; 8: water seal; 9: wet gas-flow meter
2.3. Anaerobic granular sludge and correlative parameters
Anaerobic granular sludge loaded into SAB was collected from a papermaking wastewater treatment plant. The granular sludge averaged Φ1.14 mm in diameter (d p) and had a dry density (ρ p) of 1.052 g/cm3. The SAB (Fig. 1) had the following dimensions: bed (column) diameter (D) Φ100 mm, bed height (H 0) 1 000 mm, and separation unit diameter and height Φ280 mm and 300 mm, respectively. The upper and lower end diameters of tri-phasic separator equipped in separation unit were Φ50 mm and Φ180 mm, respectively. The working and column volumes of reactor were 20 000 ml and 7 850 ml, respectively. The total volume and height of reactor were 28 000 ml and 1 600 mm, respectively. Other characteristics were: liquid dynamic viscosity μ=8.6×10−3 g/(cm·s), liquid density ρ l=1 000 g/cm3, incipient bed porosity ε 0=0.38, acceleration of gravity g=980 cm/s2, and ranges of superficial liquid and gas velocities (u l and u g) 0–1.83 mm/s and 0–0.67 mm/s, respectively.
2.4. Analytical procedures
The granular sludge was observed and photographed under microscope (Leica DFC300FX, Germany), and its diameter was analyzed by supporting image analysis software (Leica Qwin V3, Germany). The density of granular sludge and the incipient bed porosity were determined according to Summerfelt (2006). The superficial liquid velocity could be calculated by the influent volume in relation to gas production time. The superficial gas velocity was determined by gas flow meter (BSD 0.5, China) and the liquid dynamic viscosity was determined by rotating viscometer (NDJ-1, China). The height of granular sludge in bed was determined by a ruler with precision of 1 mm.
3. Results and discussion
3.1. Bed expansion behavior under unfluidization state
OLR of bioreactor was low when bed expansion behavior was studied under unfluidization state. The minimum fluidization velocity u mf=0.45 mm/s could be calculated according to Eq. (4), where ε 0=0.38, d p =Φ1.14 mm, ρ p=1.052 g/cm3, ρ l=1 000 g/cm3, g=980 cm/s2, and μ=8.6×10−3 g/(cm·s). The granular sludge held nearly still when superficial velocity u was lower than 0.45 mm/s, and bed expansion ratio E was 0. According to Eq. (14), the maximum bed sludge content V pmax=4 867 ml could be calculated, where V 0=7 850 ml, ε 0=0.38, and ε s=1−ε 0. By using Eq. (5), where we could ignore the gas holdups (ε g=0) because the OLR under the unfluidization state was very low and the gas production was very few, we have ε l=1−ε s. Together with ε 0=1−ε s=0.38 and H gls=H umax=1 000 mm, Eq. (15), the maximum bed contact time between sludge and liquid (τ max) under bed unfluidization state, could be replaced in the following equation:
| τmax=380/ul. | (16) |
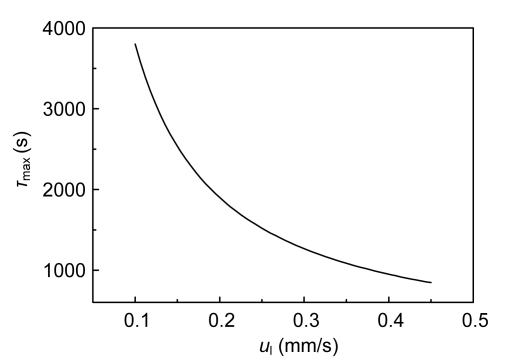
According to Eq. (16), influence curve of u l to τ max is shown in Fig. 2. From Fig. 2, τ max decreased from 3 800 s to 844 s as u l increased from 0.1 mm/s to 0.45 mm/s (with hydraulic retention time between 10 000 s and 2 222 s).
Fig. 2.
Influence of superficial liquid velocity on maximum bed contact time between sludge and liquid under unfluidization state
3.2. Bed expansion behavior under fluidization state
OLR of bioreactor was high or even super-high when bed expansion behavior was studied under fluidization state. When u was above the minimum fluidization velocity 0.45 mm/s, the unfluidization state of granular sludge was changed into the fluidization state.
3.2.1. Influence of superficial liquid velocity on bed expansion behavior under fluidization state
By combining the Eqs. (3), (5), (6), (9) and (10) where the estimation of n and u t values is based on Eqs. (11) and (12), respectively, having ε 0=0.38, d p =Φ1.14 mm, and D=Φ100 mm, the bed expansion ratio under liquid-solid bi-phasic fluidization state (ε g=0) can be translated as follows:
| E=(0.435u10.29−0.38)/(1−0.435u10.29)×100%. | (17) |
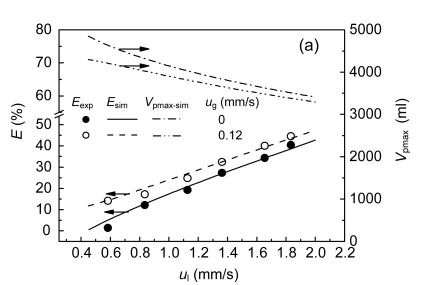
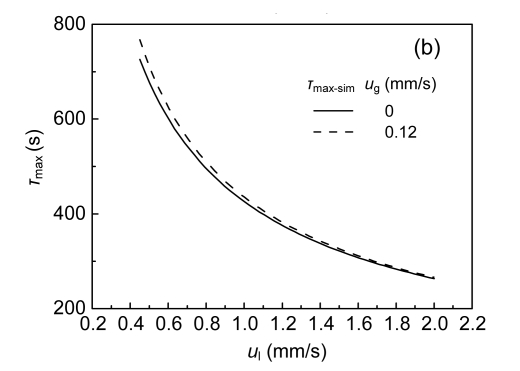
On the basis of Eq. (17) and the bed expansion ratio model of the fluidization state, Fig. 3a depicts the influence of superficial liquid velocity on bed expansion ratio and the maximum bed sludge content. The bed expansion ratio model is a close match to the experimental data. The plot indicates that bed expansion ratio E increased from 0 to 42.7% and from 11.7% to 47.4% under u g=0 and u g=0.12 mm/s, respectively, as u l increased. On the contrary, the maximum bed sludge content decreased as u l increased, in which values decreased from 4 867 ml to 3 411 ml and from 4 295 ml to 3 293 ml under u g=0 and u g=0.12 mm/s, respectively. Fig. 3b depicts the effect of superficial liquid velocity on maximum bed contact time between sludge and liquid; the τ max decreased from 726 s to 263 s and from 767 s to 266 s under u g=0 and u g=0.12 mm/s as u l increased.
Fig. 3.
Influence of superficial liquid velocity on bed expansion ratio and maximum bed sludge content (a) and maximum bed contact time between sludge and liquid (b) under fluidization state
3.2.2. Influence of superficial gas velocity on bed expansion behavior under fluidization state
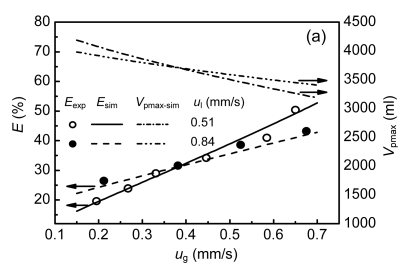
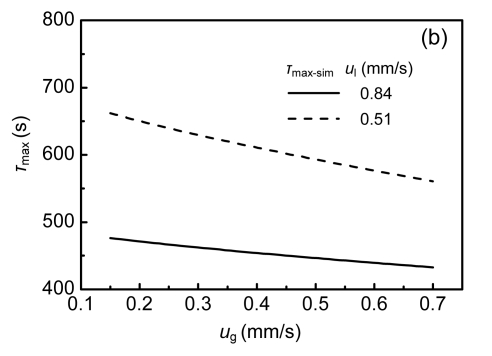
Fig. 4a depicts the effect of superficial gas velocity on bed expansion ratio and the maximum bed sludge content. A reasonable agreement existed between the experimental data and the bed expansion ratio model. What can be seen in this plot is that bed expansion ratio E increased as u g was increased for two data sets, in which values increased from 16.3% to 52.7% and from 22.2% to 42.9% under u l=0.51 mm/s and u l=0.84 mm/s, respectively. In contrast, the maximum bed sludge content decreased from 4 187 ml to 3 187 ml and from 3 982 ml to 3 407 ml under u l=0.51 mm/s and u l=0.84 mm/s as u g increased. Meanwhile, Fig. 4b depicts the effect of superficial gas velocity on the maximum bed contact time between sludge and liquid τ max; τ max decreased from 662 s to 561 s and from 476 s to 432 s under two data sets (u l=0.51 mm/s and u l=0.84 mm/s) as u g increased.
Fig. 4.
Influence of superficial gas velocity on bed expansion ratio and maximum bed sludge content (a) and maximum bed contact time between sludge and liquid (b) under fluidization state
3.2.3. Influence of superficial liquid and gas velocities on bed expansion behavior under fluidization state
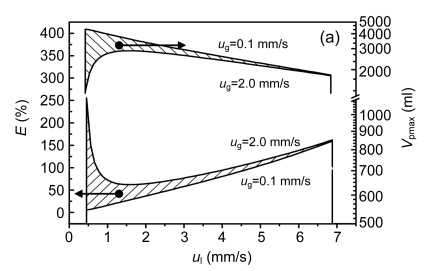
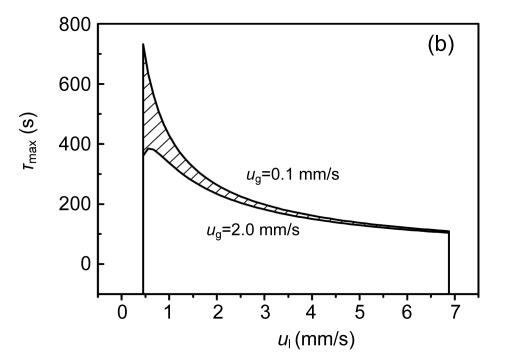
The influence curves of superficial liquid and gas velocities on bed expansion behavior are shown in Fig. 5. Bed expansion ratio E increased from 5.28% to 159.55%, while the maximum bed sludge content V pmax decreased from 4 559 ml to 1 878 ml and the maximum bed contact time between sludge and liquid τ max decreased from 732 s to 110 s when u g=0.10 mm/s. Bed expansion ratio E decreased initially, and then increased with the increase of u l, varying from 255.69% to 62.20% when u g=0.20 mm/s. Similar to the result of E, V pmax and τ max increased first, and then decreased as u l increased, varying from 1 368 ml to 3 001 ml and from 385 s to 104 s, respectively. Hence, when u l and u g were varied synchronously, the changed range of bed expansion ratio E changed from 255.69% to 5.28%, the maximum bed sludge content V pmax changed from 1 368 to 4 559 ml (as shown in the shaded part of Fig. 5a), and the maximum bed contact time between sludge and liquid τ max changed from 104 s to 732 s (as shown in the shaded part of Fig. 5b). Fig. 5 also shows that when superficial liquid velocity u l was larger, bed expansion behavior under different u l and u g tended to be more uniform. When superficial liquid velocity u l was close to the minimum transportation velocity u mt, values for E, V pmax and τ max approached 160%, 1 860 ml and 104 s (with hydraulic retention time between 145 s and 2 222 s), respectively.
Fig. 5.
Influence of superficial liquid and gas velocities on bed expansion ratio and maximum bed sludge content (a) and maximum bed contact time between sludge and liquid (b) under fluidization state
3.3. Bed expansion behavior under transportation state
Bed expansion behavior changes into transportation state when superficial liquid velocity u l of bioreactor exceeds the upper limit. According to Eq. (13) and combining Eqs. (5)–(12), where u t was based on Eq. (12) and ε s was based on Eqs. (5)–(11), together with corresponding parameters, the minimum transportation velocity u mt 6.88 mm/s was obtained. When superficial velocity u exceeded 6.88 mm/s, the fluidization state of granular sludge transitioned into the transportation state. Thus, washout of the granular sludge occurred and destabilized the SAB. Thereby, values for E, V pmax, and τ max have no utility values in practice under the transportation state.
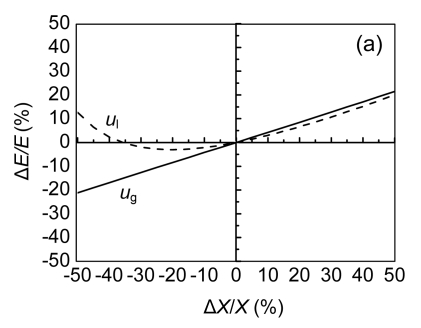
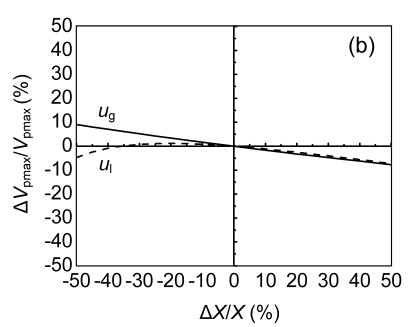
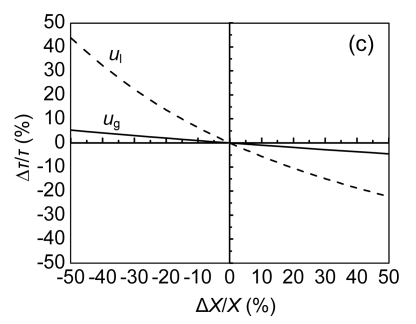
3.4. Parametric sensitivity analyses of bed expansion behavior under fluidization state
SAB can operate effectively and stably under bed fluidization state, which can maintain a fixed bed expansion ratio and provide good hydrodynamic behavior (Diez Blanco et al., 1995; Sowmeyan and Swaminathan, 2008b). Therefore, the sensitivity analyses of main parameters (X) such as u l and u g for bed expansion behavior under fluidization state were performed on the basis of the following parameter values: u l=2.00 mm/s, u g=2.00 mm/s, d p=Φ1.14 mm, D=Φ100 mm, ρ p=1.052 g/cm3, and ε g, k, vi, n, and u t obtained by using Eqs. (6), (8), (9), (11) and (12), respectively. E, V pmax and τ max were regarded as object values, where u l and u g varied within a range of ±50%. When u l=1.00–3.00 mm/s and u g=1.00–3.00 mm/s, sensitivities (S R) of E, V pmax and τ max can be calculated using Eq. (18) in the following form (Zheng and Feng, 2006):
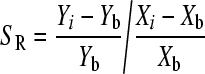 , ,
|
(18) |
where S R represents sensitivity (dimensionless); Yi represents E, V pmax, or τ max of different parameters; Y b represents the basic value of E, V pmax, or τ max; Xi represents the different parameter values; X b represents the basic parameter value.
It is evident from Fig. 6 that, for bed expansion ratio E and the maximum bed sludge content V pmax, the sensitivities of superficial liquid and gas velocities were close to each other (Figs. 6a and 6b), while for the maximum bed contact time between sludge and liquid τ max, the sensitivity of superficial liquid velocity was higher than that of superficial gas velocity (Fig. 6c), which guided us to better operate the SAB. For example, if we wanted to enhance removal efficiency of the SAB by prolonging τ max, we took some measures to reduce the superficial liquid velocity firstly as soon as possible, but not the superficial gas velocity.
Fig. 6.
Parametric sensitivity analyses of bed fluidization state on bed expansion ratio (a), maximum bed sludge content (b), and maximum bed contact time between sludge and liquid (c)
4. Conclusion
Bed expansion behavior of SAB was systemically investigated by analysis of the results obtained in this research. Under unfluidization state, u was less than 0.45 mm/s; E was 0; V pmax was 4 867 ml, and τ max was 844–3 800 s (with hydraulic retention time 2 222–10 000 s). Under fluidization state, u ranged 0.45 mm/s to 6.88 mm/s; and E, V pmax, and τ max were 5.28%–255.69%, 1 368–4 559 ml, and 104–732 s (with hydraulic retention time between 145 s and 2 222 s), respectively. Under transportation state, u was larger than 6.88 mm/s and washout of granular sludge occurred and destabilized the SAB. The predictions from these models agreed well with the experimental data; thus, they may be used to optimize the operations and designs of SAB. Under bed fluidization state of SAB, E correlated positively with u g and u l, while V pmax and τ max correlated negatively with u g and u l. For E and V pmax, the sensitivities of u g and u l were close to each other, while for τ max, the sensitivity of u l was more than that of u g.
Footnotes
Project supported by the Hi-Tech Research Development Program (863) of China (No. 2006AA06Z332) and the Ministry of Science and Technology of China (No. 2008BADC4B10)
References
- 1.Chen C, Wang AJ, Ren NQ, Lee DJ, Lai JY. High-rate denitrifying sulfide removal process in expanded granular sludge bed reactor. Bioresource Technology. 2009;100(7):2316–2319. doi: 10.1016/j.biortech.2008.10.023. [DOI] [PubMed] [Google Scholar]
- 2.Chen JW, Tang CJ, Zheng P, Zhang L. Performance of lab-scale SPAC anaerobic bioreactor with high loading rate. Chinese Journal Biotechnology. 2008;24(8):1413–1419. doi: 10.1016/S1872-2075(08)60062-X. (in Chinese) [DOI] [PubMed] [Google Scholar]
- 3.Chern HH, Fan LS, Muroyama KL. Hydrodynamics of concurrent gas-liquid-solid semifluidization with a liquid as the continuous phase. American Institute of Chemical Engineers Journal. 1984;30(2):288–294. [Google Scholar]
- 4.Diez Blanco V, Garacia Encina PA, Fdz-polanco F. Effects of biofilm growth, gas and liquid velocities on the expansion of an anaerobic fluidized bed reactor (AFBR) Water Research. 1995;29(7):1649–1654. doi: 10.1016/0043-1354(95)00001-2. [DOI] [Google Scholar]
- 5.Heijnen JJ, Mulder A, Enger W, Hoeks F. Review on the application of anaerobic fluidized bed reactors in wastewater treatment. Chemical Engineering Journal. 1989;41(3):37–50. doi: 10.1016/0300-9467(89)80029-2. [DOI] [Google Scholar]
- 6.Huang JS, Wu CS. Specific energy dissipation rate for fluidized-bed bioreactors. Biotechnology and Bioengineering. 1996;50(6):643–654. doi: 10.1002/(SICI)1097-0290(19960620)50:6<643::AID-BIT5>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
- 7.Jin RC, Zheng P, Hu AH, Mahmood Q. Performance comparison of two anammox reactors: SBR and UBF. Chemical Engineering Journal. 2008;138(1-3):224–230. doi: 10.1016/j.cej.2007.06.038. [DOI] [Google Scholar]
- 8.Khan AR, Richardson JF. The resistance to motion of a solid sphere in a fluid. Chemical Engineering Communications. 1987;62(1):135–150. doi: 10.1080/00986448708912056. [DOI] [Google Scholar]
- 9.Khan AR, Richardson JF. Fluid-particle interactions and flow characteristics of fluidized beds and settling suspensions of spherical particles. Chemical Engineering Communications. 1989;78(1):111–130. doi: 10.1080/00986448908940189. [DOI] [Google Scholar]
- 10.Lens PNL, van den Bosch MC, Poll WH, Lettinga G. Effect of staging on volatile fatty acid degradation in a sulfidogenic granular sludge reactor. Water Research. 1998;32(4):1178–1192. doi: 10.1016/S0043-1354(97)00323-0. [DOI] [Google Scholar]
- 11.Lettinga G, Field JA, Sierra-Alvarez R. Future perspectives for the anaerobic treatment of forest Industrial wastewaters. Water Science and Technology. 1991;24(3/4):91–102. [Google Scholar]
- 12.Pereboom JHF, Vereijken TLFM. Methanogenic granule development in full scale internal circulation reactors. Water Science and Technology. 1994;30(8):9–21. [Google Scholar]
- 13.Sowmeyan R, Swaminathan G. Evaluation of inverse anaerobic fluidized bed reactor for treating high strength organic wastewater. Bioresource Technology. 2008;99(9):3877–3880. doi: 10.1016/j.biortech.2007.08.021. [DOI] [PubMed] [Google Scholar]
- 14.Sowmeyan R, Swaminathan G. Performance of inverse anaerobic fluidized bed reactor for treating high strength organic wastewater during start-up phase. Bioresource Technology. 2008;99(14):6280–6284. doi: 10.1016/j.biortech.2007.12.001. [DOI] [PubMed] [Google Scholar]
- 15.Summerfelt ST. Design and management of conventional fluidized-sand biofilters. Aquacultural Engineering. 2006;34(3):275–302. doi: 10.1016/j.aquaeng.2005.08.010. [DOI] [Google Scholar]
- 16.Wu CS, Huang JS, Chou H. Influence of internal biogas production on hydrodynamic behavior of anaerobic fluidized-bed reactors. Water Research. 2006;40(1):126–136. doi: 10.1016/j.watres.2005.10.036. [DOI] [PubMed] [Google Scholar]
- 17.Yu HB, Rittmann BE. Predicting bed expansion and phase hold-ups for there-phase fluidized-bed reactors with and without biofilm. Water Research. 1997;31(10):2604–2616. doi: 10.1016/S0043-1354(97)00102-4. [DOI] [Google Scholar]
- 18.Zheng P, Feng XS. Biotechnology for Wastes Treatment. Beijing, China: Higher Education Press; 2006. (in Chinese) [Google Scholar]
- 19.Zheng P, Chen JW, Tang CJ, et al. A New Type of Spiral Automatic Circulation (SPAC) Anaerobic Reactor. ZL200720106182.6. China Patent. 2008 (in Chinese)