Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 1988 Jul;85(14):5057–5061. doi: 10.1073/pnas.85.14.5057

Monte Carlo simulations of the folding of beta-barrel globular proteins.

J Skolnick 1, A Kolinski 1, R Yaris 1
PMCID: PMC281687  PMID: 3393530

Abstract

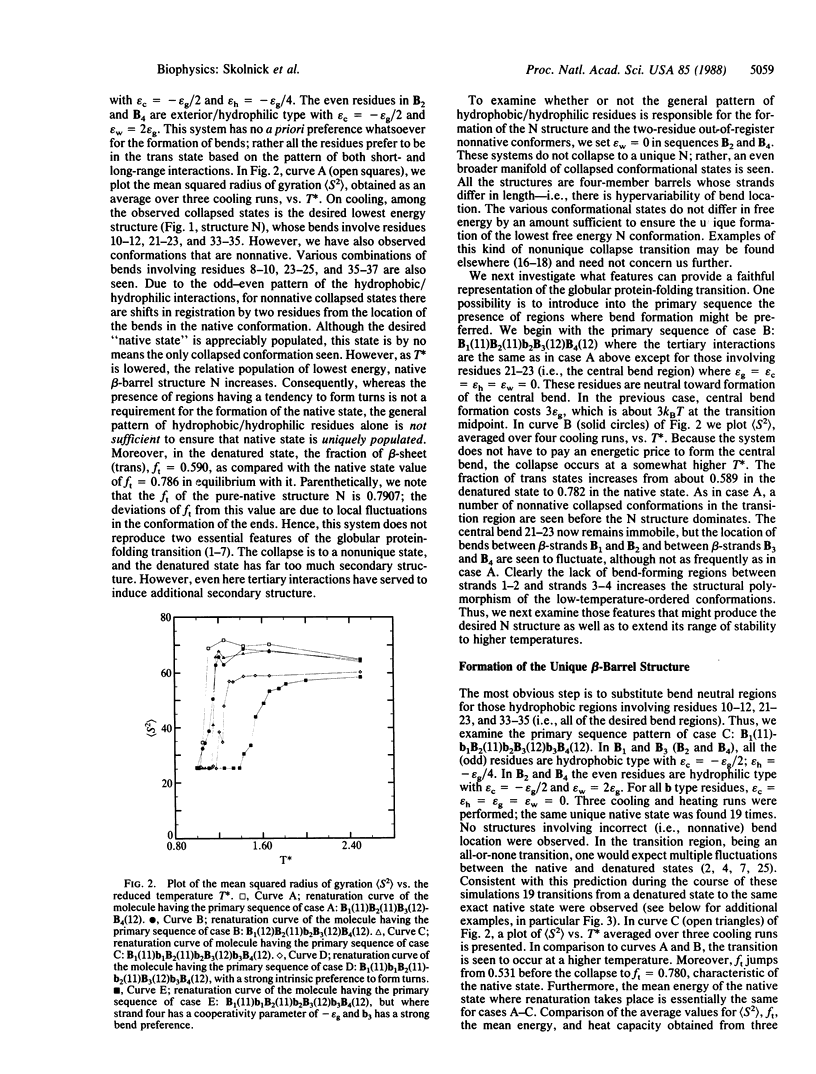
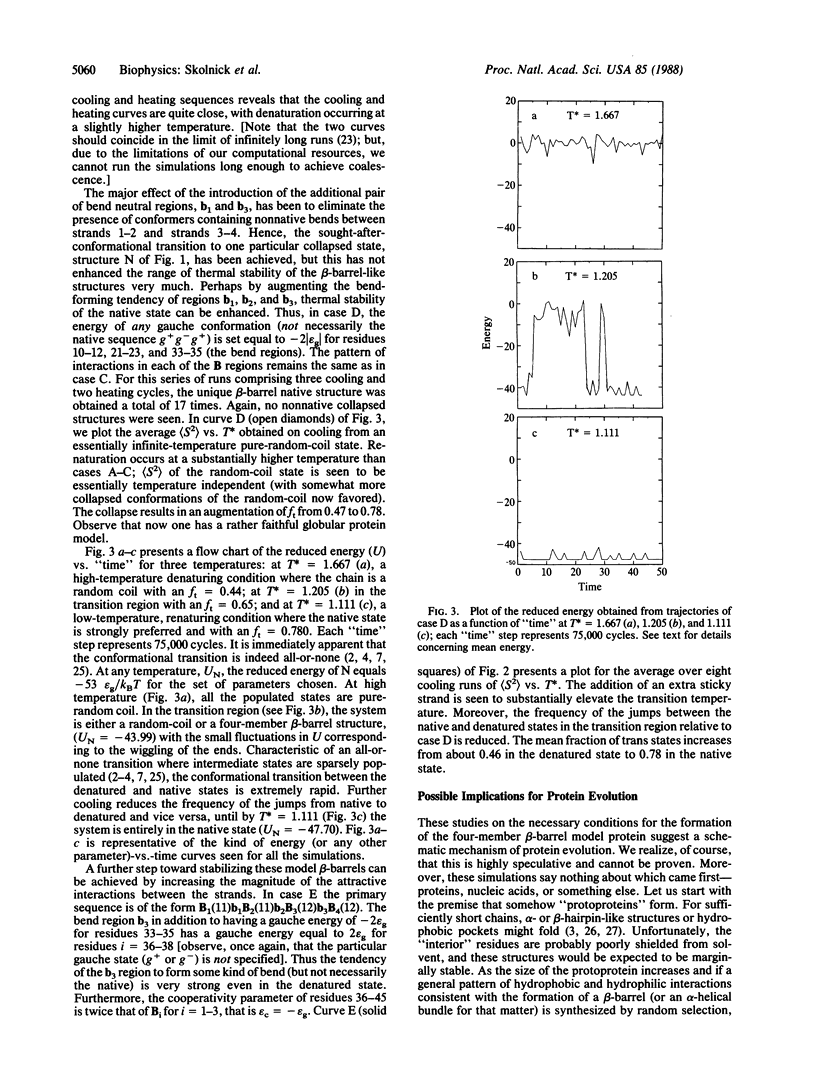
With the use of dynamic Monte Carlo simulations, the necessary conditions for the collapse from a random-coil denatured state to a structurally unique four-member beta-barrel native state of a model globular protein have been investigated. These systems are free to roam through all of configuration space--both native and nonnative interactions are allowed. The relative importance of hydrophobic and hydrophilic interactions and the presence or absence of statistical bend-forming regions for the formation of a unique native state are examined, and the conditions necessary for a denatured-to-native (and vice versa) conformational transition that is thermodynamically all-or-none and which always results in collapse to the same, four-member beta-barrel are explored. These conditions are found to be a general pattern of hydrophobic/hydrophilic residues that allows the native state to differentiate the interior from the exterior of the protein and the presence of regions that are, at the very least, neutral toward turn formation. The former set of interactions seems to define the mean length of the beta-stretch, and the latter set serves to lock the native state into the lowest free energy state, the native conformation. These folding simulations strongly suggest that the general rules of protein folding are rather robust and that site-specific tertiary interactions are only involved in structural fine tuning. The conditions required for the formation of a structurally unique native state from a manifold of collapsed conformations that are originally quite close in energy is highly suggestive of a mechanism of protein evolution by means of random mutations. The implications of these folding studies for such a mechanism are qualitatively explored.

Full text

PDF
5057

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Anfinsen C. B. Principles that govern the folding of protein chains. Science. 1973 Jul 20;181(4096):223–230. doi: 10.1126/science.181.4096.223. [DOI] [PubMed] [Google Scholar]
  2. Auer H. E., Miller-Auer H. Dynamics of the disordered-beta transition in poly(L-tyrosine) determined by stopped-flow spectrometry. Biopolymers. 1986 Sep;25(9):1607–1613. doi: 10.1002/bip.360250904. [DOI] [PubMed] [Google Scholar]
  3. Fasman G. D. The road from poly(alpha-amino acids) to the prediction of protein conformation. Biopolymers. 1987;26 (Suppl):S59–S79. doi: 10.1002/bip.360260009. [DOI] [PubMed] [Google Scholar]
  4. Go N. Theoretical studies of protein folding. Annu Rev Biophys Bioeng. 1983;12:183–210. doi: 10.1146/annurev.bb.12.060183.001151. [DOI] [PubMed] [Google Scholar]
  5. Karplus M., McCammon J. A. The internal dynamics of globular proteins. CRC Crit Rev Biochem. 1981;9(4):293–349. doi: 10.3109/10409238109105437. [DOI] [PubMed] [Google Scholar]
  6. Kolinski A., Skolnick J., Yaris R. Monte Carlo simulations on an equilibrium globular protein folding model. Proc Natl Acad Sci U S A. 1986 Oct;83(19):7267–7271. doi: 10.1073/pnas.83.19.7267. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Kolinski A., Skolnick J., Yaris R. Monte Carlo studies on equilibrium globular protein folding. I. Homopolymeric lattice models of beta-barrel proteins. Biopolymers. 1987 Jun;26(6):937–962. doi: 10.1002/bip.360260613. [DOI] [PubMed] [Google Scholar]
  8. Lewis P. N., Go N., Go M., Kotelchuck D., Scheraga H. A. Helix probability profiles of denatured proteins and their correlation with native structures. Proc Natl Acad Sci U S A. 1970 Apr;65(4):810–815. doi: 10.1073/pnas.65.4.810. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Li Z., Scheraga H. A. Monte Carlo-minimization approach to the multiple-minima problem in protein folding. Proc Natl Acad Sci U S A. 1987 Oct;84(19):6611–6615. doi: 10.1073/pnas.84.19.6611. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. McCammon J. A. Computer-aided molecular design. Science. 1987 Oct 23;238(4826):486–491. doi: 10.1126/science.3310236. [DOI] [PubMed] [Google Scholar]
  11. Privalov P. L. Stability of proteins: small globular proteins. Adv Protein Chem. 1979;33:167–241. doi: 10.1016/s0065-3233(08)60460-x. [DOI] [PubMed] [Google Scholar]
  12. Ptitsyn O. B., Finkelstein A. V. Similarities of protein topologies: evolutionary divergence, functional convergence or principles of folding? Q Rev Biophys. 1980 Aug;13(3):339–386. doi: 10.1017/s0033583500001724. [DOI] [PubMed] [Google Scholar]
  13. Richardson J. S. The anatomy and taxonomy of protein structure. Adv Protein Chem. 1981;34:167–339. doi: 10.1016/s0065-3233(08)60520-3. [DOI] [PubMed] [Google Scholar]
  14. Rose G. D., Winters R. H., Wetlaufer D. B. A testable model for protein folding. FEBS Lett. 1976 Mar 15;63(1):10–16. doi: 10.1016/0014-5793(76)80184-6. [DOI] [PubMed] [Google Scholar]
  15. Tanford C. Protein denaturation. Adv Protein Chem. 1968;23:121–282. doi: 10.1016/s0065-3233(08)60401-5. [DOI] [PubMed] [Google Scholar]
  16. Van Gunsteren W. F., Berendsen H. J. Molecular dynamics: perspective for complex systems. Biochem Soc Trans. 1982 Oct;10(5):301–305. doi: 10.1042/bst0100301. [DOI] [PubMed] [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES