Prediction of Probabilistic Sleep Distributions Following Travel Across Multiple Time Zones

Abstract

Study Objectives:

To parameterize and validate a model to estimate average sleep times for long-haul aviation pilots during layovers following travel across multiple time zones. The model equations were based on a weighted distribution of domicile- and local-time sleepers, and included algorithms to account for sleep loss and circadian re-synchronization.

Design:

Sleep times were collected from participants under normal commercial operating conditions using diaries and wrist activity monitors.

Participants:

Participants included a total of 306 long-haul pilots (113 captains, 120 first officers, and 73 second officers).

Measurement and Results:

The model was parameterized based on the average sleep/wake times observed during international flight patterns from Australia to London and Los Angeles (global R² = 0.72). The parameterized model was validated against the average sleep/wake times observed during flight patterns from Australia to London (r² = 0.85), Los Angeles (r² = 0.79), New York (r² = 0.80), and Johannesburg (r² = 0.73). Goodness-of-fit was poorer when the parameterized model equations were used to predict the variance across the sleep/wake cycles of individual pilots (R² = 0.42, 0.35, 0.31, and 0.28 for the validation flight patterns, respectively), in part because of substantial inter-individual variability in sleep timing and duration.

Conclusions:

It is possible to estimate average sleep times during layovers in international patterns with a reasonable degree of accuracy. Models of this type could form the basis of a stand-alone application to estimate the likelihood that a given duty schedule provides pilots, on average, with an adequate opportunity to sleep.

Citation:

Darwent D; Dawson D; Roach GD. Prediction of probabilistic sleep distributions following travel across multiple time zones. SLEEP 2010;33(2):185-195.

THE CURRENT GENERATION OF BIOMATHEMATICAL MODELS OF SLEEP AND PERFORMANCE ARE BROADLY BASED ON THE PHYSIOLOGICAL PRINCIPLES represented in the two-process model of sleep regulation.^1,2 In accordance, the structure and timing of the sleep/wake cycle is regulated by the interaction of two basic physiological processes: (1) a homeostatic process, that minimizes deviations from a basal quantity of sleep required for optimal neurobehavioral functioning; and (2) a light-sensitive circadian process, that determines oscillations in the propensity for sleep. The two-process model was originally conceived as an investigative tool—serving to generate and test hypotheses about the physiological mechanisms that regulate the sleep-wake cycle.³ Elaborated versions have since been developed to account for nonlinear interactions between the homeostatic and circadian processes,⁴ ultradian dynamics of electroencephalograph (EEG) slow wave activity,^5,6 photic entrainment of the circadian pacemaker,^7,8 and regulation of alertness during wake.^9,10 In conjunction with these developments, researchers have also extended the scope of their models to predict the performance impairment (or fatigue) that arises in connection with sleep loss and circadian disruption in industrial shiftwork settings.

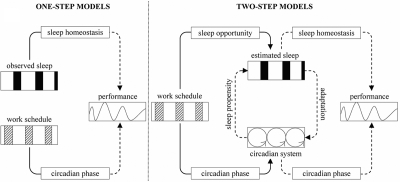
The characteristic elements of two major types of biomathematical models that have been developed for use in field-based settings are depicted in Figure 1. One-step models, shown in the left panel, estimate fatigue based on user-inputted work and sleep times.^11,12 The need to input observed sleep times limits the utility of one-step models to post hoc analyses or to highly specialized populations in which sleep times can be monitored continuously. To overcome this restriction, 2-step models, shown in the right panel, incorporate intermediary algorithms to estimate sleep times—thus allowing fatigue levels to be estimated on the basis of work schedule inputs alone.^13–15 Obtaining good estimates of sleep is critical to the utility of all 2-step model simulations. Predictive errors have the potential to prejudice subsequent estimates of fatigue and may compound across successive iterations where simulations require recursive input of previously estimated values.

Figure 1.

One-step and 2-step biomathematical models of human fatigue and performance. Continuous lines represent the passing of known values, while broken lines, the passing of estimated values. One-step models, represented on the left-side panel, generate outputs via predictive algorithms that require input of known work-rest and sleep-wake times. Two-step models, represented on the right-side panel, include intervening algorithms to estimate sleep-wake times based solely on known or planned work-rest times.

Models describing the physiological processes contributing to sleep and wakefulness have been developed based on data collected in experimental protocols. In view of this heritage, the predictions made by these models correspond remarkably well with sleep times observed in laboratory conditions.^2,5,12,16 Sleep homeostasis and circadian rhythmicity also exert control on sleep timing and duration in naturalistic settings, but may be subject to mediation by social factors and rational decisions.^17,18 Individuals may adjust the timing of sleep-wake cycles in response to non-work social zeitgebers,^19–21 and therein bias exposure to light-dark conditions. The time course of sleep homeostasis may be mediated by decisions to abstain from, or otherwise restrict, sleep in view of social activities.²² Employees may also adopt anticipatory, as opposed to reactionary, sleep strategies as a means of balancing work and social commitments.²³ These decisions are usually concomitant with the use of volitional countermeasures such as alarm clocks, stimulants, and social interaction.

Field-based studies conducted in the aviation industry indicate that most pilots adjust the timing of main sleeps in accordance with local zeitgebers during international layovers, independent of flight direction or the number of time zones crossed.^24–29 Only a minority are reported to maintain a sleep/wake cycle in phase with the domicile time zone while resting in an alternate time zone.^24–29 Pilots often facilitate these strategies by initiating short recovery and/or anticipatory sleeps around arrival and departure times.^25–28 The consistency of these observed sleep/wake patterns cannot be explained solely on the basis of sleep physiology—especially given that circadian adaptation to local zeitgebers is not instantaneous. Thus, it is our premise that strategic decisions, motivated by duty schedule constraints, local social and geophysical zeitgebers, and sleep physiology, are the main drivers of the sleep/wake cycles exhibited by pilots during layovers.

The primary aim of this study was to parameterize and validate a general model to estimate average sleep times for long-haul aviation pilots during layovers of international flight and duty patterns. The intention was to parameterize equations that could be incorporated into any 2-step biomathematical model of human fatigue and performance. To this end, the predictors were restricted to prospective variables that could be obtained or estimated from flight and duty schedules or on the basis of previous empirical research. However, in contrast to the traditional deterministic biological models of sleep, our objective was to model the probability of an individual being asleep within a given time period. This objective is consistent with our premise that volitional decision-making processes influence sleep timing and duration.

Description of the Model

Equation 1 – Baseline regression equation

The initial objective was to define a regression equation to model sleep probability quotients at time, t, under normal, or baseline, sleep/wake conditions. The criterion of normality was based on the ideal scenario that sleep/wake data were sampled from participants who were not sleep deprived, who were entrained to the exogenous day-night cycle, and whose sleep/wake times were not restricted by scheduled duty periods. A modified form of a standard cosine equation was defined to model baseline sleep probability quotients. This function is described in Equation 1 below:

where:

• f(t) = predicted sleep probability quotient at time of day, t

• t = independent variable representing time of day

• M = parameter representing the midline-estimating statistic of the rhythm (MESOR) of the cosine function

• A = parameter representing the amplitude of the cosine function

• P = parameter representing the phase of the cosine function

• S = parameter representing the slope of the distribution

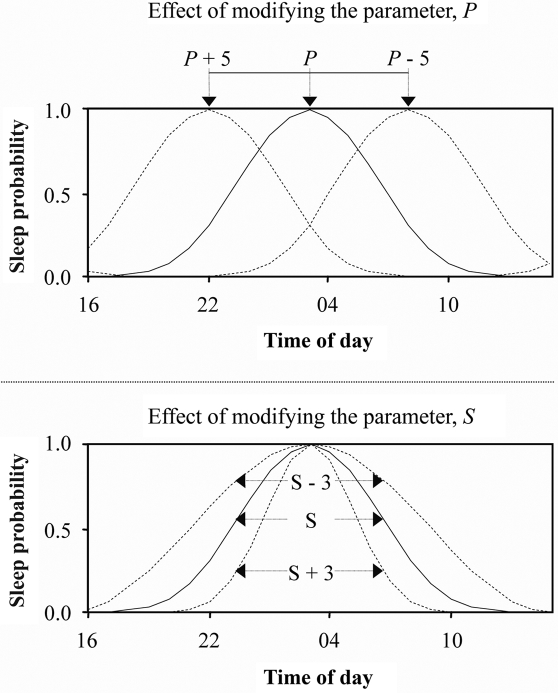
Given that observed sleep probability quotients have, a priori, a maximum value of 1.0 and a minimum value of 0.0, the MESOR, M, and the amplitude, A, were assigned constant values of 0.5. The phase offset parameter, P, and the exponential parameter, S, determine the timing of the acrophase/nadir and slope of the distribution respectively. The transformational significance of modifying the P and S parameters is demonstrated in Figure 2. Variations in these parameters produce transforms that are orthogonal to each other and to the minimum and maximum values of the fitted distribution.

Figure 2.

Effect of modifying the P (top panel) and S (lower panel) parameters of the baseline regression equation (Equation #1). Continuous lines represent distributions for any given value of P and S, respectively. Broken lines represent the curve translations that result from adding or subtracting from the given values.

Equation 2 – Transmeridian regression equation

Empirical observations of pilots' sleep during layovers in foreign destinations indicate that the timing of main sleep periods has a biphasic distribution. A certain proportion of pilots, W, initiate main sleeps during the local night, while the remainder, 1-W, initiate main sleeps at the appropriate circadian phase/domicile time. The function to model sleep probability quotients during international layovers may be stated as:

where:

• f_I(t) = predicted sleep probability quotient at time, t

• f(t) = cosine function using local time, t, as an independent variable

• f(c) = cosine function using circadian phase, c, as an independent variable (see Ancillary Equation 1)

• s = independent variable representing the impact of sleep on sleep probability (see Ancillary Equation 2)

• W = constrained weighting parameter (0 ≤ W ≤ 1) representing the proportion of pilots who adjust the timing of sleep/wake cycles in accordance with local zeitgebers

Equation 2 describes a proportionate weighting of two juxtaposed distributions. The first, (t), represents “local-time sleepers” while the second, f(c), represents “biological-time sleepers.” The phase relationship between f(t) and f(c) is dependent on the time zone difference between domicile and layover locations and the rate of circadian adaptation. Two ancillary formulae, presented below, describe the procedures used to estimate circadian phase and to account for the contribution of sleep loss and anticipatory behavior to sleep probability quotients.

Ancillary Equation 1 – Circadian phase estimates

Circadian adaptation to local zeitgebers following transmeridian travel has been studied across all flight directions and a multitude of time zone displacements.^29–34 These studies suggest that the time course of circadian resynchronization can be represented as a nonlinear, asymptotic function between the initial circadian phase and time of day in the destination time zone. A pre-existing model was used to estimate circadian resynchronization:³⁵

where:

• t_e = elapsed time since arrival, in days

• R(t_e) = the difference between circadian phase and local time at the elapsed time, t_e, in hours

• ΔΦ = the difference between circadian phase and local time when t_e = 0

• α = constant representing the rate of adaptation

The α parameter was assigned a value of 0.5. This equates to a phase shift per day of approximately 50% of the required remaining shift for both phase delays and advances. This provides a rough estimate of the time course of circadian adaptation following transmeridian flight.^34,35 Given a value for R(t_e), the function to estimate circadian phase, c, at a given local time, t, is thus be given by:

where:

• c = circadian phase at local time, t

• t = time of day in the destination time zone

Ancillary Equation 2 – Sleep homeostasis and anticipatory sleep/wake behavior

To incorporate sleep homeostatic and anticipatory sleep behavior, the S parameter of the baseline model was substituted for an independent variable, s. The equation represents the sum of sleep obtained in the 12 h before, and 12 h after, a given epoch, t. The value is expressed as a proportion of the sum of sleep probability quotients derived from the 24-h baseline model (see Equation #1). As sleep in the prior 12 h and intended sleep in the ensuing 12 h increase or decrease, so too the value of s. In turn, variation in the value of s inversely modifies predicted sleep probability quotients. The algorithm to calculate the s variable is given by:

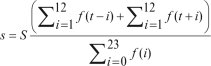where:

• s = derived variable representing the effect of sleep homeostasis and sleep anticipation on sleep probability

• S = constant value representing the parameter estimate obtained for S of Equation #1

• Σ_i=1¹²f(t−i= the sum of sleep probability quotients in the 12 hours prior to time, t

• Σ_i=1¹²f(t+i= the sum of expected sleep probability quotients in the 12 hours after time, t

• Σ_i=0²³f(i) = the sum of predicted sleep probability quotients derived from Equation #1 over the time interval T ϵ [0,23]

The s variable is based on the notion that the probability of being asleep at any point in time is: (1) inversely related to the amount of sleep obtained in the immediate past, via the biological process of sleep homeostasis; and (2) inversely related to the amount of sleep expected to be obtained in the immediate future, via an anticipatory process based on training and experience. For example, recovery sleeps taken on arrival in a destination location partly reflect the influence of sleep homeostasis. Conversely, anticipatory sleeps taken just prior to departure partly reflect an intention to sustain alertness during ensuing flights by minimizing prior wakefulness and increasing prior sleep.

To calculate sleep in the 12 h prior to time, t, previously simulated sleep probability quotients, f(t-i), are recursively input back into the simulation and summed accordingly. Conversely, to calculate sleep in the 12 h after to time, t, expected sleep probability quotients, f(t+i), are pre-calculated using the transmeridian model equation where, to avoid circularity, the S parameter is substituted in place of the relative sleep loss variable, s. Note, that for the purpose of estimating parameters, the s variable is calculated using observed rather than simulated values.

Importantly, the algorithm does not regard duty times as sleep opportunities and fully discounts any sleep that pilots might be expected to obtain in-flight. The primary reasons for this are that: (1) the model is intended as a tool to predict sleep times for layovers in advance of actual operations before in-flight sleep times are known; and (2) the factors which contribute to the timing of in-flight and the relative recovery value of in-flight sleep are uncertain.

METHODS

Ethics

Ethical approval for conducting the studies was granted by the Human Research Ethics Committee of the University of South Australia. All potential recruits were informed that participation was voluntary, that any information collected would be de-identified and confidential, and that non-participation or withdrawal from the study would not influence future employment conditions. No financial remuneration was offered to or received by participants for taking part in the study.

Participants

A total of 306 pilots were sampled from a commercial passenger airline based in Australia. Each participant collected data across successive flight and duty patterns for at least 2 weeks during the course of normal international commercial operations. The baseline regression equation was parameterized using data collected from 217 pilots (76 Captains, 86 First Officers, and 55 Second Officers). The transmeridian regression equation was parameterized using data collected from 36 pilots (14 Captains, 15 First Officers, and 7 Second Officers) and then validated using data collected from 59 pilots (25 Captains, 22 First Officers, and 12 Second Officers).

Baseline Data Set

The baseline regression equation (see Equation 1) was parameterized using 1,571 sleep periods collected in 387 domicile rest periods. Rest periods had a mean (± standard deviation) of 133.2 (± 44.9) h, but the distribution was positively skewed because only rest periods ≥ 96 h were selected for analyses (median = 120.9 h; 95% confidence interval = 96.8 to 238.6 h). To minimize the influence of flight/duty periods and circadian desynchronization on sleep/wake behavior, data in the initial and final 24 h of each rest period were excluded from all further consideration. The truncated rest periods were used to calculate a baseline sleep probability distribution using waveform eduction, wherein sleep probability quotients were calculated by dividing the total number of pilots who were asleep by the total number of pilots at rest (not on duty) for every 1-min epoch of the “24-hour” clock. This procedure yields a waveform whose sum (i.e., sum of the sleep probability quotients) is equivalent to the average amount of sleep obtained by the constituent sample/24-h period.

Parameterization and Validation Data Sets

The transmeridian regression model was parameterized using sleep/wake records from 41 data sets collected during 2 types of flight and duty patterns: (1) Australia - Bangkok - London - Singapore - Australia (LHR-p, n = 25); and (2) Australia - Los Angeles - Auckland - Australia (LAX-p, n = 16). The parameterized version of the transmeridian regression model was validated using sleep/wake records from 71 data sets collected during 4 types of flight and duty patterns: (1) Australia - Singapore - London - Singapore/Bangkok - Australia (LHR - v, n = 23); (2) Australia - Auckland - Los Angeles - Australia (LAX-v, n = 17); (3) Australia - Los Angeles - New York - Los Angeles (JFK-v, n = 18); and (4) Australia - Johannesburg - Australia (JNB-v, n = 13). The number of data sets is greater than the number of participants because some participants contributed more than one data set.

All flight and duty patterns commenced and terminated in Australia in the UTC +10 time zone—in Sydney, Melbourne, or Brisbane. The initial outbound flights from Australia departed either in the morning (LAX-p, LAX-v, and JNB-v) or early-to-mid afternoon (LHR-p, LHR-v, and JFK-v). The 2 days/nights directly preceding the initial departure times were classified as the “pre-pattern” rest period for each of the data sets. The terminal inbound flights to Australia arrived either in the morning (LHR-p, LAX-p, LHR-v, LAX-v, and JFK-v) or mid-afternoon (JNB-v). The 2 days/nights directly following the final arrival times were classified as the “post-pattern” rest period for each of the data sets. The time zone and the mean duration and timing of layovers for the parameterization and validation data sets are provided in Table 1.

Table 1.

The time zone and the duration and local timing of layovers for the parameterization and validation data sets

Flight and Duty Pattern	Time Zone	Arrive Time (time ± min)	Rest Duration (hours ± min)	Depart Time (time ± min)
LHR-p (n = 25)
Bangkok	+8	23:51 ± 17	23.8 ± 27	23:38 ± 24
London	+0	7:32 ± 48	61.7 ± 28	21:07 ± 33
Singapore	+7	19:10 ± 46	47.9 ± 38	19:05 ± 21
LAX-p (n = 16)
Los Angeles	−8	8:34 ± 69	35.9 ± 65	20:29 ± 41
Auckland	+12	6:15 ± 42	23.7 ± 52	5:57 ± 29
LHR-v (n = 23)
Singapore	+7	22:05 ± 39	24.0 ± 49	22:07 ± 40
London	+0	6:04 ± 40	39.0 ± 41	21:04 ± 32
Singapore/Bangkok	+7	17:39 ± 73	48.2 ± 37	17:52 ± 47
LAX-v (n = 17)
Auckland	+12	16:58 ± 85	24.6 ± 81	17:36 ± 34
Los Angeles	−8	11:30 ± 43	35.1 ± 37	22:35 ± 19
JFK-v (n = 18)
Los Angeles	−8	10:36 ± 29	45.3 ± 18	7:55 ± 22
New York	−5	18:09 ± 57	72.0 ± 52	18:07 ± 21
Los Angeles	−8	22:59 ± 45	46.6 ± 35	21:36 ± 26
JNB-v (n = 13)
Johannesburg	+2	16:21 ± 36	72.7 ± 34	17:04 ± 10

Separate sleep probability distributions were calculated for each layover and pre- and post-pattern rest period of each flight and duty pattern. This was done by dividing the total number of pilots who were asleep by the total number of pilots at rest (not on duty) for every 1-min epoch of the given rest period.

Data Collection Protocol

Participants recorded the timing and origin and destination locations of all flight and duty periods on a flight and duty time diary. Participants' sleep/wake behavior was determined before, during, and after international flight/duty patterns using activity monitors (Respironics) in conjunction with sleep diaries. Activity monitor records were collected in 1-min epochs and subsequently analyzed using Actiware-Sleep algorithms with sensitivity set at “medium” (threshold activity value of 40). Sleep was classified as the time in between sleep onset and sleep offset (sleep period duration) for all descriptive and inferential analyses of sleep.

Statistical analyses

Development of the sleep probability model occurred in a series of 4 stages: (1) parameterization of the baseline regression equation; (2) parameterization of the transmeridian regression equation; (3) simulation to validate the parameterized transmeridian model; and (4) assessment of goodness-of-fit for individuals. Statistical analyses were performed using Statistical Package for the Social Sciences (SPSS) for Windows version 14.0.0.

Parameterization of the Baseline Regression Equation

A nonlinear regression was performed using the Levenberg-Marquardt optimization procedure to estimate the phase, P, and the slope, S, parameters of the baseline equation. The observed baseline sleep probability quotients were used as the dependent variable and local clock-time, t, as the independent variable. Goodness-of-fit for the baseline model was determined by calculating R² and mean square error.

Parameterization of the Transmeridian Regression Equation

The parameter estimate obtained for P, as described above, was substituted into the transmeridian regression equation and treated as a constant value. The parameter estimate for S and the sum of the “fitted” baseline distribution were used to derive an independent variable, s, representing the relative degree of accumulated and anticipated sleep loss/gain (see Ancillary Equation 2). A separate global nonlinear regression was performed to estimate the W parameter of the transmeridian regression equation. The observed sleep probability quotients derived from the 2 parameterization data sets (LHR-p, LAX-p) were used as a dependent variable. Estimated circadian phase (see Ancillary Equation 1), local time, and sleep loss/gain (i.e., the s variable) were used as independent variables. Since W was a constrained parameter, the sequential quadratic programming option in the SPSS nonlinear regression module was used to optimize the procedure.

Simulation To Validate the Parameterized Transmeridian Model

A simulation program based on the parameterized transmeridian equations was developed in Microsoft Excel 2003 to validate the model. Simulated values were calculated solely on the transmeridian model equations, the parameter estimates obtained in the baseline and transmeridian regression analyses, and inputted flight and duty schedules. To validate the transmeridian model, the flight and duty schedules associated with the 2 parameterization data sets were inputted into the simulation program. For each rest period, the observed and simulated sleep probability quotients were correlated to assess the external validity of the model. Goodness-of-fit for the group average information provided by the model was determined by calculating r² and mean square error for the observed and simulated data. To further validate the model, similar procedures to those described above were applied to the 4 independent validation data sets. Specifically, the observed and simulated sleep probability quotients were correlated for each rest period to assess the external validity of the model. Goodness-of-fit for the group average information provided by the model was determined by calculating r² and mean square error for the observed and simulated data. In addition to the fit of the waveform itself, the sum of the observed, fitted, and simulated sleep probability distributions are also presented for comparison.

Assessment of Goodness-of-fit for Individuals

The purpose of the model was to predict average sleep/wake behavior, rather than the sleep/wake behavior of individuals. However, goodness-of-fit for individual pilots was also assessed by converting estimated sleep probability distributions to discrete sleep periods for every individual data set. The analysis took into account the minor variations in flight arrival and departure times across the sample and generated a unique set of predicted sleep periods for each individual data set. Importantly, the procedure used the parameter estimates obtained for the average model, and no inter-individual predictors were included. Thus, the purpose of this analysis was not to generate sleep patterns for individual pilots per se, but rather to describe the representativeness of the predicted sleep/wake times generated by the average model. Goodness-of-fit was quantified by calculating the total variance explained (R²) by the predicted sleep periods across the observed sleep periods for all individual data sets.

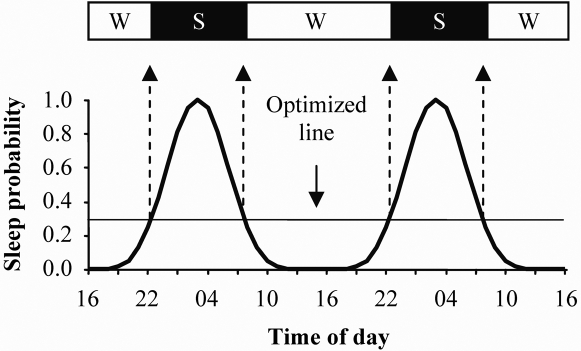
Estimated sleep probability distributions were converted to discrete sleep periods using the stepwise optimization procedure (method of steepest descent) illustrated in Figure 3. The procedure was carried out separately for every individual participant in each of the validation data sets. In accordance, the intersection of points of the horizontal line (optimized line) and the sleep probability distribution demarcate sleep onset and sleep offset times. Adjusting the height of the line modifies the relative length of sleep and wake periods. Optimization is achieved when the sum of the sleep period(s) approximates the sum of the sleep probability distribution (i.e., area under the curve) for a given rest period. For each of the validation data sets, the sum of the respective estimated sleep probability distributions were used to determine the height of the optimized line.

Figure 3.

Pictograph showing the optimization process used to convert a sleep probability distribution into sleep (S) and wake (W) periods. Optimization is achieved when the sum of the derived sleep periods is approximately equal to the sum of the area beneath the sleep probability distribution.

RESULTS

Sleep Behavior

Domicile Location

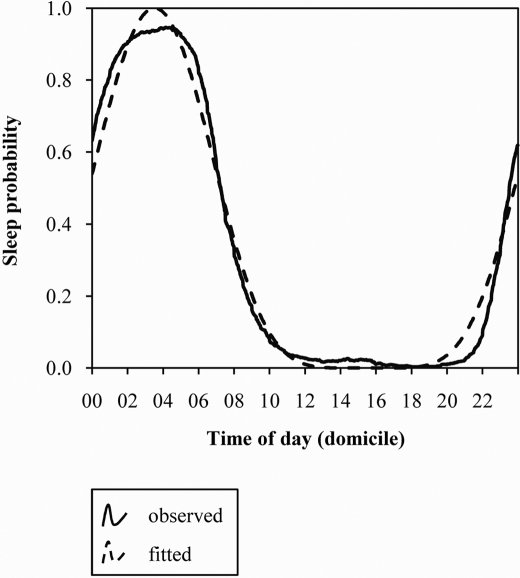
The great majority of participants exhibited normal monophasic sleep/wake cycles while resting at home for extended periods (≥ 96 h) in between flight and duty patterns. On average, sleeps sampled in the baseline dataset were associated with 7.38 (± 2.49) h in bed and 7.00 (± 2.48) h of sleep. The sleep probability distribution for this data set (Figure 4) reveals that the greatest proportion of participants were asleep between 04:00 and 06:00 (maximum = 0.946), while the fewest were asleep between 18:00 and 20:00 (minimum = 0.003). A minor secondary rise in sleep probability was evident in the post-lunch period (local maximum = 0.027 between 14:00 and 16:00). In total, only 4% of sleep was obtained in the daytime/evening period extending from 10:00 until 22:00.

Figure 4.

Observed and fitted sleep probability distributions for sleeps initiated during extended (≥ 96 h), domicile-based rest periods.

Layovers

During the layovers of the 6 flight and duty patterns, participants exhibited highly fragmented, polyphasic sleep/wake cycles (i.e., multiple sleep periods/24-h period). Participants initiated a mean of 1.74 (± 0.49) sleep periods/24-h period of each layover. These sleep periods were associated with a mean of only 5.71 (± 1.87) h in bed and 5.38 (± 1.85) h of sleep. Despite the relatively short duration of sleeps, the polyphasic sleep/wake cycles meant that participants were able to obtain a mean total of 9.25 (± 1.72) h in bed and 8.67 (± 1.69) h of sleep/24-h period of the layovers.

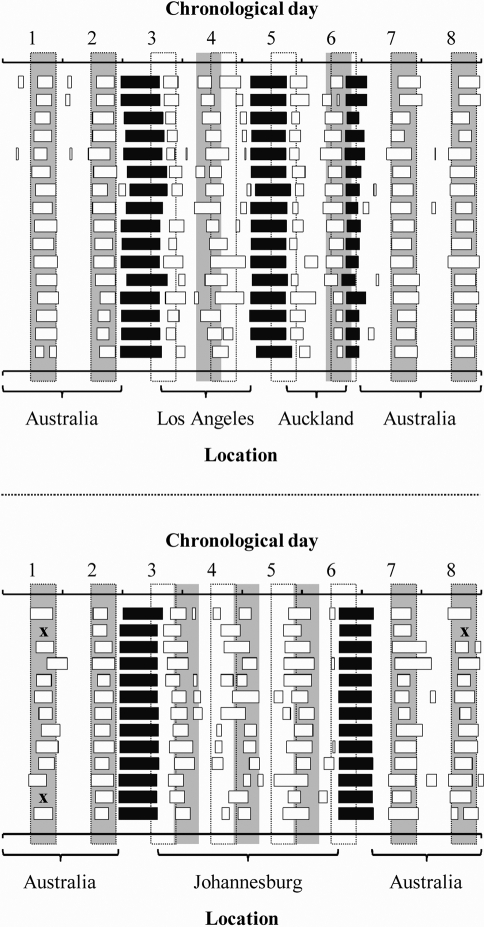
A variety of sleep patterns were evident during the layovers of each flight and duty pattern. To illustrate, the sleep/wake cycles adopted by participants in the LAX-p (eastbound) and JNB-v (westbound) data sets are depicted in Figure 5. Fragmented sleep patterns and the wide range of sleep period durations obfuscated the conventional distinction between main sleeps and naps. The majority of participants initiated relatively long sleeps during the local nights (gray-shaded areas) and shorter sleeps during the domicile nights (dotted outline areas), while a minority appeared to favor the converse strategy. Notably, sleep periods tended to cluster into particular time periods of each layover, irrespective of specific sleep strategies. These included: (1) the local nights; (2) the domicile nights; and (3) the time periods shortly before and after duty periods. These basic descriptions were also characteristic of the sleep patterns exhibited by participants in the LHR-p, LHR-v, LAX-v and JFK-v data sets (not shown).

Figure 5.

Raster plots depicting the sleep periods (white boxes), duty periods (black boxes), and local (grey-shaded areas) and domicile (areas within dotted outlines) nights from 21-07 h for 2 flight and duty patterns. The X symbol indicates missing data. The upper panel represents the 16 records for the eastbound Australia-Los Angeles-Auckland-Australia(LAX-p) pattern. The lower panel represents the 13 records for the westbound Australia-Johannesburg-Australia (JNB-v) pattern. For each plot, the upper x-axis indicates the day of the flight and duty pattern (i.e., the number of days extending from 48 h prior to departure from Australia until 48 h following arrival back in Australia), while the lower x-axis indicates location.

Parameter estimates

Baseline Model Parameter Estimates

The baseline regression model was highly significant, R² = 0.98, P < 0.001 (mean square error = 0.002). The parameter estimate and asymptotic 95% confidence intervals (CI) for the phase, P, was 5.365 (95% CI = 5.358 to 5.370) and for the slope, S, was 2.810 (95% CI = 2.776 to 2.844). The observed and fitted baseline curves are presented in Figure 4. The sums of observed and fitted distributions were 7.77 h and 7.73 h, respectively.

Transmeridian Model Parameter Estimates

The global nonlinear regression for the transmeridian model was significant, R² = 0.72, P < 0.001 (mean square error = 0.033). The parameter estimate and asymptotic 95% CI for the weighting coefficient, W, was 0.640 (95% CI = 0.632 to 0.647). Squared product-moment correlations between the observed and fitted sleep probability distributions were moderate-to-strong for both the LHR-p (r² = 0.84, P < 0.01, mean square error = 0.022) and the LAX-p (r² = 0.81, P < 0.01, mean square error = 0.025) data sets. Goodness-of-fit statistics and mean sleep quantities for the observed and fitted distributions for each rest period of the parameterization data sets are presented in Table 2. For comparison with the fitted values, Table 2 also reports goodness-of-fit statistics and mean sleep quantities for the simulated distributions that were calculated based on the flight and duty times in the LHR-p and LAX-p data sets.

Table 2.

Relationships between the observed, fitted, and simulated sleep probability curves for the parameterization data sets.

	Pearson Correlation (r)		Mean Sleep Quantity per Rest Period (hours)
	Observed × Fitted	Observed × Simulated	Observed	Fitted	Simulated
LHR-p
Pre-pattern	0.97	0.97	15.9	14.9	15.2
Bangkok	0.83	0.88	8.8	7.1	8.3
London	0.77	0.81	19.5	17.9	19.5
Singapore	0.92	0.93	18.2	14.1	15.7
Post-pattern	0.79	0.88	10.4	8.8	9.3
LAX-p
Pre-pattern	0.94	0.95	14.2	15.2	14.9
Los Angeles	0.74	0.74	13.1	9.3	10.6
Auckland	0.66	0.77	9.8	7.1	8.2
Post-pattern	0.96	0.98	8.9	8.7	8.5

All correlations were significant at the 0.01 α level.

Validation Simulations

For the 4 validation data sets, squared product-moment correlations between the averaged observed and simulated sleep probability distributions are presented in Table 3 (range = 0.73 to 0.85). The total variance explained by the average simulation model across the data sets provided by individual participants is also reported for each validation data set (range = 0.28 to 0.42). Goodness-of-fit statistics and mean sleep quantities for the observed and simulated distributions for each rest period of the validation data sets are presented in Table 4. Observed and simulated sleep probability distributions for the LHR-v and JFK-v validation data sets are presented in Figure 6 and Figure 7 respectively.

Table 3.

Goodness-of-fit statistics for validation data sets (observed × simulated)

Validation Data Sets	Pearson r2(Group)	Mean Square Error (Group)	Explained Variance R2(Individuals)
London (LHR-v)	0.85	0.023	0.42
Los Angeles (LAX-v)	0.79	0.026	0.35
New York (JFK-v)	0.80	0.031	0.31
Johannesburg (JNB-v)	0.73	0.030	0.28

All correlations were significant at the 0.01 α level.

Table 4.

Relationships between the observed and simulated sleep probability curves for the validation data sets

	Pearson Correlation (r)	Mean Sleep Quantity per Rest Period (hours)
	Observed × Simulated	Observed	Simulated
LHR-v
Pre-flight	0.98	15.7	15.5
Singapore	0.92	9.2	8.6
London	0.65	12.4	12.3
Singapore/Bangkok	0.95	17.1	15.6
Post-flight	0.85	19.2	18.5
LAX-v
Pre-flight	0.97	13.1	14.7
Auckland	0.92	10.2	7.8
Los Angeles	0.69	12.1	9.7
Post-flight	0.91	16.5	16.3
JFK-v
Pre-flight	0.94	15.3	15.6
Los Angeles	0.74	17.4	14.9
New York	0.95	24.5	23.4
Los Angeles	0.75	16.8	15.8
Post-flight	0.91	16.6	16.5
JNB-v
Pre-flight	0.92	12.5	15.1
Johannesburg	0.79	24.4	23.0
Post-flight	0.88	15.9	15.3

All correlations were significant at the 0.01 α level.

Figure 6.

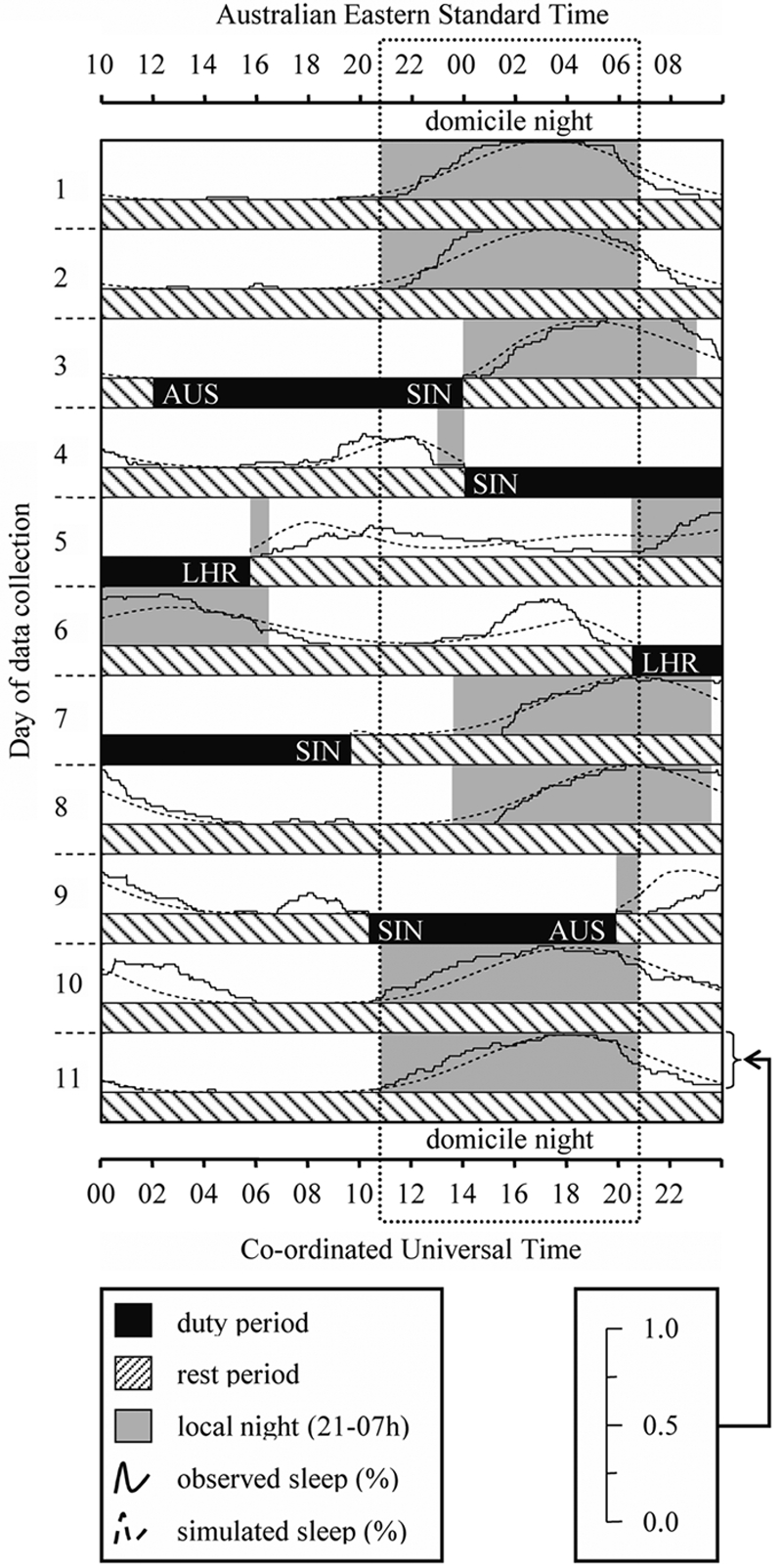
Observed and simulated sleep probability distributions for a flight pattern between Australia (AUS; Sydney, Melbourne, or Brisbane), Los Angeles (LAX), and New York (JFK). The vertical dotted box extending down each day of the plot indicates the night-time period from 21-07 h in the domicile time zone.

Figure 7.

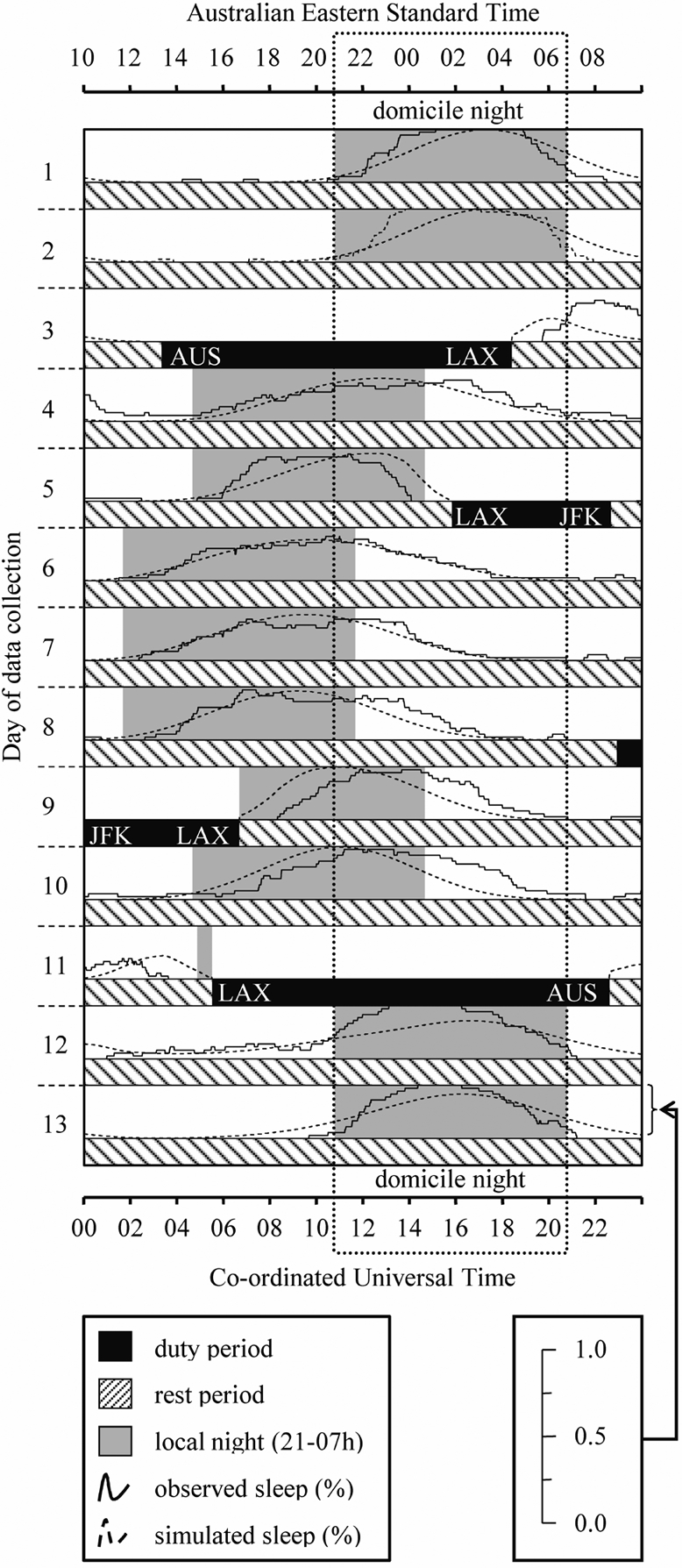
Observed and simulated sleep probability distributions for a flight pattern between Australia (AUS; Sydney, Melbourne, or Brisbane), Singapore (SIN), and London (LHR). The vertical dotted box extending down each day of the plot indicates the night-time period from 21-07 h in the domicile time zone.

DISCUSSION

The primary aim of this study was to parameterize and validate a model to estimate sleep probability distributions for long-haul pilots during layovers in international flight/duty patterns. The model is based on the premise that local social and geophysical zeitgebers exert a robust influence on pilots' volitional decisions of when to sleep. The premise was initially suggested by observations that the majority of pilots adjust the timing of their sleep/wake cycles to coincide with the local night after rapid travel across time zones.^24–29 Evidence of the validity of the model premise was provided by the moderate-to-strong goodness-of-fit estimates obtained between the model simulations and pilots' observed sleep/wake times. In our estimate, therefore, the observed predictive error resulted from the limits of the mathematical representation rather than any fundamental fault with the premise itself.

Parameter estimates for the models were obtained by conducting two successive nonlinear regression analyses, such that parameterization of the second regression was reliant on parameter estimates obtained from the first. The variance accounted for in the baseline model parameterized in the first regression was very high, and its parameters had narrow asymptotic 95% confidence intervals. This indicates that a priori biases in the ultimate transmeridian models were minimal. This was important given that models parameterized via a sequence of preliminary regressions are sensitive to the predictive power of the precursor models.

For the transmeridian model, there was a moderate-to-strong level of agreement between observed and fitted sleep probability values, indicating that the basic formulation of the model had reasonable veracity. In support of this, peaks and troughs of the fitted distributions aligned reasonably well with those of the observed distributions. Agreement between observed and fitted values was greatest for sleep probabilities in the pre- and post-pattern rest periods. This is not surprising given the explanatory power of the baseline model and the tendency for pilots to keep habitual sleep-wake cycles while at home between international flight patterns.²⁶ The comparisons of observed and simulated sleep probability values produced similar results to the comparisons of the observed and fitted values. The level of agreement between observed and simulated values was moderate-to-strong. Agreement was greatest for the pre- and post-pattern rest periods, and weakest in the post-arrival and pre-departure phases of the layovers.

The model tended to underestimate the amount of sleep obtained in the post-arrival and pre-departure phases of the layovers. This is potentially due to the formulation of the equation that accounts for the impact of sleep homeostasis and anticipatory behavior on sleep probability (i.e. Ancillary Equation 2). In particular, values close to the nadir (0) and acrophase (1) were less sensitive to changes in the power quotient (provided by Ancillary Equation 2) than values close to the MESOR. The sleep loss required to produce an appreciable change in an underlying probability quotient close to zero would have to be near total (i.e., sum of sleep obtained in the 12 h before and after a given epoch ≈ 0). However, in a model dealing with averaged, population-based data, this level of sleep loss is unlikely to eventuate.

The tendency to underestimate sleep during layovers is a limitation of the model. In the existing algorithms, there is no mechanism to directly predict the amount of sleep that occurs across an entire rest period. The total amount of sleep that is estimated for a given rest period is merely the emergent sum of the epoch-by-epoch prediction of sleep probability quotients. For applied use, underestimates of sleep amount have the potential to produce corresponding overestimates of fatigue-risk in 2-step biomathematical models of human performance (or fatigue), and vice versa. To address this limitation, our research group is currently developing modified algorithms to generate sleep probability distributions with a pre-defined amount of sleep. These pre-defined values would be estimated on the basis of a standard linear regression, using descriptive features of flight and duty patterns as dependent variables.

With the exception of the layover in New York, agreement between the observed and simulated values for layovers became weaker as the time zone difference between domicile and local time increased. One possible explanation for this outcome relates to our assumption that the proportion of pilots who sleep during local night is a fixed percent (represented by the W parameter in the model). It has previously been reported that the proportion of pilots who sleep at local time varies depending on the direction of travel.³⁶ The extent to which this reported directional asymmetry demonstrates a generalized change in pilots' preference for sleeping at local time is unclear. The majority of studies show that pilots exhibit a robust preference for sleeping at local time, despite directional asymmetries in sleep staging and sleep pattern fragmentation.^25–28 Nevertheless, separate parameter estimates for eastward and westward travel would improve the capacity for the model to account for these asymmetries.

Trait-like inter-individual differences in circadian rhythmicity,^37,38 sleep need,^39,40 and vulnerability to sleep loss^41,42 have been well documented. These findings, in conjunction with advances in the availability of statistical techniques to model individual behavior,^43,44 suggest that the next generation of biomathematical models of sleep and performance may have the potential to generate predictions for specific subpopulations and/or individuals. The success of these “individualized” models will depend greatly on the availability of algorithms to predict sleep behavior for these specific subpopulations and/or individuals. However, to date, there does not appear to be any analogous research investigating the stability of inter-individual differences in the sleep behavior of airline pilots during international flight and duty patterns.

The purpose of the transmeridian model was to predict average sleep/wake behavior, but the output sleep probability distributions can also be used to estimate discreet sleep periods for an average group of pilots. Thus, in addition to calculating goodness-of-fit statistics for the group average sleep probability data, explained variance for individual pilots was also calculated for discrete sleep periods. These analyses indicated that the explained variance for individuals' sleep/wake data was considerably less than the variance accounted for in the group sleep probability data. This was expected given that the models were developed with the aim of estimating the sleep/wake behavior of an average group of pilots, rather than the sleep/wake behavior of a particular pilot. Nevertheless, to remain in step with the next generation of biomathematical models, future versions of the transmeridian model will need to consider whether inter-individual characteristics available in organizational records (age, gender, rank, experience) exert meaningful influences on sleep/wake behavior.

The results of this study indicate that it is possible, with a reasonable degree of accuracy, to estimate sleep probability distributions for an average group of pilots operating international flight/duty patterns. Until further validations are conducted however, caution should be taken in generalizing beyond flight/duty patterns that include layovers with durations less than 24 hours and/or those that originate in Australia and turn around in Europe, the United States, or South Africa. In future, models of this type could form the basis of a stand-alone application to estimate the likelihood that a given duty schedule provides pilots, on average, with an adequate opportunity to sleep. Furthermore, models of this type could provide the sleep input information for any 2-step biomathematical model of human fatigue and performance to improve their prediction of work-related fatigue levels.

DISCLOSURE STATEMENT

This study was part of a larger study that was financially supported by a Discovery Project grant from the Australian Research Council and by a consortium comprised of Qantas Airways, the Civil Aviation Safety Authority, and the Australian and International Pilots Association. Dr. Darwent has conducted research for the Northern Territory Cattlemen's Association, the Livestock Transport Association, the Royal Flying Doctors Service, National Jet, and BP Australia. Dr. Roach has conducted research for New South Wales Police, the Northern Territory Cattlemen's Association, the Livestock Transport Association, the Australian Institute of Sport, the Royal Flying Doctors Service, and National Jet. Dr. Dawson has conducted research on behalf of the Co-operative Research Centre (CRC) for Rail Innovation; is a director of Edu.au Pty Ltd., a consulting company; has undertaken paid speaking engagements for IQPC, a for-profit conference organizing company; and receives royalties from InterDynamics Pty Ltd for a license associated with sleep opportunity prediction software (FAID™).