Coverage optimized planning: Probabilistic treatment planning based on dose coverage histogram criteria

Abstract

This work (i) proposes a probabilistic treatment planning framework, termed coverage optimized planning (COP), based on dose coverage histogram (DCH) criteria; (ii) describes a concrete proof-of-concept implementation of COP within the PINNACLE treatment planning system; and (iii) for a set of 28 prostate anatomies, compares COP plans generated with this implementation to traditional PTV-based plans generated with planning criteria approximating those in the high dose arm of the Radiation Therapy Oncology Group 0126 protocol. Let D_v denote the dose delivered to fractional volume v of a structure. In conventional intensity modulated radiation therapy planning, D_v has a unique value derived from the static (planned) dose distribution. In the presence of geometric uncertainties (e.g., setup errors) D_v assumes a range of values. The DCH is the complementary cumulative distribution function of D_v. DCHs are similar to dose volume histograms (DVHs). Whereas a DVH plots volume v versus dose D, a DCH plots coverage probability Q versus D. For a given patient, Q is the probability (i.e., percentage of geometric uncertainties) for which the realized value of D_v exceeds D. PTV-based treatment plans can be converted to COP plans by replacing DVH optimization criteria with corresponding DCH criteria. In this approach, PTVs and planning organ at risk volumes are discarded, and DCH criteria are instead applied directly to clinical target volumes (CTVs) or organs at risk (OARs). Plans are optimized using a similar strategy as for DVH criteria. The specific implementation is described. COP was found to produce better plans than standard PTV-based plans, in the following sense. While target OAR dose tradeoff curves were equivalent to those for PTV-based plans, COP plans were able to exploit slack in OAR doses, i.e., cases where OAR doses were below their optimization limits, to increase target coverage. Specifically, because COP plans were not constrained by a predefined PTV, they were able to provide wider dosimetric margins around the CTV, by pushing OAR doses up to, but not beyond, their optimization limits. COP plans demonstrated improved target coverage when averaged over all 28 prostate anatomies, indicating that the COP approach can provide benefits for many patients. However, the degree to which slack OAR doses can be exploited to increase target coverage will vary according to the individual patient anatomy. The proof-of-concept COP implementation investigated here utilized a probabilistic DCH criteria only for the CTV minimum dose criterion. All other optimization criteria were conventional DVH criteria. In a mature COP implementation, all optimization criteria will be DCH criteria, enabling direct planning control over probabilistic dose distributions. Further research is necessary to determine the benefits of COP planning, in terms of tumor control probability and∕or normal tissue complication probabilities.

INTRODUCTION

Geometric uncertainties, which include patient setup errors, interfraction and intrafraction organ motion, and structure delineation errors, are inherent in the simulation and delivery of external beam radiation therapy.^{1, 2} The traditional method of handling these uncertainties is to expand the clinical target volume (CTV) to a planning target volume (PTV), and plan treatment as if there were no uncertainty, using the PTV as target.^{3, 4} In this approach, the planner is responsible for sizing the CTV-to-PTV margin so that the CTV receives the prescription dose (PD) for a specified percentage of uncertainties. Such margin sizing is necessarily based on approximate models and∕or empirical rules, which can produce suboptimal normal tissue sparing.⁵

Probabilistic treatment planning (PTP) is an evolving approach which does away with PTVs. In PTP the treatment planning system (TPS) incorporates a mathematical model of geometric uncertainties. The planner is expected to configure this model, e.g., by supplying the probability density functions of anticipated uncertainties, and to define dose coverage criteria for the CTV instead of the PTV. The TPS then generates an expanded dose distribution around the CTV, which satisfies the specified criteria. In PTP, the treatment planner is no longer responsible for adding margins. Instead, the TPS builds its own “margins” into the dose distribution, governed by probabilistic planning criteria.

This work presents a PTP framework, referred to as coverage optimized planning (COP), in which probabilistic planning criteria take the form of dose coverage histogram (DCH) criteria. For a given patient, a DCH plotsQ_v,d≡Pr[D_v≥d] versus dose d, where D_v is the dose delivered to fraction v of a structure’s volume, and Q_v,d is by definition the probability that D_v is greater than or equal to d. For a given patient, the DCH summarizes the effect of geometric uncertainties on the metric D_v. DCH criteria are criteria which constrain Q_v,d, e.g., Q_v,d≥q or Q_v,d<q. In addition to explaining how COP can be formulated using DCH criteria, this work describes a concrete implementation using a research version of the PINNACLE TPS (Philips Medical Systems, Fitchburg, WI). For 28 prostate anatomies, it compares plans generated on one hand with this COP implementation, and on the other with a traditional PTV-based approach, using dose criteria modeled on the high dose arm of Radiation Therapy Oncology Group (RTOG) protocol 0126. This study is intended as a proof-of-concept demonstration of the COP framework.

The COP framework presented here differs from other PTP approaches that have been published to date. Most alternative PTP implementations either optimize a probability weighted dose distribution (PWDD), or use a probability weighted objective function (PWOF), to obtain a robust dose distribution. For random (per fraction) setup uncertainties,⁶ a common way of obtaining a PWDD is via the convolution method (CM).⁷ In this case, one convolves either the dose distribution or the incident fluence with the uncertainty distribution. We use the term PWDD loosely to encompass the CM, even if the CM utilizes a probability weighted fluence distribution, rather than a probability weighted dose distribution.

For conventional fractionation schemes, the convolution method provides an acceptable approximation to the cumulative blurring effect of many setup errors. The optimizer tries to “undo” the fluence convolution by deconvolving the uncertainty distribution from the prescribed dose distribution. The end result is the addition of “horns” to the (preconvolution) fluence profile.⁵ The horns counteract the effect of random errors, albeit imperfectly. Application of PWDD-type techniques to PTP has been investigated by Li and Xing,⁸ Birkner et al.,⁹ Trofimov et al.,¹⁰ Chetty et al.,¹¹ and Moore et al.¹²

McShan et al.¹³ generalized the CM approach by using a probabilistically weighted finite sum of sample dose distributions, rather than a convolution. The advantage of this technique is that errors are no longer restricted to rigid body translations. Unkelbach et al.^{14, 15, 16, 17} also developed a PWDD-type approach to PTP, based on optimization of the dose expectation (first moment). They noted that optimizing the average dose can lead to unsatisfactory doses in some cases. They avoided this problem by including a dose variance term, in addition to the expectation, in the objective function. The variance term damped the more extreme dose distributions.

A number of authors have explored PWOF approaches, including Löf et al.,¹⁸ Baum et al.,¹⁹ Sir et al.,²⁰ Yang et al.,²¹ and Witte et al.²² Löf et al.¹⁸ proposed a comprehensive adaptive control framework for fractionated radiotherapy that incorporated random setup uncertainties, and demonstrated the occurrence of horns in the resulting dose distributions. This work was pursued by Rehbinder et al.,²³ who used fluence modulation to compensate for random errors and couch corrections for systematic errors. Baum et al.¹⁹ and Sir et al.²⁰ explored objective functions in which each voxel is weighted by a coverage probability, i.e., a probability that the voxel will be included in a target or organ at risk (OAR) structure. In contrast, Yang et al.²¹ and Witte et al.²² employed objective functions that are probabilistically weighted functions of biological metrics: Equivalent uniform dose, tumor control probability, and normal tissue complication probability.

In simple cases, Unkelbach and Oelfke²⁴ showed that the above two PTP approaches, i.e., the PWDD and PWOF approaches, are mathematically related. More general optimization strategies, which fall into neither of these solution categories, are represented by Chu et al.²⁵ and Olafsson and Wright.²⁶

In general, there is a consensus that the above PTP approaches can compensate for the effect of random uncertainties. However, it is not clear that they provide good solutions for systematic uncertainties. Optimizing a dose or fluence distribution, or objective function, that is averaged over systematic uncertainties does not prevent the occurrence of unacceptable results in some cases. As noted by Unkelbach et al.,^{14, 15, 16, 17} this strategy does not eliminate the more extreme dose distributions that can be delivered to patients. The present work uses the convolution method to compensate for random uncertainties, but employs DCH criteria to compensate for systematic uncertainties. The advantage of DCH criteria is that adequate target coverage is required not just on average, but for a specified percentage of systematic uncertainties.

The COP framework was motivated by dose population histograms (DPHs), which form the basis of the van Herk margin formula (VHMF).²⁷ In deriving the VHMF, van Herk et al.²⁷ started from a well-defined probabilistic criterion: A CTV-to-PTV margin should be large enough to ensure that the CTV minimum dose D_min is greater than or equal to the planned PTV minimum dose for 90% of treatments. DCH criteria have been generalized here to apply not only to targets but also to OAR, and not just to a D_min dose metric but more generally to any dose metric D_v.

In addition, importantly, the goal of DCH criteria is to enforce coverage criteria on a single-patient basis. In contrast, the intent of the VHMF is to enforce the 90% criterion for a population of patients. DPHs plot ${\widehat{Q}}_{100,d}\equiv \mathrm{Pr}\left[D_{\min }\ge d\right]$, where the probability ${\widehat{Q}}_{100,d}$ is calculated over all geometric errors and all patients within a population. Note that ${\widehat{Q}}_{100,d}$ differs from Q_100,d as defined above because Q_100,d is calculated over all geometric errors for a specific patient. If, for a given geometric uncertainty distribution, one adopts the VHMF approach and uses margins that ensure ${\widehat{Q}}_{100,d}\ge 90\%$, it is possible for individual patients with unfavorable anatomies to have Q_100,d<90% or patients with favorable anatomies to have Q_100,d≈100%. Patient anatomies can vary substantially. Recognizing this, the COP framework attempts to achieve acceptable dose coverage for each individual anatomy.

METHODS AND MATERIALS

The introduction uses the term “geometric uncertainties” to cover all uncertainties in the geometric localization of the tissues of interest, including interfraction and intrafraction setup errors, organ motion, organ deformation, and delineation errors. The remainder of this work focuses on interfraction setup errors, though it is generalizable to other types of uncertainties, provided they satisfy relevant assumptions detailed below. As proposed by van Herk,⁶ setup errors are divided into random and systematic errors. A systematic error is the mean setup error over a course of treatment. A random error is the error relative to the mean in each fraction. For this work it is irrelevant how systematic and random errors are estimated. Estimates could be obtained from a population of patients or, in adaptive therapy, from patient-specific data. Both systematic and random errors are assumed here to be rigid and normally distributed with standard deviations Σ (systematic) and σ (random) along each axis. We consider only translational setup errors, though the framework generalizes to nontranslational errors.

The 28 prostate plans used in this work were evaluated for the specific case: Σ=σ=3 mm. Throughout this work, the nominal requirement is that plans should be able to achieve CTV coverage (i.e., CTV minimum dose) for 95% of setup errors. The same type of modeling that underlies the van Herk margin formula can be used to calculate the isotropic PTV margin required to achieve CTV coverage for 95% of random and systematic setup errors: M=1.03 cm≈1.0 cm. (The standard van Herk margin formula M=2.5Σ+0.7σ gives the margin required to achieve CTV coverage for 90% of patients. Since van Herk posited each patient to have a different systematic error drawn from the same distribution, this is equivalent to requiring target coverage for 90% of systematic errors.) In the absence of other criteria, one would therefore use isotropic 1 cm CTV-to-PTV margins to achieve acceptable PTV-based plans, and COP plans could likewise be expected to expand the dose distribution by 1 cm around the CTV to maintain coverage.

Optimization was performed with the PINNACLE treatment planning system. A PINNACLE research license enabled two nonstandard capabilities. First, the convolution method, i.e., convolution of beam fluence with a setup error distribution prior to dose calculation,⁷ could be turned on and off via a script. The CM simulated the cumulative effect on the dose distribution of random setup errors over ∼30 fraction delivery. In this work it was used in the optimization of probabilistic plans to compensate for isotropic normally distributed random setup errors having standard deviation σ=3 mm. Second, custom research objectives were used in conjunction with the standard PINNACLE optimizer to implement DCH criteria for isotropic normally distributed systematic setup errors having standard deviation Σ=3 mm. Specifically, a custom research objective was used to compute dose coverage histograms for Σ=3 mm, and return a score to the optimizer reflecting how well the dose distribution met the DCH optimization criterion.

PTV-based planning

This work utilized 28 anonymized prostate image sets taken from a clinical database with institutional review board approval. For each prostate anatomy a series of PTV-based plans and a parallel series of COP plans was generated. Baseline optimization criteria approximated the high dose arm of RTOG 0126 (see www.rtog.org). Normal tissue criteria were then varied around this baseline, in order to quantify the tradeoff between target and normal tissue doses. This section briefly describes the contouring and planning criteria used for the “PTV” plans. Following sections describe our COP planning criteria and implementation.

Treatment plans were assumed to be for localized prostate cancer, and so targeted the prostate and proximal seminal vesicles, but not the associated lymph nodes. Contouring may be summarized as follows. The prostate constitutes the gross tumor volume (GTV). The CTV consists of the GTV plus proximal bilateral seminal vesicles (BSVs), i.e., BSV lying within 1 cm of the prostate. The PTV consists of the CTV expanded by a margin of 1.0 cm. The bladder is contoured from its base to the dome, and the rectum from the anus (at the level of the ischial tuberosities) for a length of 15 cm or to the rectosigmoid flexure. Femoral heads are likewise contoured down to the level of the ischial tuberosities.

Plans utilized seven coplanar beams in the patient's transverse plane, with gantry angles 30°, 80°, 130°, 180°, 230°, 280°, and 330°. Dose volume histogram (DVH) optimization criteria for normal tissues are summarized in Table 1. Each row of the table defines a criterion set, labeled PTV_0–PTV_4. The prescription dose was 79.2 Gy, consistent with RTOG 0126. Target optimization criteria were the same for all criterion sets. In the case of PTV-based plans they were PTV D_min≥79.2 Gy and PTV D_max≤84.7 Gy.

Table 1.

Normal tissue optimization criteria used in PTV-based and COP-based optimizations. Criteria range from tight (PTV_0 and COP_0) to moderate (PTV_4 and COP_4). Criterion sets PTV_4 and COP_4 are identical and approximate the high dose arm of the RTOG 0126 protocol. The optimization criteria given below were supplemented with target criteria, with four other normal tissue criteria (left and right femoral heads were each required to have D_max≤50 Gy and D₅₀≤35 Gy), and with a maximum dose criterion for the NORM_TISSUE ring structure (NORM_TISSUE D_max≤50 Gy).

Criterion set	Bladder	Rectum
PTV_0	Dmax≤84.7, D15≤70.0, D25≤65.0, D35≤60.0, D50≤55.0	Dmax≤84.7, D15≤65.0, D25≤60.0, D35≤55.0, D50≤50.0
COP_0	Dmax≤84.7, D15≤60.0, D25≤55.0, D35≤50.0, D50≤45.0	Dmax≤84.7, D15≤55.0, D25≤50.0, D35≤45.0, D50≤40.0
PTV_1	Dmax≤84.7, D15≤72.5, D25≤67.5, D35≤62.5, D50≤57.5	Dmax≤84.7, D15≤67.5, D25≤62.5, D35≤57.5, D50≤52.5
COP_1	Dmax≤84.7, D15≤65.0, D25≤60.0, D35≤55.0, D50≤50.0	Dmax≤84.7, D15≤60.0, D25≤55.0, D35≤50.0, D50≤45.0
PTV_2	Dmax≤84.7, D15≤75.0, D25≤70.0, D35≤65.0, D50≤60.0	Dmax≤84.7, D15≤70.0, D25≤65.0, D35≤60.0, D50≤55.0
COP_2	Dmax≤84.7, D15≤70.0, D25≤65.0, D35≤60.0, D50≤55.0	Dmax≤84.7, D15≤65.0, D25≤60.0, D35≤55.0, D50≤50.0
PTV_3	Dmax≤84.7, D15≤77.5, D25≤72.5, D35≤67.5, D50≤62.5	Dmax≤84.7, D15≤72.5, D25≤67.5, D35≤62.5, D50≤57.5
COP_3	Dmax≤84.7, D15≤75.0, D25≤70.0, D35≤65.0, D50≤60.0	Dmax≤84.7, D15≤70.0, D25≤65.0, D35≤60.0, D50≤55.0
PTV_4	Dmax≤84.7, D15≤80.0, D25≤75.0, D35≤70.0, D50≤65.0	Dmax≤84.7, D15≤75.0, D25≤70.0, D35≤65.0, D50≤60.0
COP_4	Dmax≤84.7, D15≤80.0, D25≤75.0, D35≤70.0, D50≤65.0	Dmax≤84.7, D15≤75.0, D25≤70.0, D35≤65.0, D50≤60.0

RTOG 0126 properly places no requirements on the planner as to what optimization criteria should be employed to achieve target coverage. It evaluates target coverage based on D₉₈ and D₂. It attempts to achieve a target D₉₈ greater than or equal to the PD, and a D₂ less than or equal to 84.7 Gy, which is 7% greater than the PD. These criteria are not always achievable. Consequently, in RTOG 0126, target D₂’s in the range [84.7, 87.1 Gy] are recorded as a minor variation, while target D₂’s greater than 87.1 Gy are recorded as a major variation. We note that to simplify implementation and comparison with the COP algorithm, this work utilized optimization criteria for D_min and D_max, not D₉₈ and D₂. The principal interest in this work is the tradeoffs produced by varying optimization criteria. However, plan quality is also evaluated in terms of target D₉₈ and D₂.

Criterion set PTV_4 approximates the criteria from the high dose arm of the RTOG 0126 protocol. Normal tissue criteria were varied as in Table 1 in order to determine the tradeoff between target and OAR doses. OAR criteria range from tight (PTV_0) to moderate (PTV_4). The RTOG 0126 protocol additionally defines a DVH criterion for the penile bulb. This was omitted because it is typically ignored if it compromises target coverage. Criteria for the PTV, bladder, and rectum were supplemented with additional DVH criteria for the femoral heads, which are not required by the RTOG protocol, but which are used at our institution. The criteria for the femoral heads (D_max≤50 Gy and D₅₀≤35 Gy) had little impact on this work, since they were generally met by both the PTV and COP plans.

The RTOG criteria were further supplemented with a criterion limiting maximum dose to a NORM_TISSUE structure (NORM_TISSUE D_max≤50 Gy). NORM_TISSUE was an artificial ring structure, extending from 2 to 4 cm from the CTV. The maximum dose criterion for NORM_TISSUE is a common method of minimizing peripheral dose outside the immediate neighborhood of the target, and therefore also integral dose to the patient. For the criteria sets used in this study, the rectum and bladder dose-volume objectives are the primary objectives limiting the target dose. The NORM_TISSUE ring structure only plays a secondary role in reducing dose outside the CTV volume.

The OAR DVH criteria given in Table 1 were applied to the whole OAR, leading to volumes of overlap (i.e., conflict) between target and OAR. Optimization criteria were assigned weights as follows. The PTV D_min criterion had the weight of 100, while the D_max criterion had a weight of 90. Bladder and rectal criteria had weights of 20. Criteria for the femoral heads and NORM_TISSUE had weights of 5. These weights apply to all criterion sets. No attempt was made to vary optimization weights to yield improved plans (see Sec. 2F for discussion of this point).

Plans were optimized using PINNACLE’s direct machine parameter optimization (DMPO). PTV-based optimization was performed with fluence convolution turned off. The optimizer was run for up to 50 iterations, though some plans converged sooner. No attempt was made to hand-tune the resulting plans, e.g., by tweaking optimization parameters. While appropriate in a clinical setting, this would have introduced a subjective element into the tradeoff analysis which we were seeking to avoid. Specifically, by introducing additional degrees of freedom, it would have invalidated the target OAR dose tradeoff (TODT) curves introduced in Sec. 2F, and used here for plan evaluation. After optimization was complete, the dose distribution was recalculated with fluence convolution turned on to simulate the effect of random setup errors on the treatment-course integral dose distribution.

Dose volume coverage maps (DVCMs), dose coverage histograms, and percentile DVHs

Suppose one were to perform a virtual experiment, where the same treatment (i.e., beam arrangement) was delivered to the same patient anatomy N times, each time with a different systematic setup error sampled from the systematic setup error distribution. In this work, use of the convolution method to simulate the effect of random setup errors makes it unnecessary to sample from the random setup error distribution. If the convolution method were not used, one would need to sample from both random and systematic setup error distributions.

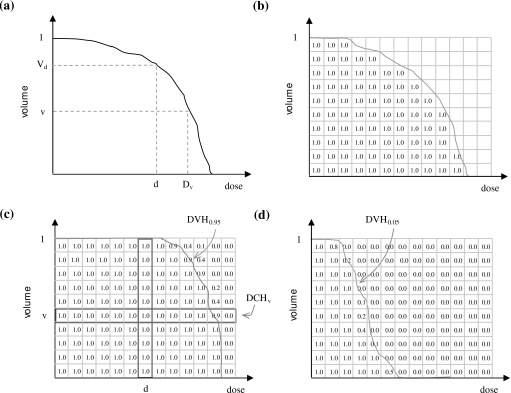
For each virtual treatment course, one would obtain a different CTV DVH, as in Fig. 1a. Now suppose the axes of the DVH are divided into small increments, creating a two-dimensional grid, and for each of the N DVHs a 1 is added (i.e., accumulated) to grid squares that fall below or to the left of the DVH, as in Fig. 1b. Finally, if one divides the total in each square by N, one obtains a DVCM, as in Fig. 1c.

Figure 1.

Steps to generate a DVCM, DCH, and PDVH for a target structure or OAR. (a) Generate DVHs for different setup errors. (b) For each DVH, increment all grid squares lying below or to the left of the DVH. (c) Divide by total number of DVHs to obtain the DVCM. Each grid square contains the probability that, in an individual treatment course, the realized DVH will lie above or to the right of that grid square. A DCH is obtained by plotting probability versus dose across a grid row. A PDVH for a target structure is obtained by connecting grid squares containing a probability of, e.g., 0.95. (d) A PDVH for an OAR is obtained by connecting grid squares containing a probability of, e.g., 0.05.

For each of the N treatment courses, let V_d denote the fractional volume of the CTV receiving dose d, and D_v the dose delivered to fractional volume v. In the DVCM, denote the probability at the intersection of lines through volume v and dose d by Q_v,d. In this work the quantity Q_v,d is referred to as a coverage probability. It is the probability that (or percent of uncertainties for which) V_d≥v or D_v≥d:Q_v,d=Pr[V_d≥v]=Pr[D_v≥d]. Note that DVCM values along a vertical line from dose d give the probabilities Pr[V_d≥v] as a function of v [see Fig. 1c for illustration]. Similarly, the values along a horizontal line from volume v give the probabilities Pr[D_v≥d] as a function of d. The latter curve is the dose coverage histogram for D_v: DCHs are plots of Q_v,d versus d.

Percentile DVHs are defined as isocoverage (or isoprobability) curves on the DVCM. Suppose one draws a pseudo-DVH, as in Fig. 1c, that connects all the squares containing a coverage value of q=0.95≡95%. This DVH might never be realized in practice or may never occur in one of the N virtual treatment courses. However, it represents a DVH in the following probabilistic sense. Across the N virtual treatments, doses D_v and volumes V_d fall above or to the right of the pseudo-DVH exactly 95% of the time. The percentile DVH can therefore be thought of as the CTV DVH that is exceeded for 95% of systematic setup errors. Conversely, if one were to generate a treatment plan that had such a percentile DVH, one could be sure that realized values of D_v and volumes V_d would fall above or to the right of the percentile DVH 95% of the time.

The above definitions may be summarized as follows. For a given structure S, a DVH plots the fractional volume of S receiving dose D. Metrics D_v and V_d can be read off the DVH. In the absence of setup errors (i.e., in the static or planned dose distribution) these quantities have unique values, denoted by D_v,static and V_d,static. However, in the presence of setup errors they assume a continuum of values. We use D_v,q and V_d,q to denote values such that Pr[D_v≥D]=q and Pr[V_d≥V]=q. That is, D_v,q and V_d,q are the qth percentiles of the random variables D_v and V_d. [Strictly, they are the (1−q)th percentiles.] We use D_v,static or D_v,st and V_d,static or V_d,st to denote the corresponding static values. A percentile DVH (PDVH) is a plot of V_d,q versus d. For clarity we denote the static DVH by DVH_static or DVH_st, and the qth percentile DVH by DVH_q. The DCH for dose D_v is a plot of Q_v,d versus d. For clarity we denote this by DCH_v.

DCH optimization criteria

PTV-based treatment planning often uses DVH criteria to drive the optimizer toward the desired dose distribution. A typical target criterion is PTV D₉₈≥TD and a typical OAR criterion is planning organ at risk volume (PRV) D₅₀≤OD, where TD is a target dose, OD is an OAR dose, and PRV denotes the planning organ at risk volume around the OAR. These criteria are referred to as “static” criteria because they are applied to the static (i.e., planned) dose distribution, which excludes the effect of setup errors.

In COP one can do away with PTVs and PRVs, and apply optimization criteria directly to the CTV and OAR. However, because the static dose distribution excludes the effect of setup errors, application of static DVH criteria directly to the CTV or OAR will not guarantee CTV coverage or OAR avoidance in the presence of setup errors.

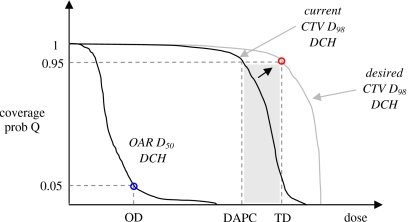
One method of achieving CTV coverage in the presence of setup errors is to supplement the static criterion CTV D₉₈≥TD with the probabilistic criterion Pr[CTV D₉₈≥TD]≥q, where q is a desired coverage probability. The probabilistic criterion should be understood as applying to the dose distribution after the effects of random and systematic setup errors are accounted for. Due to setup uncertainties, CTV D₉₈ can assume a range of values. The above criterion requires the value of CTV D₉₈ to exceed TD for q percent of setup errors. In this work we adopt q=95% as a reasonable coverage value. The probabilistic CTV criterion then becomes: Pr[CTV D₉₈≥TD]≥95%.

As shown in Fig. 2, the probabilistic criterion is a minimum DCH criterion for CTV D₉₈. Figure 2 shows hypothetical DCHs for CTV D₉₈ and OAR D₅₀. Each DCH plots coverage probability versus dose: The y-axis is the probability that the dose metric (CTV D₉₈ or OAR D₅₀) will exceed x-axis dose D in a treatment course. The above criterion is a minimum DCH criterion because it places a lower bound on acceptable DCH values. As shown in Fig. 2, it attempts to ensure that the CTV DCH will pass above or to the right of the point (TD, 95%).

Figure 2.

Example DCHs for CTV D₉₈ and OAR D₅₀ in the current optimization iteration. The DCH gives the probability that, in an individual treatment course, the realized value of the dose metric (CTV D₉₈ or OAR D₅₀) will exceed the dose on the x-axis. In this example the OAR DCH passes through the point (OD,0.05), where OD is the OAR dose, ensuring Pr[D₅₀≤OD]=95%. The CTV DCH passes to the left of the point (TD, 0.95), where TD is the target dose. The desired coverage criterion is: Pr[D₉₈≥TD]≥95%. The figure shows a strategy for meeting this criterion. At each iteration, one uses the current DCH to find the DAPC. In this example, the prescription coverage is 0.95. The objective function sums contributions from all voxels with doses d such that DAPC≤d≤TD. This causes the optimizer to increase dose to these voxels, pushing the current DCH toward the desired DCH.

A corresponding probabilistic OAR criterion is: Pr[OAR D₅₀≥OD]≤5%, which is equivalent to Pr[OAR D₅₀≤OD]≥95%. This is a maximum DCH criterion, as it places an upper bound on acceptable DCH values. As shown in Fig. 2, it attempts to ensure that the OAR DCH will pass below or to the left of the point (OD, 5%). Note that DCH plots have properties similar to DVH plots. For targets, the requirement is that DCHs, like DVHs, pass to the upper right (i.e., a minimum criterion). For OAR, the requirement is that DCHs, like DVHs, pass to the lower left (i.e., a maximum criterion).

The COP framework proposed in this work can utilize target and∕or OAR DCH criteria, with or without additional DVH criteria, to drive the optimizer toward the desired dose distribution. For this reason the approach is referred to as DCH-based. In COP, one can think of the probabilistic DCH criteria that are applied to a specific structure (e.g., the CTV) as supplementing the static DVH criteria. So, for example, one could use two criteria to ensure adequate CTV coverage: A CTV DVH criterion D₉₈≥TD, and a CTV DCH criterion Pr[D₉₈≥TD]≥95%.

In reality, however, it would be difficult, if not impossible, to satisfy the DCH criterion without also satisfying the DVH criterion. Consequently, one can use the DCH criterion alone, and consider the DVH criterion to be implied. In the proposed COP framework, the final prescription for translating PTV-based planning criteria into probabilistic criteria is to replace DVH criteria with corresponding DCH criteria. That is, one replaces static criteria with probabilistic criteria. In the case of target structures, the DCH criteria are applied to CTVs rather than PTVs. In the case of an OAR, the DCH criteria are applied to the OAR itself, instead of to a PRV.

Note that although the thrust of PTP is to eliminate PTVs, it is possible that probabilistic treatment planning could be used to compensate for a subset of geometric uncertainties, while a PTV or PRV expansion is used to accommodate others. In this case, PTVs and PRVs would still be used in a diminished role to compensate for residual geometric errors that are not modeled via COP, and DCH criteria would be applied to the residual PTVs and PRVs.

COP implementation

DCH cost function

To drive the optimizer toward satisfying DCH criteria, one can use the same strategy as for DVH criteria, which is described, e.g., in Wu and Mohan.²⁸ Its application to the CTV DCH criterion Pr[D₉₈≥TD]≥95% is illustrated in Fig. 2. At each iteration the cost (or objective) function corresponding to the DCH criterion returns a cost C to the optimizer. The cost function uses the current DCH to find the dose at prescription coverage (DAPC), which is the dose corresponding to the prescription coverage of 95%. Cost C is set equal to a sum of squared dose differences (d_n−TD)², where d_n is the dose in the nth voxel v_n. The sum extends over all voxels in the CTV neighborhood whose dose falls between DAPC and TD (the shaded region in Fig. 2),

$$C=\sum _n{{}_{v_n∊\text{CTV}̱\text{neighborhood},\text{DAPC}\le d_n\le \text{TD}}\left(d_n-\text{TD}\right)}^2.$$ (1)

Along with other component cost functions, corresponding to other criteria, the optimizer attempts to reduce the cost C. It does this by searching for beamlet intensities that will increase dose to the CTV neighborhood, and so produce lower costs C than in the current iteration. Provided other criteria do not oppose it, the optimizer will gradually move the CTV DCH in the desired direction, to the point where it meets the DCH criterion. The cost C then becomes zero, i.e., the optimizer can ignore the DCH constraint once it is satisfied. OAR criteria are satisfied in the same way, except that the score is over voxels such that OD≤d_n≤DAPC, where OD is the OAR dose, and the TPS achieves a lower score in that case by lowering (not raising) dose to neighborhood voxels.

DCH cost function implementation

In the following discussion we adopt a reference frame that is fixed relative to the patient anatomy. The CTV therefore covers the same set of anatomical voxels, independent of geometric errors. The dose distribution and voxel doses referred to below incorporate the effect of random setup errors via fluence convolution, but do not include the effects of systematic setup errors. The effect of systematic setup errors is to move this dose distribution relative to CTV voxels. The specific COP implementation used here employed the following cost function:

$$C=\sum _n{{}_{v_n∊\text{CTV},d_n\le \text{TD}}\left(d_n-\text{TD}\right)}^2+\sum _m{{}_{v_m∊\text{CTV}̱\text{RING},\text{DAPC}\le d_m\le \text{TD}}\omega }^2{\left(d_m-\text{TD}\right)}^2.$$ (2)

Equation 2 consists of two terms, the first being a sum over CTV voxels and the second a sum over CTV_RING voxels. A standard DVH objective function is only concerned with voxels that belong to the specified structure (e.g., the PTV). In order to achieve the desired DVH, the optimizer need only adjust beamlets that traverse those voxels. In contrast, although one nominally applies a DCH criterion to a structure such as the CTV, the optimizer must adjust beamlets that traverse voxels outside the structure if it is to achieve the desired DCH when the effects of patient setup uncertainties are considered. So, for example, in order to satisfy the DCH criterion Pr[CTV D_min≥TD]≥95%, the optimizer must adjust beamlets that traverse not only CTV itself, but also voxels in the neighborhood of the CTV.

Voxels having the potential to affect coverage can be determined via a simple calculation. The isotropic margin required to absorb 95% of random and systematic setup errors for σ=Σ=3 mm is 1 cm. To absorb 99.9% of random and systematic setup errors requires a 1.4 cm margin. To allow participation of the surrounding voxels in the dose optimization, voxels within 1.4 cm of the relevant structure are included in the DCH cost function. Specifically, the CTV was expanded by 1.4 cm to create structure CTV_EXP. The structure CTV_RING, used in Eq. 2, is equal to the difference: CTV_RING=CTV_EXP−CTV. We emphasize that CTV_EXP and CTV_RING are nonphysical. CTV_RING represents the neighborhood around the CTV, in which beamlet intensities must be adjusted in order to meet coverage criteria. The principle reason for defining CTV_RING is to enable precise specification of the cost function in Eq. 2, which practically extends over a finite set of voxels in the neighborhood of the CTV.

With random setup errors accounted for via fluence convolution, the DCH criterion must address systematic errors only, which reduces the necessary CTV_RING expansion to only 1.2 cm. We nevertheless employed a 1.4 cm CTV_RING. Our consideration of additional voxels out to 1.4 cm from the core structure does no harm, but is unnecessary because there is negligible probability that the structure will be displaced that far from its static or planned position. Note that the minimum expanded volume size depends on σ and Σ.

In the case of the PINNACLE TPS, a further practical consequence of the CTV_EXP structure is to force PINNACLE to set initial beamlet intensities so they cover all voxels that could potentially contribute to CTV coverage. At the start of an optimization, PINNACLE determines all target structures and initializes beamlet intensities to a nonzero value only for those beamlets that traverse a target voxel. It appears that the intensities of all other beamlets are initialized to zero, and remain zero through the optimization. It is therefore useful to initialize PINNACLE to consider the expanded set of voxels that could contribute to CTV coverage. By making CTV_EXP the nominal target structure in PINNACLE, one achieves this goal. This may or may not be necessary in other TPS∕optimization engines.

In Eq. 2, the CTV and CTV_RING voxels contribute differently to the cost function. That is, they make different contributions to C, even though they are part of the same structure CTV_EXP. Specifically, voxels inside the CTV contribute their squared differences to C provided d_n≤TD, where d_n is the voxel dose. That is, there is no lower dose bound that excludes interior CTV voxels from contributing to the DCH cost function. In contrast, voxels in CTV_RING contribute to C only if DAPC≤d_m≤TD. The DCH cost function achieved better CTV coverage using these different dose bounds, probably because the CTV term strongly penalizes low doses in CTV interior voxels that can severely degrade coverage.

Equation 2 incorporates an additional heuristic mechanism, voxel-dependent weights ω, that encourage the optimizer to modify coverage in an efficient manner. Consider the voxels in CTV_RING. If the factor ω is set equal to one in Eq. 2, all of the ring voxels contribute their unweighted squared difference (d_m−TD)² to the cost function score. In this scenario, if the optimizer wants to increase coverage to the CTV, it will tend to modify dose in any voxel having DAPC≤d_m≤TD, regardless of how weakly or strongly that voxel affects CTV coverage. For example, it might increase dose in a voxel that satisfies DAPC≤d_m≤TD, but which lies relatively far from the CTV and therefore has negligible effect on coverage.

Let δ denote the distance from a ring voxel to the nearest point on the CTV boundary. (By definition, ring voxels have δ>0). Also, let Δ(d) denote the minimum such distance taken over all voxels whose dose is equal to d. Critical voxels are defined to be those voxels for which the ratio κ=Δ(d)∕δ is close to one, where d is the voxel dose. (κ values fall in the range (0,1].) CTV coverage is effectively determined by critical voxels. Increasing dose to noncritical voxels will have little or no effect on coverage because there exist voxels with the same dose lying closer to the CTV. A potentially attractive strategy is therefore to increase the cost function contribution for those voxels having κ close to one. This should encourage the optimizer to increase coverage by preferentially boosting dose in voxels that are closer to the CTV than other voxels with the same dose d. This strategy was implemented for ring voxels in the DCH cost function by including a voxel-dependent weight ω in Eq. 2, where

$$\omega =1+4\cdot \kappa =1+4\cdot \Delta \left(d\right)∕\delta .$$ (3)

Note that ω values range from 1 to 5. Critical ring voxels having κ≈1 will have ω≈5, and so will contribute most strongly to the cost function. The optimizer will be encouraged to preferentially boost dose to those voxels, before boosting dose to noncritical voxels that lie further from the CTV. Voxel-dependent weights ω are an empirical mechanism intended to achieve more rapid convergence to the desired dose distribution. However, the scope of this study did not permit extensive experimentation. More research is therefore required to determine whether the weights given by Eq. 3 can be improved upon. Also note that the weights in Eq. 3 were applied only in optimization iterations n≥5. For iterations n<5, ω was set equal to one for all voxels. In the first few iterations, the dose distribution is fragmented; it takes a few passes for the optimizer to produce a smooth distribution that conforms approximately to the target. Applying the weights in Eq. 3 appeared to be counterproductive in the early iterations, but produced good convergence once an initial reasonable dose distribution had emerged.

Lastly, we note that the CTV maximum dose criterion employed for the COP plans (see Sec. 2E below) used a modified max dose constraint for which the cost function was

$$C=\sum _n{{}_{v_n∊\text{CTV}̱\text{EXP},d_n\ge \text{TD}}\eta }^2{\left(d_n-\text{TD}\right)}^2,$$ (4)

where TD was the relevant target dose (84.7 Gy), and η was set equal to 5, the maximum value of the weight ω in Eq. 2. PINNACLE’s own max dose cost function has the form 4 with η=1. The reason for using this variant was to ensure that cost function contributions from the min DCH criterion of Eq. 2 were adequately counterbalanced by contributions from a max dose criterion. Use of the weight ω in Eq. 2 has the effect of strongly increasing the dose in critical voxels having ω≈5. If extreme doses are not penalized with a similar weight η=5 in Eq. 4, the max dose constraint fails to have an effect and the result is that unacceptably high doses (e.g., 90+Gy) can occur in voxels that are in the middle ground between target and OAR.

COP planning

In converting the PTV-based planning criteria (Sec. 2A) into COP criteria, one has the option of replacing all, or only a subset, of the DVH criteria with corresponding DCH criteria. In this initial study, we replaced only the PTV D_min criterion with a DCH criterion. Specifically, the criterion PTV D_min≥79.2 Gy was replaced by Pr[CTV D_min≥79.2 Gy]≥95%. The criterion PTV D_max≤84.7 Gy was replaced by a similar DVH criterion CTV_EXP D_max≤84.7 Gy. However, for reasons described in Sec. 2D2, the cost function utilized in conjunction with this maximum dose constraint was the modified cost function of Eq. 4.

Table 1 gives the normal tissue criteria used for COP plans. These are similar to those used for the PTV-based plans. In the case of criterion sets PTV_4 and COP_4, they are identical. COP planning criteria had the same optimization weights as for the PTV-based plans. COP plans were optimized using PINNACLE DMPO with fluence convolution turned on. The optimizer was run for up to 50 iterations. The COP optimizations took about 6 times longer than the PTV-based optimizations, due to the numerically intensive task of computing dose coverage histograms.

Plan evaluation

In radiation therapy the principle tradeoff is between target and OAR doses. For a given treatment site, the performance of a treatment planning method may be quantified using TODT curves, examples of which are shown in Fig. 3. The curves plot an OAR dose metric (e.g., rectum D₁₅) versus a target dose metric (e.g., CTV D_min).

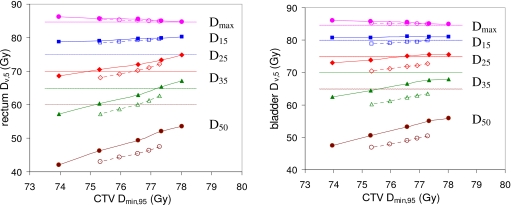
Figure 3.

Average rectum and bladder doses D_max,5 (●), D_15,5 (◼), D_25,5 (◆), D_35,5 (▲), and D_50,5 (●) plotted against CTV D_min,95. Results are averaged over 28 prostate anatomies. Results for PTV plans (criterion sets PTV_0–PTV_4, Table 1) are represented by dotted lines and hollow symbols. Results for COP plans (criterion sets COP_0–COP_4, Table 1) are represented by solid lines and solid symbols. Dotted horizontal lines mark the RTOG 0126 dose limits for rectum D_max (84.7 Gy), D₁₅ (75 Gy), D₂₅ (70 Gy), D₃₅ (65 Gy), and D₅₀ (60 Gy); and bladder D_max (84.7 Gy), D₁₅ (80 Gy), D₂₅ (75 Gy), D₃₅ (70 Gy), and D₅₀ (65 Gy).

This work uses TODT curves as the principal method of comparing the performance of PTV-based planning and probabilistic treatment planning. When comparing two planning techniques, the one that gives a lower TODT curve, i.e., lower OAR dose for the same target dose, is superior. TODT curves provide an objective method of plan comparison that is more informative than comparing individual plans.

A TODT curve can be generated in one of two ways: By varying OAR criterion doses (as in Table 1) or by varying OAR criterion weights. Both methods should give approximately the same TODT curve; this was verified to be the case for one of the 28 patients. In this study we elected to vary OAR criterion doses because they more strongly influence the optimizer, and therefore generate TODT curves that span a larger range of target doses. Criterion weights were not varied.

RESULTS

In this work, PTV_4 and COP_4 plans most closely approximate the RTOG 0126 planning criteria. For all but one of COP_4 plans, CTV D₉₈, specifically CTV D_98,95, exceeded the 79.2 Gy prescription dose. For PTV_4 plans the CTV D₉₈ averaged 81.2 Gy with a range of [80.5, 81.9 Gy]. For COP_4 plans it averaged 81.7 Gy with a range [78.6 Gy, 82.7 Gy]. (The range would have been [80.3, 82.7 Gy] except for the one plan falling below the PD). For PTV_4 plans, the CTV D₂, specifically CTV D_2,0, averaged 84.8 Gy with a range of [83.8, 85.2 Gy]. For COP_4 plans it averaged 84.8 Gy with a range [82.8, 85.6 Gy]. Based on RTOG 0126 evaluation criteria, all plans were therefore clinically acceptable in meeting the prescription dose, though maximum target dose in some of the plans slightly exceeded the 84.7 Gy threshold, and would therefore have counted as minor protocol variations. It is possible these plans could have been manually tweaked to meet the RTOG 0126 maximum dose limit. However, manual tweaking was intentionally avoided in the present work so as not to introduce subjective changes into the numerical results.

OAR optimization criteria were progressively tightened in going from PTV_4∕COP_4 plans to PTV_0∕COP_0 plans. This caused a decrease in both target and OAR doses. For PTV plans the average CTV D₉₈ fell slightly from 81.2 to 81.0 Gy while CTV D₂ varied in the range 84.8–85.2 Gy. For COP plans the average CTV D₉₈ fell from 81.7 to 80.9 Gy, while CTV D₂ varied in the range 84.8–85.9 Gy. As OAR criteria were tightened, CTV D_min was affected more strongly than CTV D₉₈. Variation in CTV D_min and OAR dose metrics are shown in Figs. 345.

Figure 4.

Patient 10 rectum and bladder doses D_max,5 (●), D_15,5 (◼), D_25,5 (◆), D_35,5 (▲), and D_50,5 (●) plotted against CTV D_min,95. Line and symbol conventions are as in Fig. 3. For this patient, bladder doses are actively limiting the CTV D_min,95, rectum doses are not.

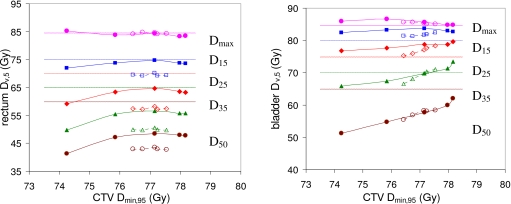
Figure 5.

Average rectum and bladder doses D_max,5 (●), D_15,5 (◼), D_25,5 (◆), D_35,5 (▲), and D_50,5 (●) plotted against CTV D_min,95. Results are averaged over 28 prostate anatomies. Rectum and bladder doses D_v,5 falling below the dose limits in Table 1 were set equal to those limits to avoid penalizing increased doses below the optimization objectives. Line and symbol conventions are as in Fig. 3.

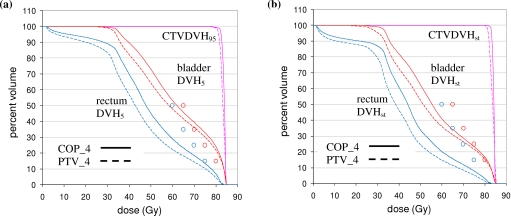
Figure 3 shows TODT curves for the rectum and bladder averaged over the 28 prostate anatomies. Each dose metric D_v,q was averaged over the 28 anatomies. Results are given for 95% coverage, since this was the intended coverage. Accordingly, as explained in Sec. 2C, CTV D_min,95 is plotted against OAR D_v,5. Dotted lines and hollow symbols represent (left to right) PTV criterion sets PTV_0–PTV_4. Solid lines and solid symbols represent (left to right) COP criterion sets COP_0–COP_4. (See Table 1). Note that TODT curves for individual anatomies vary around the average.

Dotted horizontal lines mark the RTOG 0126 dose limits for the rectum and bladder. However, it is important to note that the dose metrics plotted in Fig. 3 (D_min,95 and D_v,5) are probabilistic doses, while the dotted lines mark dose limits for static OAR doses. Consequently, the correspondence between the plotted doses and the dose limits is not an exact one. None of the plans incorporated PRVs for OAR. For an OAR the value of D_v,5 can be greater than D_v,st and, in particular, D_v,5 can exceed the static optimization dose limit while D_v,st remains below it.

Table 2 shows that maximum OAR doses change very little between static and probabilistic metrics: Rectum D_max,st is close to rectum D_max,5 and bladder D_max,st is close to bladder D_max,5. However, other dose metrics vary substantially. Average rectum D_v,5 values are 3.6–7.4 Gy greater than the corresponding D_v,st values, and average bladder D_v,5 values are 2.9–9.5 Gy greater than the corresponding D_v,st values, for v=15, 25, 35, and 50. These gaps between probabilistic and static dose metrics explain the apparently high doses received by the OAR in Fig. 3 (as measured, e.g., by D₁₅). Probabilistic dose metrics incorporate the effect of setup errors, and so are more pessimistic than static values. This applies to both PTV and COP plans.

Table 2.

Differences (Gy) between average normal tissue probabilistic doses D_v,5 and static doses D_v,st for PTV_4 and COP_4 plans. Probabilistic doses incorporate the effect of geometric uncertainties (i.e., setup errors). Static doses assume no geometric uncertainties, and are therefore optimistic.

	Rectum Dmax	Rectum D15	Rectum D25	Rectum D35	Rectum D50
PTV_4 Dv,5	84.9	79.6	72.1	62.6	47.5
PTV_4 Dv,st	85.3	74.9	64.8	55.3	42.1
PTV_4 Dv,5−Dv,st	−0.4	4.6	7.4	7.3	5.4
COP_4 Dv,5	84.7	80.3	74.8	67.1	53.6
COP_4 Dv,st	85.0	76.6	68.6	60.6	48.0
COP_4 Dv,5−Dv,st	−0.2	3.6	6.2	6.6	5.6
	Bladder Dmax	Bladder D15	Bladder D25	Bladder D35	Bladder D50
PTV_4 Dv,5	85.0	80.0	72.7	63.5	50.4
PTV_4 Dv,st	85.5	75.9	64.7	53.9	41.2
PTV_4 Dv,5−Dv,st	−0.5	4.1	7.9	9.5	9.2
COP_4 Dv,5	85.0	81.0	75.5	67.9	55.8
COP_4 Dv,st	85.5	78.1	69.2	59.6	47.7
COP_4 Dv,5−Dv,st	−0.5	2.9	6.4	8.3	8.2

The COP curves in Fig. 3 lie above the PTV-based curves, suggesting that the COP plans provide a poorer tradeoff between target and OAR doses. However, the average results in Fig. 3 mask relevant detail. For some prostate anatomies, CTV dose is actively constrained by either the rectum dose, or the bladder dose, but not both simultaneously. Figure 4 shows a case in point. For this anatomy (patient 10), bladder dose limits are actively constraining CTV dose, indicated by the fact that the bladder TODT curves are oblique and close to the RTOG dose limits (horizontal dotted lines). The D_35,5 exceeds the RTOG dose limits. In contrast, rectum dose limits are inactive, indicated by the fact that rectum TODT curves are flat and well below the RTOG dose limits.

The Fig. 4 rectum COP TODT curves plans lie noticeably higher than those for PTV-based plans. In the COP plans, the rectum curve is pushed closer to the rectum dose limit. As long as the (static) rectum dose stays below the (static) dose limit, the optimizer does not penalize the plan. The COP algorithm is therefore taking advantage of the “slack” in the rectum doses of Fig. 4 to increase dose without any optimization penalty. This is a legitimate thing for the COP algorithm to do. In Fig. 3, this nonpenalized rectal dose increase boosts the COP average values, making COP TODT curves look erroneously worse than their PTV counterparts.

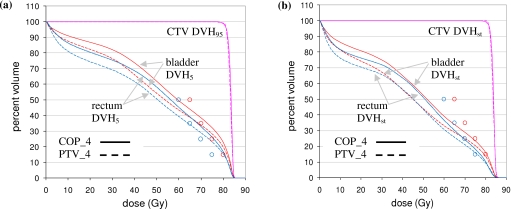
A fairer comparison between the two sets of plans can be achieved by counting any rectum or bladder dose D_v,5 that falls below the corresponding limit in Table 1 as equal to that limit. The intention is that no plan is penalized for increasing the rectum or bladder dose up to, but not beyond, its specified limit. If one regenerates Fig. 3 using this strategy, the result is Fig. 5. Figure 5 shows very similar TODT curves for PTV and COP plans, indicating that both planning techniques provide a similar tradeoff between target and normal tissue doses.

Figure 6a shows percentile DVHs for the CTV, bladder, and rectum for patient 10. Figure 6b shows the corresponding static DVHs. Note that the static DVHs are more optimistic than the percentile DVHs: The CTV DVHs are higher while the OAR DVHs are lower. The plots in Fig. 6 are for the COP_4 and PTV_4 plans, which have identical OAR optimization criteria approximating those in RTOG 0126. Static OAR criteria for bladder and rectum D₁₅, D₂₅, D₃₅, and D₅₀ are indicated by the circles on the figure.

Figure 6.

(a) Percentile DVHs for the same patient (patient 10) as in Fig. 4 for COP_4 (solid) and PTV_4 (dashed) plans. The CTV DVH is the 95% DVH (DVH₉₅), while the rectum and bladder DVHs are 5% DVHs (DVH₅). (b) Static DVHs for patient 10. In both plots, static OAR optimization criteria are indicated by circles (see Table 1).

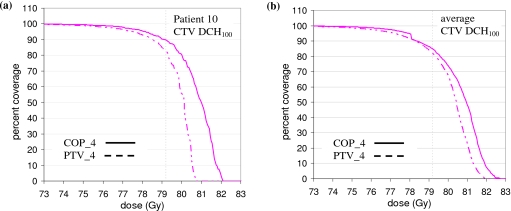
Consistent with Fig. 4, the rectum curves in Fig. 6 lie well below the optimization limits. The COP plan takes advantage of this slack to increase the rectum doses without incurring an optimization penalty. At the same time, the COP plan achieves better target coverage. Figure 8a shows the DCH for the CTV D_min dose metric (CTV DCH₁₀₀). For the benchmark coverage of 95%, the COP_4 CTV dose is 79.1 Gy while the PTV_4 dose is 77.5 Gy. The higher COP_4 CTV dose is attributed to fact that the COP algorithm does not have a predefined PTV, and so has more freedom to increase dose in the neighborhood of the CTV to achieve better target coverage.

Figure 8.

(a) CTV D_min DCH (DCH₁₀₀) for patient 10. (b) CTV D_min DCH (DCH₁₀₀) averaged over all 28 prostate anatomies. In both plots, the prescription dose of 79.2 Gy is indicated by the dotted line.

Figure 6 shows results for one patient only. Figure 7 shows equivalent plots averaged over all 28 anatomies. Figure 7 confirms the results of Fig. 6. The COP plans increase the OAR doses so that static doses are moved up to, but not beyond, their optimization limits. This results in better CTV coverage, as shown by Figs. 7b, 8b. Figure 8b, in particular, shows that for 95% coverage, the average COP_4 dose (77.9 Gy) exceeds the average PTV_4 dose (77.2 Gy) by 0.7 Gy. On a per patient basis, the 95% coverage COP_4 dose is less than the PTV_4 dose by 0–0.8 Gy for three patients. It is greater than the PTV_4 dose by 0–0.5 Gy for nine patients, 0.5–1.0 Gy for five patients, 1.0–1.5 Gy for eight patients, and >1.5 Gy for three patients. In most of the cases where the 95% coverage COP_4 dose is less than the PTV_4 dose, or greater than it by 0–0.5 Gy, the COP_4 and PTV_4 DCH curves are similar in the region of the PD, and differences could be characterized as “noise.” In the other 16 cases, the COP_4 plan provides significantly better coverage. The COP approach is able to increase target coverage because it is not constrained by a predefined PTV. Figures 678 show this more clearly than the approximate analysis in Fig. 5.

Figure 7.

(a) Percentile DVHs averaged over all 28 prostate anatomies for COP_4 (solid) and PTV_4 (dashed) plans. The CTV DVH is the 95% DVH (DVH₉₅), while the rectum and bladder DVHs are 5% DVHs (DVH₅). (b) Static DVHs averaged over all 28 prostate anatomies. In both plots, static OAR optimization criteria are indicated by circles (see Table 1).

DISCUSSION

Performance of COP versus PTV-based planning

A principal advantage of probabilistic treatment planning is that it removes the need for artificial PTV and PRV helper structures, and allows the treatment planner to deal directly with dose distributions and metrics that incorporate the effects of geometric uncertainties. A minimum requirement for PTP plans is that they provide target OAR dose tradeoffs that are no worse than corresponding PTV-based plans. However, PTP can be expected to provide better target OAR dose tradeoff in cases where (i) the anatomy, prescribed dose and∕or motion is complex, and for which it is therefore difficult to define an optimal PTV, or (ii) subtle shaping of the dose distribution can enable increases in target dose, without violating OAR constraints.

Examples of category (i) might be complex head and neck plans, where there are multiple targets receiving different levels of dose via simultaneous boost. In contrast, the prostate plans considered in this work fall into category (ii). The prostate is a quasispherical target embedded in approximately homogeneous tissue. In this scenario, an isotropically expanded PTV is likely to give near-optimal target coverage, and it follows that there is little room for COP to improve on PTV-based planning. Patient 10, for whom results are given in Figs. 46, illustrates the way in which PTP can incrementally improve the target OAR dose tradeoff.

For this patient, PTV dose is actively limited by bladder dose, i.e., by bladder D₁₅. Figure 6 shows that the COP plan increases the rectum dose, and also bladder doses D₂₅, D₃₅, and D₅₀ (but not D₁₅). Because it is not constrained by a predefined PTV, the COP algorithm can take advantage of slack in the OAR doses to increase doses beyond the PTV. This enables the COP algorithm to deliver higher target dose, as shown in Figs. 6b, 8a. The extent to which the COP algorithm can increase the target dose varies from patient to patient. This is shown by Figs. 78b, where the average increase in CTV dose is more modest than in Figs. 6b, 8a. Nevertheless, the qualitative behavior of the COP algorithm is the same as in Fig. 6: It exploits slack in OAR doses to increase dose outside what would have been the PTV, in order to increase target coverage. To maintain coverage as OAR constraints are tightened, isodose lines are expanded in directions not constrained by OARs.

COP framework and implementation

Figures 6a, 6b, 7a, 7b emphasize the difference between static and probabilistic doses. Static DVHs are more optimistic than the PDVHs: The static CTV DVHs are higher, while the static OAR DVHs are lower. Probabilistic doses∕DVHs more accurately represent the dose given to patients. An advantage of COP is that DCH criteria allow the planner to impose limits on percentile DVHs. Most prior PTP implementations either optimize a PWDD, or use a PWOF, to obtain a robust dose distribution. As discussed in Sec. 1, these approaches do not easily permit firm constraints to be placed on percentile DVHs or percentile dose metrics D_v,q. DCH criteria provide a natural method of doing this. Furthermore, because the DCH criteria that would be applied to targets or OAR look very much like DVH criteria, IMRT planners are likely to find the COP DCH framework fairly intuitive. Within the proposed framework, the prescription for moving from a traditional PTV-based plan to a probabilistic plan is simply to replace target and OAR DVH criteria with the corresponding DCH criteria.

Because DCH criteria look like DVH criteria, one can use the same strategy for meeting these criteria within the optimizer. In an optimization that uses DVH criteria, the objective function typically consists of a simple sum of squared voxel dose differences (see Secs. 2D1, 2D2). In the specific COP implementation described here, this objective function is modified to include voxel-dependent weights [see Eqs. 2, 3]. The goal of these weights is to achieve faster and more stable convergence toward a robust dose distribution.

It is useful to note that DCH and PDVH criteria are completely equivalent. A DCH criterion of the form Pr[D_v≥d]≥q is equivalent to the PDVH criterion D_v,q≥d. Consequently, the proposed COP framework can be formulated in terms of either DCH or PDVH criteria. The distinction between the two is one of notation only. If formulated in terms of PDVHs, the prescription for going from a PTV-based plan to a COP plan would be to replace all target DVH criteria D_v≥TD with corresponding PDVH criteria D_v,q≥TD. Similarly one would replace OAR criteria D_v≤OD with PDVH criteria D_v,1−q≤OD.

In theory, there is nothing to prevent a PTV-based plan from achieving the same level of target coverage as a probabilistic plan. In practice, experimenting and manually designing an anisotropic PTV margin that delivers the same level of target coverage as a probabilistic plan might be so time-consuming as to be infeasible. It is important to note that PTV-based and probabilistic plans are equally dependent on sufficiently accurate knowledge of the geometric uncertainty distribution. If the geometric uncertainty distribution model is inaccurate, both types of plan will produce underdosing of the target and∕or overdosing of OAR.

The COP implementation described here assumed normally distributed interfraction setup errors, and shift invariance of the dose distribution. That is, setup errors are assumed to simply translate the dose distribution, an assumption which breaks down in the presence of tissue heterogeneities. The implementation generalizes in a straightforward manner to other types of geometric errors, e.g., anisotropic, non-normal, and rotational errors. One can also forgo the assumption of shift invariance. However, in this case it would be necessary to recalculate the dose distribution corresponding to each geometric uncertainty.

The proposed COP DCH-based framework is more general than the specific implementation described here. DCH criteria can be applied to the case where geometric uncertainties are completely general, e.g., nonrigid body deformations of the anatomy. The only requirement is that one be able to calculate DCHs (or PDVHs) corresponding to each deformation.

CONCLUSIONS

This work (i) proposes a probabilistic treatment planning framework, referred to as coverage optimized planning, based on dose coverage histogram criteria; (ii) describes a concrete proof-of-concept implementation of COP within the PINNACLE treatment planning system; and (iii) for a set of 28 prostate patients, compares COP plans generated with this implementation to traditional PTV-based plans generated according to planning criteria approximating those in the RTOG 0126 protocol.

COP was found to produce better plans than standard PTV-based plans, in the following sense. Target OAR dose tradeoff curves were equivalent to those for PTV-based plans, so COP performance was equivalent in this respect. However, COP plans were able to exploit slack in OAR doses, i.e., cases where OAR doses were below their optimization limits, to increase target coverage. Specifically, because COP plans were not constrained by a predefined PTV, they were able to provide wider dosimetric margins around the CTV, by pushing OAR doses up to, but not beyond, their optimization limits. COP plans demonstrated improved target coverage when averaged over all 28 prostate anatomies, indicating that the COP approach can provide benefits for many patients. However, the degree to which slack OAR doses can be exploited to increase target coverage will vary according to the individual patient anatomy.

The proof-of-concept COP implementation investigated here utilized a probabilistic DCH criteria only for the CTV minimum dose criterion. All other optimization criteria were conventional DVH criteria. In a mature COP implementation, all optimization criteria will be DCH criteria, enabling direct planning control over probabilistic DVHs. Further research is necessary to determine the benefits of COP planning, in terms of tumor control probability and∕or normal tissue complication probabilities.