Technical Note: Development of a tidal volume surrogate that replaces spirometry for physiological breathing monitoring in 4D CT

Abstract

Purpose: Spirometry exhibits baseline drift and frequent measurement errors so it cannot be used by itself to provide tidal volume-based image sorting or breathing motion modeling. Other breathing surrogates, in this study an abdominal bellows system, are drift free but do not measure tidal volume. Simultaneously using spirometry and the bellows system allows the user to convert the recorded bellows signal to tidal volume but still relies on spirometry measurements. The authors therefore propose to use CT-based air content, rather than a spirometer, to convert the bellows signal to tidal volume.

Methods: 41 4D CT data sets are acquired, while the breathing cycle is simultaneously measured using spirometry and an abdominal pressure bellows system. The assumptions underlying the conversion of the bellows measurement to tidal volume by CT-based air content are analyzed. This comprises of detailed correlation studies of the spirometry-measured tidal volume, the bellows signal, and CT-based air content.

Results: For 15∕41 patients, the spirometry signals are not consistently acquired during the 4D CT session, so correlating spirometry to bellows measurements and CT-based air content leads to erroneous conversion coefficients. After introducing a minimum correlation threshold to remove these data, good correlations are obtained between the remaining breathing signals. The ratio of CT-based air content to tidal volume is measured to be 1.11±0.08; the expected value is 1.11 because room air is 11% more dense than air in the lungs.

Conclusions: The observed problems of spirometry recording illustrate the challenges encountered when using spirometers as breathing surrogate for 4D CT acquisition. The high correlation between spirometry and bellows breathing signals and the verified factor of 1.11 between CT-based air content and tidal volume mean that the bellows measurement (or other equivalent surrogates) can be reliably converted to tidal volume using the CT-based air content, avoiding the need for a spirometer.

INTRODUCTION

Different approaches exist to acquire respiration-correlated computed tomography images [4D CT data (see Ref. 1 for a brief overview)], but they all require measurement of a respiratory surrogate to guide image acquisition. Retrospective breathing motion analysis and modeling is also based on the surrogate measurement. While many surrogates have been used, they do not often provide a physiologically relevant measurement. This has been shown to be important both for validating the image sorting and for developing breathing motion models.² Tidal volume provides a physiologically relevant measurement. In this technical note, we address the problem of developing a tidal volume-based breathing surrogate for 4D CT imaging that could be used even if spirometry was not used.

The study is based on an established free-breathing ciné 4D CT protocol³ and represents a continuation of our research presented in Refs. ^{4, 5, 6}. We initially used spirometry-measured tidal volume as the sole breathing surrogate,^{3, 4} but spirometry had significant baseline drift and frequent measurement failures (e.g., air leaks)^{4, 5, 7} so spirometry had limited utility when used by itself.^{5, 6} Other breathing surrogates are in more common use, including a pneumatic belt system that is wrapped around the abdomen and provides a signal that is proportional to abdominal distension.^{8, 9} While this signal does not exhibit baseline drift, it also does not provide a physiologically relevant measurement. In principle, simultaneous use of bellows and spirometry takes advantages of both surrogates and the basic concept of such a spirometry-bellows system has been described in Ref. 6. The idea is to use the spirometer to convert the bellows signal into tidal volume. This approach is limited by an observed high failure rate for the spirometry measurements, most of the time caused by patient noncompliance. Because of an expected correlation between internal air content and tidal volume, we hypothesized that CT-based air content, rather than the spirometer, could be used to convert the bellows signal into tidal volume.

METHODS AND MATERIALS

Data acquisition

CT and breathing surrogate data sets of 41 patients (25 patients with lung tumors and 16 with abdominal tumors) were acquired as follows under an IRB-approved study:³ A 16-slice CT (Brilliance 16, Philips Medical Systems, Cleveland, OH) was operated in ciné mode (spatial resolution: 0.98×0.98×1.5 mm³) with 25 scans acquired contiguously at each couch position (CP). Each scan (360° gantry rotation) required 0.42 s and a dead time of 0.30 s was inserted by the system between each scan. The total scan time per CP was 18 s, spanning approximately three breaths. Between 17 and 30 adjacent CPs were scanned depending on the coverage required for the imaging protocol (only lungs or lungs, abdomen, and pelvis). Simultaneously, two external respiratory measurements were acquired: Tidal volume measured using a spirometer (VMM-400, Interface Associates, Laguna Niguel, CA) and a bellows pressure signal measured using a hollow pneumatic belt system that was wrapped around the abdomen. The CT scanner’s x-ray-on signal was also monitored to retrospectively synchronize the respiratory measurements with the image data.

Conversion of bellows signal to tidal volume by CT-based air content

The CT-based air content was a measurement of the amount of air in the lungs at each CP.¹⁰ It was determined by analyzing the volume-averaged Hounsfield units of lung voxels (cf. Ref. 4). The goal of this work was to convert the bellows signal to a bellows-based tidal volume using only the air content, so the correlation between the bellows signal, the spirometry signal, and air content was evaluated.

Correlation of bellows signal and spirometry-measured tidal volume

The relationship between the bellows signal and tidal volume was assumed to be linear except for a possible small time delay. This assumption was evaluated by correlating the spirometry-measured tidal volume against the bellows pressure signal. To remove the spirometry drift artifact, a linear tidal volume drift correction was applied and optimized by maximizing the normalized correlation coefficient between drift-corrected spirometry and bellows signal. A small time offset between the two surrogate signals was also applied and optimized to allow a small time delay between abdomen motion and spirometer-measured air flow. This was repeated independently for the times (18 s time windows) corresponding to image acquisitions at each CP.

The spirometry-measured and drift-corrected tidal volume was termed v_spiro, and the bellows-based signal was b. If the spirometer was being used correctly, and our assumptions were correct, the ratio dv_spiro∕db should be constant and the correlation coefficient r(v_spiro,b) should be high throughout the scan session. These were analyzed for each patient.

Correlation of bellows signal and CT-based air content

The air content was termed V. It was computed from the CT images acquired at the individual CPs. The correlation coefficient r(V,b) between V and the bellows signal was determined for each CP. Again allowing for a small time offset between the two measurements, a linear regression was performed between V and b corresponding to the image acquisition.

Quantitative relationship between CT-based air content and tidal volume

The bellows cannot be assumed to provide a signal that has a constant relationship to internal motion and physiologically relevant measurements for different patients or even for different sessions of the same patient due, for example, to varying sensor or patient positioning. Assuming that a high correlation was found in the analysis of Secs. 2B1, 2B2, the slope of a linear regression of V to v_spiro, dV∕dv_spiro, needed to be a single value for all patients in order to use the air content to convert the bellows signal to tidal volume. dV∕dv_spiro, based on the ideal gas law, should be 1.11 (room air is 11% more dense than air in the lungs, Refs. ^{6, 11}). This was evaluated using two approaches.

First, the bellows signal b was converted into the bellows-based tidal volume, v_bellows, by multiplying b by the couch position average value of dv_spiro∕db. The values of v_bellows for each image acquisition within a CP were then compared to the air content values V represented by each of those 25 image acquisitions. The slope of the comparison between V and v_bellows, dV∕dv_bellows, measured the fraction of the total lung expansion that occurred at that CP. Therefore, the sum of these slopes, ∑_CP(dV∕dv_bellows)_CP, should represent the entire lung expansion, which, when compared against tidal volume, would total 1.11.

Second, a series of 3D CT scans encompassing the entire lungs was reconstructed for 12 selected tidal volumes, and the total air content V^′ of these reconstructed scans was compared against the selected tidal volumes v_bellows to provide dV^′∕dv_bellows. The tidal volumes were equally spaced in volume from the 10th to the 90th percentile tidal volume. The ith percentile tidal volume was defined as the bellows-based tidal volume for which the patient’s v_bellows signal had that value or less for i percent of the time. In each CP, the acquisition with the closest tidal volume to the specified volume was used.

The values of ∑_CP(dV∕dv_bellows)_CP and dV^′∕dv_bellows were compared against the expected value of 1.11.

RESULTS

The correlation analysis of the bellows signal and the spirometry-measured tidal volume highlighted the unreliability of the spirometry measurements as described in Sec. 1: Due to a high failure rate of the spirometry measurements, we observed a significant variability (standard deviations >10%) in both r(v_spiro,b) and dv_spiro∕db values for 15∕41 patients.

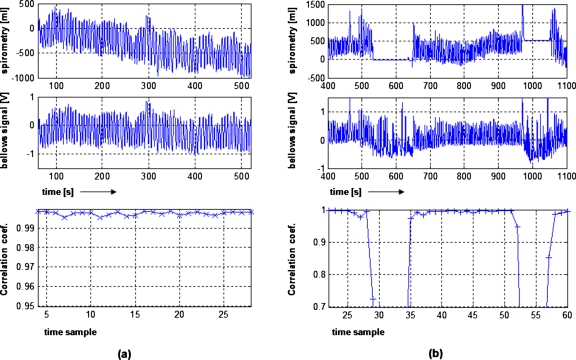
Figure 1 shows the spirometry record, bellows signal, and the correlation coefficients for two patients. For the patient in Fig. 1a, the spirometry record was reliable during the entire scanning session. The drift of the spirometry signal was compensated by combining spirometry and bellows systems. The resulting correlation coefficients r(v_spiro,b) were >0.99 for all CPs. For the patient shown in Fig. 1b, there were two periods where the spirometry record froze due to the patient or therapist removing the spirometer from the patient’s mouth. The bellows system continued to acquire breathing data, so the correlation coefficient dropped significantly dur-ing those periods. The correlation coefficients were near 1.0 for the remaining periods.

Figure 1.

Spirometry record, bellows signal, and the correlation coefficient for each of the 18 s time windows during scanning for two patients. For (a), the spirometer worked the entire session. For (b), the spirometry failed for two periods, resulting in a low correlation for the corresponding times samples and erroneous dv_spiro∕db values.

To assure that only reliable spirometry data were used to determine the relationship between spirometry and bellows data and subsequent analysis, the data were used only when the correlation coefficient r(v_spiro,b) was greater than 0.95. The spirometer data were too poor to use in 6 out of the 15 problematic data sets, so these data were removed from further analysis. On the average, 11% of the 18 s time windows had r(v_spiro,b)<0.95 and excluding these data improved the consistency of the patient-specific dv_spiro∕db values, especially for the other nine problematic cases.

The results are summarized in Table 1 (see also supplementary material¹² for more details). The table includes the average correlation coefficients r(V,b) of the bellows signal to air content correlation analysis (mean value: 0.95±0.03) and the ratios of air content to tidal volume ∑_CP(dV∕dv_bellows)_CP and dV^′∕dv_bellows, which were 1.11±0.08 and 1.12±0.08, respectively. These results were highly consistent with each other and the expected value of 1.11. Without applying the correlation threshold, the average ∑_CP(dV∕dv_bellows)_CP and dV^′∕dv_bellows values were 1.19±0.33 and 1.21±0.34, respectively, showing that the correlation threshold improved the bellows-defined tidal volume.

Table 1.

Summarized results of correlation analysis of the bellows measurement b and the spirometer-measured volume v_spiro and the CT-based air content V. The results of the evaluation of the conversion factor of air content to tidal volume are also listed; for explanation of the acronyms see Sec. 2B. Parenthesized values indicate single standard deviations. The listed values were averaged over the specified data sets; data sets whose spirometry record was completely corrupted were eliminated from the analysis.

	r(vspiro,b)	σ(dvspiro∕db)	r(V,b)	ΣCP(dV∕dvbellows)CP	dV′∕dvbellows
Data sets with reliable spirometry record (26∕41 data sets)
No thresholding	0.98 (0.02)	5.5% (1.9%)	0.96 (0.03)	1.12 (0.08)	1.15 (0.13)
5% thresholding	0.99 (0.01)	5.1% (1.9%)	n∕a	1.12 (0.08)	1.15 (0.13)
Data sets with some spurious spirometry data (9∕41 data sets)
No thresholding	0.85 (0.16)	30.5% (19.6%)	0.94 (0.03)	1.38 (0.58)	1.36 (0.59)
5% thresholding	0.99 (0.01)	7.5% (3.9%)	n∕a	1.08 (0.06)	1.04 (0.09)
Average over all data sets considered for analysis (35∕41 data sets)
No thresholding	0.95 (0.10)	11.9% (15.1%)	0.95 (0.03)	1.19 (0.33)	1.21 (0.34)
5% thresholding	0.99 (0.01)	5.6% (2.7%)	n∕a	1.11 (0.08)	1.12 (0.13)

CONCLUDING REMARKS

We hypothesized that CT-based air content, rather than a spirometer, could be used to convert the bellows signal to provide tidal volumes for 4D CT image sorting and data analysis. This was motivated primarily by the relatively large error rate in spirometry measurements.

The observed correlation coefficients r(v_spiro,b)=0.99±0.01 (after correlation thresholding) and r(V,b)=0.95±0.03 indicated linear relationships between the different breathing signals. We also verified that the conversion factor between air content and tidal volume was 1.11. Thus, the hypothesis was verified. Provided that the entire lungs were scanned, one could use the total air content V^′ to reliably convert a bellows measurement b or other surrogates with a linear relationship to air content using the equation

$$b\mapsto v_{\text{bellows}}≔(1.11\cdot \frac{d{V}^{\prime }}{db})(b-b_{\text{end}\text{expiration}})$$ (1)

where b_{end expiration} is the user-selected zero-tidal volume condition (e.g., the 5th percentile bellows signal). The individual steps of the conversion process are outlined in the flowchart in Fig. 2.

Figure 2.

Steps required for converting the bellows signal (or other surrogates with a linear relationship to air content) to tidal volume without the use of spirometry.

The intended applications are motion modeling and 4D CT research. The described approach for generating tidal volume provides, for example, a way to relate 4D CT data from different scanning sessions via tidal volume—but without being concerned with issues such as spirometer baseline drift and the problem of patient noncompliance regarding spirometer use. The requirement to scan the entire lung is a limitation of the proposed method.