Commentary: Understanding practical lot quality assurance sampling

Lot Quality Assurance Sampling (LQAS) is a statistical method emanating from the brilliant work of Dodge and Romig,¹ which, together with that of Shewhart,² developed into what is known today as Statistical Quality Control. Since the 1980s,³ LQAS has transitioned into the health sciences and has gained considerable appeal in a wide range of applications.⁴ We disagree with the statement in the obloquy by Rhoda and colleagues that LQAS has devolved into two methods;⁵ it remains a single methodology.

LQAS does consist of two stages: the first stage obtains random samples from, say, districts within a region in order to classify each as belonging to one of two classes that is often labeled either ‘acceptable’ or ‘unacceptable’; and the second stage deals with estimation. It sells LQAS short to say that it ‘is supposed to provide a rapid and inexpensive estimate of the prevalence …’.⁵ This quote reveals an academic bias in Rhoda and colleagues' view that overlooks a primary consequence of LQAS; namely, classifications carried out at the local level.³ The first stage is the focus taken by Rhoda et al.^6–8 and the one that is often the most important to practitioners in the field, although, ironically, the second stage is where prevalence estimation occurs.

Rhoda et al. cast LQAS into a hypothesis testing framework, and, as with any analogy, it should not be extended. The Dodge–Romig work preceded the Neyman–Pearson⁹ developments and the attempt by Rhoda et al. to straitjacket LQAS, does not do it justice. This is evident in Concern 1,⁵ e.g. where they admit that the manuals they assail^10,11 do not state a null hypothesis. Yet, not wishing to acknowledge that it is unnecessary to have a null hypothesis, they invent one—and then attack it! This straw man serves no purpose other than to advance a polemic.

Some think that the hypothetico-deductive method, including statistical hypothesis testing, has served us well in advancing empiricism, but the first step of LQAS simply deals with classification. To say that one of these classifications is the ‘null hypothesis’ appends unnecessary labelling baggage. For example, one ‘accepts the null’, which then leads to an addlepated admonition that ‘accepting a null hypothesis is always a statistical error’.⁵ This, of course, belies the fact that in hypothesis testing a Type II error is sometimes called the ‘acceptance’ error, as we teach our beginning students—(e.g. p. 240).¹² Perhaps the authors mean to direct their admonition toward ‘proving’ the null as opposed to accepting it, but such an assumption is kind speculation on our part. One must accept classification into one of the two established classes, which may explain why this methodology is also called acceptance sampling.¹³

In an early published application of LQAS to the health sciences they recognized that the local sample sizes were too small to provide ‘meaningful confidence intervals’ in the first stage.³ In the binomial setting we have here, there is a complete duality between confidence intervals and hypothesis testing. Thus this warning should also be taken by hypothesis testers⁵ to mean that the samples are too small for meaningful hypothesis testing—LQAS is different: at the first stage, it classifies.

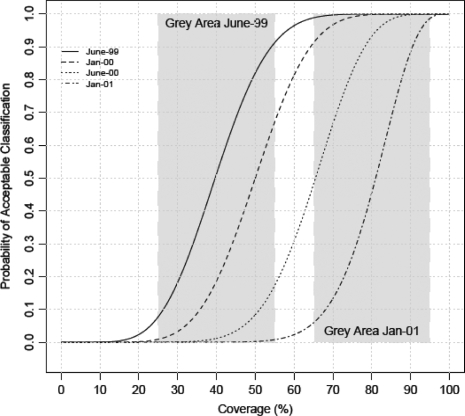
The complete probabilistic characterization of the first step in LQAS is the operating characteristic (OC) curve, such as Figure 1.⁵ This particular design was chosen by Valadez¹⁴ because the value of the OC curve at 80% is ∼90% and its value at 50% is ∼10%. These two thresholds, 50 and 80%, play a pivotal role in LQAS as opposed to the single threshold in hypothesis testing. Note that there is also a certain symmetry in the probabilities of the potential errors at these thresholds, and this is noteworthy for those who feel secure in hypothesis testing, since this equivalence equalizes the ‘value’ of the ‘null’ and ‘alternative’ hypotheses and therefore shields them from the novel and presumably much dreaded ‘bias of the null hypothesis’.⁵

Figure 1.

Figure showing the OC curves as time progressed pertaining to the health services study in Nepal.¹⁷ The first grey area and the last are also shown

A design is judged by the values at these two thresholds—call them p_L and p_U, a lower and an upper threshold, respectively—and the inner region between the two, which is called the grey area. For prevalences smaller than p_L the OC curve is <10%, and for prevalences bigger than p_U the OC curve is >90%, and this is the essence of the first stage of LQAS. The grey area is further evidence that we are sampling and open to possibly large potential errors as described in Valadez.¹⁴

Ideally, we would have a discontinuous curve equal to zero for values below p_L and one for values above p_U—and also that p_L = p_U. Because we have a finite sample, this ideal is unattainable in the binomial model—Figure 6 shows the ideal is not reached even with n = 2800.⁵ The resultant implementation is such that if the truth lies outside the grey region, the chance of making an error is small, leading to the reputation that LQAS is excellent for correctly classifying both extremes. The width of the grey region is how ‘Trainees and LQAS designers [can] be made to understand that small sample studies have low power’.⁵ This fact has not been hidden. How can it be? It is the reality of sampling.

Rhoda et al.⁵ assert that a set of often-used training materials^10,11 promote designs with Type I errors, such that ‘life-giving resources may be prematurely withdrawn from needy populations based on faulty decisions’. This egregious accusation is not supported by any reported occurrences. Indeed, the manuals are freely available (this part of the web site averages approximately 100 hits a month) and have been used extensively, so if they do lead to abuse, as claimed,⁵ it should be easy to find evidence proving such abuse.

The lack of such evidence proffered by Rhoda et al. makes it difficult to counter their predictions. We cannot prove the null, yet we offer evidence in the way of a fairly typical example,¹⁵ where LQAS was used to assess knowledge of oral rehydration therapy amongst mothers of children of age 12–23 months in Nepal (an application which is both cited and ignored by Rhoda et al.⁵). First we note in Figure 1 that the grey region shifted to the right as the study progressed and as expected conditions improved, thus adding nuance to the definition of the grey region; it is not static. Importantly, however, no resources were shifted, as threatened by Rhoda et al., but rather the poorer performing regions were helped by and learnt from the better performing regions, resulting in evident improvement by all.¹⁵ Experienced field practitioners know that when a target is achieved, the programme is maintained—it does not withdraw, as speculated by Rhoda et al.

How to attach a numeric label to the classes seems up for debate. A further imposition due to the enveloping hypothesis testing analogy is that the union of the null and alternative hypotheses must cover the whole parameter space. In search of a value to define the demarcating cut, reason would dictate that a number between p_L and p_U—p*, say—might be chosen to label the classes as having prevalences less than, or greater than or equal to, p*. Surprisingly, the reasoning behind this labelling seems to be the genesis of the ‘two kinds of methods being called LQAS’,⁵ even though the labelling differs but the resultant action is the same.

LQAS does not require this framework—it guarantees in the design above, e.g. that if the prevalence is <50% or >80%, the chance of making a mistake is <10%. These are the extreme sets of prevalences. Even though the distance between the two can be made smaller by choosing a larger sample size, they are not contiguous. This presents one of the important contrasts to hypothesis testing.

The methods supported in the manuals are a consequence of a high-level review of LQAS, which concluded that LQAS tables were difficult to interpret and that user-friendly guidelines were needed.¹⁶ Twenty-four international NGOs helped develop and field test training tools that were later refined by other NGOs (pp. vi–vii).¹⁰ The materials were intended for field workers and were based on the book,¹⁴ a fact not mentioned by Rhoda et al., although in fairness the manuals should be judged in that context. The resulting recommendation identified p* with p_U. The practical reason for this choice is programme staff set coverage targets (p_U), which is the standard operating procedure_.

Rhoda et al. disagree with these recommendations and suggest setting p* equal to p_L. Yet oddly in Recommendation 3 they suggest, as a critical point, to ‘compute the quotient (d*)/n …’. Their design guarantees that when the real prevalence is at the desired target p*, the OC curve is at ∼50%. Another way to achieve these odds is to flip a fair coin, which is much cheaper than obtaining data. Presumably, Rhoda et al. are not recommending that approach, even though their proposed design has the same assurance!

LQAS is far too important a methodology to be subordinated to a churlish and unsubstantiated critique.^17,18 If Rhoda et al. have sound, field-tested and constructive suggestions for the improvement of the manuals, these would be welcome. Their paper contains none.

Funding

National Institutes of Health (R01EB006195); International Health Group within the Liverpool School of Tropical Medicine.

Conflict of interest: None declared.