Abstract
A major goal in evolutionary biology is to understand how and why populations differentiate, both genetically and phenotypically, as they invade a novel habitat. A classical example of adaptation is the pale colour of beach mice, relative to their dark mainland ancestors, which colonized the isolated sandy dunes and barrier islands on Florida's Gulf Coast. However, much less is known about differentiation among the Gulf Coast beach mice, which comprise five subspecies linearly arrayed on Florida's shoreline. Here, we test the role of selection in maintaining variation among these beach mouse subspecies at multiple levels—phenotype, genotype and the environments they inhabit. While all beach subspecies have light pelage, they differ significantly in colour pattern. These subspecies are also genetically distinct: pair-wise Fst-values range from 0.23 to 0.63 and levels of gene flow are low. However, we did not find a correlation between phenotypic and genetic distance. Instead, we find a significant association between the average ‘lightness’ of each subspecies and the brightness of the substrate it inhabits: the two most genetically divergent subspecies occupy the most similar habitats and have converged on phenotype, whereas the most genetically similar subspecies occupy the most different environments and have divergent phenotypes. Moreover, allelic variation at the pigmentation gene, Mc1r, is statistically correlated with these colour differences but not with variation at other genetic loci. Together, these results suggest that natural selection for camouflage—via changes in Mc1r allele frequency—contributes to pigment differentiation among beach mouse subspecies.
Keywords: adaptation, divergence, gene flow, Mc1r, pigmentation, Peromyscus polionotus
1. Introduction
A long-standing goal in evolutionary biology is to understand the forces that lead populations to diverge as they colonize novel habitats, and to partition the relative roles of genetic drift and natural selection (Wright 1931, 1932; Fisher 1958). Island populations, often referred to as ‘natural laboratories of evolution’ (Mayr 1942), are ideal systems in which to explore the contributions of drift and selection to often-rapid population divergence (Emerson 2002, 2008; Grant & Grant 2008; Templeton 2008). On the one hand, genetic drift is likely to play a large role in new island populations that experience founder effects and maintain small population size. On the other hand, natural selection may be important when populations colonize new habitats, which often have novel environmental conditions to which organisms must adapt.
While both of these evolutionary forces can contribute to divergence, understanding their relative contributions can be a challenge. One approach is to compare spatial patterns of neutral genetic differentiation to phenotypic differentiation (e.g. Qst to Fst comparison for quantitative traits: Spitze 1993; Storz 2002; or discrete traits: Thorpe et al. 1996; Schneider et al. 1999; Schemske & Bierzychudek 2007), to differentiation in candidate genes (e.g. Storz et al. 2007), or to both (e.g. Hoekstra et al. 2004; Mullen & Hoekstra 2008). In the absence of strong selection, populations will achieve migration-drift equilibrium, resulting in a pattern of isolation-by-distance in which neighbouring populations are more similar than geographically distant populations (Wright 1943; Slatkin 1993). Selection, however, can disrupt the correlation between neutral genetic differentiation and either phenotypic differentiation or the genes responsible for phenotypic differentiation (Endler 1977, 1986).
The effects of selection, however, may depend on the amount of gene flow that connects populations. If there is limited gene flow among populations, selection will drive phenotypic divergence, whereas the time since population divergence will drive neutral genetic divergence (e.g. Ogden & Thorpe 2002). However, if gene flow occurs between populations, we may expect a positive correlation between phenotypic and genetic divergence because local adaptation can act to reduce gene flow among populations (e.g. selection against migrants or hybrids; Schluter 2000; Nosil et al. 2008). Indeed, in many species, there is a correlation between ecological and genetic divergence (Nosil et al. 2009). Thus, measuring gene flow among populations is key to disentangling the evolutionary forces responsible for phenotypic differentiation.
One of the classic examples of intraspecific geographic variation concerns variation in coat-colour patterns among populations of Peromyscus polionotus. For almost a century, intraspecific variation in P. polionotus has been documented (Sumner 1926, 1929a,b) and genetically analysed using crosses (Blair 1944; Bowen & Dawson 1977). Sumner's studies of P. polionotus, in particular, were considered by Sewall Wright to be ‘the best example of the experimental study of quantitative variability in geographical races of animals in nature’ (Provine 1979, p. 212). Throughout the range of this species in the southeastern US, dark-coloured mainland mice occupy densely vegetated fields with dark soils. These mice have colonized the coastal beaches and barrier islands along the Atlantic and Gulf coasts of Florida and Alabama, unique habitats characterized by brilliant white sandy dunes and sparse vegetation. Overall, these ‘beach mice’ have very light pelage and reduced pigmentation in contrast to their mainland conspecifics.
Most research on beach mice has focused on the phenotypic differences between the dark mainland forms and the light beach forms (e.g. Sumner 1926; Haldane 1948; Hoekstra et al. 2006; Mullen & Hoekstra 2008). However, there are also discrete colour pattern differences among beach mouse subspecies, and it is, in fact, these colour differences that provided the basis for their subspecific designations (Osgood 1909; Howell 1939).
Historically, the underlying forces responsible for more subtle intraspecific geographical variation have been the subject of much debate (e.g. ladybird beetles, Dobzhansky 1933; butterflies, Ford 1940; Cepea snails, Cain & Shepard 1954). The same is true for variation among beach mice. For example, while Osgood (1909) held an adaptationist interpretation of racial differentiation, he provided no evidence to support his position. Sumner, who initially held a neo-Lamarckian belief, challenged Osgood's view, suggesting that the phenotypic differences were environmentally induced (Provine 1983). Later, Bowen (1968), after demonstrating that these colour traits were inherited, largely attributed differences among subspecies to admixture between neighbouring subspecies and a complex history of island colonization. Recently, others have argued that genetic drift is responsible for differentiation among these subspecies (Van Zant & Wooten 2007). However, little is known about levels of gene flow among subspecies, and there is still uncertainty about the role of selection, if any, in phenotypic differentiation among beach mouse subspecies.
To test for a role of selection in generating diversity among beach mice, we compared variation in neutral genetic markers to pigment pattern, but, unlike most systems, we can also examine variation in the genes responsible for these phenotypic differences. In P. polionotus, genes that contribute to pigment differences have been identified (Hoekstra et al. 2006; Steiner et al. 2007). Specifically, a single mutation in one pigmentation gene, the melanocortin-1 receptor (Mc1r), explains as much as 35 per cent of the variation in colour pattern between a dark mainland and a light Santa Rosa Island beach subspecies. Whether this gene also is involved in the subtler differentiation among beach subspecies, however, remains an open question. Here, we investigate whether variation in this gene explains subspecific colour differences and, if so, by comparison with neutral genetic markers, we ask whether evolutionary divergence has been adaptive.
2. Methods
(a). Sample collection
We captured 212 individuals from five subspecies—Alabama, Perdido Key, Santa Rosa Island, Choctawhatchee and Saint Andrew beach mice (tables S1 and S4 in the electronic supplementary material). For each individual, we sampled a 2-mm tail tip and quantified colour pattern (see below), except in 16 samples for which we had only genetic data. We also collected sand samples along each trap line, representing the range of sand colour at each site. For each sample, we measured brightness following Mullen & Hoekstra (2008).
(b). Measuring colour pattern
To measure colour pattern, we scored 12 traits across the body that showed the most difference in pigmentation among individuals (fig. S1 in the electronic supplementary material). For nine traits, we used a three-category system based on the pigmentation of individual hairs within each body region: no visible pigment, partially pigmented or fully pigmented. For three additional traits, we used a five-category system to score the distribution of pigmented hairs across the flank (shadow), rump and tail (as opposed to the extent of pigmentation on individual hairs). Methods follow Steiner et al. (2007).
(c). Genetic variation
We collected genetic data from three different types of markers: microsatellite loci, mitochondrial DNA (mtDNA) sequences and single nucleotide polymorphisms (SNPs) in nuclear genes. First, we genotyped 212 individuals at 20 microsatellite markers (table S2 in the electronic supplementary material); primer sequences and reaction conditions are reported in Mullen et al. (2006). Second, for 70 individuals (10–12 individuals from each subspecies, including two diverged populations within Choctawhatchee beach mice, and one from each of two outgroups), we sequenced two mitochondrial regions: ND3 and COIII (ND3-H and CO3-L; GenBank no. GQ355691-355758; Hoekstra et al. 2004) and, separately, the control region (PL276-R and PL792-F; GenBank no. GQ355623-355690; Van Zant & Wooten 2007). Finally, we genotyped SNPs from eight nuclear genes with no known effect on pigmentation in the same 70 individuals from which we sequenced mtDNA. We also genotyped all 212 samples for a single SNP located in the Mc1r that was previously implicated in colour variation in P. polionotus (Hoekstra et al. 2006). All Taqman assays were conducted in standard conditions, visualized on an ABI 7000 and analysed using the Allelic Discrimination Assay procedure in sds v.1.1.
(d). Data analysis
(i). Phenotypes
To determine the distribution of phenotypic variation within and among subspecies, we used a novel application of Wright's F-statistics (similar to Schemske & Bierzychudek 2007). This approach allowed us to compare patterns of phenotypic divergence across traits to patterns of genetic divergence across loci. To this end, we considered each categorical trait score to be analogous to an allele at a particular locus (i.e. each trait has several discrete conditions that vary among individuals). Using Genalex v.6 (Peakall & Smouse 2005), we first calculated pair-wise phenotypic distance among all individuals following Huff et al. (1993). We then performed a principle component analysis on these phenotypic distance values. Finally, we calculated phenotypic Fst-values among subspecies for each trait using tfpga (Miller 1997).
To determine whether subspecies were phenotypically distinct, we tested for a relationship between the 12 traits (as simultaneous dependent variables) and subspecies (as the independent variable) using multivariate analysis of variance. We also calculated a ‘lightness’ score for each individual by averaging the phenotypic scores of all 12 traits, giving each trait equal weight. We then calculated the average lightness for each sampling site, population and subspecies and tested for differences among them.
(ii). Microsatellites
For each of the 20 microsatellite loci, we tested for deviations from Hardy–Weinberg equilibrium (HWE) and estimated genetic diversity (table S2 in the electronic supplementary material). We used several approaches to measure population structure among subspecies. First, we used the Bayesian clustering program Structure v.2.2 (Pritchard et al. 2000) to assign individuals to clusters based on their genotypic similarity. We ran Structure under the admixture and uncorrelated allele frequencies model, using a Markov Chain Monte Carlo (MCMC) length of 100 000 steps, discarding the first 30 000 as burn-in. No prior information on the origin of the sample was provided. The number of subpopulations (k) was determined by estimating maximum likelihood (ML) scores for runs with k = 1–9, averaged over 10 independent runs for each k-value. We then compared this ML value to those generated from the algorithm Δk (following Evanno et al. 2005). Because calculations of Δk require differences between successive likelihoods of k, this method cannot be used to confidently predict k = 1, which we considered when examining the likelihood outputs.
To measure genetic differentiation, we calculated pair-wise Fst- and Rst-values among subspecies using Arlequin v.2.000 (Schneider et al. 2000). Here, we report only Fst-values as they were not statistically different from Rst-values. We tested for a pattern of isolation by distance by regressing linearized Fst against geographical distance. We also conducted an analysis of molecular variance (AMOVA) among subspecies and ran 10 000 permutations to assess statistical significance.
We then used the microsatellite data to estimate the effective population size (ne) of each subspecies using the program ldne (Waples & Do 2008). To estimate ne, this method calculates linkage disequilibrium among multiple recombining loci with a bias-correction method. We excluded rare alleles (those less than 2%) and assumed random mating.
To measure gene flow, we used the program Migrate v.3.0.3 (Beerli & Felsenstein 1999) to estimate the per-generation effective number of migrants (Nm) for all pair-wise comparisons of subspecies. We started with the default parameters and optimized the likelihood score by using values from the previous run as the next run's starting parameters until the ln (L) peaked and stabilized.
(iii). Mitochondrial sequences
For each subspecies, we estimated genetic diversity from concatenated mtDNA sequences using the program dnasp v.4.20.2 (Rozas et al. 2003). We also calculated genetic differentiation (γst) among populations. γst is similar to Gst, which is equivalent to the weighted average of Fst for loci having more than two alleles (Nei 1973), but is a more appropriate measure for samples with unequal population sizes (Nei 1982).
(e). Phylogenetic analyses
To determine the relationships among subspecies, we combined mtDNA sequences and nuclear-gene SNPs. We included two individuals as outgroups: one mainland (P. p. subgriseus) and one from the sister species P. maniculatus. We constructed a Bayesian topology using MrBayes v.3.0 (Ronquist & Huelsenbeck 2003) on a partitioned dataset that comprises a total of three partitions (two mtDNA regions and SNPs). Models of nucleotide evolution for each partition were chosen using MrModeltest2 (Nylander et al. 2004), in which rate parameters could vary among partitions under a flat Dirichlet prior. We conducted two runs in parallel using random starting topologies, default priors, four Markov chains for two million generations, and sampled every 100 generations. To verify whether the analysis reached stationarity, we plotted generation times against log-likelihood values. We calculated Bayesian posterior probabilities for each branch.
(f). Comparing genetic, phenotypical and geographical data
We conducted Mantel tests to investigate correlations between genetic Fst (based on microsatellites) or γst scores (based on mtDNA sequences), phenotypic Fst scores (calculated for each trait) and geographical distance. Partial Mantel tests were used to identify correlations between genetic, phenotypical or geographical distance, while controlling for each variable in turn. We also tested for correlations between SNP genotype and overall colour phenotype using Kruskal–Wallis tests.
3. Results
(a). Variation in colour pattern within and between subspecies
Several patterns emerge when we compare colour patterns among individuals, traits and subspecies. First, all beach mice were lighter in overall pigmentation than mainland mice (figure 1). However, for some traits, individual beach mice were similar to mainland mice; for example, 80 per cent of Alabama beach mice have a fully pigmented rostrum like mainland mice. The amount and extent of pigmentation in beach mice varied within subspecies (figure 1)—of the five subspecies, the palest subspecies, Santa Rosa Island, showed the least variation in pattern, whereas Choctawhatchee beach mice showed the most variation among individuals. Specific pigment traits also differed in variability: overall, the cheek and ventrum were almost uniformly light, while shadow, rump and tail showed the greatest variation among individuals and subspecies.
Figure 1.
Sample sites and phenotypes of beach mouse subspecies in northwestern Florida (a representative mainland mouse is shown for comparison). Sample sizes (n) are shown. Variations in 12 pigmentation traits for each subspecies are depicted as pie charts: nine traits are scored in three categories (shown above the horizontal line) and three traits are scored in five categories (below the line). Colours in the pie diagrams correlate with pigmentation, e.g. darker colours represent more fully pigmented hairs (see text for details). Average lightness values calculated across all traits (see text) are reported.
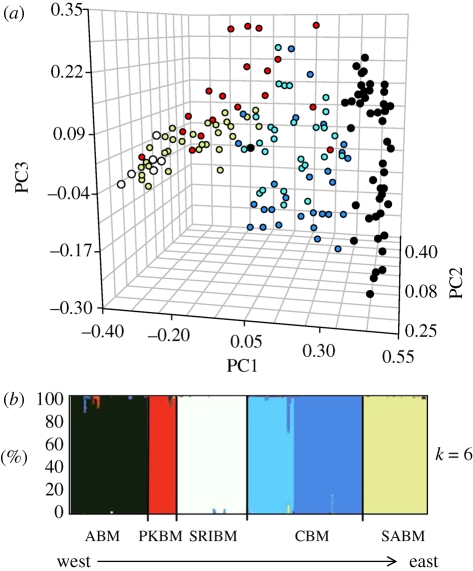
In addition to variation within subspecies, we found significant differences in colour pattern among subspecies (table S3 in the electronic supplementary material). When all 12 traits are considered together, the first three principal components explain 81.9 per cent of the variation in pigment pattern (figure 2a: PC1 = 58.7%; PC2 = 15.6%; PC3 = 7.7%), with PC1 largely corresponding to variation in overall coloration. However, we did not find a correlation between phenotypical distance and geographical distance among subspecies (r2 = −0.161, p = 0.66). Finally, all comparisons of overall lightness (the average for each subspecies) show significant differences among subspecies (analysis of variance, p < 0.0001; all post hoc comparisons Tukey HSD, p < 0.01).
Figure 2.
Phenotypic and neutral genetic divergence in beach mice. (a) Three-dimensional scatter plot of a principal components analysis for 12 phenotypic traits among beach mouse subspecies. Each dot represents an individual (in some cases, dots overlap and therefore represent more than one individual) and is colour-coded by subspecies. Choctawhatchee beach mice (CBM) are represented as both light and dark blue corresponding to the two subgroups identified in (b). Sample sizes are provided. (b) Proportion of individuals assigned by Structure to clusters estimated from microsatellite data (with no prior membership information). Vertical coloured bars represent the proportion of an individual's membership in each of the six clusters, which correspond to the five subspecies. CBM (in blue) show two genetically distinct subgroups (n = 41); ABM in black (n = 42); SRIBM in white (n = 42); PKBM in red (n = 18); SABM in pale green (n = 39).
(b). Genetic structure within and among subspecies
All 20 microsatellite loci were polymorphic within each subspecies, and most were in HWE (table S2 in the electronic supplementary material). Overall, the five beach mouse subspecies showed similar levels of genetic diversity (table S4 in the electronic supplementary material), but lower than values reported for mainland subspecies (e.g. Mullen et al. 2006; Degner et al. 2007). Accordingly, estimates of effective population size were also low (table 1)—approximately 100 individuals for each subspecies, including the two subpopulations of Choctawhatchee beach mice (see below).
Table 1.
Estimates of effective population size (ne) for each beach mouse subspecies.
| subspecies | ne | 95 per cent CI |
|---|---|---|
| Alabama beach mice | 96 | 70–144 |
| Perdido Key beach mice | 106 | 38–∞ |
| Santa Rosa Island beach mice | 165 | 99–420 |
| Choctawhatchee beach mice | ||
| Shell Island/Crooked Island | 80 | 39–836 |
| Topsail Hill State Park | 34 | 27–45 |
| St Andrew beach mice | 95 | 62–186 |
In comparisons among subspecies, we found high levels of population structure in pair-wise estimates of Fst (table 2), ranging from 0.23 to 0.63. However, we did not find a significant pattern of isolation-by-distance (r2 = −0.021, p = 0.53). Moreover, subspecies showing the lowest genetic differentiation of all pair-wise comparisons were often not neighbouring populations: the lowest Fst-value was 0.23 between Alabama (westernmost subspecies) and Santa Rosa Island (central subspecies) beach mice. There was also significant geographical structure in the distribution of genetic variation (table S5 in the electronic supplementary material): 21 per cent of the genetic variation segregates among subspecies (p < 0.001).
Table 2.
Genetic structure estimated from microsatellites and mtDNA sequences among beach mouse subspecies. Pair-wise linearized Fst were calculated from 20 microsatellites between sites (below the diagonal); γst calculated from mtDNA sequences (above the diagonal). Populations are shown from west to east.
| ABM | PKBM | SRIBM | CBM | SABM | |
|---|---|---|---|---|---|
| ABM | — | 0.444 | 0.289 | 0.643 | 0.359 |
| PKBM | 0.362 | — | 0.307 | 0.595 | 0.376 |
| SRIBM | 0.231 | 0.465 | — | 0.579 | 0.189 |
| CBM | 0.330 | 0.632 | 0.442 | — | 0.584 |
| SABM | 0.334 | 0.572 | 0.412 | 0.540 | — |
Results from the Structure analyses indicated that there were six distinct genetic clusters (figure 2b). All but two individuals were unambiguously placed into the cluster corresponding to their subspecific designation (i.e. 98% of individuals were assigned to the correct subspecies with greater than 90 per cent confidence). Similarly, Migrate analyses indicated low levels of gene flow among subspecies—Nm ranged from 0.065 to 0.792 (table 3).
Table 3.
Estimates of the effective number of migrants (Nm) among five beach mouse subspecies, which are shown from west to east, based on 20 microsatellite loci.
| ABM | PKBM | SRIBM | CBM | SABM | |
|---|---|---|---|---|---|
| ABM | — | ||||
| PKBM | 0.532 | — | |||
| SRIBM | 0.553 | 0.665 | — | ||
| CBM | 0.792 | 0.096 | 0.129 | — | |
| SABM | 0.657 | 0.366 | 0.086 | 0.065 | — |
We next tested for population structure within subspecies and found that 11 per cent of genetic variation segregates within a subspecies (table S5 in the electronic supplementary material; p < 0.0). Although multiple sites were sampled within each subspecies, only three showed any evidence of population structure. Within Alabama beach mice, individuals from one sampling site, the Gazebo Unit, clustered together, but pair-wise estimates of population structure among the four sampling sites were low (Fst = 0.02–0.09). Similarly, within Santa Rosa Island, mice collected from Eglin Air Force Base clustered together, but there was little population structure between the two sampling sites (Fst = 0.05). Most striking, however, is that Choctawhatchee beach mice form two very distinct genetic clusters. One cluster is comprised exclusively of individuals from Topsail Hill State Park, while the other cluster includes individuals from Shell Island and West Crooked Island. In fact, genetic differentiation between these two populations (Fst = 0.55) was as high as that found among subspecies (i.e. Fst = 0.23–0.63).
(c). Nucleotide diversity
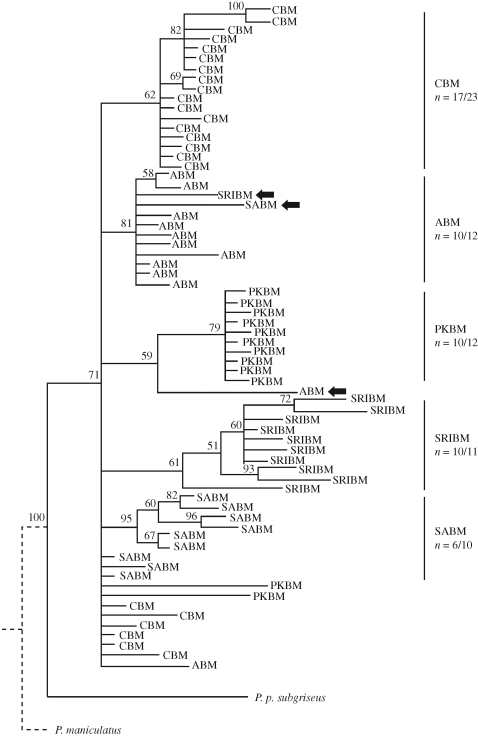
Within beach mouse subspecies, levels of nucleotide diversity were consistently low across subspecies (table S4 in the electronic supplementary material). Similar to the microsatellite results, we found a high degree of population structure among subspecies using estimates of γst (table 2), which also was mirrored in the phylogenetic analysis of mtDNA alleles (figure 2). Although not all individuals clustered perfectly with their population of origin, the Gulf Coast beach mice formed a monophyletic group (see also Steiner et al. 2009), and subspecies generally clustered into clades (figure 3).
Figure 3.
Bayesian topology of 70 individuals (rooted with P. p. subgriseus and P. maniculatus) based on 2958 bp of mtDNA (ND3–COIII and control region) sequences and eight autosomal SNPs. Individuals are labelled by their sample site, and those that do not cluster with their population of origin are highlighted with an arrow. Subspecific clades are highlighted on the right with the number of individuals from that subspecies included in the clade of the total number sampled. Bayesian posterior probabilities for each node of ≥50 are shown.
(d). Correlation between genetic and phenotypic distance
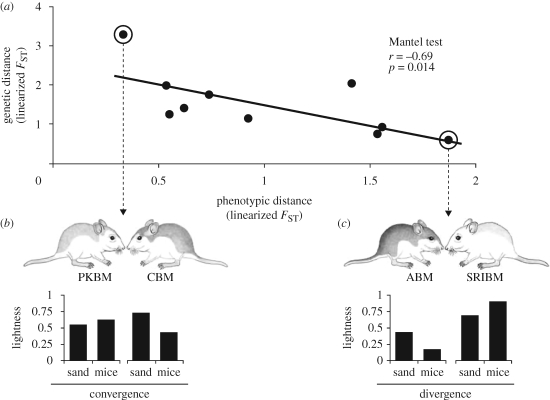
Using Mantel tests, we found a significant negative correlation between genetic and phenotypic distance when all traits are considered together (figure 4; r = −0.690, p = 0.014) even when we controlled for geographical distance (partial Mantel test; r = −0.684, p = 0.014). This trend is largely driven by two points representing phenotypic similarity between the two most distantly related subspecies and phenotypic divergence between the two most closely related subspecies (figure 4). When these two points are removed, the trend remains negative, but the correlation is no longer significant.
Figure 4.
Convergence and divergence in beach mice colour pattern. (a) Negative correlation between genetic distance and phenotypic distance in pair-wise comparisons among five beach mouse subspecies. The extreme points demonstrate (b) convergence and (c) divergence in colour pattern. The most distantly related subspecies, Perdido Key and Choctawhatchee beach mice, occupy similar-coloured sands and have similar lightness scores (see text), whereas the two most closely related subspecies, Alabama and Santa Rosa Island beach mice, occupy different coloured sands and have different lightness scores.
(e). Correlations among phenotype, melanocortin-1 receptor genotype and environment
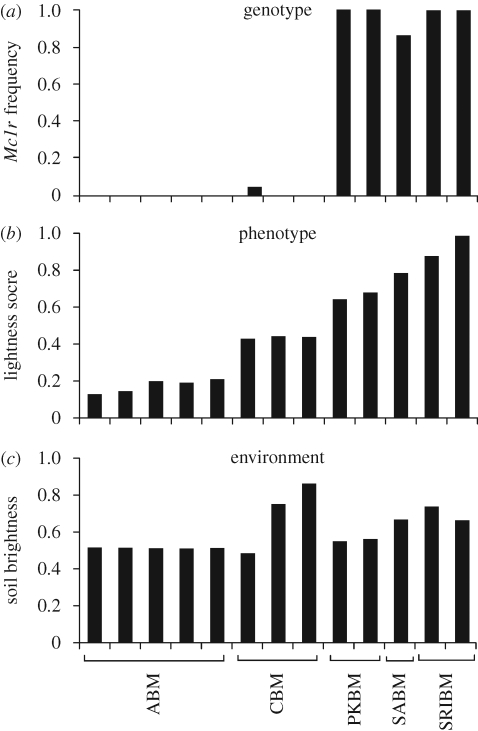
We calculated the frequency of the most common allele in eight autosomal loci (table S4 in the electronic supplementary material). For most genes, the low-frequency allele segregates in one or a few subspecies. Overall, allelic variation at these genes did not show a correlation with phenotypic variation among populations, with one exception: the pigmentation gene Mc1r. The derived light Mc1r allele was fixed or at high frequency (≥0.90) in the three lightest subspecies, but was at low frequency (0.05 in Choctawhatchee) or completely absent (Alabama) in the two darker subspecies (figure 5a). We found a strong association between Mc1r genotype and pigmentation among subspecies (Spearman's ρ = 0.83, p < 0.001).
Figure 5.
Patterns of genetic, phenotypical and environmental variation across beach mouse subspecies. Each column represents a sampling site. Columns are arranged by phenotypic score (not by geographical location). (a) Frequency of the light allele of the Mc1r pigment gene. (b) Average lightness score of mice scaled from 0–1 (see text for details). (c) Average brightness of sand sample measured using a spectrophotometer.
We also found a significant association between phenotype and environmental variation (figure 5). Sand brightness ranged from 44 to 88 per cent reflectance (figure 5c). Sand brightness was most uniform within the range of Alabama beach mice (50–51%), but varied greatly among Choctawhatchee beach populations (44–88%). Most strikingly, there was a significant positive correlation between sand brightness and phenotypic lightness score among populations (Spearman's ρ = 0.64, p = 0.02).
4. Discussion
While the overall pale pigmentation of beach mice inhabiting the sandy dunes of the Gulf and Atlantic coasts of Florida have long served as an example of adaptation (Dobzhansky 1937; Mayr 1942; Haldane 1948; Hoekstra et al. 2006), the evolutionary forces responsible for variation among beach mouse subspecies have been the subject of much speculation. Here, we document differences in pigmentation pattern among the five Gulf Coast subspecies and show that these subspecies are highly differentiated at neutral genetic markers, despite being separated by only a few kilometres in some cases. Although effective population sizes are small and drift undoubtedly occurs, we did not find a pattern of isolation by distance. Instead, we found a significant correlation between pigment phenotype and sand brightness consistent with local adaptation. Moreover, these differences in pigmentation are probably due, at least in part, to allelic variation at Mc1r, as there is also a correlation between pigment phenotype and Mc1r allele frequency among populations. Together, these data support the hypothesis that natural selection has driven the diversification of colour patterns among beach mouse subspecies.
These results also highlight how local adaptation can lead to heterogeneous divergence across the genome, and how this can inform our understanding of the genetic basis of adaptation. Here, we provide a clear case in which divergent selection acts on at least one specific pigmentation gene, Mc1r, affecting the distribution of its alleles among populations. By contrast, much of the remainder of the genome is probably diverging neutrally, primarily affected by the time since population separation (i.e. colonization of the novel beach habitat). Thus, contrasting patterns of variation at ‘adaptive’ and neutral genetic markers ultimately will allow us to better understand the timing of adaptation and the source of adaptive alleles (i.e. as novel alleles or from pre-existing genetic variation).
(a). Phenotypic and genetic differentiation
Variation in colour patterns among beach mice historically has served as the main rationale for their subspecific designations (Howell 1939; Bowen 1968). While all beach mice are lighter than their mainland conspecifics, our analysis of colour pattern quantified strong phenotypic differentiation among subspecies (Bowen 1968), which is not correlated with geographical distance. We also found substantial within-population variation. Given the small effective population sizes, it is surprising that such variation can be maintained within a subspecies over time. Thus, two main questions emerge: (i) does selection—natural or sexual—act to maintain within-population variation in pigmentation? And (ii) is colour variation maintained by the introduction of new pigmentation alleles from neighbouring populations? Future population studies examining the fine-scale distribution of phenotypic and genetic variation in relation to dispersal and environmental heterogeneity will allow us to address the first question, while genetic association studies will allow us to identify the origin of genetic variants responsible for within-population variation in pigment pattern.
In addition to phenotypic differentiation, we found high genome-wide genetic differentiation among subspecies. For example, microsatellites showed high levels of structure and no evidence for historical or current gene flow between subspecies. Similar clustering, although not monophyly, was found in phylogenetic analyses based on DNA sequences. The lack of monophyly is probably due to incomplete lineage sorting caused by recent divergence among subspecies. This level of population structure among geographically proximate populations is especially surprising given the dynamic habitats these animals occupy. Historically, the coastal shoreline has been affected by changes in the water level (for example, during the Pleistocene glaciations; McNeil 1950). Even now, these barrier islands and coastal dunes are regularly struck by hurricanes that both restructure the habitat (including splitting and fusing of beaches) and form new corridors for migration.
These results also have conservation and management implications. First, it is clear that each of the five Gulf Coast subspecies represents a distinct gene pool validating their subspecific designations. In fact, the divergence is often almost an order of magnitude higher than that reported for other mammalian subspecies (e.g. Fst = 0.06–0.16; Roy et al. 1994; Van Hooft et al. 2000; Eizirik et al. 2001). This divergence (both genetic and phenotypic), combined with evidence for post-zygotic reproductive isolation among subspecies (hybrid inviability; Bowen 1968), warrants discussion of their elevation to species. This result is particularly relevant because most of the Gulf Coast beach mouse subspecies are listed as endangered or threatened. Second, we found substantial cryptic genetic divergence within Choctawhatchee beach mice. Although the two primary populations (one inhabiting Topsail Hill State Park and the other Shell Island and West Crooked Island) are phenotypically indistinguishable, they are as genetically distinct as the currently recognized subspecies. This genetic differentiation may have accumulated in allopatry: it is possible the Topsail Hill mice were exclusively distributed along the coastal dunes, while the Shell Island/Crooked Island group was isolated on the barrier islands. In any case, these two Choctawhatchee populations should be managed as distinct evolutionarily significant units.
(b). The role of selection
Detecting evidence for selection in small populations can often be difficult. However, we have found several lines of evidence that support the role of selection in shaping pigment patterns among beach mouse subspecies. First, we found phenotypic differences between geographically proximate populations. However, because we also found little evidence for gene flow among subspecies, these data alone cannot rule out the possibility that genetic drift is responsible for their phenotypic differentiation. Second, and more convincingly, we found a statistically significant correlation between environmental variation (i.e. sand brightness at sampling sites) and phenotypic variation (i.e. average lightness of mice at that site). Such differences in brightness among the sand dunes are consistent with the complex geological history of the Gulf Coast (Stapor 1973; Johnson 1997). Although the association is not perfect, such a correlation is not predicted by genetic drift alone. This concordance between environment and phenotype is best illustrated by the most extreme comparisons: phenotypic convergence in the two most genetically divergent subspecies and phenotypic divergence in the two most genetically similar subspecies. This negative correlation is probably driven by environmental variation. Specifically, the two convergent subspecies inhabit similar sand habitats, and the two divergent subspecies occupy different habitats. Finally, spatial variation in Mc1r allele frequency is inconsistent with differentiation by drift. While populations from the three lightest subspecies occupying light habitats have similar Mc1r allele frequencies (light Mc1r allele is greater than 0.85), they are among the most genomically divergent subspecies (Fst = 0.41–0.57) at neutral loci, which is consistent with parallel selection in similar environments. Together, these results provide a strong case for the role of selection in the diversification of pigment pattern among subspecies.
5. Conclusion
Comparison of genes, phenotypes and environment provides a powerful approach to understanding the evolutionary forces responsible for phenotypic divergence. Using this integrative approach, we provide empirical evidence that natural selection acting on Mc1r alleles has not only contributed to differences between mainland and beach populations (Hoekstra et al. 2006; Mullen & Hoekstra 2008), but has also fine-tuned pigment patterns among the five Gulf Coast subspecies of beach mice to best match their local environments. As the number of genomic resources available for species with well-studied ecology continues to grow, our study provides an example of how combining data from multiple levels can provide insight into the precise evolutionary mechanisms driving phenotypic evolution.
Acknowledgements
We thank several colleagues for their help: T. Doonan, R. Hoggard, R. Loggins, A. Pries, L. Slaby, S. Sneckenberger, L. Suydan and C. Steiner for field assistance, M. Wooten and J. Weber for samples, C. Linnen and L. Turner for advice on analyses, L. Boettger for molecular data collection, and members of the Hoekstra laboratory for helpful discussion. Comments from V. Domingues, J. Losos, J. Mallet, P. Nosil and two anonymous reviewers improved this manuscript. This work was supported by an American Society of Mammalogists Grant-in-Aid, a NSF Graduate Research Fellowship and a NSF Dissertation Improvement grant to L.M.M., a University of California President's Postdoctoral Fellowship to S.N.V., and NSF grant (DEB-0344710) to H.E.H.
References
- Beerli P., Felsenstein J.1999Maximum-likelihood estimation of migration rates and effective population numbers in two populations using a coalescent approach. Genetics 152, 763–773 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blair W. F.1944Inheritance of the white-cheek character in mice of the genus Peromyscus. Contrib. Lab. Vert. Biol. Univ. Michigan 25, 1–7 [Google Scholar]
- Bowen W. W.1968Variation and evolution of Gulf Coast populations of beach mice, Peromyscus polionotus. Bull. Florida St. Mus. 1, 1–91 [Google Scholar]
- Bowen W. W., Dawson W. D.1977Genetic analysis of coat pattern variation in oldfield mice (Peromyscus polionotus) of western Florida. J. Mammal. 58, 521–530 (doi:10.2307/1380000) [Google Scholar]
- Cain A. J., Shepard P. M.1954Natural selection in Cepea. Genetics 39, 89–116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Degner J. F., Stout I. J., Roth J. D., Parkinson C. L.2007Population genetics and conservation of the threatened southeastern beach mouse (Peromyscus polionotus niveiventris): subspecies and evolutionary units. Conserv. Genet. 8, 1441–1452 (doi:10.1007/s10592-007-9295-1) [Google Scholar]
- Dobzhansky T.1933Geographical variation in ladybeetles. Am. Nat. 67, 97–126 (doi:10.1086/280472) [Google Scholar]
- Dobzhansky T.1937Genetics and the origin of species New York, NY: Columbia University Press [Google Scholar]
- Eizirik E., Kim J. H., Menotti-Raymond M., Crawshaw P. G., O'Brien S. J., Johnson E. E.2001Phylogeography, population history and conservation genetics of jaguars (Panthera onca, Mammalia, Felidae). Mol. Ecol. 10, 65–79 (doi:10.1046/j.1365-294X.2001.01144.x) [DOI] [PubMed] [Google Scholar]
- Emerson B. C.2002Evolution on oceanic islands: molecular phylogenetic approaches to understanding pattern and process. Mol. Ecol. 11, 951–966 (doi:10.1046/j.1365-294X.2002.01507.x) [DOI] [PubMed] [Google Scholar]
- Emerson B. C.2008Speciation on islands: what are we learning? Biol. J. Linn. Soc. 95, 47–52 [Google Scholar]
- Endler J. A.1977Geographic variation, speciation, and clines. In Monographs in population biology, vol. 10 Princeton, NJ: Princeton University Press; [PubMed] [Google Scholar]
- Endler J. A.1986Natural selection in the wild. In Monographs in population biology, vol. 21 Princeton, NJ: Princeton University Press [Google Scholar]
- Evanno G., Regnaut S., Goudet J.2005Detecting the number of clusters of individuals using the software STRUCTURE: a simulation study. Mol. Ecol. 14, 2611–2620 (doi:10.1111/j.1365-294X.2005.02553.x) [DOI] [PubMed] [Google Scholar]
- Fisher R. A.1958Genetical theory of evolution Oxford, UK: Clarendon Press, Oxford University [Google Scholar]
- Ford E. B.1940Polymorphism and taxonomy. In The new systematics (ed. Huxley J.). London, UK: Oxford University Press [Google Scholar]
- Grant P. R., Grant B. R.2008How and why species multiply: the radiation of Darwin's finches Princeton, NJ: Princeton University Press [Google Scholar]
- Haldane J. B. S.1948The theory of a cline. J. Genet. 48, 277–284 (doi:10.1007/BF02986626) [DOI] [PubMed] [Google Scholar]
- Hoekstra H. E., Drumm K. E., Nachman M. W.2004Ecological genetics of adaptive color polymorphism in pocket mice: geographic variation in selected and neutral genes. Evolution 58, 1329–1341 [DOI] [PubMed] [Google Scholar]
- Hoekstra H. E., Hirschmann R. J., Bundey R. A., Insel P. A., Crossland J. P.2006A single amino acid mutation contributes to adaptive beach mouse color pattern. Science 313, 101–104 (doi:10.1126/science.1126121) [DOI] [PubMed] [Google Scholar]
- Howell A. H.1939Description of five new mammals from Florida. J. Mammal. 20, 363–365 (doi:10.2307/1374266) [Google Scholar]
- Huff D. R., Peakall R., Smouse P. E.1993RAPD variation within and among natural populations of outcrossing buffalograss [Buchloe dactyloides (Nutt.) Engelm]. Theoret. Appl. Genet. 86, 927–934 (doi:10.1007/BF00211043) [DOI] [PubMed] [Google Scholar]
- Johnson A. F.1997Rates of vegetation succession on a coastal dune system in northwest Florida. J. Coast. Res. 13, 373–384 [Google Scholar]
- Mayr E.1942Systematics and the origin of species New York, NY: Columbia University Press [Google Scholar]
- McNeil F. S.1950Pleistocene shorelines in Florida and Georgia. U.S. Geol. Survey 221, 59–107 [Google Scholar]
- Miller M. P.1997Tools for Population Genetic Analyses (tfpga): a Windows program for analysis of allozyme and molecular population genetic data. See http://herb.bio.nau.edu/~miller [Google Scholar]
- Mullen L. M., Hoekstra H. E.2008Natural selection along an environmental gradient: a classic cline in mouse pigmentation. Evolution 7, 1555–1569 (doi:10.1111/j.1558-5646.2008.00425.x) [DOI] [PubMed] [Google Scholar]
- Mullen L. M., Hirschmann R. J., Prince K. L., Glenn T. L., Dewey M. J., Hoekstra H. E.2006Sixty polymorphic microsatellite markers for the oldfield mouse developed in Peromyscus polionotus and P. maniculatus. Mol. Ecol. Notes 6, 36–40 (doi:10.1111/j.1471-8286.2005.01128.x) [Google Scholar]
- Nei M.1973Analysis of gene diversity in subdivided populations. Proc. Natl Acad. Sci. USA 70, 3321–3323 (doi:10.1073/pnas.70.12.3321) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nei M.1982Evolution of human races at the gene level. Human genetics, Part A: the unfolding genome (eds Bonne-Tamir B., Cohen T., Goodman R. M.). New York, NY: Alan R. Liss [Google Scholar]
- Nosil P., Egan S. P., Funk D. J.2008Heterogeneous genetic differentiation between walking stick ecotypes: ‘isolation by adaptation’ and multiple roles for divergent selection. Evolution 62, 316–336 (doi:10.1111/j.1558-5646.2007.00299.x) [DOI] [PubMed] [Google Scholar]
- Nosil P., Funk D. J., Ortiz-Barrientos D.2009Divergent selection and heterogeneous genomic divergence. Mol. Ecol. 18, 375–402 (doi:10.1111/j.1365-294X.2008.03946.x) [DOI] [PubMed] [Google Scholar]
- Nylander J. A. A., Ronquist F., Huelsenbeck J. P., Nieves-Aldrey J. L.2004Bayesian phylogenetic analysis of combined data. Syst. Biol. 53, 47–67 (doi:10.1080/10635150490264699) [DOI] [PubMed] [Google Scholar]
- Ogden R., Thorpe R. S.2002Molecular evidence for ecological speciation in tropical habitats. Proc. Natl Acad. Sci. USA 99, 13612–13615 (doi:10.1073/pnas.212248499) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osgood W. H.1909Revision of the American genus Peromyscus. In North American Fauna, vol. 28 Washington, DC: Government Printing Office [Google Scholar]
- Peakall R., Smouse P. E.2005GENALEX 6: genetic analysis in Excel. In Population genetic software for teaching and research Canberra, Australia: Australian National University; [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard J. K., Stephens M., Donnelly P.2000Inference of population structure using multilocus genotype data. Genetics 155, 945–959 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Provine W. B.1979Francis B. Sumner and the evolutionary synthesis. In Studies in the history of biology (eds Coleman W., Limoges C.). Baltimore, MD: Johns Hopkins University Press; [PubMed] [Google Scholar]
- Provine W. B.1983The development of Wright's theory of evolution: systematics, adaptation and drift. In Dimensions of Darwinism (ed. Grene M.). Cambridge, UK: Cambridge University Press [Google Scholar]
- Ronquist F., Huelsenbeck J. P.2003MrBayes 3: Bayesian phylogenetic inference under mixed models. Bioinformatics 19, 1572–1574 (doi:10.1093/bioinformatics/btg180) [DOI] [PubMed] [Google Scholar]
- Roy M. S., Geffen E., Smith D., Ostrander E. A., Wayne R. K.1994Patterns of differentiation and hybridization in North American wolf-like canids, revealed by analysis of microsatellite loci. Mol. Biol. Evol. 11, 553–570 [DOI] [PubMed] [Google Scholar]
- Rozas J., Sanchez-DelBarrio J. C., Messeguer X., Rozas R.2003DnaSP, DNA polymorphism analyses by the coalescent and other methods. Bioinformatics 19, 2496–2497 (doi:10.1093/bioinformatics/btg359) [DOI] [PubMed] [Google Scholar]
- Schemske D. W., Bierzychudek P.2007Spatial differentiation for flower color in the desert annual Linanthus parryae: was Wright right? Evolution 61, 2528–2543 (doi:10.1111/j.1558-5646.2007.00219.x) [DOI] [PubMed] [Google Scholar]
- Schluter D.2000The ecology of adaptive radiation Oxford, UK: Oxford University Press [Google Scholar]
- Schneider C. J., Smith T. B., Larison B., Moritz C.1999A test of alternative models of diversification in tropical rainforests: ecological gradients vs. rainforest refugia. Proc. Natl Acad. Sci. USA 96, 13 869–13 873 (doi:10.1073/pnas.96.24.13869) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider S., Roessli D., Excoffier L.2000ARLEQUIN v.2.000: a software for population genetics data analysis Geneva, Switzerland: University of Geneva, Genetics Biometry Laboratory [Google Scholar]
- Slatkin M.1993Isolation by distance in equilibrium and nonequilibrium populations. Evolution 47, 264–279 (doi:10.2307/2410134) [DOI] [PubMed] [Google Scholar]
- Spitze K.1993Population structure in Daphnia obtusa: quantitative genetic and allozymic variation. Genetics 135, 367–374 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stapor F.1973History and sand budgets of the barrier island system in the Panama City, Florida region. Mar. Geol. 14, 277–286 (doi:10.1016/0025-3227(73)90006-6) [Google Scholar]
- Steiner C. C., Weber J. N., Hoekstra H. E.2007Adaptive variation in beach mice produced by two interacting pigmentation genes. PLoS Biol. 5, 1880–1889 (doi:10.1371/journal.pbio.0050219) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steiner C. C., Römpler H., Boettger L. M., Schöneberg T., Hoekstra H. E.2009The molecular basis of phenotypic convergence: pigmentation patterns of beach mice. Mol. Biol. Evol. 26, 35–45 (doi:10.1093/molbev/msn218) [DOI] [PubMed] [Google Scholar]
- Storz J.2002Contrasting patterns of divergence in quantitative traits and neutral DNA markers: analysis of clinal variation. Mol. Ecol. 11, 2537–2551 (doi:10.1046/j.1365-294X.2002.01636.x) [DOI] [PubMed] [Google Scholar]
- Storz J. F., Sabatino S. J., Hoffmann F. G., Gehring E. J., Moriyama H., Ferrand N., Monterio B., Nachman M. W.2007The molecular basis of high-altitude adaptation in deer mice. PLoS Genet. 3, 448–459 (doi:10.1371/journal.pgen.0030045) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sumner F. B.1926An analysis of geographic variation in mice of the Peromyscus polionotus group from Florida and Alabama. J. Mammal. 7, 149–184 (doi:10.2307/1373508) [Google Scholar]
- Sumner F. B.1929aThe analysis of a concrete case of intergradation between two subspecies. Proc. Natl Acad. Sci. USA 15, 110–120 (doi:10.1073/pnas.15.2.110) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sumner F. B.1929bThe analysis of a concrete case of intergradation between two subspecies. II. Additional data and interpretations. Proc. Natl Acad. Sci. USA 15, 481–493 (doi:10.1073/pnas.15.6.481) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Templeton A. R.2008The reality and importance of founder speciation in evolution. Bioessays 30, 470–479 (doi:10.1002/bies.20745) [DOI] [PubMed] [Google Scholar]
- Thorpe R. S., Black H., Malhotra A.1996Matrix correspondence tests on the DNA phylogeny of the Tenerife lacertid elucidate both historical causes and morphological adaptation. Syst. Biol. 45, 335–343 [Google Scholar]
- Van Hooft W. F., Groen A. F., Prins H. H. T.2000Microsatellite analysis of genetic diversity in African buffalo (Syncerus caffer) populations throughout Africa. Mol. Ecol. 9, 2017–2025 (doi:10.1046/j.1365-294X.2000.01101.x) [DOI] [PubMed] [Google Scholar]
- Van Zant J. L., Wooten M. C.2007Old mice, young islands and competing biogeography hypotheses. Mol. Ecol. 16, 5070–5083 (doi:10.1111/j.1365-294X.2007.03582.x) [DOI] [PubMed] [Google Scholar]
- Waples R. S., Do C.2008LDNE: A program for estimating effective population size from data on linkage disequilibrium. Mol. Ecol. Resour. 8, 753–756 (doi:10.1111/j.1755-0998.2007.02061.x) [DOI] [PubMed] [Google Scholar]
- Wright S.1931Evolution in Mendelian populations. Genetics 16, 97–159 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S.1932The roles of mutation, inbreeding, crossbreeding and selection in evolution. Proc. VI Int. Congress Genet. 1, 356–366 [Google Scholar]
- Wright S.1943Isolation by distance. Genetics 28, 114–138 [DOI] [PMC free article] [PubMed] [Google Scholar]