Abstract
Since Haldane first noticed an excess of paternally derived mutations, it has been considered that most mutations derive from errors during germ line replication. Miyata et al. (1987) proposed that differences in the rate of neutral evolution on X, Y, and autosome can be employed to measure the extent of this male bias. This commonly applied method assumes replication to be the sole source of between-chromosome variation in substitution rates. We propose a simple test of this assumption: If true, estimates of the male bias should be independent of which two chromosomal classes are compared. Prior evidence from rodents suggested that this might not be true, but conclusions were limited by a lack of rat Y-linked sequence. We therefore sequenced two rat Y-linked bacterial artificial chromosomes and determined evolutionary rate by comparison with mouse. For estimation of rates we consider both introns and synonymous rates. Surprisingly, for both data sets the prediction of congruent estimates of α is strongly rejected. Indeed, some comparisons suggest a female bias with autosomes evolving faster than Y-linked sequence. We conclude that the method of Miyata et al. (1987) has the potential to provide incorrect estimates. Correcting the method requires understanding of the other causes of substitution that might differ between chromosomal classes. One possible cause is recombination-associated substitution bias for which we find some evidence. We note that if, as some suggest, this association is dominantly owing to male recombination, the high estimates of α seen in birds is to be expected as Z chromosomes recombine in males.
Keywords: male-mutation bias, male-driven evolution, mutation, recombination, introns, rodents
Introduction
Following Haldane's (1947) discovery that most mutations in humans are male derived, it has been conventional wisdom that this male excess is owing to a difference in germ line replications (Crow 1997a, 1997b; Hurst and Ellegren 1998; Li et al. 2002; Ellegren 2007). In males, spermatogenesis is an ongoing process through a male's life, whereas in females, the number of divisions prior to oocyte production is fixed. Under the presumption of a male bias owing to replication differences, Miyata et al. (1987) proposed a simple means to assay the extent of male bias. They argued that the rate of evolution of putatively neutral sites on X, Y, and autosome should reflect the amount of time spent in the male germ line by the three chromosomal classes: The Y should evolve the fastest being exclusively in males, followed by autosomes that spend half of the time in males, followed by the X which spends only one-third of its time in males.
More formally, suppose that the mutation rate in females is μ and the ratio of male-to-female germ line replication events (prior to generation of a successful gamete) is α. Miyata et al. (1987) proposed that if germ line replication is the source of all differences in substitution rate of sequence not under selection:
| (1) |
| (2) |
| (3) |
where KN indicates the evolutionary rate of sequences of class N (Y, X, or autosomal). By considering the ratios of any two classes at a time (KX/KAuto, KY/KAuto, or KY/KX), it is possible to estimate α.
Typically, by employing just one of the three possible comparisons, various authors have attempted to assess the extent of male bias in various taxa (e.g., Shimmin et al. 1993; Chang et al. 1994; Makova and Li 2002; Sandstedt and Tucker 2005; Goetting-Minesky and Makova 2006; Bachtrog 2008). It is commonly argued (Makova and Li 2002) that results are broadly consistent with expectations, in that species with relatively long-lived males (hence, a greater discrepancy between the number of male and female replications) have higher values of α. For humans, the estimate is typically around six (Shimmin et al. 1994; Chang et al. 1996; Taylor et al. 2006), for rodents around two (Chang et al. 1994; Sandstedt and Tucker 2005), and for flies around one (Bauer and Aquadro 1997).
The case is by no means decided however. First, direct observations of male bias (rather than molecular evolutionary inferred estimates) do not agree with one another (Hurst and Ellegren 1998; Hurst 2006). In part, this reflects the fact that very high estimates of α appear to be confounded by intramale germ line selection favoring certain mutations (Qin et al. 2007; Choi et al. 2008). Although these very strong male biases were initially taken as strong support for the replication hypothesis (Li et al. 2002), they no longer arbitrate on the issue. Why some (e.g., Yin et al. 1996) might show a female bias is unresolved.
The molecular evolutionary comparisons also have a number of unresolved issues. Z–W chromosomal comparisons in birds, for example, tend to give estimates (Bartosch-Härlid et al. 2003) that are rather high given the short life spans of the species (α ∼ 5) (Hurst and Ellegren 1998). In Drosophila, one study claims there is a bias of the same magnitude claimed for rodents (Bachtrog 2008). In mammals there is also now strong evidence for within-autosome (Matassi et al. 1999; Lercher et al. 2001; Malcom et al. 2003) and between-autosome (Lercher et al. 2001) variation in rates. To account for this under the replication model, one must suppose different genomic regions are subject to different rates of replication-associated mutations, but why this might be is mechanistically unclear.
Although it has been claimed that differences in the rate of evolution of different chromosomal classes can be explained by the male mutation bias alone (Axelsson et al. 2004), others have argued that mutations arising in nonreplicating DNA also contribute substantially to rates of evolution (Huttley et al. 2000). Further, substitution rates are known to be effected by transcription (Green et al. 2003; Majewski 2003; Lercher et al. 2004), location within an inversion (Navarro and Barton 2003), GC content (Smith and Hurst 1999b; Bielawski et al. 2000; Hurst and Williams 2000), and recombination (Perry and Ashworth 1999; Rattray et al. 2001; Lercher and Hurst 2002; Hellmann et al. 2003; Bussell et al. 2006; Dreszer et al. 2007). However, the quantitative effect of these processes, if any, on Miyata et al.'s (1987) model has not yet been explored.
We propose that there is a simple test of whether replication alone is the source of the differences in evolutionary rate between X, Y, and autosome. If the logic is correct, then equations 1 to 3 must hold. If so, all of the possible pairwise comparisons (X–A, Y–A, and Y–X) should provide the same estimate for α. If they do not, then the “replication-alone” method fails and application of Miyata et al.'s (1987) commonly employed method must be questioned.
In rodents, some prior evidence suggested that the value of α is dependent on which chromosomal classes were employed (Smith and Hurst 1999a). However, sample sizes were too limited to make definitive statements and substitution rates at exonic silent sites were used. As we now know (Chamary et al. 2006) that selection can act on synonymous mutations in mammals (although estimates of KS are very similar to Ki – the intronic rate), it is worthwhile repeating this analysis using a larger sample of well-aligned intronic sequence as well as employing synonymous rates. To this end, we sequenced two rat Y-linked bacterial artificial chromosomes (BACs). Although this provides copious amounts of sequence, outside of the coding regions it proved impossible to unambiguously define orthology. We therefore confined analysis of BAC-derived sequence to well-aligned introns. In addition, we sequenced some further Y-linked cDNAs to expand the inventory for analysis of synonymous substitution rates.
Methods
BAC Isolation, Sequencing, and Annotation
By reference to known rat Y-linked genes, we identified, by screening the RZPD's rat BAC pool library RPCIB657, two Y chromosome BACs (supplementary table 1, Supplementary Material online). These were sequenced and assembled. From the assemblies, and by reference to mouse Y-linked genes and rat cDNA sequencing (supplementary table 2, Supplementary Material online), we determined the full genomic sequence of Ube1y and Eif2s3y and partial genomic sequence of Jarid1d (alias Smcy).
Genomic DNA samples obtained from male and female Wistar rats were used as controls for standardizing rat Y-specific genomic polymerase chain reactions (PCRs). If mouse genomic sequence information was available, the same was used to design primers in exons with some products spanning across introns. Where rat partial cDNA information was available, the same was used in designing primers. Specific primer pairs thus designed were used to standardize male-specific genomic PCRs in rat (supplementary table 3, Supplementary Material online). Positive amplifications were sequenced to verify the authenticity of the genes targeted.
Y-specific PCRs standardized for the various mouse orthologs in rat were used simultaneously to screen the RZPD's rat BAC pool library RPCIB657. Primary and secondary screenings were performed as prescribed by the RZPD. Positive PCR products obtained were sequenced to check the authenticity of the genes targeted. Large-scale preparations of the BACs thus identified were done using Qiagen and Clontech kits. PCR primer pairs proven Y specific were subsequently chosen for use in reverse transcriptase–polymerase chain reactions (RT-PCRs; supplementary table 3, Supplementary Material online) using RNA from brain, kidney, and testis of Wistar rats. Products obtained were sequenced. Rapid amplification of cDNA ends PCRs for Eif2s3y, Jarid1d, Uty, and Ddx3y were designed (supplementary table 3, Supplementary Material online) based on cDNA sequences from deposited sequences or mRNA/genomic sequences generated as part of the current project. The sequences thus obtained were further used in designing RT-PCRs for these genes.
BAC mapping was done by PCR and Southern hybridization. PCRs standardized earlier for the various Y-linked genes were used in mapping experiments. Gene-specific PCR products were cloned in TOPO vectors pcr4 or pcr2.1. Insert DNA fragments were isolated and used as probes in Southern hybridizations against digested BACs immobilized on Osmonics nylon membranes. BAC sequencing was done using standard Sanger Institute sequencing and assembly. Sequence analysis was done using GCG, Bioedit, HGMP's programs, NCBI, and some of our own scripts.
Sequences
Mouse (Mus musculus) and rat (Rattus norvegicus) autosomal and X-linked intronic sequences were downloaded from the University of California Santa Cruz (UCSC) Genome Bioinformatics database (Karolchik et al. 2004; www.genome.ucsc.edu). Mouse exonic and intronic sequences were obtained from the February 2006 and July 2007 builds, respectively, whereas rat exonic and intronic sequences were both obtained from the November 2004 build. Exonic sequences were concatenated by gene and filtered so that only those containing complete codons, correct start and termination codons, no premature stops, or ambiguous bases were retained. In addition to the full coding sequence of rat Ube1y and Eif2s3y and partial coding sequence of Ddx3y (alias Dby), Uty, and Jarid1d (alias Smcy) obtained by BAC sequencing, the full coding sequence of rat Sry and partial coding sequence of rat Zfy were obtained from accession files NM_012772 and X75172, respectively. The correct reading frame of partial rat Y-linked exonic sequences was established as that free from internal stop codons. Rat Y-linked sequences were subjected to a blastn search against the mouse genome to identify orthologous mouse Y-linked coding sequence. Similarly, BAC sequencing gave rise to intronic rat Y-linked sequences of Jarid1d, Ube1y, and Eif2s3y, whereas the last intron of Zfy was obtained from accession file X58934. A blastn search of rat Y-linked sequences against the mouse genome identified orthologous Y-linked mouse genes, for which intronic sequences were downloaded from the UCSC Genome Bioinformatics database (Karolchik et al. 2004).
Ortholog Identification
From an initial set of MGI-defined mouse–rat orthologs (Mouse Genome Database, Mouse Genome Informatics, The Jackson Laboratory, Bar Harbor, Maine; [URL: http://www.informatics.jax.org] [February 2007] [Eppig et al. 2007]), autosomal and X-linked orthologs were further strictly defined by reference to exon number and phase, mouse and rat having to be the same, and by genomic location, chromosomal class having to be known and of the same type. Intronic orthologs were further filtered to retain only those where the difference in coding sequence lengths was less than 5% of the mean coding sequence length. Orthologous Y-linked genes were identified from blastn search of rat sequence against the mouse genome.
Alignments
Orthologous introns were aligned individually using LAGAN (Brudno et al. 2003), with exons identified by reference to mouse and/or rat cDNA in the case of new Y-linked sequence or by RefSeq annotation in the case of X-linked and autosomal genes. This left 40,168 orthologous introns.
By reference to a set of hand-aligned mouse–rat introns (Chamary and Hurst 2004), we determined that there should not be more than 0.84 indels per base pair of alignment and alignment length should be no greater than 1.16 of the longest sequence. In all, 1,915 introns were eliminated due to poor alignment. Rates of evolution of autosomal introns derived from the LAGAN alignment (Ki = 0.1666) were in agreement with those previously obtained both by eye (Ki = 0.1533) and by a maximum likelihood protocol (Ki = 0.1791) (Chamary and Hurst 2004).
We additionally analyzed synonymous rates of evolution. Coding sequences were concatenated by gene and their translations aligned using MUSCLE (Edgar 2004) under default parameters, from which the nucleotide alignment was reconstructed. Exonic alignments of less than 300 sites, equivalent to 100 amino acids assuming no indels, were excluded from the analysis to control for bias introduced due to the influence of short sequences.
Filter for Introns With Hidden Exons or Other Constrained Domains
Given the possibility of alternative splicing, it is possible, if not likely, that some of the above introns may contain hidden exons (or indeed other residues under selection such as binding or regulatory domains). To attempt to filter out these introns, we asked whether, within an intron, substitutions/conserved residues were clustered or randomly scattered through the intron. Our premise is that if a hidden exon or a protein-binding domain is present, such regions should be relatively free of substitution, so we will see longer runs of conserved residues than expected in the absence of such domains.
The filter consisted of a linear model derived from a simulation in which varying percentages of diverged bases ranging from 10% to 90% were randomly distributed along sequences varying in length from 100 to 100,000 bases. For each sequence length and percentage divergence modeled, the number of switches in state between conserved and diverged bases as one moves down the sequence was counted. From multiple permutations ranging from 10,000 permutations for shorter sequences to 100 permutations for longer sequences due to computational limitations, the lowest one-sided 95 percentile was identified. From this, a linear model was developed from which the lowest number of switches in state per base (z) expected for a given number of aligned nucleotides (l) and a given percentage of diverged bases (d) could be predicted: z = −0.005757 + 0.00000026 (l) + 0.0192327 (d) − 0.000192 (d2) + 0.0000000136 ((l − 20350) (d − 50)) − 0.00000000014 ((l − 20350) (d2 − 3166.67)). We do not suppose this method to be perfect (it will likely miss small hidden exons), but it should eliminate those introns most profoundly affected by hidden exons.
After elimination of the 30 bp of sequence flanking exon–intron boundaries (known to be under selective constraint; Chamary and Hurst 2004), we classified sites as conserved or diverged and then calculated the number of switches in state as one moves down the intron. By reference to the linear model, we eliminated any intron showing a lower number of switches than predicted (z). In all, 21,041 (55%) introns showed such evidence of selective constraints and were excluded from the analysis. Autosomal rates of evolution remained largely unchanged between the purged and the unpurged data sets. Note that the filter removed one intron (that of Zfy) previously employed in rodents to estimate the evolutionary rate of the Y chromosome.
Assignment of Chromosomal Location and Concatenation of Intronic Sequences
The first intron of each gene was eliminated from the analysis, these being known to be unusually slow evolving (Keightley and Gaffney 2003; Chamary and Hurst 2004). Indels were removed from the remaining intronic alignments. Finally, for estimation of chromosomal rates, all introns from a given chromosome, assigned by the location of the mouse ortholog, were concatenated. This constituted the first data set and consisted of 15,625 autosomal introns (16.7 Mb), 349 X-linked introns (450 Kb), and 20 Y-linked introns (6,624 bp). For analysis of the effect of GC, expression rate, and a past history of inversions, introns from the same gene were concatenated (comprising 4,051 autosomal, 107 X-linked, and 3 Y-linked genes). Aligned coding sequences for each gene were assigned to the three chromosomal classes. This second data set was comprised of 4,474 autosomal genes (5.8 Mb), 145 X-linked genes (180 Kb), and 7 Y-linked genes (13,662 bp). As it is known that exonic synonymous mutations can be subject to selection in mammals (Chamary et al. 2006), we concentrated our attention on intronic sequences.
Distance Estimation
The rate of intronic divergence (Ki) was estimated and corrected for multiple hits according to the model of Tamura and Kumar (2002), this correcting for inhomogeneous evolution. This was used for the main analysis and all analyses at the gene level. We additionally employed several other methods, including those of Jukes and Cantor (1969), Kimura (1980), and Tamura and Nei (1993).
KS was estimated from exonic alignments using Li's (1993) protocol, correcting for multiple hits according to Kimura's two-parameter model (Kimura 1980). As methods for estimating the synonymous substitution rates are subject to overestimation (McVean and Hurst 1997), the synonymous rate at 4-fold degenerate sites (K4) was also estimated, correcting for multiple hits according to Jukes and Cantor (1969), Kimura (1980), and Tamura and Nei (1993).
α, r, and rm Estimates
Exonic chromosomal K estimates were calculated from the average substitution rate of genes assigned to each chromosomal class. This was repeated using mean, mean weighted by alignment length, and median measures of centrality.
Intronic X- and Y-linked substitution rates were determined directly from concatenated sequences assigned to each chromosome. Intronic autosomal substitution rates were calculated from the average substitution rate of each concatenated autosomal alignment. Analyses were repeated using the mean, mean weighted by alignment length, and median measures of centrality. The main analysis utilized comparisons of intronic X- and Y-linked substitution rates to the autosomal mean. For analyses at the gene level, chromosomal means weighted by alignment length were used.
The ratio of chromosomal K for each pairwise comparison (KX to KAuto, KY to KAuto, and KY to KX) were substituted into the equations of Miyata et al. (1987), namely αXA = (3(KX/KAuto) − 4)/(2 − 3(KX/KAuto)), αYA = (KY/KAuto)/(2 − (KY/KAuto)), and αYX = 2(KY/KX)/(3 − (KY/KX)), in order to calculate the male-to-female mutation rate ratio (α).
For the two-parameter model incorporating a single recombination effect, chromosomal substitution rates were substituted into the following equations to derive α and r:
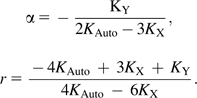 |
For the two-parameter model excluding a female recombination effect (rf = 0), chromosomal substitution rates were substituted into the following equations to derive α and rm:
 |
Error Limits
Within each chromosomal class, per-gene synonymous substitution rates derived from coding sequences were randomly sampled, with replacement and preserving sample size, from which an average substitution rate for the chromosomal type was determined, using each K estimator and measure of centrality previously described. Similarly, alignments of the same length as the concatenated intronic chromosomal sequences were created by random sampling of aligned intronic base pairs with replacement, from which chromosomal substitution rates were calculated using each K estimator previously described and average autosomal rates were determined using the three alternative measures of centrality. Substitution of chromosomal rates of evolution for any given rate estimator into Miyata et al.’s (1987) equations enabled estimation of α for each pairwise comparison. Likewise for estimates of α, r, and rm derived from the two novel models. 10,000 bootstraps enabled values for each calculated parameter to be ranked and the values lying at the 95 percentiles to be identified.
Significant differences between the rate of evolution of different chromosomal classes were determined from 10,000 permutations, whereby for each comparison, pairs of bootstrapped estimates were randomly sampled and the number of occasions on which either the estimates were equal or the chromosomal class with the higher rate was not that originally observed was counted so that significance was calculated as P = (count + 1)/10,001. Likewise for significance of differences between estimates of α.
Recombination Rates
Rat sex-averaged recombination rates over 5 Mb windows were obtained from Jensen-Seaman et al. (2004). These rates were derived from the physical position of markers placed on a previous build, 3.1. To control for potential inaccuracies arising from incorrect annotation of these positions, the relative proximity of neighboring genes in the previous build, 3.1, and the current build, 3.4, were compared. A most conservative approach did not allow for any discrepancy between the relative positions in each build. Runs of consecutive genes between which there was no discrepancy in relative positions were used to identify regions in which the position of markers and the subsequent calculation of recombination rates were likely to be accurate. Recombination windows within such regions were retained. Although relaxation of the size of the discrepancy allowed did not qualitatively affect the results, the most conservative data set was used for all subsequent analyses. Autosomal and X-linked genes were assigned positions based on the midpoint between the start and end of their coding sequence in build 3.1 and, where data were available, these positions were used to assign orthologs a sex-averaged recombination rate in rat. Data were analyzed in nonoverlapping 1 Mb windows.
For both autosomal and X-linked genes, a linear regression weighted by alignment length was performed on recombination rate as a predictor of substitution rate. Comparison of the higher steepness of the autosomal regression compared with that of the X was tested for significance using a one-sided t-test (see later).
Regionality of Substitution Rates
The substitution rate of individual Y-linked introns was estimated and subjected to an analysis of variance (ANOVA) by gene. For each autosomal and X-linked gene, the neighboring 5′ and 3′ orthologs were identified and the mean of their substitution rates determined. For these chromosomal classes, a Spearman's rank correlation of a given focal gene’s substitution rate with the mean of its neighboring orthologs was performed. A higher steepness of the autosomal regression of focal verses flanking substitution rates compared with that of the X regression was tested for significance using a one-sided t-test:
for which degrees of freedom (df) were estimated using the Welch–Satterthwaite equation (Satterthwaite 1946; Welch 1947):
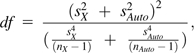 |
where bN = slope of the regression, sN = standard error of the mean (SEM), and nN = sample size of the chromosomal class N.
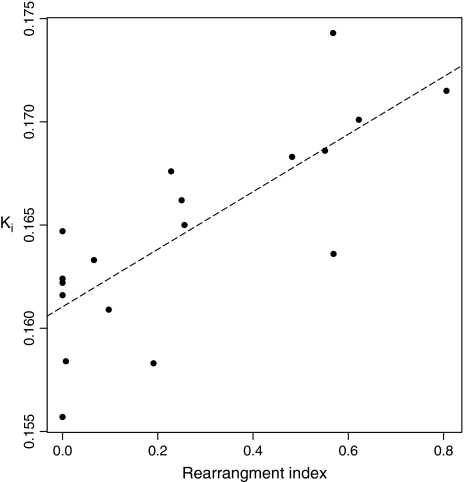
Rearrangement Index
For a given mouse autosome, the chromosomal location of the rat orthologs of two randomly selected genes on the mouse chromosome was determined. From 1,000 repeats per mouse chromosome, we counted the number of times the randomly selected pair of mouse genes had their orthologs located on two different chromosomes in rat. Division of this count by the number of repeat samplings generated a rearrangement index for each mouse autosome. A linear regression of this index as a predictor of autosomal Ki was then calculated.
Results
Estimates of α Are Dependent On Choice of Chromosomes
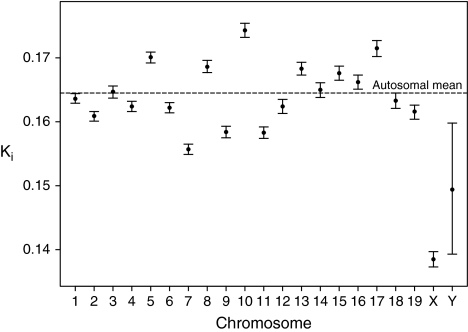
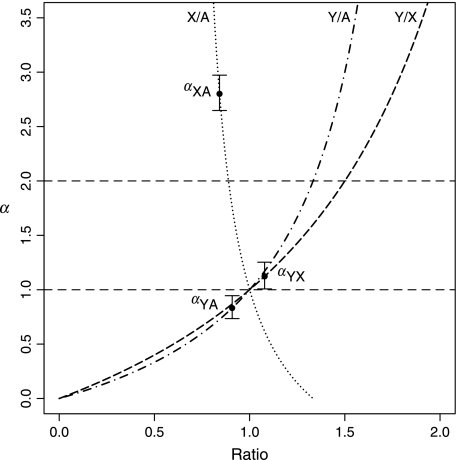
We generated two data sets: aligned introns purged of those in which conserved residues were clustered (possibly owing to hidden exons) and synonymous rates in exons. Qualitatively, estimates of α derived from each of the three pairwise between-chromosome comparisons were unaffected by which of the data sets we used. For brevity then we consider what is probably the safest data set, namely, the filtered introns. For this data set, we find that rates of evolution are in the order KAuto = 0.1645 (0.1642, 0.1647) > KY = 0.1494 (0.1393, 0.1598) > KX = 0.1385 (0.1373, 0.1397), with the autosomal rates significantly higher than the Y chromosome rate (P = 0.0031; fig. 1). As KAuto > KY, it is no surprise that the three comparators fail to agree on the estimate of α, with one supporting a moderate male bias, one a female bias, and one no or weak male bias (fig. 2). These estimates are not mutually compatible (P < 0.0001; for statistical test, see Methods).
FIG. 1.—
Rates of intronic evolution on each mouse autosome, X chromosome, and Y chromosome. For each chromosome, we plot the K estimate for the concatenation and 95% confidence intervals determined from bootstraps.
FIG. 2.—
Estimates of α from three pairwise chromosomal comparisons under the germ line replication model. For each chromosomal comparison, we plot the form of the curve relating the ratio of rates to α. The 95% confidence intervals were determined from 10,000 bootstraps.
Use of synonymous rates of evolution (supplementary information 1, Supplementary Material online) or alternative K estimators (supplementary information 2, Supplementary Material online) confirm this finding. Making allowance for weak effects of differences in expression rate (Lercher et al. 2004), past history of inversions (Navarro and Barton 2003), or GC content (Hurst and Williams 2000) does not alter the conclusion that the results are incompatible with germ line replication as a unique determinant of substitution rate differences (supplementary information 3–5, Supplementary Material online). These results strongly support the view that differences in replication rates alone do not fully explain between-chromosome differences in rates of evolution at putatively neutral sites.
Might Recombination Also Be Important?
That autosomes have a higher substitution rate than Y-linked sequence is most unexpected. Why might this be? Although the replication model has dominated thinking on between-chromosome substitution rates, there are now regular reports that both neutral single nucleotide polymorphism diversity and neutral substitution rates increase across autosomes in correspondence with the local recombination rate (Lercher and Hurst 2002; Hellmann et al. 2003). This may be owing to recombination-induced mutation (Perry and Ashworth 1999; Rattray et al. 2001; Lercher and Hurst 2002; Hellmann et al. 2003; Bussell et al. 2006) and/or recombination-associated biased gene conversion (Dreszer et al. 2007). A correlation between substitution rate and recombination rate is not, however, universally reported. Both Nachman (2001) and Spencer et al. (2006) failed to observe a correlation in humans.
That there might be disagreement between studies is unsurprising given that recombination rate data are based on relatively recent crossover events, whereas substitution rates reflect a much longer history. However, note that recombination is seen at high rates on the pseudoautosomal region of X and Y, a region known to be associated with high substitution rates (Perry and Ashworth 1999; Bussell et al. 2006) but not included in our study.
First then we ask whether we see any evidence in rodents that, across autosomes, regions with high recombination rates have high substitution rates. This issue is, however, enormously problematic. What one needs to know for any sequence is not the current recombination rate alone, but rather the recombination rate to which the sequence has been exposed in both lineages over the course of the divergence of the two species. This is impossible to know. Perhaps, then, it is optimal to consider the mean recombination rate of a sequence in mouse and in rat? This too is problematic. The mouse lineage has undergone very many rearrangements (Ramsdell et al. 2008), so the recombinational environment of a gene in today's mouse genome need not correlate in any manner to its recombinational environment in mouse and rat since divergence of the two. At the extreme, if a rearrangement is very modern, today's recombinational environment may well be a very poor guide to that to which the gene has been exposed over its evolutionary history.
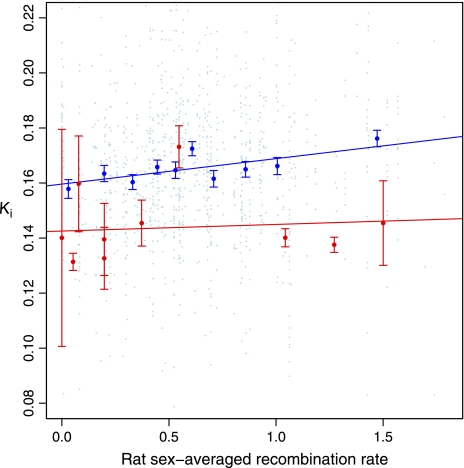
Given that the rat genome is vastly more stable than the mouse, one can, however, define a test that is defendable. If we assume that each chromosomal region has a characteristic recombination rate (on the megabase scale this is defendable), then we may presume that the recombination rate seen in rat should correlate with the recombination rate of a sequence in the rat lineage and for some early part of the mouse lineage of the gene. We therefore ask whether rat recombination rates predict substitution rates. We find that they do, with a significant relationship between substitution rate and recombination rate in rat on the autosomes (weighted linear regression R2 = 0.0346, P = 5 × 10−5; fig. 3).
FIG. 3.—
The relationship between substitution rate and recombination rate in rat. For each chromosomal class, we plot the K estimate for the gene against the sex-averaged recombination rate of the rat ortholog. Data for autosomal genes are in blue and for X chromosome in red. Also shown are bin averages (±1 SEM), where, for each chromosomal class, bins contain equal numbers of genes, 111–112 for autosomes, and 2–3 for X chromosome. Regression lines are for all data, not bin means.
With all the necessary caveats, the above result would suggest that recombination is correlated with substitution rates independent of replication rates (all autosomes undergo the same number of replications). What would be the consequence of this? Such a model could predict that if germ line replication–associated bias, α, were weak (as probably seen in rodents but not necessarily in humans; Makova and Li 2002), the fact that recombination in males is limited to autosomes should increase the autosomal substitution rate, possibly exceeding the Y-linked rate.
As a first approximation, let us then consider a simple extension to Miyata et al.'s (1987) model, whereby a recombination-associated substitution/mutation effect boosts the rate of evolution by an increment of r. Assuming an equal contribution to the recombination effect from each sex, we replace equations (2) and (3) with
| (4) |
| (5) |
respectively. Using data from all three chromosomal classes, we can solve simultaneously for α and r. From this, we find that α = 1.7263 (1.5936, 1.8720) and r = 0.5374μ (0.4666μ, 0.6143μ). This suggests that replication in males provides a boost of 0.7263 and recombination supplies a boost of about the same magnitude, probably a little weaker.
This may not be the whole story. Recent evidence suggests the effect of recombination on neutral substitution rates and clusters of biased substitutions correlates strongly with male recombination rates but not with rates seen in females (Webster et al. 2005; Dreszer et al. 2007; Duret and Arndt 2008; Tyekucheva et al. 2008; Berglund et al. 2009; Galtier et al. 2009). Allowance for this indicates a much lower replication-associated bias. To see this, consider a model excluding female recombination (rf = 0), such that equations (1) and (3) are unaltered but equation (2) is replaced with
| (6) |
where rm is a male recombination-associated substitution/mutation effect. Solving simultaneously resolves to estimates of α = 1.1229 (1.0076, 1.2528) and rm = 0.3496μ (0.3182μ, 0.3805μ). If recombination in males alone is associated with a substitution bias, then these results suggest that in rodents, at least, the effect of replication may have been much overestimated.
Discussion
We find strong evidence that replication alone cannot explain differences in the rates of evolution of X, Y, and autosomes. This is important to know as it suggests that the method of Miyata et al. (1987), although commonly employed, is fundamentally incorrect. Whether the method is grossly misleading, however, will depend on many parameters.
First, if the true replication effect is very large compared with the recombination effect (or whatever causes the disparity), then Miyata et al.'s (1987) method is unlikely to greatly mislead. This may well be the case in humans where a priori, if replication is associated with mutation, a male bias should be very pronounced.
For example, Makova and Li (2002) estimate KY/KAuto to be 1.68 and estimate α = 5.25. Assuming rm = 0.35μ, we can correct this estimate by considering that KY/KAuto = 2α/(1.35 + α) and so estimate α = 7.08. This corrected estimate and the original are both around the proposed α = 6 derived from germ line anatomy. Whether it is legitimate to suppose that any recombination effect is the same in rodent and human is unclear. The reason for this approximate insensitivity is that, if α, the replication-associated bias, is high, the relative impact of male recombination on between-chromosome estimates is reduced. Conversely, the evolutionary rates of rodents may be especially instructive, as any recombination and replication effects are likely to be more balanced.
The models above also suggest that whether any recombination effect is associated with males alone may be very important. A priori given a lack of understanding of any substitution–recombination correlation on a mechanistic basis, it seems impossible to arbitrate at the present. The observation that gene conversion predominantly occurs in the mitotically dividing spermatogonia (Böhme and Högstrand 1997) might be important, but the regular finding of increased pseudoautosomal evolutionary rates (Perry and Ashworth 1999; Filatov and Gerrard 2003; but see Yi et al. 2004) is more obviously consistent with meiotic events.
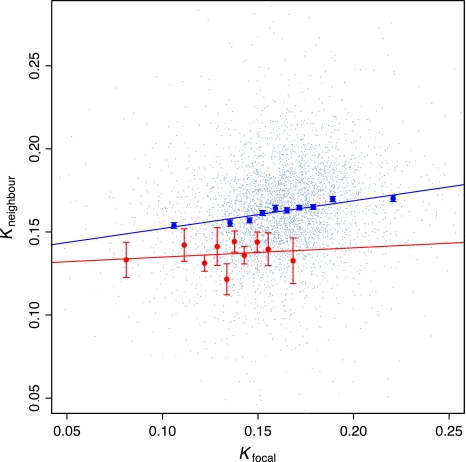
We find some weak evidence consistent with a male bias to recombination-associated substitution bias, but this is not definitive. If male recombination is the sole or dominant source of within-autosome heterogeneity in substitution rates, then we might expect to see no or lesser regionality of substitution rates on the X chromosome and the Y chromosome, these never being subject to recombination in males (nor to translocations from autosomes). Data remain limited on the Y, as it has too few genes on it. Nonetheless, ANOVA reports no gene effect on substitution rates for Y-linked sequences (P = 0.5628). For X and autosome, we can compare the rate of evolution of a gene with its immediate chromosomal neighbors (one 5′ and one 3′). On the X chromosome, there is no correlation (Spearman's rank correlation ρ2 = 0.007, P = 0.40), whereas on autosomes, we find a correlation an order of magnitude higher (Spearman's rank correlation ρ2 = 0.054, P = 2.2 × 10−16; fig. 4). As expected, the slope of the regression line of focal versus flanking for autosomes is steeper than that on the X (slope for autosomes = 0.167 ± 0.01 [SEM], for X = 0.0472 ± 0.07 [SEM], t = 1.69, df = 107, P < 0.05). These data are consistent with a dominant effect of recombination in the male germ line. However, this test suffers two problems. First, the gene density on the X is lower than on autosomes, so immediate neighbors on the X from our ortholog sample are less likely to be in the same recombination block. Second, recombination in females is more scattered along chromosomes than in males (Paigen et al. 2008), hence any female effect on the X need not be visible in a comparison between neighbours, while nonetheless a potent force in determining the overall rate of evolution of the X.
FIG. 4.—
No evidence for local similarity of substitution rates on the X chromosome. For each gene we compare a focal gene's intronic substitution rate with the mean of its 5′ and 3′ nearest neighbors for which we have data. Data for autosomal genes are in blue and for X chromosome in red. Also shown are bin averages (±1 SEM), where for each chromosomal class bins contain equal numbers of genes, 100 for X chromosome, and 401 for autosomal. Regression lines are for all data, not bin means.
Further, if only male recombination is mutagenic, then we would not expect to see a relationship between recombination rate and substitution rate for X-linked genes, these not recombining in males. Indeed, although we find that recombination rate in rat can predict the substitution rate on the autosomes, no such effect is observed on the X chromosome (weighted linear regression for autosomes R2 = 0.0346, P = 5 × 10−5; for X, R2 = 0.004, P = 0.8122). However, given the weakness of the effect, it is unsurprising that we do not find a steeper slope on the autosomes than on the X (slope for autosomes = 0.0086 ± 0.0021 [SEM], for X = −0.0026 ± 0.0111 [SEM], t = 1.0, df = 13.949, P = 0.167). We are therefore unable to completely exclude a female recombination effect.
We further wish to make two observations. Any theory to explain why X, Y, and autosomes evolve at different rates should also attempt to account for why different autosomes evolve at different rates. We suggest that a recombination model might be able to explain one curious observation. We find a striking correlation (ρ = 0.7488, P < 0.00009) between the probability that two randomly chosen genes on a given mouse chromosome have their ortholog on the same chromosome in rat and the evolutionary rate of the mouse chromosome (fig. 5). We suggest that two factors might link this observation to recombination. Let us assume that regions associated with high recombination rates have high substitution rates. Such high-recombination, fast-evolving domains may be expected to be associated with genomic rearrangements, first because, at least in some species, rearrangements tend to occur in regions of high recombination (Akhunov et al. 2003), and second because when chromosomal fusions and translocations occur, they tend to move telomeres rendering them nontelomeric (Dreszer et al. 2007). If high rates of telomeric recombination are associated with increased substitution rates, fusions of such regions should have elevated rates of evolution, as recently reported at the fusion point of human chromosome 2 (Dreszer et al. 2007).
FIG. 5.—
The relationship between between-chromosome rearrangement rates and rates of sequence evolution of genes on mouse autosomes. For each mouse chromosome, we determined a rearrangement probability by repeatedly taking random genes on a given mouse chromosome for which 1:1 orthologs are known in rat and asking whether the two genes reside on the same chromosome in rat. The index is the proportion of times this is not true. As nearly all chromosomal rearrangements occur down the mouse lineage, we employ mouse as the focal chromosome set. The chromosomal rate is derived from intron concatenation. Spearman's ρ = 0.7488, P = 8.098 × 10−5.
Second, if recombination in females has little or no effect on substitution rates but male recombination is important, then, in birds, in which Z chromosomes can recombine in males, we expect Z–W comparisons to produce estimates of α that are biased upward. It has indeed been noted (Hurst and Ellegren 1998) that given their life span, the Z-W derived estimates of α are sometimes unusually high, although this in part may be related to extrapair paternity influencing the number of replication events (Bartosch-Härlid et al. 2003). Comparably, if male recombination is the cause of disparity between estimators of α, assuming nothing else peculiar about the X chromosome, X–Y comparisons are probably best to estimate α, as male recombination should not influence these predictions. It is probably for this reason that X–Y comparisons are those that in the past have more accurately reflected presumed differences in germ line replication ratios (Li et al. 2002; Sandstedt and Tucker 2005; Goetting-Minesky and Makova 2006), whereas X–autosome comparisons have suggested remarkably high (Smith and Hurst 1999a), sometimes impossible (α > infinity) (McVean and Hurst 1997) estimates for α.
Supplementary Material
Supplementary tables 1–18, information 1–5, and references are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).
Supplementary Material
Acknowledgments
We would like to thank the members of the Sanger Institute sequencing teams for their assistance with sequencing of the rat BAC clones, in particular, Sian Hammond, Carl Henderson, and Owen McCann. C.J.P. is funded by an Medical Research Council Capacity Building Studentship; S.K.S. was funded by a Biotechnology and Biological Sciences Research Council grant to L.D.H. and A.W. L.D.H is a Royal Society Wolfson Research Merit Award Holder. We thank The Wellcome Trust for funding.
References
- Akhunov ED, et al. The organization and rate of evolution of wheat genomes are correlated with recombination rates along chromosome arms. Genome Res. 2003;13:753–763. doi: 10.1101/gr.808603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Axelsson E, Smith NGC, Sundstrom H, Berlin S, Ellegren H. Male-biased mutation rate and divergence in autosomal, Z-linked and W-linked introns of chicken and turkey. Mol Biol Evol. 2004;21:1538–1547. doi: 10.1093/molbev/msh157. [DOI] [PubMed] [Google Scholar]
- Bachtrog D. Evidence for male-driven evolution in Drosophila. Mol Biol Evol. 2008;25:617–619. doi: 10.1093/molbev/msn020. [DOI] [PubMed] [Google Scholar]
- Bartosch-Härlid A, Berlin S, Smith NG, Møller AP, Ellegren H. Life history and the male mutation bias. Evolution. 2003;57:2398–2406. doi: 10.1554/03-036. [DOI] [PubMed] [Google Scholar]
- Bauer VL, Aquadro CF. Rates of DNA sequence evolution are not sex-biased in Drosophila melanogaster and D. simulans. Mol Biol Evol. 1997;14:1252–1257. doi: 10.1093/oxfordjournals.molbev.a025734. [DOI] [PubMed] [Google Scholar]
- Berglund J, Pollard KS, Webster MT. Hotspots of biased nucleotide substitutions in human genes. PLoS Biol. 2009;7:e26. doi: 10.1371/journal.pbio.1000026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bielawski JP, Dunn KA, Yang Z. Rates of nucleotide substitution and mammalian nuclear gene evolution: approximate and maximum-likelihood methods lead to different conclusions. Genetics. 2000;156:1299–1308. doi: 10.1093/genetics/156.3.1299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Böhme J, Högstrand K. Timing and effects of template number for gene conversion of major histocompatibility complex genes in the mouse. Hereditas. 1997;127:11–18. doi: 10.1111/j.1601-5223.1997.00011.x. [DOI] [PubMed] [Google Scholar]
- Brudno M, et al. LAGAN and Multi-LAGAN: efficient tools for large-scale multiple alignment of genomic DNA. Genome Res. 2003;13:721–731. doi: 10.1101/gr.926603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bussell JJ, Pearson NM, Kanda R, Filatov DA, Lahn BT. Human polymorphism and human-chimpanzee divergence in pseudoautosomal region correlate with local recombination rate. Gene. 2006;368:94–100. doi: 10.1016/j.gene.2005.10.020. [DOI] [PubMed] [Google Scholar]
- Chamary JV, Hurst LD. Similar rates but different modes of sequence evolution in introns and at exonic silent sites in rodents: evidence for selectively driven codon usage. Mol Biol Evol. 2004;21:1014–1023. doi: 10.1093/molbev/msh087. [DOI] [PubMed] [Google Scholar]
- Chamary JV, Parmley JL, Hurst LD. Hearing silence: non-neutral evolution at synonymous sites in mammals. Nat Rev Genet. 2006;7:98–108. doi: 10.1038/nrg1770. [DOI] [PubMed] [Google Scholar]
- Chang BH, Shimmin LC, Shyue SK, Hewett-Emmett D, Li WH. Weak male-driven molecular evolution in rodents. Proc Natl Acad Sci USA. 1994;91:827–831. doi: 10.1073/pnas.91.2.827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang BHJ, Hewett-Emmett D, Li WH. Male-to-female ratios of mutation rate in higher primates estimated from intron sequences. Zool Stud. 1996;35:36–48. [Google Scholar]
- Choi SK, Yoon SR, Calabrese P, Arnheim N. A germ-line-selective advantage rather than an increased mutation rate can explain some unexpectedly common human disease mutations. Proc Natl Acad Sci USA. 2008;105:10143–10148. doi: 10.1073/pnas.0801267105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crow JF. Molecular evolution—who is in the driver's seat? Nat Genet. 1997a;17:129–130. doi: 10.1038/ng1097-129. [DOI] [PubMed] [Google Scholar]
- Crow JF. The high spontaneous mutation rate: is it a health risk? Proc Natl Acad Sci USA. 1997b;94:8380–8386. doi: 10.1073/pnas.94.16.8380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dreszer TR, Wall GD, Haussler D, Pollard KS. Biased clustered substitutions in the human genome: the footprints of male-driven biased gene conversion. Genome Res. 2007;17:1420–1430. doi: 10.1101/gr.6395807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duret L, Arndt PF. The impact of recombination on nucleotide substitutions in the human genome. PLoS Genet. 2008;4 doi: 10.1371/journal.pgen.1000071. e1000071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edgar RC. MUSCLE: multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res. 2004;32:1792–1797. doi: 10.1093/nar/gkh340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellegren H. Characteristics, causes and evolutionary consequences of male-biased mutation. Proc R Soc Lond B Biol Sci. 2007;274:1–10. doi: 10.1098/rspb.2006.3720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eppig JT, et al. The mouse genome database (MGD): new features facilitating a model system. Nucleic Acids Res. 2007;35:D630–D637. doi: 10.1093/nar/gkl940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Filatov DA, Gerrard DT. High mutation rates in human and ape pseudoautosomal genes. Gene. 2003;317:67–77. doi: 10.1016/s0378-1119(03)00697-8. [DOI] [PubMed] [Google Scholar]
- Galtier N, Duret L, Glemin S, Ranwez V. GC-biased gene conversion promotes the fixation of deleterious amino acid changes in primates. Trends Genet. 2009;25:1–5. doi: 10.1016/j.tig.2008.10.011. [DOI] [PubMed] [Google Scholar]
- Goetting-Minesky MP, Makova KD. Mammalian male mutation bias: impacts of generation time and regional variation in substitution rates. J Mol Evol. 2006;63:537–544. doi: 10.1007/s00239-005-0308-8. [DOI] [PubMed] [Google Scholar]
- Green P, et al. Transcription-associated mutational asymmetry in mammalian evolution. Nat Genet. 2003;33:514–517. doi: 10.1038/ng1103. [DOI] [PubMed] [Google Scholar]
- Haldane JBS. The mutation rate of the gene for hemophilia and its segregation ratios in males and females. Ann Eugen. 1947;13:262–271. doi: 10.1111/j.1469-1809.1946.tb02367.x. [DOI] [PubMed] [Google Scholar]
- Hellmann I, Ebersberger I, Ptak SE, Paabo S, Przeworski M. A neutral explanation for the correlation of diversity with recombination rates in humans. Am J Hum Genet. 2003;72:1527–1535. doi: 10.1086/375657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hurst LD. Mutation rate: sex biases. In: Kehrer-Sawatzki H, editor. Encyclopedia of life sciences. Chichester (United Kingdom): John Wiley & Sons; 2006. [Google Scholar]
- Hurst LD, Ellegren H. Sex biases in the mutation rate. Trends Genet. 1998;14:446–452. doi: 10.1016/s0168-9525(98)01577-7. [DOI] [PubMed] [Google Scholar]
- Hurst LD, Williams EJ. Covariation of GC content and the silent site substitution rate in rodents: implications for methodology and for the evolution of isochores. Gene. 2000;261:107–114. doi: 10.1016/s0378-1119(00)00489-3. [DOI] [PubMed] [Google Scholar]
- Huttley GA, Jakobsen IB, Wilson SR, Easteal S. How important is DNA replication for mutagenesis? Mol Biol Evol. 2000;17:929–937. doi: 10.1093/oxfordjournals.molbev.a026373. [DOI] [PubMed] [Google Scholar]
- Jensen-Seaman MI, et al. Comparative recombination rates in the rat, mouse, and human genomes. Genome Res. 2004;14:528–538. doi: 10.1101/gr.1970304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jukes TH, Cantor CR. Evolution of protein molecules. In: Munro HN, editor. Mammalian protein evolution. New York: Academic; 1969. pp. 21–132. [Google Scholar]
- Karolchik D, et al. The UCSC Table Browser data retrieval tool. Nucleic Acids Res. 2004;32:D493–D496. doi: 10.1093/nar/gkh103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keightley PD, Gaffney DJ. Functional constraints and frequency of deleterious mutations in noncoding DNA of rodents. Proc Natl Acad Sci USA. 2003;100:13402–13406. doi: 10.1073/pnas.2233252100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura K. A simple method for estimating evolutionary rates of base substitutions through comparative studies of nucleotide substitution. J Mol Evol. 1980;16:111–120. doi: 10.1007/BF01731581. [DOI] [PubMed] [Google Scholar]
- Lercher MJ, Chamary J-V, Hurst LD. Genomic regionality in rates of evolution is not explained by clustering of genes of comparable expression profile. Genome Res. 2004;14:1002–1013. doi: 10.1101/gr.1597404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lercher MJ, Hurst LD. Human SNP variability and mutation rate are higher in regions of high recombination. Trends Genet. 2002;18:337–340. doi: 10.1016/s0168-9525(02)02669-0. [DOI] [PubMed] [Google Scholar]
- Lercher MJ, Williams EJ, Hurst LD. Local similarity in evolutionary rates extends over whole chromosomes in human-rodent and mouse-rat comparisons: implications for understanding the mechanistic basis of the male mutation bias. Mol Biol Evol. 2001;18:2032–2039. doi: 10.1093/oxfordjournals.molbev.a003744. [DOI] [PubMed] [Google Scholar]
- Li W-H. Unbiased estimation of the rates of synonymous and nonsynonymous substitution. J Mol Evol. 1993;36:96–99. doi: 10.1007/BF02407308. [DOI] [PubMed] [Google Scholar]
- Li WH, Yi SJ, Makova K. Male-driven evolution. Curr Opin Genet Dev. 2002;12:650–656. doi: 10.1016/s0959-437x(02)00354-4. [DOI] [PubMed] [Google Scholar]
- Majewski J. Dependence of mutational asymmetry on gene-expression levels in the human genome. Am J Hum Genet. 2003;73:688–692. doi: 10.1086/378134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makova KD, Li WH. Strong male-driven evolution of DNA sequences in humans and apes. Nature. 2002;416:624–626. doi: 10.1038/416624a. [DOI] [PubMed] [Google Scholar]
- Malcom CM, Wyckoff GJ, Lahn BT. Genic mutation rates in mammals: local similarity, chromosomal heterogeneity, and X-versus-autosome disparity. Mol Biol Evol. 2003;20:1633–1641. doi: 10.1093/molbev/msg178. [DOI] [PubMed] [Google Scholar]
- Matassi G, Sharp PM, Gautier C. Chromosomal location effects on gene sequence evolution in mammals. Curr Biol. 1999;9:786–791. doi: 10.1016/s0960-9822(99)80361-3. [DOI] [PubMed] [Google Scholar]
- McVean GT, Hurst LD. Evidence for a selectively favourable reduction in the mutation rate of the X chromosome. Nature. 1997;386:388–392. doi: 10.1038/386388a0. [DOI] [PubMed] [Google Scholar]
- Miyata T, Hayashida H, Kuma K, Mitsuyasu K, Yasunaga T. Male-driven molecular evolution: a model and nucleotide sequence analysis. Cold Spring Harb Symp Quant Biol. 1987;52:863–867. doi: 10.1101/sqb.1987.052.01.094. [DOI] [PubMed] [Google Scholar]
- Nachman MW. Single nucleotide polymorphisms and recombination rate in humans. Trends Genet. 2001;17:481–485. doi: 10.1016/s0168-9525(01)02409-x. [DOI] [PubMed] [Google Scholar]
- Navarro A, Barton NH. Chromosomal speciation and molecular divergence—accelerated evolution in rearranged chromosomes. Science. 2003;300:321–324. doi: 10.1126/science.1080600. [DOI] [PubMed] [Google Scholar]
- Paigen K, et al. The recombinational anatomy of a mouse chromosome. PLoS Genet. 2008;4:e1000119. doi: 10.1371/journal.pgen.1000119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perry J, Ashworth A. Evolutionary rate of a gene affected by chromosomal position. Curr Biol. 1999;9:987–989. doi: 10.1016/s0960-9822(99)80430-8. [DOI] [PubMed] [Google Scholar]
- Qin J, et al. The molecular anatomy of spontaneous germline mutations in human testes. PLoS Biol. 2007;5:e224. doi: 10.1371/journal.pbio.0050224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsdell CM, et al. Comparative genome mapping of the deer mouse (Peromyscus maniculatus) reveals greater similarity to rat (Rattus norvegicus) than to the lab mouse (Mus musculus) BMC Evol Biol. 2008;8:65. doi: 10.1186/1471-2148-8-65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rattray AJ, McGill CB, Shafer BK, Strathern JN. Fidelity of mitotic double-strand-break repair in Saccharomyces cerevisiae: a role for SAE2/COM1. Genetics. 2001;158:109–122. doi: 10.1093/genetics/158.1.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sandstedt SA, Tucker PK. Male-driven evolution in closely related species of the mouse genus Mus. J Mol Evol. 2005;61:138–144. doi: 10.1007/s00239-004-0279-1. [DOI] [PubMed] [Google Scholar]
- Satterthwaite FE. An approximate distribution of estimates of variance components. Biometrics Bull. 1946;2:110–114. [PubMed] [Google Scholar]
- Shimmin LC, Chang BH, Li WH. Male-driven evolution of DNA sequences. Nature. 1993;362:745–747. doi: 10.1038/362745a0. [DOI] [PubMed] [Google Scholar]
- Shimmin LC, Chang BHJ, Li W-H. Contrasting rates of nucleotide substitution in the X-linked and Y-linked zinc finger genes. J Mol Evol. 1994;39:569–578. doi: 10.1007/BF00160402. [DOI] [PubMed] [Google Scholar]
- Smith NG, Hurst LD. The causes of synonymous rate variation in the rodent genome. Can substitution rates be used to estimate the sex bias in mutation rate? Genetics. 1999a;152:661–673. doi: 10.1093/genetics/152.2.661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith NGC, Hurst LD. The effect of tandem substitutions on the correlation between synonymous and nonsynonymous rates in rodents. Genetics. 1999b;153:1395–1402. doi: 10.1093/genetics/153.3.1395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer CCA, et al. The influence of recombination on human genetic diversity. PLoS Genet. 2006;2:1375–1385. doi: 10.1371/journal.pgen.0020148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamura K, Kumar S. Evolutionary distance estimation under heterogeneous substitution pattern among lineages. Mol Biol Evol. 2002;19:1727–1736. doi: 10.1093/oxfordjournals.molbev.a003995. [DOI] [PubMed] [Google Scholar]
- Tamura K, Nei M. Estimation of the number of nucleotide substitutions in the control region of mitochondrial DNA in humans and chimpanzees. Mol Biol Evol. 1993;10:512–526. doi: 10.1093/oxfordjournals.molbev.a040023. [DOI] [PubMed] [Google Scholar]
- Taylor F, Tyekucheva S, Zody M, Chiaromonte F, Makova KD. Strong and weak male mutation bias at different sites in the primate genomes: insights from the human-chimpanzee comparison. Mol Biol Evol. 2006;23:565–573. doi: 10.1093/molbev/msj060. [DOI] [PubMed] [Google Scholar]
- Tyekucheva S, et al. Human-macaque comparisons illuminate variation in neutral substitution rates. Genome Biol. 2008;9:R76. doi: 10.1186/gb-2008-9-4-r76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Webster MT, Smith NG, Hultin-Rosenberg L, Arndt PF, Ellegren H. Male-driven biased gene conversion governs the evolution of base composition in human alu repeats. Mol Biol Evol. 2005;22:1468–1474. doi: 10.1093/molbev/msi136. [DOI] [PubMed] [Google Scholar]
- Welch BL. The generalization of “student's” problem when several different population variances are involved. Biometrika. 1947;34:28–35. doi: 10.1093/biomet/34.1-2.28. [DOI] [PubMed] [Google Scholar]
- Yi S, Summers TJ, Pearson NM, Li WH. Recombination has little effect on the rate of sequence divergence in pseudoautosomal boundary 1 among humans and great apes. Genome Res. 2004;14:37–43. doi: 10.1101/gr.1777204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin L, Seri M, Barone V, Tocco T, Scaranari M, Romeo G. Prevalence and parental origin of de novo RET mutations in Hirschsprung's disease. Eur J Hum Genet. 1996;4:356–358. doi: 10.1159/000472232. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.