Abstract
Inversions are among the most common mutations acting on the order and orientation of genes in a genome, and polynomial-time algorithms exist to obtain a minimal length series of inversions that transform one genome arrangement to another. However, the minimum length series of inversions (the optimal sorting path) is often not unique as many such optimal sorting paths exist. If we assume that all optimal sorting paths are equally likely, then statistical inference on genome arrangement history must account for all such sorting paths and not just a single estimate. No deterministic polynomial algorithm is known to count the number of optimal sorting paths nor sample from the uniform distribution of optimal sorting paths.
Here, we propose a stochastic method that uniformly samples the set of all optimal sorting paths. Our method uses a novel formulation of parallel Markov chain Monte Carlo. In practice, our method can quickly estimate the total number of optimal sorting paths. We introduce a variant of our approach in which short inversions are modeled to be more likely, and we show how the method can be used to estimate the distribution of inversion lengths and breakpoint usage in pathogenic Yersinia pestis.
The proposed method has been implemented in a program called “MC4Inversion.” We draw comparison of MC4Inversion to the sampler implemented in BADGER and a previously described importance sampling (IS) technique. We find that on high-divergence data sets, MC4Inversion finds more optimal sorting paths per second than BADGER and the IS technique and simultaneously avoids bias inherent in the IS technique.
Keywords: genome rearrangement, MCMC, Yersinia, inversion
Introduction
As genome-sequencing costs continue their downward spiral, sequencing of closely related organisms has become increasingly viable. Initial efforts to sequence groups of closely related organisms have focused largely on human-pathogenic bacteria. The most striking result has been the discovery that members of the same bacterial species exhibit a diversity of genome structures, including extensive differences in gene content (Perna et al. 2001) and large-scale changes in genome arrangement (Deng et al. 2002).
Genomic inversion is the best known and most common mechanism by which bacteria rearrange their chromosomes. Inversions typically occur with end points in oppositely oriented repetitive elements. The repetitive elements form a homologous substrate for replication-associated DNA repair, the malfunction of which leads to inversion. Associations between the abundance of repetitive DNA and the frequency of inversion are well demonstrated (Achaz et al. 2003).
However, bacteria do not tolerate inversion of some portions of their chromosomes, and accumulating evidence suggests that inversions are subject to strong selective forces and possibly also recombination bias (for an overview, see Darling et al. 2008). As such, it is clear that going beyond inversion distance estimation to reconstruct actual inversion history is useful to elucidate patterns of natural selection and recombination bias.
Some bacterial lineages, particularly host-restricted pathogens like Yersinia pestis, have undergone such extensive genomic rearrangement that numerous possible inversion histories exist which are all equally parsimonious in the total number of inversions. In such organisms, the true history of rearrangement events is uncertain. To make robust inference regarding biological implications of the genome rearrangement history in such organisms, one must average across all likely histories of inversion events.
For the present work, we are interested in methods to reconstruct parsimonious inversion histories and, in particular, to sample from the uniform or other prescribed distribution of possible parsimonious inversion histories. The first polynomial-time algorithm to compute inversion history was given by Hannenhalli and Pevzner (1995). It runs in O(n4) time, where n is the number of conserved segments in the genome. Further work by others improved the running time to O(n2) (Kaplan et al. 1997), and the current best known algorithm has subquadratic running time (Tannier and Sagot 2004). These algorithms not only calculate the minimum number of inversions needed to transform one genome into another but also generate a series of such inversions. When computing only the minimum number of inversions, without reconstructing history, the time complexity drops down to O(n) (Bader et al. 2001). Other work has investigated techniques to determine whether any particular inversion can be part of a parsimonious scenario. Such inversions are termed “sorting” inversions. Because there are O(n2) possible inversions acting on a given genome, the naive algorithm that considers all possible inversions and decides in O(n) time whether each is a sorting inversion can generate the list of all sorting inversions in O(n3) time. Siepel (2002, 2003) introduced a faster algorithm that generates all sorting inversions significantly faster than the naive algorithm in practice. However, the worst-case running time of Siepel's algorithm is still Ω(n3).
If we are interested in all parsimonious inversion histories and not only the set of sorting inversions that decrease the inversion distance by 1 for a particular genome, the situation gets more complicated. It has been shown that the size of the network formed by overlaying common subpaths of minimal sorting scenarios might grow exponentially with the length of the genome (Bergeron et al. 2002). Moreover, the best algorithm for enumerating all sorting paths has O(n2n+3) running time (Braga et al. 2007). Ajana et al. (2002) introduced an importance sampler for parsimonious inversion histories; however, the sampling distribution might be very far from the uniform one (Mélykúti 2006).
In the present work, we describe a method to efficiently sample from the uniform or other prescribed distribution of all parsimonious inversion histories. We describe the expected mixing time of our method and demonstrate that in practice, it mixes quickly. In doing so, we provide an empirical comparison of our method's mixing time to that of Larget et al. (2005) as implemented in the BADGER software. We also compare our method with the importance sampling (IS) approach of Ajana et al. (2002), and we show that the IS technique cannot be used in practice. We further compare the results of our method with the results provided by IS on a pair of Y. pestis genomes, and we estimate the bias present when the IS distribution is treated as if it was the uniform one. Even if the IS is corrected with importance weights, the estimated expectation of statistics of interest has a huge sampling variance caused by the large importance weights.
Finally, we demonstrate how samples generated by our method can be marginalized to obtain distributions for statistics of interest, such as the length distribution of inversions and breakpoint usage. We discuss implications of our efficient sampler and possible applications to phylogenetic inference.
Methods
Preliminaries
Genome Rearrangement and the Reality–Desire Graph
The genome rearrangement problem involves finding a series of mutations from a set of allowable mutation types that transform one genome into another. Allowable mutation types might include inversions, transpositions, translocations, and more generally k-break rearrangements (Alekseyev and Pevzner 2008), which breaks the chromosome at k places and rejoins the so-emerging end points. Genomes are typically described as signed permutations: numbers represent the different genes and the signs represent the reading directions of genes. Although bacterial genomes usually contain a circular chromosome, they can be represented as a linear permutation: We choose an arbitrary gene, and we say that it always has a positive sign (reading direction), and this gene is the first gene in the linear permutation. When a reversal acts on a segment that contains this gene, we replace that mutation with a reversal of the other part of the genome instead. It is easy to see that the alternative mutation has the same effect on the order of the genes. In algebraic terminology, it can be shown that signed permutations with the usual permutation composition and sign multiplication form a group that is isomorphic to where n is the length of the signed permutation. Mutations act on the permutations as a group action. Therefore, transforming a genome arrangement (a permutation) z1 into z2 is equivalent to sorting into the identity permutation, +1, +2, … +n (writing products from left to right and hence assuming that mutations act from the right). In biological terms, the same observation can be realized by numbering the genes as they appear in the target genome. Moreover, the positive sign for each gene is defined as the reading direction in the target genome. Hence a gene in the starting genome has positive direction exactly when the reading direction is the same as in the target genome. Therefore, we can talk about “sorting a signed permutation” instead of transforming one permutation into another.
Inversions (also called reversals) are mutations that invert the order of a consecutive part of the permutation and change the sign of the numbers. It is possible to invert a single number, in which case the sign of the number is changed. When inversions are the only mutations that can act on signed permutations, it is possible to calculate the minimum number of mutations needed to sort a genome. This number is the “reversal sorting distance” of a permutation. An inversion is called a sorting inversion if it decreases the sorting distance of a signed permutation.
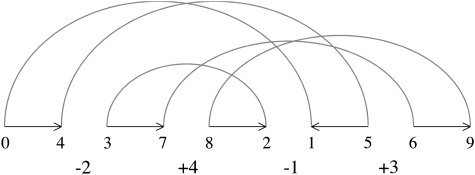
Signed permutations are traditionally represented as graphs of desire and reality (see, e.g., Bader and Ohlebusch 2006 and also fig. 1). To get this representation, we first transform the signed permutation into a double-length nonsigned permutation replacing +i by 2i − 1, 2i and replacing −i by 2i, 2i − 1. Then, we frame this unsigned permutation into 0 and 2n + 1; 0 and 2n + 1 represents the beginning and the end of the permutation. Vertices of the graph of desire and reality are the numbers of the unsigned permutation together with 0 and 2n + 1. We connect every other pair of vertices in the unsigned permutation with a black line, starting with 0. These edges are called “reality edges” because they show the reality, that is, what the neighbor of 0 is and so on. The position of a reality edge is the smallest index of its numbers in the unsigned permutation. Also starting with 0, we connect every node 2i and 2i + 1 with a gray arc above the row of vertices, and these gray arcs are called “desire edges” because they show which nodes should be neighbors to get the identity permutation. The graph falls into cycles because each vertex of the graph has a degree of 2, and we can distinguish “oriented” and “unoriented” cycles. A cycle is oriented if there are two reality edges with different directions on a traversal of the cycle, otherwise it is unoriented. The span of a desire edge is the interval of the permutation between the end points of the desire edges. Two desire edges are said to cross each other if their spans intersect, but neither contains the other. Two cycles intersect if at least one or more desire edges from each of them cross one another. By definition, intersecting cycles form “components” that partition the graph. A component is oriented if it contains at least one oriented cycle; otherwise it is unoriented. The span of a component is the interval from the smallest position of its reality edges to the largest position of its reality edges.
FIG. 1.—
The unsigned representation of the signed permutation −2, +4, −1, +3, and its graph of desire and reality. In the graph of desire and reality, every second number of the unsigned permutation is connected with a line (reality edges, the numbers that are next to each other), and each even number is connected to the next odd number by an arc (desire edges, which numbers should be neighbors to get the +1, +2, …, +n permutation). The graph of desire and reality can be decomposed into cycles. This graph contains two intersecting cycles. Arrows on the reality edges indicates a possible walk around the cycles.
Unoriented components play a central role in the theory of sorting signed permutations by reversals. An unoriented component is called a “hurdle” if its span does not contain the span of any unoriented component or its span contains the spans of all unoriented components. A hurdle is called a “superhurdle” if deleting the hurdle would transform a nonhurdle unoriented component into a hurdle. A permutation is called a “fortress” if all of its hurdles are superhurdles and the number of superhurdles is an odd number. The Hannenhalli–Pevzner theorem says that the inversion distance of permuation z is
| (1) |
where n is the length of the signed permutation, c(z) is the number of cycles, h(z) is the number of hurdles in z, and f(z) is 1 if z is a fortress, otherwise 0.
Finally, a pair of inversions are said to be commuting inversions if they are either nonoverlapping or one is nested inside the other. Because they commute, application of the two inversions to a genome will result in the same final genome arrangement regardless of which inversion is applied first.
Markov Chain Monte Carlo
The Metropolis–Hastings algorithm (Metropolis et al. 1953; Hastings 1970) can be used to construct a Markov chain that converges to a prescribed distribution π over state space S. The algorithm can tailor any Markov chain to converge to π if the following are true for the Markov chain:
- Reversible: If the Markov chain can step to state y from state x, then it can also step to x from y. More formally,
where T(y|x) is the probability that the chain steps into states y given that it is in state x.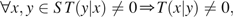
(2) - Irreducible: There is a path with positive probability between any pair of states. If P is the transition matrix of the Markov chain, then this property can be formalized that
where 1x is a vector containing 1 in coordinate x and 0 in all other coordinates, T denotes transposition, and denotes scalar product.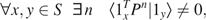
(3)
The Metropolis–Hastings algorithm is comprised of two steps. The first step is called the “proposal,” in which a random state y is drawn from the conditional distribution T(·|x). In the second step, a random decision is made to decide whether or not the proposed y is accepted. A random number u is drawn from the uniform distribution U[0,1] and the next state of the Markov chain is y if
| (4) |
otherwise, the next state of the Markov chain will be also x. It is easy to show that the so-generated Markov chain converges to the prescribed distribution π (see, e.g., Liu 2001).
Markov Chain Monte Carlo Strategy
The Setup of the Markov Chain
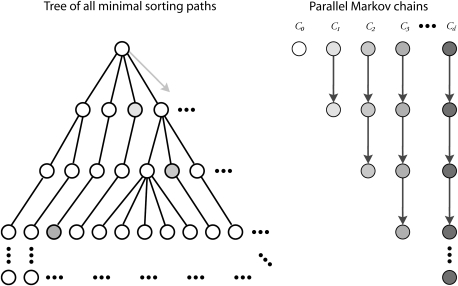
Our sampling strategy for inversions is a realization of a general framework for sampling from nested models (Miklós I, unpublished data [http://ramet.elte.hu/∼miklosi/msis.pdf]). It also can be viewed as a generalization of the (MC)3 method also known as parallel tempering (Altekar et al. 2004). Assume that the minimal number of inversions required to transform the source genome arrangement into the target is d inversions. In our method, we utilize a set of d chains to sample inversion paths in parallel. The “cold” chain Cd always maintains a complete sorting path of length d from the source arrangement to the target arrangement. Each additional chain Ci ∈ {C0 … Cd−1} maintains an i-long prefix of a sorting path. The target distribution in chain Ci is the uniform distribution of possible prefixes of length i, regardless of the number of ways to elongate a prefix into an optimal sorting path of length d. Note that the number of elongations might be different for different prefixes; however, we are unable to calculate these numbers, not even the ratio of the number of possible elongations for two different prefixes cannot be calculated. At each step in the Markov chain, either a pair of neighboring chains Ci, Ci+1 are swapped with each other or the order of commuting reversals within a single chain is swapped. Figure 2 shows an overview of the sampler. We presently describe each type of move.
FIG. 2.—
Overview of the sampler. The set of all optimal sorting paths can be represented as a tree where nodes represent genome arrangements (signed permutations) and edges represent application of a sorting inversion. The root is the starting genome arrangement, and the leaves are the target arrangement so that every path from root to leaf represents an optimal sorting path. In most cases, the tree will be too large to compute in its entirety so we desire instead to take a representative sampling of the sorting paths embedded in the tree. To do so, we construct a sampler with d chains, where d is the minimum sorting distance. Each chain Ci samples uniformly from the nodes at depth i in the tree, thereby sampling uniformly from the i-long prefixes of optimal sorting paths. Chain Cd samples complete paths. The chains perform a random walk through the tree by swapping with each other and within themselves (see text). In practice, we do not even compute the full set of edges (sorting reversals) below a node, instead use rejection sampling to find an arbitrary edge quickly.
Swapping States between Chains
Unlike in parallel tempering (Geyer 1991), where different chains have different distributions over the same state space, here different chains make random walks in different state spaces. Therefore, the states have to be transformed to states in other state spaces when we swap two parallel chains. This simply means that when states in chains Ci and Ci+1 are swapped, we elongate the i-long prefix of a sorting path in chain Ci by one sorting reversal, yielding an i + 1 long prefix as candidate for the new state in chain Ci+1. In the other direction, the last sorting reversal is removed form the current i + 1 long prefix of the chain Ci+1 to get a new candidate for chain Ci. As with parallel tempering, it is sufficient to calculate the probabilities up to unknown normalizing constants for each distributions, these normalizing constants cancel out in the Metropolis–Hastings ratio. Furthermore, as the target distributions are the uniform distribution of prefixes in all parallel chains, the equilibrium probabilities also cancel out from the Metropolis–Hastings ratio. Unlike in parallel tempering, the Metropolis–Hastings ratio contains the ratio of transition probabilities because the states are not simply swapped but are also transformed.
Thus, the Metropolis–Hastings ratio for chain swaps contains the probability of proposing a particular elongation of the shorter chain. Specifically, if the current prefix in chain Ci is pi and it is proposed to be elongated by a sorting reversal ri, and the current prefix in chain Ci+1 is pi+1 ∘ ri+1, where ∘ denotes the concatenation of paths, then the Metropolis–Hastings ratio is
| (5) |
The Metropolis–Hastings ratio accounts for the fact that two different prefixes may each have a different number of sorting reversal elongations, and the method to compute the size of the set of reversals is given below.
Steps Inside a Chain
The random walk inside a chain is performed by swapping two consecutive commuting reversals in a sorting prefix. Namely, our algorithm enumerates all ks for which reversals rk and rk+1 in the sorting prefix are commuting reversals. We select a random k and swap rk and rk+1. The Metropolis–Hastings ratio is the ratio of the cardinality of the set of ks in the resultant prefix and the old prefix.
Proving the Convergence of Our Chain
The proposed Markov Chain Monte Carlo (MCMC) strategy can be described as a random walk by a single master Markov chain. This master chain walks on the set product of i-long prefixes of sorting scenarios, where i runs from 0 to d, the reversal sorting distance. The prescribed distribution is the uniform distribution over the entire set product, which is guaranteed by the Metropolis–Hastings algorithm if the two conditions in equations (2) and (3). are satisfied. But they are indeed satisfied as all steps in the proposed Markov chain are reversible and any prefix can be grown from the empty prefix using swaps between the parallel chains. Namely, it is possible to grow a full-length path from the empty prefix by swaps, then a d − 1 long prefix from the empty prefix without disturbing the full-length path, and so on; we can grow an i-long prefix from the empty prefix without disturbing any j > i long prefixes.
Theoretical Mixing Time
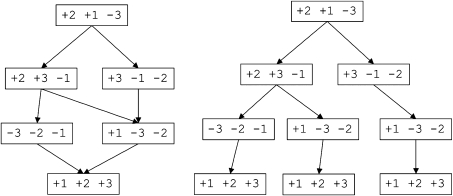
The first theoretical result on the mixing time of Markov chains slightly resembling the one presently described was given by Sinclair and Jerrum (1989). Unfortunately, we could not apply their results to our method. Instead, we can give the following theoretical bounds for the mixing time of the so-constructed Markov chain. Consider the tree of all optimal sorting paths, where the root is labeled with the starting genome, the children of the root are labeled with the possible genomes after the first step of possible optimal sorting paths, and so on. We would like to mention that all optimal sorting paths also could be described as a network; however, this network can be opened to a tree, see figure 3. We recently showed that the network might contain arbitrary big gaps, and hence, from the point of view of convergence of Markov chains on all optimal sorting paths, the tree representation is essentially as efficient as the network representation (Miklós et al. 2009). Let Lj(u) define the leaf nodes below node u at depth j, and let Di denote the set of nodes in depth i. We define the “hiddenness rate” of a tree as
| (6) |
where |·| denotes the cardinality of the set. We recently proved (Miklós 2009) that the mixing time of the Markov chain that applies only the swapping steps between the chains is
| (7) |
where k is the hiddenness rate defined above, a is the inverse of the smallest transition probability of the Markov chain, and d is the inversion distance of the input permutation. We conjecture that the mixing time is a polynomial function of both d and k and that the upper bound in equation (7) might be significantly improved.
FIG. 3.—
The network representing all shortest sorting paths of signed permutation +2,+1,−3, and the corresponding tree representing all shortest sorting paths.
However, swapping across chains alone does not guarantee fast mixing, as one can construct a series of signed permutations for which the hiddenness rate k grows exponentially with the length of the permutations. Briefly, the counterexample contains several oriented components with the same reversal distances but different numbers of sorting reversals as a first step and a different number of optimal sorting paths per component. Let us call the components with more sorting reversals “rich components,” and the components with fewer sorting reversals “poor components.” Assume the number of the poor and rich components is the same in the counterexample. The half-length prefixes containing only sorting reversals that act on poor components will have many more elongations than other prefixes. All elongations of these prefixes involve rich components, and so, they will have many more elongations than average and by definition, they are hidden parts of the tree. However, if the Markov chain also swaps commuting inversions within a path, then the chain becomes quickly mixing for this particular case. Still, we have not proved that the Markov chain with both move types mixes quickly.
Efficiently Sampling a Sorting Reversal
Rejection Sampling
The MCMC algorithm needs samples from some distribution of sorting reversals. The distribution must be such that the acceptance ratio can be estimated. The best algorithm to enumerate all sorting reversals for a given genome has Ω(n3) worst-case running time (Siepel 2002), which might be too slow in practice. Here, we introduce a rejection method (von Neumann 1951; Liu 2001) that we use as a transition kernel in our MCMC strategy. The rejection method first calculates the size of a set of reversals which contains all sorting reversals and some nonsorting reversals. We refer to that set of reversals as the sampling set, denoted s. A member from s is then chosen, uniformly at random. It takes O(n) time to compute the sampling set and choose a member at random. Next, we apply the algorithm of Bader et al. to decide if the sampled reversal is a sorting reversal. If the proposed reversal is a sorting reversal, then we propose it in the Metropolis–Hastings algorithm and accept it with a prescribed probability; otherwise, we reject it and the next state of the Markov chain will remain unchanged from the current state. Because the Bader et al. algorithm to decide whether or not a reversal is sorting also runs in O(n) time, the overall running time for one sampling is O(n). If we use |si| to refer to the sampling set size for prefix pi, and |si+1| for the sampling set size on prefix pi+1, then the Metropolis–Hastings ratio in equation (5) can be replaced by
| (8) |
Indeed, proposing a particular sorting reversal in the above described procedure is 1/|si| if the set of the reversals from which we select a random reversal has size |si|.
Below, we describe how the rejection method defines a set of reversals and samples a random reversal from it. As we found that in practice, a constant percentage of the set will contain sorting reversals, the rejection rate is small, and hence, this method works very fast in practice. The experience that the majority of the proposed reversals are indeed sorting reversals is in accordance with previous works (Bergeron et al. 2002; Swenson et al. 2008).
We used the following facts for the rejection method (Siepel 2002):
If a signed permutation does not contain a hurdle, all sorting reversals increase the number of cycles in the graph of desire and reality. “Cycle-increasing” reversals act on a single cycle and the two reality edges on which they act have different orientations when traversing the cycle.
If a signed permutation contains only one hurdle, then all sorting reversals either increase the number of cycles or act on a single cycle belonging to the hurdle. The latter inversions are called “hurdle-cutting” inversions.
If a signed permutation contains more than one hurdle, then all sorting permutations fall into one of the three categories: (1) cycle increasing (see above), 2) hurdle cutting (see above), and 3) “hurdle merging.” Inversions of the latest type have end points belonging to the spans of different hurdles. The reality edges might not necessarily belong to the hurdles; it is enough to be in the span of the hurdle. Recall that the span of the hurdle is the inclusive interval of the leftmost and the rightmost reality edges of the hurdle.
Note that not all cycle-increasing inversions will be sorting reversals as some of them might create a hurdle. On the other hand, it is possible to count the number of cycle-increasing reversals and sample uniformly one of them in linear time (see Miklós and Hein 2005).
The efficient algorithm by Bader et al. (2001) gives not only the inversion distance in linear time but also the number of hurdles, superhurdles, and which cycle belongs to which hurdle (if it belongs to any). In this way, it is possible to construct an algorithm similar to the one in Miklós and Hein (2005) that runs in linear time and counts the number of inversions acting on one cycle belonging to a hurdle. Note that not all hurdle-cutting inversions will be sorting inversions. Cutting a superhurdle creates a new hurdle, and we can transform the permutation to a fortress by cutting a hurdle.
The algorithm of Bader et al. (2001) also gives the position of the leftmost and the rightmost reality edge of a hurdle. If we traverse the reality edges of the signed permutation one more time from left to right, we can tell for each position i how many reality edges are in spans of hurdles and how many are in the span of each hurdle. In this way, we can tell in O(1) time how many reality edges are to the right of position i that give a hurdle-merging inversion together with the reality edge in position i. The sum of these numbers gives the number of hurdle-merging inversions. Moreover, we can perform a weighted sample from the reality edges where the weights are the above-mentioned numbers. The sampled reality edge will be considered as the left reality edge of a hurdle-merging inversion, and we choose uniformly from the suitable right reality edges. It is easy to see that we sample uniformly from the hurdle-merging inversions in this way in O(n) time. Note that not all the hurdle-merging inversions will be sorting inversions as merging two hurdles of a double superhurdle will create a new hurdle, too (for a definition of “double superhurdles,” see Siepel 2002).
The rejection method first calls Bader‘s algorithm and decides what categories it has to consider (cycle increasing, hurdle cutting, and hurdle merging). It then calculates the number of inversions falling into each category, chooses a category weighted by their cardinalities, and uniformly samples an inversion from that category. If the sampled inversion is indeed a sorting inversion (decided by Bader's algorithm in linear time), the change is accepted with the probability in equation (8). Our gamble is that a high fraction of the proposed reversals will be sorting reversals. This is in accordance with the recently published result claiming that hurdles are rare, so many of the cycle-increasing reversals are indeed sorting reversals (Swenson et al. 2008).
Estimating the Number of Sorting Paths
Estimation for IS
We now describe how the total number of optimal sorting paths can be estimated during an IS procedure similar to that of Ajana et al. (2002) and described further below in Results. Let q denote the IS distribution, and let π denote the uniform distribution. In our case q(y) is the inverse of the product of the number of sorting reversals of each intermediate genome on the sorting path y because random sorting paths are generated by choosing uniformly from the available sorting reversals at each step. π(y) is the same for all sorting path y and is equivalent with the inverse of the number of all sorting paths, N. To estimate N, we first write down how to estimate the constant 1 function using importance weights (Liu 2001). Indeed, the following is true for any two distributions π and q:
| (9) |
If we have a set of samples y1, y2, …, ym following the distribution q, then the unbiased estimation for 1, according to equation (9), is
| (10) |
(note that we sample from distribution q and would like to estimate expectation of function π/q). Because 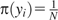 for any i, we get the following estimation for N
for any i, we get the following estimation for N
| (11) |
Estimation for the New Sampling Method
Because the equilibrium distribution of our new sampler is uniform over all sorting prefixes, the product of the expected number of sorting reversals over all Cis yields the total number of sorting paths. Therefore, if we calculate the average number of sorting reversal extensions for each Ci during the MCMC run, their product across all Ci will converge to the total number of sorting paths. To avoid counting the exact number of sorting reversals extending each chain Ci, we can instead make an unbiased estimation for it and we can draw uniformly a fixed number of reversals from the sampling set on Ci. Recall that this is the set of cycle-increasing reversals and also hurdle-merging and hurdle-cutting reversals when hurdles exist in the signed permutation. The size of the sampling set is then multiplied by the fraction of randomly chosen reversals that are indeed sorting reversals. In our experiments, we make estimations from 10 randomly chosen reversals. To reduce the effect of sampling variance, we average the number of estimated descendants at each Ci across steps in the Markov chain.
Given that the Markov chain is run long enough to converge, the method is thus guaranteed to correctly estimate the true number of sorting reversals in an unbiased fashion.
Results
We implemented the methods described above in Java 1.5 software called “MC4Inversion.” MC4 stands for Model Changing Metropolis-Coupled MCMC. ‘Model Changing’ emphasizes the fact that parallel Markov chains walk on different state spaces. The method implements d + 1 Markov chains denoted by C0, C1, …, Cd, where d is the reversal distance of the input permutation. The chain Ci takes a random walk on the i-long prefixes of possible sorting scenarios as described in “MCMC Strategy.” The program is downloadable from http://phylogeny-cafe.elte.hu/MC4Inversion.tar.gz.
The program is fast in practice; about 15 min is enough for 5 million Markov chain steps on a permutation of inversion distance 68 using a Macintosh MacBook with an Intel 2.0GHz Core 2 Duo processor.
Empirical Benchmarks of Mixing Time
In the Methods, we explain the relationship between our method and previous ones, providing some upper and lower compute time bounds for our methods. Unfortunately, we cannot prove that the proposed Markov chain always converges quickly to the prescribed distribution.
Comparing MC4Inversion and BADGER
Despite the lack of a theoretical guarantee regarding the mixing time of any known inversion sampling method, they may mix very well in practice. To examine whether our method improves upon the mixing time in practice, we compare the performance of our method to that of BADGER (Larget et al. 2005). When operating on a pair of genomes, BADGER's MCMC sampler keeps a single complete sorting path as its current state. The sorting path is updated by randomly choosing a portion of the path, deleting those inversions, and proposing new inversions to replace them. BADGER does not restrict the proposed sorting paths to only sorting inversions, thereby allowing sorting paths with more than the minimum number of inversions to be sampled. The default BADGER sampler parameters propose sorting inversions with high probability, neutral inversions (which do not change the reversal distance) with lower probability, and “bad” inversions (which increase the reversal distance) with still lower probability.
When running in parallel tempering mode (c > 1), BADGER runs multiple Markov chains in parallel, each with their own sorting path and “temperature.” Chains with a higher temperature have a flattened probability distribution relative to the cold chain (temperature 1) from which posterior samples are drawn. Chains with higher temperature are thus more likely to accept moves that have low probability in the cold chain. In that way, heated chains can in theory avoid getting stuck in local optima in the likelihood surface and by periodically swapping with the cold chain, facilitate jumps among distant local optima that improve mixing. In BADGER's probability model, heated chains are more likely to accept sorting paths longer than the minimum possible length.
We compare BADGER with and without parallel tempering to our method on several data sets. Each data set represents a pair of complete Yersinia genome sequences and were chosen to represent organisms with low, moderate, and high levels of rearrangement relative to each other (table 1). The Progressive Mauve genome alignment method (Darling 2006) was applied to each pair of organisms to identify synteny blocks and generate a signed permutation matrix (table 1). Data sets with few rearrangements are expected to have only a small number of optimal sorting paths, whereas our high-divergence data set has so many optimal sorting paths that enumeration of all sorting paths within a reasonable amount of time is not possible.
Table 1.
Data Sets Used for Empirical Evaluation of Mixing Time
| Divergence | Organisms |
Breakpoints | Min. Inversions | |
| Low | Y. pestis KIM** | Y. pestis Nepal516* | 16 | 11 |
| 1, 5, −13, 7, −10, 9, −8, 11, −12, −6, 3, −14, 16, −4, 2, −15, 17 | ||||
| Medium | Y. pestis KIM [2] | Y. pestis Antiqua* | 36 | 25 |
| 1, −11, 7, 6, −26, −23, −24, −25, −22, 21, −20, 19, −18, 17, −16, 15, −14, 13, −12, −36, 28, −34, 27, −4, −8, −5, 2, 32, 29, −9, −3, −33, 31, −10, −30, 35, 37 | ||||
| Medium 2 | Y. pestis Antiqua* | Y. pestis 91001*** | 51 | 35 |
| 1, 2, −41, 6, −37, −33, 32, −31, −49, −4, −34, −30, 13, −15, −17, −11, 29, −12, −16, 14, 18, −19, 20, −22, −23, 21, 24, 28, −27, 26, −25, −10, 9, −36, −3, 45, 5, −40, 47, 51, 38, 7, −8, 42, −43, 44, −50, 48, −46, −39, −35, 52 | ||||
| High | Y. pestis Antiqua* | Y. pestis Angola | 97 | 79 |
| 1, −81, 11, 8, −84, −13, 75, 59, −60, 51, 49, 56, −85, 9, −77, 2, −95, 6, 93, 83, −97, 91, −69, 72, 76, −88, −92, −62, 5, −94, −30, 21, 32, 31, 22, −33, −29, 50, 61, −80, 52, 24, 23, 34, −39, 35, 37, −42, 41, −40, −38, −43, −36, 44, −20, 54, −87, −47, 46, −53, −63, 70, 82, 26, 64, 28, −55, 18, −65, −27, 25, −17, 67, 14, 16, 66, 79, −19, 68, −71, 86, 48, −45, 58, −57, −10, 78, −74, −12, 15, −7, −3, 96, −4, −73, −89, 90, 98 | ||||
NOTE.—The four data sets were chosen to represent low, medium, and high degrees of genomic rearrangement. All genomes are circular. Signed permutations for each data set are given in the next row. *Chain et al. (2006); **Deng et al. (2002); ***Song et al. (2004).
Based on the results in table 2, we find MC4Inversion and BADGER to be competitive in speed. When the inversion distance of the input permutation is small, MC4Inversion and BADGER find a comparable number of optimal sorting paths per second. For high-divergence data sets, BADGER finds substantially fewer optimal sorting paths per second. This is in part because at higher inversion distances, suboptimal paths have greater probability mass in the posterior distribution sampled by BADGER. However, we observe that BADGER with c = 4 samples many more optimal paths than with c = 1 in the case of the high-divergence data set, suggesting that parallel tempering is required to sample effectively and that BADGER with c = 1 may be mixing very slowly.
Table 2.
Mixing Speed of Our Method and of BADGER (Larget et al. 2005) with Various Numbers of Parallel Chains
| Unique Optimal Samples per Second |
All Unique Samples per Second |
|||||||
| Program | Low | Medium | Medium 2 | High | Low | Medium | Medium 2 | High |
| MC4 | 1887.0 | 398.0 | 206.0 | 29.0 | 1887.0 | 398.0 | 206.0 | 29.0 |
| BADGER c = 1 | 1493.0 | 102.0 | 112.0 | 0.08 | 2577.0 | 645.0 | 365.0 | 55.0 |
| BADGER c = 4 | 437.0 | 30.0 | 34.0 | 0.97 | 790.0 | 184.0 | 113.0 | 18.0 |
| BADGER c = 16 | 33.0 | 2.6 | 4.7 | 0.0 | 57.0 | 17.0 | 12.0 | 3.2 |
| BADGER c = 64 | 5.7 | 1.3 | 1.0 | 0.0 | 10.0 | 4.2 | 2.8 | 0.7 |
NOTE.—For each level of divergence, the mixing time is given as the number of unique optimal sorting paths discovered per second and the total sorting paths discovered per second. Each program was run for exactly 10 min of CPU time. BADGER only used updates which modify sorting paths (i.e., tree topology updates were disabled) and a number of parallel chains given by c with temperatures ranging from 1 to 1.04. Other BADGER parameters were fixed at default values. At low levels of divergence, BADGER and the new method perform comparably. At medium and high divergence, the new method samples optimal paths more efficiently.
We also investigated the diversity of paths sampled by MC4 and BADGER. One way to measure the diversity of paths is to calculate the average inversion distance between the intermediate genomes at a given position on different sampled paths. We calculated that metric and found that the average distance was slightly greater for MC4 than for BADGER (data not shown). The analysis suggests that MC4 visits a slightly larger area of the total solution space than does BADGER.
Estimating the Total Number of Optimal Sorting Paths
For each data set, we estimated the total number of sorting paths using the method described above. In practice, we do not estimate the number of sorting paths at each MCMC step, but instead do it periodically, after every 25,000 steps. To initially verify that our method provides correct estimates of the number of optimal sorting paths, we compare results from our stochastic method to solutions given by the exact method (Braga et al. 2007). Because the exact method requires O(n2n+3) compute time, it was only feasible to run the method on the low-divergence data set, where n = 16. For that data set, the exact number of optimal sorting paths is computed to be 24,631,200, using about 45 min of compute time. On the same machine, our stochastic method converges within seconds on an estimate of sort paths. To further verify that our method correctly estimates the true number of sorting paths, we constructed a permutation wherein all inversions commute. In that case, the method correctly estimates that there are k! sorting paths, where k is the number of oriented small cycles in the reality–desire graph.
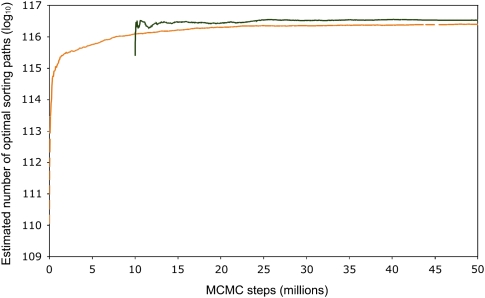
We then investigated how well our method estimates the number of sorting paths for the high-divergence Yersinia data set, which is too large for exact estimation. Figure 4 shows the base-10 logarithm of the estimated number of sorting paths for that data. The change in estimates over 50 million MCMC steps subsampled every 25,000 steps is shown. The light orange line indicates the estimation when all samples in the Markov chain contribute. At the beginning of the chain, the estimation was too small, implying that the initial sampling visited only a negligible portion of the solution space. The continual and gradual increase of the light line happens because the averages of estimated descendant counts at each Ci contain samples from the beginning of the chain, which was far from the equilibrium distribution. Initially, the chain started at nodes in the tree that had fewer than average descendants.
FIG. 4.—
Estimated number of sorting paths for the highly divergent permutation in table 1. The y axis shows the base-10 logarithm of the estimated number of sorting paths, and the x axis shows the index of the samples from the Markov chain. The estimation is based on our MCMC sampler, see the text for details. In total 50 million Markov chain steps were made, and the total sorting path count estimates were sampled every 25,000 steps. The orange curve shows the estimations based on all the samples up to the current index, and the black curve shows the estimations when the first 10 million steps were discarded as burn-in of the MCMC. As more samples are taken, our estimates converge on the true number of sorting paths.
The dark line in figure 4 shows the estimated number of sorting paths when the first 10 million MCMC steps are discarded. The estimated number of sorting paths reaches a plateau, suggesting that 10 million steps are enough to get MCMC convergence on the high-divergence Yersinia data set.
Because the target distribution is the uniform one, the usual log-likelihood trace cannot be used for empirical testing of convergence. Instead, we suggest comparison of this estimator across independent chains as an empirical check for convergence.
Comparing IS and MC4 Sampling
Ajana et al. (2002) proposed a method for sampling optimal sorting paths. In that method, random paths were generated by uniformly choosing from the sorting reversals of the actual intermediate genome. Because the number of sorting path extensions that exist after application of the first sorting reversal might be unequal for each initial reversal, this method will not generate samples from the uniform distribution. Likewise for reversals sampled at intermediate genomes. Samples could be reweighted such that estimations for expectations of interesting statistics will remain unbiased after weighting, and such a sampling strategy is called Importance Sampling (Liu 2001). An importance sampler might be superefficient and simultaneously yield a smaller sampling variance than a regular sampler. On the other hand, if the importance sampler visits a part of the distribution very rarely, the sampling variance will be extremely large. Indeed, if the upper tail of a distribution is undersampled, then the importance sampler will underestimate the statistics of interest with high probability. Although expected values of estimates will be identical to that of the background distribution (and hence, the sampling method will yield unbiased estimates), such an importance sampler will be unreliable in practice due to the large sampling variance. We now show that this is the case with the method of Ajana et al. (2002).
Comparing the Estimated Number of Sorting Paths
To test the hypothesis that the IS underestimates the total number of paths, we generated 100,000 independent samples of sorting paths for the highly divergent permutation in table 1 using the method of Ajana et al. (2002). Based on those samples, we estimated the number of complete sorting paths, see Methods for details. The estimation is 10109.75 ± 0.75, which is a significant underestimation. The MC4 method estimates the true number of sorting paths to be nearly seven orders of magnitude larger (about 10116.54).
Generating 100,000 samples under the IS protocol took substantially more time—more than 12 hours—than 50 million MCMC steps under the MC4 protocol (less than 3 h). There are two reasons for this. First, generating a sorting path with 79 steps in the Ajana et al. protocol invokes calculating the set of proposed reversals 79 times and then taking random reversals until one of them is indeed a sorting reversal (see also “Rejection Sampling”). Hence, this procedure takes about two orders more running time than an MCMC step. Second, estimating the portion of reversals that are indeed sorting reversals takes significantly more time than an MCMC step. In the MCMC run, we had only 2,000 samples, and thus, called this procedure only 2,000 times. On the other hand, the estimation procedure has to be called for all the 100,000 samples coming from the IS protocol.
We can thus conclude that the IS strategy has an extremely large sampling variance. Although in theory the method yields unbiased estimates, the estimation based on 100,000 samples is a huge underestimation. Many more samples would be needed to get the first large overestimation that compensates for the general underestimation, and even more samples would be needed to get a reasonably small standard error for the estimation.
Sampling Histories with Short Inversions
Previous studies showed that short inversions are more frequent than long inversions (Sankoff et al. 2005; Darling et al. 2008). Therefore, one might want to consider sampling from a distribution of sorting scenarios wherein short inversions are preferred. To demonstrate that our method is capable of sampling from such a distribution, we defined the following Boltzmann distribution of sorting scenarios:
| (12) |
where the sum runs over the inversions in the sorting scenario S, l(inv) is the length of a particular inversion inv, and T is a hypothetical temperature. As T tends to 0, the distribution gets frozen in a distribution of sorting scenarios that have the minimum sum of inversion lengths. When T tends to ∞, the distribution tends to the uniform one.
We set the prescribed distributions for all parallel chains as in equation (12), and we changed the Metropolis–Hastings ratio such that all chains converge to their prescribed distributions. In our experiments, we set T = 100. The convergence of the Markov chain was quick based on the log-likelihood trace (data not shown)
We also calculated the length distribution and the expected breakpoint usages for this modified distribution. The results are shown on figures 5 and 6.
FIG. 5.—
Distribution of inferred inversion lengths. Estimates based on three methods are shown: IS (orange), MC4 (blue), and MC4 modeling a preference for short inversions (black). Short inversions are more common than long inversions, and the IS method exhibits an unexplained bias away from short inversions that can be ascribed to its high sampling variance. When modeling a preference for short inversions we use equation (12) with T = 100.
FIG. 6.—
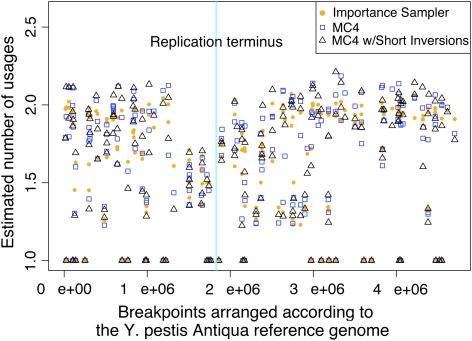
Estimated number of times each block boundary has been used as an inversion endpoint. Block boundaries are arranged according to their occurrence in the reference genome. Some blocks are extremely short, leading to points that appear to overlap. Estimates made by three methods are shown: IS (orange dots), MC4 (blue squares), and MC4 with a preference for short inversions (black triangles). When modeling a preference for short inversions, we set T = 100 in equation (12) as described in the text. As previously reported (Darling et al. 2008), we find fewer inversions surrounding the replication terminus, which is marked with a cyan vertical bar.
One shortcoming of the approach to sampling short inversions is that the temperature parameter is rather arbitrary. The lower the temperature, the more short inversions are preferred, but at sufficiently low temperatures, the mixing will be poor because scenarios with long inversions cannot be easily “bubbled out.” We now give an example that would lead to poor mixing. Consider a partial scenario, S, in which the final step is a short reversal, but it is not commutative, so that it must be the last reversal. Assume also that S contains some very long reversals, so it is otherwise a low probability scenario. Imagine a situation where partial scenarios U with one fewer inversion than S contain mostly short reversals and end with a longer reversal. Should that be the situation, such scenarios U and S cannot be swapped because shortening S means creating a scenario with only long inversions, whereas extending U means adding a longer reversal to U. So the acceptance probability will be low. Although bubbling out S (i.e., shortening S until it becomes the empty partial scenario) would be desirable, our method cannot handle this situation.
Inversion Lengths Distributions
We estimated the distribution of inversion length from the 1600 samples collected on the high-divergence data set using the IS method, the MC4 method, and the MC4 with short-inversions method. The distributions are shown on figure 5.
In general, all methods give qualitatively similar results for inversion length statistics. However, the relative difference in probabilities between the IS method and MC4 method is more than 10% in some cases, despite the fact that they supposedly sample from the same distribution. The largest difference is observed for the shortest inversions. Although both estimators indicate that short inversions are more frequent than long inversions, the MC4 protocol finds more sorting paths with short inversions than the IS protocol.
Estimates of Breakpoint Usage
By definition, the left and right boundaries (breakpoints) of every synteny block have been end points of at least one inversion event. However, some block boundaries have been end points for multiple inversion events. In previous work, we demonstrated that block boundaries located near the origin of chromosome replication tend to be used as inversion end points more frequently than those near the terminus. We now evaluate how each method estimates those values. Based on the estimation of the number of sorting paths (fig. 4), we discarded the first 10 million MCMC steps as burn-in. From the remaining 40 million steps, we sampled 1600 sorting paths, one after every 25,000 steps. From these paths, we computed the average number of times each breakpoint had been used and plotted the results on figure 6 with blue color.
We also estimated the number of breakpoint usages using the IS protocol. The estimations are plotted on figure 6 as orange dots. The difference between the two estimations is not as striking as differences in estimates of the total number of sorting paths. However, there are differences between the two statistics, and the difference is more than 10% in several cases. Such a difference would be statistically significant if we had 1600 and 100,000 independent samples from each protocol. However, MCMC methods give correlated samples, and hence, calculating statistical significance is not possible. Regardless, the 10% difference would be statistically significant even if the effective sample size of the MCMC was only 100.
Discussion
We introduced a novel parallel MCMC method for sampling optimal reversal sorting scenarios. The parallel Markov chains walk in different state spaces. State spaces are nested and range from trivial to complete. The trivial Markov chain walks in empty prefixes of any sorting scenario, the complete chain walks in optimal sorting scenarios, and intermediate chains Ci walk in the i-long prefixes of possible optimal sorting scenarios. In Methods, we describe theoretical lower and upper bounds on the mixing time of the Markov chain and showed that the new sampler can outperform another sampling methodology in some cases of interest.
Efficiency
In terms of speed, MC4Inversion and BADGER are comparable, but MC4Inversion appears to sample a slightly larger portion of the solution space on the Yersinia data in a fixed amount of time. The sampling strategy used by MC4Inversion could potentially be made faster in practice because our implementation was written in Java. BADGER is written in C++, which generally yields faster running programs. MC4Inversion also offers a natural extension to multiprocessor parallelization that should scale linearly in the number of CPUs up to the inversion distance, modulo interprocess communication overhead. In such a parallelization, a swap between chains Ci and Ci+1 can be performed independently from the swap among Cj and Cj+1, where i + 1 < j.
We believe MC4Inversion's performance is due to both better Markov chain mixing and the rejection method that proposes a new inversion in O(n) time instead of the theoretical Ω(n3) worst-case scenario, whereas the acceptance probability of the applied rejection method decreases by only a constant factor.
Future Directions
Attention toward Bayesian approaches for reconstructing inversion distance and scenarios has been growing in recent years. Such methods have been applied to mitochondrial genomes (Larget et al. 2002, 2005), bacterial genomes (Darling et al. 2008), fly genomes (York et al. 2002, 2007), and even metazoans (Durrett et al. 2004). In every case, Bayesian analysis provides a statistically robust framework for testing hypotheses regarding the rates and patterns of genome rearrangement in the organisms of interest. We anticipate that our new methods will further enable such studies by making analysis of large data sets and development of phylogenetic methods more practical.
One possible extension of our method would allow sampling suboptimal sorting paths and their prefixes, and the prescribed sampling distribution would be similar to those of programs like BADGER (Larget et al. 2005) or ParIS Genome Rearrangement (Miklós et al. 2005), which implements a method to sample inversion and transposition histories. In such a context, the shorter sorting paths are taken to be more likely than longer paths according to some prescribed distribution such as an exponential. Such a sampler might involve construction of a series of additional chains for each suboptimal sorting path length.
The new inversion sampling methodology would be most useful as a component in a phylogenetic sampler for inversions. Such samplers propose new inversion scenarios in a pairwise fashion that is compatible with our method. When used in conjunction with a method like delayed rejection (also known as a minisampler), the technique could provide substantially improved mixing time, not only because it can resample histories on an individual branch efficiently but it might also improve acceptance of topology updates. Complex topology updates can require multiple new sorting path proposals and the ability to quickly propose an optimal sorting path is essential to good mixing. As we showed, the IS protocol does not sufficiently explore the state space, and hence, good sorting scenarios on the changed topology might not be proposed frequently. We would like to emphasize that all previously implemented methods propose a new sorting scenario on the new topology in an IS way (Larget et al. 2002, 2005). A novel protocol based on the ideas introduced in this manuscript might improve the mixing of multiple genome rearrangement MCMC samplers. Indeed, in a previous work, we found that parsimonious sorting scenarios of the same Yersinia genomes contain many breakpoints that have been reused three times (Darling et al. 2008). As the IS method seems to undersample scenarios with intensive breakpoint reuse, the probability that a most parsimonious scenario is proposed by a Partial IS technique—the technique applied in BADGER and also in ParIS (Miklós et al. 2005)—will be very small, and hence, the mixing of the MCMC will be slow.
Funding
This work was is supported by a Bolyai postdoctoral fellowship [to I.M.]; Orszagos Tudomanyos Kutatasi Alap [grant F 61730]; Biotechnology and Biological Sciences Research Council [grant BB/C509566/1]; and National Science Foundation [grant DBI-0630765 to A.E.D.].
Acknowledgments
We would like to thank the three anonymous reviewers from a previous edition of this manuscript for providing excellent feedback.
References
- Achaz G, Coissac E, Netter P, Rocha EP. Associations between inverted repeats and the structural evolution of bacterial genomes. Genetics. 2003;164:1279–1289. doi: 10.1093/genetics/164.4.1279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ajana Y, Lefebvre JF, Tillier ERM, El-Mabrouk N. WABI ’02: Proceedings of the Second International Workshop on Algorithms in Bioinformatics. 2002. Exploring the set of all minimal sequences of reversals—an application to test the replication-directed reversal hypothesis. 2002 Sep 17–21, Rome, Italy. London: Springer-Verlag. p. 300–315. [Google Scholar]
- Alekseyev MA, Pevzner PA. Multi-break rearrangements and chromosomal evolution. Theor Comput Sci. 2008;395:193–202. [Google Scholar]
- Altekar G, Dwarkadas S, Huelsenbeck J, Ronquist F. Parallel Metropolis coupled Markov chain Monte Carlo for Bayesian phylogenetic inference. Bioinformatics; 2002 Sep 17–21, Rome, Italy. 2004;20:407–415. doi: 10.1093/bioinformatics/btg427. [DOI] [PubMed] [Google Scholar]
- Bader DA, Moret BM, Yan M. A linear-time algorithm for computing inversion distance between signed permutations with an experimental study. J Comput Biol. 2001;8:483–491. doi: 10.1089/106652701753216503. [DOI] [PubMed] [Google Scholar]
- Bader M, Ohlebusch E. Sorting by weighted reversals, transpositions, and inverted transpositions. Lect Notes Bioinformatics. 2006:563–577. doi: 10.1089/cmb.2007.R006. [DOI] [PubMed] [Google Scholar]
- Bergeron A, Chauve C, Hartman T, St-Onge K. Coste F, Lebret E, editors. Proceedings of JOBIM; 2002 Jun 10–12, St Malo, France. Available from: http://www.irisa.fr/manifestations/2002/jobim/index_en.html. 2002. On the properties of sequences of reversals that sort a signed permutation; pp. 99–107. [Google Scholar]
- Braga A, Sagot MF, Scornavacca C, Tannier E. The solution space of sorting by reversals. Lect Notes Bioinformatics. 2007;4463:293–304. doi: 10.1109/TCBB.2008.16. [DOI] [PubMed] [Google Scholar]
- Chain PS, et al. Complete genome sequence of Yersinia pestis strains Antiqua and Nepal516: evidence of gene reduction in an emerging pathogen. J Bacteriol. 2006;188:4453–4463. doi: 10.1128/JB.00124-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darling AE. Computational analysis of genome evolution. [PhD thesis], Chapter 5. Alignment of genomes with lineage-specific content. [Madison (WI)]: University of Wisconsin-Madison; 2006. [Google Scholar]
- Darling AE, Miklós I, Ragan MA. Dynamics of genome rearrangement in bacterial populations. PLoS Genetics. 2008;4:e1000128. doi: 10.1371/journal.pgen.1000128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng W, et al. Genome sequence of Yersinia pestis KIM. J Bacteriol. 2002;184:4601–4611. doi: 10.1128/JB.184.16.4601-4611.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durrett R, Nielsen R, York TL. Bayesian estimation of genomic distance. Genetics. 2004;166:621–629. doi: 10.1534/genetics.166.1.621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geyer C. Keramigas EM, editor. Proceedings of Computing Science and Statistics: The 23rd symposium on the interface. 1991. Markov chain Monte Carlo maximum likelihood; pp. 156–163. [Google Scholar]
- Hannenhalli S, Pevzner PA. FOCS ’95: Proceedings of the 36th Annual Symposium on Foundations of Computer Science (FOCS’95) Washington, DC: IEEE Computer Society; 1995. Transforming men into mice (polynomial algorithm for genomic distance problem) [Google Scholar]
- Hastings W. Monte Carlo sampling methods using Markov chains and their applications. Biometrika. 1970;57:97–109. [Google Scholar]
- Kaplan H, Shamir S, Tarjan RE. SODA: ACM-SIAM Symposium on Discrete Algorithms. (A Conference on Theoretical and Experimental Analysis of Discrete Algorithms); 1997 Jan 3–7; New Orleans (LA): ACM press. 1997. Faster and simpler algorithm for sorting signed permutations by reversals. [Google Scholar]
- Larget B, Simon DL, Kadane J. On a Bayesian approach to phylogenetic inference from animal mitochondrial genome arrangements. J R Stat Soc B. 2002;64:681–693. [Google Scholar]
- Larget B, Simon DL, Kadane JB, Sweet D. A Bayesian analysis of metazoan mitochondrial genome arrangements. Mol Biol Evol. 2005;22:486–495. doi: 10.1093/molbev/msi032. [DOI] [PubMed] [Google Scholar]
- Liu JS. Monte Carlo strategies in scientific computing. New York: Springer-Verlag; 2001. [Google Scholar]
- Mélykúti B. Budapest, Hungary: Eötvös Loránd University; 2006. The mixing rate of Markov Chain Monte Carlo methods and some applications of MCMC simulation in bioinformatics. [master's thesis] Available from http://ramet.elte.hu∼/;miklosi/Melykutithesis.pdf. [Google Scholar]
- Metropolis N, Rosenbluth A, Rosenbluth M, Teller A, Teller E. Equations of state calculations by fast computing machines. J Chem Phys. 1953;21:1087–1091. [Google Scholar]
- Miklós I, Hein J. Genome rearrangement in mitochondria and its computational biology. Lect Notes Bioinformatics. 2005;3388:85–96. [Google Scholar]
- Miklós I, Ittzés P, Hein J. ParIS Genome Rearrangement server. Bioinformatics. 2005;21:817–820. doi: 10.1093/bioinformatics/bti060. [DOI] [PubMed] [Google Scholar]
- Miklós I, Mélykúti B, Swenson K. The Metropolized Partial Importance Sampling MCMC mixes slowly on minimum reversal rearrangement paths. IEEE/ACM Trans Comput Biol Bioinform. Forthcoming 2009 doi: 10.1109/TCBB.2009.26. [DOI] [PubMed] [Google Scholar]
- Perna NT, et al. Genome sequence of enterohaemorrhagic Escherichia coli O157:H7. Nature. 2001;409:529–533. doi: 10.1038/35054089. [DOI] [PubMed] [Google Scholar]
- Sankoff D, Lefebvre J, Tillier E, Maler A, El-Mabrouk N. The distribution of inversion lengths in bacteria. Lect Notes Bioinformatics. 2005;3388:109–122. [Google Scholar]
- Siepel AC. RECOMB ’02: Proceedings of the sixth annual international conference on Computational biology. New York: ACM; 2002. An algorithm to enumerate all sorting reversals; pp. 281–290. [Google Scholar]
- Siepel AC. An algorithm to enumerate sorting reversals for signed permutations. J Comput Biol. 2003;10:575–597. doi: 10.1089/10665270360688200. [DOI] [PubMed] [Google Scholar]
- Sinclair A, Jerrum M. Approximate counting, uniform generation and rapidly mixing Markov Chains. Inform Comput. 1989;82:93–133. [Google Scholar]
- Song Y, et al. Complete genome sequence of Yersinia pestis strain 91001, an isolate avirulent to humans. DNA Res. 2004;11:179–197. doi: 10.1093/dnares/11.3.179. [DOI] [PubMed] [Google Scholar]
- Swenson K, Lin Y, Rajan V, Moret B. Hurdles hardly have to be heeded. Lect Notes Comput Sci. 2008;5267:241–251. [Google Scholar]
- Tannier E, Sagot MF. Sorting by reversals in subquadratic time. Lect Notes Comput Sci. 2004;3109:1–13. [Google Scholar]
- von Neumann J. Various techniques used in connection with random digits. Monte Carlo methods. Natl Bur Stand. 1951;12:36–38. [Google Scholar]
- York T, Durrett R, Nielsen R. Bayesian estimation of inversions in the history of two chromosomes. J Comp Biol. 2002;3:808–818. doi: 10.1089/10665270260518281. [DOI] [PubMed] [Google Scholar]
- York TL, Durrett R, Nielsen R. Dependence of paracentric inversion rate on tract length. BMC Bioinformatics. 2007;8:115. doi: 10.1186/1471-2105-8-115. [DOI] [PMC free article] [PubMed] [Google Scholar]