The hydrodynamic and conformational properties of denatured proteins in dilute solutions

Abstract

Published data on the characterization of unfolded proteins in dilute solutions in aqueous guanidine hydrochloride are analyzed to show that the data are not fit by either the random flight or wormlike chain models for linear chains. The analysis includes data on the intrinsic viscosity, root-mean-square radius of gyration, from small-angle X-ray scattering, and hydrodynamic radius, from the translational diffusion coefficient. It is concluded that residual structure consistent with that deduced from nuclear magnetic resonance on these solutions can explain the dilute solution results in a consistent manner through the presence of ring structures, which otherwise have an essentially flexible coil conformation. The ring structures could be in a state of continual flux and rearrangement. Calculation of the radius of gyration for the random-flight model gives a similar reduction of this measure for chains joined at their endpoints, or those containing loop with two dangling ends, each one-fourth the total length of the chain. This relative insensitivity to the details of the ring structure is taken to support the behavior observed across a range of proteins.

Introduction

In a 2005 article devoted to the discussion of “the case for (and against) residual structure in chemically denatured proteins” the authors cited a number of articles to that date suggesting that “nuclear magnetic resonance (NMR) studies suggest that significant secondary structure and long-range hydrophobic clusters persist in unfolded proteins even at high concentrations of urea or guanidine hydrochloride (GuHCl)”, whereas “intrinsic viscosity, hydrodynamic radii, and small-angle scattering experiments, some of which date back almost four decades, have been taken as evidence that the unfolded state is an effectively random coil ensemble.”¹ Since that publication, studies have continued to reveal secondary structure in strongly denatured proteins and polypeptides in dilute solution, mostly based on NMR analysis, with such studies often motivated by interest in the folding of the denatured chain. The aforementioned use of the random flight model, which has dominated most of the interpretations of hydrodynamic behavior of proteins and polypeptides in dilute solution, starting with the seminal studies of Tanford et al.,² led to the conclusion that the chains may be modeled by an ensemble of random flight chains with excluded volume effects.^1,3 One study treated the same data to conclude that the data on the intrinsic viscosity could be represented by a wormlike chain model with the chain having an appreciable persistence length, but negligible excluded volume.⁴ In this study, we suggest that taken together the experimental data on intrinsic viscosity, hydrodynamic radii, and the radius of gyration suggest a somewhat compact structure of the denatured proteins and polypeptides studied above, possibly owing to intramolecular association to form transient loops among chain elements widely separated along the chain backbone.

Results and Discussion

The published data

The addition of data on the root-mean-square radius of gyration R_G for a number of denatured proteins and polypeptides in aqueous (2–6)M GuHCl or (4–8) urea,⁵ motivates this reconsideration of the previously available data on the intrinsic viscosity [η], second virial coefficient A₂, and hydrodynamic radius R_H as functions of the molecular weight M in (5–6)M GuHCl. The data on R_H = Ξ/6πη_solv, with the molecular friction coefficient Ξ determined from the sedimentation coefficient in the original study,² have been augmented in recent study by estimates based on NMR studies on denatured proteins in a gradient field and by dynamic light scattering, discussed in detail in Ref. 6; here, η_solv is the solvent viscosity. The experimental data on these parameters are reproduced in Figure 1, where M is replaced by the number N of residues in the backbone, to more nearly represent the behavior in terms of the chain contour length L.

Figure 1.

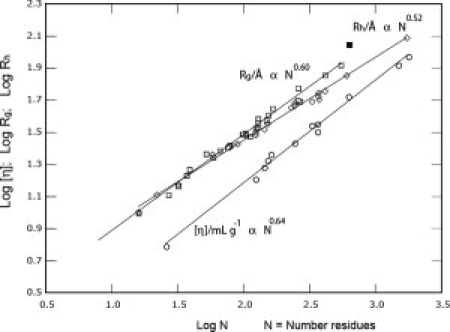
Experimental data reported in the literature on various proteins in strongly denaturing solvents giving the dependence on the number of residues N for the intrinsic viscosity,² [η] (circles), the root-mean-square radius of gyration,⁵R_G (squares) and hydrodynamic radius,⁶R_H (diamonds).

As noted above, prior treatments based on the behavior of [η], A₂, and R_H as functions of M have utilized a random flight flexible model for linear chains or a wormlike chain model in an attempt to elucidate the dependence of R_G on M, and the value (R_G/√M)_θ of R_G/√M under Flory theta conditions, for which A₂ = 0. As the GuHCl solvent system is found to be a thermodynamically good solvent for the proteins studied, with MA₂ ≈ [η], as often observed for solutions of flexible or wormlike chains,⁷ the evaluation of (R_G/√M)_θ from the dependence of [η] on M requires the use of models and extrapolations to zero M, both of which introduce opportunities for error, especially in view of the relatively narrow range of M for which data are available. For example, the analyses with the random flight and wormlike chain models, though quite different in conformational interpretations, provide reasonable fits to the data on [η] as a function of M in the aqueous GuHCl solutions.^2,4 However, both treatments provide estimates of (R_G/√M)_θ that are too large in comparison with the recent experimental data on R_G/√M,⁵ unavailable to those earlier studies.

As may be seen in Figure 1, although the data are somewhat scattered, it appears that ∂ln [η]/∂ln M = 0.64₀, ∂ln R_G/∂ln M = 0.59₇, and ∂ln R_H/∂ln M = 0.51₆. If interpreted alone, the value of ∂ln R_G/∂ln M would indicate a very strong intramolecular excluded volume effect, and that has been the usual interpretation.^1,5 Similarly, if taken alone the values of ∂ln [η]/∂ln M and ∂ln R_H/∂ln M would each represent a more modest excluded volume effect. As mentioned above the data in the intermolecular thermodynamics given by the dependence of A₂ versus M would suggest a so-called good solvent, consistent with a substantial intramolecular excluded volume for a flexible-coil chain, but irrelevant to such behavior for rodlike or even wormlike chains with a large persistence length â.⁷ The significance of these possibly disparate tendencies is considered next.

An analysis involving [η]

In a previous study, theoretical expressions for the parameter K were presented for a number of models, including linear and branched random flight chains, linear rodlike, and wormlike chains and ellipsoids of revolution (including spheres), where⁸

(1)

with N_AV the Avogadro number. Of course, K is trivially related to the more familiar Flory-Fox parameter φ′ given by⁹

(2)

so that φ′ = πN_AV(R_H/R_G)K includes the dependence of R_H on M encoded into the definition for K such that for linear flexible or wormlike chain models K spans a much smaller range of values and is much more weakly dependent on M than is φ′. For example, calculations with the random flight or wormlike chain models without intramolecular excluded volume show that K₀ ≤ K ≤ K_∞, with K₀ and K_∞ the limiting values of K as M tends to zero and infinity, respectively; for example, K₀ = 1 and K_∞ ≈ 3 for linear chains, depending on the details of the model used.⁸ Values of K_∞ for branched chains tend to exceed that for linear molecules, as does K_∞ for the random flight or wormlike chain models for ring-shaped molecules without intramolecular excluded volume, for example, for a ring-shaped molecule, K_∞,RING = 1.519K_∞,LIN, with K_∞,LIN the value for the same model for a linear chain.¹⁰

Values of K calculated as a function of M_w for the data on proteins and polypeptides for the data in Figure 1 are shown in Figure 2, along with data on synthetically prepared well-defined model linear and ring-shaped macromolecules. In fact, there are not many such studies, owing principally to the difficulty of preparing well-defined models. Two studies on ring-shaped polymers prepared by the anionic polymerization of styrene, followed by ring closure give comparable results.^11–13 Thus, for linear polystyrene, the experimental K ≈ K_∞ is constant for 10⁴ < M < 10⁶ (K ≈ 2.6) under Flory theta conditions, and in a good solvent (toluene) it decreases from this value as K ∝ M^−0.04 with increasing M, reflecting the differing effects of intramolecular excluded volume on [η] and 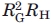.^14–16 Neither of these studies provided the behavior in good solvents needed to compute K. The data on the ring-shaped polystyrene determined under Flory Theta conditions depart from expectations in two ways: (i) K_RING is not expected to depend on M under these conditions and (ii) K_RING is smaller than the value 3.95 expected by comparison with K_LIN for the same polystyrene. The unexpected behavior may reflect the presence of linear chains remaining from the difficult synthesis of the ring-shaped polymers, as observed in some chromatography studies.¹⁷ The data on proteins and polypeptides are seen to be scattered, but with a tendency to decrease from about 3.4 to 2.7 with increasing M over the range studied, with K ∝ 10^−0.07. As the protein and polypeptide samples used in the various studies differ, resort is made to the smoothed correlations shown in Figure 1 to compute K. It is seen that the resulting K for the large M limit is comparable to K_∞ for a linear random-flight or wormlike chain for large M under Flory theta conditions, but increases to larger values with decreasing M, so that the overall pattern is similar to that seen in Figure 1 for ring-shaped polystyrenes. The effects on K or related to those note on the Flory-Fox parameter φ′ in recent considerations of size exclusion chromatography on denatured proteins.^18,19 It may also be noted in Figure 1 that R_H ≈ R_G for the lower values of M. Although one can conclude that the protein conformation appears to be more compact than a linear random flight or wormlike chain at the lower range of N, and that such behavior is not an indication of free draining hydrodynamics, which would decrease K, it is not possible to interpret these data in terms of a definitive model. Possibilities are discussed in the following.

Figure 2.

The function 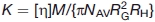for several systems: unfolded proteins based on the data in Figure 1, filled circles; linear polystyrene under Flory theta conditions and good solvent conditions, unfilled and filled diamonds, respectively;^14–16 and ring-shaped polystyrene, unfilled circles.^11–13

The effects of association among chain residues

Intermolecular association would lead to branch-shaped aggregates, and as mentioned above, K will tend to be increased above that for the linear counterpart, offering one possible interpretation. However, this possibility is discounted as the existence of such intermolecular association would be expected to have characteristic features in the dependence of the viscosity and light (or X-ray) scattering behavior, not reported for the studies cited.

Studies by NMR and MCD over the past decade have revealed that the so-called denatured state of proteins and polypeptides contain locally ordered sections of a helical nature, even in solvents that strongly suppress hydrogen bonding.^1,20–22 This includes evidence that these sections may be involved in intramolecular association among units far removed along the chain backbone, forming loops that flicker in and out of existence. As observed above, the result that K for the lower molecular weight proteins in aqueous GuHCl solutions is comparable to the behavior seen for the ring-shaped polystyrene, suggesting the presence of ring-shaped molecules or chains with containing loops, at least in that range of M. As with the data on polystyrene, the modestly decreasing value of K noted with the data on the protein solutions in aqueous GuHCl solution may reflect a modest intramolecular excluded volume effect, with the higher value obtained at low M closer to the limit that would be observed under Flory theta solvent conditions.

The data on R_G/N^1/2 and R_H/N^1/2 for the data in Figure 1 are shown in Figure 3, along with data on (R_G/N^1/2)_STAT computed via statistical coil model for the unfolded state of a range of proteins as a function of N, including excluded volume effects, and taking account of conformational constraints consistent with NMR analysis revealing (non-H-bond stabilized) helical sequences in aqueous GuHCl solution,²³ and a constant value of (R_G/N^1/2)_RIS calculated for the rotational-isomeric-state model in the limit of large N.²⁴ It may be seen that the experimental values of R_G/N^1/2 are about equal to √0.7(R_G/N^1/2)_STAT. Thus, if (R_G/N^1/2)_STAT is presumed to be an accurate measure of R_G/N^1/2 for the chain without any intramolecular association producing ring structures, 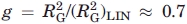, larger than the value g = 1/2 expected for a pure ring-shaped polymer. Although not impossible and perhaps possible for some unfolded proteins,²⁵ it would perhaps be unlikely for transient intramolecular hydrophobic clusters to form rings by association of their endgroups, so it is of interest to consider values of g for a model with a loop formed by association of more generally placed repeating units.

Figure 3.

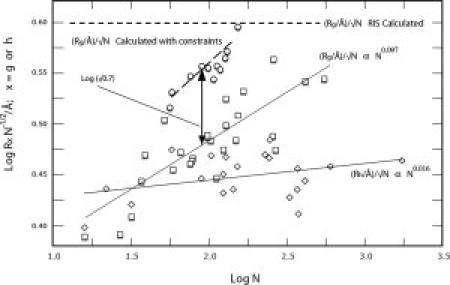
Experimental data on R_G/N^1/2 and R_G/N^1/2 versus log N using the data in Figure 1, along data on (R_G/N^1/2)_STAT calculated via a statistical model with conformational constraints (aside from intramolecular association)²³ and (R_G/N^1/2)_STAT versus calculated with rotational-isomeric-state model.²⁴

A simplified model with the results shown in Figure 4 comprises a chain with an association of residues each a distance xL from the ends of a chain of length L, resulting in a loop with (1 − 2x)N residues, or length (1 − 2x)L, and two “branches,” each with xL residues, emanating from the crosslink locus. Use of the random flight model to compute g including the constraint imposed by the effective intrachain crosslink site according to the usual expression for a chain with n statistical segments of length b = L/n:²⁶

(3)

where the sums are over all possible segments i and j, consistent with the crosslink constraint. The calculation may be conveniently accomplished by summing the contributions segment pairs confined to several components of the total structure: (1) a loop with n – 2xn segments, (2) a linear chain with 2xn segments made from the two branches, (3) four linear chains, each with n/2 segments, comprising a 1/2 loop + one branch, and (4) less the over-count from four linear chains, each with (n – 2xn)/2 segments from four 1/2 loops and four linear chains, each with xn segments from four branches. The calculation gives g as a function of the fraction 1 – 2x of the chain in the loop as shown in Figure 4, with

(4)

Figure 4.

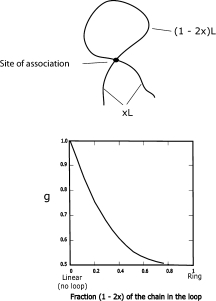
Upper: schematic diagram of a loop of length (1 – 2x) L, and two “branches,” each of length xL, emanating from the site of the association creating the structure. Lower: a plot of g versus the fraction 1 – 2x of the residues in the loop.

As required, g is unity or one-half for fractions of residues in the loop equal to zero (x = 1/2) or unity (x = 0), respectively. Although this model is certainly too simplified to permit a definitive quantitative conclusion, it may be noted that the observed g ≈ 0.7 would correspond to about a fraction 0.25–0.3 of the residues in the loop. However, even if the conclusion cannot be considered to be quantitatively accurate, the existence of such transient structures with a life-time long enough to be seen in the parameters of interest here would seem to be reasonable in view of the properties found in the NMR studies and could be relevant to the refolding process of the denatured protein.

Conclusions

Based on the preceding analysis of published data on the characterization of proteins in dilute solutions in aqueous GuHCl, it is concluded that the data are not fit by either the random flight or wormlike chain models for linear chains, but can be rationalized if it is assumed that transient intramolecular association form temporary ring conformers among the chain units. The analysis includes data on the intrinsic viscosity, root-mean-square radius of gyration, from small-angle X-ray scattering, and hydrodynamic radius, from the translational diffusion coefficient. Such residual ring structures in a state of continual flux and rearrangement in otherwise unfolded proteins are consistent with behavior deduced from NMR on these solutions. Calculation of the radius of gyration for the random flight model gives a similar reduction of this measure for chains joined at their endpoints, or those containing loop with two dangling ends, each one-fourth the total length of the chain. This relative insensitivity to the details of the ring structure is taken to support the behavior observed across a range of proteins.

Glossary

Abbreviations:

NMR

nuclear magnetic resonance;