Bar Charts Enhance Bland-Altman Plots When Value Ranges are Limited

Abstract

Objective

A common form of validation study compares alternative methods for collecting data. Bland and Altman [1–3] recommend a graphic approach that pairs observations across methods and plots their mean values versus their difference. This method provides only limited information, however, when the range of observed values is small relative to the number of observations. This brief report shows how adding a simple bar chart to a Bland-Altman plot adds essential additional information.

Study Design and Setting

The methodological approach is illustrated using data from a randomized, controlled clinical trial of patients in a U.S. county health system.

Results

When the number of unique values is small a Bland-Altman plot alone may provide inadequate information. Adding a bar chart yields new and essential information about agreement, bias, and heteroscedasticity.

Conclusion

Studies validating one data collection method against another can be performed successfully even when the range of observed values is small.

What Is New

• * Bland-Altman plots are often used to assess concordance between two competing data sources. When the number of unique points is small relative to the number of observations, however, a Bland-Altman plot alone provides inadequate information.

• * Supplementing Bland-Altman plots with bar charts reveals important information about agreement, bias, and heteroscedasticity.

• * Graphical comparisons of data from alternative sources can be done effectively even when the number of unique values is limited.

INTRODUCTION

A valid method for obtaining health care data is essential in order to understand the true effect of clinical and health services interventions. A common validation approach is to compare values generated through one method to those from a “gold standard” method. Cohen’s weighted kappa statistic is a convenient summary statistic often used when the values are categorical in nature [4–5]. A complementary method, the Bland-Altman plot [1–3], offers a graphical representation of agreement. Suppose that two machines are used to test systolic blood pressure. For each observation there are two values, one from each machine. Each point on the Bland-Altman plot represents the difference between values from each machine (Y axis) and their mean (X axis). The kappa statistic, a single number ranging from 0–100%, is easy to understand and readily comparable across data sets but reveals nothing more than overall agreement. The Bland-Altman plot lacks the straightforward interpretation of a single statistic but reveals information about measurement bias and heteroscedasticity in addition to overall agreement.

The Bland-Altman plot is typically used for continuously valued outcomes because the advantages of plotting data rest on having a relatively large number of average/difference pairs and a small number of observations per pair. Bland and Altman’s 1986 Lancet paper [1] presented data on peak flow meter readings in which 17 subjects produced 17 unique average/difference pairs. They later presented similar plots using blood pressure data in which 200 observations produced more than 120 unique pairs [2], while in a third 85 observations on systolic blood pressure yielded more than 80 unique pairs [3].

A small number of observations per plot point is beneficial. If most points reflect only a single observation then the plot as a whole necessarily reveals much about the data distribution. A Bland-Altman plot will reveal outliers, and yet such points are difficult to interpret without their associated frequencies. An extreme value that represents a single observation would be interpreted differently from one that represented many. This situation occurs frequently in studies of medical care. The count of health care encounters, for example, a common outcome in health services research, is naturally integer-valued and bounded by zero. In most populations only a few people will have more than two hospital stays in a 12-month period. A plot of annual hospitalizations will likely have a small number of possible average/difference pairs unless one of the two measures being compared is wildly inaccurate.

METHODS

Here we illustrate the benefits of adding a bar chart to a Bland-Altman plot when the number of unique values observed is small, as is often the case for categorical variables. We use data from a randomized, controlled trial, “Stanford and San Mateo County Heart to Heart Project” (HTH; registration identifier NCT00128687). HTH evaluated a case-management intervention in 419 patients served by the health care system of San Mateo County, California. Its rationale, design, and methods have been reported elsewhere [7]. HTH patients were randomly assigned to one of two treatment arms, immediate and delayed intervention. They were interviewed at seven and 15 months after randomization by research assistants blinded to study assignment. Patients were asked about emergency department visits and overnight hospital stays since the last interview, and where they occurred. The analyses presented here are limited to emergency department and hospital use reported at county health care facilities. We analyzed data from the 402 patients who completed both follow-up data collections, comparing self-report and County administrative data for the same period. Each pair of observations represents the self-reported number of emergency department or hospital stays at county facilities and the corresponding count from County administrative records.

HTH enrolled an ambulatory care population and hence hospital stays in particular were expected to be uncommon. We therefore expected that the 402 observations would be distributed into fewer than 20 average/difference pairs.

RESULTS

Exact Agreement

Any point along the Y=0 horizontal line represents exact agreement between the two measures. Because all values are non-negative, an observation pair can average zero only when both values equal zero. Graphically this implies that there can be only a single point at the left margin, (0,0).

Table 1 presents three possible sets of values for hospital use. The two leftmost columns of Table 1 show the actual range of values for a subset of HTH enrollees. Column (1) shows the actual distribution of values and the proportion of pairs that agreed exactly (55.4%). Columns (2) and (3) represent the most extreme hypothetical distributions that yield identical Bland-Altman plots. Due to the small number of unique observed pairs, the plot is consistent with a wide range of possible levels of exact agreement. The same plot could be generated in a variety of ways that imply poor, moderate, or even excellent agreement.

Table 1.

Three Distributions Producing Identical Bland-Altman Plots

		(1)	(2)	(3)
County vs. Self-report		Actual	Most	Least
average	difference	HTH	Agreement	Agreement
0	0	41	64	1
0.5	−1.0	8	1	1
0.5	1.0	14	1	1
1.0	−2.0	2	1	1
1.0	0	1	1	1
1.0	2.0	2	1	1
1.5	3.0	1	1	1
2.0	−4.0	2	1	1
2.5	−5.0	1	1	1
2.5	1.0	1	1	1
3.0	−6.0	1	1	64
Exact agreement:		55.4%	87.8%	2.7%

Notes: The average and difference columns show the actual range of values among HTH enrollees interviewed in English about hospital use. Column (1) shows the true distribution of values in the HTH study. Columns (2) and (3) are distributions that produce the most and least agreement, respectively, while maintaining the same Bland-Altman plot; other distributions are possible that would produce similar levels of agreement to those in (2) and (3).

The range of exact agreement consistent with a Bland-Altman plot is readily calculated. Suppose that there are N observations, k unique average/difference pairs, and m unique pairs where difference = 0. Then greatest possible proportion of exact agreement is (N+m−k)/N and the lowest possible is m/N. The outer bounds of the Bland-Altman plot become tighter as m and k rise relative to N. In the case of the HTH data in Table 1, we see that the Bland-Altman plot of the data could reflect a very wide range of exact agreement, from 2.7% to 87.8%. Thus the plot alone fails to convey the level of exact agreement between the sources.

Defining agreement less stringently, such as a difference of 1 unit or less on the scale of measurement, will in many cases raise the apparent level of agreement between two sources. It could also affect the upper and lower bounds of agreement, although whether it does, and by how much, will depend on the data.

These agreement limits should not be confused with the “95% limits of agreement” proposed by Bland and Altman [1], which consist of the mean value +/− 1.96 SD. Those bands are heuristic limits that rely on the observation that nearly all points fall within that range in a normal distribution.

Bias and Heteroscedasticity

Bland-Altman plots also can reveal measurement bias and heteroscedasticity. If one measurement method is accepted as correct, bias exists when the second measurement method yields a different mean. Heteroscedasticity occurs when the mean difference between measurement methods changes as their average changes. If errors in measurement are a constant proportion of the true value, for instance, then error will rise with the average measured value.

Heteroscedastic errors often develop in self-reported data due to salience of memory. Salience refers to the extent that an event seems memorable to the subject; the more salient an event, the more likely a subject is to recall it accurately [8]. A hospital stay may be quite salient for someone who usually has few or none, whereas the fifth stay in a year would likely be less memorable because the person has necessarily experienced four others in the same period. We therefore expect to see more errors in non-zero counts of service use than zero counts. We also expect that underreporting will increase as the true level rises [8, 9].

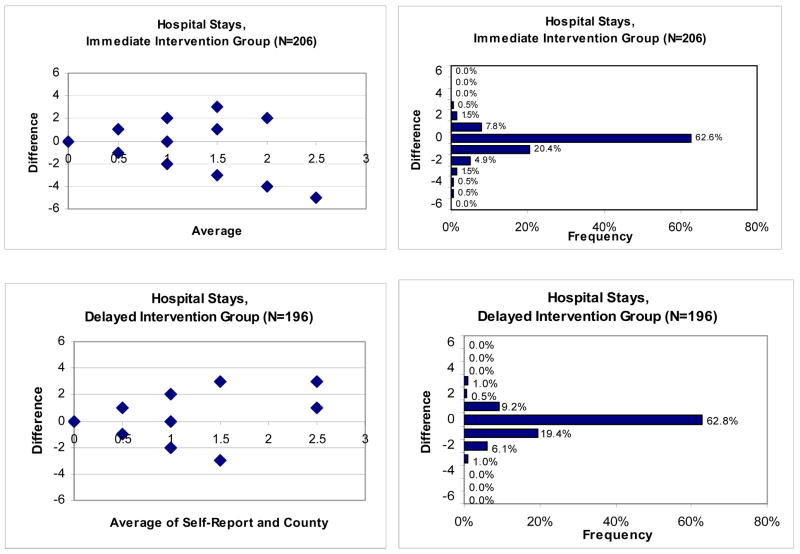
A first look at the HTH data supports these expectations. Figure 1 shows the Bland-Altman plots of hospital stays for individuals in the immediate intervention and delayed intervention arms. Superficially it appears that there is little or no bias until the average reaches 2.0 visits. The plotted pairs beneath or above the midline of difference = 0, however, may not reflect the same number of underlying observations. In a situation like this with few pairs but many observations, assessing bias is difficult using a Bland-Altman plot alone.

Figure 1.

Bland-Altman Plots and Corresponding Bar Charts for Hospital Stays, by Study Arm

The trumpet or conic shape of the plot points suggests that the average difference between values is rising in absolute value as the average rises. This is consistent with heteroscedastic measurement error. As with agreement, an assessment of heteroscedasticity is harder when the range of values is small. Both low and high heteroscedasticity are possible in this plot depending on how many observations are represented by each plot point.

Adding a Bar Chart

The Bland-Altman plot is a useful tool for graphically representing the agreement between measures. Our suggestion when there are relatively few unique average/difference pairs is to augment the plot with a bar chart that illustrates the number of observations corresponding to each level. The idea was proposed by Altman and Bland [10] many years ago, but few validation studies have used it.

Figure 1 shows the bar charts that correspond to the Bland-Altman plots for hospital use. They provide key additional information about agreement between the self-report and administrative data, such as the level of agreement between self-report and County data in both cohorts. The bar charts enable the viewer to easily determine levels of agreement with other bands, such as ±1.0. In these data 91% of both cohorts had a difference of 1.0 or less, a reasonably high concordance unless one’s goal is to distinguish users from non-users. The chart further reveals that there are differing proportions of values above and below a difference of zero: 9.8% above (over-reporting) and 27.8% below (under-reporting) for the immediate-intervention group, and similar figures (11.7%, 26.5%) for the delayed-intervention group. We also observe that the heteroscedasticity apparent in the Bland-Altman plot corresponds to plotted points with low numbers of observations. Thus the trumpet shape of the plot is somewhat misleading, as the majority of observations fall on or very near to a difference of zero. And because they do, one would expect a fairly high level of exact agreement even by chance.

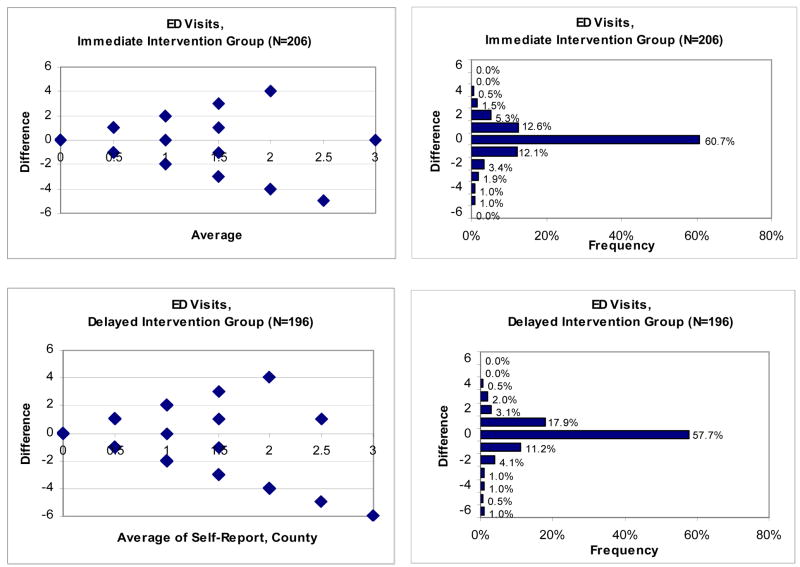
Figure 2 presents similar plots and bar charts for emergency department (ED) use. The Bland-Altman plots point to possible heteroscedasticity and a downward bias at higher levels of use. The charts instead reveal an even distribution above (19.9%) and below (20.4%) the no-difference line for the immediate intervention group. For the delayed intervention group there are somewhat more above than below (23.5% vs. 18.8%), corresponding to slight over-reporting. Heteroscedasticity will be small due to the small number of observations at high difference levels.

Figure 2.

Bland-Altman Plots and Corresponding Bar Charts for emergency department Visits, by Study Arm

DISCUSSION

Bland-Altman plots are sometimes employed for variables with few categorical values but are most common for continuous variables. Weighted kappa plots, with their corresponding tables with agreement by category, are also common. The two have a direct connection: the diagonal line in weighted kappa plots represents the 0 line for perfect agreement in Bland-Altman plots. For the categorical measurements in this paper, however, there are a number of reasons to prefer Bland-Altman over weighted kappa, including easy interpretation of the scale of measurement and the greater insight found in graphical representation.

Our discussion of agreement in relation to Bland-Altman plots has not touched on statistical testing. The statistical significance of observed differences can be calculated through t-tests, Z-tests, or chi-square tests, depending on distributional characteristics and assumptions [11, 12]. Testing could be employed to determine, for example, whether an apparent bias noted through graphical methods is more than can be attributed to chance.

Many charting programs offer the option of showing the count of observations next to each bar. If the chart will be physically small in printed form, then these numbers may be too small for some readers and may perversely make the table appear cluttered. With sufficient space, however, adding the numbers will give the reader useful additional information.