Joint Registration and Segmentation of Serial Lung CT Images for Image-Guided Lung Cancer Diagnosis and Therapy

Abstract

In image-guided diagnosis and treatment of small peripheral lung lesions the alignment of the pre-procedural lung CT images and the intra-procedural images is an important step to accurately guide and monitor the interventional procedure. Registering the serial images often relies on correct segmentation of the images and, on the other hand, the segmentation results can be further improved by temporal alignment of the serial images. This paper presents a joint serial image registration and segmentation algorithm. In this algorithm, serial images are segmented based on the current deformations, and the deformations among the serial images are iteratively refined based on the updated segmentation results. No temporal smoothness about the deformation fields is enforced so that the algorithm can tolerate larger or discontinuous temporal changes that often appear during image-guided therapy. Physical procedure models could also be incorporated to our framework to better handle the temporal changes of the serial images during intervention. In experiments, we apply the proposed algorithm to align serial lung CT images. Results using both simulated and clinical images show that the new algorithm is more robust compared to the method that only uses deformable registration.

1 Introduction

Lung cancer is the most common cause of cancer death in the world, and peripheral lung cancer constitutes more than half of all lung cancer cases. Decades of research in early detection and treatment methods have little progress to impact the long term survival of lung cancer patients [1]. It is generally believed that the key to improve long term survival of cancers are early detection and intervention with novel therapies. The traditional approach of Computed Tomography (CT) screening alone to lung cancer now appears to result in high false positive rates. On initial screening of high risk populations, most studies report false positive rates between 10% and 20% [2]. The Mayo Clinic experience showed that when high risk individuals are screened for lung cancer with CT, the likelihood that they undergo a thoracic resection for lung cancer is increased by ten folds [3]. These observations suggest that a better diagnostic and therapeutic strategy is needed to identify the early staged lung cancer and treat them accordingly in order to make CT screening cost-effective [4] and to eliminate unnecessary surgeries. Molecular imaging guided diagnosis has the advantage to fill this gap by high sensitivity detection to avoid biannual screening, and the image-guided platform offers the possibility to treat immediately after confirmed diagnosis.

To tackle the common difficulties in identifying small lung lesions (< 1.5cm) at an early stage, an image-guided therapy approach is most promising. This approach relies on pre-procedural CT images and real-time electromagnetic (EM) tracking to guide a fiber-optic microendoscope to the small lesion of interest. With the injection of fluorescent molecular imaging agent prior to the procedure, a high sensitivity molecular imaging diagnosis can be performed intraoperatively. It also offers the possibility to treat the small lung lesion simultaneously and eliminates unnecessary surgeries and the procedure related mortality. This type of workflow integration has a tremendous financial implication to lower healthcare cost as well as detect and treat peripheral lung cancer earlier. Segmentation of suspected lesion and vascular structures in pre-procedural high resolution lung CT images can be used to accurately guide the physicians during intraoperative procedures when it is used in conjunction with EM tracked real-time guidance system. Compared to the non-real-time guided interventional lung procedure, fewer punctures and lower radiation dose is expected without the iterative CT imaging to confirm the needle location.

Image-guided system plays an important role in this procedure in order to accurately and efficiently guide the interventional device to the target of interest. To reduce the intra-procedural procedure time, a pre-procedural lung CT image is often captured days before the procedure, thus the lung image and suspected lesion and vascular structures can be segmented for surgical planning. During the interventional procedure, the image and its segmentation information can be quickly warped onto the CT scan right before the intervention to highlight the target and surgical path. Then, with the help of the electromagnetic tracking and the visualization system, physicians can efficiently and accurately perform the microendoscopic optical imaging or radio frequency ablation, should the lesion is confirmed by the molecular imaging results. Thus, the alignment of the pre-procedural lung CT images as well as the intra-procedural serial images is an important step to accurately guide and monitor the interventional procedure in the diagnosis and treatment of these small lung lesions.

Traditional pairwise [5, 6, 7] and group-wise [8, 9] image registration algorithms have been used in these applications. However the pairwise algorithms warp each image separately, and they often cause unstable measures of the serial images because no temporal information of the serial images has been used in the registration procedure. Groupwise image registration methods simultaneously process multiple images, however they often consider the images as a group, not a time series. Thus the temporal information has not been used efficiently. For serial image registration, the relationship between temporally neighboring images is much more important than that of the images with larger time intervals, since both anatomical structure and tissue properties of neighboring images tend to be more similar for neighboring images than others; moreover these temporal changes can be characterized using specific physical processes models.

Recently, several 4-D image processing algorithms as well as joint segmentation and registration algorithms have been proposed in the literature [10, 11, 12, 13, 14, 15, 16, 17, 18]. Serial image processing aims at calculating the image series in the 4-D space wherein temporal deformations among images are estimated simultaneously [10, 11, 12], while segmentation and registration can be combined together since image registration significantly benefits from segmentation and vice versa [13, 14, 15, 16, 17, 18]. Accurate registration of serial images often relies on correct extraction and matching of robust and distinctive image features. Thus it is an important step to segment the image into different tissue regions, which act as additional features in the image registration to further improve the temporal alignment of the serial images. Moreover the deformations across serial images also provide more robust image segmentation.

This paper presents a joint serial image registration and segmentation, wherein serial images are segmented based on the current temporal deformations so that the temporally corresponding tissues tend to be segmented into the same tissue type, and at the same time, temporal deformations among the serial images are iteratively refined based on the updated segmentation results. Notice that the simultaneous registration and segmentation framework had been studied in [19, 12, 20] for MR images. The previous work, CLASSIC [20], relies on a temporal smoothness constraint, and it is particularly suitable for longitudinal analysis of MR brain images of normal healthy subjects, where the changes from one time-point to another is small. Nevertheless, in that algorithm the registration is purely dependent on the segmented images. In this new algorithm, no temporal smoothness about the deformation fields is enforced so that our algorithm can tolerate larger or discontinuous temporal changes that often appear during image-guided therapy. Moreover, physical procedure models could also be incorporated to our algorithm to better handle the temporal changes of the serial images during intervention.

We first demonstrate that, based on the Bayes’ rules, the registration of the current time-point image is not only related to the baseline image, but also to its temporally neighboring images. Based on this principle, a new serial image similarity measure is defined, and the deformation is modeled using the traditional Free Form Deformation (FFD) [6]. Based on the current estimate of temporal deformations, a 4-D clustering algorithm is applied for segmenting the serial images. No adaptive centroids are used because of relatively small effect of inhomogeneity in CT. The proposed joint algorithm then iteratively refines the serial deformations and segments the images until convergence. The advantage of the proposed method is that it is particularly suitable for registering serial images in image-guided therapy applications with possible large and discontinuous temporal deformations.

We have applied the proposed algorithm to both simulated and real serial lung CT images and compared it with the FFD. The dataset used in the experiments consists of anonymized serial lung CT images of lung cancer patients (N = 20). The spatial resolutions of the images from the same patient are different due to different settings and imaging protocols. For the serial images of the same patient, all the subsequent images have been globally aligned and re-sampled onto the space of the first image using the ITK package [21]. The results show that the proposed algorithm yields more robust registration results and more stable longitudinal measures.

2 Method

2.1 Software Workflow for Image-Guided Intervention

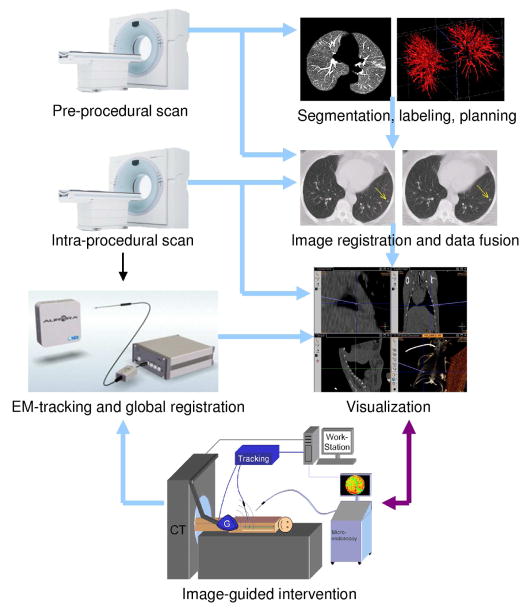
Fig. 1 illustrates the software workflow of the image-guided interventional system. First, a pre-procedural lung CT image is captured before the intervention. Then, the lung image, vascular structures, suspected lesions can be segmented for surgical planning. In the interventional procedure, the intra-procedural image is first obtained, and the image registration and data fusion step is then performed in order to transfer all the diagnosis and surgical planning data onto the current image accurately and efficiently. During the interventional procedure, with the help of the electromagnetic (EM) tracking system, the coordinates of the EM tracking and the CT images are registered or calibrated before visualization. Using this system, physicians can efficiently perform the intervention by referring to the feedback from the visualization system, which shows the real-time location of the interventional device in the 3D CT images. This paper will focus on the segmentation and registration algorithms used in the image-guided interventional system.

Figure 1.

The interventional system.

2.2 Algorithm Framework

The algorithm incorporates an iterative serial image segmentation and registration strategy in order to improve the longitudinal stability for 3-D image series. It iteratively performs two steps [18]:

• Step 1: Given the current segmentation results, the algorithm refines the underlying longitudinal deformations among the serial images using the 4-D elastic image warping algorithm. In Section 2.3, the new serial registration algorithm is proposed.

• Step 2: Given a current estimate of the longitudinal deformations necessary to align serial 3-D images, the algorithm jointly segments the image series using the 4-D clustering algorithm. This algorithm had been proposed in [18] and is briefly introduced in Section 2.4.

Fig. 2 illustrates the flowchart of this iterative algorithm. After inputting a series of images, the initial 3-D segmentation of the serial images is performed using AdpkMean [22]. Then, these segmented images can be used as the input for the 4-D elastic deformable registration, and after the longitudinal deformations among the serial images have been estimated, the 4-D clustering algorithm for serial images will refine the segmentation. These 4-D registration and segmentation procedures can be performed iteratively, and the algorithm stops when the difference between two consequent iterations is smaller than a prescribed threshold.

Figure 2.

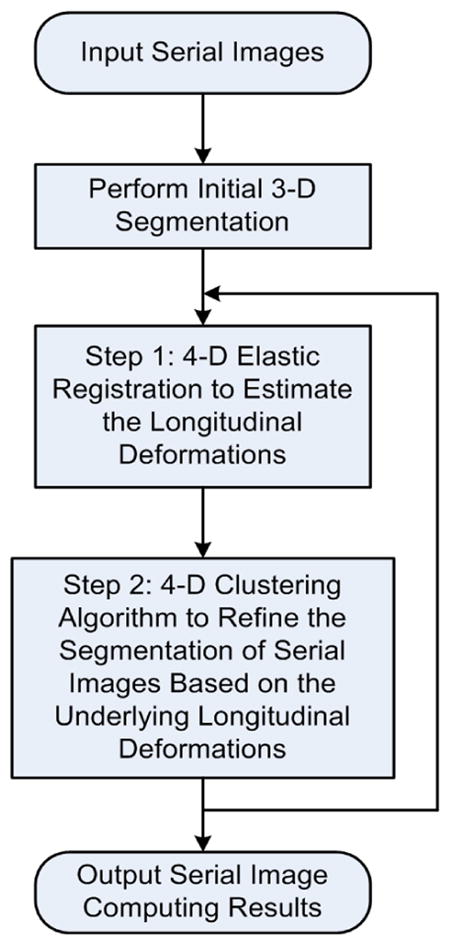
The framework of the algorithm.

In the registration algorithm, no temporal smoothness about the deformation fields is enforced so that our algorithm can tolerate larger or discontinuous temporal changes that often appear during image-guided therapy. Moreover, physical procedure models could also be incorporated to our algorithm to better handle the temporal changes of the serial images during intervention.

2.3 The Serial Image Registration Algorithm

Given a series of images I_t, t = 0,..., T (I₀ is usually called the baseline, and all the subsequent images have been globally aligned onto the space of the baseline by applying the rigid registration in Insight Toolkit (ITK)), we often need to estimate the deformations from the baseline onto each image, i.e., f_{0 → t} or simply denoted as f_t. Since no longitudinal information is used in pairwise registration, the temporal stability of the resultant serial deformations cannot be preserved. Groupwise registration jointly registers all the images with the baseline, however no temporal information has been considered effectively.

In this work, we formulate the serial image registration in the Bayes’ framework, so that the registration of the current time-point image is related to not only the previous but also the following images (if available). No longitudinal smoothness constraints are applied to the serial deformations so that our algorithm can tolerate temporal anatomical and tissue property changes. For the current image I_t, if the deformation of its previous image I_t−1, f_t−1, and that of the next image I_t+1, f_t+1, are known, the posterior probabilities of the current deformation f_t can be defined as p(f_t|I₀, I_t−1, I_t, f_t−1) and p(f_t+1|I₀, I_t, I_t+1, f_t), respectively. By jointly considering both the previous and the next images, we calculate the deformation of the current image, f_t, by maximizing the combined posterior probabilities,

$${\mathbf{f}}_t^{\ast }=argmax\{p({\mathbf{f}}_t\mid I_0,I_{t-1},I_t,{\mathbf{f}}_{t-1})p({\mathbf{f}}_{t+1}\mid I_0,I_t,I_{t+1},{\mathbf{f}}_t)\}.$$ (1)

Using the chain rule of probability equations, we can easily calculate Eq. (1) as,

$${\mathbf{f}}_t^{\ast }=argmax\{\lambda (t)p(I_{t+1}\mid I_0,I_t,{\mathbf{f}}_t,{\mathbf{f}}_{t+1})p(I_t\mid I_0,I_{t-1},{\mathbf{f}}_{t-1},{\mathbf{f}}_t)p({\mathbf{f}}_{t-1}\mid {\mathbf{f}}_t)p({\mathbf{f}}_{t+1}\mid {\mathbf{f}}_t)p({\mathbf{f}}_t)\},$$ (2)

where λ(t) gives other probability terms, which are not related to f_t. p(f_t+1|f_t) and p(f_t+1|f_t) are the conditional probability of the serial deformation fields. Since in this work, no temporal smoothness about the deformation fields is enforced so that our algorithm can tolerate larger or discontinuous temporal changes that often appear during image-guided therapy, these two conditional probabilities are assumed to be constants. Therefore, ${\mathbf{f}}_t^{\ast }$ can be calculated by minimizing,

$${\mathbf{f}}_t^{\ast }=argmin\{E_{s,t}(I_0,I_{t-1},I_t,I_{t+1},{\mathbf{f}}_{t-1},{\mathbf{f}}_t,{\mathbf{f}}_{t+1})+{\lambda }_r(t)E_r({\mathbf{f}}_t)\},$$ (3)

where E_s,t() is the serial image difference/similarity measure, and E_r() is the regularization term of the deformation field. λ_r is the weight of E_r. The serial image difference measure can be defined as,

$$\begin{array}{l}{E}_{s,t}=\sum _{\mathbf{v}\in \mathrm{\Omega }}\{\mid \mathbf{e}[I_t({\mathbf{f}}_t(\mathbf{v}))]-\mathbf{e}[I_0(\mathbf{v})]{\mid }^2\\ +\sum _{i=-1,1}\mid \mathbf{e}[I_t({\mathbf{f}}_t(\mathbf{v}))]-\mathbf{e}[I_{t+i}({\mathbf{f}}_{t+i}(\mathbf{v}))]{\mid }^2\},\end{array}$$ (4)

where e[] is the operator for calculating a feature vector, and Ω is the image domain. In this work, the feature vector for each voxel consists of the intensity, gradient magnitude, and the fuzzy membership functions calculated from the segmentation step, i.e., e[v] = [I(v), | ∇ I(v)|, μ_v,1, μ_v,2,..., μ_v,K]^T. When a physical process model is available, it can be incorporated into the second term of Eq. (4) or the conditional probabilities of deformations (such as p(f_t+1|f_t) and p(f_t+1|f_t)), so that any feature changes from one image onto another can be considered. Further, the deformations of neighboring images might not be independent by embedding a temporal model of deformations according to the physical model. However that is out of the scope of this study. E_r in Eq. (3) is the regularization energy of deformation field f_t, and it can be derived from the prior distribution of the deformation. If no prior distribution is available, the regularization term can be some continuity and smoothness constraints. In this work, since the cubic B-Spline is used to model the deformation field, the continuity and smoothness is guaranteed, thus the regularization term E_r is omitted.

The serial image registration algorithm then iteratively calculates/refines the deformation field f_t of each time-point image by minimizing the energy function in Eq. (3) until convergence. Notice that in the first iteration, since the registration results for neighboring images are not available, only the first term of Eq. (4) is used, which is essentially a pairwise FFD.

2.4 The 4-D Clustering Algorithm for Image Segmentation

Given the serial images I_t, t = 0, 1,..., T and the longitudinal deformations f_t, t = 1,..., T, the purpose of the 4-D segmentation is to calculate the segmented images $I_t^{(\text{seg})}$ by considering not only the spatial but also the temporal neighborhoods. The clustering algorithm is performed to classify each voxel of the serial image into different tissue types by minimizing the objective function,

$$\begin{array}{l}E(\mu ,c)=\sum _{t=0}^T\sum _{\mathbf{v}\in \mathrm{\Omega }}\{\sum _{k=1}^K[{\mu }_{(t,\mathbf{v}),k}^q{(I_{(t,\mathbf{v})}-c_{t,k})}^2]\\ +\frac{\alpha }{2}{\rho }_{(t,\mathbf{v})}^{(s)}\sum _{k=1}^K[{\mu }_{(t,\mathbf{v}),k}^q{\overline{\mu }}_{(t,\mathbf{v}),k}^{(s)}]+\frac{\beta }{2}{\rho }_{(t,\mathbf{v})}^{(t)}\sum _{k=1}^K[{\mu }_{(t,\mathbf{v}),k}^q{\overline{\mu }}_{(t,\mathbf{v}),k}^{(t)}]\},\end{array}$$ (5)

where voxel v in image I₀ corresponds to voxel f_t(v) in image I_t, referred to as voxel (t, v), and μ, c, q, K follow the FCM formulation [23].

$${\overline{\mu }}_{(t,\mathbf{v}),k}^{(s)}=\frac{1}{N_1}\sum _{(t,\mathbf{u})\in N_{(t,\mathbf{v})}^{(s)}}\sum _{m\in M_k}{\mu }_{(t,\mathbf{u}),m}^q,\text{and}{\overline{\mu }}_{(t,\mathbf{v}),k}^{(t)}=\frac{1}{N_2}\sum _{(\tau ,\mathbf{v})\in N_{(t,\mathbf{v})}^{(t)}}\sum _{m\in M_k}{\mu }_{(\tau ,\mathbf{v}),m}^q,$$ (6)

where $N_{(t,\mathbf{v})}^{(s)}$ and $N_{(t,\mathbf{v})}^{(t)}$ are the spatial and temporal neighborhoods of voxel (t, v), and M_k = {m = 1,..., K; m ≠ 6 k}. The fuzzy membership functions μ are subject to, ${\sum }_{k=1}^K{\mu }_{(t,\mathbf{v}),k}=1$, for all t and v.

The second term of Eq. (5) reflects the spatial constraints of the fuzzy membership functions, which is analogous to the FANTASM algorithm [24]. The difference is that an additional weight ${\rho }_{(t,\mathbf{v})}^{(s)}$ is used as an image-adaptive weighting coefficient, thus stronger smoothness constraints are applied in the image regions that have more uniform intensities, and vice versa. ${\rho }_{(t,\mathbf{v})}^{(s)}$ is defined as, ${\rho }_{(t,\mathbf{v})}^{(s)}=exp\{-{\sum }_r[{(D_r\ast I_t)}_{(t,\mathbf{v})}^2/2{\sigma }_s^2]\}$, where (D_r * I_t)_(t,v) refers to first calculating the spatial convolution (D _r * I_t), and then taking its value at location (t, v), where D_r is a spatial differential operator along axis r. Similarly, the third term of Eq. (5) reflects the temporal consistency constraints, and ${\rho }_{(t,\mathbf{v})}^{(t)}$ is calculated as, ${\rho }_{(t,\mathbf{v})}^{(t)}=exp\{-{(D_t\ast I_{(t,\mathbf{v})})}_t^2/2{\sigma }_t^2\}$, where D_t is the temporal differential operator, and (D_t * I_(t,v))_t refers to first calculating the temporal convolution (D_t * I_{(t, v)}) and then taking its value at t. It is worth noting that the temporal smoothness constraint herein does not mean that the serial deformations have to be smooth across different time-points.

Using Lagrange multipliers to enforce the constraint of fuzzy membership function in the objective function Eq. (5), we get the following two equations to iteratively update the fuzzy membership functions and calculate the clustering centroids,

$${\mu }_{(t,\mathbf{v}),k}=\frac{{[{(I_{(t,\mathbf{v})}-c_{t,k})}^2+\alpha {\rho }_{(t,\mathbf{v})}^{(s)}{\overline{\mu }}_{(t,\mathbf{v}),k}^{(s)}+\beta {\rho }_{(t,\mathbf{v})}^{(t)}{\overline{\mu }}_{(t,\mathbf{v}),k}^{(t)}]}^{\frac{-1}{q-1}}}{{\sum }_{m=1}^K{[{(I_{(t,\mathbf{v})}-c_{t,m})}^2+\alpha {\rho }_{(t,\mathbf{v})}^{(s)}{\overline{\mu }}_{(t,\mathbf{v}),m}^{(s)}+\beta {\rho }_{(t,\mathbf{v})}^{(t)}{\overline{\mu }}_{(t,\mathbf{v}),m}^{(t)}]}^{\frac{-1}{q-1}}},$$ (7)

$$c_{t,k}=\frac{{\sum }_{\mathbf{v}\in \mathrm{\Omega }}{\mu }_{(t,\mathbf{v}),k}^q{I}_{(t,\mathbf{v})}}{{\sum }_{\mathbf{v}\in \mathrm{\Omega }}{\mu }_{(t,\mathbf{v}),k}^q}.$$ (8)

In summary, the proposed joint registration and segmentation algorithm iteratively performs the serial registration and the segmentation algorithms until the difference between two iterations is smaller than a prescribed value. No temporal smoothness about the deformation fields is enforced in order to tolerate larger or discontinuous temporal changes that often appear during image-guided diagnosis and treatment. Another advantage of this method is that physical procedure models could also be incorporated to our framework to better handle the temporal changes of the serial images during intervention. However, relatively simple clustering segmentation algorithm is used in the iterative procedure, where no anatomical information such as airway, blood vessels, and others are available. A sophisticated segmentation might be used to better represent the lung information for more robust registration.

3 Experimental Results

The dataset used in the experiments consists of anonymized serial lung CT images of lung cancer patients (N = 20). The spatial resolutions of the images from the same patient are different due to different settings and imaging protocols. The typical voxel spacing in our data is 0.81mm×0.81mm×5mm, 0.98mm×0.98mm×5mm, and 0.7mm × 0.7mm × 1.25mm. For the serial images of the same patient, the time interval between different scans for our data set is between two to three months, and all the subsequent images have been globally aligned and re-sampled onto the space of the first image using the ITK package.

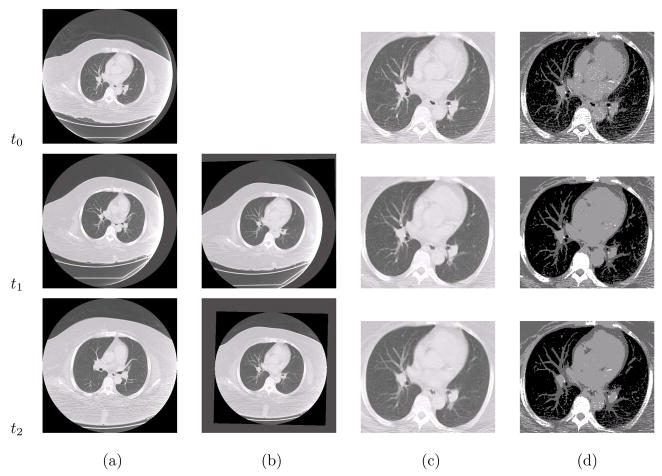
Fig. 3 gives an example of the segmentation results of our dataset. It can be seen that after global registration of the original images in Fig. 3(a), the lung regions can be roughly aligned in Fig. 3(b). By performing the joint registration and segmentation for such serial images, the lung region can be precisely aligned as shown in Fig. 3(c) and (d). The parameters used in the experiments are as follows: K = 3, α = 200, β = 200, σ_s = 2, σ_t = 1, and the spatial and temporal neighboring voxels are used. All algorithms have been implemented using the standard GNU C language on an Intel Core 2 Duo CPU 2.2GHz with 2GB RAM. Based on the number of CPU cores, the program can divide the images to be processed into 2, 4 or 8 overlapping subimages, and perform registration of each subimage in parallel. The communication and updating of the data within the overlapping regions among the subimages are achieved by using the shared memory of the Linux system. For dual-core CPU, the processing time for a series of 3 images with size 512 × 512 × 55 is about 2.5 minutes. The algorithm typically stops with 2 or 3 iterations.

Figure 3.

Illustration of the joint registration and segmentation algorithm. (a) Input serial images, (b) the globally registered images, (c) the results of the proposed algorithm, and (d) the corresponding segmented images.

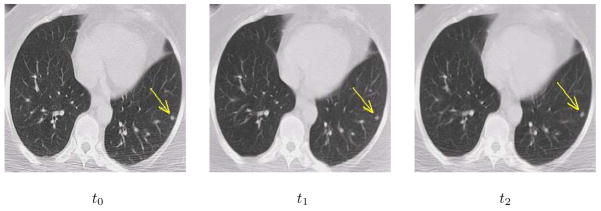
Fig. 4 illustrates the registration results of serial images with small lesion. It can be seen that the lesion appears in the same slice and the same location in the registered serial images. Using this technique, we can easily calculate the longitudinal changes of the lesion for diagnosis and assessment, and also precisely guide the interventional devices toward the lesion during image-guided therapy.

Figure 4.

Registration results of serial images with lesion. The arrows point to the lesion.

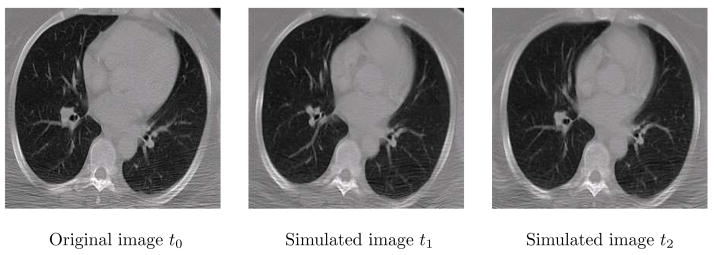
We evaluated the performance of the proposed algorithm using simulated images. The images are simulated by randomly sampling the statistical model trained from the sample deformation fields. First, for each series of the sample images, the demon’s algorithm was used to register the subsequent images onto the first time-point image. Then, one sample image is selected as the template image, and all the other first time-point images of other subjects are deformed onto the template space using the same deformable registration algorithm. Finally the statistical model about the spatially warped/normalized temporal deformations are calculated, which is then used to randomly generate the longitudinal deformation of the template image. In this paper, the statistical model of deformation (SMD) presented in [25] was used to train such a model. In our image datasets, one image was selected as the template and other 19 images were selected as the training samples. Fig. 5 shows an example of the simulated serial images from the template image.

Figure 5.

Example of the simulated serial images.

After applying the algorithm on the ten randomly simulated images, the registration errors with the ground truth were calculated reflecting the accuracy of the registration. The results show that the mean registration errors (resolution 0.7mm×0.7mm×1.5mm) is 0.9mm, and for images with resolution 0.81mm×0.81mm×5mm, the mean registration error is 4.1mm. In general, the registration errors are found less than the largest voxel spacing of the simulated images.

In order to illustrate the advantages of joint registration and segmentation, we also calculated the temporal stability of the segmentation results. For each image series, we calculate the total number of tissue type changes along the serial deformation fields and normalize this number by the total number of voxels. It turns out that for 20 series of images we tested, the proposed algorithm has about 25% voxels with tissue type changes across the temporal domain, while the FFD yields about 32% tissue type changes across the image series. The results indicate that the joint registration and segmentation generates relatively stable measures for serial images.

4 Conclusion

Integrated image-guided lung cancer diagnosis and therapy provides a paradigm shift in the workflow of early stage lung cancer care. Image-guided molecular imaging has the potential to increase the diagnostic specificity and sensitivity in detecting small peripheral lung cancer in real-time. The confirmed lesion can be treated immediately under image guidance. This change in the workflow will greatly reduce healthcare cost and provide a window of opportunity to detect and treat small peripheral lung cancer earlier. In our image-guided diagnostic and therapeutic system of small peripheral lung lesions the alignment of the pre-procedural lung CT images as well as the intra-procedural serial images is an important step to accurately guide and monitor the interventional procedure. We proposed a joint registration and segmentation algorithm for serial image processing in lung cancer molecular image-guided therapy. In this algorithm, the serial image registration and segmentation procedures are performed iteratively to improve the robustness and temporal stability for serial image processing. A new serial image registration algorithm has been proposed based on the Bayes’ framework, and the registration of the current time-point image is not only related to the baseline image, but also to its temporally neighboring images. Based on this principle, a new serial image similarity measure is defined, and the deformation is modeled using the traditional Free Form Deformation (FFD). Experimental results using both simulated and real lung CT images show the accuracy and robustness compared to the free form deformation. Future works include incorporation of physical procedure models into our algorithm to better handle the temporal changes of the serial images during intervention, and the integration to the real-time EM-guided fiber-optic microendoscope system.