A Partial Nudged Elastic Band Implementation for Use with Large or Explicitly Solvated Systems

Abstract

The nudged elastic band method (NEB) can be used to find a minimum energy path between two given starting structures. This method has been available in the standard release of the Amber9 and Amber10 suite of programs. In this paper a novel implementation of this method will be discussed, in which the nudged elastic band method is applied to only a specific, user-defined subset of atoms in a particular system, returning comparable results and minimum energy pathways as the standard implementation for an alanine dipeptide test system. This allows incorporation of explicit solvent with simulated systems, which may be preferred in many cases to an implicit solvent model. From a computational standpoint, this implementation of NEB also reduces the communication overhead inside the code, resulting in better performance for larger systems.

Introduction/Background

One of the most relevant problems currently in molecular dynamics (MD) simulations is how to study conformational changes which occur along a defined path. Many approaches to finding minimum energy transitions involve beginning in one energy minimum and proceeding stepwise along the slowest ascent path of the surrounding energy landscape.¹ These methods are inherently serial which limits their performance and thus applicability to complex systems. From a computational perspective arguably the best approach to solving this problem is to use a method which can take advantage of current massively parallel computing resources by distributing multiple simulations among many processors. An example of such an approach is umbrella sampling.² In such methods a reaction coordinate is typically chosen along which the system is forced to move. In practice, however, these methods can lead to discontinuous paths and require a prior definition of a reaction coordinate along which to bias the simulation. Such prior definition of a reaction coordinate is often impractical in systems of interest which typically involve many degrees of freedom.

An alternative solution to generating the minimum energy path of a conformational change is to use a chain-of-states method. In such methods, two images are used as endpoint conformations, additional images are then generated between these two end points, and all are optimized at once. For biological systems, the chain-of-states method was pioneered by Elber & Karplus³, whose plain elastic band method used first-derivatives to optimize the path between endpoint structures subject to restraints. Spring forces were added between the images which force each image to remain at an average separation between its partner images along the current path. The plain elastic band method is, however, highly dependent on the initial path chosen. This leads to minimum energy pathways that are local rather than global minima. Elber & Karplus proposed using simulated annealing as an optimization technique to find the global minimum energy path.

The plain elastic band method falls short in determining the transition state geometries and energies of the path because the spring forces which keep the images evenly spaced interfere with the energy of each independent image. For too rigid a spring constant, the images over-estimate the energies in the saddle point region, causing corner cutting and preventing the path from resolving saddle point structures. For too weak a spring constant, the forces on each image from the force field are too prominent, and images slide down the path back toward the minima and do not resolve the saddle points.⁴

To combat these problems, the nudged elastic band (NEB) method^4–6 was developed as a chain-of-states method which finds a minimum energy path of a conformational transition given only two initial structures to use as the energy minimized endpoints. The NEB approach implements a tangent definition, which is the tangent of the current path defined by the images. The tangent is calculated at every step in the simulation, and is used to decompose the force described by the force field and the spring forces into perpendicular and parallel forces with respect to the path.⁷ The two endpoint images are fixed in space, and copies of these images can be used as initial seed structures for the pathway calculation. Additional images may be used to seed the starting path, but these are not exempt from the NEB force calculation as the endpoint structures are. Each image is connected to its neighbor images by the virtual springs along the path which contribute only to the parallel part of the force. The springs serve to maintain spacing of the images along the path. The force described by the force field is then only applied orthogonal to the path tangent, that is, projected out from each image and not along the bath between images. From their initial coordinates, the images are pulled into an interpolating path between the two endpoint structures. This initial path is then optimized^8,9 to minimize the energy. The result is a minimum potential energy path that represents the conformational change between the two endpoint structures, independent of timescale.

Despite the ability of NEB to find minimum energy paths, the previous implementation, within Amber, inherently imposes limitations in the choice of systems to be simulated. One issue is the requirement of applying NEB forces to all atoms of the system of interest, meaning system sizes in general had to be small to be computationally efficient to simulate. Applying NEB forces to all atoms necessarily restricted systems to implicit solvent. If water molecules exist, they could cause simulation artifacts since they would be forced to move between their locations at the endpoints, perhaps through the system itself, and not allowed to equilibrate in response to the conformational change.

In the previous implementation of the NEB method in Amber9, any system used had to be set up inside the addles functionality of Amber, where all images distributed along the path were treated as one simulation. In that implementation one coordinate file was used, which grouped together all the coordinates of every image, and then split them into discrete structures at the end of the NEB simulation. The parameter file contained a copy of the system for each bead. The nonbonded exclusion list, which was the same for each image and not copied, was used to keep the images from interacting. Using particle mesh Ewald^10,11 (PME) was impractical because of the large size (#beads * (#atoms)²) of the nonbonded exclusion list, each of which would need a distance calculation with PME to remove their interaction in reciprocal space¹². This essentially limits the potential applications to small systems. Furthermore, the entire set of beads uses a single reciprocal space grid (which typically limits scaling due to fast Fourier transform calculations).

To address these issues, a new implementation of the nudged elastic band method to be released as part of Amber11 is discussed in this paper. In this new implementation the user may decide which parts of a system to apply the NEB forces to, for example, just the solute and not the solvent atoms. Rearrangement and rewriting of the code itself also allows for greater parallel efficiency, as well as accommodation of periodic systems, since the coordinates used for the root mean square (RMS) fit can be defined as a subset of the image’s atoms. The multisander functionality in the Amber MD engine (SANDER) runs multiple SANDER jobs simultaneously under a single Message Passing Interface (MPI) program, and has been applied to the NEB method, allowing each image to remain a discrete simulation, and allowing PME with no exclusion list beyond that for the standard system, and a separate reciprocal space calculation for each bead. This means each image writes output and trajectory information during its own MD simulation. This new implementation allows smaller systems to be simulated faster and larger systems to be more easily accommodated. The new method, termed partial nudged elastic band (PNEB), was validated using an alanine dipeptide model, for which the potential and free energy landscapes can be readily calculated using standard MD and minimization approaches thus allowing for a direct comparison. The PNEB method reproduces the minimum potential energy pathway of alanine dipeptide phi/psi isomerization in both implicit and explicit solvent. To convert the structural information along the path to free energies, umbrella sampling based on the PNEB path coordinates was performed with restraints, and 2D WHAM post processing of the umbrella sampling trajectories yielded free energies.

Theoretical Background

The NEB method uses multiple simulations of the system, connected by springs, to map conformational changes along a path (Equation 1), except for the two endpoint structures which are fixed in energy and space. The tangent vector to the path is used to decouple the perpendicular component of the force, described only by the standard force field, and the parallel component, described only by the springs which keep the images evenly spaced along the path, shown in Equation 2 and Equation 3, below. This way, the optimization of each discrete image is not affected by the springs holding it evenly spaced along the path, and the force field does not cause images to move along the path. The tangent τ can be based on the position of the neighboring images or their energies, the latter yielding a more stable definition of the path.⁷

$${\mathrm{F}}_i={\mathrm{F}}_i^{\perp }+{\mathrm{F}}_i^{\parallel }$$ (1)

$${\mathrm{F}}_i^{\perp }=-\nabla V({\mathrm{P}}_i)+((\nabla V({\mathrm{P}}_i))·\tau )\tau$$ (2)

$${\mathrm{F}}_i^{\parallel }=[(k_{i+1}({\mathrm{P}}_{i+1}-{\mathrm{P}}_i)-k_i({\mathrm{P}}_i-{\mathrm{P}}_{i-1}))·\tau ]\tau$$ (3)

In the above equations, the total force F on each image i is decoupled (Equation 1) to a perpendicular force and a parallel force by the tangent vector. The tangent vector defines the path between the two endpoint conformations at every image on the path, and when the dot product is taken with the potential defined by the force field for each image, represents the contribution of the force field for that image along the path. As shown in Equation 2, this is subtracted from the force field description (V) of each image (P_i) to remove any force contribution along the path from each image’s individual potential. This component is termed the perpendicular force, since it represents each image as it moves in potential energy space normal to the path, fulfilling the requirement for the minimum energy path calculation.

The parallel component of the force accounts for the artificial springs linking each image together. In Equation 3, k_i is equal to the spring constant between images P_i and P_i−1, and P is the 3N-dimensional position vector of image i. Again, the tangent definition is used to subtract out the spring forces which act normal to the path. This way, the spring force which keeps the images evenly spaced along the path does not affect the relaxation of the individual images. The discrete images are maintained at specific intervals as to resolve saddle points; otherwise, they would fall back down to the local minima where they began.

In the PNEB implementation, communication and distribution of the decoupled force calculation was changed from the previous version of the code. Many images are linked together and simulated simultaneously using the multisander functionality in Amber. In this way, each image is simulated independently, and each can be distributed to multiple processors. An MPI communicator spanning each of these individual image simulations allows the transfer of the information necessary to perform the NEB force calculation. Each simulation along the chain is assigned a MPI master process; these masters perform the NEB force calculation. The force calculation routine calls the NEB force subroutine at each time step. For each image in the chain, with the exception of the first and last which are fixed in space, the coordinates of its two neighbor images are sent to each image’s master process using MPI point-to-point communication. The master then performs an RMS fit of the neighbor coordinates to the image’s self coordinates to remove rotational and translational motions for atoms in a user-specified mask. In this manner each image remains an individual continuous simulation, where there is no change in the coordinates due to NEB imposed RMS fitting for each image. This is important for simulations with periodic boundary conditions. The master process gathers potential energies and determines spring constants, which it then uses to calculate and normalize tangent vectors depending on energy differences as described elsewhere¹³. Following this, the spring forces are calculated, and from all of this data the NEB forces are compiled and stored. After returning to the force calculation the NEB forces are broadcast to the other MPI threads for this image and added to the main force array for use in the parallelized coordinate/velocity integration step.

In the Amber11 implementation of NEB, an increase in communication timings when compared to a multisander simulation on the same system without the NEB force calculation can be expected (see Figure 1S and Table 1S in the Supplementary information for detailed timing data). This is attributed to the master process requiring forces for all atoms in a NEB calculation, which is not needed in a standard parallel MD calculation. Additionally, at every time step, an MPI master must send and receive the coordinates of the neighbor images for each image and potential energies of every bead before performing the additional work of tangent normalization and calculating the spring forces. The NEB forces must be broadcast via MPI from each image to the main force array. All of these processes are in addition to calculating the dynamics of each image along the path, and yields increased timings when compared to standard multisander (see supplementary information).

An important additional feature of this new implementation allows the NEB forces to be applied to specific subsets of atoms. Masks in the input files designate specific atoms to apply NEB forces to as well as specific atoms to be broadcast for RMS overlapping to remove rotational and translational motion. The atom selection uses the standard mask notation described in the Amber manual. In a SANDER input file with the ineb flag =1, the tgtrms mask denotes which atoms to apply NEB forces to, and the tgtfit mask denotes atoms to be broadcast for overlap of partner images to the self images. In this way, the NEB force decoupling is performed for only part of the system of interest, while the remainder is simulated with standard MD.

The tgtfit and tgtrms designations allow incorporation of explicit solvent, where the solvent atoms are not specified by either the tgtfit or tgtrms flags. This means that the NEB forces are not calculated for solvent molecules, nor are they used to overlap structures when removing the rotational and translational motion. The latter proves impossible, due to diffusion of water molecules which precludes overlapping between structures. Eliminating solvent from the NEB force calculation is important because this allows the solvent environment to react independently to the conformational change that is being studied. Additionally, communicating only part of the coordinates can dramatically improve parallel scaling. However, this approach necessarily means that more familiarity with the system of interest is required, and optimization methods must be carefully monitored to assure sufficient exploration of conformational space for the NEB part of the system while maintaining the integrity of the non-NEB part. Careful attention must be paid to annealing temperatures if this method of optimization is chosen otherwise non-physical structural deformations can be induced in the sections of the system that are not subject to NEB restraints.

Since only part of the system is simulated with NEB forces, it is important to monitor convergence of the non-NEB part of the system. The NEB forces ensure spacing of the NEB atoms along the minimum energy path. The non-NEB part of the system must be allowed more time to respond to this conformational change, since it essentially acts as a standard MD simulation. Since NEB is a timescale independent method, many of the conformational transitions this method could be applied to occur over long biological timescales. The NEB part of the system is simulated in a timescale independent manner, but the non-NEB part is not. However, in many cases the transitions in the non-NEB part of the system are expected to respond to that part of the system which is moving in a timescale independent manner, and converge faster than they would if no NEB driving forces were applied to the region of interest. Testing this point could be done by comparing the continuity of any structural differences in the endpoints that were not included in the mask of atoms to which NEB spring were applied.

Computational Details

This work was done using the Amber9 and Amber10 suite of programs. The alanine dipeptide (N-acetylalanyl-N-methyl-amide) was built from the sequence ACE ALA NME in the leap module of the Amber9 suite of programs. The impose command was used to generate two structures with phi/psi angles of 66° and 9°, and −82° and −6°, respectively. The Amber ff99SB force field was used¹⁴. The coordinates were subjected to 400 steps of conjugate gradient minimization, with 5 kcal mol⁻¹ Å⁻² restraints on all atoms except hydrogen. The implicit solvent model used in these calculations was the GB-HCT model (igb=1 in the SANDER module) with the mbondi radii set ^15–17.

Well minimized endpoints are critical for NEB simulations, since it is assumed that the transition endpoints are low energy structures. For explicit solvent simulations, the GB minimized coordinates were then solvated with 378 TIP3P¹⁸ water molecules and further minimized and equilibrated. This round of minimization began with 1000 steps of steepest descent minimization with restraints on the dipeptide. The next step was 25ps of restrained MD to increase the system temperature from 0K to 300K. Two subsequent rounds of steepest descent minimization were performed, in which the restraints were reduced to 0.1 kcal mol⁻¹ Å⁻². This was followed by 25ps each of equilibration with restraints on all atoms except water and hydrogen at 1.0 kcal mol⁻¹ Å⁻² which were reduced to 0.5 kcal mol⁻¹ Å⁻². The last steps of equilibration were to reduce the restraints to just the backbone atoms, in two rounds of 25ps with restraints of 0.5 kcal mol⁻¹ Å⁻² decreasing to unrestrained MD for 50ps. This same equilibration was performed for both endpoint structures. After the initial 400 step minimization mentioned above, the structures were subjected to 10ns of unrestrained dynamics.

Simulated annealing was used to optimize the alanine dipeptide isomerization pathway. This protocol was adapted from Mathews & Case 2006¹³. The longer simulated annealing protocol described was used here, with the exception of the high temperature range which was taken from the shorter protocol description. Here, a 760ps protocol was used, and the communication of atoms was specified by the tgtfit mask only in the case of PNEB runs. For the first 40ps the system was heated to 300K with a Langevin¹⁹ collision frequency of 1000 ps⁻¹ and pulled into an interpolating path using 10 kcal mol⁻¹ Å⁻² spring forces. The system equilibrated along this path for 100ps after increasing the spring forces to 50 kcal mol⁻¹ Å⁻², where they remained for the rest of the NEB simulation. Heating of the system from 300K to 500K and subsequent cooling back to 300K was performed stepwise over 300ps. Further cooling to 0K to remove kinetic energy occurred over 120ps, and quenched MD was run for 200ps. SHAKE²⁰ was used to constrain bonds to hydrogen. Structure distribution of images along the minimum energy path at each step in this optimization procedure are shown in the Supplementary information, Figure 2S. The same protocol was used for all three systems, regardless of solvent environment, to examine consistency of the method. A lower collision frequency is more likely relevant when solvent is present, as it is related to the viscosity of the system.

The potential energy surface was calculated by restrained energy minimization of alanine dipeptide at 2° intervals over the entire phi/psi plane. 50 kcal mol⁻¹ rad⁻² restraint forces on the phi and psi angles were used, and 500 steps of steepest descent minimization were followed by 500 steps conjugate gradient minimization.

A common way to calculate free energy using Molecular Dynamics is to use the umbrella sampling technique. The free energy surface of the alanine dipeptide system was calculated using umbrella sampling by first building and minimizing independent structures where the phi and psi were rotated every 5° to cover the complete periods (−180° to 180°) of both backbone dihedrals, totaling 1296 simulations. During the minimization process the phi and psi dihedrals were restrained with a force constant of 500 kcal mol⁻¹ rad⁻² and the minimization was run for 1000 steps. Each minimized phi/psi structure was used as the starting structure of an independent umbrella simulation, yielding 1296 windows. The force constant for the production dynamics was 75 kcal mol⁻¹ rad⁻² on the phi and psi dihedrals, and each window was simulated for 10ps at 300K. The phi and psi values were saved at every time step. Data was postprocessed into free energy profiles using the Weighted Histogram Analysis Method (WHAM)^21–23, using a program provided by Alan Grossfield, (freely available at http://membrane.urmc.rochester.edu/Software/WHAM/WHAM.html).

The umbrella sampling and subsequent free energy calculation for the PNEB path were performed using starting structures from the last step of the PNEB simulated annealing protocol, the 200ps quenched MD simulation. A grid was mapped along the path at every 10° of phi and psi using a 20° buffer in each direction along the PNEB path. The grid indicating initial phi/psi angles of each window, overlapped with the PNEB path, is shown in supplementary information Figure 3S. Structures closest to these values from each bead’s 200ps trajectory were restrained to the angles described by the grid with a 75 kcal mol⁻¹ rad⁻² restraint force. 25ps of dynamics at 300K were run for each of the 147 windows. Overlapping populations of each window are shown in the supplementary information, Figure 4S. 2D WHAM²⁴ analysis was used to calculate free energies.

Results and Discussion

The PNEB method was tested on the isomerization of an alanine dipeptide (Figure 1). This system was chosen because of its small size and the relative ease of determining its underlying energy surface in both implicit and explicit solvent. The energy surface of the alanine dipeptide is dominated by rotations around the phi and psi angles, and can be represented topographically as seen in Figure 2, where restrained minimizations at 2° intervals give potential energy over the entire plane. The starting conformations of the alanine dipeptide were chosen from the right handed helix (negative phi and psi angles) and left handed helix (positive phi and psi angles) basins. 15 copies of each image were used as the initial structure distribution along the path (30 total).

Figure 1.

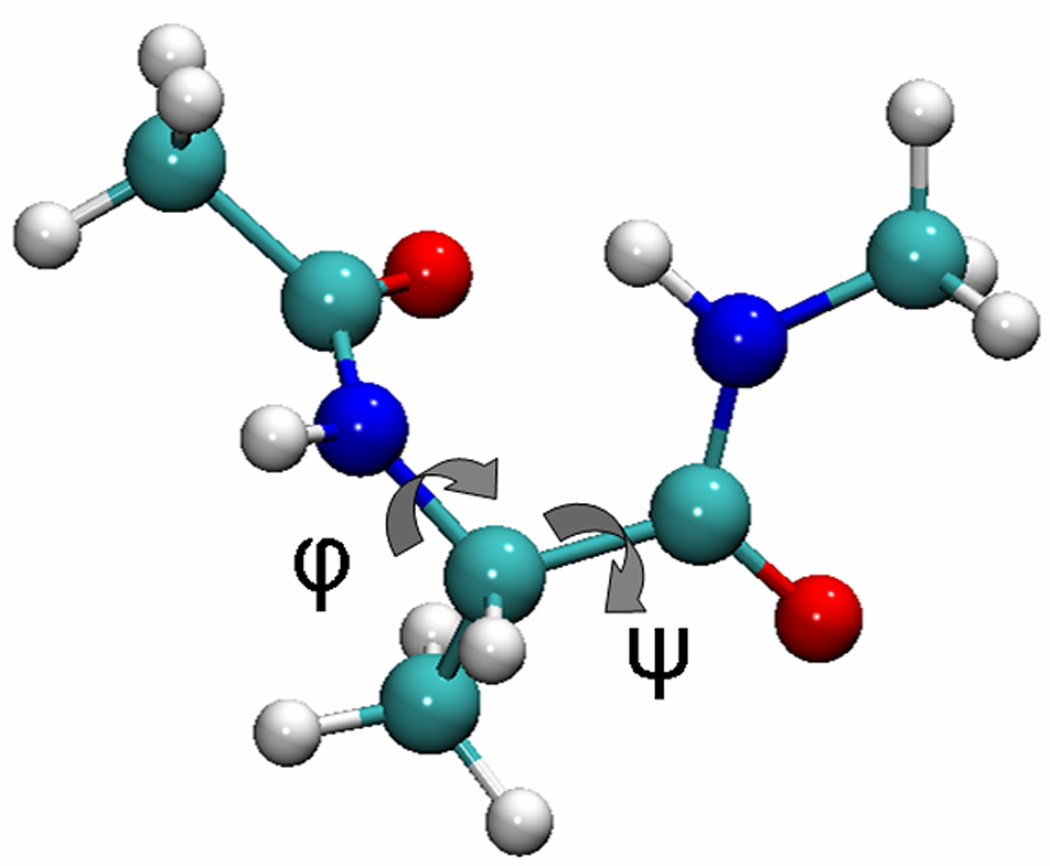
The structure of alanine dipeptide. Rotation around the phi and psi angles dominates the energy landscape. Image generated with VMD 1.8.6.²⁷

Figure 2.

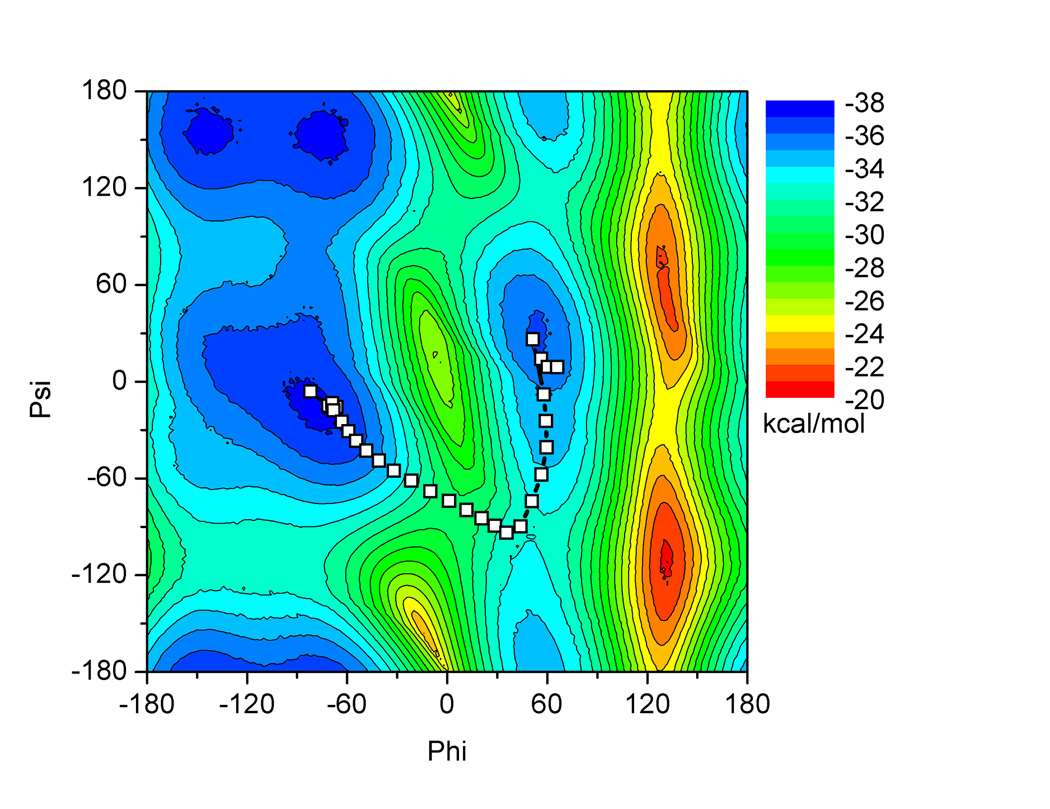
The potential energy landscape for alanine dipeptide isomerization around the phi/psi dihedral angles. Minimum energy path for standard NEB implementation is shown using squares for each bead. Contours are shown at 2 kcal/mol intervals. The surface was generated by performing restrained minimizations at every 2° of the phi and psi angles.

The purpose of performing alanine dipeptide simulations in implicit solvent was to verify that changes made to the force decoupling and communication would not change the behavior of the method in finding the minimum energy pathway since full NEB could also be used. The minimum energy path reported in Figure 2 shows that the standard NEB implementation, where forces are applied to every atom in the system, returns a minimum energy path consistent with previously published results.^9,13 The path proceeds perpendicular to the contour lines on the underlying potential energy landscape, and passes through the saddle point, indicating it is a minimum energy path.

In the standard NEB test performed on the alanine dipeptide system, NEB forces were applied to every atom, shown colored by atom name in Figure 3a. To test the implementation of the PNEB method, and assure it returned the same minimum energy path as the standard NEB implementation, two test systems were utilized where the NEB forces were applied to a subset of the atoms of the alanine dipeptide. The PNEB implementation was verified for non-periodic and periodic systems by performing two tests. In the first test, NEB forces were applied to only the backbone C and N atoms of an implicitly solvated alanine dipeptide, as specified by the orange atoms in Figure 3b. The second test of the method was to apply NEB forces to the same backbone atoms of an explicitly solvated alanine dipeptide, shown in Figure 3c. Rotational and translational motion between images was effectively removed before the tangent calculation by rms fitting on every atom of the alanine dipeptide for both of these systems.

Figure 3.

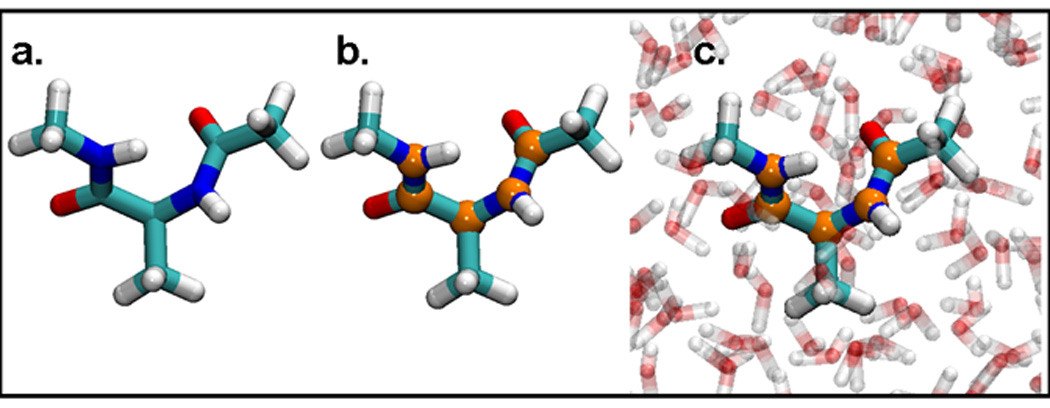
Alanine dipeptide test systems: Alanine dipeptide in implicit solvent with a) NEB forces applied to all atoms b) NEB forces applied to atoms in orange. c) Alanine dipeptide in explicit solvent with NEB forces applied to atoms in orange. Images generated with VMD 1.8.6.²⁷

In Figure 4 it is shown that the test systems for PNEB return the same minimum energy path between the endpoint conformations. In all three cases, the minimum energy transition follows a path from the right handed helix (negative values of phi and psi) to a saddle point of ~(50°,−100°) and from there to positive phi/psi values in the left handed helix.

Figure 4.

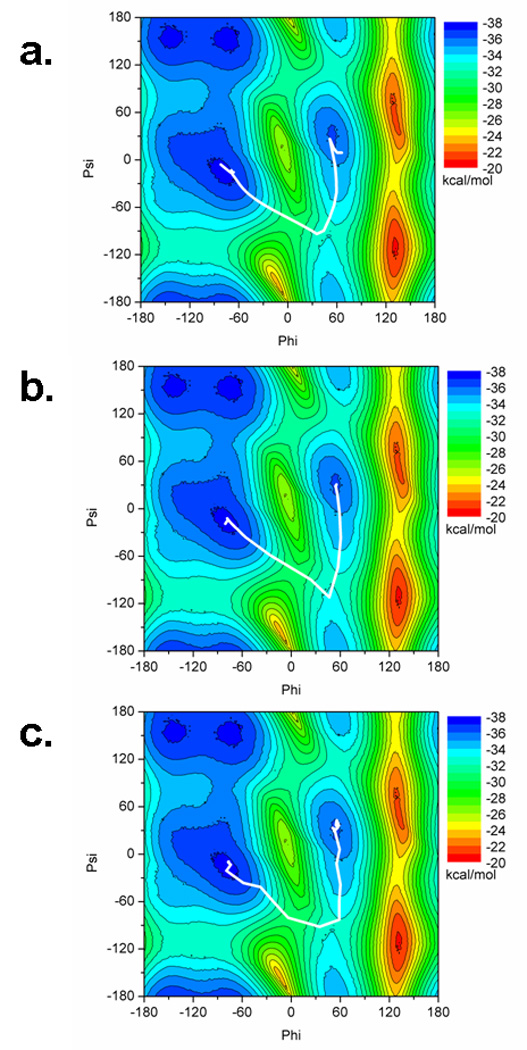
Potential energy surface of alanine dipeptide with minimum energy paths determined by a) standard NEB, b) PNEB in implicit solvent, and c) PNEB in explicit solvent. The minimum energy path is reproducible between all three systems.

Even though all three systems reproduce the same overall minimum energy path, the paths differ slightly. The endpoint structures undergo a conformational motion that is not represented by the phi/psi plane. For the standard NEB in implicit solvent, shown in Figure 4a, the movement in the images close to the endpoint structures is attributed to rotation of the end methyl groups, which is a conformational motion not represented by the phi/psi angles. The PNEB motion would not account for movement in the hydrogen atoms, since these are not included in the part of the molecule for which we calculate NEB forces. What occurs in Figure 4b is the methyl group of the C terminus rotates from the right handed helix endpoint structure, which is at an imperfect angle, to a slightly more stable structure where the angle along the C–N bond becomes completely anti conformer with regards to the rest of the structure. The N terminus methyl group also rotates its hydrogen away from the carbonyl oxygen. In Figure 4c, when explicit solvent PNEB is used, there is a larger population of structures which remain near the ending points than in the other two simulations. This is due to a few images’ trajectories along the path forming a hydrogen bond between the NH group of the N terminus and the oxygen of the C terminus, which is energetically unfavorable to break. This hydrogen bond forms more readily due to the inclusion of explicit solvent, and it is less favorable to form during implicit solvent simulations.²⁵ Since we are using PNEB, however, the NEB forces applied to the backbone atoms ultimately force the images along the minimum energy path to sample the transition state region.

Although the NEB method provides the user with a minimum potential energy path of a conformational transition, in some cases it may be desirable to determine free energies along this path. 2D-WHAM analysis was used to generate free energies along the PNEB derived minimum energy path. For many systems, the problem with applying umbrella sampling is twofold; the path cannot be easily defined by a small number of reaction coordinates that can be used as restraints, or the transition that is forced to occur along the reaction coordinate introduces artifacts along the transition path. In the alanine dipeptide example, the definition of a two dimensional reaction coordinate along which the isomerization occurs is clearly described by the phi and psi angles. For larger systems with more degrees of freedom, PNEB itself can define important reaction coordinates upon analysis of the resulting path. As shown in Figure 5a, the 2D WHAM procedure which uses PNEB derived structures as a starting path returns reasonable free energies. Figure 5b shows that the free energy along the NEB path is almost identical to that from the full free energy surface calculated independently. In this way we can generate free energies along the minimum potential energy path calculated with NEB.

Figure 5.

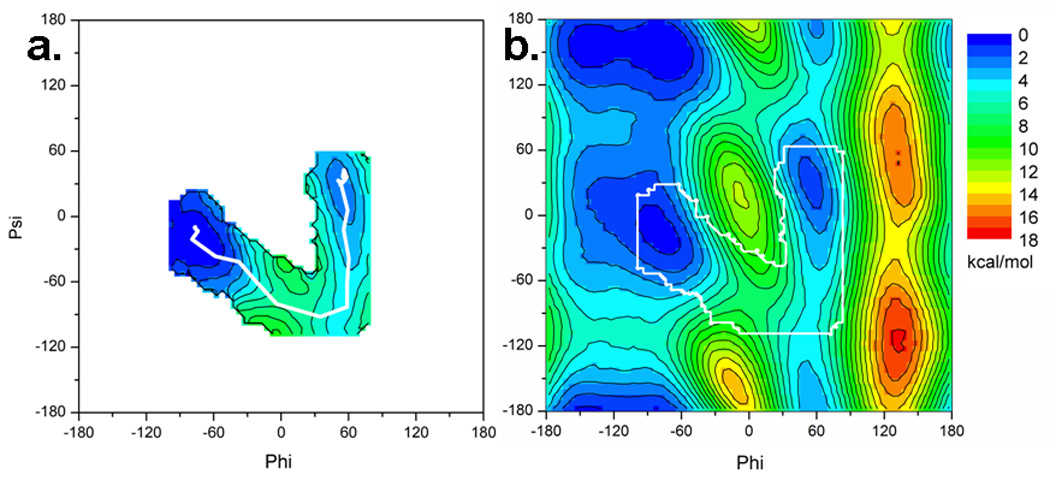
a) Free energy profile in the region of the transition calculated using the PNEB path as a starting point. b) Full free energy surface of alanine dipeptide calculated by restrained umbrella sampling followed by 2D-WHAM. Boundary corresponding to a) is outlined in white to show similarity between calculated free energy using only the PNEB path and that calculated for the entire surface.

Conclusion/Summary

The NEB method available in the Amber10 suite of programs has been updated to a partial nudged elastic band method where the NEB calculation is performed on a subset of the system, defined by user specified masks. Each image along the path is an independent MD simulation coupled to the others in a coarse grain manner through an MPI communicator. Testing on the alanine dipeptide model system, where the underlying potential energy surface can easily be determined, shows that the partial NEB method returns the same minimum energy pathway as the standard NEB method, even when the system is explicitly solvated. This verifies the method performs the same function, namely, finding the minimum energy pathway of a conformational change, even when only a subset of the system’s atoms are specified for the NEB force decoupling.

It is worth noting, however, that the alanine dipeptide system is only a model, chosen because the “answer,” in our case, the potential energy surface, is straightforward to calculate. It has been shown that dipeptide phi/psi preferences are different from phi/psi behavior in larger protein systems.²⁶ This presents a unique challenge in adapting this method to larger protein systems: as the number of degrees of freedom in a system increase, the conformational changes become more difficult to quantify. It is thus recommended that the PNEB or NEB methods be run a statistically relevant number of times, so reproducibility of the minimum energy pathway can be measured.