Subdivision Meshes for Organizing Spatial Biomedical Data

Abstract

As biomedical images and volumes are being collected at an increasing speed, there is a growing demand for efficient means to organize spatial information for comparative analysis. In many scenarios, such as determining gene expression patterns by in situ hybridization, the images are collected from multiple subjects over a common anatomical region, such as the brain. A fundamental challenge in comparing spatial data from different images is how to account for the shape variations among subjects, which make direct image-to-image comparisons meaningless. In this paper, we describe subdivision meshes as a geometric means to efficiently organize 2D images and 3D volumes collected from different subjects for comparison. The key advantages of a subdivision mesh for this purpose are its light-weight geometric structure and its explicit modeling of anatomical boundaries, which enable efficient and accurate registration. The multi-resolution structure of a subdivision mesh also allows development of fast comparison algorithms among registered images and volumes.

1 Introduction

The advance of imaging techniques has created an ever increasing body of spatial data (in the form of 2D images or 3D volumes) that requires efficient organization and analysis. Oftentimes, such data is collected over a common anatomical structure (such as the brain or the heart) from a large number of subjects. The anatomical variations among these subjects underline the main computational challenges involved in comparing data collected from different subjects.

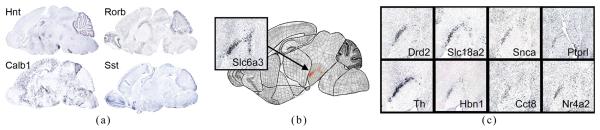
As an example, substantial effort has been made around the world to determine spatial expression patterns of genes in the mammalian genome (particularly the mouse genome [1-3]) using experimental techniques such as in situ hybridization (ISH) [4]. The result of ISH on one subject is a stack of tissue sections of an anatomical structure, such as the brain, where cells expressed by a particular gene are highlighted (Fig. 1(a)). Performing ISH on multiple subjects yields expression images of various genes over the common anatomical structure. Comparing these images reveals the spatial relations between genes, which are often key to understanding their functional relations [5]. However, as observed in Fig. 1(a), brains of individual mice may exhibit significant variation in their anatomical shape, making direct image-to-image comparisons unsuitable.

Fig. 1.

(a) Example ISH images. (b,c) An example search using our 2D prototype system at Geneatlas.org that explores genes with similar expression patterns.

In this paper, we describe the use of subdivision meshes, a geometric modeling tool, in organizing spatial data for efficient and accurate queries. Subdivision is a fractal-like process for generating smooth geometry from coarse meshes [6]. While often used for modeling animated characters [7], subdivision meshes can be an ideal form of a deformable anatomical atlas. Subdivision meshes can explicitly model the anatomical divisions interior to the structure while providing a smooth coordinate space within each division. After deforming the subdivision atlas to fit the anatomical shape of each individual image, these images can be compared within a common coordinate space established by the atlas. The key advantage of a subdivision mesh over previous atlas representations is that it can be more efficiently and accurately deformed onto individual images, due to its geometric nature and the explicit modeling of anatomical boundaries.

Using subdivision meshes, spatial data can be organized into a geometric database allowing fully customizable spatial queries. The multi-resolution structure of a subdivision mesh further gives rise to fast algorithms for processing queries. As an example, Fig. 1(b) depicts a query interface in a 2D subdivision-powered prototype database of ISH images developed by the authors at Geneatlas.org [8,5]. A cross-section of the mouse brain is overlayed with a subdivision atlas partitioned into anatomical regions. Using the query interface, a user has selected a portion of the midbrain containing the substantia nigra (the highlighted area) and asked for those genes whose expression patterns in the selected region are similar to that of a target gene Slc6a3. The top gene candidates (out of over 200 genes currently in our system) and their ISH images are shown in Fig. 1(c). Note that the comparison of expression patterns is performed despite the anatomical variations among the subjects from which the images were collected.

2 Method

We shall first describe the geometric method of subdivision and the representation of anatomical atlases as subdivision meshes. We will then elaborate on the techniques we developed to utilize subdivision atlases in mapping 2D or 3D image data. As concrete examples to illustrate these methods, we will consider the problem of mapping 2D gene expression patterns in ISH images and 3D bone density patterns in CT images. Note however that the techniques presented here can be applied to any 2D or 3D anatomical data. The following description is mainly compiled from previous work [5,8-11].

2.1 Subdivision meshes as deformable atlases

A standard approach in comparing images collected from subjects with varying shapes is mapping all images into a standard coordinate space, often known as an atlas. The typical atlas representation consists of a 3D volume where each voxel has been annotated with its anatomical region [12], or a stack of 2D images where each pixel has been annotated [2,1]. The voxelated or pixelated atlas is coupled with a deformation mechanism, typically an affine transformation [13] or a spline-based free-form deformation (FFD) [14,15], in order to register onto images from individual subjects (for a more detailed account of brain atlases, see the survey by Toga [16]). However, a global affine transformation cannot account for local shape changes (although sufficient as an initial alignment in applications such as anatomical labelling [13]). On the other hand, the rectilinear grid used in FFD inherently lacks the flexibility to account for subtle, local variation in anatomical shapes, as the grid itself is not aligned with the anatomical boundaries [9]. While such limitation can be alleviated by using a finer grid over which the FFD is defined, solving the deformation at the larger number of grid nodes will significantly increase the computation time.

We describe a different, geometric atlas representation that gives rise to more accurate and efficient registration procedures. The atlas is represented as a mesh, which consists of a collection of connected geometric elements. In particular, a 2D atlas (for a single cross-section of an anatomical structure) is represented as a planar mesh consisting of polygonal elements such as quadrilaterals. A 3D atlas (for the whole structure) is represented as a volumetric mesh consisting of polyhedral elements such as tetrahedra.

In either case, the atlas is partitioned into sub-meshes representing the anatomical partitions within the structure. The partitioning polylines (2D) or polygons (3D) are called creases.

Given an atlas represented as a coarse mesh M⁰, we generate a smooth atlas using subdivision. Subdivision is a fractal-like process that produces a sequence of increasingly fine meshes (with smaller but more elements) that converge to a limit mesh M^∞ following the shape of M⁰ [6]. The limit mesh contains a network of smooth curves (2D) and surfaces (3D) that accurately models the anatomical boundaries. We discuss our choice of subdivision algorithms in 2D and 3D, respectively.

2.1.1 2D subdivision

In 2D, we focus on Catmull-Clark subdivision [17], a subdivision scheme for quadrilateral meshes that produces provably smooth meshes in the limit. The scheme was further modified in [18] to allow smooth subdivision of crease polylines embedded in the coarse mesh.

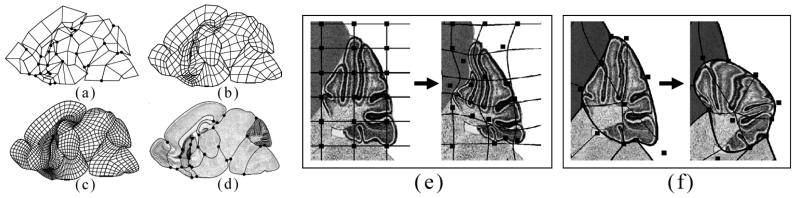
We use the simple example in Fig. 2(a) to illustrate the subdivision algorithm. Here, the coarse mesh M⁰ consists of three quadrilaterals where a subset of the quad edges and quad vertices are marked (darkened) as creases. The crease edges form a network that partitions M⁰ into disjoint pieces. Subdivision is an iterative process, where two steps are performed in each iteration. First, we split each quad into four sub-quads with new vertices placed at the midpoints of old edges and at the centroids of old faces (Fig. 2(b)). Next, for each vertex p in the mesh, compute the centroids of those quads that contain p, and reposition p at the centroid of those quad centroids (Fig. 2(c)). To yield smooth subdivision of creases, each vertex on a crease edge is repositioned at the centroid of the midpoints of only those crease edges that contain the vertex. The positions of crease vertices are left unchanged. As more subdivision iterations are performed (Fig. 2(d-f)), the limit is a smooth mesh M^∞ partitioned by a network of cubic B-spline curves that interpolate crease vertices of M⁰ and approximate the network of crease edges in M⁰.

Fig. 2.

Initial mesh with eight crease edges and a crease vertex (a), results after bi-linear sub-division (b), and centroid averaging (c), and after 2 (d), 3 (e) and 4 (f) subdivision iterations, respectively.

To construct an atlas for a 2D cross-section of an anatomical structure, we model the cross-section as a Catmull-Clark mesh partitioned by a network of crease curves. Fig. 3(a) shows such a coarse mesh M⁰ for one sagittal cross-section of the mouse brain. We mark vertices shared by more than two crease edges as crease vertices (round dots). Fig. 3(b,c) show the quad meshes M¹,M² generated by successive iterations of subdivision. The crease curves (highlighted in Fig. 3(d)) partition the mesh into 15 disjoint sub-meshes, corresponding to 15 anatomical regions. Note that the interior of each partitioned region is filled with a smooth parameterization of quadrilaterals suitable for storing spatial data after the atlas is deformed onto individual images. In addition, observe that the subdivision process itself bestows a natural hierarchical structure to the mesh, giving rise to efficient algorithms to compare data stored on the atlas (to be discussed in Section 2.2.2).

Fig. 3.

2D atlases of the mouse brain modeled as a coarse subdivision mesh (a), after sub-division (b,c), and overlaying its defining image showing the curve networks (d). Comparing free-form deformation (e) and subdivision mesh deformation (f).

An important advantage of a subdivision atlas over pixelated or voxelated atlases is that it enables fast and accurate deformation onto tissue sections. Such advantage is obtained in two ways. First, the shape of the smooth limit mesh M^∞ is entirely determined by the location of the vertices in the coarse mesh M⁰, since the rules used in constructing the mesh M^k+1 from M^k involve simple fixed combinations of vertex positions in M^k. As a result, the deformation of the entire mesh reduces to the movement of the small number of vertices in the coarse mesh M⁰. In contrast, a typical FFD deformation for pixelated atlases needs to solve for all points on a rectilinear grid. Second, unlike the regular grid used in FFD, the vertices of a subdivision mesh are aligned to the anatomical boundaries, lending direct control over fitting of these boundary curves onto those in the image, as compared in Fig. 3(e,f).

2.1.2 3D subdivision

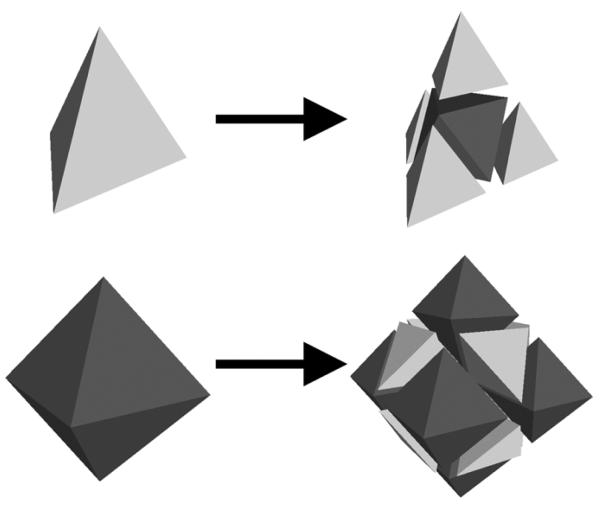
In 3D we utilize the recently developed tetrahedral subdivision scheme [9], which promises a smooth volumetric mesh at the limit. One of the reasons for considering tetrahedral elements, rather than hexahedra, is that the former are simplices in 3D and are more flexible in modeling structures with irregular shapes and fine details.

The subdivision algorithm follows a similar two-step procedure as in 2D Catmull-Clark subdivision. To produce a subdivided mesh M^k+1 from M^k, the algorithm first splits each tetrahedron in M^k into smaller elements by inserting mid-points on edges. Since there is no symmetric way of splitting a tetrahedron into only tetrahedra, the algorithm splits one tetrahedron into 4 tetrahedra and one octahedron in the center, as shown in Fig. 4. Likewise, an octahedron in M^k is split into 6 octahedra and 8 tetrahedra. In the second step, the algorithm re-positions each newly inserted vertex to the centroid of the weighted centroids of the adjacent elements (see [9] for the detailed weight mask). Similar to 2D, a volumetric subdivision mesh M⁰ can be partitioned into sub-meshes by a network of “crease” triangles. By applying surface-based averaging rules, such as Loop subdivision [19], to vertices on the crease triangles in the second step of each subdivision iteration, the subdivided crease triangles will form a smooth surface in the limit mesh M^∞. The crease triangles can further contain crease edges and vertices, whose subdivision rules follow that in the 2D discussion above.

Fig. 4.

Splitting rules for tetrahedral and octahedral elements. Image courtesy of Scott Schaefer [9].

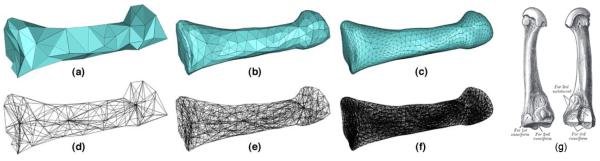
To construct an anatomical atlas, we model the anatomical structure by a volumetric subdivision mesh partitioned by a network of crease triangles that represent the boundaries of anatomical regions. If there is only a single anatomical region present, the crease triangles form the outer boundary of the anatomical structure. This is illustrated in Fig. 5, showing the subdivision atlas of a human foot bone (second metatarsal) after successive iterations of subdivision [11]. Note that repeated subdivision yields a volumetric mesh consisting of smooth boundaries as well as a smooth interior parameterization of tetrahedral and octahedral elements, which can be used for storing spatial image data. If there are multiple anatomical regions in the structure, subdivision yields a smooth network of crease surfaces modeling the boundaries between these regions. Similar to 2D subdivision atlases, we mark edges shared by more than two crease triangles as crease edges, and vertices shared by more than two crease edges as crease vertices. Just as in 2D, the explicit modeling of anatomical boundaries in 3D and the small number of vertices in the initial coarse mesh is the base for efficient and accurate registration.

Fig. 5.

The subdivision atlas of a second metatarsal after zero (a, d), one (b, e) and two (c, f) iterations of subdivision, where (a, b, c) show the exterior surfaces as a result of subdividing the crease triangles and (d, e, f) show the wire frame internal tetrahedral and octahedral elements. An illustration of the metatarsal bone is shown in (g) (image source: Gray's Anatomy).

2.2 2D subdivision atlases for mapping images

A 2D subdivision atlas can be used to map cross-section tissue image data collected from various subjects. The key steps involved in this process include constructing the atlas, deforming the atlas to fit each image, and data mining on the registered images. We explain the techniques we developed for each step, which have been successful in mapping 2D gene expression patterns in ISH images.

2.2.1 Building the atlas

Due to the low geometric complexity of a 2D subdivision atlas (such as the one shown in Fig. 3 (a) top-left), we construct these atlases manually using a graphics interface. The interface allows one to create a coarse quadrilateral mesh with crease elements, given a reference tissue image. If the tissue sections are taken at multiple cross-sections of the anatomical structure, an atlas is constructed for each cross-section where mapping is desired.

2.2.2 Deforming the atlas

We adopt the standard two-step process in which the atlas is first aligned to the image using a global rigid-body transformation and then locally fit. This global alignment accounts for rotations and translations introduced during the sectioning and imaging process. The local fitting accounts for variations in the anatomical shape of the mouse brain and tissue distortion resulting from the sectioning process.

To compute the global alignment, we perform Principle Component Analysis (PCA) to the image and the subdivision atlas. Specifically, given a tissue section (e.g., the one in Fig. 6(a)), the tissue is first identified in the image using intensity thresholding (gray area in Fig. 6(b)). A covariance matrix is then constructed as $M=\frac{1}{n}{\Sigma }_{i=1}^n{(a_i-c)}^T(a_i-c)$, where a_i is a pixel in the tissue region and c is the centroid of all such pixels. A similar matrix is built for all pixels within the outer boundary of the un-deformed subdivision atlas at some subdivision level k (we used k = 3). The centroid c and the two eigenvectors of the matrix M give an orthogonal coordinate system of the image and of the atlas, which can be used to rotate and translate the atlas onto the image (Fig. 6(c)).

Fig. 6.

(a) Overlay of the un-deformed atlas on an ISH image (showing only the crease curves). (b) The identified tissue region (gray) and sampled points on the tissue boundary with normal directions. (c) The atlas after global rigid-body alignment. (d) The atlas after local fitting.

Due to variations in the anatomical shape among individual subjects, a global rigid-body deformation is not sufficient to produce an accurate fit of the atlas onto the image, as observed in Fig. 6(c). The key step in registration involves locally repositioning the vertices of the coarse mesh M⁰ to form a new subdivision mesh M̂⁰ whose associated limit mesh M̂^∞ fits the image accurately.

To compute this mesh M̂⁰, we let X = {x₁, x₂,…} denote the vertex positions in M⁰ after global deformation. We use M^k(X) to denote the mesh resulting from subdividing M⁰ with vertex positions X k times. Our goal is to compute new positions X̂ such that M^∞(X̂) fits the tissue anatomy accurately while deforming M^∞(X) as little as possible. To this end, we formulate a minimization problem that seeks to minimize an energy function of the form:

$$E^k\left(\widehat{X}\right)=E_f^k\left(\widehat{X}\right)+E_d^k\left(\widehat{X}\right),$$ (1)

where $E_f^k\left(\widehat{X}\right)$ measures the fit of M^k(X̂) to the tissue and $E_d^k\left(\widehat{X}\right)$ measures the energy used in deforming M^k(X) to M^k(X̂).

While the fitting term $E_f^k$ may assume various forms, for simplicity, we demonstrate a simple error that measures the distance between the outer boundary of the mesh M^k(X̂) and the tissue boundary in the image. For each sampled point b_j on the tissue boundary (Fig. 6(b)), we compute the vertex p_j of the mesh M^k(X̂) that is closest to b_j and then minimize the quadratic function:

$$E_f^k\left(\widehat{X}\right)=\underset{j}{\Sigma }{w}_j{(n_j\cdot (b_j-p_j\left(\widehat{X}\right)))}^2,$$ (2)

where p_j(X̂) is the vertex of M^k(X̂) corresponding to p_j, and n_j is an estimated outward unit normal of the tissue boundary at b_j (arrows in Fig. 6(b)). The weight term w_j is the cosine of twice the angular difference between n_j and the normal for the chosen p_j on the atlas boundary, giving preference to fit points with aligned normals. The energy function penalizes the deviation of the mesh vertices p_j(X̂) from the tangent lines defined by the pairs (b_j, n_j).

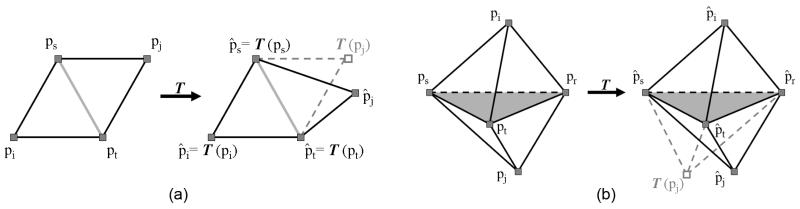
Due to the irregularity of tissue shapes, minimizing the fitting term alone may result in a significantly distorted mesh. To maintain the overall shape of the mesh, we design the deformation term $E_d^k$ to penalize non-affine deformations of the mesh M^k(X) incurred during the fitting process. To understand the structure of this term, we consider deforming a pair of adjacent triangles consisting of points {p_i, p_s, p_t} and {p_j, p_s, p_t} sharing a common edge {p_s, p_t} (see Fig. 7(a)). There exists a unique affine transformation T satisfying T ({p_i, p_s, p_t}) = {p̂_i, p̂_s, p̂_t}. However, this transformation does not necessarily map p_j into p̂_j. We therefore formulate a quadratic term that penalizes the sum of the residual T (p_j) − p̂_j for each pair of triangles:

$$E_d^k\left(\widehat{X}\right)=\underset{\{i,j,s,t\}}{\Sigma }{\left(\frac{a_{\mathit{ijt}}{\widehat{p}}_s+a_{\mathit{ijs}}{\widehat{p}}_t-a_{\mathit{jst}}{\widehat{p}}_i-a_{\mathit{ist}}{\widehat{p}}_j}{4^k{(a_{\mathit{ist}}+a_{\mathit{jst}})}^2}\right)}^2,$$ (3)

where a_ist denotes the unsigned area of the triangle formed by {p_i, p_s, p_t}. The summation is taken over all pairs of triangles in a triangulation of the original mesh M^k(X). The normalization at the denominator is used to make the term converge to a continuous energy matrix as k → ∞ for underlying continuous deformation.

Fig. 7.

Notations used in deriving the deformation penalty term in 2D (a) and 3D (b).

To minimize the energy function E^k(X̂) defined in Equation 1 at a selected subdivision level k (we use k = 3), we observe that all of its component terms (Equations 2 and 3) are quadratic, and hence the minimizer can be found using a linear solver such as conjugate gradients. We then recompute the fit term $E_f^k\left(\widehat{X}\right)$ from the deformed mesh M^k(X̂) and recompute the minimizer X̂. Iterating the process several times yields a subdivision mesh M^k(X̂) that fits the tissue boundary accurately with a minimum amount of deformation. Since the number of unknowns in this optimization process is proportional to the number of vertices in M⁰ as opposed to the number of vertices in M^k, the total fitting process takes only a few seconds to run on a consumer-grade PC.

Figure 6(d) depicts the result after applying the local fitting. Note that, although the fit term so far uses only data points from the external boundary of the tissue, the deformation term causes the internal anatomical boundaries of the deformed atlas to approximate the corresponding internal anatomical boundaries of the tissue. Based on specific characteristics of the image modality, it is possible to augment $E_f^k$ with more complex terms that measure the fitting of the mesh to interior image features. For ISH images, we have shown that more accurate fitting can be achieved by learning landmarks, boundary features and anatomical shapes, expressing them as quadratic terms, and incorporating them into the same minimization framework [20].

2.2.3 Storing and mining

Having deformed the atlas onto an image, we can store the image data onto the quadrilateral elements in the deformed atlas at a chosen subdivision level (e.g., k = 4). Such data could be the number of cells, the pixel colors, or any detected features in the image within the quadrilateral region. Note that the use of the deformed mesh corrects for anatomical variations in individual subjects.

Once the image data is stored onto the atlas, we can now allow users to answer queries of the following form: “For a given anatomical region, which image exhibits a particular spatial pattern?” Using the atlas, users may specify the target region by name or by interactively painting the desired region onto the atlas. Spatial patterns can either be uniform patterns (such as a particular gene expression level) or data from a given image in the database (such as the gene expression pattern in Fig. 1(b)). The query is processed by comparing the vector of data in the target pattern within each quad of the selected atlas region at subdivision level k, denoted as H^k, to the vector of data in those quads of every image i in the database, denoted as $G_i^k$. The error between two vectors $e(H^k,G_i^k)$ can be measured using a number of norms, such as L₁, L₂ and χ² [21]. For example, the L₁ norm has the form:

$$e(H^k,G_j^k)=\Vert H^k-G_j^k{\Vert }_1.$$ (4)

When the number of images mapped onto the atlas is large, naive comparison for every image i at the finest level of subdivision of the atlas can be very time-consuming. By exploiting the multi-resolution structure of subdivision mesh M^k, we can substantially accelerate the search by generalizing the multi-resolution search technique proposed by Chen et al. [22] from rectangular images to subdivision meshes. Specifically, we can compute a multi-resolution summary $G_i^j$ where j ∈ [0, k − 1] for each quad q in M^j that consists of the sum of data over all quads in M^k that are subdivided from q. The accelerated search first computes $e(H^0,G_i^0)$ for all images i in the database and orders the images in terms of their relative error at level 0 using a priority queue. Next, the method repeatedly extracts the image with the smallest error from the priority queue, compares it with the target pattern at a finer resolution, and inserts the image back into the queue using the newly computed error. The search terminates when the error for the image at the head of the priority queue has been previously computed on the fully subdivided atlas. The search is guaranteed to return the image with minimal error if the norm e satisfies $e(H^0,G_j^0)\le e(H^1,G_j^1)\le \cdots \le e(H^k,G_j^k)$. Both the L₁ norm and the χ² norm satisfy this criteria. In our experiments, we have noticed that the two norms yield qualitatively similar search results for gene expression patterns in ISH images.

A prototype database has been constructed that demonstrates the capability of 2D subdivision atlases in comparing gene expression data from ISH images of mouse brains. The online database, Geneatlas.org, currently contains mapped expression data of over 200 genes on 11 key cross-sections of the mouse brain, and features a graphical interface for performing customized queries (Fig. 1(b)) [8,5]. The pipeline of collecting, processing, and organizing ISH images using subdivision meshes is detailed in a concurrent article.

2.3 3D subdivision atlases for mapping volumes

While the use of a 2D atlas is limited to mapping image data on a single cross-section, a volumetric atlas would enable mapping of fully 3D spatial data within an entire anatomical structure among different subjects. The pipeline of spatial mapping using a 3D tetrahedral subdivision atlas closely follows that of a 2D quadrilateral subdivision atlas. First, the atlas is constructed to accurately model the anatomical boundaries in the organ or tissue of interest. Next, given a new data volume, the atlas is deformed to fit its anatomical shape. After atlas deformation, the spatial data of interest in the volume is stored back onto corresponding elements in the deformed atlas and ready for subsequent mining.

Working with an image volume and a 3D mesh, in contrast to a single image and a 2D mesh, brings additional challenges to atlas construction and deformation. In particular, the complexity of a tetrahedral mesh and the difficulty in manipulating 3D geometry using 2D input and display devices makes manual construction of a 3D atlas infeasible. Also, the deformation penalty term in Equation 3 is designed only for 2D triangle meshes. We next discuss the extensions to the techniques presented in the previous section that are necessary to utilize 3D subdivision atlases for mapping volumetric data. These techniques have enabled comparative analysis of 3D bone density in CT volumes [11].

2.3.1 Building the atlas

While a 2D quadrilateral mesh is easy to create by hand given a reference tissue section, manually building a 3D tetrahedral mesh representing the anatomical divisions of a whole organ is considerably harder. To increase the automation of the construction process while maintaining the accuracy of the atlas, we proceed in two stages:

• (1) Surface creation: We first create the network of crease triangles in the subdivision atlas, which represent the boundary surfaces of anatomical regions. These triangles are created by first constructing a fine-resolution triangular surface from a segmented reference volume, simplifying the surface using a quadratic-error based algorithm [23], and finally deforming the simplified crease triangles either interactively or automatically (see next section) so that the subdivided crease surface fits the original fine-resolution surface.

• (2) Volume creation: Next, the spatial volumes partitioned by the network of crease triangles are filled with tetrahedral elements using a Delaunay meshing algorithm [24]. Note that human interactions may be necessary in this stage to ensure both the validity of the input for tetrahedral meshing (e.g., the crease triangles need to be free of self-intersections) and the quality of the tetrahedral elements (e.g., free of degenerate or flat tetrahedra).

In the example of Fig. 5, the metatarsal bone atlas is created following these two stages from a segmented CT volume [25]. The initial fine-resolution bone surface is extracted using the Marching Cubes algorithm [26]. Only a small amount of manual interaction was involved in fine-tuning the fitting of the subdivided crease surface to the initial bone surface and in adjusting the tetrahedral connectivity.

2.3.2 Deforming the atlas

Once the atlas is constructed, it can be deformed onto the reconstructed image volume following the same two-step procedure as fitting a 2D atlas to a single image. First, the atlas is translated and rotated onto the volume by Principle Component Analysis. Next, individual vertices of the coarse tetrahedral mesh M⁰ are re-positioned to minimize the energy function defined in Equation 1.

Note that the deformation penalty term $E_d^k$ in Equation 1, defined in Equation 3, is designed for 2D triangles. To build a similar term for tetrahedra elements, we follow the same intuition of penalizing residues in affine transformations for each pair of adjacent tetrahedra. Specifically, consider all pairs of two tetrahedra {p_i, p_s, p_t, p_r} and {p_j, p_s, p_t, p_r} that share a common triangle {p_s, p_t, p_r} (see Fig. 7(b)). The penalty term is a summation of the following quadratic forms [11]:

$$E_d^k\left(\widehat{X}\right)=\underset{\{i,j,s,t,r\}}{\Sigma }{\left(\frac{a_{\mathit{ijtr}}{\widehat{p}}_s+a_{\mathit{ijsr}}{\widehat{p}}_t+a_{\mathit{ijst}}{\widehat{p}}_r-a_{\mathit{jstr}}{\widehat{p}}_i-a_{\mathit{istr}}{\widehat{p}}_j}{4^k{(a_{\mathit{istr}}+a_{\mathit{jstr}})}^2}\right)}^2,$$

where a_istr denotes the unsigned volume of the tetrahedron formed by {p_i, p_s, p_t, p_r}. The summation is taken over all pairs of tetrahedra in a tetrahedralization of the deformed mesh M^k(X̂).

2.3.3 Storage and mining

After the atlas is deformed onto the volume, we can store the volume data (e.g., intensity values, features, etc.) onto the tetrahedral or octahedral elements in the deformed atlas at a chosen subdivision level. In this way, volumes exhibiting different anatomical shapes can be compared using a common, atlas-based coordinate system. Like the 2D subdivision atlas, the 3D subdivision atlas too has a intrinsic hierarchical structure induced by the subdivision process. As a result, the coarse-to-fine pattern search algorithm discussed in Section 2.2.3 can be equally applied to volumes registered by a 3D subdivision atlas.

As an example of data mining using 3D subdivision atlases, we recently applied the metatarsal bone atlas (in Fig. 5) in studying bone mineral density (BMD) in the foot bones of diabetes patients [11]. The BMD is obtained by the intensity values at each voxel in volumetric quantitative computed tomography (VQCT). Registering the atlas to multiple CT volumes allows the BMD distribution in the metatarsal bones of different subjects or of the same subject at different time points to be visualized and compared in a common coordinate space. In Fig. 8(a), the BMD of one subject is visualized on the atlas, where each colored dot represents the BMD (higher BMD has redder color) in a tetrahedral or octahedral element of the atlas at subdivision level 2. Atlas registration further allows measuring BMD in a user-specified region-of-interest (ROI). In the example of Fig. 8(b,c), the user defines two ROIs on the un-deformed atlas based on the distance to the proximal (left) end of the bone. After the atlas is deformed onto a CT volume, the BMD in each region can be automatically computed on the deformed atlas.

Fig. 8.

Visualizing bone mineral density (BMD) of the second metatarsal in the human foot. (a) The BMD is visualized as colored dots, one for each tetrahedral or octahedral element in the subdivided atlas, such that redder dots represent higher BMD. (b, c) BMD within two user-defined regions of interests, which are defined at a distance of 80% or 20% from the proximal (left) end of the bone.

3 Conclusion and discussion

Cross-subject comparison of spatial data in 2D images and 3D volumes plays an important role in biological and medical research. We describe and demonstrate the use of subdivision meshes as a geometric tool to organize spatial data collected from different subjects for comparative analysis. Modeling an anatomical structure by a subdivision mesh has a number of desirable features, including a light-weight structure that allows efficient deformation, explicit modeling of anatomical boundaries that enables accurate registration, smooth interior parameterization for data storage, and a hierarchical structure for multi-resolution visualization and query processing.