Exploring Ion Permeation Energetics in Gramicidin A Using Polarizable Charge Equilibration Force Fields

Abstract

All-atom molecular dynamics simulations have been applied in the recent past to explore the free energetics underlying ion transport processes in biological ion channels. Roux and co-workers, Kuyucak and coworkers, Busath and coworkers, and others have performed rather elegant and extended timescale molecular dynamics simulations using current state-of-the-art fixed-charge (non-polarizable) force fields in order to calculate the potential of mean force defining the equilibrium flux of ions through prototypical channels such as Gramicidin A. An inescapable conclusion of such studies has been the gross overestimation of the equilibrium free energy barrier, generally predicted to be from 10 – 20 kcal/mole depending on the force field and simulation protocol used in the calculation; this translates to an underestimation of experimentally measurable single channel conductances by several orders of magnitude. Next-generation polarizable force fields have been suggested as possible alternatives for more quantitative predictions of the underlying free energy surface in such systems¹. Presently, we consider ion permeation energetics in the gramicidin A channel using a novel polarizable force field. Our results predict a peak barrier height of 6 kcal/mole relative to the channel entrance; this is significantly lower than the uncorrected value of 12 kcal/mol for non-polarizable force fields such as GROMOS and CHARMM27 which do not account for electronic polarization. These results provide promising initial indications substantiating the long-conjectured importance of polarization effects in describing ion-protein interactions in narrow biological channels.

All-atom molecular dynamics simulations have been applied in the recent past to explore the free energetics underlying ion transport processes in biological ion channels. Roux and co-workers^1–4, Kuyucak and coworkers⁵, Busath and coworkers⁶, and others have performed rather elegant and extended timescale molecular dynamics simulations using current state-of-the-art fixed-charge (non-polarizable) force fields in order to calculate the potential of mean force defining the equilibrium flux of ions through prototypical channels such as Gramicidin A. Such studies overestimate the permeation free energy barrier, generally predicting maximum heights from 10 – 20 kcal/mole depending on the force field and simulation protocol used. This translates to an underestimation of experimentally measurable single channel conductances by several orders of magnitude. Next-generation polarizable force fields^7–9 have been suggested as possible alternatives for more quantitative predictions of the underlying free energy surface in such systems¹. Presently, we consider ion permeation energetics in the gramicidin A channel using a polarizable force field.

We apply a charge equilibration polarizable force field for lipids, water, and protein; the small, hard potassium cation is treated as a non-polarizable entity. This is a sufficiently justified approximation as the polarizability of potassium¹⁰ is 0.83 ų, which is smaller than the polarizability of solvent, lipid, and protein constituents. Moreover, without performing full hydration free energy calculations to assess the ion-water and ion-protein interactions, we computed gas-phase interaction energies for K⁺ with TIP4P-FQ (solvent model employed currently) and the N-Methylacetamide molecule (an often-used proxy for interactions with a peptide backbone). The current force field combination yields a TIP4P-FQ to ion interaction energy of −15.7 kcal/mole and an NMA to potassium ion interaction energy of −28.5 kcal/mole. The respective ab initio values (calculated for this work at the MP2/cc-pVTZ level) are −15.65 and −30.02 kcal/mole and experimental binding affinity (enthalpy) values are −16.2 and −29.83 kcal/mole, respectively. Thus the current force field captures the relative driving force for partitioning between bulk solvent and peptide channel (at least at the level of matching gas-phase binding affinity from experiment and ab initio calculations)¹¹.

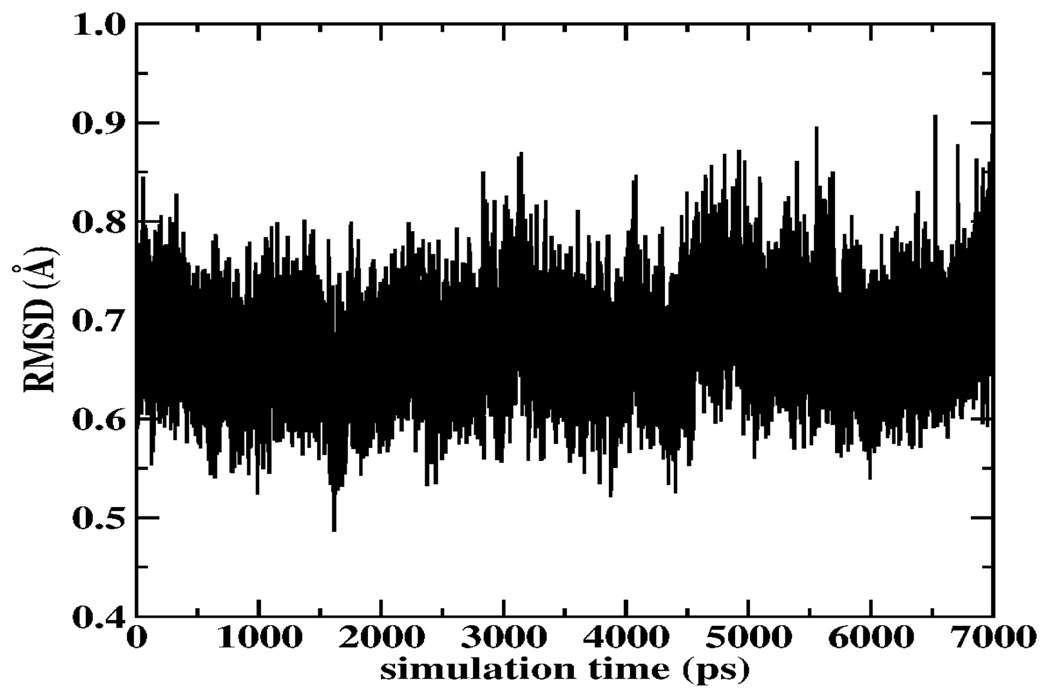
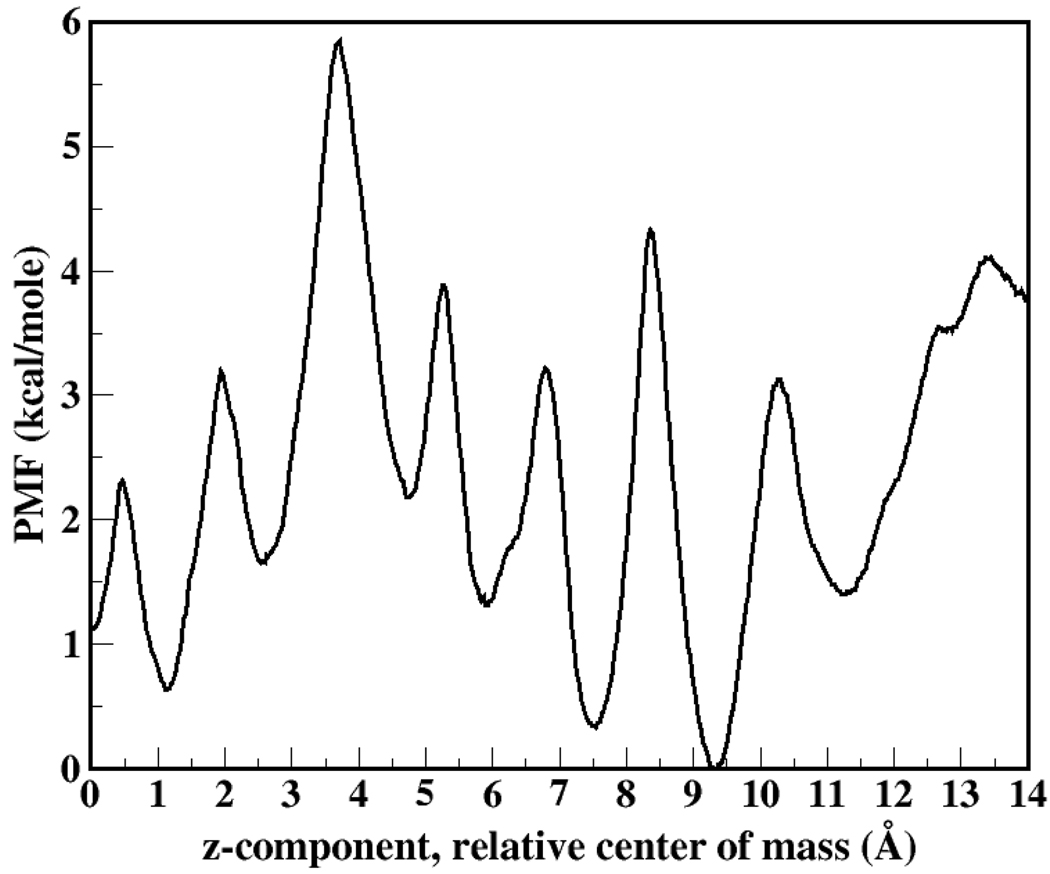
Further details of the simulation system and MD protocol are given in Supplementary information. Structural integrity of the gA channel is monitored via the root-mean-squared deviation from the initial structure, obtained by equilibrating the crystal structure (PDB entry 1JNO)¹². From Figure 1 it is evident that over the course of extended time-scale MD simulations, the structure of the channel is robust for the calculations at hand. Data is shown for simulations with a free gA channel in a DMPC bilayer; similar behavior is observed for the channel structure with restrained ion. Figure 2 shows the one-dimensional potential of mean force computed using umbrella sampling with post-simulation data processing using the WHAM equations^{13, 14}. The current polarizable force field shows a dramatic decrease in the central barrier to ion permeation. Furthermore, we stress that no corrections to the PMF (for ionic strength and system periodicity) have been included (though the effects of such corrections will no doubt further reduce inherent barriers; such a study is outside the scope of the present Communication, and is reserved for a future study). Assuming a constant channel K+ diffusion coefficient (reduced by one-tenth from the bulk value), we estimate a maximum conductance of 57pS, in semiquantitative agreement with the experimental value of 24 pS (picoSiemens)^1,3 (Supplementary Information). The global minimum occurs at 9.5Å relative center of mass separation, in excellent agreement with the solid state N¹⁵ NMR chemical shift anisotropy experiments of Tian et al¹⁵. Moreover, the site at 7.5 Å is seen to be of low free energy (almost commensurate in stability to the global binding site) but separated by a significant free energy barrier of 5 kcal/mole. This further coincides with the NMR measurements¹⁵ suggesting an internal binding site of significantly reduced signal relative to the external binding sites (conjectured to be of equal free energy). We note that non-polarizable force fields in general predict similar locations of local minima, but the relative energetics are force field-dependent. For the CHARMM nonpolarizable force field, the global minimum is 12.5 Å, while the current polarizable force field shows a global minimum at 9.5 Å.

Figure 1.

Backbone rmsd for gA embedded in a DMPC bilayer. RMSD relative to PDBID:1JNO structure¹².

Figure 2.

1-D Potential of Mean Force. The x-axis corresponds to the z-component of the center of mass separation between the gA dimer and K⁺ ion.

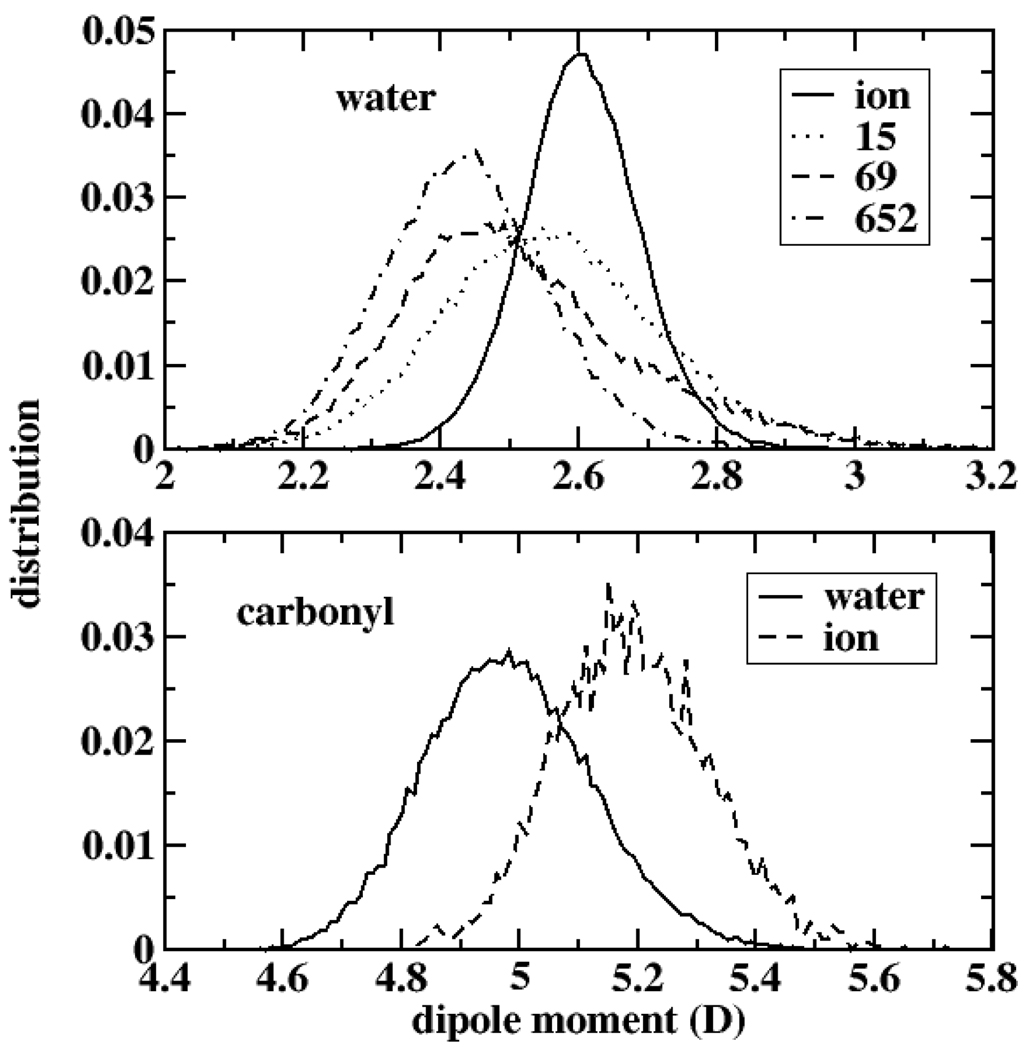
Since the subtle, local interactions between the ion and coordinating ligands and channel water primarily impact ion translocation within this channel, we consider in Figure 3 dipole moment distributions of ion-coordinating water molecules and backbone carbonyl groups; Figure 3 (top panel) shows the distributions for water molecules only in the channel for the cases where the water is interacting only with backbone carbonyl groups and when the water is also coordinating the ion. Likewise, for the carbonyl groups (Figure 3, bottom panel), we investigate the dipole moment for groups coordinating one water molecule and those coordinating the ion. We also consider specific residues in order to highlight the residue dependence (local environmental dependence) of the water and carbonyl electrostatics that is possible to capture with polarization effects. The bottom panel of Figure 3 shows the shift in carbonyl dipole moment between coordination with water (solid curve) and ion (dashed curve). This shift is on the order of 0.2 Debye, and this in conjunction with the enhanced water dipole moments agrees with the deep free energy minima corresponding to the binding sites along the channel axis. The induced dipole thus provides a compensatory stabilization for the ion being desolvated. This stabilization is lacking in non-polarizable force fields. Furthermore, the binding site stability is evidenced by the larger barriers presenting as the ion moves out of the binding sites; for the inner binding sites, the polarizable force field PMF shows barriers of 4–5 kcal/mole (i.e. moving towards the inner channel from sites at 9.5, 7.5, and 5 Å).

Figure 3.

Water dipole moment distributions (top panel) for water coordinating with ion (solid line) and channel waters coordinating with gA backbone carbonyl groups. The numbers 15, 69, and 652 label channel waters starting at the channel opening and moving to the channel center. Bottom panel shows distributions for backbone carbonyl groups (residue TRP13) coordinating with channel waters (solid line) and restrained channel ion (dashed line).

Supplementary Material

1_si_001

SUPPORTING INFORMATION AVAILABLE Supporting information containing simulation protocol and information on force fields is given on the web.