Abstract
Group analysis of structure or function in cerebral cortex typically involves as a first step the alignment of the cortices. A surface based approach to this problem treats the cortex as a convoluted surface and coregisters across subjects so that cortical landmarks or features are aligned. This registration can be performed using curves representing sulcal fundi and gyral crowns to constrain the mapping. Alternatively, registration can be based on the alignment of curvature metrics computed over the entire cortical surface. The former approach typically involves some degree of user interaction in defining the sulcal and gyral landmarks while the latter methods can be completely automated. Here we introduce a cortical delineation protocol consisting of 26 consistent landmarks spanning the entire cortical surface. We then compare the performance of a landmark-based registration method that uses this protocol with that of two automatic methods implemented in the software packages FreeSurfer and BrainVoyager. We compare performance in terms of discrepancy maps between the different methods, the accuracy with which regions of interest are aligned, and the ability of the automated methods to correctly align standard cortical landmarks. Our results show similar performance for ROIs in the perisylvian region for the landmark based method and FreeSurfer. However, the discrepancy maps showed larger variability between methods in occipital and frontal cortex and also that automated methods often produce misalignment of standard cortical landmarks. Consequently, selection of the registration approach should consider the importance of accurate sulcal alignment for the specific task for which coregistration is being performed. When automatic methods are used, the users should ensure that sulci in regions of interest in their studies are adequately aligned before proceeding with subsequent analysis.
Keywords: Cortical Surface Registration, Landmark-based, Automatic, FreeSurfer, BrainVoyager, BrainSuite
1 Introduction
Registration of cortical anatomy is essential to a broad range of neuroimaging studies. The creation of probabilistic brain atlases, the analysis of differences in anatomical structure associated with neurological disease, and studies of genetic and epigenetic factors affecting cortical development and aging all require that the data first to be transformed to a common coordinate system in which anatomical structures are aligned. Similarly, both longitudinal and cross-sectional functional MRI studies require registration in order to pool brain activation data from multiple experimental units and identify experimental effects.
The majority of brain registration methods compute a volumetric alignment. These methods range in complexity from the piece-wise linear transformation of the Ta-lairach method (Talairach and Szikla, 1967) through lower dimensional polynomial warps (Woods et al., 1998) to very high dimensional transformations based on energy minimization using, for example, linear elastic and viscous fluids models (Johnson and Christensen, 2002; Shen and Davatzikos, 2003; Joshi et al., 2007). Since these methods do not explicitly constrain cortices to align, the maps typically exhibit poor correspondence between cortical features in the aligned volumes. Recently, there has been an increasing interest in analyzing the cerebral cortex based on alignment of surfaces rather than volumes. This is because functional and architectonic boundaries of the human cortex have been linked to the shape of sulci and gyri since the pioneering work of Brodmann (1909) and continuing in several more recent studies (Watson et al., 1993; Roland and Zilles, 1994; Fischl et al., 2008). In particular, there is evidence for a good relation between primary sulci and limits of cytoarchitectonic fields in primary cortices. Even though the relationship is more variable when it comes to secondary and tertiary sulci and association cortices, there is no better process currently available to align the macroscopic elements of the brain and, by proxy, expect an alignment of functional units. We note that recently developed methods are able to combine surface and volume alignment to compute a volumetric correspondence in which sulcal features are aligned (e.g. Joshi et al. (2007); Postelnicu et al. (2009)). However, here we will restrict our attention specifically to surface alignment.
Surface-based registration methods differ mainly in the features or similarity metrics that are used when aligning cortical surfaces. One general approach uses manually or automatically defined landmark contours to constrain the registration (Joshi and Miller, 1997; Thompson et al., 2000; Thompson and Toga, 2002; Joshi et al., 2007; Van Essen et al., 1998; Van Essen, 2004, 2005; Glaunes et al., 2004). The second approach allows automatic registration by optimizing the alignment of shape metrics, such as sulcal depth, cortical convexity, and conformal factor, computed over the entire cortical surface (Fischl et al., 1999b; Tosun et al., 2004; Wang et al., 2005; Goebel et al., 2006).
The main advantage of automatic methods is that they do not require user interaction or neuroanatomical expertise. They are therefore suitable for large-scale studies involving registration of hundreds of subjects. They also have the benefit of removing inter-rater variability and subjectivity on the part of the rater. However, this consistency does not guarantee that the correspondences are accurate and does not directly make use of expert knowledge of the location and variability of specific sulcal features as in landmark-based methods. Landmark-based methods are also more flexible, because registration features can be customized for the particular study. For example, registration of lesioned brains to a normal brain, a challenging task for any automatic method due to the lack of a one-to-one mapping between the brains at the lesioned cortex, can be achieved by constraining landmarks surrounding the lesion. Furthermore, it is reasonable to expect that manual landmark-based methods are more accurate, as they incorporate precise knowledge of sulcal anatomy when registering brains. Even the most consistent gyri and sulci appearing in all normal subjects exhibit pronounced variability in size and configuration, a fact already pointed out by Talairach and Szikla (1967) and reiterated more recently in Roland and Zilles (1994) and Damasio (2005). There are also anatomical features, for instance the sulcus of Jensen, double cingulate sulcus and supra-orbital sulcus, that are not always present, violating the one-to-one correspondence between a target and the brains to be aligned, and making registration a difficult task. Despite the widespread use of both approaches, no detailed comparison of their relative performance has yet been published.
Volumetric registration techniques have been far more widely evaluated than their surface-based counterparts (Zuk and Atkins, 1996; Strother et al., 1994; Hsu et al., 2002; Joshi et al., 2007; Shen and Davatzikos, 2003). Most analysis of surface registration methods has focused on demonstrating the advantages of surface-based against volumetric-based fMRI data analysis (Fischl et al., 1999b; Jo et al., 2007; Andrade et al., 2001; Anticevic et al., 2008; Desai et al., 2005). Ju et al. (2005) compared three cortical flattening methods, but the performance criteria were geometric distortion and computational speed, rather than registration accuracy. Desai et al. (2005) have demonstrated that landmark-based surface registration is superior to an automatic surface registration, but their work was limited to the auditory cortex. Given that five landmarks were used to constrain a small cortical region, the increased accuracy of the landmark-based method would be expected.
In this article we introduce a cortical delineation protocol comprising 26 well de-fined and consistent landmarks spanning the entire cortical surface. We demonstrate that despite the variable anatomy of the cortex these landmarks generally align well with a landmark-based registration method. We then evaluate the performance of two automatic surface registration methods, implemented in two popular software packages, FreeSurfer (Fischl et al., 1999a,b) and BrainVoyager (Goebel, 2000; Goebel et al., 2006). To the best of our knowledge, this is the first study that compares the registration accuracy on the entire cortex of automatic vs. landmark-based cortical methods.
Our studies used two groups with 12 subjects in each. The first was used for optimization of the new cortical delineation protocol. For each group, one brain was selected as a target to which the remaining 11 brains were coregistered. We then computed various performance metrics for both groups as reported below; results not included in the paper can be found in the supplemental online material. We begin by comparing how well both curvature and the individual sulcal curves are aligned for each of the three registration methods. We also compute discrepancy maps that quantify the pairwise differences between the three methods as a function of cortical location to identify those cortical regions in which the biggest differences should be expected. Finally we evaluate the absolute and relative accuracy with which each of the three methods is able to align cortical regions of interest as defined by an expert neuroanatomist.
2 Materials and methods
2.1 Sulcal Delineation Protocol
Landmark-based registration methods are only as accurate as the landmarks used to constrain the cortical alignment. An efficient set of landmarks should have a number of properties, the most important being consistency, i.e. landmarks should be typically present in normal brains, with similar configuration and extent for most of the subjects. They should also be easily identified, to reduce inter- and intra-tracer variability, and easily traced, so that delineating the landmarks is not exceedingly time-consuming. To achieve accurate registration everywhere in the cortex, a delineation protocol should include features throughout the cortical surface, so that most cortical areas are constrained by nearby landmarks.
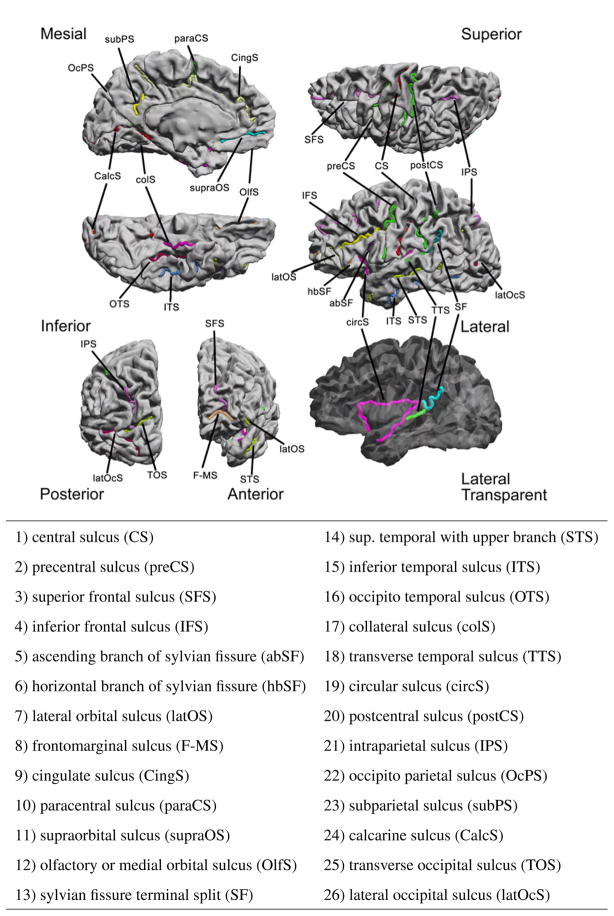
Cortical delineation protocols have been developed by investigators who typically use landmark-based registration. For example, the Laboratory of Neuro Imaging (LONI) at UCLA (http://www.loni.ucla.edu) has defined a set of 23 surface sulci and fissures for cortical registration, or a set of 25 landmarks, mostly gyri, for the creation of a probabilistic brain atlas. These protocols have been developed for surfaces that represent the cerebral hull, i.e. a mostly convex segmentation boundary that runs along gyral margins only slightly dipping into sulci. However, this is not suitable for our purposes, because we use surfaces that follow the cortical surface from gyral crowns into the sulcal fundi. Our protocol assumes a surface corresponding to the midcortex, midway between the pial surface and the gray - white interface. As a result the sylvian fissure is handled as a virtual space whose depth is in fact the circular sulcus which is traced, as is the transverse temporal sulcus, also buried in the virtual space of the sylvian fissure. Van Essen (2005) used a 6-curve protocol, comprising the central sulcus, sylvian fissure (traced along the superior branch of the circular gyrus), anterior half of the superior temporal gyrus, calcarine sulcus, pericallosal sulcus, and the ventral boundary of the corpus callosum, to register the entire cortex and create a human brain atlas. We have defined a protocol that uses many more sulci as curves, to ensure that as many areas as possible will be constrained by nearby sulcal boundaries.
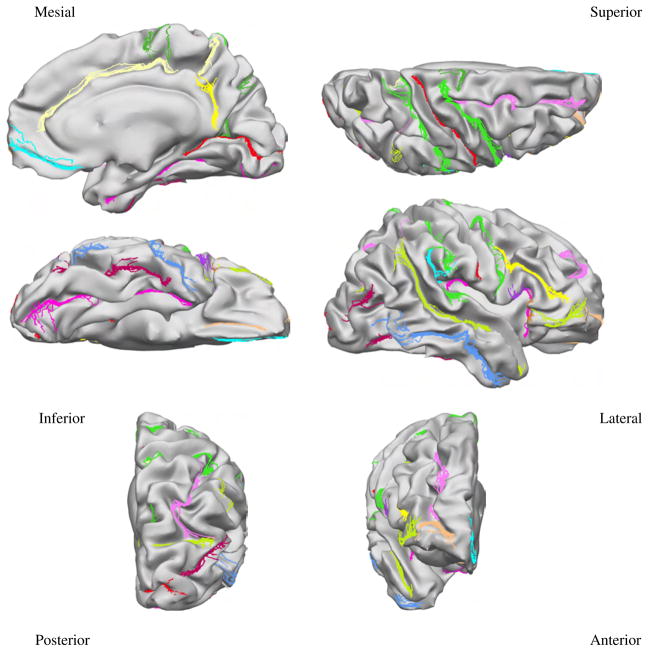
Our protocol uses the 26 sulcal curves listed in Fig. 1. The sulci are consistently seen in normal brains, and are distributed throughout the entire cortical surface. A thorough description of the sulcal curves with instructions on how to trace them is available on our website (http://neuroimage.usc.edu/CurveProtocol.html). Recommended sources of further information for sulcal and gyral identification are Damasio (2005), Duvernoy (1999), and Ono et al. (1990).
Fig. 1.
The set of 26 sulcal curves used for landmark-based cortical registration.
We trace the curves on the midcortical surface because it provides better access to the depth of the sulci than the pial surface, and the valleys of the sulci are more convex than the white-matter surface allowing more stable tracing of the curves. Curves are traced using the software BrainSuite (Shattuck and Leahy, 2002), available at http://brainsuite.usc.edu, which allows visualization of white-matter, midcortex or pial surfaces to assist identification of cortical anatomy. For deep cortical structures, such as the insula, locations can be selected from three orthogonal sections through the MRI volume, which are then directly transferred to the nearest surface points. Sulci are traced by selecting a few points on the cortical surface that are then automatically connected with the minimum distance path on the surface using Dijkstra’s algorithm (Dijkstra, 1959), a graph search algorithm that solves the shortest path problem for a graph with nonnegative edge. Path distance is weighted based on the cortex curvature to ensure that the curves follow the sulcal valleys. When sulci are interrupted by gyri, the weight can be interactively modified to allow the curve to cross the gyrus to complete the sulcal curve (Shattuck et al., 2009). If some of the sulci are missing or cannot be identified, they do not need to be traced, in which case the remaining landmarks will constrain the registration. When we encounter a double sulcus, as is often the case with the cingulate sulcus, we select the most external segment. Rules used for tracings can be found in the aforementioned website.
2.2 Participants
The study involved two groups of subjects: Group 1 was used to develop a curve delineation protocol for the landmark-based method. Group 1 and Group 2 were used to evaluate the cortical registration performance of landmark-based and automatic methods.
The structural scans of Group 1 were obtained as part of a functional imaging study (Bernstein et al., in revision) independently from the present study, and comprised 12 subjects (6 male, 6 female) with mean age 26 years and range 22 to 28 years. They were all right-handed (score of +70 or more on the Edinburgh handedness inventory). Informed consent was obtained from all participants, and the experiment was approved by the Institutional Review Board at the University of Southern California. Group 2 also consisted of 12 right handed subjects, age and gender matched to Group 1 (6 male, 6 female; mean age 24.9; range 22 to 28) all right handed (Oldfield-Geschwind score of +85 or more). Group 2 was retrieved from the subject registry of the Division of Cognitive Neuroscience, Department of Neurology, University of Iowa, and was part of previous studies in comparative normal neuroanatomy (Allen et al., 2002). All participants had given informed consent in accordance with Institutional and Federal guidelines.
2.3 Image Acquisition
Group 1 was scanned at the Dornsife Cognitive Neuroscience Imaging Center at the University of Southern California using a 3T Siemens MAGNETOM Trio scanner. High-resolution T1-weighted anatomical volumes were acquired for each subject with an MPRAGE scan using the following protocol: TR = 2350 ms, TE = 4.13 ms, 192 slices, field-of-view = 256 mm, voxel size = 1.0 × 1.0 × 1.0 mm.
Group 2 was scanned at the University of Iowa using thin-cut MR coronal images obtained in a General Electric Signa Scanner operating at 1.5 Tesla, using the following protocol: SPGR/50, TR 24, TE 7, NEX 1 Matrix 256 × 192, FOV 24 cm, which yielded 124 contiguous coronal slices, 1.5 or 1.6 mm thick, with an interpixel distance of 0.94 mm. Three data sets were obtained for each subject. These were co-registered and averaged post-hoc using Automated Image Registration (AIR 3.03, Woods et al. (1998)). The final data for each subject had anisotropic voxels with an interpixel spacing of 0.7 mm and interslice spacing of 1.5–1.6 mm.
Using different imaging protocols for the two groups allows us to demonstrate the generalizability of our analysis. Surface registration results should not depend on the imaging protocol as long as cortical surface extraction algorithms work well, and this is indeed the case as we show later.
2.4 Cortical Surface Registration
For automatic cortical registration we used the programs FreeSurfer (version 4.0.1) (Fischl et al., 1999a,b) and BrainVoyager (version 1.9.10) (Goebel, 2000; Goebel et al., 2006). For landmark-based registration we used the method described in Joshi et al. (2007). One target for each group was selected among the 12 brains in that group, with the criterion that all 26 sulci in the protocol could be identified and traced. All subjects were then registered to the target of the same group. Since Group 1 was used to develop the 26-curve cortical delineation protocol, we used Group 2 to repeat all analysis and verify we do not introduce any bias favoring the landmark-based method when reporting registration results.
The technical approach taken in each of the three registration methods can be summarized as follows. In both FreeSurfer and BrainVoyager each folded cortex is first mapped to a sphere, which provides a parameterization for the subsequent cortical alignment. Registration of an individual brain to a target or atlas is then computed with respect to this intermediate spherical representation. In FreeSurfer, the alignment of the cortical surface is carried out by minimizing the mean squared difference between the average convexity (Fischl et al., 1999a) across a set of subjects (the cortical atlas) and that of the individual subject. The squared error is weighted by the variance of the convexity across subjects at each location and integrated over the entire cortex (Fischl et al., 1999b). The use of the variance of the convexity in FreeSurfer allows consistent folding patterns such as the central sulcus, the sylvian fissure etc., to have a greater effect on the alignment than more variable patterns. In BrainVoyager, the curvature information is computed in the folded representation and is preserved as a curvature map on the spherical representation. The curvature is then smoothed with respect to the surface to provide spatially extended gradient information that drives intercortex alignment by minimizing the mean squared differences between the curvature of a source and a target sphere using a coarse to fine strategy (Goebel et al., 2006). Negative and positive values of curvature indicate gyral and sulcal regions, respectively. In our manual landmark based registration method (Joshi et al., 2007), sulcal landmarks are traced on the subject and target brains and then a parameterization for the two surfaces is generated so that the sulcal landmarks are aligned. The parameterization maps each cortical hemisphere to a unit square. The mapping is computed by modeling the cortical surface as an elastic sheet and solving Cauchy-Navier’s linear elastic equilibrium equation using the Finite Element Method (FEM) to minimize the elastic energy of the mapping. The elastic energy is minimized subject to the constraint that the corpus callosum separating the two brain hemispheres is mapped to the boundary of the unit square. A quadratic mismatch penalty was added for the corresponding sulcal landmarks in the subject and atlas so that they align in the two simultaneously computed flat maps.
We used the same cortical surface representations for all registration methods to facilitate comparison of the registration results. For this purpose we used FreeSurfer to extract the midcortical surface. We acknowledge that this may favor the program used for surface extraction when comparing registration methods. For the subjects in Group 1 we also extracted surfaces with BrainVoyager. In this case, BrainVoyager produced similar registration results to the ones described in this study. We decided to use only FreeSurfer surfaces for the comparison because they provided a more accurate representation of the outer gray-matter boundary than the Brain-Voyager surfaces and also because FreeSurfer surfaces can subsequently be coregistered using BrainVoyager while the reverse is more difficult to do.
Preprocessing included transforming the MRIs of the 12 subjects of Groups 1 and 2 into the Talairach coordinate system, as required by the BrainVoyager automatic registration procedure for optimal results. This transformation, an affine registration aligning the anterior and posterior commissures and forcing each brain in the same bounding box, was performed in BrainVoyager. Cortical surfaces were then extracted with the FreeSurfer software using default parameters, which also automatically produced cortical registration maps of each subject to an average FreeSurfer template. This is the optimal registration procedure for FreeSurfer, because it is modulated by the variance of the convexity across subjects comprising the atlas, allowing consistent folding patterns such as the central sulcus, the sylvian fissure, etc., to have a greater effect on the alignment than more variable patterns (Fischl et al., 1999b).
To evaluate the registration accuracy of BrainVoyager with an identical dataset, the same FreeSurfer surfaces were imported into BrainVoyager and registered to the target of each group using the default program parameters. We used the midcortical surface, an average of the white-matter and pial surface, for registration. We found that BrainVoyager is very sensitive to initialization of the registration procedure; whenever the initial overlap of the curvature maps was poor, the algorithm diverged, for example mapping the superior temporal sulcus of one subject into the insula of a different subject. For this reason, we manually rotated the cortical spheres whenever necessary, to provide a better initialization, which usually resolved the problem. It is important to note that the BrainVoyager results presented below are all based on this limited degree of user interaction. Also, even though BrainVoyager also offers the option to register all subjects to the group average, our registration results were worse than individually registering each subject to a target, therefore we followed the latter approach.
To compare the FreeSurfer and BrainVoyager registrations directly, we converted the FreeSurfer registration maps from the average FreeSurfer template to the target subject from each group. This conversion is straightforward, because the FreeSurfer spherical atlas naturally forms a coordinate system in which point-to-point correspondence between subjects can be achieved.
Even though preprocessing the MRIs with a Talairach transformation is nonstandard procedure for FreeSurfer, we did this because we wanted to use the extracted cortical surfaces for BrainVoyager registration. Even though it can be considered a confound for our analysis, we believe it did not negatively impact our registration results with FreeSurfer, because 1) the first step of FreeSurfer analysis is to convert the volumes into Talairach space, which is exactly what we did, and 2) the extracted surfaces were very accurate representations of the cortex, indicating that FreeSurfer did not have any interpolation problems resulting from our resampling of the volumes into the Talairach space.
For the manual landmark-based registration, we used the sulci delineation protocol described above. We traced the set of 26 cortical landmarks in BrainSuite (Shattuck and Leahy, 2002). All curves were checked and corrected whenever necessary by one of the authors (HD), an expert neuroanatomist. We then used the manual registration procedure described in Joshi et al. (2007), with the default parameters μ = 100 and λ= 1 defining the linear elastic equilibrium equation, to map all surfaces to the target cortical surface.
2.5 Comparison of Registration Methods
Here we summarize the methods that were used to compare the three surface registration methods. As a first step we compared the alignment of curvature maps and sulcal curves at the individual and group level. Curvature maps measure the amount of cortical folding by assigning positive values at gyral crowns and negative values at sulcal fundi. In this paper, we calculated curvature maps using an approximation of mean curvature, which we refer to as the convexity measure, as described in Shattuck et al. (2009). We expect automatic methods to better align curvature because they primarily optimize the match of cortical folding patterns, and the landmark-based method to better align the sulcal protocol curves because they directly constrain them during registration. We quantified the effects of coregistration on curvature by computing the curvature maps as a function of cortical location averaged over all 11 subjects that were registered to the template for each group. We also computed and compared the curvature histograms, again averaged over the group, before and after coregistration.
To compare the alignment of curves, we mapped the 26 protocol curves from all subjects to the target surface. We then quantified their clustering using their variance on the target surface, which is estimated as follows. We use a distance measure based on the Hausdorff distance (Dubuisson and Jain, 1994):
| (1) |
where d(Di, Dj) is the distance between curves Di and Dj, each discretized by a number of points Ni and Nj on the cortical surface, respectively. The first term in the above equation is the average minimum distance of each point in curve Di to a point in curve Dj, and the second term is the average minimum distance of each point in Dj to a point in Di. Using the above distance metric, we calculate the variance of a population of K curves as:
| (2) |
Since registration produces a one-to-one correspondence between cortical surfaces, we can use the Talairach-based x, y, and z coordinates of each cortical location to identify where registration methods differ the most. A given cortical location on the target surface is mapped to different cortical locations on the subject surface, depending on which registration method is used. For example, the landmark-based method and FreeSurfer may map two different cortical locations of a subject to the same point on the target surface. In such a case, an indication of the registration difference between the two methods is given by the Euclidean distance between the two subject locations mapped to the same point on the target. By repeating this procedure over all target locations, we obtain a discrepancy map between two registration methods. To get reliable results and make group inferences, we average these maps over all 11 subjects of the same group (since each group has 12 subjects and one is used as the target).
While geodesic rather than Euclidean distances are a more appropriate metric for measuring distances on the cortical surface, it is computationally infeasible to compute the former for all cortical locations, subjects, and pairs of registration methods considered here. However, we would not expect a significant qualitative change in the disparity maps between the two metrics since the distances are relatively short and the same metrics were used for each of the pair-wise comparisons.
Cortical registration methods typically have penalty functions that trade off goodness of fit of the sulci vs. smoothness of the transformation. Despite the latter term, cortices are considerably distorted during alignment, because they are highly convoluted surfaces with variable sulcal and gyral patterns. We measured the local area distortion everywhere in the cortex resulting from coregistration to the template for each of the 3 registration methods. In particular, since a cortical surface is represented by multiple connected triangles, we measured how much the area of each surface triangle increased or decreased during registration. Normalized area distortion at a cortical location is defined as the area of the corresponding triangle on the target surface, divided by the area of the subject surface mapped into the same triangle.
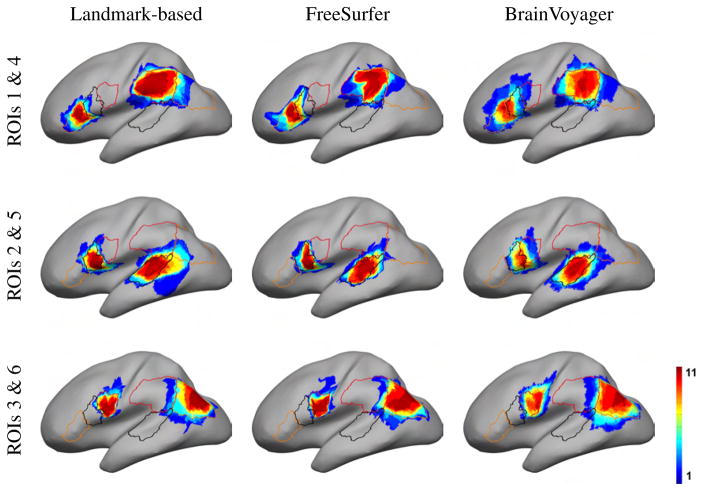
To better investigate the performance of the registration methods in terms of aligning anatomy, an expert neuroanatomist (coauthor HD) traced 6 Regions Of Interest (ROIs) on the left hemisphere of the 12 brains of Group 2 (right of Fig. 12); ROI 1: pars triangularis (anterior region of Broca’s area); ROI 2: pars opercularis (posterior region of Broca’s area; ROI 3: lower portion of the precentral gyrus (face and mouth area); ROI 4: supra marginal gyrus; ROI 5: posterior sector, behind the transverse temporal gyrus, of the middle temporal gyrus (classically Wernicke’s area); ROI 6: angular gyrus. The selection of these regions reflected areas of interest for an fMRI study exploring language related cortical areas in the Group 1 subjects (Bernstein et al., in revision).
Fig. 12.
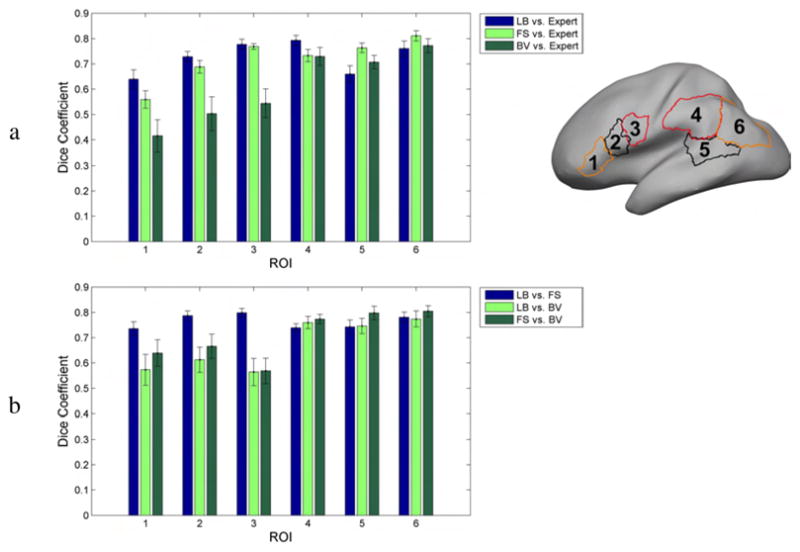
Average Dice coefficients for 6 cortical ROIs: (a) between mapped ROIs for each registration method and the neuroanatomist delineation on the target surface (b) between mapped ROIs for different pairs of registration methods. The bars indicate 1 standard error from the mean.
To evaluate accuracy, we computed the Dice coefficients between the target ROIs and the subject ROIs mapped to the target. The Dice coefficient measures overlap between two sets representing ROIs S1 and S2, and is defined as (2|S1∩S2|)/(|S1|+|S2|) where |.| denotes area of the ROI (Zijdenbos et al., 1994). Below we show the Dice coefficients between the registered ROIs and the expert defined ROIs on the target. We also perform pairwise comparisons between the three registration methods. Statistical significance of the observed differences was assessed using pairwise t-tests.
3 Results
All 26 curves were identified and traced for most of the subjects, with a few exceptions. Right hemisphere of Group 1: latOcS was not traced for one subject; Left hemisphere of Group 1: TOS was not traced for one subject and F-MS and latOcS for two subjects; Right hemisphere of Group 2: latOcS was not traced for one subject; Left hemisphere of Group 2: latOS, OTS, and latOcS were not traced for one subject each. No subject had more than one missing curve in either hemisphere. We registered both groups of 12 subjects with the FreeSurfer and BrainVoyager automatic methods, and the landmark-based method, using one subject selected from the same group as the target, with the criterion that no sulci were missing from the target and therefore all of the 26 protocol curves could be identified.
3.1 Curvature
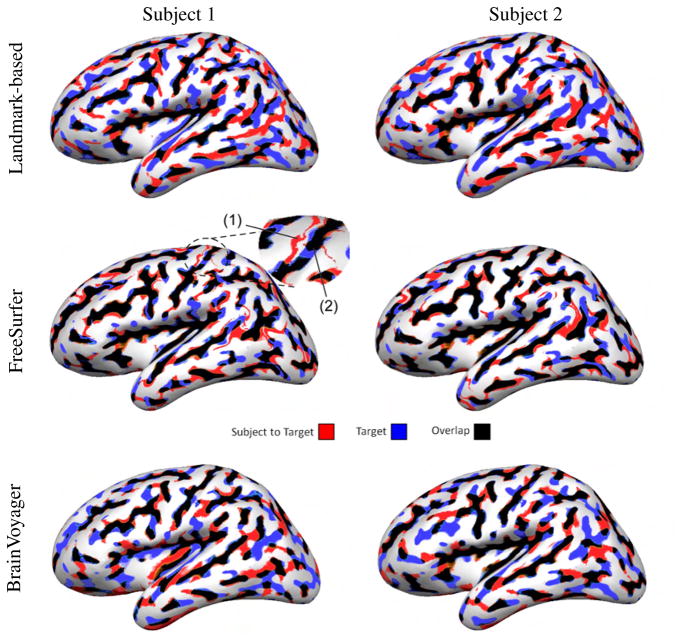
Fig. 2 shows how well curvature maps overlap after registration of two subjects from Group 1 to the target brain with the three methods. We selected Subject 2 and Subject 1 as examples respectively of more and less successful FreeSurfer registration. Curvature maps are plotted on the smoothed target anatomy, where the blue and red colors represent respectively the sulci of the target and the sulci of the subject mapped to the target. The black color represents regions of overlap of the two maps. Ideally, a perfect registration of curvature for two compatible anatomies should contain only black areas, since blue and red represent areas where sulci are mapped to gyri or vice versa.
Fig. 2.
Registration of the left hemisphere of two different subjects from Group 1 to the target brain. Curvature overlap between the subject and the target is color coded. The enlarged area indicates misregistration of the central sulcus, which happened once with FreeSurfer: (1) the subject’s central sulcus (thin red line) was mapped to the precentral gyrus of the target (white area); (2) the subject’s postcentral sulcus was mapped to the central sulcus of the target (thick black line) resulting in a mismatch between the precentral and postcentral sulci.
As can be seen in Fig. 2, FreeSurfer produces a stronger overlap of the curvature maps than the landmark-based and BrainVoyager methods. Cortical areas where there is a mismatch in curvature are compressed, as illustrated by the thin red lines in the second row of Fig. 2. In these areas, sulci of the subject are mapped to very small gyral cortical areas in the target. Subject 1 was the only case out of all 24 subjects of both groups where FreeSurfer misaligned the central sulcus; we verified that the thin red line, indicating the subject’s central sulcus, was mapped to the precentral gyrus of the target (enlarged area in Fig. 2). FreeSurfer alignment was much better for Subject 2. Since the landmark-based method does not rely on curvature for registration, we did not expect it to align curvature as well as FreeSurfer.
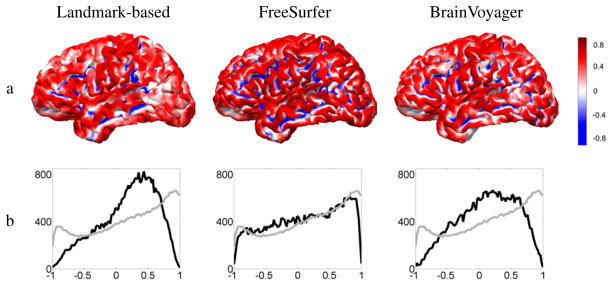
To quantify effects of registration on curvature we computed the average curvature map as a function of cortical location across all 11 coregistered surfaces as shown in Fig. 3a. To illustrate the effect of averaging, we represent cortical folds with continuous curvature maps ranging from +1 for a gyrus to −1 for a sulcus. After averaging curvature maps, large values represent areas for which gyri consistently map together (0.8 for 80 percent of the subjects). The same holds true for small values and sulci. Areas for which gyri are mapped to sulci, or the original cortical surfaces are locally flat (for example sulcal banks) have average curvature close to zero and are represented in white.
Fig. 3.
a: Average curvature of Group 1 cortical surfaces on the target brain; b: Histogram of the average curvature after registration (black), and average of the curvature histograms before registration (gray). In other words, black denotes the histogram of the curvature map displayed in row (a), and gray the typical curvature histogram a cortical surface has before registration.
The landmark-based and BrainVoyager methods have more white areas than FreeSurfer, even in locations where there are gyral crowns or sulcal fundi on the target anatomy. This is also indicated in Fig. 3b, where the average histogram of the curvature of the 12 subjects is shown before and after registration. To compute the curvature histogram of a typical brain, we averaged the curvature histograms of the 12 brains of Group 1 (shown in gray). After registration, curvature maps were aligned and averaged to compute the average curvature map, whose histogram is shown in black. The landmark-based method and BrainVoyager distort the histograms by shifting them close to zero, whereas FreeSurfer preserves the histogram reasonably well.
3.2 Curves
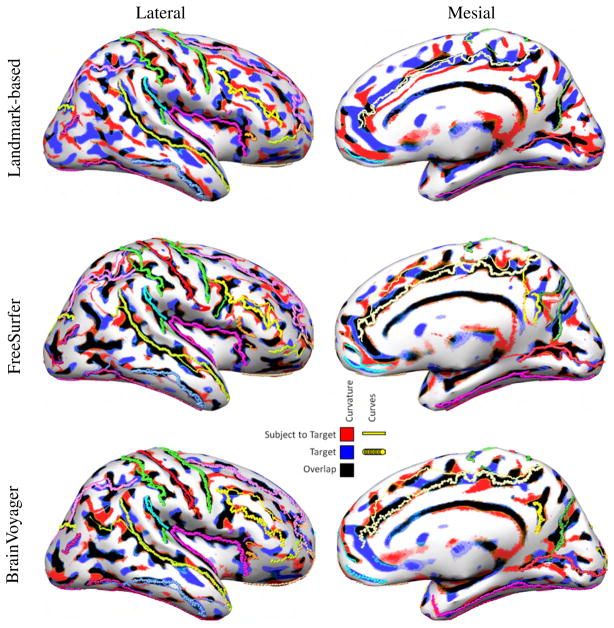
Automatic methods are expected to do better in curvature alignment than landmark-based methods because their cost function has terms that explicitly minimize discrepancies in folding patterns. However, in cortical registration it is important to map corresponding sulci and gyri to each other rather than simply ensuring that regions of positive and negative curvature are aligned. To illustrate this issue, we show in Fig. 4 not only the curvature overlap between Subject 1 of Group 1 (the same subject as in the left column of Fig. 2) and the target, but also the 26 sulcal curves for the target and Subject 1 mapped to the target. Thick lines represent the target sulci, and thin lines the subject sulci mapped to the target.
Fig. 4.
Alignment of curvature and sulcal curves after registration of the right hemisphere of Subject 1 (Fig. 2) to the target. The subject was selected to demonstrate a case of misregistration of sulcal curves with automatic methods, even when curvature aligns well.
Since the landmark-based method constrains specific sulci to match each other, it is not surprising that they align in most cases. There are a few cases, though, where the curves do not align perfectly, such as the ascending branch of the superior temporal sulcus or the paracentral sulcus (first row of Fig. 4). The landmark-based method uses a penalty function that trades off goodness of fit of the sulci vs. smoothness of the transformation, and in some cortical areas the later term dominated the registration leading to a misalignment of the corresponding curves. Automatic methods are not as successful in aligning the curves (second and third row of Fig. 4). For example, the inferior frontal sulcus is very poorly aligned both with FreeSurfer and BrainVoyager, and the same is true for the ascending branch of the superior temporal sulcus, the cingulate sulcus, and the parieto-occipital sulcus. There are also unexpected results, as for instance the behavior of the intraparietal sulcus and inferior frontal sulcus in FreeSurfer suddenly making large jumps, only to continue in the correct path later on, or the case of misregistration of the central sulcus in FreeSurfer. We note that the subject in Fig. 4 was selected to demonstrate cases when automatic methods fail to properly align curves despite apparently good curvature overlap. The performance of FreeSurfer for Subject 1 was the worst among the 22 registrations performed over the two groups and should not be taken as reflecting typical performance, which we now investigate in more detail by looking at the mapping of sulci for all 11 subjects in Group 1 (the equivalent results for Group 2 are shown in the supplemental material and are qualitatively very similar to those shown here).
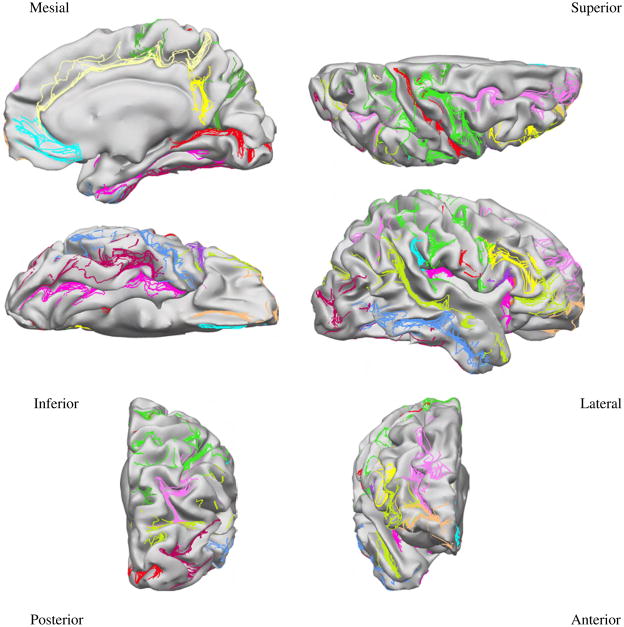
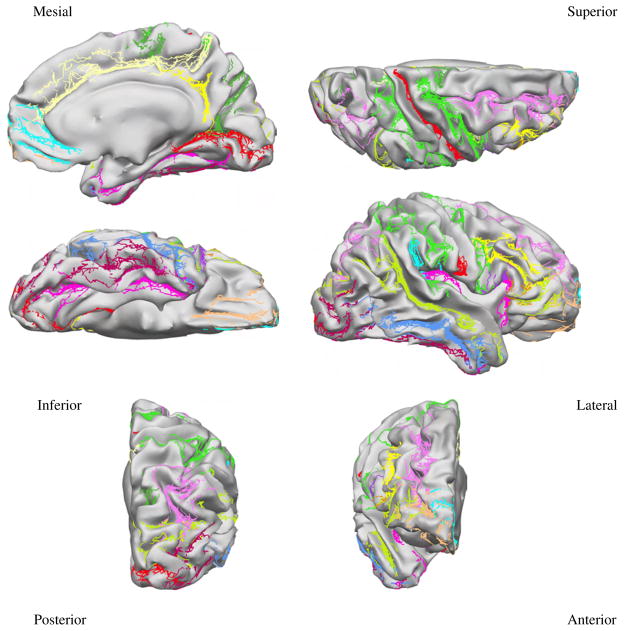
Mapping the 26 protocol curves from all subjects to the target surface provides an indication on how accurately each method registers anatomy. Figures 5, 6, and 7 show the curves from all subjects of Group 1 mapped to the target surface using each of the 3 registration methods, and Fig. 8 displays their variance. As expected, the manual landmark-based method produces substantially closer alignment of the curves than the automatic methods (FreeSurfer and BrainVoyager). Even so, the manual landmark-based method does not completely align all curves; the paracentral sulcus, the ascending branch of sylvian fissure, and the posterior sector of the collateral sulcus among others, are not perfectly aligned. On the other hand, the automatic methods show poorer registration of the traced curves in most cortical regions.
Fig. 5.
Protocol curves for Group 1 surfaces mapped onto the target surface using landmark-based registration. The target surface is displayed with less smoothing than the previous figures, to demonstrate the clustering of the curves in relation to the shape of the cortex.
Fig. 6.
Protocol curves for Group 1 surfaces mapped onto the target surface using FreeSurfer registration.
Fig. 7.
Protocol curves for Group 1 surfaces mapped onto the target surface using Brain-Voyager registration.
Fig. 8.
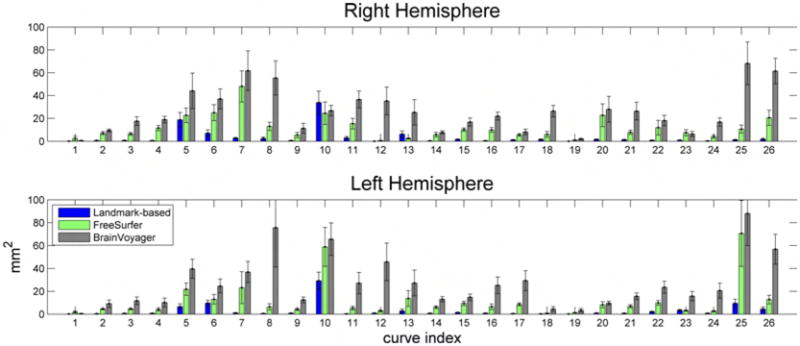
Variance of protocol curves of Group 1 after being mapped onto the target surface using the 3 registration methods. Figs. 5, 6, and 7 display the curves for the right hemisphere. Curves are numbered based on Fig. 1. The error bars indicate 1 standard error from the mean, and are calculated by bootstrapping the original curves 100 times.
3.3 Discrepancies
Average registration discrepancy maps for Group 1 are plotted in Fig. 9 and indicate in units of mm the pairwise differences between the three registration methods. Distances are computed as the root mean square distance in Talairach space between corresponding cortical locations in subject and target. Averaging is performed over the 11 subjects to target mappings in Group 1 (similar results for Group 2 can be found in the supplemental material). Fig. 9 shows that the main differences between any of the three possible pairs of methods are in the lateral and mesial occipital cortex, the posterior and inferior temporal lobe, and the lateral and mesial frontal lobe, all areas with quite variable sulci.
Fig. 9.
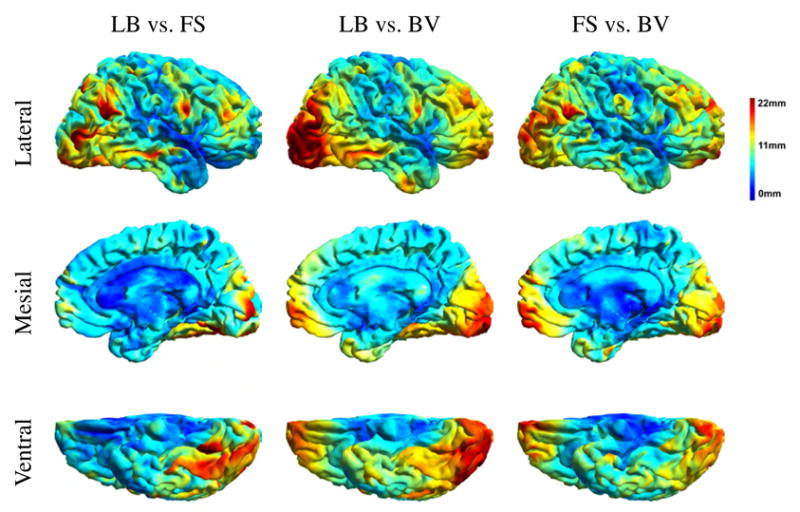
Color-coded cortical maps indicating averaged pairwise root mean square Euclidean distance in mm between registration methods averaged over the 11 subjects in Group 1. Distances are computed with respect to the Talairach coordinates. LB: landmark-based, FS: FreeSurfer, BV: BrainVoyager. The results were obtained for the subjects of Group 1.
3.4 Distortion
As described in Section 2.5 we computed the area distortion for each registration method. Fig. 10 shows the cumulative distribution function (CDF) of the normalized area distortion for all triangles comprising the tessellated surfaces of all 11 subjects in Group 1. The value of the CDF at 0.25 represents the percentage of triangles that become at least 4 times smaller after registration. Similarly, 1 - CDF at 4 represents the percentage of triangles that become at least 4 times larger after registration. The landmark-based method resulted in 4.4% of triangles becoming at least 4 times smaller, as compared to 6.6% for FreeSurfer and 8.5% for Brain-Voyager. For triangles becoming at least 4 times larger, BrainVoyager resulted in 4.2%, as compared to 5.9% for the landmark-based and 6.5% for FreeSurfer. These results are very similar between methods, indicating that all registration methods cause comparable distortions when aligning cortical surfaces.
Fig. 10.
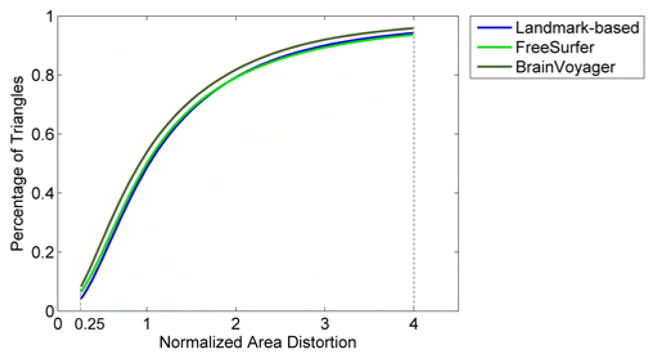
Cumulative distribution function (CDF) of the normalized area distortion of triangles forming the tessellated cortical surface after registration with the 3 methods. Results are averaged over all brains comprising Group 1. Normalized area distortion at a cortical location is defined as the area of the corresponding triangle on the target surface, divided by the area of the subject surface mapped into the same triangle. The value of the CDF at 0.25 represents the percentage of triangles that become at least 4 times smaller after registration. Similarly, 1 - CDF at 4 represents the percentage of triangles that become at least 4 times larger after registration.
We repeated the analysis of curvature and curve alignment as well as discrepancy maps and triangle distortion on Group 2 with similar results: landmark-based method achieved better curve registration, and automatic methods better curvature alignment. The analysis is available as supplementary material on the journal’s website.
3.5 Regions of Interest
Finally, we applied the ROI analysis described in Section 2.5 to the Group 2 subjects (Fig. 11). Fig. 12a shows that the landmark-based method has the highest Dice coefficients in ROIs 1–4, and FreeSurfer in ROIs 5–6. A pairwise t-test showed that all Dice coefficient differences in Fig. 12a were significant at a 0.05 level (uncorrected), apart from ROI 3 between Landmark-based and FreeSurfer, ROIs 4,5 and 6 between Landmark-based and BrainVoyager, and ROIs 4 and 6 between FreeSurfer and BrainVoyager. When considering data from all ROIs, the landmark-based method, FreeSurfer, and BrainVoyager had mean Dice coefficients 0.7265, 0.7209 and 0.6121 respectively. An overall pairwise t-test with data from all ROIs showed significant difference between Landmark-based and BrainVoyager (p = 2 · 10−6), FreeSurfer and BrainVoyager (p = 10−7), but there was no significant difference between Landmark-based and FreeSurfer (p = 0.64).
Fig. 11.
ROIs of the 12 subjects of Group 2 mapped on the target surface. The color indicates the number of subjects whose ROI registers to each cortical location. Also shown are the outlines of each cortical region as originally drawn on the template by our neuroanatomist.
We also used the above ROIs to examine registration differences between the 3 methods in the corresponding cortical regions. Instead of computing Dice coefficients between the target and the mapped ROIs as in Fig. 12a (and effectively comparing a human expert delineation with an automated registration method), we computed Dice coefficients between the mapped ROIs of pairs of different registration methods given in Fig. 12b (and thus measuring the overlap of two registration methods in mapping the same ROI to the target). In the frontal ROIs 1–3, the Landmark-based method and FreeSurfer overlap much more than either does with BrainVoyager. In the posterior ROIs 4–6, all methods overlap similarly with each other, with Dice coefficients around 0.7–0.8. When considering all ROIs simultaneously, the Dice coefficients between pairs of methods were: Landmark-based vs. FreeSurfer: 0.76, Landmark-based vs. BrainVoyager: 0.67, and FreeSurfer vs. BrainVoyager: 0.71. This indicates that registration methods differ considerably from each other, with Dice coefficients much smaller than 1.
4 Discussion
Landmark-based methods register anatomy by constraining a set of curves on the cortex, whereas automatic methods align continuously varying shape metrics, such as sulcal depth, cortical convexity and others. We have demonstrated that each method performs best in its own similarity metric, i.e. our landmark-based method achieved better alignment of the traced contours, even if it was not as accurate in matching curvature, with the opposite being true for FreeSurfer and BrainVoyager. However, as we mentioned in the Introduction, there is evidence for a good relationship between primary sulci and the boundaries of cytoarchitectonic fields in primary cortices. Even though the relationship is more variable when it comes to secondary and tertiary sulci and association cortices (Watson et al., 1993; Roland and Zilles, 1994; Fischl et al., 2008), there is no better process currently available to align the macroscopic elements of the brain. Therefore, the fact that curvature is aligned at the expense of misaligned sulci seems to point to a problem with curvature-driven automatic alignment methods: corresponding cortical areas that are bounded by standard sulcal curves will not be aligned in those cases where the curvature matching constraint results in the misalignment of sulci.
None of the methods perfectly optimized its similarity metric. The landmark-based method achieved an efficient clustering of the traced curves (Fig. 5), but not a perfect match. Mathematically, the reason is that the smoothness term in the optimization function balances the goodness-of-fit term and prevents severe distortions that would fully align all sulci. Anatomically, the reason resides with the fact that brains have, generally, very different cortical folding patterns, sometimes as extreme as to require unacceptable cortical foldings in order to achieve perfect sulcal alignment. In such cases, the landmark-based method has the following desirable behavior: aligning anatomy to the best possible extent while preserving the normal geometry of the cortex.
In the same way that the landmark-based method did not align the curves perfectly, automatic methods did not align curvature perfectly. However, FreeSurfer produced substantial better alignment than BrainVoyager (Fig. 3). Anatomical variabilities, such as the absence of sulci or their interruption by gyri, prevent an accurate match of curvature, unless large spatial distortions are allowed. The intraparietal and inferior frontal sulcus jumps in FreeSurfer registration in Fig. 4 represent such a case.
All methods produce different registration results, with disagreements reaching as much as 2.2cm (Fig. 9). These differences have been primarily observed in the occipital, frontal, and posterior temporal lobes. These are regions where cortical anatomy shows marked variability in folding patterns.
We have identified several reasons why landmark-based methods and automatic methods disagree. There are cases where automatic methods incorrectly align sulci. This is the case, even with the very reliable and consistent central sulcus, which is mapped onto the precentral sulcus in the FreeSurfer registration in Fig. 4. Many more instances of incorrectly mapped sulci are shown in Figures 6 and 7. We do not expect gross errors, such as mislabeling of the central sulcus, for curves traced by a user trained in neuroanatomy. However, there are cases where it is difficult to create a continuous curve for a particular sulcus, allowing for differences in the final sulcal curve which will result in differences in registration. For example, the superior frontal sulcus is often interrupted into several segments allowing for multiple possible paths to be chosen during manual delineation, in which a single continuous curve has to be produced. There are also cases where a particular sulcus is simply absent, in which case it cannot be used to constrain alignment. In cases where it is difficult to trace a single continuous sulcal curve, automated curvature registration removes the subjectivity that arises when tracing by hand. However, this does not imply that the resulting registrations are correct. The fact that many standard sulci are misaligned in cases where there is no ambiguity in their location (Figs 6 and 7) means that one should be particularly cautious when assessing the reliability of cortical alignment in areas where sulci are more variable.
The ROI analysis in Fig. 12a showed that the Dice coefficient measure of the overlap between the mapped ROIs and the manually delineated ROIs on the target surface was around 0.6–0.8. The limited overlap between the ROIs has to be attributed not only to registration errors, but also to subjective factors affecting selection of the ROIs for different subjects in the human tracings. The Dice coefficients where higher for the landmark-based registration in ROIs 1–4 and for FreeSurfer in ROIs 5 and 6. The anterior and posterior border of ROI 5 is not limited by specific sulci. Similarly, the posterior limit of ROI 6 was not constrained by nearby curves, and the anterior limit was variable depending on whether the sulcus of Jensen was present or not. It is noteworthy that taken as a whole, there was no significant difference in performance between FreeSurfer and the landmark-based method.
The language related ROIs we selected happened to be in the perisylvian region, the sector where registration differences among the three methods were overall smaller than the rest of the brain, as shown in Fig. 9. Therefore, our results of ROI registration may be better than they would be in most other locations where the methods differ more.
Overall, landmark-based and FreeSurfer registration results agreed more than either with BrainVoyager. This is supported in Fig. 9 where registration differences of the other methods with BrainVoyager were the highest, and Fig. 12b where Dice coefficients for ROIs 1–3 were much larger for landmark-based vs. FreeSurfer comparisons.
All methods caused similar local area distortions when aligning brains, even though they use different regularizing terms. In particular, regularizing (elastic energy) was computed in the folded surface geometry in the landmark-based method. On the other hand, FreeSurfer and BrainVoyager compute their regularizing energies (changes in edge length and areas) in the spherical geometry, but again they minimize metric distortion relative to the original folded surface.
Identification of cortical landmarks presupposes anatomical expertise. A common problem concerning all landmark-based techniques is error and human variability in the identification of the landmarks. Such variability can obviously affect the registration efficacy. Here, all curves were carefully identified and cross-checked by an expert neuroanatomist. In a separate study (Shattuck et al., 2009), we have demonstrated that assisted tracing of sulci using Dikstra’s algorithm within BrainSuite helps reduce inter-rater variability and improve delineation accuracy of sulci. However, neuroanatomical knowledge is considerably more important than the software used to delineate the curves. The large number of sulci identifications needed in the method described here can be seen as a potential problem. We recently described an approach for selection of an optimal subset of the 26 sulci used in the current study, in order to reduce the time required by the rater to identify sulci (Joshi et al., 2009).
It is necessary to have all 26 sulci present in the target brain in order to use all the curves as constraints in the landmark approach. Consequently we selected a single target from the group of 12 brains for the comparisons shown here. Using a single target may have led to an unknown bias in these comparisons. To address this issue we repeated the analysis with the second set of 12 brains, for which detailed results are presented in the supplemental material. Results are very similar for both groups. If any of the sulci were missing from the target then we would expect some loss in performance when using the landmarked based approach, so that careful selection of the target is important in this method.
Both the FreeSurfer and BrainVoyager software packages are updated regularly, and newer versions have been released since the completion of this study. A possible confound in our analysis is the different ways in which we performed the registration for each method; for the landmark-based and BrainVoyager methods we directly registered each subject to the target, but for FreeSurfer we indirectly achieved this registration by first mapping all subjects to an atlas and then finding the point correspondence between subjects and target. We chose this approach for FreeSurfer, because registration is optimal when it uses the variance of the convexity across subjects comprising the atlas (Fischl et al., 1999b) and we wanted to maximize the performance of all methods we were comparing. For the same reason, even though BrainVoyager offers the option to register all subjects to the group average, we found that registration results were worse using the group average than when individually registering each subject to the target, therefore we followed the latter approach.
In summary, the results of this comparison show that for the task of aligning the set of ROIs chosen for this study, FreeSurfer and the landmark-based method do not differ significantly in performance. Both methods produce significantly better results than BrainVoyager. However, the comparison of sulcal curve alignment shown in Figs 5–7 indicate that curvature matching often results in the misidentification or misalignment of well established sulcal anatomy. Given that, to date, there are no landmarks available that better correlate with underlying functional and cytoarchitectonic boundaries (Brodmann, 1909; Watson et al., 1993; Roland and Zilles, 1994; Fischl et al., 2008) it is important that results of curvature mapping be verified for reasonable correspondence of sulcal features in cortical areas in which experimental effects are reported.
5 Conclusion
We compared landmark-based and automatic cortical registration techniques using as criteria curve alignment, curvature alignment, comparison with expert delineated ROIs, and local area distortion. Each method optimizes best its own similarity metric; landmark-based methods align the traced contours, and automatic methods align curvature. ROI analysis showed no statistically significance difference between the landmark-based method and FreeSurfer, however the ROIs were restricted to language related areas in which there is relatively little intersubject variability in sulcal anatomy. The discrepancy maps also reported above indicate that larger differences may be found in occipital and frontal cortex. The ROI results from BrainVoyager gave significantly smaller overlap with the expert identified ROIs than either of the other two methods and also produced a larger number of misaligned sulci than FreeSurfer.
Overall, the landmark-based method proved to be more reliable in the sense that it did not produce crude registration errors that are often present in automatic registration methods, such as the mismapping of the central sulcus to the precentral and occipito-parietal sulcus to a more anterior sulcus in FreeSurfer (second row, Fig. 4), or the frequent mapping of calcarine to incorrect nearby regions in BrainVoyager (Fig. 7).
Requirements for accurate registration vary among neuroimaging studies and depend on many parameters, such as the number of subjects, cortical areas of interest, and imaging modality. As our studies have shown, there are cases where automatic alignment can produce poor registration results. Consequently, the practice of blindly applying registration across a group should be avoided. Instead, users of these packages should ensure that sulci in regions of interest in their studies are adequately aligned after registration before proceeding with subsequent analysis.
Supplementary Material
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Allen JS, Damasio H, Grabowski TJ. Normal neuroanatomical variation in the human brain: An mri-volumetric study. American Journal of Physical Anthropology. 2002;118 (4):341–358. doi: 10.1002/ajpa.10092. [DOI] [PubMed] [Google Scholar]
- Andrade A, Kherif F, Mangin JF, Worsley KJ, Paradis AL, Simon O, Dehaene S, Bihan DL, Poline JB. Detection of fmri activation using cortical surface mapping. Human Brain Mapping. 2001;12 (2):79–93. doi: 10.1002/1097-0193(200102)12:2<79::AID-HBM1005>3.0.CO;2-I. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anticevic A, Dierker DL, Gillespie SK, Repovs G, Csernansky JG, Van Essen DC, Barch DM. Comparing surface-based and volume-based analyses of functional neuroimaging data in patients with schizophrenia. NeuroImage. 2008;41 (3):835–848. doi: 10.1016/j.neuroimage.2008.02.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernstein LE, Jiang J, Pantazis D, Lu Z-L, Joshi A. Visual phonetic processing localized using speech and non-speech face gestures in video and point-light displays. Human Brain Mapping. doi: 10.1002/hbm.21139. in revision. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brodmann K. Vergleichende Lokalisationslehre der Grosshirnrinde in ihren Prinzipien dargestellt auf Grund des Zellenbaues. Johann Ambrosius Barth Verlag 1909 [Google Scholar]
- Damasio H. Human Brain Anatomy in Computerized Images. 2 Oxford University Press; 2005. [Google Scholar]
- Desai R, Liebenthal E, Possing ET, Waldron E, Binder JR. Volumetric vs. surface-based alignment for localization of auditory cortex activation. NeuroImage. 2005;26 (4):1019–1029. doi: 10.1016/j.neuroimage.2005.03.024. [DOI] [PubMed] [Google Scholar]
- Dijkstra EW. A note on two problems in connexion with graphs. Numerische Mathematik. 1959;1 (1):269–271. [Google Scholar]
- Dubuisson M-P, Jain A. A modified Hausdorff distance for object matching. Proceedings of the 12th IAPR International conference on computer vision & image processing; 1994. pp. 566–568. [Google Scholar]
- Duvernoy HM. The Human Brain: Surface, Blood Supply and Three-Dimensional Sectional Anatomy. 2 Springer Verlag; 1999. [Google Scholar]
- Fischl B, Rajendran N, Busa E, Augustinack J, Hinds O, Yeo BTT, Mohlberg H, Amunts K, Zilles K. Cortical folding patterns and predicting cytoarchitecture. Cerebral Cortex. 2008;18 (8):1973–1980. doi: 10.1093/cercor/bhm225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Dale AM. Cortical surface-based analysis: II: Inflation, flattening, and a surface-based coordinate system. NeuroImage. 1999a;9 (2):195–207. doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Tootell RBH, Dale AM. High-resolution intersubject averaging and a coordinate system for the cortical surface. Human Brain Mapping. 1999b;8 (4):272–284. doi: 10.1002/(SICI)1097-0193(1999)8:4<272::AID-HBM10>3.0.CO;2-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glaunes J, Vaillant M, Miller MI. Landmark matching via large deformation diffeomorphisms on the sphere: Special issue on mathematics and image analysis. Journal of Mathematical Imaging and Vision. 2004;20(22):179–200. [Google Scholar]
- Goebel R. A fast automated method for flattening cortical surfaces. NeuroImage. 2000;11:S680. [Google Scholar]
- Goebel R, Esposito F, Formisano E. Analysis of functional image analysis contest (fiac) data with brainvoyager qx: From single-subject to cortically aligned group general linear model analysis and self-organizing group independent component analysis. Human Brain Mapping. 2006;27 (5):392–401. doi: 10.1002/hbm.20249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsu Y-Y, Schuff N, Du A-T, Mark K, Zhu X, Hardin D, Weiner M. Comparison of automated and manual mri volumetry of hippocampus in normal aging and dementia. 2002 doi: 10.1002/jmri.10163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jo HJ, Lee JM, Kim JH, Shin YW, Kim IY, Kwon JS, Kim SI. Spatial accuracy of fmri activation influenced by volume- and surface-based spatial smoothing techniques. NeuroImage. 2007;34 (2):550–564. doi: 10.1016/j.neuroimage.2006.09.047. [DOI] [PubMed] [Google Scholar]
- Johnson HJ, Christensen GE. Consistent landmark and intensity-based image registration. IEEE Transactions on Medical Imaging. 2002;21 (5):450–461. doi: 10.1109/TMI.2002.1009381. [DOI] [PubMed] [Google Scholar]
- Joshi A, Pantazis D, Li Q, Damasio H, Shattuck D, Leahy R. Optimizing sulcal landmark selection for cortical surface registration. Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition; 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joshi A, Shattuck D, Thompson P, Leahy R. Surface-constrained volumetric brain registration using harmonic mappings. Medical Imaging, IEEE Transactions on. 2007 Dec;26 (12):1657–1669. doi: 10.1109/tmi.2007.901432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joshi SC, Miller MI. On the geometry and shape of brain sub-manifolds. International Journal of Pattern Recognition and Artificial Intelligence. 1997;11 (8):1317–1343. [Google Scholar]
- Ju L, Hurdal MK, Stern J, Rehm K, Schaper K, Rottenberg D. Quantitative evaluation of three cortical surface flattening methods. NeuroImage. 2005;28 (4):869–880. doi: 10.1016/j.neuroimage.2005.06.055. [DOI] [PubMed] [Google Scholar]
- Ono M, Kubick S, Abernathey C. Atlas of the Cerebral Sulci. Thieme Medical Publishers; 1990. [Google Scholar]
- Postelnicu G, Zollei L, Fischl B. Combined volumetric and surface registration. IEEE Transactions on Medical Imaging. 2009;28 (4):508–522. doi: 10.1109/TMI.2008.2004426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roland PE, Zilles K. Brain atlases - a new research tool. Trends in Neurosciences. 1994;17 (11):458–467. doi: 10.1016/0166-2236(94)90131-7. [DOI] [PubMed] [Google Scholar]
- Shattuck DW, Joshi AA, Pantazis D, Kan E, Dutton RA, Sowell ER, Thompson PM, Toga AW, Leahy RM. Semi-automated technique for delineation of landmarks on models of the cerebral cortex. Neuroscience Methods. 2009;178 (2):385–392. doi: 10.1016/j.jneumeth.2008.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shattuck DW, Leahy RM. Brainsuite: An automated cortical surface identification tool. Medical Image Analysis. 2002;8 (2):129–142. doi: 10.1016/s1361-8415(02)00054-3. [DOI] [PubMed] [Google Scholar]
- Shen D, Davatzikos C. Very high-resolution morphometry using mass-preserving deformations and hammer elastic registration. NeuroImage. 2003;18 (1):28–41. doi: 10.1006/nimg.2002.1301. [DOI] [PubMed] [Google Scholar]
- Strother SC, Anderson JR, Xu XL, Liow JS, Bonar DC, Rottenberg DA. Quantitative comparisons of image registration techniques based on high-resolution mri of the brain. 1994 doi: 10.1097/00004728-199411000-00021. [DOI] [PubMed] [Google Scholar]
- Talairach J, Szikla G. Atlas of stereotaxic anatomy of the telencephalon. Paris: Masson and Cie; 1967. [Google Scholar]
- Thompson PM, Toga AW. A framework for computational anatomy. Computing and Visualization in Science. 2002;5 (1):1–34. [Google Scholar]
- Thompson PM, Woods RP, Mega M, Toga AW. Mathematical/computational challenges in creating deformable and probabilistic atlases of the human brain. Human Brain Mapping. 2000;9 (2):81–92. doi: 10.1002/(SICI)1097-0193(200002)9:2<81::AID-HBM3>3.0.CO;2-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tosun D, Rettmann ME, Prince JL. Mapping techniques for aligning sulci across multiple brains. Medical Image Analysis. 2004;8:295–309. doi: 10.1016/j.media.2004.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen D. Surface-based approaches to spatial localization and registration in primate cerebral cortex. NeuroImage. 2004;23 (Supplement 1):S97–S107. doi: 10.1016/j.neuroimage.2004.07.024. [DOI] [PubMed] [Google Scholar]
- Van Essen D. A population-average, landmark- and surface-based (pals) atlas of human cerebral cortex. NeuroImage. 2005;28 (3):635–662. doi: 10.1016/j.neuroimage.2005.06.058. [DOI] [PubMed] [Google Scholar]
- Van Essen DC, Drury HA, Joshi S, Miller MI. Functional and structural mapping of human cerebral cortex: solutions are in the surfaces. Proc Natl Acad Sci. 1998;95 (3):788–95. doi: 10.1073/pnas.95.3.788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Chiang M-C, Thompson PM. Medical Image Computing and Computer-Assisted Intervention MICCAI. 2005. Automated surface matching using mutual information applied to riemann surface structures; pp. 666–674. [DOI] [PubMed] [Google Scholar]
- Watson JDG, Myers R, Frackowiak RSJ, Hajnal JV, Woods RP, Mazziotta JC, Shipp S, Zeki S, March 1. Area v5 of the human brain: Evidence from a combined study using positron emission tomography and magnetic resonance imaging. Cereb Cortex. 1993;3 (2):79–94. doi: 10.1093/cercor/3.2.79. [DOI] [PubMed] [Google Scholar]
- Woods R, Grafton ST, Holmes CJ, Cherry SR, Mazziotta JC. Automated image registration: I. general methods and intrasubject, intramodality validation. J Computer Assisted Tomogr. 1998;22(1):139–152. doi: 10.1097/00004728-199801000-00027. [DOI] [PubMed] [Google Scholar]
- Zijdenbos A, Dawant B, Margolin R, Palmer A. Morphometric analysis of white matter lesions in mr images: method and validation. Medical Imaging, IEEE Transactions on. 1994 Dec;13 (4):716–724. doi: 10.1109/42.363096. [DOI] [PubMed] [Google Scholar]
- Zuk T, Atkins M. A comparison of manual and automatic methods for registering scans of the head. Medical Imaging, IEEE Transactions on. 1996 Oct;15 (5):732–744. doi: 10.1109/42.538950. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.