The Optimal Template Effect in Hippocampus Studies of Diseased Populations

Abstract

We evaluate the impact of template choice on template-based segmentation of the hippocampus in epilepsy. Four dataset-specific strategies are quantitatively contrasted: the “closest to average” individual template, the average shape version of the closest to average template, a best appearance template and the best appearance and shape template proposed here and implemented in the open source toolkit Advanced Normalization Tools (ANTS). The cross-correlation similarity metric drives the correspondence model and is used consistently to determine the optimal appearance. Minimum shape distance in the diffeomorphic space determines optimal shape. Our evaluation results show that, with respect to gold-standard manual labeling of hippocampi in epilepsy, optimal shape and appearance template construction outperforms the other strategies for gaining data-derived templates. Our results also show the improvement is most significant on the diseased side and insignificant on the healthy side. Thus, the importance of the template increases when used to study pathology and may be less critical for normal control studies. Furthermore, explicit geometric optimization of the shape component of the unbiased template positively impacts the study of diseased hippocampi.

1. Introduction

The role of the reference template or atlas, in current medical imaging practice, is fundamental to many aspects of magnetic resonance image processing, particularly in neuroimaging (Senjem et al., 2005). The image template provides a standardized neuroanatomical space for clinical imaging studies (Ashburner et al., 1998; Thompson et al., 2000) and spatial prior probabilities for a variety of segmentation methods (Zhang et al., 2001; Leemput et al., 2003; Prastawa et al., 2005; Awate et al., 2006; Ashburner and Friston, 2009). Template-based segmentation is particularly needed for labeling substructures in the brain that have diffuse boundaries, such as the hippocampus. The hippocampus plays an important role in diseases such as epilepsy which is characterized by seizures originating most often in the medial temporal lobe (mTL) (Gastaut, 1975), where the hippocampus resides. Segmenting the hippocampus is particularly important for assessing disease stage in epilepsy, the range of the disease’s effect, and surgical planning (Engel, 1996; Watson et al., 1997).

Many papers exist on general computational hippocampal anatomy and a special issue of Hippocampus was recently devoted to documenting the state of the art in 2009. Deformable image registration is commonly used for template-based segmentation of hippocampal neuroanatomy, (Hogan et al., 2000b,a; Hammers et al., 2007). One such study showed that hippocampus focused diffeomorphic mapping improves estimates of functional activation (Miller et al., 2005). Hippocampus segmentation, in particular, is aided by template-based approaches due to indistinct intensity boundaries with other structures, such as the amygdala and parahippocampal gyrus. Prior knowledge in the form of a labeled template coordinate system is required to delineate this structure automatically. Methods for building population-specific templates have gained prominence due to the difficulty of determining an appropriate template or set of templates for a given population. Such templates statistically summarize the average shape and appearance of the population on which the template-building algorithm is trained.

Further motivating these approaches, the coordinate system chosen for a particular structural or functional study influences the quantitative outcome, as the reference frame affects the measurement in the nonlinear world of morphometry (Thompson et al., 2000; Senjem et al., 2005). The statistically conservative approach thus requires least-biased coordinate systems where average anatomical configurations are estimated from a spatially normalized population. Prior work on this problem falls into two categories: deformation-based averaging and intensity-based averaging. The advantage of intensity averaging is that it removes dependence on the intensity signature of any single, specific anatomy. However, intensity averaging may create false structures by averaging tissues that are not in correspondence and it does not directly find a shape mean. That is, the residual of the geometric (or shape) component of the average may be far from zero. Examples of these types of diffeomorphic methods are in (Joshi et al., September 2004; Lorenzen et al., 2006). Shape-based averaging, on the other hand, guarantees that tissues are in correspondence before averaging and gives a minimal shape residual. However, initialization is with respect to a specific anatomical space, inducing a dependence on the initial anatomy. Examples of such methods are (Guimond et al., 2000; Twining et al., 2005) and, with diffeomorphisms, (Vaillant et al., 2004; Beg and Khan, 2006; Younes, preprint). An additional variation of template-building approaches are full group-wise approaches (Studholme and Cardenas, 2004) where one solves a n² optimization problem, where n is the number of images in the dataset. A very recent study used optimal shape estimation to find template-based tissue priors (Ashburner and Friston, 2009).

Our method, symmetric group-wise normalization (SyGN), is distinct from those cited above in that we derive an optimal template that is unbiased with respect to both shape and appearance, in the diffeomorphic space, and with fully symmetric methods (Avants et al., 2008). Symmetric performance, with respect to input data, is an important property for a measurement tool as it guarantees continuous dependence with the data. Symmetry is also a basic requirement for measuring distances between shapes. Furthermore, symmetric approaches have been shown to outperform closely related asymmetric methods in quantitative evaluation studies (Avants et al., 2008; Beg and Khan, 2007; Geng et al., 2009). Because we use a symmetric diffeomorphic method, both the pairwise and group-wise maps are unbiased with respect to the input data and with respect to the role of “template” and “target” imagery. We also use an unbiased optimization strategy that accounts for appearance and shape variation and allows us to fully automate the template derivation, reduce dependence on individual anatomy and produce a template with high feature sharpness. An argument can be made that symmetry should not be combined with optimal template strategies due to statistical differences in template and target. However, low-noise T1 acquisition and advances in template construction greatly reduce the gap in noise levels and, at the same time, the benefit of having symmetric use of image information is likely to outweigh potential disadvantages.

Here, we extend this methodology to statistically characterize disease effects that appear sporadically and asymmetrically, as in unilateral temporal lobe epilepsy (TLE). In the majority of cases, TLE is characterized by unilateral mesial temporal sclerosis, i.e., neuron cell loss in the hippocampus, amygdala and parahippocampal gyrus (NIH, 1990) that is restricted to one side of the brain. This induces often visible asymmetry in the affected individual, as in Figure 1. The atrophy in the hippocampus and ventricles can cause the hippocampus to take on an apparent appearance and topology, in typical one millimeter resolution MRI, that is distinct from an unaffected hippocampus. Because TLE produces disease-specific effects, we expect that our explicit symmetric diffeomorphic template model will result in notable performance improvements in TLE hippocampus segmentation.

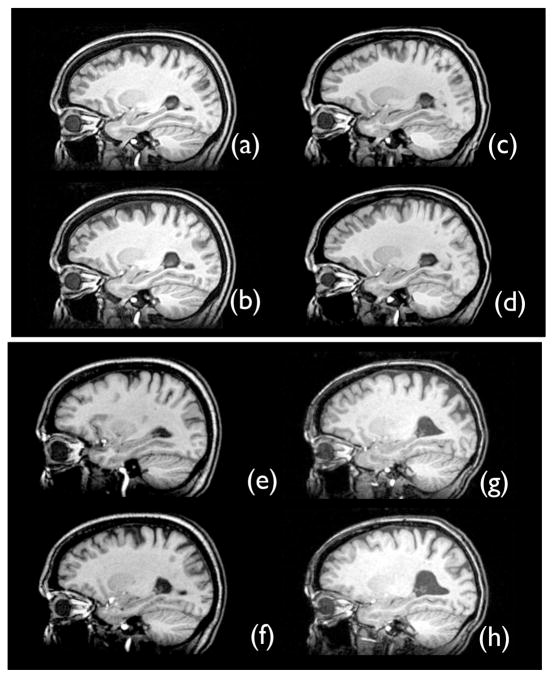
Figure 1.

The SyGN template healthy side hippocampus is in (a), while the SyGN template diseased side hippocampus is in (b). The optimal appearance template healthy side hippocampus is in (c), while its diseased side hippocampus is in (d). The individual shape-optimal template healthy side is in (e), while its diseased side is in (f). The individual template healthy side hippocampus is in (g), while the diseased side hippocampus is in (h). The template in (e) and (f) is derived from the image shown in (g) and (h). All of these templates show the asymmetric effect of unilateral sclerosis on temporal lobe neuroanatomy.

We evaluate this hypothesis with respect to expert-generated gold standard labelings of the hippocampus. We thus establish the impact of template selection on hippocampus segmentation, for both the diseased side of the brain and the contralateral (healthy) side. Our results show that our novel approach to template-based segmentation—here specialized to capture disease laterality in TLE—provides a significant improvement. In contrast, we also show that template selection is much less important for the young, healthy hippocampus. This paper is the first, to our knowledge, to state and concretely establish the impact of different optimal template approaches in the context of template-based segmentation with and without disease. The evaluation uses methodology available in an open-source toolkit that compares favorably with other available algorithms (Klein et al., 2009) and, thus, our findings are likely to be relevant and extendible to independently developed methodology.

2. Methods

2.1. Pairwise Normalization

Diffeomorphisms, differentiable maps with differentiable inverse, recently gained prominence due to their ability to capture large deformation without compromising performance or causing topological problems. This transformation space also allows one to perform a pure gradient descent on the similarity metric of choice, without inducing folds in the underlying anatomy. In the sense that one registers images in a well-defined, closed transformation space, diffeomorphic registration algorithms are much closer, in principle, to rigid registration algorithms than to the Demons (Thirion, 1998), B-Spline (Rueckert et al., 2003) or small deformation elastic registration algorithms (Gee et al., 1993). The Diff space is traversed along paths of transformations generated through the o.d.e.,

$$\frac{d\phi (\mathbf{x},t)}{dt}=\mathit{v}(\phi (\mathbf{x},t),t),$$

where the velocity, ν, is bounded and regularized by a linear operator, t is time and φ(x, t) is a diffeomorphism of domain Ω with x ∈ Ω (Arnold, 1991). Maps may also be generated in an Eulerian (or moving) reference frame (Christensen et al., 1996). Typically, φ(x, 0) = Id, where Id is the identity diffeomorphism and φ(x, 1) is the end-point of the path of diffeomorphisms starting at Id. Additional, related theoretical advantages of diffeomorphisms generated by o.d.e.s are their continuous dependence on initial conditions and differentiability in time and space (Ebin and Marsden, 1970).

Shape Distances in deformable space may be computed using Diff. Diffeomorphic transformations have a natural distance measure which is defined by

$$D(\phi (\mathbf{x},0),\phi (\mathbf{x},1))={\int }_0^1\left|\right|\mathit{v}(\mathbf{x},t)\mid {\mid }_{L}dt,$$

where L is a linear operator such as ∇² + Id, where Id denotes the identity. This distance, locally at each position in the domain, is analogous to a curve length. Taking the infimum of this distance—over all admissible velocity fields—generates a true mathematical metric and allows one to define shortest paths (geodesics) and associated distances between images, when the images are represented by the transformations that map them.

Appearance Distances between images I and J may also be metric distances or may provide a “softer” notion of dissimilarity, as in the case of mutual information. Here, we use the correlation,

$$X(I,J)(x)=\frac{<I(\mathbf{x})-{\mu }_n(I(\mathbf{x})),J(\mathbf{x})-{\mu }_n(J(\mathbf{x})){>}_n^2}{<I(\mathbf{x})-{\mu }_n(I(\mathbf{x})){>}_n<J(\mathbf{x})-{\mu }_n(J(\mathbf{x})){>}_n}=\frac{A^2}{BC},$$ (1)

where the < · >_n represents the inner product of a n–vector with itself, <·, · >_n represents the inner product of two n–vectors, μ_n represents the mean of n variables and the metric is assessed over a local neighborhood around x with n voxels. We define n by choosing the size of a square (two-dimensions) or cubic (three-dimensions) voxel neighborhood with radius typically equal to four. The derivative of this metric with respect to I is:

$$X_I=\frac{2A}{BC}(J(\mathbf{x})-{\mu }_n(J(\mathbf{x}))-\frac{A}{B}(I(\mathbf{x})-{\mu }_n(I(\mathbf{x})))),$$ (2)

where one multiplies this term by the spatial gradient to find the derivative with respect to the spatial transformation, as in (Avants et al., 2008). The cross-correlation metric was shown to perform well, with a symmetric diffeomorphic transformation model, for challenging normalization problems such as those posed by aging and neurodegeneration (Avants et al., 2008). This similarity metric is integrated over Ω to assess the total (dis)similarity between I and J where we denote the integrated value of Π(·, ·) without a spatial index, (x). The dissimilarity between a pair of mapped images may then be written Π(I(φ(x, 1)), J) = −X(I(φ(x, 1)), J(x)). Here, Π(I(φ(x, 1)), J) should be smaller than Π(I, J).

Pairwise Symmetry may be induced in the mapping space by distributing the transformation equally to both images I and J. Define two mappings that have equivalent length such that,

$$D({\phi }_1(\mathbf{x},0),{\phi }_1(\mathbf{x},0.5))=D({\phi }_2(\mathbf{x},0),{\phi }_2(\mathbf{x},0.5)),$$

and the mapped image pair is I(φ₁(x, 0.5)) = J(φ₂(x, 0.5)). This concept of “splitting” the deformation equally between the pair of images is termed pairwise symmetric normalization (SyN) and was introduced in (Avants and Gee, 2004), further formalized in (Avants et al., 2006) and evaluated in (Avants et al., 2008; Klein et al., 2009). The method was shown to perform well and is used to perform group-wise SyN. Note that, although transformations operate on both images, full transformations from I(x) to J(x) may easily be computed by composing φ₁(x, 0.5) and ${\phi }_2^{-1}(\mathbf{x},0.5)$. The variational SyN optimization minimizes

$$\begin{array}{l}{E}_S(I,J,\phi )=D^2({\phi }_1(\mathbf{x},0),{\phi }_1(\mathbf{x},0.5))+D^2({\phi }_2(\mathbf{x},0),{\phi }_2(\mathbf{x},0.5))\\ +\mathrm{\Pi }(I({\phi }_1(\mathbf{x},0.5)),J({\phi }_2(\mathbf{x},0.5))),\end{array}$$ (3)

where φ is composed of φ₁ and φ₂. This method is explained in full in (Avants et al., 2008).

2.2. Population Normalization and Template Creation

Fundamentally, a full group-wise registration problem dictates that we want to find the template and set of transformations that gives the “smallest” parameterization of a dataset. The size of the parameterization, here, is given by the SyN energy terms which measure image similarity and diffeomorphism lengths. No specific guess for the initial template should be required. Instead, the template should be derived completely from the database of n images, {Jⁱ}. We denote such a template as image Ī. Generally, then, Ī = ℰ({Jⁱ}) where ℰ will optimize Ī with respect to the selected similarity criterion. We elaborate on our method for updating Ī with respect to correlation—equation 1—in section 2.2.1.

Our method also allows Ī to change shape via a diffeomorphism, ψ, such that we can explore possible template shapes Ī(ψ (x)). SyN normalization studies find a set of diffeomorphisms, {φⁱ}, and a template shape, represented by Ī, such that we optimize a similarity criterion with respect to a given template and set of initial conditions,

$$E_{\overline{I}}=\sum _i{E}_S(\overline{I},J^i,{\phi }^i)\text{where}\forall i,{\phi }^i(\mathbf{x},0)=\psi (\mathbf{x}),$$ (4)

where ψ is a diffeomorphism representing the initial conditions of each φⁱ and each pairwise problem is solved with SyN. We now describe an algorithm for iteratively minimizing E_Ī with respect to the initial conditions, ψ, for the diffeomorphisms and where Ī is defined by the optimal template appearance. We denote our algorithm as symmetric group-wise normalization (SyGN), pronounced “sign”.

Symmetric Group-wise Normalization (SyGN): The energy E_Ī of equation 4 is minimized iteratively with respect to the set of φⁱ, the template appearance and ψ (template shape). All φⁱ and ψ are initialized as identity. The template at the first iteration is the Euclidean average appearance image obtained after affine alignment, which provides a good initialization for the gradient algorithm later used to update appearance. Our affine registration, evaluated on neurodegenerative data, is described in (Song et al., 2007). The SyGN algorithm then performs a coordinate-descent style optimization, where we optimize one term at a time while rest are fixed. This approach has the advantage of being simple to implement, memory efficient, easily distributable across many computational nodes and relatively fast. The procedure first optimizes the mappings with fixed template, second, optimizes the template appearance with fixed shape and mappings and, finally, optimizes the template shape. The process then repeats.

1. With fixed template, compute the set of φⁱ by minimizing E_S for each image, J_i.

2. Update Ī to reduce the Π term with respect to template appearance. See subsection 2.2.1 below.

3. Estimate the Frechet mean (Frechet, 1948) (a nonlinear, intrinsic mean) in the space of diffeomorphisms by minimizing ${\sum }_i{D}^2({\phi }_1^i(\mathbf{x},0),{\phi }_1^i(\mathbf{x},1))$ with respect to ψ at time zero. This calculation results in an average velocity field, ν̄(x, t), at time zero. The fundamental theorem of o.d.e.s allows one to find a new ψ by integrating ν̄(x, t) over small time, t̄. This computation is described in subsection 2.2.2.

4. Set Ī ← Ī(ψ(x, t̄)). Then ψ(x, t̄) defines the identity with respect to this new template. Set the φⁱ(x, 0) = ψ (x, t̄), identity in this coordinate space, and go to 1.

The method typically converges well under 10 iterations (usually three to five depending upon the complexity of the deformations in the data). A shape-focused version of this algorithm was proposed in (Avants and Gee, 2004). Figure 3 shows an example of convergence for a simple ground truth dataset with known average shape. This example illustrates reasonable performance in a well constrained, theoretically clear case study. The overall SyGN approach is similar to that given by Fletcher, et al (Fletcher et al., 2004) for computing intrinsic means for the statistics of medial shapes. Note that we minimize each pairwise problem with the SyN approach, defining the φⁱ via ${\phi }_1^i$ and ${\phi }_2^i$ for each registration. The initial conditions for each ${\phi }_1^i$ are given by ψ, which is chosen to be the coordinate system that is least biased with respect to our metric on the diffeomorphic space, D. This algorithm guarantees a fully unbiased, symmetric result and yields an optimal template with respect to the correlation and shape space.

Figure 3.

Above, in (a), we see four binary images, ellipses, in a synthetic dataset with known radii, R₁ and R₂ and identical center. The unbiased template optimization initializes the template appearance by averaging these images, given the image in the upper right, (b), which has four gray levels, 0, 0.25, 0.5, 0.75 and 1. The geometric ground truth is shown in (c). The SyGN algorithm result, in (d), converges—up to interpolation error—to the expected shape and appearance. Error between SyGN and the ground truth is shown in (g). If the shape update step is removed—and we use only an optimal appearance (OA) template–the algorithm converges to a result with the wrong shape, shown in (e) and (f). The implication is that methods without explicit shape optimization will be more sensitive to initialization and are thus less likely to find the optimal minimum shape distance image. Theoretically, methods such as congealing (Learned-Miller, 2006) and (Joshi et al., September 2004), neither of which use explicit shape optimization, would converge to this type of reasonable, but geometrically less than optimal, solution. This is because the optimal solution for the problem above, with a matching criterion related to intensity difference, is to map all images to the 0.5 level set of the initial image shown in (b).

There are three key differences between SyGN and related methods. First, SyGN uses pairwise SyN for the pairwise problem. SyN treats both template and target symmetrically, thus guaranteeing that image features from the individual and template are used to drive the mapping throughout the optimization. Second, we optimize the template appearance with respect to a correlation-based model of template appearance—to our knowledge, this is the first work to do so. Third, SyGN includes an explicit geometric update step, in addition to a novel approach to estimating the expected template appearance. That is, SyGN optimizes the total distance value, ${\sum }_{i}D(\psi ,{\phi }_1^i(1))+{\mathrm{\Pi }}_i$, by varying the geometric origin of the population study, ψ, as well as template appearance and diffeomorphism lengths. SyGN is a contrast to methods such as congealing (Learned-Miller, 2006) or (Joshi et al., September 2004) in that neither method explicitly represents ψ, the geometric component of the template. As shown in Figure 2, varying the geometric origin of the study is fundamental to minimizing the total distance between the template and the population. The final estimate to the average anatomy satisfies two important properties: 1) the image appearance is independent of any specific anatomy; 2) the image shape is independent of any individual’s anatomical coordinate system. We now provide details on our specific approaches to updating Ī and ψ, the template appearance and shape, respectively.

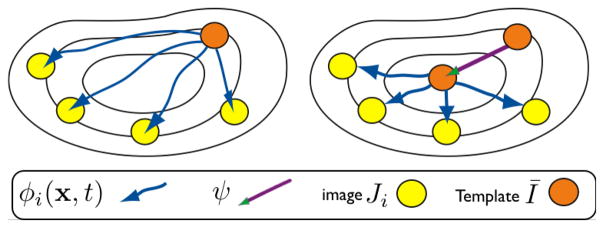
Figure 2.

We illustrate two steps in our optimization of a population template through a symmetric diffeomorphic parameterization. The shape of an initial template guess (orange circle) is updated by first estimating the diffeomorphic paths, φ_i. We then change the initial conditions, ψ, to the maps between the template, Ī, and the individual images, J_i, to shorten their total length. The template shape also changes under ψ. We term this approach “symmetric” because it uses symmetric pairwise mapping, symmetrically optimizes the two terms in normalization methods (geometry and appearance) across the population and is unbiased, that is, does not prefer any specific image or require user input.

2.2.1. Finding the Optimal Appearance

Our similarity metric of choice is the cross-correlation, a metric which maximizes the similarity of regional intensity patterns, where linear intensity transformations between corresponding neighborhoods of image I and J are factored out. The cross-correlation performs well in the presence of local tissue inhomogeneity and slowly varying distortions in tissue appearance. The cross-correlation is therefore able to capture complex intensity relationships between a template and a dataset of images. That relationship may be different from image to image and even from position to position within an image. This complex assumption is rather distinct from the Gaussian noise model usually used in template estimation methods and which invites directly averaging the aligned images.

It is possible to perform a gradient descent, with respect to cross-correlation, to optimize the template appearance. The goal is to estimate Ī(x) from the set of currently deformed images where each deformed image is $J_d^i=J^i({\phi }^{-1^i}(\mathbf{x},1))$. The gradient-based algorithm takes the following steps:

1. Normalize the intensity of all images to be in the range [0, 1].

2. For each image, compute the gradient of the similarity term $X_{J_d^i}$ with respect to appearance as given in equation 2. Reduce high frequencies in the appearance gradient by smoothing with a Gaussian of sigma σ_cc = 1.0 in voxel space (assuming isotropic image spacing). Smaller σ_cc gives greater fidelity to image features.

3. Average all $X_{J_d^i}$ to gain X̄_J.

4. Define gradient step-size γ = 0.1, and update Ī by Ī = Ī + γX̄_J.

5. Repeat from step 2 until convergence (typically a few iterations).

Hence, we are able to optimize template appearance in a way that is consistent with our selected similarity criterion. The difference between our approach and standard averaging is illustrated in Figure 4. Note that our strategy, is defined completely by equation 4: we maximize the correlation via updating normalization parameters and also template appearance. So, in summary, template appearance is not explicitly optimized by a separate strategy, but rather is determined implicitly by the selected normalization method performance and optimization criterion.

Figure 4.

The SyGN optimal template image, derived from (a) through (e) in the top row, is in (l). The Euclidean mean of images (a) through (e) is in (f). The gradient update X_Jⁱ is in (g) through (k). The SyGN image appearance—derived from maximizing the template appearance with respect to correlation—has more contrast and better captures the eyebrows than the Euclidean average, thus providing more realistic features to guide mapping. This data is available in ANTS, along with scripts to compute this example (Avants et al., 2009). We use face images to illustrate the concepts due to their ease of interpret-ability and familiarity in comparison to brain images. Furthermore, faces have biological variability and detailed features (such as mustache) that may not match perfectly between subjects. Similar challenges to correspondence are also present in brain mapping.

2.2.2. Shape Update

A diffeomorphism is defined uniquely by its initial conditions and the associated velocity field. The average diffeomorphism, with respect to some template, then, is determined by averaging the set of initial conditions defining the diffeomorphisms from this template to a population. This defines a new diffeomorphism, then, that, when applied to the template, reduces the total shape-based distance. The shape update step is, in essence, a statistical evolution of diffeomorphism, ψ, from averaged initial velocities.

Two facts are needed to establish the validity of this approach. First, averaging in the space of regularized velocity fields is permissible as the space is closed under addition (while the space of diffeomorphisms is not). Thus, averaging initial velocity fields indeed determines a permissible velocity field. Second, we establish that integrating this velocity field with an o.d.e. permits an acceptable diffeomorphism. The standard existence and uniqueness theorem for ordinary differential equations (Ebin and Marsden, 1970; Arnold, 1991) guarantees the existence/uniqueness of our statistically defined solutions.

The theorem above provides a direct motivation for using averaged initial velocities to evolve towards average shape. However, the value of ν̄(x, t) may also be defined by performing a first-order minimization of the total population-based shape distance, with the result being identical to that established by the argument above. To see this, we find the conditions defining an extremum of the total distance measure by taking the partial derivative with respect to ψ at time zero, where ψ(x) = x. The shape update, then, is derived from

$$\frac{\partial }{\partial \psi }\sum _i\left|\right|{\mathit{v}}^i(\psi ,0)\mid {\mid }_L^2=0.$$

We approximate this space using a linear regularization matrix L (containing, for example, Gaussian derivative kernels along the diagonal as in (Ashburner and Friston, 2009)),

$$\sum _i\frac{\partial }{\partial \psi }{\mathit{v}}^i{(\psi ,0)}^T\mathbf{L}{\mathit{v}}^i(\psi ,0)=0.$$

This yields the condition:

$$\sum _i{\mathit{v}}^i(\psi ,0)=\overline{\mathit{v}}=0,$$

which indicates that the average of the time zero velocity fields should be the identity. We may allow ψ to evolve in this gradient direction under the o.d.e.

$$\frac{d\psi }{d\overline{t}}=\overline{\mathit{v}}(\psi ,\overline{t}).$$ (5)

Noting that $({\phi }_1^i(\psi ,\mathrm{\Delta }t)-\psi )/\mathrm{\Delta }t\approx {\mathit{v}}^i(\psi ,0)$, we may break this equation down with further small-time, small-deformation approximations to find our simple, gradient-based update strategy for template shape,

$$\frac{{\psi }_{\mathrm{\Delta }\overline{t}}-\psi }{\mathrm{\Delta }\overline{t}}=\sum _i({\phi }_1^i(\psi ,\mathrm{\Delta }t)-\psi )/\mathrm{\Delta }t$$

Without loss of generality, if we set ψ = x, then

$${\psi }_{\mathrm{\Delta }\overline{t}}=\mathbf{x}+\frac{\mathrm{\Delta }\overline{t}}{\mathrm{\Delta }t}\sum _i{\phi }_1^i(\psi ,\mathrm{\Delta }t),$$

or a scaling and summing of the mapping values, ${\phi }_1^i$. This equation establishes a local condition for the minimization of Σ_iD². One can see that if we are at the (locally optimal) average configuration, then ψ will not evolve under equation 5. Otherwise, the o.d.e. gives a valid for small time gradient-based update of ψ. This strategy is implemented in Advanced Normalization Tools (Avants et al., 2009).

An alternative to this optimization—perhaps with stronger convergence properties—is the geodesic shooting approach, using a momentum representation, described in (Beg and Khan, 2006) and (Wang et al., 2007; Younes et al., 2009). The momentum-based minimization approach is, theoretically, equivalent to the approach used as the momentum and velocity are related to each other through a linear operator. That is, initial momenta and initial velocity fields are uniquely related to each other and define the same set of transformations.

2.3. Lateralized Optimal Template Algorithm

We apply SyGN to gain a template from data that is processed such that disease is constrained to the left side of the brain, while the right side represents the contralateral, “control” side. Thus, our template contains an averaged healthy (non-diseased) side with the opposite side capturing the average affect of epilepsy on the anatomy.

The key component of this strategy is defining the mid-sagittal plane in each individual image with disease on the right side. We then flip only those images across the mid-sagittal plane. To achieve this, we first use SyGN to create an initial template. We then manually align this template such that its mid-sagittal plane is coplanar with the central sagittal slice in the voxel domain. We then affinely align all images to this template. We have found that this approach accurately maps the individual mid-sagittal plane to our template. We are then able to flip individuals with right-sided disease across the estimated mid-sagittal plane. We compose the flip with the affine map. We then run SyGN again, on this preprocessed dataset, which yields an optimal template where disease is left-lateralized.

2.4. Evaluation Strategy

Our evaluation strategy assesses the impact of the SyGN template on template-based hippocampus segmentation by contrasting performance with both manual segmentation and template-based segmentation with alternative template choices. The evaluation is performed on a dataset of 16 epilepsy subjects in order to establish the impact of disease on algorithm performance.

2.5. Subject Data

Patients with refractory nonlesional or lesional temporal lobe epilepsy (TLE) undergoing presurgical evaluation for temporal lobectomy were recruited from the Penn Epilepsy Center at the Hospital of the University of Pennsylvania and the Comprehensive Epilepsy Center at Thomas Jefferson University. A combination of clinical MRI findings, EEG, IAT, and neuropsychological testing was used to lateralize the side of seizure. Patients with brain tumors or vascular lesions involving the temporal lobe were excluded. Patients who had extratemporal epilepsy, had prior temporal lobectomy, or who had contraindications to MRI were excluded. Patients with severe mental retardation who are likely to be unable to cooperate with the MRI examination were also excluded. A combination of clinical MRI findings, EEG, IAT, and neuropsychological testing was used to lateralize the side of seizure. Data for sixteen patients is included in this analysis. Six of the participants had TLE localized to the right temporal lobe, eight had TLE localized to the left temporal lobe and two had bitemporal TLE with more severe disease effects on the left. The mean age of participants was 41.3 (SD=13.8), with a range of 18–67 years of age. Twelve of the participants were right-handed, three were left handed (one localized to the right side and two localized to the left side), and one was ambidextrous and localized to the left side. Eleven participants were female and five were male. Nine patients had hippocampal sclerosis, four did not have sclerosis, and sclerosis was indeterminate in the remaining three patients.

All subject images were acquired with a Siemens Trio 3.0 T MRI scanner. Each study began with a rapid sagittal T1-weighted scan to determine patient position. A T1 structural acquisition was then acquired with TR (repetition time) = 1620ms, TE (echo time) = 3s, slice thickness: 1 mm, in-plane resolution: .9766mm × .9766mm and field of view (FOV) 256 × 256 × 192.

2.5.1. Manual Labeling Protocol

Bilateral hippocampi were manually segmented by trained operators using ITK-SNAP. Three experienced operators (MK, JP, DM) were trained in temporal lobe anatomy by a board certified epileptologist in the University of Pennsylvania Department of Neurology. The hippocampus mask was defined by the appearance and disappearance of sulci observed in sagittal slices. Although sagittal slices were used to perform all segmentations, axial and coronal planes were used continuously as references to distinguish and confirm the anatomical boundaries and landmarks in three-dimensional space in consecutive slices. Anteriorly, the temporofrontal junction was used as the initial reference point for measurements for temporal lobe substructures, while posterior boundaries were defined by the gradual disappearance of gray and white matter of each structural region and associated sulci. The alveus and fimbria served as the superior boundary for the hippocampal segmentations while the inferior boundary was the parahippocampal gyrus. Laterally, the appearance of the temporal horn of the lateral ventricle initially defined the hippocampus, which also served as the anterior point at which to begin segmentations of the hippocampus. Posteriorly, the hippocampus was limited by the coalescing of the temporal horn of the lateral ventricle with the simultaneous appearance of the crux fornicis. The anatomical validity of hippocampus segmentations was confirmed by a board certified neuroradiologist.

Images from five subjects were selected for reliability analysis. Interrater and intrarater reliability was evaluated using the Dice similarity coefficient, an unbiased measure of overlap. The Dice statistic, O, counts the number of voxels, between two labelings A and B, that agree about the hippocampus labeling and the number that disagree such that, $O=\frac{2\mid A\cap B\mid }{\mid A\mid +\mid B\mid }$. The statistic produces a measure that varies in [0, 1] where 1 is perfect agreement. The average intrarater Dice overlap was 0.87 for JP and 0.92 for DM. Average interrater overlap was 0.82. These values are higher than overlap-based reliability measurements reported for several manual and automatic segmentation approaches Haller et al. (1997); Carmichael et al. (2005). JP was the only rater to complete segmentation of the full dataset. The other raters performed independent segmentation on the subset of the data and collaborated with JP on making decisions about hippocampal boundaries in challenging cases.

2.5.2. Alternative Template Selection

In order to evaluate our proposed template building strategy, and argue for its importance, we compare the impact of different template selection strategies on the performance of template-based hippocampus segmentation,

1. SyGN: The template provided by SyGN, an unbiased optimal shape and appearance template, given training by cross-correlation;

2. Optimal Appearance (OA): A template that is derived with an identical strategy to that used by SyGN but without explicitly estimating the optimal shape by minimizing the shape-based distance term. For this approach, only the appearance and estimated φⁱ change at each iteration. The value of ψ is not explicitly manipulated;

3. Individual (Indi): An individual template that is selected to be “closest” to the average image. This template individual was selected by computing the distance metrics involved in equation 3, for all individuals, with respect to the SyGN derived template and taking the closest subject. An expert visually inspected this image to confirm the absence of image artifacts that may impair its usefulness as a reference image. Note that using an individual as the template reduces the size of the test dataset by one.

4. Individual with Average Shape (Shape): The individual template, above, is selected to initialize the optimal template derivation strategy. The appearance of the individual image is kept fixed while the shape of the image is updated as in the SyGN algorithm.

We use an identical pair-wise registration strategy for estimating the φⁱ for each template and individual normalization problem. We factor out all effects, except for that of the template itself on our ultimate results.

2.5.3. Cross-Validation

Given n test images, we use a leave-one-out cross-validation strategy to define the spatial prior in the template space from n−1 individual hippocampi, mapped to the template. We then compute h̄, the hippocampus appearance, with respect to Ī, using the same method as outlined above. This defines the hippocampus probability map in the template space. We then map this estimated hippocampus to the individual that did not contribute to the spatial prior. Note that a probabilistic object boundary value with a probability of 0.5 would, after deformation with linear interpolation, take on the value of 0.25 due to partial voluming with a background value. The mapped hippocampus probability is thus thresholded at 0.25 to define the template-based labeling of the individual. The approach is repeated for each individual in the dataset.

3. Results

The disease-lateralized templates produced by SyGN and by the other methods are shown in Figure 1. We quantify performance of the selected templates for template-based segmentation by contrasting two measures: the Dice overlap ratio and the maximum shortest Euclidean distance between the estimated and manually labeled hippocampus surface. Surface distance, in contrast to the Dice score, compares the distance between labeled surface voxels alone—it is insensitive to variations in labeling within the object boundaries. We calculate surface distance by thresholding the estimated hippocampus segmentation, labeling surface voxels, and then masking the distance map from the target hippocampus with the estimated surface. We also measure the distance from the individual hippocampus to the estimated hippocampus, thus providing a symmetric estimate of the segmentation’s surface distance. This provides a symmetric spatially varying measure of the distance from the mapped template hippocampus to the manually labeled hippocampus. Both measures are affected by the relative smoothness of the labelings. As the template-based method is notably smoother than the manual labelings, some error is not surprising due to this systematic difference alone.

The average Dice statistic and average of mean surface distances, for segmentation of both the control side and the diseased side based on our templates, is shown in Table 1. The healthy side shows no significant difference in performance between the approaches. The diseased side, however, shows a significant improvement that is strongest with the SyGN template in terms of the the overlap and mean surface distances. Overall, these results show that SyGN, which produces a template that is theoretically close to the “true” average shape and appearance, indeed yields the best average performance. The average volumetrically rendered left and right hippocampus, along with the average surface distance, are rendered in Figure 6. The individual template and the shape-optimized individual template have only small differences in performance that may be attributed to interpolation. Therefore, we continue the comparison mainly with the individual template rather than comparing SyGN and OA with the redundant, highly correlated shape-template data.

Table 1.

Evaluation results for four template-based segmentation approaches.

Side and Template	Dice Mean ± SD	Dice Min/Max	Surface Dist Mean ± SD	Mean Max Surface Dist
Diseased SyGN Template	0.740 ± 0.07	0.6/0.85	0.78 ± 0.27	3.73
Diseased OA Template	0.728 ± 0.08	0.59/0.84	0.81 ± 0.28	3.66
Diseased Individual Template	0.690 ± 0.10	0.51/0.81	1.43 ± 1.2	5.1
Diseased Shape Template	0.686 ± 0.12	0.54/0.83	1.32 ± 1.1	4.9
Healthy SyGN Template	0.800 ± 0.09	0.52/0.88	1.01 ± 1.6	4.00
Healthy OA Template	0.802 ± 0.09	0.53/0.89	0.98 ± 1.6	3.48
Healthy Individual Template	0.781 ± 0.12	0.42/0.88	1.55 ± 2.1	5.47
Healthy Shape Template	0.776 ± 0.13	0.48/0.88	1.42 ± 1.7	5.01

Dice Measure Comparison	T-value	P-value	Distance Measure Comparison	T-value	P-value
Diseased SyGN vs OA	2.60	0.021*	Diseased SyGN vs OA	1.70	0.11
Diseased SyGN vs Indi	3.52	0.004*	Diseased SyGN vs Indi	2.86	0.012*
Diseased OA vs Indi	2.41	0.037*	Diseased OA vs Indi	1.69	0.12
Diseased SyGN vs Shape	3.55	0.004*	Diseased SyGN vs Shape	2.80	0.014*
Diseased OA vs Shape	2.44	0.037*	Diseased OA vs Shape	1.62	0.13
Healthy SyGN vs OA	0.34	0.738	Healthy SyGN vs OA	−1.27	0.22
Healthy SyGN vs Indi	2.11	0.055	Healthy SyGN vs Indi	1.72	0.11
Healthy OA vs Indi	1.70	0.112	Healthy OA vs Indi	1.73	0.11
Healthy SyGN vs Shape	2.13	0.055	Healthy SyGN vs Shape	1.72	0.11
Healthy OA vs Shape	1.71	0.112	Healthy OA vs Shape	1.73	0.11

^*The * denotes significance.

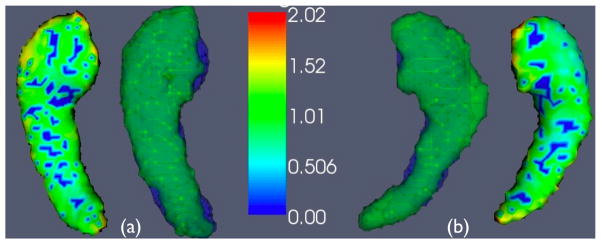
Figure 6.

The average SyGN template hippocampi are shown with (a), the healthy side mean surface distances, and (b) the diseased side mean surface distances. An individual that is near the average performance for both sides is also shown (in blue) overlaid in order to visualize the expected performance. Note the asymmetry in the expected size of the diseased versus healthy side hippocampus.

We further compare performance, across each individual, by graphing the values of $(O_i^{\mathit{SyGN}},O_i^{OA}),(O_i^{\mathit{SyGN}},O_i^{\mathit{Ind}})$ and ( $O_i^{OA},O_i^{\mathit{Ind}}$), as gained by each template-based method. The values of $O_i^{\mathit{Shape}}$ are not included as they are redundant with $O_i^{\mathit{Ind}}$. These graphs indicate, for each individual, which method performed best. We note that when SyGN outperformed the other methods, the improvement was high. However, the converse is not true. These results are shown in Figure 5.

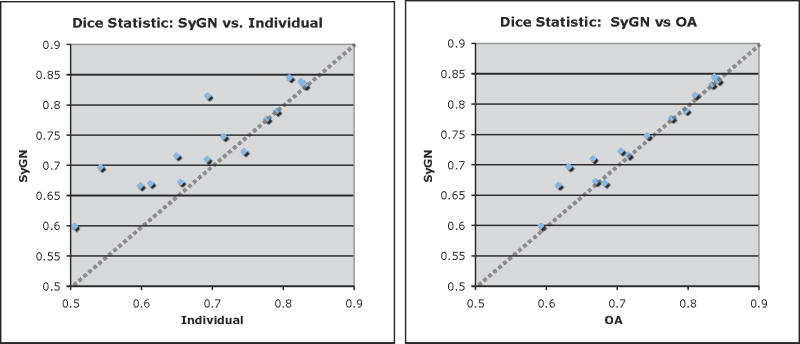
Figure 5.

We contrast the performance of OA vs SyGN and Indi vs SyGN, for segmenting the diseased-side hippocampus, by graphing their relative values. Identical performance would fall along the dotted line. SyGN, relatively, performs notably better—on nearly all data—than the individual template. SyGN’s performance is comparable to the OA template except on a few individuals where SyGN’s overlap ratio is superior by approximately 0.05.

Finally, we assess the ability of each method to provide estimates of hippocampal asymmetry that mirror those of the manual rater, JP. Here, asymmetry is measured by differences in hippocampal volume between the diseased side and the healthy side. We define the asymmetry as (V_c − V_d)/(0.5(V_c + V_d)) where V_c is the healthy side hippocampal volume and V_d is the diseased side hippocampal volume. As before, we use labeling results generated from cross-validation. The Pearson correlation of asymmetry measures provided by SyGN and JP was 0.831, considered a large correlation. The correlation of asymmetry between the OA algorithm and JP was 0.748, also considered a large correlation. The individual template produced a medium level correlation with JP’s volumetric asymmetry, 0.618. The shape template produced a correlation of 0.625.

4. Discussion

The key finding of our application is that the diseased population of hippocampi, showing greater shape and appearance variation, is labeled with significantly greater accuracy, in terms of Dice statistic, with SyGN than with other approaches. In terms of mean surface distance, SyGN is only significantly better than the individual image and optimal shape image. The SyGN template also produces measures of hippocampal asymmetry that, of the templates tested, correlate most strongly with the manual rater.

The importance of an optimal appearance template is that it seeks to estimate the most common or most likely “topology” of the local anatomy, as represented by the input dataset. In the case of the hippocampus, differences in topology may occur due to differences in the size and location of cerebrospinal fluid spaces that separate the hippocampus from amygdala and other surrounding mTL structures. We hypothesize that our integrated shape and appearance template most closely captures the expected local structures—and topology—in the mTL region and that this is the reason for improved performance. This claim is supported by the fact that the closest to average individual is only a small deformation/diffeomorphism away from the SyGN template. However, there are topological idiosyncracies that are specific to the anatomy of this (or any) individual and that cannot be captured by the diffeomorphic space. These idiosyncracies are what is “averaged out” by optimal appearance strategies that lead to templates that have improved overall performance across the dataset. Our results also show that the SyGN template finds a different local minimum of shape and appearance/topology that improves performance with respect to either the individual or average appearance template.

We note that the spectrum of our results, while reasonable on average, do not have the consistency that would be desirable for an unsupervised clinical application of this methodology. Causes of performance challenges are apparent and potentially real topology differences between the hippocampi, uncertainty and irregularity in the manual segmentation approach and lack of an accurate initialization—in the region of the hippocampus—provided by the affine transform. The worst case results are due largely to a poor affine initialization of the template relative to the diseased side hippocampus.

Our results compare favorably with three closely related approaches. Carmichael, et al. (Carmichael et al., 2005) investigated template based segmentation of the hippocampus in Alzheimer’s disease, which also induces hippocampal atrophy. Similar to our results, Carmichael showed that a dataset derived template was superior to standard templates such as that provided by SPM (Ashburner et al., 2003). Hogan, et al. (Hogan et al., 2000b) reported overlap values for normalization-based segmentation of epileptic hippocampi in a study similar to our own. Their work used a semi-automated, landmark-driven diffeomorphic hippocampus segmentation method that produced overlap values that are close to inter-rater overlap. However, their reported values for overlap (0.73, for both sides) were lower than those provided by SyGN (0.77, for both sides), on average. We note that firm conclusions cannot be made by comparing performance values derived from different datasets. However, it is of note that our fully automated approach yields performance values that appear to be similar to the semi-automated method. Finally, our method also produced performance, for automated hippocampus segmentation in epilepsy, that is similar to a recent study reported by Hammers, et al (Hammers et al., 2007). The Hammers study, in contrast, based their segmentation on a more computationally intensive approach that used 20 templates and a subsequent refinement of hippocampal boundaries by a three tissue segmentation. We note that our method would also benefit from further refining the hippocampus prior by using gray, white and cerebrospinal fluid data-derived probability maps. Another strategy that is available to improve performance is segmentation bootstrapping as in Khan et al. (2008); Yassa and Stark (2009). Both methods combine information from different algorithms to improve performance of template-based hippocampus/mTL labeling. However, for this study, we restrict ourselves to using a shape prior alone in order to evaluate the impact of the template on normalization quality. In summary, our efficient approach uses less user-input and fewer processing steps than previous algorithms that were evaluated for segmenting the hippocampus in epilepsy. However, minimum performance values, for this dataset, suggest that the near 100% reliability necessary for clinical application is not achievable by this method alone. Landmarks, whether placed by a user or by landmark discovery methods, and refinement by tissue probability maps would likely be adequate to enable the method to achieve the desired level of reliability (Pluta et al., 2009). Alternatively, a multiple atlas selection approach (Wu et al., 2007) or combination of multiple atlas-based classifiers would also aid performance (Rohlfing et al., 2004). Despite these other possibilities, our evaluation protocol, here, focuses on the impact of optimal shape on performance.

5. Conclusion

Epilepsy induces lateralized atrophy on the brain that affects the apparent topology and appearance of the hippocampus in standard approximately 1mm³ resolution T1 magnetic resonance images. These changes in appearance/topology are difficult to describe or capture in a model based on normal anatomy. Therefore, we developed a disease-specific average shape and appearance template for imaging-studies of neuroanatomy in epilepsy. The template is derived from data that is processed, with a novel protocol, such that disease is on one side of the brain. We showed that this template outperforms other dataset-specific templates in terms of automatically segmenting the diseased hippocampus from epilepsy data. This template also produced measures of hippocampal asymmetry that correlate strongly with asymmetry measures provided by an expert manual rater.

We built this model with a novel approach that derives a template with average shape and best with respect to cross-correlation appearance. This new approach to template creation uses a more flexible optimal appearance model that interfaces clearly with a well-known, high performance (Klein et al., 2009) normalization objective, the cross-correlation. Furthermore, as is standard in contemporary template creation algorithms, the method is unbiased and does not require user selection of an initial template. Our philosophy prefers to estimate the template appearance only from the completed group normalization solutions, rather than incrementally updating appearance before pairwise solutions are fully optimized. That is, SyGN only re-estimates the template shape/intensity after the template to individual mappings achieve the desired level of accuracy. We iterate template updates over the end-point condition of the group mapping. This avoids making decisions about appearance based on incomplete mappings, which may lead to persistent errors. On the other hand, SyGN comes at the cost of requiring full estimates of the mapping before determining appearance.

Finally, theoretical advantages of this method are that we minimize pairwise shape and appearance error measures via normalization and then, given optimal mappings, use these results to learn the best update to template appearance and shape. Despite benefits of this strategy in mapping the diseased hippocampus, we also found that, for the healthy side of the data, the impact of the template on template-based segmentation performance is small. However, an optimal template approach indeed improves segmentation for the epilepsy affected hippocampus data. Disease-affected hippocampi may undergo severe atrophy or deformation relative to a normal control. One may hypothesize that the optimal template represents an image/anatomical model that is more generalizable than the alternatives tested here. We expect future work to focus on using more complex statistical models for template creation and hippocampus labeling as a single template approach, while effective, may be fundamentally limited for unsupervised, hippocampus segmentation in large-scale datasets with pathology induced variation. It is likely that careful quantification of neuroanatomical variation for specific diseases will be necessary to define a small set of templates on which to base automated segmentation. Alternatively, manual or automated landmark placement approaches may also be adequate to bootstrap single-template based segmentation performance to an acceptable level of reliability. Both of the approaches—careful development of sub-template creation and automatic landmark placement—comprise our future work.