How does an fMRI voxel sample the neuronal activity pattern: compact kernel or complex spatiotemporal filter?

Abstract

Recent studies suggested that fMRI voxel patterns can convey information represented in columnar-scale neuronal population codes, even when spatial resolution is insufficient to directly image the patterns of columnar selectivity (Kamitani & Tong 2005; Haynes & Rees 2005). Sensitivity to subvoxel-scale pattern information, or “fMRI hyperacuity”, would greatly enhance the power of fMRI when combined with pattern-information analysis techniques (Kriegeskorte & Bandettini 2007). An individual voxel might weakly reflect columnar-level information if the columns within its boundaries constituted a slightly unbalanced sample of columnar selectivities (Kamitani & Tong 2005), providing a possible mechanism for fMRI hyperacuity. However, Op de Beeck (in press) suggests that a coarse-scale neuronal organization rather than fMRI hyperacuity may explain the presence of the information in the fMRI patterns. Here we argue (a) that the present evidence does not rule out fMRI hyperacuity, (b) that the mechanism originally suggested for fMRI hyperacuity (biased sampling by averaging within each voxel's boundaries; Kamitani & Tong 2005) will only produce very weak sensitivity to fine-grained pattern information, and (c) that an alternative mechanism (voxel as complex spatiotemporal filter) is physiologically more accurate and promises stronger sensitivity to fine-grained pattern information: We know that each voxel samples the neuronal activity pattern through a unique fine-grained structure of venous vessels that supply its blood-oxygen-level-dependent signal. At the simplest level, the drainage domain of a venous vessel may sample the neuronal pattern with a selectivity bias (Gardner in press; Shmuel et al. in press). Beyond biased drainage domains, we illustrate with a simple simulation how temporal properties of the hemodynamics (e.g. the speed of the blood in the capillary bed) can shape spatial properties of a voxel's filter (e.g. how finely structured it is). This suggests that a voxel, together with its signal-supplying vasculature, may best be thought of as a complex spatiotemporal filter. Such a filter may well have greater sensitivity to high spatial frequencies than the Gaussian or averaging-box kernels typically invoked to characterize voxel sampling (compact kernels, both of which would act like anti-aliasing filters that minimize such sensitivity). Importantly, the complex-spatiotemporal-filter hypothesis of fMRI hyperacuity can account for the observed robustness to slight shifts of the voxel grid caused by head motion: Because the fine-grained components of the filter are vascular, they will remain in a constant relationship to the neuronal patterns sampled as the voxel grid is slightly shifted.

Introduction

Functional MRI is thought to give us “images” of neuronal activity patterns as reflected in the hemodynamic response (Ogawa et al. 1990; Ogawa et al. 1992; Bandettini et al. 1992; Kwong et al. 1992; Blamire et al. 1992; Logothetis et al. 2001). The images are blurred and distorted locally (within a range of a few millimeters), but approximately accurate at a larger spatial scale. If the technique really simply gives us blurred “images” of neuronal activity, then standard-resolution fMRI should not allow us to detect fine-grained differences, such as the difference between the columnar activity patterns elicited in visual area V1 by the viewing of two gratings of different orientation. This would require nonstandard fMRI techniques with higher resolution and a reduced contribution from larger vessels (Cheng et al. 2001; Harel et al. 2006; Yacoub et al. 2007; Shmuel et al. 2007; Yacoub et al. 2008).

Contrary to this reasoning, recent studies have shown that standard blood-oxygen-level-dependent (BOLD) fMRI activity patterns acquired from V1 with (3-mm)³ voxels contain enough information to allow robust decoding of grating orientation (Kamitani and Tong 2005; Haynes and Rees 2005). Decoding worked even though the fMRI patterns were much too coarse to depict the fine-grained patterns of orientation columns. The authors explained their finding by suggesting that each voxel samples columns selective to all orientations, but not in a precisely balanced fashion (for an intuitive illustration of this interpretation, see Boynton 2005). As a result, each voxel may respond slightly more strongly to some orientations than to others. Combining the orientation information in these slight biases across many voxels would then allow robust decoding of orientation.

The issue is of great practical significance to neuroscientists working with fMRI: If 3-mm-wide isotropic voxels really reflected neuronal patterns of columnar grain, then pattern-information fMRI (Haxby et al. 2001; Cox and Savoy 2003; Carlson et al. 2003; Hanson et al. 2004; Kriegeskorte 2004; Mitchell et al. 2004; and too many more to list since 2005, for reviews see Haynes and Rees 2006; Norman et al. 2006; Kriegeskorte and Bandettini 2007) would be even more useful than previously thought: allowing sensitive population-code analyses not only of the coarse activity patterns directly imaged by fMRI (i.e. the lower spatial-frequency band of neuronal population activity), but even of fine-grained within-voxel columnar patterns. These fine-grained patterns reside in the “hyper band”, the spatial-frequency band above the Nyquist frequency (i.e. half the sampling frequency), which cannot be represented directly given the spacing of the voxels and the additional hemodynamic blurring.

Op de Beeck (in press) introduced the apt term “fMRI hyperacuity” for fMRI sensitivity to above-Nyquist (i.e. “hyper band”) spatial frequencies of the underlying neuronal activity pattern. However, he argues against this possibility on the basis of his finding that fMRI pattern-decoding accuracy did not suffer when the fMRI data were spatially smoothed prior to decoding grating orientation from V1 or object category from LOC. Similar results have been reported previously (Gardner et al. 2006, but see also: Friston et al. 2008). If we think of fMRI as simply giving us images of neuronal activity patterns, then every spatial-frequency band of the neuronal pattern should be reflected in the same spatial-frequency band of the fMRI pattern (Fig. 1, left column). Spatial smoothing reduces high spatial frequencies, but in Op de Beeck's experiments this does not reduce decoding performance.¹ On this basis, the author suggests that decoding may utilize lower spatial frequencies of the fMRI and neuronal signals. While this is one plausible explanation (see also Shmuel et al. in press), we will see that the present evidence is also consistent with the presence of high- and hyper-band neuronal pattern information in standard BOLD fMRI patterns.

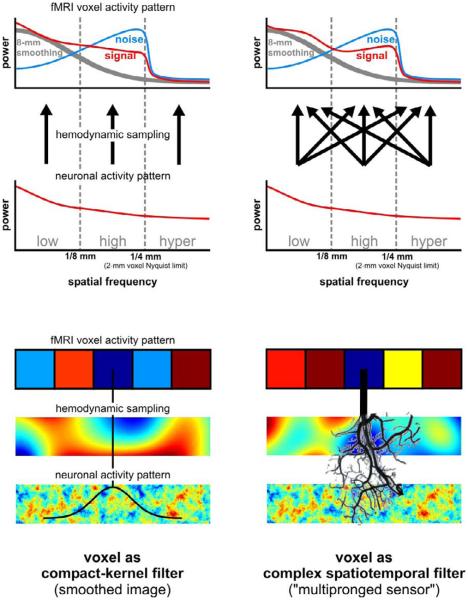
Fig. 1. Two models for how fMRI voxels sample neuronal activity patterns.

In the compact-kernel filter model (left column), the neuronal activity pattern is sampled by local averaging to generate each voxel's signal (bottom). The compact kernel defines the weights for the local averaging and could implement an averaging box (constant weights inside, zero weight outside the voxel) as well as a Gaussian-weighted average. In the complex-spatiotemporal-filter model (right column), the neuronal activity pattern is sampled through the finely structured vascular architecture supplying each voxel with its signal and the precise spatiotemporal properties of the filter are unique to each voxel and depend on both the signal-supplying vascular architecture and the dynamics of blood flow into the voxel (bottom). The two models suggest different predictions as to how different spatial frequencies of the neuronal activity pattern are reflected in the voxel pattern (top). In the compact-kernel filter model, the voxel pattern essentially provides a blurred image of the neuronal pattern. Thus each spatial frequency of the neuronal pattern will be represented by the same spatial frequency in the voxel pattern (upward arrows in the left column). Aliasing of hyper-band spatial frequencies can also occur (not shown), but the aliased components should be weak in amplitude. The complex-spatiotemporal-filter model suggests a more complicated relationship between neuronal patterns and voxel patterns, in which aliasing of a given frequency of the neuronal pattern into a different frequency of the voxel pattern is more prevalent (crossing arrows in the right column), although the voxel pattern may also contains an image of the neuronal activity pattern (upward arrows in the right column) for the frequency range the voxel grid can represent.

Neuronal pattern information may be present in the low spatial-frequency band

Why is it plausible that the lower spatial-frequency band (or, equivalently, a coarse-scale organization) contributes to decoding? Columnar organizations are often fine-grained. For example, V1 orientation and ocular-dominance domains are small and approximately uniformly distributed across the cortical area. This implies that the activity contrast patterns will have a lot of energy in the high spatial-frequency band. However, it does not imply that there will be exactly zero energy in lower spatial-frequency bands. For intuition, consider the fact that line drawings have a lot of their energy in the high band. But two different drawings will not be exactly identical after low-pass filtering. Similarly, neuronal activity contrast patterns known to have a lot of energy in the high band may also have some energy in lower bands (preview Fig. 4a, for low-band energy in ocular-dominance patterns). It has never been shown, to our knowledge, that orientation columns or, in fact, any other neuronal activity patterns do not also have a low spatial-frequency component. Low-band neuronal pattern information may, thus, contribute to pattern-decoding performance.

Fig. 4. Aliasing is weak for compact-kernel models and stronger for filters with high-frequency energy.

(a) The pattern of ocular-dominance strips contains some low-spatial-frequency components. Here we used the same image of the pattern of ocular-dominance strips as in Fig. 2a. In order to create a larger pattern, we added a replication of the pattern that was rotated by 180°. This resulted in a roughly point-symmetrical pattern (top). Smoothing by convolution with a Gaussian kernel of 8-mm FWHM greatly reduces the image contrast, reflecting the fact that most of the pattern energy is in the higher spatial-frequency band (middle). When we scale the smoothed pattern to full range (bottom), however, we find that there is some low-spatial-frequency components are present. The low-band pattern reflects the point-symmetry of the replicated original pattern. (b) To simulate 3-mm-wide fMRI voxels, we sampled the fine-grained pattern of ocular-dominance strips (a, top) with different kernels. This is equivalent to sampling the left-eye and right-eye patterns separately and subtracting the sampled patterns (as the right-eye domain was indexed by −1 and the left-eye domain by 1 in the original pattern). The kernels were scaled so as to have the same overall energy. Assuming independent identically distributed noise in each neuron of the original pattern, the voxels outputs thus all have an equal noise component in all cases (rows) and we need only consider the contrast in order to assess the contrast-to-noise ratio. For the single-point filter (top row), we observe substantial aliasing in the unsmoothed voxel pattern (central column). However, the contrast-to-noise ration is weak, because the kernel does not reduce the neuronal noise within each voxel by averaging but instead samples a single pixel (or “neuron”) of the original fine-grained pattern. The weak-contrast voxel pattern includes low frequencies that remain after smoothing the voxel patterns (right column). For the averaging-box filter (second row), each voxel benefits from noise reduction through averaging within a square of 3-mm width. However each voxel also suffers from contrast reduction caused by cancellation between the ocular domains. Overall, the voxel pattern contains more information about the stimulated eye than for the single-point filter. When we smooth the voxel pattern, we see the low-band of the original neuronal pattern (a, bottom). This suggests that the low-band of the voxel pattern reflects the low-band of the neuronal pattern for this filter and aliasing of hyper-band components into the low band of the voxel pattern is limited. Similar results obtain for a 3-mm-FWHM Gaussian filter (third row). A complex-kernel filter (bottom row) was constructed by spatially bandpassing a noise pattern and imposing a 3-mm-FWHM Gaussian envelope. Such a filter has a greater sensitivity to hyper-band neuronal pattern information. As a result the voxel pattern it predicts discriminates left and right-eye stimulation with greater contrast. When the voxel pattern is smoothed (right column), we see that the low band of the voxel pattern does not resemble the low band of the original neuronal pattern (a, bottom). This suggests that this filter produces more pronounced aliases of higher frequency components of the neuronal pattern in the low band of the voxel pattern. The voxel patterns have all been scaled to match, so the visual contrast of each pattern (center and right columns) reflects the expected decoding performance. Numbers above the voxel contrast patterns are standard deviations across space, which are monotonically related the d' and t value on an ideal observer's linear combination of the voxel outputs and to the decoding performance. Greater numbers indicate greater contrast to noise and higher decoding performance. Standard deviations are computed across space within the central part of the pattern indicated by the green contours in (a).

High noise may obscure information in the high band of the fMRI patterns

If smoothing does not affect decoding performance (Op de Beeck in press), can we conclude that the high band of the fMRI pattern contains no information? The answer is no. Low-pass filtering (e.g. smoothing) reduces not only high-band signal, but also high-band noise. If there were no signal in the high band at all, then low-pass filtering would only reduce the noise. As a result, we would, in fact, expect an improvement in decoding performance after smoothing. However, the converse implication need not hold: If removing higher frequencies of the fMRI patterns did improve decoding, this would not imply that the high band does not contain any information. The high band of the fMRI patterns could still contain information at a lower signal-to-noise ratio than the low band, such that the cost of the high-band noise is greater than the benefit of the high-band signal. For these reasons, finding decoding performance unaffected (or even improved) by low-pass filtering, does not have any strong implications about the presence or absence of information in the fMRI high band.

The signal-to-noise ratio is likely to be lower in the high band of fMRI patterns because of head-motion artefacts. Although motion correction algorithms remove a substantial proportion of the variance induced by movement, their method of rigid-body realignment does not correct the complex patterns of distortion that result from magnetic-field inhomogeneities, parenchymal motion, and other artifacts of echoplanar imaging (Andersson et al. 2001; Cusack et al. 2003). Motion correction may quite successfully reduce artefacts in the low band. However, the high band typically remains strongly affected, such that head-motion parameter time courses explain substantial variance in the signal even after head-motion correction. To address whether the high band contains information about the stimulus, it might be better to remove the low band (i.e. to spatially high-pass the data or remove the regional-average level of activity for a small region) and test for pattern information.²

Hyperacuity: Both the low and the high band of the fMRI pattern may contain hyper-band neuronal pattern information

Up to this point, we have assumed that fMRI simply gives us “images” of neuronal activity patterns. But under this assumption sensitivity to the hyper band is impossible to begin with: anything of higher spatial frequency than the voxel grid can capture cannot be represented in the signal. Hyper-band sensitivity requires that hyper-band frequencies are reflected in the frequency range the voxels can represent. So a hyper-band frequency must appear in a lower frequency band. This can happen through the small sampling biases hypothesized by Kamitani and Tong (2005) and intuitively illustrated by Boynton (2005). In signal and image processing, this phenomenon is known as aliasing (although the cited authors did not use this concept). Aliasing is the transposition of energy from the hyper band (i.e. the band above the Nyquist frequency) into the band that the sampling grid can represent (i.e. the band below the Nyquist frequency). Note that fMRI hyperacuity implies some form of aliasing by definition. Aliasing works by the same mechanism that produces “beats” and “moirés” as signals of two different frequencies interfere so as to alternately sum and cancel.

If aliasing occurs when neuronal activity patterns are sampled with fMRI voxels, then there is no reason to believe that the hyper-band frequencies should be transposed into the high band of the below-Nyquist range only. Aliasing has no preference for close-by frequency bands. For example, beats and moiré patterns can be of very low frequency (i.e. slowly varying). A given hyper-band frequency component in the signal will create an alias at a frequency that depends on the relationship between the frequency of the hyper-band component and the sampling frequency.

For complex neuronal patterns that are not precisely regular (e.g. patchy columnar organizations), we may expect each voxel to acquire an independent, essentially random selectivity bias if aliasing plays a role. An image of independent random intensities has equal power in all frequency bands. So hyper-band neuronal pattern information would be reflected in both the high and the low band of the fMRI patterns. So we see that fMRI hyperacuity cannot be ruled out based on the finding that smoothing (Op de Beeck in press) or even downsampling³ (Gardner et al. 2006), does not hurt decoding performance. Even if smoothing improved decoding performance, we could not rule out fMRI hyperacuity, because smoothing might strongly reduce the noise in the high band while preserving hyper-band information aliased into the low band.

We will address the possibility of fMRI hyperacuity in greater depth by considering two alternative models of how fMRI voxels sample the neuronal activity pattern: (1) Each voxel samples the neuronal pattern like a simple compact-kernel filter (e.g. an averaging box or a Gaussian). (2) Each voxel samples the neuronal activity pattern through a complex spatiotemporal filter determined by the unique architecture of its signal-supplying vasculature and the temporal properties of the hemodynamics. An overview of the main properties and predictions of the two models is given in Fig. 1 and Table 1.

Table 1.

Properties and predictions of the two models of fMRI voxels.

	compact-kernel filter (voxel as averaging box or Gaussian kernel)	complex spatiotemporal filter (voxel and signal-supplying vasculature as uniquely structured “multipronged sensor”)
imaging properties	The voxel pattern is essentially a blurred image of the neuronal activity pattern. As a result, each spatial frequency band of the neuronal pattern will be reflected in the same spatial frequency band of the voxel pattern, except for above-Nyquist frequencies, which will be eliminated. Aliasing of above-Nyquist frequencies into the entire represented range can occur but will be weak in amplitude.	The voxel pattern reflects the neuronal activity pattern like an image at a coarse scale, but represents it in a more complex fashion within local clusters of voxels. Above-Nyquist frequencies can alias into the entire frequency range represented by the voxel pattern, even affecting the coarse scale of the voxel patterns.
useful analogies	pixelated photograph pixelated movie	visual representation in V1 wavelet transform
low-band sensitivity (to spat. freq. below 1/8mm)	high
high-band sensitivity (to spat. freq. between 1/8mm and voxel Nyquist frequency)	compromised by head-motion related noise in the high band (Even if the high band contains substantial signal, the greater noise may lead to a low signal-to-noise ratio. As a result, decoding could be more accurate if the data are smoothed, even if the high band is informative.)	higher (to the extent that the complex filters of the voxels contain frequencies in the high and hyper bands; direct imaging of high-band information is compromised by head- motion related noise as for the compact-kernel filter)
hyper-band sensitivity (to spat. freq above voxel Nyquist freq., requires aliasing)	low (not zero, but strongly diminished because the filter functions like anti- aliasing in image processing)
effect of subvoxel shifts of the voxel grid	Shifting the voxel grid by a small fraction of the voxel width can invert the weak selectivity of a voxel to properties represented at the columnar level. Head-motion artefact could therefore substantially reduce the already small sensitivity to such hyper-band information.	The fine-grained portion of the filter is in the vasculature and will thus not shift with the voxel grid. A voxel sampling a fine-grained pattern through a larger venule will maintain its selectivity, as long as the voxel samples the same venule after the shift.
effect of smoothing and downsampling of the voxel data (assuming that high-band fMRI frequencies are completely removed)	Sensitivity to high-band frequencies should be diminished by smoothing and downsampling. Sensitivity to hyper-band frequencies should be low either way (only present based on weak aliasing from hyper to low band).	Sensitivity to high- and hyper-band frequencies could be more robust to smoothing, since the filters alias frequencies from these bands into the low band to a greater degree.

In a nutshell, we will argue that compact-kernel weighted averaging (model 1) will strongly reduce the contrast (i.e. the amplitude of the aliased frequency components) like an anti-aliasing filter in image processing. Moreover, any hyper-band information reflected in the voxels through aliasing would be highly sensitive to slight shifts of the voxel grid, rendering decoding across independent data sets impossible, because of head-motion artefacts that cannot be corrected (see Fig. 3 for a preview). The complex-spatiotemporal-filter model (model 2) is not only physiologically more realistic, but might turn out to better account for the substantial information about fine-grained neuronal activity patterns that appears to be present in fMRI patterns. At the simplest level, the drainage domain of a venous vessel sampled by a voxel may in turn sample the neuronal pattern with a selectivity bias (Gardner in press; Shmuel et al. in press). In V1, for example, a particular venule's drainage domain may sample more columns responding to horizontal than vertical orientations. Gardner (in press) suggested in particular that vascular structure may be functionally organized in a way that respects neuronal columnar selectivity. But even without such biological design, small venule biases are expected to arise by chance. Beyond biased drainage domains, a simple simulation (see Fig. 6 for a preview) illustrates how temporal properties of the hemodynamics (e.g. the speed of the blood in the capillary bed) can shape spatial properties of a voxel's filter (e.g. how finely structured it is). Importantly, the complex-spatiotemporal-filter hypothesis of fMRI hyperacuity can account for the observed robustness to slight shifts of the voxel grid caused by head motion: Because the fine-grained components of the filter are vascular, they will remain in a constant relationship to the neuronal patterns sampled as the voxel grid is slightly shifted.

Fig. 3. Aliasing is extremely sensitive to slight shifts of the sampled pattern relative to the sampling grid.

A hypothetical fine-scale grating pattern (top left) is sampled by a coarse voxel grid (top right). The voxels are 3 mm wide, so the voxel grid can represent spatial frequencies of up to 1/(6 mm), i.e. the Nyquist frequency. The grating's spatial frequency is 1/(0.8 mm), which is above the Nyquist frequency (i.e. in the hyper band). The voxel pattern cannot accurately represent the fine-scale grating, but the hyper-band energy is aliased into it. If the fine-scale grating's contrast polarity were inverted, then the voxel pattern's contrast polarity would invert as well. Pattern information in the hyper band could therefore be decoded from the voxel pattern. However, a slight shift and rotation of the grating at a scale much finer than that of the voxels (0.23 mm shift and 1.15° rotation, bottom panels) completely changes the voxel pattern. Pattern decoding would therefore not be successful unless training and test data are acquired with the voxel grid in precisely the same position at the scale of the spatial frequencies to be decoded. Subject head motion essentially always produces much larger shifts of the voxel grid. Head-motion correction cannot solve this problem at all, because the slight shifts have large-scale consequences in the voxel pattern (resampling the voxel pattern in the lower right panel to correct for the shift and rotation will not recover the voxel pattern in the upper right panel). Note that the rotation of the grating is not required: a slight shift by itself will cause similar large changes in the voxel pattern. In fact, the same phenomenon could be illustrated using a unidimensional signal resampled at regular intervals before and after a slight shift. The rotation was included here to produce a slightly more complex and realistic two-dimensional illustration. This toy simulation uses averaging-box voxels, but the sensitivity of aliases of hyper-band components to slight shifts does not depend on the shape of the sampling kernel. Similar results would therefore obtain for all the kernels of Fig. 4b. For averaging-box voxels, the voxel patterns have much lower contrast than the original grating. Here, the voxel patterns have been scaled to full range (black to white) so as to more clearly reveal the aliasing.

Fig. 6. A simple toy simulation of hemodynamic sampling suggests that the voxel filter is not space-time separable and that its spatiotemporal structure depends on the unique vascular architecture supplying each voxel with its signal and on the dynamics of blood flow.

(a) Hemodynamic delay map for a cross-section of the human cortical ribbon (pial surface at the top). This map has been computed by a two-dimensional toy simulation based on a modification of a drawing of cortical vasculature (Fig. 248 in Duvernoy et al. 1999). At each location, the color encodes the time in seconds required for the blood drained from that location to reach the pial surface (top. Because the drawing contained only venules and no capillaries, we simulated capillary drainage assuming that the blood drains in a straight line toward the closest venule end point at a speed of 0.5mm/s. For the venules, we assume a drainage speed of 5mm/s. (Keener and Sneyd (1998) report values of 0.3mm/s for the capillary bed and 5mm/s for venules, so our toy simulation should be slightly conservative, yielding coarser-than-actual spatial filters.) The simulation suggests spherical iso-delay surfaces and Voronoi-type drainage domains. The white square indicates the position of a 1×1 mm² voxel. (b) Based on the hemodynamic delay map (a) and assuming that the fMRI acquisition averages across 100 ms (typical EPI slice acquisition time) and is repeated at 100-ms intervals, we computed the spatiotemporal filter of the voxel. Each panel shows the spatial domain, whose BOLD signal (reflecting neural activity at time 0) would be reflected in the voxel (white square in a and b) in each of 9 consecutive acquisitions. Note that the voxel essentially samples its contents in the first acquisition. In the ninth acquisition, by contrast, it samples a discontiguous set of domains distributed around it, whose spatial extent depends on the EPI-slice acquisition time and capillary blood velocity, not on the size of the voxel.

In sum, there are three potential explanations for the results reported by Kamitani & Tong (2005) and Haynes & Rees (2005), which are not mutually exclusive:

• (a) Lower-band effects directly imaged with fMRI: Sensitivity to fine-grained organizations (as in Kamitani & Tong, 2005) actually relies on lower spatial-frequency band information that can be directly imaged with fMRI (Op de Beeck in press).

• (b) Hyper-band effects aliased into fMRI patterns (fMRI hyperacuity): Hyper-band neuronal pattern effects are aliased into the fMRI patterns because individual voxels sample fine-grained neuronal patterns in a biased fashion.

  • (b1) Compact-kernel filter produces aliases: Local averaging produces slight voxel biases that are highly sensitive to columnar-scale shifts of the voxel grid (Kamitani & Tong 2005, illustrated in Boynton 2005).

  • (b2) Complex spatiotemporal filter produces aliases: Voxel biases result from the complex way a voxel samples the neuronal activity through its fine-grained signal-supplying vasculature.

We argue that explanations a and b2 are more plausible than b1 and explore the intriguing possibility of b2 in some detail.

Two models of how an fMRI voxel samples the neuronal activity pattern

(1) Voxel as compact-kernel filter

We like to think of voxels as averaging boxes. Like a pixel of a digital image, an averaging-box voxel would give us the average signal within its boundaries. This is a simple way to discretize an image. We know that the averaging-box model is a simplification: neuronal activity outside a voxel's boundary can be reflected in the voxel's fMRI signal as hemodynamic effects are washed into the voxel from the outside.⁴

To accommodate hemodynamic blurring, we can think of the voxel as sampling the neuronal activity pattern by weighting each location according to a little spatial kernel (e.g. a Gaussian), which is centered on the voxel and whose spatial extent exceeds the voxel's boundaries. This is the way voxel sampling is typically conceptualized in the literature (e.g. Engel et al. 1997, Parkes et al. 2005, Shmuel et al. 2007; but see Olman et al. 2007; for a review see Uğurbil et al. 2003). Both the averaging-box and the Gaussian model are compact-kernel models in that a voxel samples activity by weighting inputs with a kernel that has all its weight concentrated in a compact local region. What predictions does the compact-kernel model suggest?

In this section we argue that a compact-kernel model is essentially consistent with the idea that fMRI quite simply provides an “image” of neuronal activity – albeit a blurred one. In the spatial frequency-domain description, this means that each spatial frequency band of the neuronal pattern is reflected in the same spatial frequency band of the voxel pattern – with the exception of hyper-band spatial frequencies, which are eliminated or greatly diminished (Fig. 1, left column).

Aliasing can occur but is expected to be weak

What will happen to above-Nyquist spatial frequencies (i.e. the hyper band) under the compact-kernel model of voxel sampling? Hyper-band information may still be reflected in single voxels. However, these signals are expected to be weak. For the voxels not to contain any hyper-band information at all, the different selectivities sampled would have to be exactly balanced when weighted with the voxel's compact kernel. Consider the case of decoding grating orientation from V1, assuming that each voxel simply samples its contents by averaging. The voxel would have to contain an exactly equal number of columns preferring each orientation in order not to have any bias at all. This is unlikely to be the case, even if the organization were very fine-grained, regular, and had no low-spatial-frequency component (see illustration in Boynton 2005). Therefore slight biases are expected. However, the local averaging does reduce the strength of the bias. In the language of image sampling, the local averaging acts as a low-pass filter preceding the subsampling of the image at the voxel locations. In image processing, low-pass filtering is applied prior to subsampling as a method of “anti-aliasing”. Anti-aliasing serves to prevent hyper-band components from projecting into the samples. (Aliases are undesirable if our goal is simply to obtain an image of the original signal.) The Gaussian filter approximating fMRI voxel sampling (including the hemodynamic blurring effect) may not achieve perfect anti-aliasing, so some hyper-band information might pass. However, we expect a greatly weakened signal from the hyper band.

Population decoding performance should drop sharply as voxel width increases beyond the grain of the organization

A simple simulation of sampling the pattern of ocular dominance strips with averaging-box voxels (Fig. 2) shows that the functional contrast between a voxel's response to left-eye and right-eye stimulation drops sharply as voxel width increases beyond the width of the ocular-dominance strips (Fig. 2b). Although slight biases remain, population decoding performance (or the contrast of an ideal observer's linear combination of all voxels covering the pattern) reflects the loss of functional contrast and also drops sharply as voxel width increases (Fig. 2c, solid black line).

Fig. 2. Sampling the ocular-dominance pattern with averaging-box voxels of increasing size: population decoding suffers, but single-voxel contrast t values remain approximately constant.

A simple two-dimensional simulation of sampling the pattern of ocular-dominance strips with averaging-box voxels. (a) The pattern of ocular-dominance strips in the monkey in a drawn reconstruction by S. LeVay (http://hubel.med.harvard.edu/b27.htm; LeVay et al., 1975). To simulate the spatial scale of the human ocular-dominance pattern, we assumed a strip width of 0.75 mm and superimposed square voxels (right) of up to 6-mm width. (b) For voxels of any given width placed in random locations on the pattern, we determined the probability density function of the voxel contrast, i.e. (L-R)/voxel area, where L and R are the areas of left and right ocular dominance within the voxel, respectively. When voxels are very small (width: 0.2 mm), almost all of them are located either entirely in the left or entirely in the right ocular-dominance domain; few voxels straddle the boundary between the domains. When voxels are large (width: 3-6 mm), each voxel samples both domains and most of their contrast, thus, cancels out. (c) The expected decoding information predicted by the simulation (ideal-observer t value, vertical axis) plotted as a function of voxel width for single voxels (dotted gray) and for a voxel population covering the entire pattern (solid black). As shown in (b) larger voxels suffer from contrast cancellation. However, larger voxels also benefit from greater noise reduction through averaging the signal within their boundaries. Consider the single voxel case (dotted gray line). As voxel size increases for very small voxels, noise reduction through averaging improves decoding (dotted gray line rises). Single-voxel decoding performance peaks when voxel width approximately matches domain width (i.e. 0.75 mm). As voxel size increases further, signal cancellation becomes an issue and single-voxel decoding suffers. However, for large voxels (width: 3-6 mm), the two effects end up balancing each other, for the following reason: When voxel width doubles, voxel area squares, and noise (i.e. standard error of the contrast estimate) is divided by two. What happens to the signal (i.e. the contrast estimate)? For intuition, we can imagine the strips as a vertical grating. Adjacent ocular dominance strips in the voxel cancel and any signal comes from at most a single strip at the edge of the voxel that ends up without a partner. When voxel width is doubled, the area of the non-cancelling strip relative to the area of the voxel (i.e. the contrast) is divided by 2. So as voxel width doubles, the contrast and its standard error are both divided by 2, thus the voxel's t value remains unaffected. This holds only for strip patterns, such as ocular dominance columns. For a checkerboard pattern, for example, the t value would roughly be divided by 2 each time voxel width doubles. However, there would still be some contrast, even for large voxels covering many squares of the checkerboard (unless the voxel's width is an exact multiple of the checkerboard period).

For the entire population of voxels (solid black line), the picture is different: decoding performance drops monotonically as the voxels get larger. Note, however, that the whole-volume performance using all voxels in the pattern area (black axis on the left) is much higher than the single-voxel performance (gray axis on the right). The ideal observer will optimally weight each voxel, thus benefiting from high contrast in single small voxels, while the overall factor by which the noise is reduced through combining the evidence across the pattern area is the same for all voxel sizes (square root of the total pattern area). In the plot, the decoding information is represented by the ideal-observer t value, which is the contrast t value obtained by optimally weighting the voxel input. Assuming Gaussian independent and identically distributed noise at each location of the neuronal pattern, the ideal-observer t value is monotonically related to d', decoding accuracy, and stimulus-response mutual information in bits. The units are arbitrary as they scale with the noise level in the neuronal input.

Interestingly, even large voxels can retain some bias, responding more to stimulation of one eye than the other (Fig. 2c, dotted gray line). Larger voxels suffer from greater contrast cancellation. However, larger voxels also benefit from greater noise reduction through averaging the signal within their boundaries. For the strip patterns in this simulation, these two effects balance out when the voxels are large (for details, see legend of Fig. 2). While a single large voxel may have a similar contrast-to-noise ratio as a single smaller one, the set of smaller voxels filling the large voxel conveys much more information.

Our simulation of ocular-dominance strip sampling with averaging-box voxels suggests that decoding performance should drop sharply as voxel width increases. This prediction, of course, depends on the spatial-frequency spectrum of the neuronal contrast pattern, so different results may obtain for different neuronal representations.

Decoding may be based mainly on below-Nyquist neuronal-pattern frequencies

Let us assume we sampled the ocular-dominance pattern with voxels of 3-mm width. Fig. 2c (solid black line) suggests that averaging-box voxels would still convey some information at this voxel width. Is the pattern information that produces the ocular contrast from the lower spatial-frequency bands of the ocular-dominance pattern that can be directly imaged with 3-mm voxels or is the information aliased into the voxel pattern from the hyper band?

In a separate simulation (Fig. 4), we sampled the pattern of ocular-dominance strips with different kernels, including a single-point, an averaging-box, and a Gaussian kernel. The single-point filter samples the input pattern at a single point at the center of the voxel. This is not realistic as a model of an fMRI voxel, but included here because point sampling entails maximal aliasing as there is no reduction of the amplitude of high-frequency components through local averaging (i.e. no contrast cancellation). As expected, point sampling of the ocular-dominance strips with a 3-mm grid leads to substantial aliasing. The resulting “voxel” pattern contains low as well as high frequency energy, but the low-frequency band does not resemble the low-passed version of the original pattern. Instead the low band of the voxel pattern is dominated by aliases from high frequencies, whose amplitude is undiminished for point sampling. (The point-sampling pattern nevertheless provides only weak decoding information, because it does not benefit from the noise reduction associated with local averaging. This is illustrated in Fig. 4b by scaling the voxel pattern intensities according to noise standard deviation units, yielding a weaker-contrast voxel pattern than for the other kernel filters.)

For the averaging-box and Gaussian kernels, each voxel benefits from noise reduction through averaging within a local neighborhood. However each voxel also suffers from contrast reduction caused by cancellation between the ocular domains. The local averaging works as a low-pass filter, strongly reducing (though perhaps not cleanly eliminating) hyper-band spatial frequency components. When we smooth or downsample the voxel pattern, we see the low-band of the original neuronal pattern (compare Fig. 4a, bottom and Fig. 4b, right column). This is in contrast to the single-point filter, for which the low band of the “voxel” pattern was dominated by aliases from high frequencies. For averaging-box and Gaussian kernel filters, the low band of the voxel pattern essentially reflects the low band of the neuronal pattern. Aliases of hyper-band components may also be present in the low band of the voxel pattern, but they are weak in amplitude.

Aliasing will be highly sensitive to head-motion-induced subvoxel shifts of the voxel grid that cannot be corrected

Aliasing is extremely sensitive to small shifts of the sampling grid relative to the sampled signal (Fig. 3). If a coarse sampling grid is shifted by half a period of an above-Nyquist-frequency signal to be sampled, the low-frequency alias will invert (i.e. shift its phase by half a period). This holds for point sampling as well as for compact-kernel sampling (only aliases will be weaker in the latter case).

When sampling a very fine-grained organization such as orientation or ocular-dominance columns, shifting the voxel grid by a small fraction of the voxel width is expected to completely change the aliasing pattern of weak selectivities across the voxels. As a consequence, linear decoding would require a completely different set of weights.

Given that some degree of head motion is inevitable, shifts of the voxel grid cannot be avoided altogether during image acquisition. The shifts would have to be small in relation to the length of the period of the spatial organization studied. This appears an unrealistic assumption for orientation columns.

Importantly, once the voxel patterns have been acquired, it is not possible to correct the hyper-band aliases for the shifts by head-motion correction (i.e. by resampling the voxel pattern). For an intuition on this, consider the voxel patterns in Fig. 3 (right column, top and bottom). Resampling of the voxel patterns can only improve the representation of the below-Nyquist range, where the voxel pattern represents the underlying activity like an image. (This may explain why cutting-edge high-resolution fMRI can represent these fine-grained patterns accurately.)

In our opinion, these considerations further weaken the idea that substantial amounts of hyper-band information enter the voxel pattern through aliasing if voxels are essentially compact-kernel filters. There are two alternative explanations: (a) The decoding information is from the below-Nyquist-spatial-frequency band of the neuronal patterns, which the voxels can directly image without aliasing (Op de Beeck in press). (b) The fMRI voxels are not compact-kernel filters.

(2) Voxel as complex spatiotemporal filter

We know that the compact-kernel model of voxel sampling is a simplification. A voxel samples vessels of various sizes, which can include capillaries, venules, and draining veins. Each larger vessel sampled washes in signals from a particular direction. The distribution of wash-in directions is not going to be isotropic around the center of the voxel as the compact-kernel model would suggest. Moreover, the precise architecture of the signal-supplying venous vasculature is different for each voxel, so each voxel actually samples the neuronal pattern with a unique filter. Finally, the spatiotemporal structure of the filter depends not only on the vascular architecture, but also on the dynamics of the blood flow. The compact-kernel model glosses over all of these complications. Here we argue that the spatiotemporal complexities of the hemodynamics may be of practical significance as they suggest the possibility of enhanced sensitivity to columnar-level neuronal information.

Voxel + venules = multipronged sensor?

Conventionally, the complexities of the hemodynamics are considered a nuisance that limits the spatiotemporal accuracy and precision of fMRI. But we can look on the bright side and suggest, somewhat provocatively, that an fMRI voxel, together with its signal-supplying vasculature, could serve as a uniquely shaped, finely branched, “multipronged sensor” of neuronal activity patterns. Although obtaining an accurate high-resolution image of the fine-grained spatial pattern of neuronal activity may prove elusive with fMRI, each such voxel may sample the activity pattern with a unique and finely structured spatiotemporal filter, whose spectral sensitivity profile in space and time may have some unexpected properties. For example, complex spatiotemporal filters of this type might be sensitive to spatial frequencies of the neuronal activity pattern that exceed the Nyquist limit suggested by voxel size and hemodynamic point spread.

Sensitivity to hyper-band information might be stronger than for a compact kernel

Consider our simulation of sampling the pattern of ocular-dominance strips with different filters (Fig. 4). As discussed above, the compact-kernel filters may have benefited from some aliasing of the hyper band frequencies, but the voxel pattern's low band was dominated by a simple image of the low band of the neuronal patterns. We constructed a complex-kernel filter (Fig. 4b, bottom row) by spatially bandpassing a noise pattern and imposing a 3-mm-FWHM Gaussian envelope. Because of its fine-grained structure, the filter has a greater sensitivity to hyper-band neuronal pattern information. As a result the voxel pattern it predicts discriminates left and right-eye stimulation with greater contrast. When the voxel pattern is smoothed (right column), we see that the low band of the voxel pattern does not resemble the low band of the original neuronal pattern (a, bottom). This suggests that this filter produces more pronounced aliases of higher frequency components of the neuronal pattern in the low band of the voxel pattern than the compact-kernel filters.

A voxel's filter may not be space-time separable and space-invariant

The hemodynamic response to neuronal activity has been independently characterized in time (e.g. Boynton et al. 1996; de Zwart et al. 2005) and space (e.g. Engel et al. 1997; Parkes et al. 2005; Shmuel et al. 2007; for a review see Uğurbil et al. 2003). This approach implicitly assumes that the spatial profile does not change over time (or, equivalently, that the temporal profile does not depend on spatial location, i.e. space-time separability) and that the filter properties will be similar across different voxels (i.e. space invariance). The assumptions of space-time separability and space invariance may have led us to overestimate the smoothness of the actual spatiotemporal kernel with which a single voxel samples the local neuronal activity pattern. The two assumptions (a) lead to smoother estimates of the spatial and the temporal mode and (b) invite us to imagine the spatiotemporal kernel defining a voxel's sampling of the neuronal activity pattern as the outer product of the spatial and the temporal mode (Fig. 5, left). However, the same smooth temporal and spatial modes (when independently estimated) are also consistent with a complex and non-smooth spatiotemporal filter that is not space-time separable (Fig. 5, right). Such a filter could be much more sensitive to hyper-band spatial and temporal frequencies of the neuronal activity patterns.

Fig. 5. A complex spatiotemporal filter with high-spatial frequency sensitivity could have the same spatial and temporal mode and across-voxel average as a simple outer-product filter.

Conventionally, the spatial and temporal aspects of the filter, by which an fMRI voxel samples neuronal activity, are characterized independently. The implicit assumption of this approach is that the spatiotemporal filter is space-time separable, i.e. that the spatial profile does not change over time (or, equivalently, vice versa) and hence the spatiotemporal kernel obtains as the outer product of the spatial and temporal modes (left). However, the assumption of space-time separability of the filter is questionable and the same spatial and temporal modes could obtain for a complex non-space-time-separable spatiotemporal filter, when characterized independently by a spatial and a temporal mode (right). Note that for this complex filter the spatial profile changes over time (and, equivalently, the temporal profile depends on the spatial location). So the appearance of smoothness and compactness of the filter could arise as an artefact of considering space and time separately. Moreover, the fine structure of the complex spatiotemporal filter would be unique for each voxel, so characterizing all voxels jointly by a single spatiotemporal kernel might artefactually give rise to the appearance of a compact kernel filter. The figure illustrates the two scenarios for the simplified case of a single spatial dimension.

Imagining a voxel's complex spatiotemporal filter

In order to help us imagine the actual structure of the spatiotemporal filter, with which an intracortical voxel may sample the neuronal activity pattern, we performed a toy simulation in two dimensions (Fig. 6). The simulation is based on a depiction of intracortical venules in a cortical cross-section (Fig. 248 in Duvernoy et al. 1999). First we computed a hemodynamic delay map (Fig. 6a) indicating, for each location in the cortex, how long it takes the blood from that location to reach the pial surface. To compute the delay map, we assumed that the blood in the capillary bed will drain in a straight line toward the closest venule entry point. We then placed an intracortical voxel in the scene (white square in Fig. 6a) and simulated fMRI acquisitions averaging signal across 100 ms (typical EPI slice acquisition duration) and repeated immediately (every 100 ms).

The hemodynamic delay map allowed us to compute how a neuronal-pattern impulse at time 0 (the start of the first acquisition) would influence each subsequent fMRI acquisition. The neuronal pattern at time 0 produces hemodynamic signals inside and outside of the voxel. These signals are then drained toward the pial surface. For all the blood passing through the voxel on a given acquisition, we computed the cortical location of origin at time 0 (i.e. the time of the neuronal impulse). The set of these cortical locations provides the input to the voxel for the acquisition in question. Each panel of Fig. 6b corresponds to an acquisition and shows the spatial region (black) of the neuronal impulse at time 0 sampled by that acquisition. Jointly these temporal snapshots characterize the spatiotemporal filter, with which the voxel samples neuronal activity.

So far we have imagined how a neuronal-pattern impulse (i.e. a spatial activity pattern with no temporal extent) occurring at time 0 would influence a temporal sequence of acquisitions. Conversely, we can ask how a given single acquisition is influenced by a temporally-extended neuronal activity pattern preceding it. We can think of the spatiotemporal neuronal pattern as a sequence of neuronal pattern impulses. If we assume linear summation of the hemodynamic effects of these neuronal pattern impulses, then the spatiotemporal filter, with which a given acquisition samples the spatiotemporal neuronal pattern, is also described by the panels of Fig 5b.

Our toy simulation shows that an fMRI voxel samples neuronal activity with a spatiotemporal filter that depends not only on the size of the voxel and the time between acquisitions, but on two other factors: (1) the structure of the voxel's signal-supplying vasculature, (2) the hemodynamics (particularly the speed of blood flow). The voxel essentially samples its contents in the first acquisition (resembling the averaging-box model). By the ninth acquisition, it samples a discontiguous set of domains distributed around it, whose spatial extent depends on the speed of the blood and the EPI-slice acquisition time, not on the size of the voxel. Each latency is associated with its own unique spatial characteristic, because hemodynamically more remote input will be washed into the voxel at a greater latency. Thus, the filter is not space-time separable. Finally, shifting the voxel off the venule it samples would completely change the structure of the spatiotemporal filter. Thus, the filter is not space invariant: Each voxel samples the neuronal pattern in a unique manner.

This toy simulation is restricted to two dimensions and unrealistic in a number of other respects. However, the further complications ignored here are unlikely to simplify the picture and support a compact-kernel filter model, space-time separability, or space invariance of the filter.

We assumed a realistic EPI slice acquisition of 100 ms and a realistic capillary drainage speed of 0.5mm/s. This results in spatial profiles for a single acquisition that are quite finely structured. We emphasize that the spatial scale of this structure depends on capillary blood speed and slice acquisition time duration, not on the size of the voxel. A voxel may therefore have sensitivity to spatial frequencies beyond the Nyquist limit that would apply if voxels simply averaged neuronal activity within their boundaries. High-spatial-frequency neuronal information may, thus, be present in a low spatial frequency sampling of the hemodynamic response even with voxels of conventional sizes in the millimeter range.

More generally, the model suggests that information can be projected from one spatiotemporal frequency band to another (Fig. 1, right column) and that temporal properties of the neuronal pattern can be reflected in spatial properties of the voxel pattern and that spatial properties of the neuronal pattern can be reflected in temporal properties of the voxel pattern.

Aliasing will be less sensitive to subvoxel shifts of the voxel grid

In the context of the compact-kernel-filter model, we noted that slight shifts of the voxel grid would completely change pattern of lower-frequency aliases of hyper-band neuronal pattern information. The same would hold if a complex fine-grained kernel were shifted slightly relative to the sampled pattern (e.g. by half a period of a hyper-band frequency it samples). In the complex-spatiotemporal-filter model, however, the vasculature provides the fine-grained component of the filter. Since the vasculature stays in place when the voxel grid is slightly shifted, the hyper-band aliases in the filter output could be much less sensitive to such shifts. This would explain why the inevitable head-motion artefact present in fMRI data does not prevent us from decoding what might be fine-grained neuronal pattern information.

Empirical evidence

So far two studies have empirically addressed the origin of the decoding information first utilized by Kamitani and Tong (2005) and Haynes and Rees (2005). The first study by Gardner et al. (2006) suggested that the signal allowing the decoding of grating orientation from early visual cortex stems from large draining veins (as ascertained by T2*-weighted venograms). As a result, decoding performance was robust to downsampling and remained above chance level even at an in-plane resolution of about (1 cm)².

The second study by Shmuel et al. (in press) addressed the question for ocular-dominance columns in V1 using human high-field (7 Tesla) fMRI. These authors as well argue for a contribution to decoding from veins that reflect a biased sample of the ocular-dominance domains. However, they also suggest a contribution from gray-matter voxels and it is unclear whether the signals in those voxels could be accounted for by a compact-kernel filter model or would require the assumption of a complex spatiotemporal filter (as for the gray matter voxel in our simulation, Fig. 6).

Consistent with these reports, optical imaging sometimes shows orientation specificity in large veins. Such venous sampling biases suggest that the hemodynamics can transpose high-spatial-frequency neuronal effects into low-spatial-frequency hemodynamic effects sampled by fMRI voxels. This appears consistent with a complex-spatiotemporal-filter model. However, Gardner et al. (2006) correctly point out that the venous biases could also reflect a large-scale organization (i.e. low-band neuronal pattern information).

The more detailed consequences of the complex-spatiotemporal-filter model are challenging to test directly by experiment. They include the possibility that pure gray-matter voxels are sensitive to fine-grained neuronal activity patterns and that a voxel's filter depends on properties of the hemodynamics, such as the speed of blood flow. At present the complex-spatiotemporal-filter model serves as a reminder that we do not know enough to rule out the presence of unexpectedly fine-grained spatiotemporal information in fMRI voxel patterns.

Concluding remarks

Hyperacuity is a term borrowed from vision science. In vision, hyperacuity refers to the fact that human observers can localize a visual stimulus with a precision corresponding to about one fifth of the width of a retinal cone receptor (Wandell 1995; Westheimer and McKee 1977). The analogy does not yield any simple answers, but leads us straight into the complexities discussed in this paper. Consider the fact that the imperfect optics of the eye disperse the retinal image of a stimulus, but this does not hurt hyperacuity. Similarly, fMRI hyperacuity cannot be ruled out by the finding that low-passing the voxel pattern does not hurt decoding performance. Hyper-band information aliased into the voxel pattern would not be restricted to the high band of the voxel pattern eliminated by low-passing. Moreover, each fMRI voxel samples the neuronal activity pattern through a unique local structure of vessels and a complex hemodynamic process, about which we know too little to be sure that it cleanly eliminates hyper-band information. Herrmann von Helmholtz (1868) famously noted that given its substantial imperfections, the human eye – if it were an optical device – would have to be returned to the manufacturer (quoted from Biedermann 2002). He went on to say that he would be happy nevertheless to keep his own eyes, defects and all, as long as possible. In neuroimaging, as in biological vision, the essential function may depend on the information transmitted, irrespective of whether intermediate stages conform to the simplest possible representation of the input pattern: a perfect image.