Abstract
This paper describes the combination of three-way contingency tables and geostatistics to visualize the non-linear impact of two putative covariates on individual-level health outcomes and test the significance of this impact, accounting for the pattern of spatial correlation and correcting for multiple testing. The methodology is used to explore the influence of distance to mammography clinics and census-tract poverty level on the rate of late-stage breast cancer diagnosis in three Michigan counties. Incidence rates are significantly lower than the area-wide mean (18.04%) mainly in affluent neighbourhoods [0-5% poverty], while higher incidences are mainly controlled by distance to clinics. The new simulation-based multiple testing correction is very flexible and less conservative than the traditional false discovery rate approach that results in a majority of tests becoming non-significant. Classes with significantly higher frequency of late-stage diagnosis often translate into geographic clusters that are not detected by the spatial scan statistic.
Keywords: Breast cancer, Multiple testing, Semivariogram, scan statistic, Poverty, Screening
Introduction
Many studies in the literature report association between late-stage breast cancer diagnosis and covariates, such as socio-economic status, access to health care, marital status, ethnicity and neighbourhood of residence (Farley and Flannery, 1989; Barry and Breen, 2005; MacKinnon et al., 2007). Such relationships are explored using a variety of techniques that depend primarily on the spatial support of the data (aggregated versus individual-level data) and are typically based on a linear or log-linear model. For individual-level data, logistic regression is fitted to indicators of early/late stage diagnosis; see examples in Barry and Breen (2005) or Hahn et al. (2007). On the other hand, Poisson regression is the method of choice for modeling count data, such as the number of late-stage breast cancer cases aggregated at the level of ZIP codes (Wang et al., 2008) or counties (Thomas and Carlin, 2003; Lin and Zhang, 2007). Multilevel models are also increasingly used to include information about the individual woman residence (e.g., see Gumpertz et al., 2006). In all cases, little attention is paid to the visual description of the relationships among variables. Yet, visualization is a vital tool for the analyst, often providing a more intuitive view of the association or interaction than numerical summaries along with characteristics of her neighbourhood of alone.
The use of multiway contingency tables is here proposed to help visualize the impact of putative factors on categorical health outcomes, such as cancer stage at diagnosis. Meyer et al. (2008) review the main tools available to visualize multiway tables, such as mosaic, association and sieve plots, and an example of the application of mosaic plots to visualize three-way loglinear models is given in Theus and Lauer (1999). For the simple case of two covariates and one binary health outcome (i.e. early versus late-stage diagnosis) a simple table of the frequency of occurrence of either outcome, say late stage, provides a much more intuitive and interpretable graphical display. This tool has been used, for example, to display the likelihood of observing a particular geological facies as a function of the recorded value of two seismic attributes (Hong et al., 2008).
Besides the exploratory visualization of the impact of covariates, the health scientist is usually interested in flagging any statistically significant behavior which could confirm or invalidate a particular hypothesis. At first glance, a simple randomization approach (Edgington and Onghena, 2007) could be used to test whether the observed frequency of late-stage diagnosis is significantly lower or higher than what is expected under the assumption of no impact of putative factors. However, such a procedure would overlook the presence of spatial autocorrelation in the data (Fortin and Jacquez, 2000): residences of late-stage cancer diagnosis might not be distributed randomly in space. In addition, one would like to conduct such test for different levels of the covariates (e.g. different poverty levels) to account for non-linear relationships, thereby increasing the number of tests and the risk that some tests will turn out significant by chance alone. In this paper, a geostatistical simulation-based approach (Goovaerts, 2009a) is developed to incorporate spatial dependence and multiple testing correction in the testing procedure. This innovative approach is used to explore the influence of distance to mammography clinics and census-tract poverty level on the rate of late-stage breast cancer diagnosis in three Michigan counties.
Data and Methods
Invasive breast cancer cases, diagnosed during the calendar years 1985 through 2002 in Michigan, were used to illustrate the methodology. Approximately 92% of these records, which were compiled by the Michigan Cancer Surveillance Program (MCSP), were successfully geocoded at residence at time of diagnosis. The present study focused on cases diagnosed for white women in 83 census tracts of three counties in Southwestern Michigan: Berrien, Cass and Van Buren; see Figs. 1A and 1B (data are aggregated for confidentiality reasons). Out of the 2,118 women diagnosed with breast cancer during that time period, 18% of cases were defined as late-stage (i.e. regional and distant metastatic cancer) according to the SEER General Summary Stage classification (Young et al., 2001).
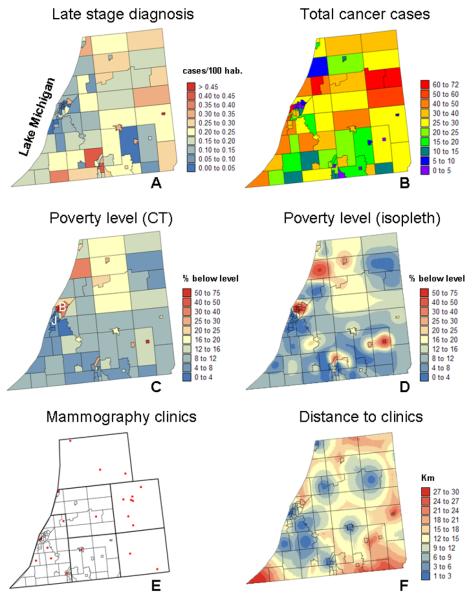
Fig. 1.
Maps of late-stage breast cancer incidence rate (A) and number of cancer cases (B) in three Michigan counties, by census tract (CT), 1985-2002. Maps of percentage of habitants living below the federally defined poverty line in 1990: original census tract data (C) and results of disaggregation using ATP kriging (D). Location of mammography clinics in 2006 (E), and map of population-based distance to the closest clinic (F). Note the contrasted economic statistics for the Twin Cities of Benton Harbor and St Joseph, denoted by letters B and J in Fig. 1C.
Two covariates that according to the literature (e.g. Barry and Breen, 2005; MacKinnon et al., 2007; Wang et al., 2008) could potentially explain the spatial pattern in late-stage diagnosis were considered: percentage of habitants living below the federally defined poverty line in 1990, and distance to mammography clinics located in these three counties and adjacent counties in Michigan (Figs. 1C & F). Poverty data, which were available at the census-tract level, were disaggregated using the Area-to-Point (ATP) kriging method introduced in Goovaerts (2008) to map the within-tract variation (Fig. 1D). In this illustrative example, access to screening facilities was quantified using two simple metrics: Euclidian distance between each residence and the nearest clinic based on 2006 location (Fig. 1E), and a population-based Euclidian distance to account for lower travel speeds expected in urban versus rural census tracts. In the second case, the following heuristic procedure was developed: 1) census-tract population data were disaggregated to the nodes of a 300-m grid using the same method as for poverty data in Fig. 1E, 2) each patient residence and clinic was relocated to the closest node on that 300-m grid, 3) each residence was then linked to each of the 22 clinics by a suite of linear segments joining grid nodes to form an approximately straight travel path, 4) the population data Pd at each node along the path were then combined using the heuristic formula: Σ300×log(1+10^Pd), and 5) the smallest of the 22 distances was rescaled by the average population density and used as the population-based Euclidian distance. The rank correlation between the two metrics was 0.90. Since the population-based distance yielded a slightly larger R-square and odd ratio in a logistic regression using cancer stage as dependent variable, it was adopted in the present study. Beware that this paper does not pretend to conduct a thorough analysis and interpretation of the spatial pattern of breast cancer incidence for this small area in Michigan, but rather, the main objective is to showcase some of the features of the proposed methodology.
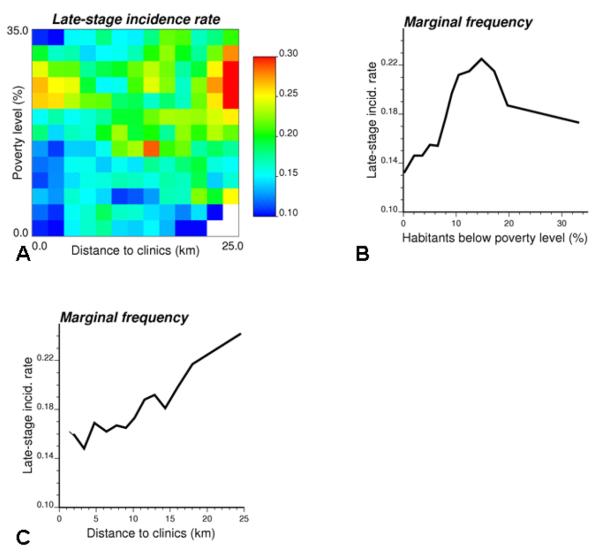
Fig. 2.
Late-stage breast cancer incidence rates computed for 169 classes of poverty level × distance to mammography clinics (A), and their row and column averages (B,C). Rates based on less than 10 cases are considered missing and displayed in white in the frequency table.
Characterization of spatial patterns
The information about each cancer case, referenced geographically by its residence's spatial coordinates uα=(xα,yα), takes the form of an indicator of early/late stage diagnosis:
| (1) |
The spatial pattern of these indicator data can be characterized using the experimental semivariogram computed as:
| (2) |
where N(h) is the number of pairs of cases within a given class of distance and direction, known as spatial lag and denoted h. The spatial increment [i(uα )–i(uα + h)]2 is non-zero only if cases at uα and uα+h are diagnosed at different stages. The indicator variogram 2 γ̂ I (h) thus measures how often the stage of diagnosis of two cases a vector h apart is different. In other words, it quantifies the transition frequency between early and late-stage diagnosis as a function of h. In presence of spatial clusters of early or late-stage diagnosis, the variogram value is expected to increase with the lag h and reaches a plateau at a distance, called range, which corresponds to the average size of these clusters. If these clusters are non-circular, different ranges will be observed along different directions, a situation referred to as spatial anisotropy. The study of indicator semivariograms can thus provide important information about the nature and scale of the process responsible for the spatial distribution of cancer stages at diagnosis.
Quantifying the impact of covariates
The impact of covariates, such as proximity to screening facilities or area-based measures of economic deprivation, can be assessed by computing the frequency of occurrence of the event of interest (i.e. late-stage diagnosis) for a given combination of these factors. For example, the frequency for late-stage diagnosis at residence u with poverty level v(u) within the class ]vl-1;vl] (e.g. 0-5%) and distant from the closest screening facility by s(u) miles within the class ]sl'-1;sl'] (e.g. 0-5 miles) is simply computed as the proportion of late-stage diagnosis for all nll' cases residing in this poverty×distance class:
| (3) |
where n is the total number of cases, with i(uα; vl)=1 if vl-1 < v(uα) ≤ vl and zero otherwise, while i(uα; sl')=1 if sl'-1 < s(uα) ≤ sl' and zero otherwise. As the number L and L' of classes increases, fewer cases might fall within each class, resulting in less reliable frequencies. In this paper, joint frequencies fll' were smoothed by application of a 3×3 moving window: the frequency fll' is estimated using data from classes ]vl-2;vl+1] and ]sl'-2;sl'+1]. The marginal frequency, that is the frequency within the class of a single attribute, is simply computed as:
| (4) |
with .
Both joint and marginal frequencies can be assembled into a L×L' frequency table and marginal frequency plots to visualize the joint and individual impacts of covariates on health outcomes. For example, Figure 2 shows the table and plots obtained for 13 classes of poverty level and distance to clinics (L=L'=13). The frequency table can be viewed as a particular case of a three-way contingency table where the third variable takes only two possible values: late or early stage of diagnosis. The use of marginal and joint frequencies offers a flexible alternative to parametric models such as logistic regression since no assumption is made regarding the form of the relationship (e.g. linearity). Furthermore, the large number of observations usually available (e.g. more than 100,000 cases for the entire state of Michigan) allows one to consider many classes of values ]vl-1;vl] and the interaction between multiple covariates, such as poverty and access to health care in Equation (3).
Detection of significant impact using spatial randomization
Testing the significance of the impact of a covariate on the rate of late-stage diagnosis amounts at testing whether the frequency fl or fll' is significantly different from the frequency f computed over the entire dataset regardless of the covariate values. For example, the null and alternative hypotheses for the joint frequency fll' are formulated as follows:
With:
| (5) |
This step typically requires computing the probability of obtaining a result as extreme as the test statistic fl or fll' by chance alone, under the null hypothesis of absence of impact of covariates. This probability, called the p-value of the test, is obtained by comparing the test statistic to its expected distribution under the null hypothesis H0. A straightforward approach to derive the null distribution of the test statistic fl or fll' is through randomization: the frequency (3) or (4) is computed after a random swapping of the indicators i(uα) over all n residences, which amounts at assuming that the likelihood of being diagnosed late or early does not depend on any of the covariates. This operation is repeated many times (e.g. K=4,999 draws), yielding a distribution of simulated frequency values under the null hypothesis. The p-value of the j-th test, noted Pj with j=l+(l'-1)L, is then computed simply as the proportion of simulated frequencies that are smaller (larger) than the observed frequency fll′ if fll′ is smaller (larger) than the global frequency f:
| (6) |
with if , and zero otherwise.
By using the randomization procedure, one implicitly assumes that late and early stage cases are randomly distributed in space, once the impact of covariates has been taken into account. Yet, for the Michigan dataset the indicator semivariogram (Equation 1) reveals the existence of a spatial structure (range of autocorrelation = 50 m) at a scale smaller than the census tracts, hence independent of the socio-demographic variables. Such a short distance is also unlikely to impact the travel time and access to screening facilities. This local spatial structure can be incorporated in the testing procedure by replacing the random swapping of indicators by a spatially ordered swapping whereby indicators are shuffled so that the indicator semivariogram is reproduced. This spatial randomization was here performed in two steps: 1) sequential Gaussian simulation (Goovaerts, 1997) is used to assign to each of the 2,118 residences a random number so that the set of random numbers reproduces the spatial pattern inferred from the semivariogram model, and 2) the residences are ranked according to these random numbers and the top f percent (i.e. 18% for this case study) are assigned an indicator i(k)(uα)=1 (late stage) while the rest is classified as early stage (i(k)(uα)=0). These “simulated indicators” are then used to compute frequencies and according to expressions (3) and (4). The two steps are repeated K=4,999 times to generate the reference distribution of the joint and marginal frequencies.
Multiple testing correction
The last step in the testing procedure consists of rejecting the null hypothesis if the p-value does not exceed the significance level α, which is typically set to 0.05 (significant difference) or 0.01 (highly significant difference). In other words, one rejects the null hypothesis if it appears very unlikely (i.e. 0.05 or 0.01 probability) that the frequency for a given class vl or sl′, or a combination of both, could be observed if the covariate(s) were not influencing the rate of late-stage diagnosis. Using the notation Pj for the p-value of the j-th test, the decision rule can be expressed as:
The significance level a of α test represents the probability of incorrectly rejecting the null hypothesis, that is declaring a covariate significant when it has, in fact, no significant impact. This wrong decision is known as a “false positive” or a “type I error”.
In the present application with L=L′=13, the test will be repeated for each of the J=169 classes of poverty level and access to screening facilities, increasing the likelihood that some tests will turn out significant by chance alone (even if the null hypothesis of no impact of covariates is true in all cases). Multiple testing corrections reduce the significance level applied to each test so that the overall false positive rate is kept to less than or equal to the user-specified significance level α. Methods to correct for multiple testing differ in their ease of implementation and their stringency. In this paper, the false discovery rate (FDR) approach was adopted since it is less restrictive and more powerful than other approaches, such as the simple Bonferroni correction (Castro and Singer, 2006). In particular, the step-up FDR procedure proposed by Benjamini and Hochberg (1995) for independent tests was used. The first step is to rank all Jp-values by ascending order (smallest p-value has rank 1) and apply a correction that increases as the rank r of the p-value decreases, i.e. the multiplication factor is r/J. The decision rule is however sequential and involves checking that the p-value of rank r does not exceed the adjusted significance level, starting with the largest p-value (r=J). Once this condition has been met for a given rank r′, the adjusted significance level αFDR is set to r′α/J and applied to all tests of hypothesis. The decision rule can then be formulated as:
A limitation of this procedure is the assumption of independence of tests (p-values), which is not satisfied if a moving window is applied to the frequency table. Several techniques have been proposed recently to account for correlated test statistics in the FDR approach (Benjamini and Yekutieli, 2001; Romano et al., 2008). In this paper, a new simulation-based approach is proposed to take advantage of the fact that the randomization procedure allows the computation of the probability for several frequency classes to be significant simultaneously; for example, the joint p-value for two classes (R=2) is computed empirically as:
| (6) |
with , and zero otherwise. The indicator function I[.] takes a value of 1 if, for the k-th randomization, the proportion of non-significant tests exceeds a given threshold β. For example, if β =0, the p-value P12 will report the proportion of randomizations where at least one of the two classes is non-significant. The objective is to find the largest subset of R classes that have a high probability of being jointly all significant, that is associated with a small p-value: P1..R ≤ α. Therefore, the decision rule is applied once to the joint p-value instead of sequentially to p-values computed for each individual test as in all variants of the FDR approach. Unlike Benjamini and Hochberg's approach, the new procedure, coined Joint Empirical Frequency (JEF) approach, is step-down (Romano and Shaikh, 2006) in that it starts with the smallest p-value (i.e. the most significant test, rank r=1). For the example of Expression (6), the two classes and would then correspond to the two tests with the smallest p-values. If the condition P12 ≤ α is satisfied, then the test with the third smallest p-value is considered next for inclusion in the subset. The decision rule can then be formulated as:
Results
Logistic regression
The influence that poverty level and distance to screening facilities, as well as their interaction, exert on late-stage diagnosis at the individual level was first explored using a traditional logistic regression. The spatial coordinates of residences was used in the computation of the population-based Euclidian distance to screening facilities. On the other hand, two options were considered for poverty level: constant within each census tract (CT) or spatially varying according to the kriging map of Fig. 1D. The odds ratios, reported in Table 1, show that cancer patients are more likely to be diagnosed late if they live in poor neighborhoods and away from mammography clinics. Although the impact of poverty level is enhanced by the use of kriged estimates relative to census tract aggregates, all the 95% confidence intervals include an odds ratio equal to one, indicating that none of the findings are statistically significant.
Table 1.
Results of logistic regression (odds ratios and 95% confidence intervals) using three covariates: logtransformed poverty level and distance to screening facilities, and their interaction. Poverty level is either assumed constant within each census tract (CT) or spatially varying according to the kriging map of Fig. 1D.
| Poverty estimation | Poverty level | Distance to clinics | Interaction |
|---|---|---|---|
| CT-constant | 1.20 0.53-2.73 |
1.25 0.63-2.47 |
0.99 0.74-1.34 |
| Kriging | 1.43 0.71-2.88 |
1.38 0.75-2.51 |
0.95 0.73-1.22 |
Frequency table and plots
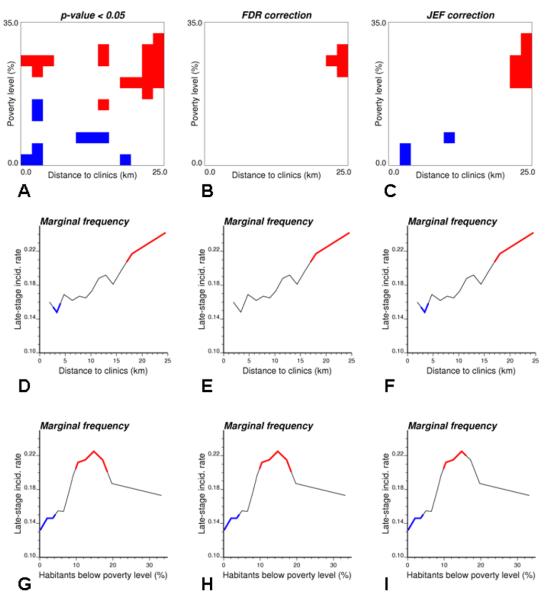
An easy way to look at the individual-level correlations without making any assumption regarding the linearity of the relationship is to compute joint frequencies according to expression (3). Based on logistic regression results, kriging estimates of poverty level were preferred to census tract values in the analysis. Thirteen equal-frequency classes were formed for each covariate, resulting in 169 joint classes of poverty level and distance to mammography clinics to which each cancer case was assigned. The rate of late-stage diagnosis was computed for each class and then smoothed using rates from adjacent classes in that table. The separate impact of each covariate was captured by the marginal distributions that were obtained simply by averaging the table rows and columns according to Expression (4). The first frequency plot (Fig. 2B) shows that late-stage incidence rate increases up to a 16% poverty level, and then it declines and reaches the area-wide rate of 0.18. The second graph (Fig. 2C) shows a steady increase in late-stage diagnosis that accelerates once the distance to mammography clinics exceeds 15 km.
The smoothed frequency table in Fig. 2A facilitates the visualization of the interaction among the two covariates. It reveals that proximity to clinics has almost no impact on incidence rates for affluent neighbourhoods [0-5% poverty], while for the 10-15% poverty level the incidence rate always exceeds the area-wide rate regardless of proximity to clinics. As expected, late-stage cancer incidence is the largest for high poverty and long driving time to mammography clinics (top right corner in the frequency table). The table also highlights the unexpected decrease in late-stage diagnosis for cases residing in economically distressed urban census tracts with short driving distance to screening facilities. This non-linear impact of poverty level was already noticed on the frequency plot of Fig. 2B. This surprising decline is caused by low incidence rates recorded in Benton Harbor, a city with high poverty level and 90% African-American population. This result suggests that the area-based measure of economic distress might not be an accurate descriptor for white women in these census tracts. Another, more optimistic, explanation is that these patients benefitted from access to three mammography clinics located in the “Twin City” of St Joseph that has very different demographics: 90% white and $37,000 household income instead of 5.5% white and $17,500 for Benton Harbor.
Significance and multiple testing correction
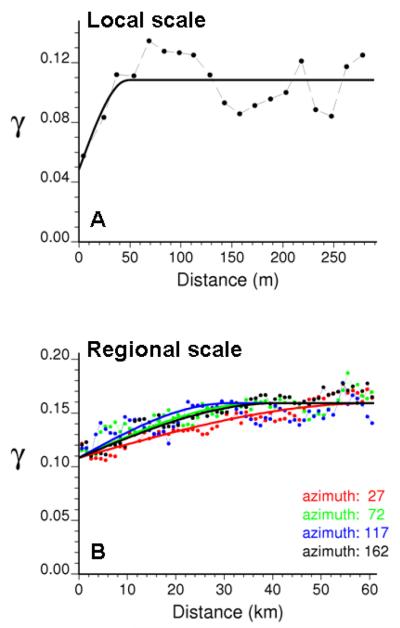
The statistical significance of the visual trends detected on the graphs of Figure 2 was assessed by testing each joint and marginal frequency for significant differences with the area-wide rate of late-stage diagnosis. A geostatistical randomization procedure that accounts for the pattern of spatial correlation of indicator data was implemented. The spatial connectivity of late-stage cancer cases was first explored using the indicator semivariogram (equation 2). To account for the wide range of separation distances between cancer cases (from a few meters to 112 km), two semivariograms with different lag classes were computed: 20 lags of 15 meters to characterize the small-scale variation of the data, and 62 lags of 1km to look at the regional patterns. The first indicator semivariogram (Fig. 3A) indicates that late detection cases do not occur randomly in space, yet individual-level factors such as age or family history generate a large variability over very short distances (1st range = 48 meters). At a larger scale (Fig. 3B), the connectivity becomes direction-dependent: the semivariogram, hence the lack of connectivity, increases more slowly in the NE-SW direction (azimuth = 27° as measured in degrees clock-wise from the N-S axis). This spatial anisotropy reflects the gradient of decreasing late-stage cancer incidence towards the lake shore which was apparent on the incidence map of Fig. 1A. For the present application, the focus is on the local scale of variability which was modelled using a nugget effect and a spherical model with a range of 48.2 meters (Goovaerts, 2009b).
Fig. 3.
Experimental indicator semivariograms with the model fitted (solid line) computed for different options: omnidirectional for short distances (A) and directional for long distances (B).
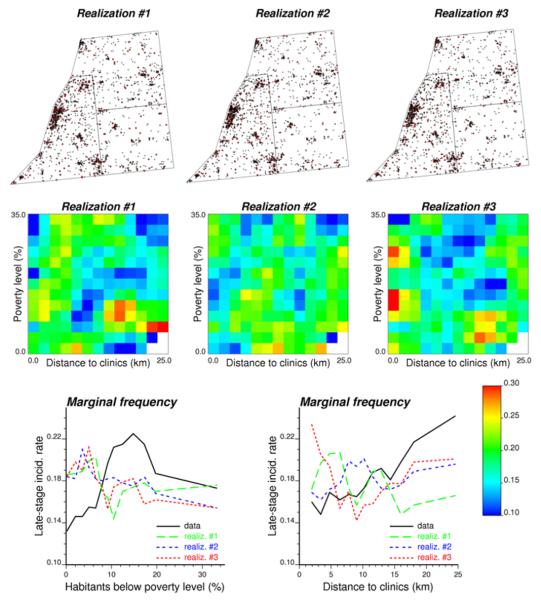
Based on the semivariogram of Fig. 3A, 4,999 realizations of the spatial distribution of late-stage cancer diagnosis were generated by sequential Gaussian simulation. The first three realizations are displayed at the top of Figure 4. Each randomized map of late-stage cases was processed using the same procedure as the original data, yielding a frequency table and two plots of marginal frequencies; see results for first three realizations in Figure 4. The simulated joint and marginal frequencies were then used to compute the p-value of the tests according to Expression (6). Figure 5 (1st column) shows that for multiple classes of poverty level and distance to screening facilities the frequency of late-stage cancer incidence is significantly smaller or larger than the tri-county average of 18% for α=0.05. Poverty level mainly explains significantly low incidences (blue segments), while high incidences (red segments) are mainly controlled by distance to clinics. Such significant impact of both covariates was missed by the logistic regression approach.
Fig. 4.
Location of patient residences and the simulated stage at diagnosis (x = early stage, ● = late stage). Frequency tables and marginal frequency plots are generated for each of the three simulated maps and compared to results obtained from actual data in Figure 2 in order to compute the p-values of the tests of hypothesis.
Fig. 5.
Impact of multiple testing correction on the significance of joint and marginal frequencies computed in Figure 2: No correction (1st column), False discovery rate (FDR) correction (2nd column), and simulation-based procedure (3rd column). In all graphs, blue (red) pixels and segments represent incidence rates that are significantly lower (higher) than the incidence rate expected under the assumption of no impact of covariates on late-stage diagnosis (α=0.05).
One might argue that significant tests are bound to occur given the large number of classes being tested. This effect was corrected using the well-established FDR approach (Figure 5, 2nd column) and the innovative simulation-based JEF approach that accounts for correlation among frequencies in multiple testing correction (Figure 5, 3rd column). As expected, both types of correction reduce the number of significant frequency classes, yet both covariates still exert a significant impact. The FDR approach appears to be more conservative than the JEF procedure for the frequency table (see also Table 2, 2nd row), which confirms results obtained for other procedures incorporating the dependence of p-values (e.g. Romano and Shaikh, 2006). On the other hand, both types of correction yield fairly similar results for the frequency plots.
Table 2.
Impact of the randomization procedure (random swapping versus spatially ordered swapping of indicators of late-stage diagnosis) on the results of the test of hypothesis. The number of incidence rates in the contingency table of Figure 2A that are declared significantly larger or smaller than the tri-county average of 18% are reported for α=0.05 and three types of multiple testing correction: No correction, False discovery rate (FDR) correction, and simulation-based procedure (JEF).
| Multiple testing correction |
|||
|---|---|---|---|
| Swapping | None | FDR | JEF |
| Random | 20/15 | 3/2 | 9/4 |
| Spatially ordered | 19/9 | 4/0 | 8/3 |
The impact of the geostatistical randomization procedure on the results was investigated by repeating the analysis using a traditional random swapping of indicator data. Spatially ordered randomization yields slightly larger p-values for the test of hypothesis: mean = 0.188 versus 0.178 for traditional randomization, which translates into fewer frequency classes being declared significantly different from the tri-county average. Accounting for the spatial connectivity of late-stage cancer cases is expected to create clusters of cases of similar stage (either late or early stage) in the simulations, leading to wider distributions of the simulated test statistic and larger p-values. Table 2 indicates that this increase mainly impacts the testing of lower frequencies: 9 significant classes versus 15 for the random swapping. Multiple testing correction, however, greatly reduced differences between the two randomization schemes.
Geographic clusters
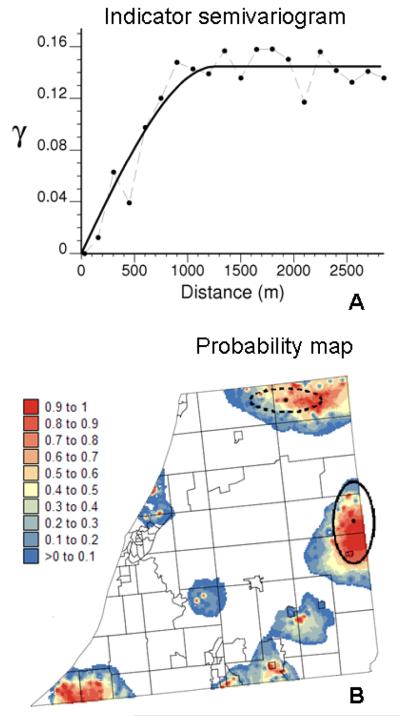
Since both covariates are spatially structured (recall Figs. 1D&F), one should expect the cases that belong to the same poverty × distance class in the frequency table to display some type of spatial clustering. Mapping cases from a class of significantly high frequency of late-stage diagnosis would thus help delineating areas that should be targeted for intervention. The spatial connectivity of cases within classes of significantly high frequency after JEF correction was quantified using the indicator semivariogram (1) where i(uα)=1 if the case uα is within a red cell in Fig. 5C, and zero otherwise. The semivariogram model in Figure 6A has a range of autocorrelation of 1,263 meters, which indicates the average size of clusters of higher frequency. This model was used with indicator kriging (program AUTO-IK, Goovaerts, 2009c) to map the likelihood of observing a significantly high frequency of late-stage diagnosis across the three counties (Figure 6B). The probability map reflects the impact of distance to screening facilities on the likelihood of being diagnosed late (compare to Fig. 1F), which agrees with the interpretation of the frequency plots in Figure 5F.
Fig. 6.
Map of the probability of occurrence of significantly higher frequency of late-stage diagnosis (B) obtained using kriging and the semivariogram model inferred from indicator data (A). Ellipses represent the primary (solid) and secondary (dashed) clusters of high relative risks of late-stage diagnosis detected using the spatial scan statistic.
For comparison purpose, areas of excess of late-stage diagnosis were also delineated using the spatial scan statistic implemented in SatScan 8.0 (Kulldorff, 2009). A Bernoulli model was chosen with a maximum cluster size of 5% of the total number of cases. Elliptic windows were allowed (medium penalty for non-compactness) and the default of no geographic overlap was used so that secondary clusters would not overlap the most significant cluster. The statistic was adjusted for more likely clusters, which required an iterative procedure (analysis stopped when the p-value exceeds 0.05). Results were overlaid on the kriged map of Figure 6B: a primary cluster (solid line) and a secondary cluster (dashed line), both bearing strong similarity with areas of high risk, were found. The analysis of clusters in the attribute space (i.e. frequency table), however, revealed several geographic clusters that were not detected by the spatial scan statistic, in particular in the southwest corner of the study area with lower access to screening.
5. Conclusions
Frequency tables and plots provide a straightforward non-parametric visualization tool to explore the impact of two continuous or ordered categorical covariates on the likelihood of health outcomes, such as cancer stage at diagnosis. Although this paper describes the analysis of individual-level data, the same approach can be applied to data aggregated over small census geographies like census tracts. The new procedures for spatial randomization and multiple testing correction, which proved to be less conservative than the traditional FDR approach, could be easily applied to other statistical tests for cluster or boundary detection. Statistical significance can be established for specific combinations of covariate values and results can be mapped to gain insight about the geographic distributions of classes with significantly high or low frequencies, supplementing the application of traditional spatial scan statistics.
The analysis of breast cancer data in three Michigan counties shed some light on the non-linear impact of distance to mammography clinics and census-tract poverty level on the rate of late-stage diagnosis. Proximity to clinics has almost no impact on incidence rates for affluent neighbourhoods [0-5% poverty] and poor neighbourhoods [10-15% poverty] where incidence consistently exceeds the area-wide mean (18.04%). The frequency table also flagged the outlying behaviour of Benton Harbor community: the incidence of late-stage diagnosis recorded for the small white population is low despite the magnitude of the area-based measure of economic distress, which might lead one to question the use of such measure for a small fraction of the census-tract population. Last, the disaggregation of census poverty data using area-to-point kriging enhanced the impact of that covariate in the logistic regression.
Although the predictive variables in the frequency analysis were significant, the census-derived poverty measure and the as-a-bird-flies measure of proximity to screening facilities are surrogate estimates of individual-level income and screening experiences, respectively. No data were available on individual income or screening practices. In addition, the locations of the screening facilities were from 2006 while poverty data were from the 1990 census, a temporal mismatch from the 1985-2002 breast cancer dataset. The next step is to apply the same methodology to the entire state of Michigan using more robust measures of access to mammography clinics (e.g., two-step floating catchment method described in Wang et al., 2005) and county-level rates to allow a finer analysis in time and reduce temporal mismatch with screening practices and poverty data. Another area of research is the extension of the approach to more than two covariates; for example by conducting a factor analysis to summarize the information contained in multiple covariates using a few descriptors (e.g., see Wang and Luo, 2005). Last, contextual variables could be incorporated into the analysis by creating multiple neighborhood-level contingency tables and exploring how results change between neighborhoods.
ACKNOWLEDGEMENTS
This research was funded by grants R44-CA132347-02 and R43-CA135814-01 from the National Cancer Institute. The views stated in this publication are those of the author and do not necessarily represent the official views of the NCI.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- Barry J, Breen N. The importance of place of residence in predicting late-stage diagnosis of breast or cervical cancer. Health & Place. 2005;11:15–29. doi: 10.1016/j.healthplace.2003.12.002. [DOI] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. (Series B).Journal of the Royal Statistical Society. 1995;57(1):289–300. [Google Scholar]
- Benjamini Y, Yekutieli D. The control of the false discovery rate in multiple testing under dependency. The Annals of Statistics. 2001;29(4):1165–1188. [Google Scholar]
- Castro MC, Singer BH. Controlling the false discovery rate: a new application to account for multiple and dependent tests in local statistics of spatial association. Geographical Analysis. 2006;38:180–208. [Google Scholar]
- Edgington ES, Onghena P. Randomization Tests. 4th Edition Chapman & Hall; New York, NY: 2007. [Google Scholar]
- Farley TA, Flannery JT. Late-stage diagnosis of breast cancer in women of lower socioeconomic status: public health implications. American Journal of Public Health. 1989;79:1508–1512. doi: 10.2105/ajph.79.11.1508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fortin M-J, Jacquez GM. Randomization tests and spatially auto-correlated data. Bulletin of the Ecological Society of America. 2000;81(3):201–205. [Google Scholar]
- Goovaerts P. Geostatistics for Natural Resources Evaluation. Oxford University Press; New York, NY: 1997. [Google Scholar]
- Goovaerts P. Kriging and semivariogram deconvolution in presence of irregular geographical units. Mathematical Geosciences. 2008;40(1):101–128. [PMC free article] [PubMed] [Google Scholar]
- Goovaerts P. Medical geography: a promising field of application for geostatistics. Mathematical Geosciences. 2009a;41(3):243–264. doi: 10.1007/s11004-008-9211-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goovaerts P. Combining area-based and individual-level data in the geostatistical mapping of late-stage cancer incidence. Spatial and Spatio-temporal Epidemiology. 2009b;1:61–71. doi: 10.1016/j.sste.2009.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goovaerts P. AUTO-IK: a 2D indicator kriging program for the automated non-parametric modeling of local uncertainty in earth sciences. Computers and Geosciences. 2009c;35:1255–1270. doi: 10.1016/j.cageo.2008.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gumpertz ML, Pickle LW, Miller BA, Bell BS. Geographic patterns of advanced breast cancer in Los Angeles: associations with biological and sociodemographic factors (United States) Cancer Causes Control. 2006;17(3):325–339. doi: 10.1007/s10552-005-0513-1. [DOI] [PubMed] [Google Scholar]
- Hahn KME, Bondy ML, Selvan M, Lund MJ, Liff JM, Flagg EW, Brinton LA, Porter P, Eley JW, Coates RJ. Factors associated with advanced disease stage at diagnosis in a population-based study of patients with newly diagnosed breast cancer. American Journal of Epidemiology. 2007;166:1035–1044. doi: 10.1093/aje/kwm177. [DOI] [PubMed] [Google Scholar]
- Hong S, Ortiz JM, Deutsch CV. Multivariate density estimation as an alternative to probability combination schemes for data integration. In: Ortiz J, Emery X, editors. Geostatistics. GECAMIN Ltd; Santiago, Chile: 2008. pp. 197–206. 2008. [Google Scholar]
- Kulldorff M, Information Management Services, Inc. SaTScanTM v8.0: Software for the spatial and space-time scan statistics. 2009 http://www.satscan.org/
- Lin G, Zhang T. Loglinear residual tests of Moran's I autocorrelation and their applications to Kentucky breast cancer data. Geographical Analysis. 2006;39:293–310. [Google Scholar]
- MacKinnon JA, Duncan RC, Huang Y, Lee DJ, Fleming LE, Voti L, Rudolph M, Wilkinson JD. Detecting an association between socioeconomic status and late stage breast cancer using spatial analysis and area-based measures. Cancer Epidemiology Biomarkers & Prevention. 2007;16:756–762. doi: 10.1158/1055-9965.EPI-06-0392. [DOI] [PubMed] [Google Scholar]
- Meyer D, Zeileis A, Hornik K. Visualizing contingency tables. In: Chen C, Härdle W, Unwin A, editors. Handbook of Data Visualization. Springer-Verlag; Berlin: 2008. pp. 590–616. [Google Scholar]
- Romano JP, Shaikh AM. Stepup procedures for control of generalizations of the familywise error rate. The Annals of Statistics. 2006;34(4):1850–1873. [Google Scholar]
- Romano JP, Shaikh AM, Wolf M. Control of the false discovery rate under dependence using the bootstrap and subsampling. TEST. 2008;17(3):417–442. [Google Scholar]
- Theus M, Lauer SRW. Visualizing loglinear models. Journal of Computational and Graphical Statistics. 1999;8(3):396–412. [Google Scholar]
- Thomas AJ, Carlin BP. Late detection of breast and colorectal cancer in Minnesota counties: an application of spatial smoothing and clustering. Statistics in Medicine. 2003;22:113–127. doi: 10.1002/sim.1215. [DOI] [PubMed] [Google Scholar]
- Wang F, Luo W. Assessing Spatial and Nonspatial Factors for Healthcare Access in Illinois: Towards an Integrated Approach to Defining Health Professional Shortage Areas. Health and Place. 2005;11:131–146. doi: 10.1016/j.healthplace.2004.02.003. [DOI] [PubMed] [Google Scholar]
- Wang F, McLafferty S, Escamilla V, Luo L. Late-stage breast cancer diagnosis and health care access in Illinois. Professional Geographer. 2008;60:54–69. doi: 10.1080/00330120701724087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young JL, Jr., Roffers SD, Ries LAG, Fritz AG, Hurlbut AA. SEER Summary Staging Manual - 2000: Codes and Coding Instructions, National Cancer Institute. National Institutes of Health; Bethesda, MD: 2001. (Pub. # 01-4969). [Google Scholar]