Abstract
Conventional methods widely available for the analysis of spike trains and related neural data include various time- and frequency-domain analyses, such as peri-event and interspike interval histograms, spectral measures, and probability distributions. Information theoretic methods are increasingly recognized as significant tools for the analysis of spike train data. However, developing robust implementations of these methods can be time-consuming, and determining applicability to neural recordings can require expertise. In order to facilitate more widespread adoption of these informative methods by the neuroscience community, we have developed the Spike Train Analysis Toolkit. STAToolkit is a software package which implements, documents, and guides application of several information-theoretic spike train analysis techniques, thus minimizing the effort needed to adopt and use them. This implementation behaves like a typical Matlab toolbox, but the underlying computations are coded in C for portability, optimized for efficiency, and interfaced with Matlab via the MEX framework. STAToolkit runs on any of three major platforms: Windows, Mac OS, and Linux. The toolkit reads input from files with an easy-to-generate text-based, platform-independent format. STAToolkit, including full documentation and test cases, is freely available open source via http://neuroanalysis.org, maintained as a resource for the computational neuroscience and neuroinformatics communities. Use cases drawn from somatosensory and gustatory neurophysiology, and community use of STAToolkit, demonstrate its utility and scope.
Keywords: Computational neuroscience, Information theory, Neural coding, Neurodatabases, Data sharing
Introduction: Unrealized Potential of Information-Theoretic Measures for Neurophysiology
Understanding how the brain represents and processes information is an extraordinarily complex problem, requiring a wide range of experimental preparations, measurement techniques, physical scales, experimental paradigms, and computational methods. Effective collaboration across each of these domains is crucial to progress in neuroscience. Computational neuroinformatics can aid many such collaborations by synthesizing computational neuroscience—analyses of neural representation and information processing—and the standards-based methods for archiving, classifying, and exchanging neuroscience data embodied in this journal’s title and reviewed in its pages by Gardner et al. (2003, 2008a, b), Kennedy (2004, 2006), and Koslow and Hirsch (2004).
The neural coding problem—how neurons represent and process information with spike trains—can be approached in a rigorous, quantitative manner. Information theory, originally developed as a means of studying modern communication systems (Shannon 1948), is now being applied to questions of neural coding by many laboratories (Ince et al. 2009, Quian Quiroga and Panzeri 2009, Victor 2006). Although many of these newly-developed methods have high potential significance for our understanding of neural coding and classification in health and in disease states, they are not easily adapted, adopted, or utilized widely throughout the neurophysiology community because they require significant time for implementation, testing, and matching to appropriate datasets. Toward reducing these barriers to wider utilization of such methods, we have developed and released STAToolkit, an open source and open access suite of information-theoretic analytic methods.
STAToolkit is a component of an evolving computational neuroinformatic resource for the sharing and analysis of spike train data. This resource integrates the neurophysiology data repository at Neurodatabase.org (Gardner et al. 2001a, b, 2005) with a suite of complementary methods for information theoretic and other advanced analyses of spike trains. The goal of this component is to make emerging and significant analysis techniques available to the experimental neurobiologist who is not a computational expert or programmer.
A specific motivating focus of the project was on the analysis of data from neurophysiology experiments where stimuli can be divided into discrete categories, and responses are in the form of spike trains. Information theoretic analyses here quantify how well the stimuli can be distinguished based on the timing of neuronal firing patterns. We illustrate the utility of STAToolkit with examples from parietal cortex and a brainstem gustatory nucleus (nucleus tractus solitarius), and other neural systems. Each of these advances the goal of understanding the dimensions of neural coding.
Another motivation for making available a suite of tools was in order to facilitate testing of three overarching meta-hypotheses:
different regions, networks, or modalities within the nervous system may utilize different neural codes or coding strategies,
individual regions, networks, or modalities may utilize different coding at different times, or in different contexts, and
the mechanisms of neural or mental disorders may be better understood by discriminating neural coding correlates of such disorders.
These remain meta-hypotheses because they can only be explored by the independent action of individual investigators whose work is enabled by such algorithms and tools as those the project make available. The union of results so obtained—made available through conventional literature and new-modality channels—may develop and test such meta-hypotheses.
The application of information theoretic concepts to the study of neural coding is non-trivial, because straightforward estimates of information theoretic quantities often require prohibitively large amounts of data. Alternative methods reduce the amount of requisite data, but do so at the expense of making assumptions about the neural system under study. Because we lack a priori knowledge about the appropriateness of these assumptions, it is essential that multiple methods be made available to analyze datasets from multiple systems.
This provides the third motivation for implementing a suite of selected analytical methods: not all methods are applicable to all data sets. The applicability of a particular method to a specific data set depends upon:
The amount of experimental data
Assumptions about the topology of the response space
Assumptions about the nature of the neural code
In addition, different methods provide different insights, and the dependence of information on method parameters provides insight about the nature of the encoding.
Earlier versions of this material have appeared in abstract form (Gardner et al. 2007a; Goldberg et al. 2006a, b, c, d, 2007; Vaknin et al. 2005).
STAToolkit Design and Methodology
Information and Entropy
In describing the capabilities of the toolkit, we distinguish between information methods and entropy methods. Information methods are those that estimate the mutual information (in the Shannon 1948 sense) between an ensemble of spike trains and some other experimental variable. We further distinguish between formal information and attribute-specific information, as proposed by Reich et al. (2001a). Formal information concerns all aspects of the response that depend on the stimulus. It is estimated from the difference between the entropy of responses to an ensemble of temporally rich stimuli and the entropy of responses to an ensemble of repeated stimuli. Attribute-specific information refers to the amount of information that responses convey about a particular experimental parameter. If the parameter describes one of several discrete categories, we refer to it as category-specific information. Entropy methods are those methods that estimate entropy from a discrete histogram, a computation common to many information-theoretic methods. Although information is defined as a difference in entropies and usually calculated in this fashion, there are strategies (e.g., the “binless” method, see below) that largely bypass this step.
Information Methods
A recent survey of information-theoretic methods is provided in Victor (2006). Our design principles included the following criteria for selecting methods to be incorporated into the initial version of the STAToolkit:
They were useful but new and therefore not generally available,
Multiple methods were needed because of the inability of any one method to give useful results for each of several common experimental designs and the data they yield,
We could offer verification of each method and provide instruction in its applicability and use.
The current version contains implementations of three information methods:
Direct method, providing formal and category-specific information (Strong et al. 1998)
Metric space method, providing category-specific information (Aronov 2003; Victor 2005; Victor and Purpura 1997)
Binless method, providing category-specific information (Victor 2002)
Each of these methods informs us about a different aspect of neural coding. The direct method makes no assumptions about the underlying neural code, but requires a prohibitive amount of data in many cases. The binless method exploits the continuity of time in order to reduce data requirements. The metric space method gives us information about the temporal precision of the neural code. The methods also have differing degrees of suitability to the analysis of multiple simultaneously recorded neurons, data for which are rapidly becoming more readily available. The direct method and the metric space method are suitable for this but the binless method is not readily applied to the multineuronal setting. A more thorough analysis of the concepts behind these methods and others for which implementation is planned as STAToolkit is enhanced, as well as an expanded rationale for applying multiple complementary methods, is found in Victor (2006).
Entropy Methods
The toolkit includes a module that includes several entropy methods. Users select methods by specifying any of several entropy_estimation_method options. The included methods are:
Plug-in, the classical estimator, based on the entropy formula H = − Σipi log2 pi.
Asymptotically debiased (Carlton 1969; Miller 1955; Treves and Panzeri 1995).
Jackknife debiased (Efron and Tibshirani 1993).
Debiased Ma bound (Ma 1981; Strong et al. 1998).
Best upper bound (Paninski 2003)
Coverage-adjusted (Chao and Shen 2003).
Bayesian with a Dirichlet prior (Wolpert and Wolf 1995).
All entropy estimation techniques have some degree of bias. The toolkit currently includes two basic bias reduction techniques: the jackknife and the classical method popularized by Treves and Panzeri (1995). Even with these techniques, it is often impossible (depending on the preparation and the choice of estimation technique) to collect enough data for entropy estimates to be useful. (For example, the “direct method” is impractical for the parietal cortex data described below). We have adopted several recently-developed and sophisticated bias-reduction techniques. One such method is the best upper bound method (Paninski 2003) which finds the polynomial entropy estimator that minimizes the error (bias squared plus variance) in the worst case. The toolkit also provides estimates of the variance of entropy estimates, which can in turn be used to compute confidence limits. These results can be obtained by setting the option variance_estimation_method for jack-knife or bootstrap.
Our choice of entropy estimation methods included in the initial STAToolkit release was based on several considerations. A necessary condition was that the methods needed to have a rigorous mathematical foundation, backed up by peer-reviewed publications. But we also recognize that criteria for utility of entropy estimation methods for neural data analysis differ from criteria in other contexts, e.g., biological sequence analysis (Hausser and Strimmer 2008). In neural data analysis, the quantity of interest is often information, which is a difference in entropies. This differencing operation can have major effects on bias properties: methods that have poor bias properties as entropy estimators may be quite useful for information, if the biases tend to cancel when entropies are subtracted; conversely, methods that have good properties as entropy estimators may have undesirable properties if the biases tend to reinforce. Moreover, neural data are intrinsically event sequences in continuous time, and the continuity of time allows for approaches that do not readily apply to discrete symbol sequences.
Because of this, we placed a high priority on including methods that were diverse in terms of their basic approaches and assumptions, rather than being prescriptive. To increase awareness of these issues by our users, we include in the STAToolkit distribution a script ( demo_entropy) that demonstrates all of the entropy methods included in the toolkit on examples drawn from a binomial distribution with ten bins and provides as well expected results as a check. We anticipate that with continued use of the STAToolkit by investigators with a variety of kinds of data and goals, heuristics will emerge that suggest that specific estimators are preferable in particular contexts—and we will collect this knowledge into documentation in future releases, and/or a knowledge base.
Input/Output
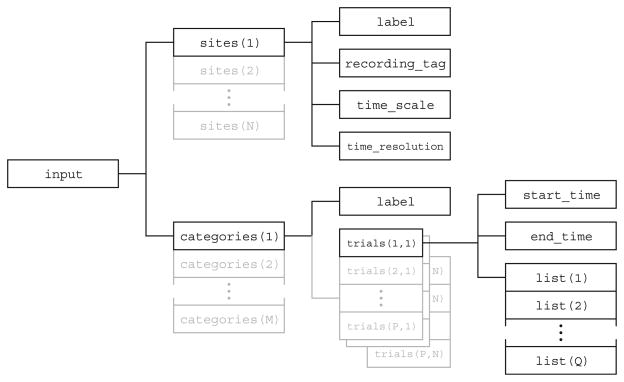
In order to modularize the development of the different components of the project, and facilitate re-use of STAToolkit modules by the community and for parallel computational engines, we developed a standard categorical data container (Fig. 1) that is:
Fig. 1.
The STAToolkit project-designed input data container facilitates application of analytic methods, including multiple information-theoretic methods to datasets. The sites tag accommodates multielectrode recordings; the categories and trials tags provide an organization broadly compatible with current experimental protocols. Variable indexed elements of the structure are extended in grey
Agnostic to the procedure that generated the data
Appropriate for both single and multichannel data
General enough to handle episodic or time-stamped data such as spike trains as well as continuously-sampled signals such as field potentials.
Each input data set is described by two easy-to-generate text-based, platform-independent files, each described in detail at http://neuroanalysis.org/toolkit/releases/1.0g/format.html:
A data file, denoted by a .stad file extension
A metadata file, denoted by a .stam file extension
The metadata file is a text file consisting of name=value pairs that describe the data in the data file. The metadata file provides information about four types of elements: the data file itself, recording sites (including multi-electrode and multi-site recordings), categories associated with any experimental/control, timed, or normal/diseased distinction, and trial-associated metadata. Users also have the option of bypassing the text-based file format and using other means to read the data into the Matlab input data structure. Documentation for the analysis options and parameters for information methods and entropy methods is available.
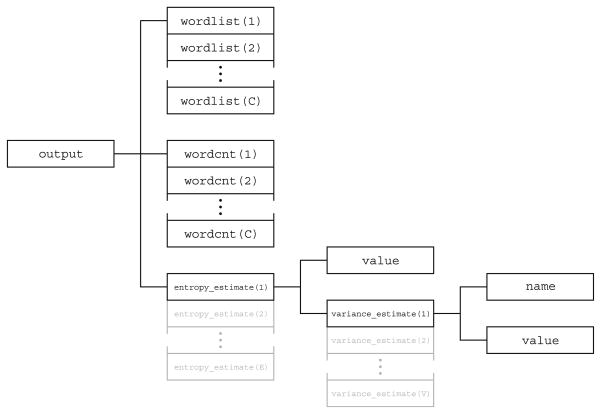
In parallel, we have developed an output data container (Fig. 2) that provides an intuitive structure for results of analyses. This specialized container stores discrete histograms and associated statistics, commonly used for estimation of entropy, and accommodates bias corrections and variance estimates.
Fig. 2.
The output data container provides an intuitive structure for the results generated by any of several information-theoretic analytic methods
Both input and output data structures are organized in a hierarchical manner. To facilitate the segregation of stimulus and response traces into categories, we have developed a framework for grouping traces on the basis of their relationships in time, recording locations, and stimulus attributes. (In parallel, we augmented the data submission procedure at neurodatabase.org to accommodate the metadata concerned with grouping, and developed methods to visualize the relationships among traces in large datasets.)
Input Structure
The input structure (Fig. 1) is organized to naturally store multineuron data and to facilitate the application of analytic methods. The top level of the input structure contains an array of sites structures and an array of categories structures. The sites structures describe the physical locations where the signals were recorded. An individual input structure can simultaneously accommodate data that consists of time-stamped events (episodic) or data sampled at regular intervals (continuous). Because the notion of categorization is central to information theoretic analysis, the recorded data is segregated into categories at the top level. These categories could be based on an attribute of the stimulus or an observed behavior that coincided with the recording. Each element in the categories array holds a two-dimensional array of trials structures, each of which corresponds to a distinct recording trial in the same category. All of the elements in a single row of the trials array correspond to a single instance of a simultaneous recording. All of the elements in a single column of the trials array correspond to repeated recordings at a single physical location. Finally, each trials array consists of a list structure with the raw data: event times for episodic data, and sampled signal levels for continuous data.
Output Structure
Many of the functions in the toolkit yield estimates of information-theoretic quantities. The output data structure (Fig. 2) is organized to facilitate intuitive storage of analysis results obtained with several different methods, and to allow for future expansion. Because the estimation of entropy from discrete probability distributions is one of the main functions of the toolkit, the output structure is organized around a histogram construct with auxiliary information such as variance estimates. The basic one-dimensional histogram ( hist1d) consists of paired arrays wordlist and wordcnt, which list the labels of the unique elements in the data set and the number of times they appear, respectively. Also present is the entropy, which is held in an array of estimate structures. Each element in the array corresponds to a different entropy estimation method. An estimate structure holds not only the estimated quantity, but also estimates of the entropy estimates’ variances, each obtained with a different variance estimation method. The hist1d structure can also be used to construct more complicated histograms. For example, a two-dimensional histogram ( hist2d) consists of hist1d structures that describe the marginal histograms across rows and columns and their corresponding marginal entropies, a hist1d structure that describes the joint histogram and the joint entropy, as well as an estimate structure that holds the mutual information.
Modular and Iterative Design
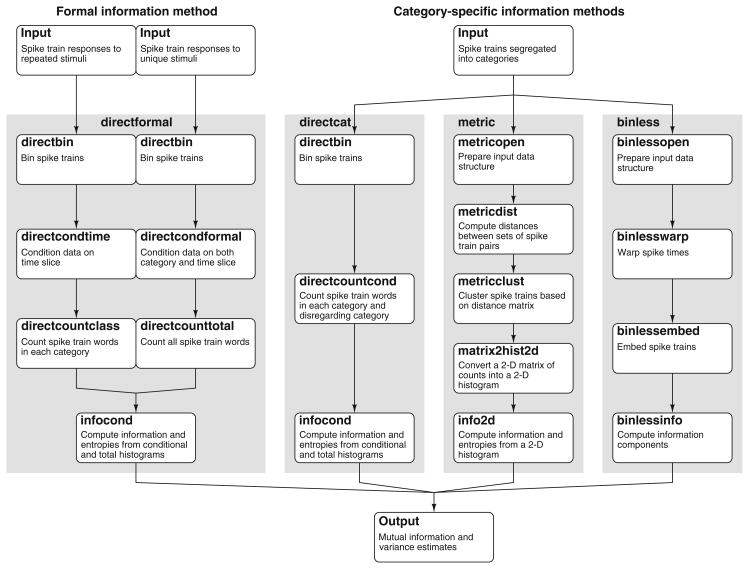
The information methods are implemented in a modular fashion (Fig. 3). While the goal of the information methods is to compute mutual information from a set of spike trains, intermediate results may be of interest to the user. Toward this goal, each algorithm has been partitioned into modules corresponding to steps that provided useful intermediate results. An additional shared module estimates entropy from a discrete histogram, a computation that arises in almost all information theoretic methods. This module provides classical bias corrections (Treves and Panzeri 1995) as well as more sophisticated methods (e.g., Paninski 2003). Further, the user has the option to use only those modules that provide the intermediate variable of interest, rather than being required to run each method to the end.
Fig. 3.
Modular implementation facilitates design of current and projected STAToolkit information-theoretic analytical methods. Computation of information and entropies for each of the direct, binless, or metric space methods is implemented as sequences of basic modules that not only provide intermediate results, but allow re-utilization as additional capabilities are added to the STAToolkit. For example, direct calculations of either formal or category information share modules for binning ( directbin), and for calculation of information and entropies from histograms ( infocond). Distinct modules are used for formal ( directcondtime, directcountclass, directcondformal, directcounttotal) and category ( directcountcond) calculations. Grey backgrounds outline modular flow. Further detail in text
In addition to being modular, code development is versioned and commented, in conformance to standard professional software practice. Development of the STAToolkit proceeded via several beta releases, each of which added significant functional enhancements. Release 0.2 (March 2006) added functions for calculation of formal information via the Direct method of Strong et al. Release 0.9 (June 2006) added the Ma entropy estimate and augmented the metric space method via the spike interval metric. It provided statistical tools for assessing the significance of information methods (a bootstrap variance estimator, and efficient routines for shuffling and jackknifing), and facilitated the use of parallel algorithms for the spike time metric, described below (Victor et al. 2007). Release 0.9.1 added Paninski’s “best upper bound” method, which is computationally intensive but provides accurate estimates with less data than the Direct method. Public release 1.0 (November/December 2006) added the Chao-Shen entropy estimator, which, though less principled than the “best upper bound” method, is very fast, and appears to provide more reliable results in some undersampled regimes, and the Wolpert-Wolf estimator, that makes explicit Bayesian use of a Dirichlet prior. There were of course in addition improvements to increase robustness, modularity, and extensibility. Successive releases included a number of tools to facilitate implementation and further development: versioning, didactic demos, exercising routines that validate the installation, and full documentation of functions and data structures.
Victor et al. (2007) presented new algorithms for analyzing multineuronal recordings that calculate similarity metrics in parallel. This dramatically increases the efficiency of analyses whose target is to characterize neural coding strategies, since this kind of analysis requires exploration of a wide range of parameters. These algorithms have been incorporated into STAToolkit, along with options to allow selection of the non-parallel versions of the calculation when the latter will be more efficient.
STAToolkit Release 1.0
Spike Train Analysis Toolkit: Capabilities and Options
In order to reach the widest possible audience, the toolkit was designed to be compatible with the most common computing environments—Windows, Mac OS, and Linux. The computational engine is written in C, which lends itself to fast execution that is critical for some of the computationally intensive toolkit components. Free C compilers are available for all of the major computing environments. The toolkit takes advantage of the advanced numerical capabilities of the free, open source GNU Scientific Library. The user interfaces with the toolkit through Matlab, which communicates with the computational engine through the MEX framework. We chose Matlab because it is a de facto standard for many members of the computational neuroscience community, and because Matlab combines a convenient means for performing additional calculations with the toolkit results with sophisticated visualization tools. Native C/C++ access is also available. This Matlab/C hybrid approach provides the toolkit with the portability and speed of C and the intuitive user interface of Matlab.
The Spike Train Analysis Toolkit Version 1.0 (STAToolkit) is implemented for use on desktop workstations and available now open source for download at http://neuroanalysis.org/toolkit. The toolkit distribution includes:
Full C and Matlab source code for the information-theoretic and entropy routines described above,
scripts for compilation and installation for Windows, Linux, and MacOS,
sample data sets,
demonstration scripts that verify that the toolkit has been properly installed and compiled and also illustrate typical usage.
A simple, platform-independent, human-readable data format
Extensive online documentation for installation and use (for example, see Fig. 4).
Fig. 4.
Extensive STAToolkit instructions at neuroanalysis.org include these descriptions of options available for precise application of STAToolkit methods to users’ datasets
Didactic Data, Demos, and Documentation
The toolkit distribution includes example data sets and demonstration scripts that verify that the toolkit has been properly installed and compiled. These scripts also illustrate typical usage. The example data sets include synth, a synthetic data set of sinusoidally modulated Poisson spike trains as described by Victor and Purpura (1997), taste, responses of taste-sensitive neurons in the nucleus tractus solitarius in rat (Di Lorenzo and Victor 2003), drift, responses of neurons in V1 to drifting gratings (Reich et al. 2001b), phase, multineuron responses described in Aronov (2003), and inforate_rep and inforate_uni, synthesized data inspired by Reinagel and Reid (2000) that is used to illustrate the calculation of formal information. The demo_entropy script is described above in the section on entropy methods.
STAToolkit includes user documentation for verifying hardware and software compatibility, installation, and use, including its utility and applicability to our target audience of neurophysiologists. One example of the level of coverage and detail is shown in Fig. 4. Documentation describes how all of the modules are used, the input and output data structures, and the options and parameters for all of the analysis techniques. The documentation also includes literature references citing the originators of the various methods we have implemented in STAToolkit, both to guide proper use of the routines and also to properly acknowledge the intellectual property of each of those who devised such methods.
STAToolkit-Enabled Spike Train Analyses
As part of the verification and testing of STAToolkit, and also to stimulate more widespread adoption of information-theoretic methods for the analysis of neural coding, we developed several collaborative use cases combining proof of concept with neuroscience significance. One of these is illustrated in some detail; two others are briefly noted below. Many of the datasets used in these analyses are available via neurodatabase.org.
STAToolkit Analyses of Neurons Encoding Information About Primate Prehension
Using STAToolkit, we analyzed single neurons and neuronal ensembles in parietal cortex of awake behaving monkeys during a series of prehension tasks, using data collected in the laboratory of E.P. Gardner. When the primate hand performs sensorimotor tasks such as grasping objects, successful performance requires sensory feedback. Tactile information sensed by mechanoreceptors in glabrous skin encodes physical properties of objects. These receptors also provide somatosensory information about the actions of the hand. Toward analyzing processing of such sensorimotor information in posterior parietal cortex, we analyzed spike trains of neurons in the hand representation of areas 5 and 7b/AIP recorded as each of two monkeys performed a trained reach-and-grasp prehension task (Gardner et al. 2007b, c). We used STAToolkit’s metric space and multineuron metric space methods to investigate which aspects of these sensorimotor behaviors are encoded by the firing of individual neurons, and by pairs and triplets of neurons:
Digital video images of hand kinematics were synchronized to recorded single- or multi-neuron spike trains, and were used to delineate the timing of task actions.
Responses on individual task trials were characterized by knob identity (location in the workspace, size and shape), approach style (forward, lateral, local/regrasp), and grasp style (power, precision, ulnar).
In some trials, the animal’s view of the target objects was unobscured (“sighted”); in others, an occluder plate prevented visualization of targets (“blocked”).
We analyzed the spike trains with the metric space method to determine how much information their temporal structure conveyed about the task kinematics and the properties of the grasped object. The efficiency of the toolkit enabled a comprehensive search of the parameter space, using different analysis window positions and sizes. STAToolkit metric space analysis of the parameter space revealed particular aspects of task kinematics and object features encoded by specific neurons in parietal cortex. In addition, the routines provided insight about what aspects of spike timing conveyed information about kinematics. Our analysis found that spike trains convey the greatest information immediately prior to hand contact, distinguishing trials in which the animal reached to the object from those in which no reach was necessary because the hand was already close to the object.
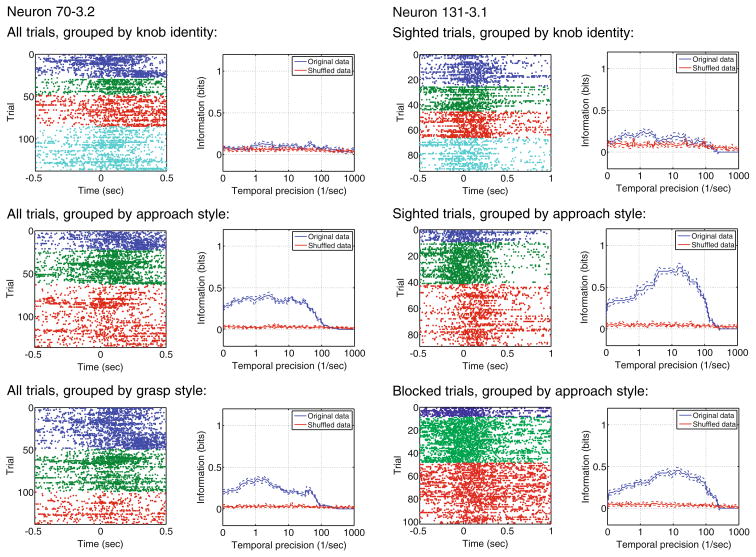
Figure 5 shows our initial analysis using STAToolkit routines. Neuron 70-3 conveys information about kinematics of grasp, not knob identity. About 0.4 bits of information are conveyed for both approach style and grasp style, with information peaking at temporal precision q=1 s−1 (corresponding to a timescale of 2 s). There was no significant difference between sighted and blocked trials in this test. Figure 5 also shows that neuron 131–3.1 again does not convey information about the knob identity. Here, significantly more information is conveyed about approach style during sighted (0.7 bits) than during blocked conditions (0.4 bits). There was a strong peak in information for both sighted and blocked trials at q=10 s−1 (corresponding to a timescale of 200 ms). A simultaneously-recorded neuron (131–3.2) displayed qualitatively similar characteristics.
Fig. 5.
Metric space analysis reveals which aspects of task kinematics are encoded by specific neurons in parietal cortex. Spike trains color-coded (top to bottom) by knob identity (1–4, rectangular or round), approach style (forward, lateral, local/regrasp), and grasp style (power, precision, ulnar) were analyzed using the metric space method. Neuron 70–3.2 codes for approach and grasp style; neuron 131–3.1 reports approach style in both sighted and occluded trials. Neither neuron reports knob identity. In each panel, rasters show raw spike timings, grouped by knob or style for visualization. Graphs report STAToolkit-derived spike information for original compared to shuffled data, as a function of spike timing
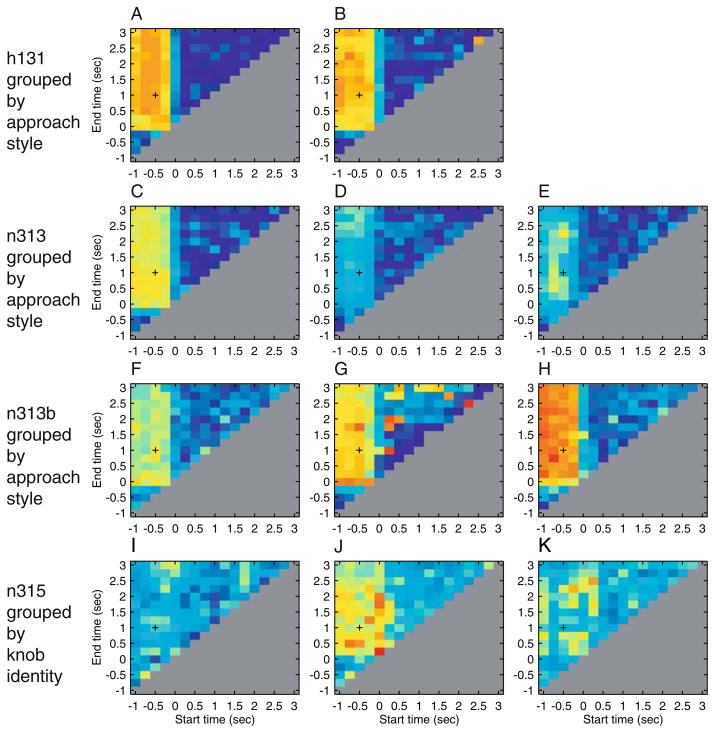
Of the 20 units analyzed from a series of single- or multi-neuron recordings, the spike trains of 11 conveyed information about approach style or knob identity. Most of the information about these features is conveyed in a brief (100 to 250 ms) window shortly before contact (Fig. 6). Demonstrating success of the approach, the metric space analysis extended conventional analyses by giving the timescales over which the spike trains convey information about the attributes of the task, and reduced the amount of a priori knowledge that is needed for analysis by eliminating the need for binning the spike train.
Fig. 6.
STAToolkit analysis of aspects of timing used to convey information. Of the 11 units shown, recorded from awake behaving monkey, eight (units A through H, from tracks h131, n313, and n313b, recorded in area 5) coded approach style and three (units I, J, and K, from track n315, recorded in area AIP) coded identity of knob grasped. These analyses of hand kinematics show that spike trains convey the greatest information immediately prior to hand contact. For each of the 11 units shown, most of the information about approach style and knob identity is conveyed in a brief (250 ms) window shortly before contact. Information above is color-coded and displayed as a function of analysis window start and end times. Red = 1.0 bit, blue = 0 bit. Four tracks are shown, each with two or three units recorded
Neighboring Neurons Convey Largely Redundant Information
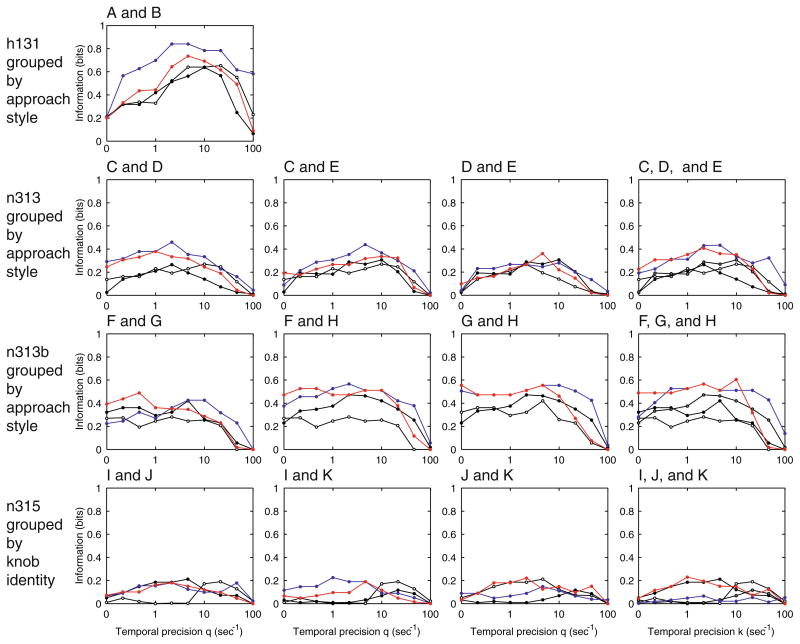
In several cases, pairs or triplets of simultaneously recorded neurons on the same or nearby electrodes were analyzed by STAToolkit routines to reveal what information about sensorimotor behaviors might be represented by the ensemble of simultaneously activated neurons. This multi-neuron analysis showed that the number of trials, although standard for experiments of this type, was marginal for the multi-neuron metric space method. (Orders of magnitude more data would be required for the direct method.) Nevertheless, we were able to show that in each of the cases examined, neighboring neurons convey largely redundant information. In some examples, the activity of the cluster is more informative than individual neurons. However, the increase in information is carried by a summed population temporal code: the neuron of origin of each spike is not significant (Fig. 7). Thus knowledge of a spike’s neuron of origin does not increase the task-related information conveyed. It is possible that a larger sample size would reveal such an increase.
Fig. 7.
Neighboring neurons convey largely redundant information. In this application of the STAToolkit to multi-neuron analyses, each of the pairs or triples shown compares joint to individual information as a function of temporal precision. Although in some examples multiple neurons convey more information than one neuron alone, this is due to a summed population code. That is, knowing the neuron in which a spike occurred does not convey more information about the task. It is, however, possible that larger sample sizes than those recorded here might have revealed such an increase. Track and unit designators correspond to those in Fig. 6
Other Use Cases
In ongoing formal collaboration with Dr. Patricia Di Lorenzo (SUNY Binghamton), the project has applied STAToolkit routines to analyze single-neuron recordings of rat brainstem gustatory neurons in nucleus tractus solitarius. This analysis yielded the first demonstration of temporal coding of flow rate of stimuli. Analyses of responses to chemically distinct substances of similar taste quality and taste mixtures showed that temporal coding contributes proportionally more for discriminations among similar tastants, than for discriminations among tastants of different qualities (Di Lorenzo and Victor 2007; Roussin et al 2008). That is, while spike counts may suffice for gross discriminations, temporal pattern is required for subtle ones. This collaboration has also yielded a menu-driven Matlab user interface that can serve as a model to aid the application of STAToolkit routines to an individual’s data, and pilot development of multidimensional scaling routines that use STAToolkit output to construct a “perceptual space” of a neuron or neural population.
The project has investigated the formal properties of the “binless” entropy method in the highly undersampled regime, with the ultimate goal of using this approach to investigate the statistics of natural scenes. This illustrates the utility of the toolkit routines to domains beyond neurophysiology, namely, digitized images.
With Igor Bondar (Moscow), STAToolkit routines were used to analyze temporal contributions to selectivity of inferotemporal cortex neurons, and to neural code stability over several weeks of recording. This illustrates the utility of intermediate results provided by the toolkit—this application only required calculation of measures of spike train similarity (the output of the module metricdist of Fig. 3).
From outside our group, one sample use case is provided by Huetz et al. (2009), who used STAToolkit and neuro-analysis.org for information-theoretic analyses of thalamo-cortical spike timing.
Toward Expansion and Further Adoption of STAToolkit
STAToolkit is one Component of a Computational Neuroinformatic Resource
STAToolkit, and other resources available via neuroanalysis.org, complement those offered via our neurodatabase.org and brainml.org sites. The three open resources together offer a metadata-searchable database of neurophysiological data from a broad spectrum of preparations and techniques, group type definitions allowing easy correlational analyses of data with sensory inputs or behavior or performance measures, instructions for applying algorithms and preparing data and algorithms for community submission, guidelines for applicability of algorithms to datasets, a neurodatabase construction kit, enabling terminologies for neurodatabase development, and guidelines for submission of new or extended terminologies. Toward further integration of the stand-alone STAToolkit with the data repository at neuro-database.org and a linked 64-processor parallel array, a suite of tools will allow our user community to select, segment, concatenate, and group datasets, select information and entropy methods, and schedule custom analyses.
Planned Expansion Leverages Modular Design
As noted above, STAToolkit design is modular, to allow additional information-theoretic and other algorithms to be implemented within the overall structure and data formats, thus expanding utility for the study of neural coding. In addition to further entropy and information methods, system design allows the planned addition of both variability and synchrony metrics. Common to all of these, enhancements originally scheduled for later implementation or suggested by users include multi-parameter methods to further characterize and match algorithms and data types, expanded grouping and classification types, relating each of these to lab-developed terminologies, expanded data converters and viewer types provided by colleagues at related projects, and versioning for multiple Matlab and Octave versions, libraries, and compilers. Expanding user interest suggests the utility of a Sourceforge site in parallel with the one at neuroanalysis.org, and a user course or workshop at one or more computational neuroscience or general meeting.
We plan expansion of entropy and bias methods, including the Nemenman-Shafee-Bialek estimator (Nemenman et al. 2002), a Bayesian technique based on a unique distribution of Dirichlet priors, and the Hausser and Strimmer (2008) estimator based on the James-Stein “shrinkage” approach. Theoretical insights developed by Paninski (2003) point to rigorous bounds on the bias and variance of several techniques. While rigorous bounds require knowledge of the underlying probability distribution of the data (which is unknown), we are nevertheless working to incorporate these ideas into the toolkit via Monte Carlo or analytic approximations of Bayesian estimates based on observed data.
STAToolkit is an Open Resource, Accepting User Contributions
In keeping with goals for open analysis and data and algorithm sharing, the STAToolkit has been designed to allow community submission of complementary information-theoretic or other algorithms. Version 1.0 includes instructions for external contributions to the STAToolkit, at http://neuroanalysis.org/toolkit/releases/1.0g/contribute.html. This includes specifications for input, output, options and parameters, and coding conventions for either Matlab or C/MEX, with guidelines for each. We continue to work with members of the computational neuroscience community to incorporate additional information theoretic techniques, as well as looking beyond information theory to other methodologies for analyzing neurophysiology data. A recent paper on entropy estimation from interspike intervals in J. Neurosci. Meth. (Dorval 2008) reports successful porting of STAToolkit to Octave, an open software package with capabilities similar to Matlab.
The STAToolkit is acknowledged as well as an exemplar by computational neuroinformatics developers. The sig-TOOL project, providing GUI-driven MATLAB-centric spike train data input and analysis, has requested that we collaborate on adding STAToolkit capability and combining interface development (Lidierth 2009; http://sigtool.sourceforge.net/). In addition, the developers of FIND (Finding Information in Neural Data; http://software.incf.org/software/finding-information-in-neural-data-find/home) at the Bernstein Centre in Freiburg note that “…we will incorporate other open source toolboxes (e.g. http://neuroanalysis.org/toolkit, an information theory based toolbox).” The Brian project (http://brian.di.ens.fr/) notes that for analysis “Brian currently includes a module for simple spike train statistics. It would be good to have more analysis functions (for example porting the Spike Train Analysis Toolkit).” Panzeri et al. (2007) and Ince et al. (2009) cite the STAToolkit and its relation to Panzeri and others’ complementary development of Python tools. Scripts for interchange between STAToolkit and Chronux (Mitra and Bokil 2008; http://chronux.org), an independent spectral analysis toolkit, are available by searching http://wiki.neufo.org, associated with the neuroinformatics summer course at the Marine Biological Laboratories, Woods Hole, MA, USA.
Acknowledgments
The STAToolkit and related computational neuroscience resources are supported by the U.S. Human Brain Project/Neuroinformatics program via MH068012 from NIMH, NINDS, NIA, NIBIB, and NSF to D. Gardner, with partial support via EY09314 from NEI to J.D. Victor. Parallel development of neurodatabase.org and related terminology, including BrainML are supported by Human Brain Project/Neuroinformatics MH057153 from NIMH, with past support from NIMH and NINDS. Data from E.P. Gardner’s lab used in the STAToolkit tests and demonstrations reported here supported by NS011862 from NINDS and Human Brain Project/Neuroinformatics NS044820 from NINDS, NIMH, and NIA, both to E.P. Gardner.
We thank the many developers of the information-theoretic and entropy measures we have implemented in the toolkit, and the many users of this software. In addition to those named elsewhere, the project has benefited from consultations with Sheila Nirenberg (Weill Cornell), Ron Elber and Ramin Zabih (Cornell), Simon Schultz (Imperial College London), Emery N. Brown and R. Clay Reid (Harvard Medical School), Pamela Reinagel (UCSD), Barry J. Richmond (NIMH), Partha Mitra (Cold Spring Harbor Labs), and A.B. Bonds (Vanderbilt). We are also indebted to Keith Purpura for demonstration datasets included with STAToolkit, as well as Eliza Chan, Ajit Jagdale, Adrian Robert, and Ronit Vaknin for many helpful discussions, contributions to, and testing of the software and its in-development extensions.
Footnotes
Information Sharing Statement
The STAToolkit and documentation are available freely and open source at http://neuroanalysis.org.
References
- Aronov D. Fast algorithm for the metric-space analysis of simultaneous responses of multiple single neurons. Journal of Neuroscience Methods. 2003;124:175–179. doi: 10.1016/S0165-0270 (03)00006-2.. [DOI] [PubMed] [Google Scholar]
- Carlton AG. On the bias of information estimates. Psychological Bulletin. 1969;71:108–109. doi: 10.1037/h0026857.. [DOI] [Google Scholar]
- Chao A, Shen T-J. Nonparametric estimation of Shannon’s index of diversity when there are unseen species in a sample. Environmental and Ecological Statistics. 2003;10:429–443. doi: 10.1023/A:1026096204727.. [DOI] [Google Scholar]
- Di Lorenzo PM, Victor JD. Taste response variability and temporal coding in the nucleus of the solitary tract of the rat. Journal of Neurophysiology. 2003;90:1418–1431. doi: 10.1152/jn.00177.2003. [DOI] [PubMed] [Google Scholar]
- Di Lorenzo PM, Victor JD. Neural coding mechanisms for flow rate in taste-responsive cells in the nucleus of the solitary tract of the rat. Journal of Neurophysiology. 2007;97:1857–1861. doi: 10.1152/jn.00910.2006.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dorval AD. Probability distributions of the logarithm of inter-spike intervals yield accurate entropy estimates from small datasets. Journal of Neuroscience Methods. 2008;173:129–139. doi: 10.1016/j. jneumeth.2008.05.013.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron B, Tibshirani RJ. An introduction to the bootstrap. New York: Chapman & Hall; 1993. [Google Scholar]
- Gardner D, Abato M, Knuth KH, DeBellis R, Erde SM. Dynamic publication model for neurophysiology databases. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences. 2001a;356:1229–1247. doi: 10.1098/rstb.2001.0911.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner D, Knuth KH, Abato M, Erde SM, White T, DeBellis R, et al. Common data model for neuroscience data and data model interchange. Journal of the American Medical Informatics Association. 2001b;8:17–31. doi: 10.1136/jamia.2001.0080017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner D, Toga AW, Ascoli GA, Beatty J, Brinkley JF, Dale AM, et al. Towards effective and rewarding data sharing. Neuroinformatics. 2003;1:289–295. doi: 10.1385/NI:1:3:289.. [DOI] [PubMed] [Google Scholar]
- Gardner D, Abato M, Knuth KH, Robert A. Neuroinformatics for neurophysiology: The role, design, and use of databases. In: Koslow SH, Subramaniam S, editors. Databasing the brain: The role, design, and use of databases. New York: Wiley; 2005. pp. 47–67. [Google Scholar]
- Gardner D, Chan E, Goldberg DH, Jagdale AB, Robert A, Victor JD. Neurodatabase.org and Neuroanalysis.org: Tools and resources for data discovery. (Abstract) Program No. 100.10. Washington, DC: Society for Neuroscience; 2007a. [Google Scholar]
- Gardner EP, Babu KS, Reitzen SD, Ghosh S, Brown AM, Chen J, et al. Neurophysiology of prehension: I. Posterior parietal cortex and object-oriented hand behaviors. Journal of Neurophysiology. 2007b;97:387–406. doi: 10.1152/jn.00558.2006.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner EP, Babu KS, Ghosh S, Sherwood A, Chen J. Neurophysiology of prehension: III. Representation of object features in posterior parietal cortex of the macaque monkey. Journal of Neurophysiology. 2007c;98:3708–3730. doi: 10.1152/jn.00609.2007.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner D, Akil H, Ascoli GA, Bowden DM, Bug W, Donohue DE, et al. The neuroscience information framework: a data and knowledge environment for neuroscience. Neuroinformatics. 2008a;6(3):149–160. doi: 10.1007/s12021-008-9024-z.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner D, Goldberg DH, Grafstein B, Robert A, Gardner EP. Terminology for neuroscience data discovery: multi-tree syntax and investigator-derived semantics. Neuroinformatics. 2008b;6(3):161–174. doi: 10.1007/s12021-008-9029-7.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldberg DH, Victor JD, Gardner D. Computational neuroinformatic toolkit: Information-theoretic analysis of spike trains. (Abstract) Biophysical Society Annual Meeting; 1244-Pos, Salt Lake City, UT. 2006a. [Google Scholar]
- Goldberg DH, Victor JD, Gardner EP, Gardner D. Computational neuroinformatics: toward distributed neuroscience data discovery. (Abstract) Computational Neuroscience Society Annual Meeting; Edinburgh, UK. 2006b. [Google Scholar]
- Goldberg DH, Gardner EP, Gardner D, Victor JD. Metric space analysis of neuronal ensembles in parietal cortex during prehension (Abstract) Program No. 147.7. Washington, DC: Society for Neuroscience; 2006c. [Google Scholar]
- Goldberg DH, Victor JD, Gardner D. Neuroinformatic resources for the information theoretic analysis of spike trains. (Abstract) Dynamical Neuroscience Satellite Symposium at Society for Neuroscience; Atlanta. 2006d. [Google Scholar]
- Goldberg DH, Chan E, Jagdale AB, Victor JD, Gardner D. Computational neuroinformatics: web-enabled tools for neuroscience data discovery. (Abstract) Biophysical Society Annual Meeting; 531-Pos, Baltimore, MD. 2007. [Google Scholar]
- Hausser J, Strimmer K. Entropy inference and the James-Stein estimator, with application to nonlinear gene association networks. 2008 Dec 31 arXiv:0811.3579v2 [stat.ML] [Google Scholar]
- Huetz C, Philibert B, Edeline J-M. A spike-timing code for discriminating conspecific vocalizations in the thalamocortical system of anesthetized and awake guinea pigs. The Journal of Neuroscience. 2009;29(2):334–350. doi: 10.1523/JNEUROSCI.3269-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ince RAA, Petersen RS, Swan DC, Panzeri S. Python for information theoretic analysis of neural data. Frontiers in Neuroinformatics. 2009 doi: 10.3389/neuro.11.004.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennedy DN. Barriers to the socialization of information. Neuroinformatics. 2004;4:367–368. doi: 10.1385/NI:2:4:367.. [DOI] [PubMed] [Google Scholar]
- Kennedy DN. Where’s the beef? Missing data in the information age. Neuroinformatics. 2006;6:271–274. doi: 10.1385/NI:4:4:271.. [DOI] [PubMed] [Google Scholar]
- Koslow SH, Hirsch MD. Celebrating a decade of neuroscience databases. Looking to the future of high-throughput data analysis, data integration, and discovery neuroscience. Neuroinformatics. 2004;4:267–270. doi: 10.1385/NI:2:3:267.. [DOI] [PubMed] [Google Scholar]
- Lidierth M. sigTOOL: a MATLAB-based environment for sharing laboratory-developed software to analyze biological signals. Journal of Neuroscience Methods. 2009;178:188–196. doi: 10.1016/j.jneumeth.2008.11.004.. [DOI] [PubMed] [Google Scholar]
- Ma S. Calculation of entropy from data of motion. Journal of Statistical Physics. 1981;26:221–240. doi: 10.1007/BF01013169.. [DOI] [Google Scholar]
- Miller GA. Note on the bias on information estimates. Information Theory in Psychology Problems and Methods. 1955;II-B:95–100. [Google Scholar]
- Mitra P, Bokil H. Observed Brain Dynamics. New York: Oxford University Press; 2008. [Google Scholar]
- Nemenman I, Shafee F, Bialek W. Entropy and inference, revisited. In: Dietterich TG, Becker S, Ghahramani Z, editors. Advances in neural information processing systems 14: Proceedings of the 2002 Conference; Cambridge, MA: MIT; 2002. pp. 471–478. [Google Scholar]
- Paninski L. Estimation of entropy and mutual information. Neural Computation. 2003;15:1191–1253. doi: 10.1162/089976603321780272.. [DOI] [Google Scholar]
- Panzeri S, Senatore R, Montemurro MA, Petersen RS. Correcting for the sampling bias problem in spike train information measures. Journal of Neurophysiology. 2007;98:1064–1072. doi: 10.1152/jn.00559.2007.. [DOI] [PubMed] [Google Scholar]
- Quian Quiroga R, Panzeri S. Extracting information from neuronal populations: information theory and decoding approaches. Nature Reviews. Neuroscience. 2009;10(3):173–185. doi: 10.1038/nrn2578. [DOI] [PubMed] [Google Scholar]
- Reich DS, Mechler F, Victor JD. Formal and attribute-specific information in primary visual cortex. Journal of Neurophysiology. 2001a;85:305–318. doi: 10.1152/jn.2001.85.1.305. [DOI] [PubMed] [Google Scholar]
- Reich DS, Mechler F, Victor JD. Temporal coding of contrast inprimary visual cortex: when, what, and why. Journal of Neurophysiology. 2001b;85:1039–1041. doi: 10.1152/jn.2001.85.3.1039. [DOI] [PubMed] [Google Scholar]
- Reinagel P, Reid RC. Temporal coding of visual information in the thalamus. The Journal of Neuroscience. 2000;20:5392–5400. doi: 10.1523/JNEUROSCI.20-14-05392.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roussin AT, Victor JD, Chen J-Y, Di Lorenzo PM. Variability in responses and temporal coding of tastants of similar quality in the nucleus of the solitary tract of the rat. Journal of Neurophysiology. 2008;99:644–655. doi: 10.1152/jn.00920.2007.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shannon C. A mathematical theory of communication. The Bell System Technical Journal. 1948;27:379–423. [Google Scholar]
- Strong SP, Koberle R, de Ruyter van Steveninck RR, Bialek W. Entropy and Information in Neural Spike Trains. Physical Review Letters. 1998;80:197–200. doi: 10.1103/PhysRevLett.80.197.. [DOI] [Google Scholar]
- Treves A, Panzeri S. The upward bias in measures of information derived from limited data samples. Neural Computation. 1995;7:399–407. doi: 10.1162/neco.1995.7.2.399.. [DOI] [Google Scholar]
- Vaknin R, Goldberg DH, Victor JD, Gardner EP, Debowy DJ, Babu KS, et al. Metric space analysis of spike trains in parietal cortex during prehension. Society for Neuroscience Abstracts. 2005;2005:984.20. [Google Scholar]
- Victor JD. Binless strategies for estimation of information from neural data. Physical Review E: Statistical, Nonlinear, and Soft Matter Physics. 2002;66:051903. doi: 10.1103/PhysRevE.66.051903. [DOI] [PubMed] [Google Scholar]
- Victor JD. Spike train metrics. Current Opinion in Neurobiology. 2005;15:585–592. doi: 10.1016/j.conb.2005.08.002.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Victor JD. Approaches to information-theoretic analysis of neural activity. Biological Theory. 2006;1(3):302–316. doi: 10.1162/biot.2006.1.3.302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Victor JD, Purpura KP. Metric-space analysis of spike trains: theory, algorithms and application. Network: Computation in Neural Systems. 1997;8:127–164. doi: 10.1088/0954-898X/8/2/003.. [DOI] [Google Scholar]
- Victor JD, Goldberg DH, Gardner D. Dynamic programming algorithms for comparing multineuronal spike trains via cost-based metrics and alignments. Journal of Neuroscience Methods. 2007;161(2):351–360. doi: 10.1016/j.jneumeth.2006.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolpert DH, Wolf DR. Estimating functions of probability distributions from a finite set of samples. Physical Review E. 1995;52:6841–6854. doi: 10.1103/physreve.52.6841. (Erratum in Physical Rev. E (Norwalk, Conn), 54, 6973. [DOI] [PubMed] [Google Scholar]