Intervening Inhibition Underlies Simple-Cell Receptive Field Structure in Visual Cortex

Bao-hua Liu; Pingyang Li; Yujiao J Sun; Ya-tang Li; Li I Zhang; Huizhong Whit Tao

doi:10.1038/nn.2443

. Author manuscript; available in PMC: 2010 Jul 1.

Published in final edited form as: Nat Neurosci. 2009 Nov 29;13(1):89–96. doi: 10.1038/nn.2443

Intervening Inhibition Underlies Simple-Cell Receptive Field Structure in Visual Cortex

Bao-hua Liu ¹, Pingyang Li ¹, Yujiao J Sun ¹, Ya-tang Li ¹, Li I Zhang ^1,^3,^†, Huizhong Whit Tao ^1,^2,^†

PMCID: PMC2818750 NIHMSID: NIHMS165647 PMID: 19946318

Abstract

Synaptic inputs underlying spike receptive fields (RFs) are key to understanding mechanisms for neuronal processing. Here, whole-cell voltage-clamp recordings from neurons in mouse primary visual cortex revealed the spatial patterns of their excitatory and inhibitory synaptic inputs evoked by On and Off stimuli. Surprisingly, neurons with either segregated or overlapped On/Off spike subfields exhibited substantial overlaps between all the four synaptic subfields. The segregated RF structures are generated by the integration of excitation and inhibition with a stereotypic pattern: the peaks of excitatory On/Off subfields are separated and flank co-localized peaks of inhibitory On/Off subfields. The small mismatch of excitation/inhibition leads to an asymmetric inhibitory shaping of On/Off spatial tunings, resulting in a great enhancement of their distinctiveness. Thus, slightly separated On/Off excitation together with intervening inhibition can create simple-cell RF structure, and the dichotomy of RF structures may arise from a fine-tuning of the spatial arrangement of synaptic inputs.

Simple and complex cells were first defined in the primary visual cortex (V1) of cats according to their distinctive spike receptive field (RF) structures¹. Simple-cell receptive fields are made up of spatially segregated On and Off subregions, within which bright and dark stimuli respectively increase the cell’s firing. In contrast, complex cells exhibit overlapped On and Off subregions in their RFs¹^,². A popular circuit model for simple-cell RFs, known as “push-pull” circuit³^–⁷, proposes that the segregation of On and Off subfields results largely from the spatial arrangement of On- and Off-center excitatory inputs from thalamic relay cells, while the arrangement of inhibitory inputs is thought to be antagonistic to that of the excitatory thalamic inputs⁵^,⁶^,⁸^,⁹. The push-pull model predicts that inhibitory and excitatory inputs evoked by the same contrast are largely segregated spatially, and that inhibition does not contribute significantly to the segregation of the On and Off subfields. However, several experimental results contradict this model. Firstly, an intracellular study in cats has suggested that the On and Off responses of simple cells may consist of both excitatory and inhibitory inputs¹⁰. Secondly, blocking GABA receptors extracellularly or intracellularly could convert simple-cell RFs to those similar to complex cells¹¹^,¹². These experimental data suggest that there may be a significant spatial overlap between excitation and inhibition in simple cells, and that inhibition may play a crucial role in generating the segregated On/Off RF structure. More recently, it has been proposed that the spike threshold increases the difference in functional properties of simple and complex cells, which otherwise lie on a continuum if distributions of synaptic responses are considered¹³^–¹⁶. This model implies that the push-pull circuit may only apply to the “purest” simple cells.

In order to comprehend how specific RF structures are generated, it is critical to understand the distribution patterns of the underlying synaptic inputs. Most of the experimental evidence for the push-pull was based on extracellular recordings of spike responses¹⁷^–²⁰ or intracellular recordings of membrane potential responses³^,⁸^,⁹^,¹⁶^,²¹. These responses are the result of integrating excitatory and inhibitory synaptic inputs as well as voltage-dependent conductances, and may not be taken directly as either excitatory or inhibitory synaptic inputs. The synaptic circuit underlying simple-cell RFs requires further examination. Recent studies have demonstrated that whole-cell voltage-clamp recordings can be reliably carried out in rodent cortices in vivo²²^–²⁶, and that the basic functional properties, such as simple/complex RF structures as well as orientation and direction selectivity, are preserved in the mouse V1²⁷^–³¹,, potentially making it a good model for dissecting synaptic input circuits underlying fundamental cortical processing of visual information. In this study, by applying whole-cell voltage-clamp recordings, we mapped four synaptic subfields for layer 2/3 neurons in the mouse V1: excitatory On and Off (Eon and Eoff), and inhibitory On and Off (Ion and Ioff) subfields. Surprisingly, we found that in all the neurons recorded, the four synaptic subfields overlapped substantially. Spike RFs with segregated On and Off subfields are in fact generated from the synaptic integration of excitation and inhibition with a stereotypic spatial pattern: with the peaks of the Eon and Eoff segregated and those of the Ion and Ioff largely co-localized. More importantly, the peaks of the Ion and Ioff were located between those of the Eon and Eoff. This configuration enables inhibition to exert an asymmetric shaping effect on the spatial tuning of On and Off responses, leading to a significant enhancement of the spatial segregation between spike On and Off subfields. Our results demonstrate a novel synaptic mechanism for the generation of simple-cell RF structure.

RESULTS

Subthreshold responses underlying spike RF structures

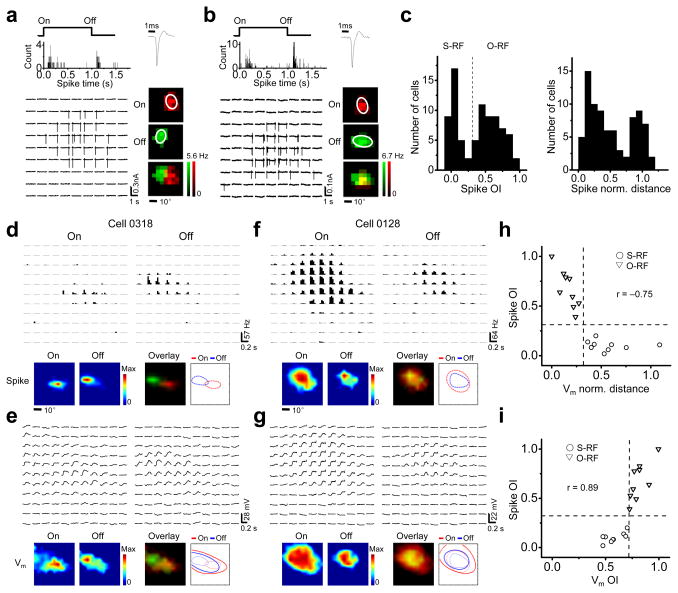
Previous studies suggest that simple- and complex-cell RFs primarily appear in layer 2/3 of the mouse V1²⁸^,²⁹^,³¹. Two examples of layer 2/3 excitatory neurons were shown in Figure 1a and 1b. They exhibited spatially segregated and overlapped spike On and Off subfields respectively, as detected by cell-attached recordings (see Methods). To quantify the spatial overlap between the On and Off subfields, we calculated an overlap index (OI) after fitting the subfields with two-dimensional Gaussian ellipses⁶^,⁸ (see Methods). The histogram of OI values revealed a dichotomy in the RF structures (Fig. 1c, left, Hartigan’s dip test, p < 0.05, n = 82). The OI of 0.33 (the value for two identical subfields that are half separated and half overlapped) appeared to divide the cells into two groups. Cells with OI < 0.33 (~45%) were named neurons with segregated RF structure (or S-RF neurons). Otherwise, they were named neurons with overlapped RF structure (or O-RF neurons)³¹. The normalized peak distance between the spike On and Off subfields²⁰ also exhibited a bimodal distribution (Fig. 1c, right, Hartigan’s dip test, p < 0.05, n = 82). In contrast to the S-RF/O-RF structures in layer 2/3, layer 4 neurons mostly responded only to one contrast (see Supplementary Fig. 1), consistent with previous reports²⁸^,²⁹^,³¹. Since classic simple-cell RF structures were primarily found in layer 2/3, we focused on layer 2/3 neurons in this study.

Membrane potential (V_m) responses underlying S-RF and O-RF structures in layer 2/3 of the mouse V1. (a–b) Example S-RF (a) and O-RF (b) cells. Top left, the peri-stimulus-spike-time histograms (PSTH) for evoked spikes. “On” and “Off” mark the onset and offset of the stimuli respectively. Top right, the spike shape. Bottom left, each small trace represents the recorded spike response (vertical deflections) in one trial to a unit stimulus displayed at the corresponding spatial location. Bottom right, color maps of the spike subfields. The white ellipses depict the outlines of the spike subfields determined by Gaussian fittings. (c) Left, histogram of OI of spike subfields (spike OI) for the recorded excitatory neurons. The dash line marks OI = 0.33. Right, histogram of normalized distance between the peaks of spike On and Off subfields. (d) Spike RF for an example S-RF cell. Top, each small trace represents the PSTH for spike responses to a unit On or Off stimulus. Bottom, color maps and outlines of spike On/Off subfields. Color scale: 14.8 (On) and 39.1 Hz (Off). (e) V_m responses of the same cell in d. Top, traces of average V_m responses. Bottom, color maps and outlines of V_m subfields. Color scale: 22 (On) and 26 mV (Off). (f–g) An example O-RF cell. Data are presented in the same way as in **d–e**. Color scale: 42.3 and 21.5 Hz in f; 20 and 18 mV in g. (h) Spike OI versus normalized distance between the peaks of V_m subfields. The two dash lines (OI = 0.33, norm. distance = 0.32) separate S-RF and O-RF structures. “r”, correlation coefficient. (i) Spike OI versus OI of V_m subfields (V_m OI). The vertical and horizontal lines mark V_m OI = 0.71 and spike OI = 0.33 respectively.

In order to understand the patterns of subthreshold synaptic inputs underlying the S-RF/O-RF structures, we carried out current-clamp recordings to record both sub- and suprathreshold membrane potential responses. As shown for an example S-RF cell, the subthreshold response regions were much larger than the spike subfields (Fig. 1d,e). While the spike On and Off subfields were largely segregated, the subthreshold On and Off regions substantially overlapped (Fig. 1e). The peaks of the subthreshold subfields (where the maximum depolarizing response appears) were clearlyoffset spatially, with their locations consistent with those of the spike subfields (Fig. 1d,e, bottom). In comparison, the subthreshold On and Off responses of an O-RF cell exhibited a similarly large overlap (Fig. 1f,g), but without an apparent segregation between the peak depolarizing On and Off responses (Fig. 1f,g, bottom). In fact, the OI of spike subfields (spike OI) was strongly correlated with the normalized distance between the peaks of subthreshold subfields, decreasing monotonically with the increase of the latter (Fig. 1h). The S-RF and O-RF cells could be best separated by a normalized peak distance at 0.32, based on the Youden’s Index (see Methods). The spike OI was also correlated strongly with the OI of subthreshold subfields (see Methods, Fig. 1i), with a subthreshold OI at 0.71 best separating the S-RF from O-RF cells. These results suggest that the spatial pattern of subthreshold On and Off responses may predict the structure of the spike RF, and that the spike threshold is required to generate the segregated spike On and Off subfields in the S-RF cells. It should be noted that the level of the spike threshold is not associated with the RF type, as no significant difference of it was observed between the S-RF and O-RF cells (25.1 ± 2.6 mV for S-RF cells and 23.9 ± 5.2 mV for O-RF cells).

The observed membrane potential responses consisted mostly of depolarizing responses (Fig. 1e,g), which indicate the arrival of excitatory synaptic inputs. Thus, the largely overlapped depolarizing On and Off responses predict that in both the S-RF and O-RF cells, the excitatory On and Off synaptic subfields may overlap substantially.

Subfields of excitatory and inhibitory inputs

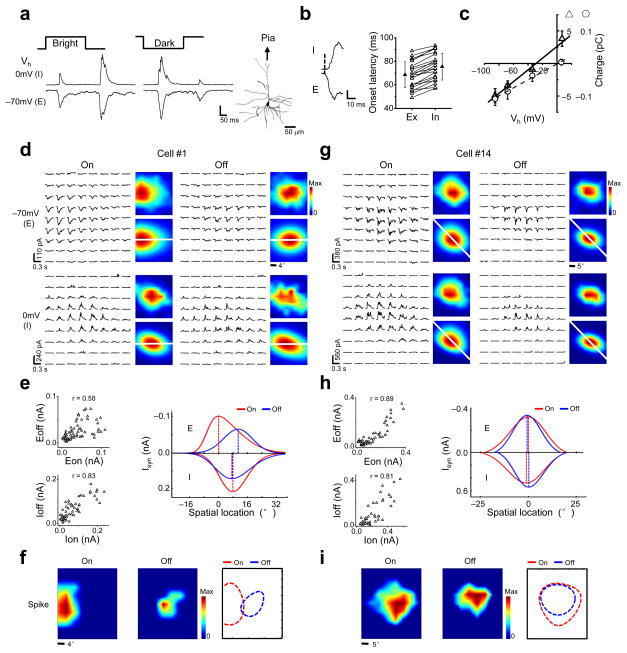
To further elucidate the patterns of excitatory and inhibitory synaptic inputs, we carried out whole-cell voltage-clamp recordings to dissect synaptic excitation and inhibition (see Methods). Sample responses of a neuron to a bright or dark square flashed at the same location, recorded at two clamping voltages, were shown in Figure 2a. The inward currents recorded at −70 mV and the outward currents at 0 mV were primarily contributed by excitatory and inhibitory synaptic inputs respectively²⁵^,²⁶, with the inhibitory input temporally closely following the co-activated excitatory input²²^–²⁴^,³² (Fig. 2b). The observed synaptic inputs were reasonably controlled by the somatic voltage clamp, as suggested by a linear I–V relationship and the derived reversal potential of the excitatory currents, which was close to 0 mV (Fig. 2c and Supplementary Fig. 2). This is likely due to the proximity of the visually-activated synapses to the soma of layer 2/3 neurons³³.

Synaptic subfields examined by voltage-clamp recordings. (a) Individual synaptic responses of a layer 2/3 pyramidal neuron to stimuli displayed at the same location. Scale: 118 (E) and 203 pA (I). Right, the reconstructed morphology of the cell. (b) Left, onset phase of synaptic responses. The onset of the excitatory response was marked by dash line. Scale: 80 (E) and 160 pA (I). Right, onset latencies of excitatory (Ex) and inhibitory (In) synaptic responses. The values from the same cell are connected with a line. Solid symbol = mean, error bar = SD. (c) I–V curves for a cell under white noise stimulation. Synaptic charges were measured in a 0–5ms (circle) and 10–150ms (triangle) time window after the onset of excitatory synaptic responses. (d–f) A putative S-RF cell. (d) Arrays of trial-averaged excitatory (E) and inhibitory (I) synaptic responses to On and Off stimuli. Color maps are the smoothed (top) and skew-normal fitted (bottom) synaptic subfields. White lines pass through the peaks of the excitatory On and Off subfields. Color scale: 109, 73, 236, and 178 pA for Eon, Eoff, Ion and Ioff respectively. (e) Left, correlation between the strengths of synaptic responses (Eon-Eoff, Ion-Ioff). Right, spatial tuning curves of the four synaptic inputs along the white lines in d. Dash lines mark their peaks. (f) Derived spike subfields of the same cell and their boundaries. Color scale: 25 (On) and 10 Hz (Off). (g–i) Synaptic subfields of a putative O-RF cell. Data are presented in the same manner as in d–f. Color scale in g: 381, 352, 560 and 412 pA (Eon, Eoff, Ion, Ioff). Color scale in i: 25 (On) and15 Hz (Off).

We mapped excitatory On and Off (Eon, Eoff) and inhibitory On and Off (Ion, Ioff) subfields by recording synaptic currents evoked bybrief bright and dark stimuli while clamping the cell at −70 mV and 0 mV respectively. For the example cell #1 (Fig. 2d), average traces of excitatory and inhibitory currents responding to all the On and Off stimuli are arranged and displayed in accordance with the location of the corresponding stimulus. The distribution of the peak amplitude of the synaptic currents is depicted by a smoothed color map (Fig. 2d, top right corners). We observed a considerable overlap between the Eon and Eoff, which is further demonstrated by the positive correlation between the strengths of the excitatory On and Off responses (Fig. 2e, top left). Despite this overlap, it is clear that the peaks of the Eon and Eoff (where the strongest response is elicited) were spatially offset (Fig. 2d). Interestingly, the Ion and Ioff almost completely overlapped, as demonstrated by a strong correlation between the inhibitory On and Off responses (Fig. 2e, bottom left). In order to quantitatively describe the spatial relationship between each pair of the four synaptic subfields, the subfields were fitted with two-dimensional skew-normal distribution function (Fig. 2d, bottom right corners; see Methods), which better described the asymmetrical distribution of the synaptic strengths than the Gaussian function in some cells (Supplementary Fig. 3 and 4). The tuning curves for the four sets of synaptic inputs in the one-dimensional slice that passed through the peaks of both the Eon and Eoff were plotted together (Fig. 2e, right). The plotting clearly showed that the peaks of the Eon and Eoff were segregated with a normalized distance of 0.53 (see Methods), while those of the Ion and Ioff were overlapped and located between the former two. The separation between the peaks of the Eon and Eoff is reminiscent of that of depolarizing subfields in the S-RF cells (Fig. 1e). Indeed, the derived spike On and Off subfields (see Methods) of the cell #1 exhibited an almost complete segregation, suggesting that it is likely an S-RF cell (Fig. 2f). In comparison, the cell #14 exhibited almost completely overlapped four synaptic subfields (Fig. 2g,h, left), with a good co-localization of all of their peaks (Fig. 2h, right). The derived spike On and Off subfields overlapped well, suggesting that the cell is likely an O-RF cell (Fig. 2i).

Spatial relationships of synaptic subfields

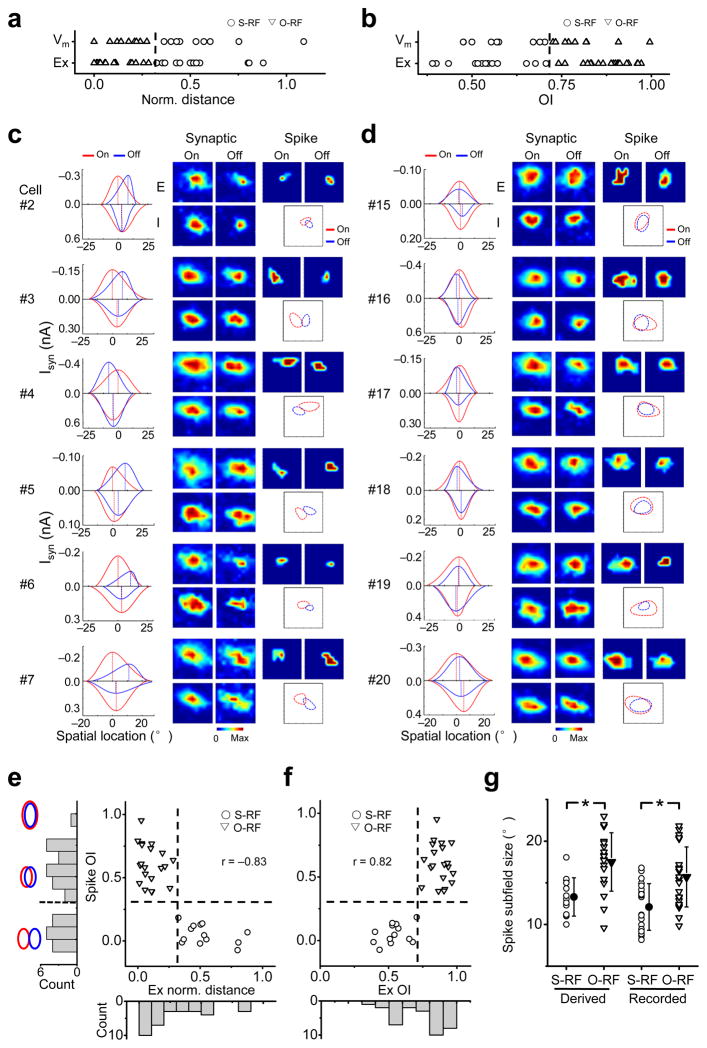
Synaptic subfields were obtained for a total of 33 neurons. In all of these neurons, the four synaptic subfields substantially overlapped, but there was a relatively larger variation in the separation between the Eon and Eoff (Supplementary Fig. 5). According to spike response data (Fig. 1c), about half of these cells were potential S-RF cells. To understand how different spatial patterns of synaptic inputs result in different spike RF structures, first we roughly categorized the recorded cells into putative S-RF and O-RF cells. As the spatial relationship between the Eon and Eoff primarily determined that of the subthreshold depolarizing responses (Supplementary Fig. 6), and the latter could predict the S-RF/O-RF structures (Fig. 1h,i), we applied the same separation criteria to the patterns of excitatory inputs in order to categorize cells (i.e. S-RF cells having normalized peak distance < 0.32, or OI < 0.71) (Fig. 3a,b). Interestingly, the grouping was the same based on either the OI or the normalized peak distance (Fig. 3b).

Grouping of cells based on the structure of synaptic subfields. (a) The distributions of the normalized distances between the peaks of V_m On/Off subfields, and between the excitatory On/Off subfields (Ex). The two distributions are not different (Mann-Whitney test, p = 0.14). The dash line marks norm. distance = 0.32, which was used to group the cells from V-clamp recordings. (b) The distributions of the OIs of V_m and excitatory subfields. Mann-Whitney test, p = 0.21. The dash line marks OI = 0.71, which separated the cells from V-clamp recordings the same as in a. (c) Synaptic subfields and derived spike subfields of six putative S-RF cells. For each cell, shown from left to right are the synaptic tuning curves in the slice that passes through the peaks of the Eon and Eoff, the four synaptic subfields, the derived spike subfields and the superimposed outlines of fitted spike subfields. Color scale: 337, 404,543, 528 pA for synaptic subfields (in the sequence of Eon, Eoff, Ion, Ioff), 15, 10 Hz for spike On/Off subfields in cell #2; 163, 165, 288, 196 pA, 10, 15 Hz in cell #3; 280, 342, 638, 854 pA, 10, 10 Hz in cell #4; 122, 106, 142, 141 pA, 10, 10 Hz in cell #5; 225, 153, 245, 161 pA, 15, 20 Hz in cell #6; 311, 184, 412, 149 pA, 10, 5 Hz in cell #7. (d) Six putative O-RF cells. Plots are organized in the same way as in c. Color scale: 74, 54, 141, 82 pA, 5, 10 Hz in cell #15; 398, 347, 595, 563 pA, 10, 10 Hz in cell #16; 141, 154, 298, 145 pA, 15, 15 Hz in cell #17; 187, 172, 218, 173 pA, 15, 15 Hz in cell #18; 232, 154, 356, 329 pA, 20, 5 Hz in cell #19; 280, 253, 415, 221 pA, 15, 15 Hz in cell #20. (e) OI of derived spike subfields versus the normalized distance between the peaks of the Eon and Eoff for all recorded neurons (n = 33). The vertical and horizontal dash lines mark Ex norm. distance = 0.32 and spike OI = 0.33 respectively. Left, histogram of spike OI. The schematic drawings depict the extent of overlap between two identical subfields for OI = 0, 0.5 and 1 respectively. Bottom, histogram of Ex norm. distance. (f) OI of derived spike subfields vs. the OI between the Eon and Eoff. The vertical and horizontal dash lines mark Ex OI = 0.71 and spike OI = 0.33 respectively. Bottom, the histogram of Ex OI. (g) The distribution of the subfield size of the derived and recorded spike responses. Solid symbol = mean, error bar = SD. *, p < 0.01, t-test.

More example putative S-RF and O-RF cells are shown in Figure 3c & d. All the putative S-RF cells exhibited similar patterns of synaptic inputs: there was a clear segregation between the peaks of the Eon and Eoff while the extent of these subfields substantially overlapped, and the peaks of the Ion and Ioff were largely co-localized and located somewhere between those of the Eon and Eoff. Their derived spike subfields showed a significant segregation, supporting the categorization of them as S-RF cells (Fig. 3c, right). In comparison, the putative O-RF cells exhibited more closely localized peaks of all the synaptic subfields, and their derived spike subfields showed a large overlap (Fig. 3d). The summary graph in Figure 3e & f revealed that there was a strong correlation between the derived spike OI and the normalized peak distance or OI of the Eon and Eoff, consistent with the current-clamp recording results (Fig. 1h,i). The OI of derived spike subfields formed a bi-modal distribution (Fig. 3e, left, Hartigan’s dip test, p < 0.05), while the normalized peak distance or OI between the Eon and Eoff exhibited a continuous distribution (Fig. 3e, bottom, Hartigen’s dip test, p = 0.38 and Fig. 3f, bottom, Hartigen’s dip test, p = 0.25.), again consistent with the results of cell-attached and current-clamp recordings (Fig. 1c,h,i). The distribution of the size of derived spike subfields is also similar to that of the extracellularly recorded RFs (Fig. 3g). These similarities suggest that the derived spike RFs had not significantly underestimated or exaggerated the separation between the bona fide spike subfields.

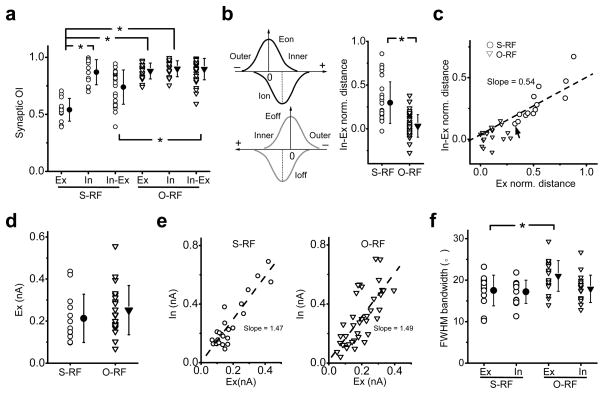
The level of overlap between the Ion and Ioff, as well as between the excitatory and inhibitory subfields of the same contrast (“Ex-In”) was then compared between the putative S-RF (n = 13) and O-RF cells (n = 20) (Fig. 4a). While the Eon and Eoff were more segregated in the S-RF cells than the O-RF cells, the overlap between the Ion and Ioff is similarly large in the two groups. In the S-RF cells, the average OI of Ex-In is higher than that of Eon-Eoff, but lower than that of Ion-Ioff, consistent with the notion that the peaks of the inhibitory subfields were usually located between those of the Eon and Eoff. To further illustrate the Ex-In relationship, we measured the normalized peak distance, using “+” or “−” sign to indicate that the inhibitory peak locates on the inner or outer side of the excitatory subfield respectively (Fig. 4b, left). In the S-RF cells, almost all the values were positive, indicating that inhibition always peaked at the inner side of the excitatory subfield (Fig. 4b, right). On the other hand, in O-RF cells, the relative locations of inhibitory peaks were rather random and all close to 0, indicating that the inhibitory and excitatory peaks were essentially co-localized. The normalized peak distance for Ex-In was linearly correlated with that of Eon-Eoff, and was about half of the latter (Fig. 4c). Based on the distances of In-Ex and Eon-Eoff, the cells could be statistically separated into two clusters by TwoStep Cluster analysis, and the two clusters matched well with the cell type categorization (concordance = 32/33). The two groups of cells do not differ significantly in synaptic strengths or the size of inhibitory subfields, only differ slightly in the size of excitatory subfields (Fig. 4d–f). This suggests that the spatial relationship between synaptic subfields primarily determines RF structures.

Summary of the spatial relationships between synaptic subfields. (a) The distributions of OIs between the Eon and Eoff (Ex), the Ion and Ioff (In) as well as between the excitatory and inhibitory subfields of the same contrast (In-Ex). Solid symbol = mean, error bar = SD. *, p < 1e–5, t-test. (b) Left, we defined the inner side of an excitatory tuning curve as the one facing towards the other excitatory tuning curve of the opposite contrast. The value of In-Ex distance is positive if the peak of the inhibitory field is located on the inner side of the excitatory field of the same contrast, but negative if it is on the outer side. Right, the distribution of the normalized In-Ex distance. Solid symbol = mean, error bar = SD. *, p < 1e–6, t-test, n = 26 (S-RF) and 40 (O-RF). (c) Normalized In-Ex distance (averaged for On and Off subfields) versus the normalized distance between the peaks of the Eon and Eoff. The dash line is the best-fit linear regression line. Arrow points the only cell that would be grouped differentlyunder TwoStep Cluster analysis. (d) The maximal amplitude of the excitatory currents. Solid symbol = mean, error bar = SD. P = 0.34, t-test. (e) The maximum strength of inhibitory input (In) versus that of excitatory input (Ex) in the same subfield. The dash line shows the best-fit linear regression line. (f) The full-width at half-maximum bandwidth of excitatory and inhibitory spatial tuning curves. Solid symbol = mean, error bar = SD. *, p = 0.02, t-test.

An inhibitory mechanism for the S-RF structure

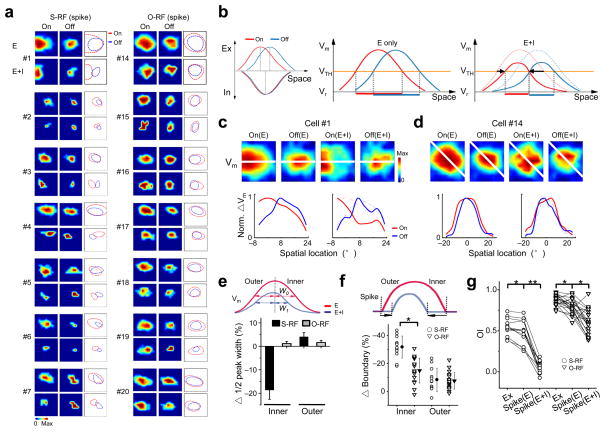
The largely overlapped excitatory and inhibitory subfields as observed indicated that the inhibition would spatiotemporally interact with the excitation. To determine the impact of inhibition on spike RF structures, we derived spike RFs in the absence of inhibitory inputs (see Methods). For the S-RF cells, the spike On and Off subfields derived from excitatory inputs only (“E”) showed substantial overlaps, while the integration of inhibition (“E+I”) resulted in largely increased On/Off segregation (Fig. 5a,g and Supplementary Fig. 7a). In the O-RF cells, the spike subfields only reduced in size with no apparent improvement in the segregation. Thus, the small segregation between the Eon and Eoff cannot fully account for a complete segregation of spike subfields. Rather, inhibition plays a crucial role in determining their spatial distinctiveness.

The inhibitory mechanism for the generation of the S-RF structure. (a) Derived spike subfields without (E) and with the integration of inhibition (E+I) of the cells in Figure 2 and 3. Dashed curves represent the outlines of the subfields. Color scale in the order of On(E), Off(E), On(E+I) and Off(E+I): from cell #1 to #7, 30, 25, 25, 10 Hz; 20, 15, 15, 10 Hz; 25, 20, 10, 15 Hz; 25, 20, 10, 10 Hz; 15, 10, 10, 10 Hz; 25, 20, 15, 20 Hz; 15, 10, 10, 5 Hz; and from cell #14 to #20: 35, 20, 25, 15 Hz; 20, 15, 5, 10 Hz; 30, 15, 10, 10 Hz; 25, 20, 15, 15 Hz; 20, 15, 15, 15 Hz; 30, 20, 20, 5 Hz; 20, 15, 15, 15 Hz. (b) Schematic drawings to show how inhibition plays a role in the generation of S-RFs. Left, the spatial tuning curves of excitatory and inhibitory inputs. The peak locations are marked by dotted lines. Middle, the spatial tuning curves of V_m responses without inhibition. V_TH and V_r stand for spike threshold and resting potential respectively. The thick red and blue lines below the tuning curves represent the one dimensional regions of the suprathreshold On/Off responses respectively. Note that they overlap significantly. Right, the V_m tuning curves after integrating inhibition (solid curves), overlayed with the tuning curves without inhibition (dashed). The suprathreshold On/Off response regions are now segregated. Arrows indicate the shrinkage of suprathreshold subfield boundaries. (c) Top, color maps of V_m responses derived without (E) and with (E+I) integrating inhibition for cell #1. Scale from left to right: 47, 40, 39, 26 mV. White line was defined the same as before. Bottom, normalized spatial tuning curves of V_m responses along the white line, in the absence (left) and presence (right, solid) of inhibition. Note a strong suppression of the right part of the On tuning curve. (d) Similar plottings for cell #14. Scales: 54, 53, 32, 36 mV. (e) The percentage change in the half-peak width of the V_m tuning curve after integrating inhibition. Top, schematic drawings of V_m tuning curves before and after integrating inhibition, with the half-peak widths at the inner side labelled by W₀ and W₁ respectively. The percentage change is then defined as *(W₁* − *W₀)/W*, where W is the full-width at half-maximum of the tuning curve without inhibition. Error bar = SE. (f) Percentage shift of spike subfield boundaries after integrating inhibition. Arrows in the schematic drawings depict the boundary shift on the inner and outer side. The absolute value was divided by the size of spike subfields without inhibition to obtain the percentage shift. (g) OIs between Eon and Eoff (Ex), and between spike On/Off subfields derived without (spike(E)) and with inhibition (spike(E+I)). Values for the same cell are connected with lines. *, p < 0.005; **, p < 0.0001, paired t-test.

How does inhibition shape spike RF structures? Based on the largely overlapping, but subtly mismatched spatial relationship between the excitatory and inhibitory inputs to S-RF cells (Fig. 5b, left), we propose that inhibition can enhance the distinctiveness of spike On and Off subfields through an asymmetric suppression effect. Because of the large overlap between Eon and Eoff, the spike threshold alone may not be sufficient to generate a complete On/Off segregation (Fig. 5b, middle). The integration of inhibition will reduce the size of spike subfields by suppressing the level of the membrane excitation (Fig. 5b, right). More importantly, due to the locations of the inhibitory peaks at the inner sides of the excitatory tunings, the inhibition will exert a stronger suppression effect on the inner side of the membrane potential tuning curve than on its outer side. This can result in a more effective separation of suprathreshold On and Off response regions (Fig. 5b, right). To illustrate this effect, maps of the membrane potential changes in the absence and presence of inhibition, as well as the corresponding spatial tuning curves were shown for two example cells (Fig. 5c,d). For the cell #1, a putative S-RF cell (Fig. 2e, right), the inclusion of inhibition markedly changed the shape of the On membrane potential tuning curve, with a strong suppression on its inner side (Fig. 5c, bottom). This reshaping greatly increased the distinctiveness of the On and Off tunings, resulting in almost completely segregated spike subfields (Fig. 2f). On the contrary, for the putative O-RF cell (the cell #14, Fig. 2h, right), inhibition had little effect on the distinctiveness of the On and Off tunings (Fig. 5d). As a result, the spike On and Off subfields remained overlapping after the integration of inhibition (Fig. 2i).

The asymmetric shaping effect on the On/Off tunings was summarized in Figure 5e. In the S-RF cells, the half-peak width of the membrane potential tuning was significantly reduced after the integration of inhibition at the inner side but not at the outer side. As a result, the spike subfield boundary shrank to a larger degree at the inner side than the outer side (Fig. 5f). In contrast, the shape of membrane potential tunings was largely unchanged in the presence of inhibition in the O-RF cells (Fig. 5e). Thus, empowered by the slightly mismatched spatial relationship between excitation and inhibition, the inhibition can exert a powerful asymmetric shaping effect on the On/Off tunings in S-RF cells, leading to a more pronounced reduction in the OI of spike subfields (Fig. 5g). This effect greatly increases the functional difference between the two groups of cells.

Modelling the generation of the S-RF structure

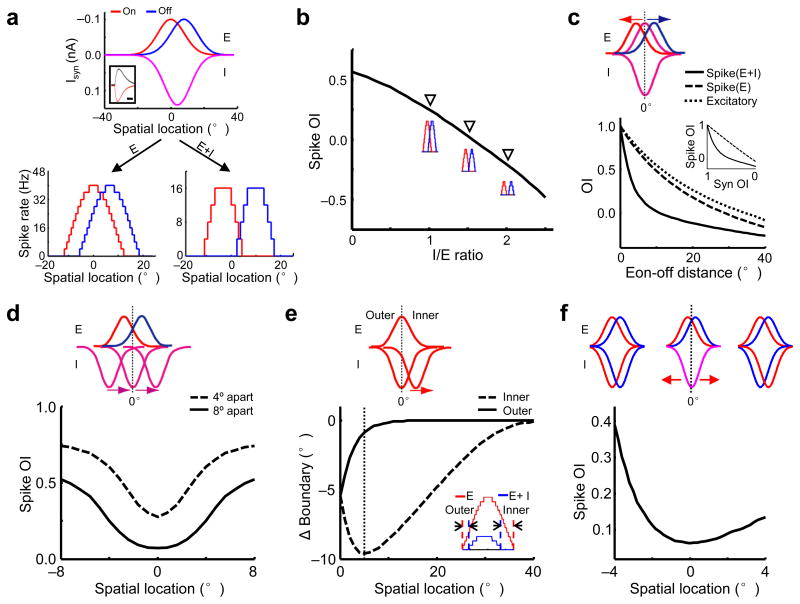
From the above experimental results, we have identified two essential factors for the generation of On/Off segregation: the slightly segregated Eon and Eoff, and a specific mismatch between the excitation and inhibition. To further understand how spatial patterns of synaptic inputs may contribute to spike RF structures, a simple neuron model was applied, based on the parameters derived from our experimental data (Fig. 6a; see Methods). Consistent with the experimental data, the slightly segregated excitatory On and Off inputs were not sufficient to generate the S-RF structure, while integrating inhibition resulted in an almost complete On/Off segregation (Fig. 6a, bottom). The level of inhibition significantly affects the level of the On/Off segregation. With the synaptic distributions and the strength of excitation fixed, an increase in the strength of inhibition led to a monotonic enhancement of the On/Off segregation, as indicated by the decrease in the OI of spike subfields (“spike OI”, Fig. 6b).

Modelling how the spatial relationships between synaptic subfields affect the segregation of spike On/Off subfields. (a) Top, the spatial tuning curves of synaptic currents (I_syn) used in the model. Inset, the temporal profiles of evoked excitatory (red) and inhibitory currents (black). Scale: 125 ms. Bottom, the tuning curves of spike responses without (left) and with inhibition (right). (b) With the strength of excitation fixed at 0.1nA, the spike OI decreases as the level of inhibition increases. Inset, spike tuning curves at I/E ratio=1, 1.5, 2. (c) Top, modelling scenario: the excitatory On (red) and Off (blue) subfields are initially co-localized with the overlapping inhibitory fields (purple) and then move away from each other at the same speed. Bottom, OIs between the Eon and Eoff (dotted), and between spike subfields without (dashed) and with inhibition (solid) versus the distance between the peaks of the Eon and Eoff. Inset, spike OI versus the OI between the Eon and Eoff (Syn OI). (d) Top, the peaks of the Eon and Eoff are separated by 4° (dashed) or 8° (solid), and the overlapping inhibitory subfields move together across different locations. Bottom, spike OI versus the spatial location of the inhibitory fields. (e) Top, the Ion is initially co-localized with the Eon and then moves in the direction towards the Eoff (not shown). Bottom, shift of the spike subfield boundary after integrating inhibition versus the location of the Ion peak. The dotted line marks the location of inhibitory subfield (~5°) where it shrinks the inner boundary most. Inset, spike tuning curves without (red) and with inhibition (blue) when the Ion peak is located at 4°. Arrows mark the boundary shifts on the two sides. (f) Top, the positions of the excitatory subfields are fixed, with an 8° separation. The initially overlapping inhibitory subfields move in opposite directions to form either exquisitely balanced excitation and inhibition (left) or an antagonistic configuration similar to the push-pull (right). Bottom, spike OI versus the location of the Ion peak, which equals to −4°, 0° and 4° for the three above scenarios respectively.

We next systematically varied the spatial relationships between synaptic subfields. With the inhibitory subfields fixed and the separation between the Eon and Eoff gradually increased, we found that inhibition most effectively reduced the spike OI when the separation between the Eon and Eoff was small (6° apart or OI of 0.72, Fig. 6c). On the other hand, with the positions of the Eon and Eoff fixed, the inhibitory subfields had the largest effect of reducing spike OI when they were located right in the middle of the Eon and Eoff (Fig. 6d). We further examined the asymmetric inhibitory shaping by sliding an inhibitory subfield away from its excitatory field of the same contrast towards that of the opposite contrast (Fig. 6e). By integrating inhibition, the shrinkage of the spike subfield boundary at the inner side was larger than the outer side, and reached the maximum when the inhibitory subfield shifted by ~5° (Fig. 6e). These simulation results further demonstrate that a small spatial shift of the inhibitory tuning results in a greatly enhanced separation between the spike On and Off responses through the asymmetric shaping effect.

DISCUSSION

The spatial patterns of excitatory and inhibitory On and Off inputs revealed in this study are apparently different from the push-pull model. In the push-pull circuit, cortical inhibition is spatially antagonistic to excitation, and the On/Off segregation is mainly determined by the spatial segregation of excitatory On and Off inputs. In this study, we found that neurons with either segregated or overlapped spike On and Off subfields all exhibit substantial overlaps between all the four synaptic subfields. The segregated RF structure of S-RF cells is created by a specific spatial arrangement of synaptic subfields: the slight separation between the peaks of excitatory On and Off subfields, and the intervening inhibitory subfields. The slightly separated excitatory On and Off subfields are not sufficient to generate the S-RF structure. Instead, the small mismatch between the excitation and inhibition leads to an asymmetric inhibitory shaping of the On and Off tunings, resulting in a strong suppression in their common region and a greatly increased segregation of spike subfields. As suggested by the results of our modelling study, the level of the On/Off segregation is sensitive to the relative location of inhibitory subfields (Fig. 6f). In fact, in a “push-pull”-like configuration (with more separation between the excitation and inhibition of the same contrast), inhibition does not further improve the segregation (Fig. 6f, top right). The substantial spatial overlap between excitation and inhibition in visual cortical neurons is reminiscent of the balanced excitation and inhibition observed in the auditory and somatosensory cortices²²^–²⁴^,²⁶.

The different synaptic organizations between the push-pull and the current study could be due to the species difference, since S-RF cells are primarily found in layer 2/3 in the mouse V1²⁷^–³¹, whereas in cats simple cells appear in the thalamo-recipient layers 4 & 6¹^,⁶^,²¹. Nonetheless, the patterns of synaptic inputs observed in this study provide a potential explanation for the previous observations in cats that blocking intracortical inhibition led to a loss of On/Off segregation¹¹^,¹², and that inhibitory conductances could be activated by both On and Off stimuli in both On and Off subfields¹⁰. In addition, our data suggest that On/Off RF structures are sensitive to the delicate relationship between the spatial tunings of the four synaptic inputs, and may potentially be modified by neuronal activity³⁴ or changed developmentally since excitatory and inhibitory tuning patterns can be developmentally regulated³⁵^,³⁶. The overlap-mismatch of synaptic subfields can produce seemingly antagonistic On and Off responses (Supplementary Fig. 8). This is because the spatial mismatch between the excitatory and inhibitory tunings can result in relatively stronger inhibition at one side of the excitatory tuning. Thus, the push-pull-like phenomenon could be generated from synaptic circuits other than the push-pull circuit. The inhibitory inputs to most of layer 2/3 neurons in the mouse V1 are mainly from local inhibitory neurons³⁷^,³⁸. The overlapped Ion and Ioff suggests that inhibitory neurons with S-RF structures may not be required to provide input to excitatory S-RF cells. Indeed, our recent study has shown that layer 2/3 inhibitory neurons in the mouse V1 mostly have overlapping spike On and Off subfields³¹.

The separation between excitatory On and Off subfields forms a contiguous distribution among our recorded cells, consistent with a previous observation of membrane potential responses in cats¹⁶. Recently it has been proposed that the nonlinearity of spike mechanism can create a dichotomy between simple and complex cells from a continuous distribution of intracellular properties¹⁴^–¹⁶. Our results suggest that, although the intrinsic neuronal mechanism of spike thresholding reduces the overlap between On and Off responses, the dichotomy of RF structures becomes much more evident after the incorporation of inhibition (Fig. 3e, 5g and Supplementary Fig. 7). Thus, besides the spike threshold, the inhibitory shaping may be an indispensable mechanism contributing to the dichotomy of the spatial organizations of RFs. Taken together, our results have revealed an alternative synaptic circuitry mechanism by which a fine-tuning of spatial patterns of synaptic inputs can create the simple-cell receptive field, as well as the dichotomy in RF structures.

Methods

Animal preparation

All experimental procedures used in this study were approved by the Animal Care and Use Committee of USC. Female adult mice (12–16 weeks, C57BL/6) were anesthetized with urethane (1.2 g/kg) and sedative chlorprothixene (0.05 ml of 4 mg/ml), as previously described²⁸^–³⁰^,³⁹. Lactated Ringer’s solution was administrated at 3 ml/kg/hour to prevent dehydration. The animal’s body temperature was maintained at ~37.5° by a heating pad (Havard Apparatus, MA). Trachotomy was performed to maintain a clear airway, and a ventilator (Havard Apparatus, MA) was connected. Cerebrospinal fluid draining was performed to prevent the cortex from swelling. The animal was placed in a custom-built stereotaxic holder. The part of the skull and dura mater (~1×1 mm) over the V1 was removed. Artificial cerebrospinal fluid solution (ACSF, containing (in mM) 140 NaCl, 2.5 KCl, 2.5 CaCl₂, 1.3 MgSO₄, 1.0 NaH₂PO4, 20 HEPES, 11 glucose, pH 7.4) was applied onto the exposed cortical surface when necessary. Throughout the surgical procedure, the lids were sutured. After surgery, right eyelid was reopened and drops of 30k silicone oil were applied to prevent the eye from drying. The whole procedure of RF mapping was finished within 25 minutes. Previous studies showed that in nonparalyzed mice the drift of the measured RF was negligible within an hour, compared to the average RF size²⁷^–²⁹^,³⁹. Our cell-attached recording also showed that the drift of the measured RF of single unit was never more than 2–3° per hour, so that the largely overlapped excitation was not due to the eye movement.

In vivo cell-attached recording, whole-cell current-clamp recording and whole-cell voltage-clamp recording

Whole-cell recording (Axopatch 200B) was performed according to previous studies²⁵^,²⁶^,⁴⁰^,⁴¹. The patch pipette had a tip opening of ~2 μm (4.5 – 6 MΩ). The intrapipette solution for V-clamp recording contained (in mM) 125 Cs-gluconate, 5 TEA-Cl, 4 MgATP, 0.3 GTP, 8 phosphocreatine, 10 HEPES, 10 EGTA, 2 CsCl, 1.5 QX-314, 0.5% biocytin, 0.75 MK-801, pH 7.25. And that for I-clamp recording contained (in mM) 130 K-gluconate, 2 KCl, 1 CaCl₂, 4 MgATP, 0.3 GTP, 8 phosphocreatine, 10 HEPES, 11 EGTA, 0.5% biocytin, pH 7.25. To prevent pulsation, 3.25% agarose was applied on the exposed cortex before recording. The whole-cell and pipette capacitance were completely compensated and the initial series resistance (20–50 MΩ) was compensated for 50–60% to achieve an effective series resistance of 10–25 MΩ. Signals were filtered at 2 kHz for V-clamp and 5 kHz for I-clamp and sampled at 10 kHz. No current injection was applied under I-clamp mode. Only neurons with resting membrane potentials lower than −55 mV and stable series resistance (less than 15% change from the beginning of the recording) were used for further analysis. Histological staining of some of the recorded cells indicated that the whole-cell recording method under our condition biased sampling toward pyramidal neurons, consistent with previous studies²⁵^,²⁶^,⁴⁰^,⁴¹. The recorded cell was first clamped at −70 mV, which is around the reversal potential of inhibitory currents, to obtain evoked excitatory currents. The cell was then clamped at 0 mV, which is around the reversal potential of excitatory currents, to obtain evoked inhibitory currents. Loose-patch cell-attached recording was performed as described previously²⁶^,³¹^,³². Glass electrodes with the same opening size containing ACSF were used. Instead of a giga-seal, a 100–250 MΩ seal was formed on the targeted neuron. All the neurons recorded under this condition showed regular-spike property, consistent with sampling bias toward excitatory neurons. The pipette capacitance was completely compensated, minimizing the distortion of the recorded spike shape. The spike signal was filtered at 10 kHz and sampled at 20 kHz. The apparent lack of hyperpolarizing responses in I-clamp recordings may be attributed to the fact that the reversal potential of inhibitory currents was close to the resting membrane potentials of the recorded cells.

Visual stimulation

Softwares for data acquisition and visual stimulation were custom-developed with LabView (National Instrument) and MATLAB (Mathworks) respectively. Visual stimuli were provided by a 34.5 × 25.9 cm monitor (refresh rate 120 Hz, mean luminance ~10 cd/m²) placed 0.25 m away from the right eye. Mouse eye has a large depth of focus of about ±10D, which means that the change in image quality of an object located from infinity to 0.1 m distance cannot be discerned by the mouse eye⁴²^–⁴⁴. Thus 0.25 m from the mouse eye is equivalent to infinity. The center of monitor was placed at 45° Azimuth, 0° Elevation⁴⁰, and it covered ±35° horizontally and ±27° vertically of the mouse visual field. To map spatial RF, two types of stimulation were used. For the first type, a set of bright squares (contrast 90%) within an 11×11 grid (grid size 4 – 5°) were displayed individually in a pseudo-random sequence, with a 1sec duration and 1sec inter-stimulus-interval. The On and Off subfields were derived from the responses to the onset and offset of the bright squares respectively¹⁷. For the second type, a set of bright and dark squares over a grey background (contrast 70% and −70% respectively) within an 11×11 grid (grid size 4 – 5°) were flashed individually (duration = 200 ms, inter-stimulus-interval = 300 ms) in a pseudo-random sequence, similar to the sparse stimuli used in the cat visual cortex³^,⁸^,¹⁶^,¹⁹. Each location was stimulated for 3–6 times for synaptic RF and ≥ 5 times for spike RFs, and the same number of On and Off stimuli were applied. The On and Off subfields were derived from responses to the onset of bright and dark squares respectively. . To be consistent with previous studies, synaptic subfields were mapped with the second type of stimulation. Spike RFs mapped with the two types of stimulation were similar and were pooled. The size of the stimulus was relatively small compared to that of the synaptic subfield, which was usually more than 35° (Fig. 3c,d). The mean overlap between synaptic subfields in the S-RF cells was larger than 25° (Supplementary Fig. 9). This large overlap between synaptic subfields cannot be explained by the possibility that some stimuli occur on the boundary between synaptic subfields.

Data analysis

Spikes were sorted offline after cell-attached recording. For the first type of stimulation, On and Off spike responses were measured within a 70–250 ms and 1070–1250 ms window after the onset of stimuli, respectively. For the second type of stimulation, spikes were counted within a 70–220 ms window after the onset of stimuli. The baseline activity was subtracted from stimulus-evoked spike rates. Response with the peak firing rate larger than threefold of standard deviation of baseline activity was considered as significant. The averaged firing rate was used to make RF color maps, which were normally smoothed with bilinear interpolation.

For intracellular recording, the peak amplitudes of synaptic responses (average from 3–6 trials) or V_m responses (averaged from >8 trials after removing spikes with an 8 ms median filter⁴⁵) were used for the RF color maps (smoothed with bilinear interpolation) and the spatial correlation plots. Excitatory and inhibitory synaptic conductances were derived according to¹⁰^,²²^,²³^,²⁵^,²⁶^,³²^,⁴⁵.

I (t) = G r (V (t) - E r) + G e (t) (V (t) - E e) + G i (t) (V (t) - E i) .

I is the amplitude of current at any time point; Gr and Er are the resting leak conductance and resting membrane potential respectively, and were derived from the baseline current of each recording; Ge and Gi are the excitatory and inhibitory synaptic conductance respectively; V is the membrane voltage, and Ee (0 mV) and Ei (−70 mV) are the reversal potentials. V(t) is corrected by V(t) = Vh − Rs*I(t), where Rs was the effective series resistance and Vh is the applied holding voltage. A 12 mV junction potential was corrected. By holding the recorded cell at two different voltages, Ge and Gi were calculated from the equation. Ge and Gi reflect the strength of pure excitatory and inhibitory synaptic inputs respectively. The visually-evoked synaptic currents are primarily mediated by AMPA and GABA_A receptors.

In the voltage-clamp recordings we were not able to experimentally examine the spike responses of the recorded cell, because our intracellular solution contained QX-314, a blocker of voltage-dependent Na⁺ channels, as to increase the clamping quality. Nevertheless, we could estimate membrane potential and spike responses by feeding the experimentally derived excitatory and inhibitory conductances into an integrate-and-fire model²³^,²⁵^,⁴⁶,

V_{m} (t + d t) = - \frac{d t}{C} [G_{e} (t) * (V_{m} (t) - E_{e}) + G_{i} (t) * (V_{m} (t) - E_{i}) + G_{r} (V_{m} (t) - E_{r})] + V_{m} (t)

where V_m(t) is the membrane potential at time t, C the whole-cell capacitance, G_r the resting leak conductance, E_r the resting membrane potential (−65 to −60 mV). To simulate spike response, 20 mV above the resting membrane potential was set as the spike threshold and a 10ms refractory period was used. C was measured during experiments and G_r was calculated based on the equation G_r = C*G_m/C_m, where G_m, the specific membrane conductance is 2e 5 S/cm², and C_m, the specific membrane capacitance is 1e−6 F/cm² (Ref. ⁴⁷). The derived spike RFs were similar to those recorded directly (Fig. 3e,g), suggesting that the integrate-and-fire model provides reasonable estimations of spike RFs.

To quantify the separation between On and Off subfields, an overlap index (OI) ²¹^,⁴⁸ was calculated for cells exhibiting both On and Off responses. The OI is defined as:

O I = \frac{W_{1} + W_{2} - d}{W_{1} + W_{2} + d}

where d is the distance between the peaks of two subfields, W₁ and W₂ are the half widths on the inner side of the two subfields respectively, defined as the segment of the line connecting the two subfield peaks between the peak and boundary on the inner side of the subfield. To determine d and W, we first fit the subfields separately with 2-D skew-normal distribution⁴⁹,

S N (x, y) = 2 φ (x, y) * Φ (x, y, α_{x}, α_{y})

where ϕ is 2-D Gaussian function and Φ is the 2-D integration of Gaussian function. α_x and α_y are parameters regulating the shape of the distribution. When α_x and α_y equal 0, the function is a normal Gaussian. The fitting was performed to the raw data. The outlines of subfields were drawn where the values of fitted distribution are three fold of standard deviation of baseline activity.

The distance between the peaks of spike On and Off subfields was normalized to the mean width of the subfields along the axis determined by their peaks. The distance between the peaks of membrane potential subfields or between those of synaptic subfields was normalized to the mean full-width at half-maximum of the two subfields along the axis determined bytheir peaks. The subfield size for spike RFs, the full-width at half-maximun bandwidth of synaptic RFs and the percentage shift of spike subfield boundaries were averaged for On and Off subfield.

The Youden’s Index was used to identify the boundary that best separate S-RF and O-RF cells.

Youden’s index = sensitivity + specificity − 1

Sensitivity = Probability(S-RF |V_m norm. distance > a)

Specificity = Probability(O-RF|V_m norm. distance < a)

We changed the value of a to obtain the maximum Youden’s index. The corresponding a value was the criteria to split S-RF and O-RF cells.

Modelling

A simple neuron model was built with a neuron receiving four sets of synaptic inputs evoked by On/Off stimuli. The spatial tuning curves of excitatory and inhibitory On responses were obtained by averaging the tuning curves from all the recorded S-RF cells. The Off tuning curves were obtained by flipping the On tuning curves horizontally. The peaks of the Eon and Eoff were separated by 8° (average separation in the recorded S-RF cells), and the overlapped Ion and Ioff located in the middle between the Eon and Eoff (Fig. 6a, top). The temporal profile of the evoked synaptic response was generated by fitting the average synaptic current of the cell #1 with an alpha function:

G = G_{max} * (t - onset) / τ * exp (- (t - onset - τ) / τ), for t > onset

with τ 63 ms for the excitatory response and 83ms for the inhibitory response (Fig. 6a, top, inset). The onset of the inhibitory current was set at 5ms after that of the excitatory current. The peaks of the excitatory and inhibitory tuning curves were set at 0.1 nA and 0.14 nA, respectively. The peak amplitudes of the evoked synaptic currents for each spatial location were determined from the tuning curves.

The spike response to On or Off stimulus at each spatial location was derived from the modelled synaptic inputs, based on the integrate-and-fire model. OIs were calculated based on the spatial tuning curves in a similar way as described above. For synaptic tuning curves, the boundary was set at 10% of maximum response. For spike tuning curves, the boundarywas set at where the first spike occurred.

Supplementary Material

Supplementary Figure 1. Layer 4 is dominated by monocontrast cells in the mouse V1

Supplementary Figure 2. Synaptic currents examined by voltage-clamp recordings

Supplementary Figure 3. Comparison between skew-normal fitting and Gaussian fitting of synaptic subfields

Supplementary Figure 4. Asymmetric distribution of synaptic strengths is characteristic of some subfields

Supplementary Figure 5. The distribution of correlation coefficient r between excitatory On and Off (Ex) and between inhibitory On and Off (In) subfields

Supplementary Figure 6. The relationship between the OI of derived membrane potential subfields and the OI of excitatory synaptic subfields

Supplementary Figure 7. Spike threshold cannot fully account for the dichotomy of spike RFs in our data set

Supplementary Figure 8. The ON/OFF spatial tuning curves of excitatory conductance (G_e), inhibitory conductance (G_i) used in the model, and of the derived. membrane potential responses (V_m) at two resting potentials

Supplementary. Figure 9 The level of overlap between three pairs of synaptic subfields

NIHMS165647-supplement-1.pdf^{(659.5KB, pdf)}

Acknowledgments

We thank Drs. Alapakkam Sampath and Dalin Li for their very helpful suggestions. This work was supported by grants to H.W.T. from the US National Institutes of Health (EY018718 and EY019049) and The Karl Kirchgessner Foundation. L.I.Z. is supported by the Searle Scholar Program, the Klingenstein Foundation, and the David and Lucile Packard Foundation.

Footnotes

AUTHOR COBTRIBUTIONS

B.H.L. and P.L. performed most of the experiments and data analysis. B.H.L. and Y.J.S. did the modelling. Y.T.L. helped with current-clamp recording experiments. H.W.T. and L.I.Z. designed the experiments and wrote the manuscript.

References

1.Hubel DH, Wiesel TN. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J Physiol. 1962;160:106–154. doi: 10.1113/jphysiol.1962.sp006837. [DOI] [PMC free article] [PubMed] [Google Scholar]
2.Heggelund P. Quantitative studies of the discharge fields of single cells in cat striate cortex. J Physiol. 1986;373:277–292. doi: 10.1113/jphysiol.1986.sp016047. [DOI] [PMC free article] [PubMed] [Google Scholar]
3.Hirsch JA, Alonso JM, Reid RC, Martinez LM. Synaptic integration in striate cortical simple cells. J Neurosci. 1998;18:9517–9528. doi: 10.1523/JNEUROSCI.18-22-09517.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
4.Troyer TW, Krukowski AE, Priebe NJ, Miller KD. Contrast-invariant orientation tuning in cat visual cortex: feedforward tuning and correlation-based intracortical connectivity. J Neurosci. 1998;18:5908–5927. doi: 10.1523/JNEUROSCI.18-15-05908.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Miller KD. Understanding layer 4 of the cortical circuit: a model based on cat V1. Cereb Cortex. 2003;13:73–82. doi: 10.1093/cercor/13.1.73. [DOI] [PubMed] [Google Scholar]
6.Hirsch JA, Martinez LM. Circuits that build visual cortical receptive fields. Trends Neurosci. 2006;29:30–39. doi: 10.1016/j.tins.2005.11.001. [DOI] [PubMed] [Google Scholar]
7.Ferster D, Miller KD. Neural mechanisms of orientation selectivity in the visual cortex. Annu Rev Neurosci. 2000;23:441–471. doi: 10.1146/annurev.neuro.23.1.441. [DOI] [PubMed] [Google Scholar]
8.Hirsch JA, Martinez LM, Pillai C, Alonso JM, Wang Q, Sommer FT. Functionally distinct inhibitory neurons at the first stage of visual cortical processing. Nat Neurosci. 2003;6:1300–1308. doi: 10.1038/nn1152. [DOI] [PubMed] [Google Scholar]
9.Ferster D. Spatially opponent excitation and inhibition in simple cells of the cat visual cortex. J Neurosci. 1988;8:1172–1180. doi: 10.1523/JNEUROSCI.08-04-01172.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Borg-Graham LJ, Monier C, Fregnac Y. Visual input evokes transient and strong shunting inhibition in visual cortical neurons. Nature. 1998;393:369–373. doi: 10.1038/30735. [DOI] [PubMed] [Google Scholar]
11.Sillito AM. The contribution of inhibitory mechanisms to the receptive field properties of neurones in the striate cortex of the cat. J Physiol. 1975;250:305–329. doi: 10.1113/jphysiol.1975.sp011056. [DOI] [PMC free article] [PubMed] [Google Scholar]
12.Nelson S, Toth L, Sheth B, Sur M. Orientation selectivity of cortical neurons during intracellular blockade of inhibition. Science. 1994;265:774–777. doi: 10.1126/science.8047882. [DOI] [PubMed] [Google Scholar]
13.Carandini M, Ferster D. Membrane potential and firing rate in cat primary visual cortex. J Neurosci. 2000;20:470–484. doi: 10.1523/JNEUROSCI.20-01-00470.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Mechler F, Ringach DL. On the classification of simple and complex cells. Vision Res. 2002;42:1017–1033. doi: 10.1016/s0042-6989(02)00025-1. [DOI] [PubMed] [Google Scholar]
15.Abbott LF, Chance FS. Rethinking the taxonomy of visual neurons. Nat Neurosci. 2002;5:391–392. doi: 10.1038/nn0502-391. [DOI] [PubMed] [Google Scholar]
16.Priebe NJ, Mechler F, Carandini M, Ferster D. The contribution of spike threshold to the dichotomy of cortical simple and complex cells. Nat Neurosci. 2004;7:1113–1122. doi: 10.1038/nn1310. [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Palmer LA, Davis TL. Receptive-field structure in cat striate cortex. J Neurophysiol. 1981;46:260–276. doi: 10.1152/jn.1981.46.2.260. [DOI] [PubMed] [Google Scholar]
18.Dean AF, Tolhurst DJ. On the distinctness of simple and complex cells in the visual cortex of the cat. J Physiol. 1983;344:305–325. doi: 10.1113/jphysiol.1983.sp014941. [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Jones JP, Palmer LA. The two-dimensional spatial structure of simple receptive fields in cat striate cortex. J Neurophysiol. 1987;58:1187–1211. doi: 10.1152/jn.1987.58.6.1187. [DOI] [PubMed] [Google Scholar]
20.Mata ML, Ringach DL. Spatial overlap of ON and OFF subregions and its relation to response modulation ratio in macaque primary visual cortex. J Neurophysiol. 2005;93:919–928. doi: 10.1152/jn.00668.2004. [DOI] [PubMed] [Google Scholar]
21.Martinez LM, Wang Q, Reid RC, Pillai C, Alonso JM, Sommer FT, Hirsch JA. Receptive field structure varies with layer in the primary visual cortex. Nat Neurosci. 2005;8:372–379. doi: 10.1038/nn1404. [DOI] [PMC free article] [PubMed] [Google Scholar]
22.Zhang LI, Tan AYY, Schreiner CE, Merzenich MM. Topography and synaptic shaping of direction selectivity in auditory cortex. Nature. 2003;424:201–205. doi: 10.1038/nature01796. [DOI] [PubMed] [Google Scholar]
23.Wehr M, Zador AM. Balanced inhibition underlies tuning and sharpens spike timing in auditory cortex. Nature. 2003;426:442–446. doi: 10.1038/nature02116. [DOI] [PubMed] [Google Scholar]
24.Higley MJ, Contreras D. Balanced excitation and inhibition determine spike timing during frequency adaptation. J Neurosci. 2006;26:448–457. doi: 10.1523/JNEUROSCI.3506-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
25.Liu BH, Wu GK, Arbuckle R, Tao HW, Zhang LI. Defining cortical frequency tuning with recurrent excitatory circuitry. Nat Neurosci. 2007;10:1594–1600. doi: 10.1038/nn2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
26.Wu GK, Arbuckle R, Liu BH, Tao HW, Zhang LI. Lateral Sharpening of Cortical Frequency Tuning by Approximately Balanced Inhibition. Neuron. 2008;58:132–143. doi: 10.1016/j.neuron.2008.01.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
27.Drager UC. Receptive fields of single cells and topography in mouse visual cortex. J Comp Neurol. 1975;160:269–290. doi: 10.1002/cne.901600302. [DOI] [PubMed] [Google Scholar]
28.Mangini NJ, Pearlman AL. Laminar distribution of receptive field properties in the primary visual cortex of the mouse. J Comp Neurol. 1980;193:203–222. doi: 10.1002/cne.901930114. [DOI] [PubMed] [Google Scholar]
29.Metin C, Godement P, Imbert M. The primary visual cortex in the mouse: receptive field properties and functional organization. Exp Brain Res. 1988;69:594–612. doi: 10.1007/BF00247312. [DOI] [PubMed] [Google Scholar]
30.Niell CM, Stryker MP. Highly selective receptive fields in mouse visual cortex. J Neurosci. 2008;28:7520–7536. doi: 10.1523/JNEUROSCI.0623-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
31.Liu BH, Li P, Li YT, Sun YJ, Yanagawa Y, Obata K, Zhang LI, Tao HW. Visual receptive field structure of cortical inhibitory neurons revealed by two-photon imaging guided recording. J Neurosci. 2009;29:10520–10532. doi: 10.1523/JNEUROSCI.1915-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
32.Tan AYY, Zhang LI, Merzenich MM, Schreiner CE. Tone-evoked excitatory and inhibitory synaptic conductances of primary auditory cortex neurons. J Neurophysiol. 2004;92:630–643. doi: 10.1152/jn.01020.2003. [DOI] [PubMed] [Google Scholar]
33.Petreanu L, Mao T, Sternson SM, Svoboda K. The subcellular organization of neocortical excitatory connections. Nature. 2009;457:1142–1145. doi: 10.1038/nature07709. [DOI] [PMC free article] [PubMed] [Google Scholar]
34.Debanne D, Shulz DE, Fregnac Y. Activity-dependent regulation of ‘on’ and ‘off’ responses in cat visual cortical receptive fields. J Physiol. 1998;508:523–548. doi: 10.1111/j.1469-7793.1998.00523.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
35.Tao HW, Poo MM. Activity-dependent matching of excitatory and inhibitory inputs during refinement of visual receptive fields. Neuron. 2005;45:829–836. doi: 10.1016/j.neuron.2005.01.046. [DOI] [PubMed] [Google Scholar]
36.Liu Y, Zhang LI, Tao HW. Heterosynaptic Scaling of Developing GABAergic Synapses: Dependence on Glutamatergic Input and Developmental Stage. J Neurosci. 2007;27:5301–5312. doi: 10.1523/JNEUROSCI.0376-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
37.Dantzker JL, Callaway EM. Laminar sources of synaptic input to cortical inhibitory interneurons and pyramidal neurons. Nat Neurosci. 2000;3:701–707. doi: 10.1038/76656. [DOI] [PubMed] [Google Scholar]
38.Yoshimura Y, Callaway EM. Fine-scale specificity of cortical networks depends on inhibitory cell type and connectivity. Nat Neurosci. 2005;8:1552–1559. doi: 10.1038/nn1565. [DOI] [PubMed] [Google Scholar]
39.Wagor E, Mangini NJ, Pearlman AL. Retinotopic organization of striate and extrastriate visual cortex in the mouse. J Comp Neurol. 1980;193:187–202. doi: 10.1002/cne.901930113. [DOI] [PubMed] [Google Scholar]
40.Moore CI, Nelson SB. Spatio-temporal subthreshold receptive fields in the vibrissa representation of rat primary somatosensory cortex. J Neurophysiol. 1998;80:2882–2892. doi: 10.1152/jn.1998.80.6.2882. [DOI] [PubMed] [Google Scholar]
41.Margrie TW, Brecht M, Sakmann B. In vivo, low-resistance, whole-cell recordings from neurons in the anaesthetized and awake mammalian brain. Pflugers Arch. 2002;444:491–498. doi: 10.1007/s00424-002-0831-z. [DOI] [PubMed] [Google Scholar]
42.de la Cera EG, Rodriguez G, Llorente L, Schaeffel F, Marcos S. Optical aberrations in the mouse eye. Vision Res. 2006;46:2546–2553. doi: 10.1016/j.visres.2006.01.011. [DOI] [PubMed] [Google Scholar]
43.Green DG, Powers MK, Banks MS. Depth of focus, eye size and visual acuity. Vision Res. 1980;20:827–835. doi: 10.1016/0042-6989(80)90063-2. [DOI] [PubMed] [Google Scholar]
44.Remtulla S, Hallett PE. A schematic eye for the mouse, and comparisons with the rat. Vision Res. 1985;25:21–31. doi: 10.1016/0042-6989(85)90076-8. [DOI] [PubMed] [Google Scholar]
45.Anderson JS, Carandini M, Ferster D. Orientation tuning of input conductance, excitation, and inhibition in cat primary visual cortex. J Neurophysiol. 2000;84:909–926. doi: 10.1152/jn.2000.84.2.909. [DOI] [PubMed] [Google Scholar]
46.Somers DC, Nelson SB, Sur M. An emergent model of orientation selectivity in cat visual cortical simple cells. J Neurosci. 1995;15:5448–5465. doi: 10.1523/JNEUROSCI.15-08-05448.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
47.Hines M. NEURON a program for simulation of nerve equations. In: Eeckman F, editor. Neural Systems: Analysis and Modeling. Norwell, MA: Kluwer; 1993. pp. 127–136. [Google Scholar]
48.Schiller PH, Finlay BL, Volman SF. Quantitative studies of single-cell properties in monkey striate cortex. I Spatiotemporal organization of receptive fields. J Neurophysiol. 1976;39:1288–1319. doi: 10.1152/jn.1976.39.6.1288. [DOI] [PubMed] [Google Scholar]
49.Azzalini A, Capitanio A. Statistical applications of the multivariate skew-normal distribution. J Roy Statist Soc B. 1999;61:579–602. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials