Distinct nonuniform cable properties optimize rapid and efficient activation of fast-spiking GABAergic interneurons

Abstract

Fast-spiking, parvalbumin-expressing basket cells (BCs) play a key role in feedforward and feedback inhibition in the hippocampus. However, the dendritic mechanisms underlying rapid interneuron recruitment have remained unclear. To quantitatively address this question, we developed detailed passive cable models of BCs in the dentate gyrus based on dual somatic or somatodendritic recordings and complete morphologic reconstructions. Both specific membrane capacitance and axial resistivity were comparable to those of pyramidal neurons, but the average somatodendritic specific membrane resistance (R_m) was substantially lower in BCs. Furthermore, R_m was markedly nonuniform, being lowest in soma and proximal dendrites, intermediate in distal dendrites, and highest in the axon. Thus, the somatodendritic gradient of R_m was the reverse of that in pyramidal neurons. Further computational analysis revealed that these unique cable properties accelerate the time course of synaptic potentials at the soma in response to fast inputs, while boosting the efficacy of slow distal inputs. These properties will facilitate both rapid phasic and efficient tonic activation of BCs in hippocampal microcircuits.

Fast-spiking, parvalbumin-expressing basket cells (BCs) play an important role in feedforward and feedback inhibition, providing rapid control over the frequency and timing of action potential initiation in principal neuron ensembles (1–6). Although inhibition comprises several steps, including activation of excitatory input synapses on BCs, dendritic integration of excitatory postsynaptic potentials (EPSPs), action potential initiation and propagation, and GABA release from output synapses, the kinetics of disynaptic inhibition can be very rapid, with ≈2 ms total onset time at physiologic temperature (3, 7). Several synaptic specializations contribute to the remarkable speed of feedforward and feedback inhibition. At the glutamatergic input synapses of BCs, the fast clearance of transmitter from the synaptic cleft and the expression of molecularly specialized L-α-amino-3-hydroxy-5-methyl-4-isoxazolepropionate receptors (AMPARs) contribute to rapid signaling (8, 9). At the GABAergic output synapses of BCs, the use of rapidly gated P/Q-type Ca²⁺ channels and the tight coupling of these channels to the Ca²⁺ sensors of exocytosis may serve a similar function (10, 11). Thus, functional specializations at both input and output synapses maximize the speed of BC-mediated disynaptic inhibition.

Synaptic location, dendritic structure, and electrical cable properties will also contribute to rapid signaling in GABAergic interneurons. For example, the proximal location of excitatory synapses may promote rapid activation of BCs. The significance of this factor, however, is unclear, because many glutamatergic synapses terminate on distal dendrites of BCs (12). Furthermore, rapid signaling could be promoted by the extensive axon, which may accelerate the somatic EPSP decay time course by generating a current sink. Although the axon contributes substantially to the time course of somatic EPSPs in cerebellar interneurons (13), its contribution in hippocampal BCs is not evident. Finally, the cable parameters, specific membrane resistance (R_m), membrane capacitance (C_m), and intracellular resistivity (R_i), will shape neuronal signaling (14–22). For example, a low value of R_m, which may be generated by a high density of leak channels (23), would accelerate the decay of EPSPs by speeding up the membrane time constant. Similarly, a low R_i value, which may be caused by a high intracellular Cl^- concentration in BCs (24), could accelerate dendrosomatic propagation of synaptic signals.

Whether BCs differ from principal cells in any of these cable parameters, however, is presently unclear. Although a number of cable models are available for principal neurons, previous attempts to model inhibitory interneurons were only partially successful. In one study, estimated values of R_i varied by almost an order of magnitude (50–484 Ω cm; ref. 25), whereas another study concluded that the value of R_i could not be determined (26). Furthermore, the axonal arborization was not included in any of these studies, and a possible nonuniformity of R_m was not considered (27, 28). However, complete passive cable models will be necessary for understanding the mechanisms of both dendritic integration and action potential initiation in GABAergic interneurons (13, 29).

To address these questions, we developed detailed passive cable models (27, 28, 30–32) of BCs in the dentate gyrus. To obtain accurate measurement of R_i and somatodendritic nonuniformity of R_m, both dual somatic and somatodendritic recordings were performed. To probe both proximal and distal electrotonic compartments, short- and long-pulse responses were simultaneously analyzed. In all cases we reconstructed neurons entirely, including the complex axonal arborization (13).

Results

To develop detailed cable models of dentate gyrus BCs, two-electrode whole-cell recordings were made in hippocampal slices, using dual somatic or somatodendritic configurations. The experimental protocol was as follows. First, the input resistance and the action potential phenotype were determined using sub- and suprathreshold current pulses. Next, passive responses were evoked in the presence of tetrodotoxin, ZD 7288, AMPAR antagonists, and GABA_AR blockers. To reveal the morphologic properties, neurons were filled with biocytin during recording. After a ≈60-min recording period the slice was fixed, and the somatodendritic and axonal morphology was visualized using 3,3′-diaminobenzidine as chromogen (SI Methods). Six BCs with stable recording conditions and optimal labeling were chosen for full reconstruction (Fig. S1; Table S1).

Consistent with previous reports (33), BCs had a fast-spiking action potential phenotype and a low input resistance, with a mean value of 82.6 ± 11.8 MΩ (n = 6; Fig. S1B). Furthermore, BCs had a large soma in the granule cell layer (GCL) or at the border between GCL and the hilar region, smooth dendrites, and an extensive axonal arbor that was mainly located in the GCL (Fig. S1 A and C).

Dual Somatic and Somatodendritic Recording of Passive Responses.

To probe the passive membrane properties of BCs, we first measured voltage responses in the dual somatic configuration, allowing the separation of voltage recording and current feeding electrode (Fig. 1 A–C). A major advantage of this configuration is that the fast components of charge redistribution can be accurately measured at the voltage recording electrode, as required for reliable estimation of R_i (32).

Fig. 1.

Passive voltage transients in BCs obtained by dual somatic and somatodendritic recordings. (Ai) Infrared differential interference contrast photomicrograph of a BC during dual somatic recording. (Aii) Current pulse (Upper) and voltage responses (Lower) at voltage recording (black) and current injecting (blue) electrodes. Note artifacts caused by residual uncompensated series resistance and pipette capacitance in the current injecting electrode but not the voltage recording electrode. (B) Current pulses and corresponding voltage responses evoked by short (Upper) and long pulses (Lower). Traces are averages of 272, 233, 181, and 190 single sweeps, respectively. Dashed lines indicate baseline voltage levels. (C) Semilogarithmic plot of the decay phase of normalized average responses to short and long current pulses. Data in Aii, B, and C from BC2; image in Ai from a different cell. (D) Photomontage of confocal images (pseudocolor representation) of a BC filled with Alexa Fluor 488 during somatodendritic recording. (E) Voltage responses evoked by short (Upper) and long pulses (Lower). Blue traces, somatic injection, dendritic recording. Black traces, dendritic injection, somatic recording. Traces are averages from 158, 95, 84, and 87 single sweeps, respectively. Data in E from BC6; image in D from a different cell. (F) Test of linearity (Upper) and reciprocity (Lower) for short (Left) and long (Right) current pulses. For linearity test, amplitude of hyperpolarizing responses was plotted vs. that of depolarizing responses at the same time point (decay phase after the pulse; BC2). For reciprocity test, amplitudes of the somatic voltage responses evoked by dendritic current injection were plotted against dendritic voltage responses evoked by somatic current injection at the same time point (decay phase after the pulse; BC6). Note that data points were close to the identity lines (continuous gray lines) in all cases, indicating both linearity and reciprocity. Amplitudes of voltage signals were divided by the maximum of the injected current.

Comparison of voltage responses to short and long de- and hyperpolarizing current pulses (Fig. 1B) revealed that the decay of the long-pulse response was substantially slower than that of the short-pulse response in the same cell (Fig. 1C). Similar results were obtained in all three dual somatic recordings; the rate of decay at t = 25–35 ms was 1.89 ± 0.13-fold slower for long-pulse than for short-pulse responses. Short pulses will charge proximal compartments, whereas long pulses charge both proximal and distal membrane areas. Therefore, the marked difference in decay time course would be consistent with a nonuniform membrane time constant. To confirm the linearity of the recorded signals, the amplitudes of de- and hyperpolarizing responses were normalized to the maximal amplitude of the injected current, and voltages at the same time points after the peak were plotted against each other (Fig. 1F). Linear regression revealed that the data points were located close to the identity line (mean slope 1.01 ± 0.02 for short-pulse responses and 1.04 ± 0.004 for long-pulse responses). This corroborates the passive nature of the measured responses, as required for cable modeling (e.g., ref. 30).

Confocally guided dendritic patch-clamp recording has recently allowed us to gain direct access to BC dendrites (34). To further constrain the value of R_i and possible nonuniformities of dendritic R_m (27, 28), we performed simultaneous recordings from somata and apical dendrites of BCs 60–254 μm from the soma (Fig. 1 D and E). Similar to the dual somatic recordings, the rate of decay at t = 25–35 ms was slower for long-pulse than for short-pulse responses (1.75 ± 0.11-fold for all four combinations of injection and recording sites). To confirm reciprocity, a hallmark of passive systems (18, 30), we plotted the dendritic response to a current pulse delivered to the soma against the somatic response to the same current pulse delivered to the dendrite (Fig. 1F). Linear regression revealed that the data points were close to the identity line (mean slope 0.98 ± 0.02 for short-pulse responses and 1.00 ± 0.01 for long-pulse responses), demonstrating that the system obeyed reciprocity.

Comparison of Uniform and Nonuniform BC Cable Models.

We next analyzed the recorded passive voltage transients with cable models based on the morphology of the recorded neuron (Fig. 2). In the dual somatic recordings, only responses at the voltage recording electrode were considered. In dual somatodendritic recordings, both somatic and dendritic voltage transients evoked by somatic current injection were analyzed, but analysis of somatic responses was restricted to the decay phase. Initially, R_m, C_m, and R_i were assumed to be uniform throughout the entire cell (Fig. 2A). Although the time course of the passive responses was approximated by the uniform model, detailed analysis revealed that the different decay time courses of short- and long-pulse responses could not be reproduced (Fig. 2 A and E).

Fig. 2.

Nonuniform cable models are required to fit passive experimental voltage transients. (A–C) Voltage responses (black, soma; blue, dendrite) in the somatodendritic recording configuration to brief and long current pulses applied at the soma, superimposed with the prediction of the uniform model (U, red; A), the type 1 nonuniform model (NU1, green; B), and the type 2 nonuniform model (NU2, green; C). Plotting range of the model curves is identical to the fitting range. (D) 3D reconstruction of the same BC shown in A–C and E (BC6; somatodendritic domain in black, axon in red). (E) Semilogarithmic plot of the decay of the long-pulse responses superimposed with the predictions of models (continuous red curve, somatic and dendritic responses for model U; continuous green curve, somatic response for NU2; dashed green curve, dendritic response for NU2). (F) Comparison of SSE values for different models. (G and H) Summary of R_m (G), C_m (H, Left), and R_i (H, Right) of the six BCs fitted with the type 2 nonuniform model (NU2). Bars represent means ± SEMs. Data from individual dual somatic recordings are represented by circles, data from somatodendritic recordings are depicted as triangles. Data from the same cell are connected by lines. Pr, proximal dendritic R_m (R_{m, prox}); Di, distal dendritic R_m (R_{m, dist}); De, weighted average dendritic R_m (R_{m, dend}); Ax, axonal R_m (R_{m, axon}).

We therefore tested two alternative models with nonuniform R_m: a model with simple nonuniformity with different R_m values in somatodendritic and axonal compartments (type 1 nonuniformity; Fig. 2B) and a model with complex nonuniformity in which R_m was different between axon, proximal somatodendritic compartments (≤120 μm), and distal dendritic compartments (>120 μm; type 2 nonuniformity; Fig. 2C). Both nonuniform models provided a substantially better fit of the experimental voltage responses than the uniform model (Fig. 2 A–C and E; P < 0.05), indicating nonuniformity of R_m. On average, the type 1 model reduced the sum of squared errors (SSE) by 63.1% ± 11.5% in comparison with the uniform model, and the type 2 model further reduced the SSE by 28.0% ± 11.0% in comparison with the type 1 model (Fig. 2F). In contrast, no further improvement of the fit was obtained using alternative models with sigmoidal or linear gradients (1.4–3.3% increase of average SSE in comparison with the type 2 nonuniform model). Thus, our results indicate nonuniformity of R_m across soma, dendrites, and axon.

Analysis of somatodendritic recordings (which are expected to provide maximal information about dendritic nonuniformity) with the type 2 nonuniform model revealed R_{m, prox} (soma + proximal dendrites) = 7.6 ± 1.7 kΩ cm² and R_{m, dist} (distal dendrites) = 74.3 ± 56.1 kΩ cm² (n = 3). Furthermore, analysis of both dual somatic and somatodendritic recordings with the type 2 model revealed R_{m, axon} = 281.6 ± 108.2 kΩ cm², C_m = 0.93 ± 0.04 μF cm⁻², and R_i = 172.1 ± 18.5 Ω cm (n = 6; Fig. 2 G and H; Table S2 and Table S3). In conclusion, R_m in BCs was markedly nonuniform, with a 37-fold higher value in the axon and a 10-fold higher value in the distal dendrites than in the proximal dendrites and the soma. Potential sources of errors are analyzed in Fig. S2. Bootstrap analysis revealed that statistical errors were small, with coefficients of variation (CV) ranging from 1.7% to 31.4% (Fig. S2A; Table S2). Variation of diameter of all processes in the reconstructed cells by ±10% or ± 0.1 μm indicated only small systematic errors in the range of 2.6–18.0%, except for R_{m, axon} (106.6% for a −0.1 μm change; Fig. S2B). Likewise, variation of length of all processes by ±10% suggested only minor systematic errors in the range of 0.3–9.1%. Finally, analysis of the SSE in the parameter space revealed that the solution obtained by direct fitting was unique for all models tested (Fig. S2 C and D).

Unique Type of Somatodendritic Nonuniformity of R_m.

Our finding that R_m was higher at distal than at proximal dendrites was surprising, because previous analysis suggested an opposite gradient in hippocampal and neocortical pyramidal neurons (27, 28). Additional information about the somatodendritic R_m gradient may be obtained by comparison of the decay time course of dendritic and somatic voltage transients evoked by brief current pulses. If R_m is nonuniform and current is injected into the low-R_m region, local voltage transients will decay more rapidly than remote transients, leading to a crossing of the responses at the two sites (27, 35). We confirmed this prediction using our detailed passive cable model. If the original BC-type nonuniformity is implemented (R_{m, dist}:R_{m, prox} = 10:1), crossing of responses occurs during the first 10 ms for somatic, but not apical dendritic current injection (Fig. 3A). Conversely, if the previously proposed pyramidal-type nonuniformity is implemented (R_{m, dist}:R_{m, prox} = 1: 10), early crossing occurs selectively for the apical dendritic current injection (Fig. 3B). Thus, analysis of the time course of responses at different locations allows us to probe the direction of the somatodendritic R_m gradient.

Fig. 3.

Crossing of voltage transients recorded at different sites directly demonstrates a somatodendritic nonuniformity of R_m. (A and B) Predictions of the model for different R_m gradients. Simulation of passive responses at soma (black) and apical dendrite (≈230 μm from the soma; blue) after brief current pulses injected into the soma (Left) or the dendrite (Right). (A) BC-type gradient (R_{m, dist}:R_{m, prox} = 10:1), (B) pyramidal-type gradient (R_{m, dist}:R_{m, prox} = 1:10). Gray curves, difference between local voltage at injection site and remote voltage. Red arrows, time points where differences become minimal (≤10 μV). Note early crossing for somatic current injection in A and dendritic current injection in B. Simulations were performed using the BC2 cable model. (C) Measured responses for somatodendritic recording for somatic (Left) and apical dendritic (Right) current injection. Traces are averages of 144, 110, 144, and 139 individual sweeps; dendritic recording site 227 μm from soma. Crossing for somatic current injection is consistent with a higher R_m in distal than in proximal dendrites. (D) Plot of crossing time for somatic (filled symbols) and dendritic current injection (open symbols) vs. distance of dendritic recording site from the soma. Twenty-three somatodendritic recordings from BCs. Triangles, data from BC4–6. Continuous curve, linear regression of data for somatic injection. Dashed curve, fit of data for dendritic injection with a sigmoidal function (midpoint constrained to 120 μm).

We next compared the time course of apical dendritic and somatic voltage transients in dual recordings from somata and dendrites 60–254 μm from the soma. For distances >100 μm, dendritic and somatic voltage traces intersected at early time points for somatic current injection but converged at later times for dendritic current injection (Fig. 3 C and D; n = 23 BCs). These results provide direct experimental evidence that the somatodendritic R_m in BCs is nonuniform and that the direction of the gradient is opposite to that in pyramidal cells (27, 28).

EPSP Speeding by Structural Factors.

In the dentate gyrus, feedforward and feedback excitatory inputs on BCs are segregated to different dendrites [commissural/associational (C/A), medial perforant path (MPP), and lateral perforant path (LPP) inputs on apical dendrites, granule cell (GC) inputs on basal dendrites; e.g., ref. 9]. To test for possible differences in signaling properties between apical and basal dendrites, we simulated EPSPs generated by synapses at various locations, using the type 2 nonuniform BC cable model with reconstructed morphology and best-fit parameters. Although synapses located on basal dendrites showed larger local EPSP amplitudes than those on apical dendrites (Fig. 4A), the somatic EPSP amplitudes were comparable (Fig. 4C). Local EPSP amplitudes were approximately predicted by the input impedance (Z_in) (36), at a frequency of 100 Hz (Fig. 4B). Furthermore, synapses on basal dendrites showed a higher EPSP propagation velocity than those on apical dendrites (116 μm ms⁻¹ vs. 79 μm ms⁻¹ for distances ≤200 μm; Fig. 4D). Finally, somatic EPSP decay time constants and half-durations were faster for basal than for apical synapses (Fig. 4 E and F). Thus, the timing of somatic EPSPs depended on both synaptic location and the type of target dendrite. The fastest somatic EPSPs were generated if the synaptic input was located on basal dendrites close to the soma.

Fig. 4.

EPSP amplitude and time course in BCs depend on both synaptic location and target dendrite. (A) Local EPSP peak amplitude as a function of distance of the simulated synapse from the soma. (B) Plot of input impedance (Z_in) for high-frequency signals (100 Hz). Note that the distance dependence of local EPSP amplitude is similar to that of input impedance. (C) Somatic EPSP peak amplitude. (D) Latency between the onset of the postsynaptic conductance and peak of the somatic EPSP. Gray dashed lines represent the result of linear regression (0–200 μm; data from basal and apical dendrites fitted separately). (E) Decay time constant of somatic EPSP (monoexponential fit). (F) Half-duration of somatic EPSP. Note faster conduction velocity and somatic EPSP time course for basal than apical synapses. Insets in A, C, and D: EPSP traces generated by synapses on basal dendrites at different distances from the soma (20–180 μm, 40 μm step). Synapses were sequentially placed on all dendritic segments, and the parameter of interest was plotted against the distance of the activated synapse from the soma (positive distances, apical dendrites; negative distances, basal dendrites). Data points for the same dendritic path were connected by lines. All simulations were performed using the type 2 nonuniform model of BC2. Synaptic peak conductance was 2 nS throughout.

Unlike principal neurons, BCs are characterized by an extensive axonal arbor, which provides a major contribution to the total surface area of the cells (Fig. S1D). Previous studies in cerebellar interneurons suggested that the axon may act as a somatic current sink, leading to speeding of the EPSP decay time course (13). We tested this hypothesis by removing the axon from our BC cable model (Fig. S3, red curves). Axon removal had moderate effects on somatic EPSP peak amplitude and propagation velocity (Fig. S3 A and B) but prolonged both EPSP decay time constant and half-duration (Fig. S3 C and D). In contrast, removal of the basal dendrites markedly increased somatic EPSP peak amplitude, whereas the effects on the other parameters were moderate (Fig. S3, green curves). For the half-duration, axon and dendrite removal had opposite effects (Fig. S3D). Thus, whereas the basal dendritic tree represents a fast current sink that attenuates somatic EPSP peak amplitude, the axonal arbor provides a slow current sink that accelerates EPSP decay time course (13).

EPSP Speeding by Specific Cable Parameters.

Our results indicate that the specific cable parameters of BCs differ from those of principal neurons, especially regarding a low and nonuniform R_m (27, 28, 30, 32). How do these unique cable properties affect the signaling characteristics of BCs? To address this question, the mean value or the spatial profile of R_m was altered, while the original BC structure was maintained (Fig. S4). First, we tested the effects of uniform changes in R_m (Fig. S4, red and orange curves). Increasing R_m in all somatodendritic sections by a factor of 3 increased the amplitude of somatic EPSPs (Fig. S4A), decreased EPSP propagation velocity (Fig. S4B), and increased both decay time constant and half-duration of somatic EPSPs (Fig. S4 C and D). Decreasing R_m had opposite effects on all parameters. Thus, the low R_m value is a key factor of rapid signaling in BCs, which ensures rapid dendrosomatic propagation and fast termination of EPSPs.

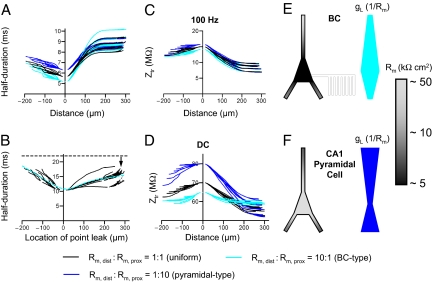
Next, we explored the effects of somatodendritic nonuniformity in R_m, changing the ratio of distal to proximal dendritic R_m (Fig. 5A; Fig. S4, cyan and blue); the total leak conductance was kept constant. Intriguingly, the model with the BC-type gradient (R_{m, dist}:R_{m, prox} = 10:1) for proximal synapses produced faster somatic EPSP half-durations than the model with the reverse (i.e., pyramidal-type; refs. 27, 28) gradient (R_{m, dist}:R_{m, prox} = 1:10; Fig. 5A). To systematically analyze the relation between the location of the leak and half-duration of the somatic EPSP, the model with the BC-type gradient (R_{m, dist}:R_{m, prox} = 10:1) was modified by uniformly increasing R_m to R_{m, dist}, while reducing R_m at a defined single dendritic segment; again, the total leak conductance was maintained. Fig. 5B shows a plot of the half-duration of the somatic EPSP generated by a distal synapse against the location of the low-R_m segment. The EPSP half-duration was markedly dependent on the location of the leak conductance, showing a minimum at the center of the soma. Thus, a somatically located conductance generates maximal EPSP speeding, whereas a distally located conductance is much less effective.

Fig. 5.

Nonuniform R_m ensures rapid phasic and efficient tonic activation of BCs. (A) Half-duration of somatic EPSP plotted against distance of the activated synapse from the soma for uniform dendritic R_m (R_{m, dist}:R_{m, prox} = 1:1; black), BC-type nonuniformity (R_{m, dist}:R_{m, prox} = 10: 1; cyan), and pyramidal-type nonuniformity (R_{m, dist}:R_{m, prox} = 1:10; blue). (B) Speeding of somatic EPSPs by a perisomatic point leak. Plot of half-duration of somatic EPSP as a function of location of the leak. R_m was uniformly set to R_{m, dist} of the BC-type model (R_{m, dist}:R_{m, prox} = 10:1), and the difference conductance was inserted at defined points of the dendritic tree. I_h conductance was uniformly set to its default value. Cyan dashed curve represents a doubly linear function with a sigmoidal transition. Note that the minimum is close to 0, indicating that a point leak has maximal speeding effects if located perisomatically. Arrow indicates location of the activated synapse. Black dashed line represents the somatic EPSP half-duration in the absence of any leak. Synaptic peak conductance was 2 nS in A and 8 nS in B. (C and D) Plot of transfer impedance (Z_tr) for high-frequency (100 Hz; C) and low-frequency signals (DC, identical to transfer resistance; D). Color code as in A. Note that in comparison with the scenario with uniform dendritic R_m, pyramidal-type nonuniformity preferentially enhances transfer resistance for proximal inputs, whereas BC-type nonuniformity selectively increases transfer resistance for distal inputs. All simulations were performed using the type 2 nonuniform model of BC2. (E and F) Schematic illustration of nonuniformity of R_m and leak conductance (g_L = 1/R_m) in BCs (E) and pyramidal neurons (F). Grayscale indicates the approximate value of R_m (Right).

To test the previous suggestion that dendritic nonuniformity may enhance the signal transfer from distal dendrites (35), we further computed the dendrosomatic transfer impedance for different dendritic locations in the two nonuniform scenarios (Fig. 5 C and D). Both types of nonuniformity had only minimal effects on the transfer impedance for high-frequency signals (100 Hz; Fig. 5C) but markedly influenced transfer impedance for low-frequency signals (i.e., transfer resistance; Fig. 5D). A pyramidal-type gradient primarily increased the transfer resistance from proximal dendritic locations to the soma, whereas a BC-type gradient selectively increased the transfer resistance from distal dendritic locations (Fig. 5D). Thus, the BC-type R_m gradient shapes dendritic signaling in a unique manner. It results in speeding of somatic EPSPs generated by fast distal inputs and at the same time enhances signal transfer for slow distal inputs.

Discussion

Cable Properties of BCs Differ from Those of Principal Neurons.

Our results demonstrate that the average somatodendritic R_m in BCs is substantially lower than that in principal neurons. In BCs, the average somatodendritic R_m in the presence of I_h channel blocker was 14.2 kΩ cm², 2- to 12-fold lower than in hippocampal principal neurons, including dentate gyrus GCs (uniform R_m = 38 kΩ cm²; ref. 32), CA3 pyramidal neurons (uniform R_m = 170 kΩ cm²; ref. 30), and CA1 pyramidal neurons (weighted mean R_{m, dend} = 26 kΩ cm², assuming a distal:proximal membrane area ratio of 2:1; ref. 28). Furthermore, our results indicate that the direction of the somatodendritic R_m gradient in BCs is the reverse of that in principal cells. In BCs, proximal dendrites are leakier (R_m ≈ 8 kΩ cm²) than distal dendrites (R_m ≈ 70 kΩ cm²) and axon (R_m ≈ 300 kΩ cm²). In contrast, an opposite gradient was found in CA1 pyramidal neurons and layer 5 neocortical pyramidal cells, where distal dendrites are leakier than proximal ones (R_{m, prox} ≈ 90 kΩ cm²; R_{m, dist} ≈ 20 kΩ cm²; ref. 28; R_{m, prox} ≈ 35 kΩ cm²; R_{m, dist} ≈ 5 kΩ cm²; ref. 27).

However, the values of both C_m and R_i in BCs are similar to those in principal neurons. In BCs, the mean value of C_m was 0.93 μF cm⁻², similar to estimates in dentate gyrus GCs (1.01 μF cm²; ref. 32), CA3 pyramidal neurons (0.75 μF cm²; ref. 30), and CA1 pyramidal neurons (1.50 μF cm²; ref. 28). Intriguingly, our estimate of C_m in BCs is almost identical to a previous measurement of somatic C_m based on capacitance and area of nucleated patches isolated from different types of neurons, including hippocampal pyramidal cells (0.90 μF cm⁻²; ref. 37). In BCs, the mean value of R_i was 172 Ω cm, similar to that obtained in dentate gyrus GCs (194 Ω cm; ref. 32; dual somatic recordings) and CA1 pyramidal neurons (178 Ω cm; ref. 28; somatodendritic recordings). Thus, whereas previous estimates of R_i based on single-electrode recording were highly variable (e.g., refs. 30, 38), estimates based on dual somatic and somatodendritic recordings converge toward the conclusion that R_i significantly exceeds the value in aqueous solutions (but see ref. 27).

Nonuniform R_m Helps to Achieve a Balance Between Speed and Efficacy.

Our results demonstrate that, in addition to synaptic characteristics, dendritic cable properties markedly contribute to rapid signaling in BCs. First, somatic EPSPs generated at basal dendrites propagate with higher velocity and show a faster time course at the soma than those generated on apical dendrites. These specific signaling properties can be explained by the smaller diameter and the more pronounced tapering of basal dendrites (Fig. S1E; ref. 36). Because GC inputs selectively terminate on the basal dendrites, whereas MPP and LPP inputs impinge on apical dendrites of BCs, BC cable properties will give a kinetic advantage to feedback over feedforward synapses. Second, the extensive axonal arborization generates a substantial perisomatic current sink, accelerating the decay of the somatic EPSP. Thus, axonal “speeding” contributes to the rapid time course of the EPSP in BCs (13). Finally, the low average dendritic R_m value of BCs makes a major contribution to the fast propagation velocity and rapid EPSP kinetics. Because the preferential action potential initiation site in BCs is the axon (34), and the axon originates perisomatically (Table S1), the low R_m will facilitate rapid action potential initiation in BCs and at the same time ensure that only a single spike rather than a burst of action potentials is triggered by a single synaptic stimulation. Likewise, the low R_m will restrict the window of temporal summation (9).

A potential disadvantage of the low average somatodendritic R_m is that the efficacy of distal inputs is reduced. Although this reduction is moderate for fast synaptic inputs, it can be very severe for slow inputs. How is this potential problem solved? Nonuniform R_m provides an answer to this question. On the one hand, the BC-type nonuniformity (R_{m, dist} > R_{m, prox}) accelerates the time course of somatic EPSPs in comparison with a pyramidal-type nonuniformity (R_{m, dist} < R_{m, prox}). This effect is prominent in the extreme scenario in which the proximal leak conductance is concentrated at a somatic point (Fig. 5B). On the other hand, the BC-type nonuniformity selectively increases the efficacy of slow synaptic inputs at the distal dendrites, equalizing the strength of C/A, MPP, and LPP inputs (Fig. 5D). In contrast, a pyramidal cell-type nonuniformity preferentially increases the transfer resistance for proximal inputs. This increase in efficacy of distal inputs by the BC-type nonuniformity could have multiple functional consequences. For example, it may help to relay low-frequency (e.g., theta) activity from the entorhinal cortex to the BC soma via the perforant path (39). Furthermore, it may promote tonic activation of BCs via metabotropic glutamate receptors, which are required for the generation of gamma oscillations in interneuron networks (40).

In conclusion, the cable properties of BCs are substantially different from those of pyramidal neurons (Fig. 5 E and F). These specific cable properties define unique signaling characteristics, promoting phasic activation of BCs by fast EPSPs and at the same time tonic activation by slow distal inputs. This may explain rapid and efficient recruitment of BCs during different forms of network activity, such as feedback inhibition, feedforward inhibition, and high-frequency oscillatory activity (1, 3, 4, 40).

Methods

Details of the methods are specified in SI Methods. In brief, dual somatic or somatodendritic recordings were made from BCs in the dentate gyrus using hippocampal slices from 17–20-day-old rats. Recording temperature was 30°C–34°C. Neurons were filled with biocytin during recording and fully reconstructed. Cable parameters R_m, C_m, and R_i were determined by minimizing the SSEs between experimental and simulated voltage transients, using the morphology of the reconstructed cell as a constraint.