Precipitation extreme changes exceeding moisture content increases in MIROC and IPCC climate models

Abstract

Precipitation extreme changes are often assumed to scale with, or are constrained by, the change in atmospheric moisture content. Studies have generally confirmed the scaling based on moisture content for the midlatitudes but identified deviations for the tropics. In fact half of the twelve selected Intergovernmental Panel on Climate Change (IPCC) models exhibit increases faster than the climatological-mean precipitable water change for high percentiles of tropical daily precipitation, albeit with significant intermodel scatter. Decomposition of the precipitation extreme changes reveals that the variations among models can be attributed primarily to the differences in the upward velocity. Both the amplitude and vertical profile of vertical motion are found to affect precipitation extremes. A recently proposed scaling that incorporates these dynamical effects can capture the basic features of precipitation changes in both the tropics and midlatitudes. In particular, the increases in tropical precipitation extremes significantly exceed the precipitable water change in Model for Interdisciplinary Research on Climate (MIROC), a coupled general circulation model with the highest resolution among IPCC climate models whose precipitation characteristics have been shown to reasonably match those of observations. The expected intensification of tropical disturbances points to the possibility of precipitation extreme increases beyond the moisture content increase as is found in MIROC and some of IPCC models.

Precipitation extreme events are of considerable interest because of their disproportionate damages on the social and natural systems including flooding and soil erosion. In spite of a great deal of uncertainty, there has emerged a broad understanding of the change in the climatological-mean hydrological cycle (1), mainly based on atmospheric thermodynamics. Similarly, thermodynamic arguments have helped interpret precipitation extreme changes. Studies pointed out that because precipitation is constrained by the availability of atmospheric water vapor, the change in precipitation extremes would scale with or be constrained by precipitable water changes (2, 3). Under a constant relative-humidity condition precipitable water increases at the rate of change in saturation vapor pressure described by the Clausius–Clapeyron (CC) relation. Applying typical lower tropospheric temperatures, one arrives at a rate of change of approximately 7% K, a number often quoted.

The thermodynamic postulate rests on the assumption that changes in vertical motion do not have a significant effect on precipitation changes and ignores a possible feedback between the upward velocity and thermodynamics, which is by no means trivial (4). Nevertheless, studies using general circulation models (GCMs) have generally confirmed that in the midlatitudes precipitation changes scale with changes in water vapor content (5–7).

A more detailed look reveals the limitations of the CC scaling, however. The changes in hourly (rather than daily) precipitation have been found to increase with temperature about twice as fast as expected from the CC relation in both observations and a regional climate model (4). The observed interannual variability in the frequency of tropical precipitation extremes has been shown to exceed the CC prediction (8). A parameter-sweeping analysis with an idealized GCM showed that a successful scaling for precipitation extremes needs to incorporate the effect of atmospheric dynamics and the temperature changes associated with extreme events (9).

Moreover, studies that provided support for thermodynamic arguments themselves identified the deviations from CC predictions for the tropics (5–7). They did not elaborate on the physical mechanism for the discrepancies, however. A recent study (10) applied a dynamically based scaling to models participating in the Fourth Assessment Report of the IPCC and found that such a scaling can predict the modeled precipitation extremes. In the same spirit we analyze daily precipitation extremes in the IPCC climate models but focus on the superCC increases of precipitation extremes in the IPCC models in particular the high-resolution version of MIROC (11), a coupled GCM that was not analyzed by O’Gorman and Schneider in ref. 10. We examine the very high percentile of precipitation by constructing a space–time cumulative distribution function (CDF) of daily precipitation (3, 6).

Precipitation Extremes in IPCC Models

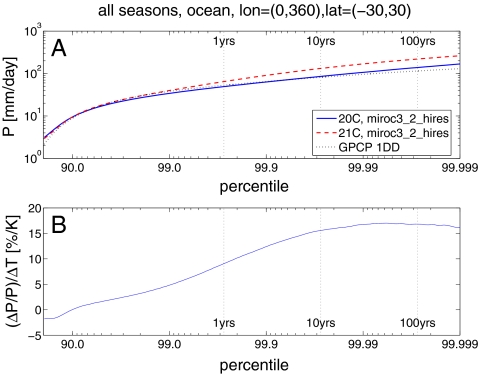
Fig. 1A shows the inverse CDFs of daily precipitation for the tropical oceans from the high-resolution version of MIROC. The CDF combines both space and time to increase the sample size and is not representative of a particular grid point. The model’s resolution is approximately 1.1° in equivalent grid, the highest among the IPCC climate models. The figure shows the results from the two scenarios: Special Report on Emissions Scenarios (SRES) A1B (2081–2100) and 20th Century Climate in Coupled Models (20C3M) (1981–2000). MIROC reproduces the observed precipitation characteristics as represented by the Global Precipitation Climatology Project (GPCP) one degree daily (1DD) dataset based on multiple satellites (12). Fig. 1B displays the fractional change of precipitation per unit regional warming as a function of the CDF. The fractional change increases with CDF and seems to asymptote to about 17% K, exceeding that expected from the CC relation.

Fig. 1.

(A) Inverse cumulative distribution functions CDFs of daily precipitation over the tropical (30°S–30°N) oceans from the high-resolution version of MIROC and the observational dataset GPCP 1DD (1997–2005). The vertical dotted lines represent the CDF values that correspond to the return periods of 1, 10, and 100 yr. (B) Fractional changes in precipitation per unit warming of the target area.

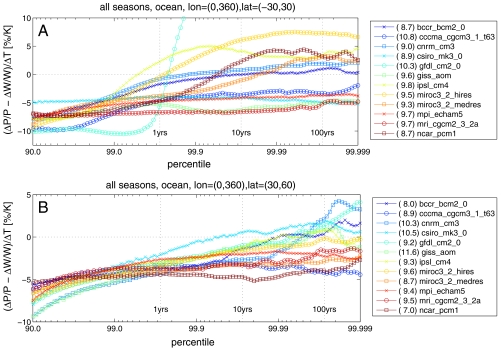
Fig. 2 extends the analysis shown in Fig. 1A to the selected climate models from the World Climate Research Program (WCRP) Coupled Model Intercomparison Project phase 3 (CMIP3) multimodel dataset (13). In Fig. 2, fractional changes in climatological-mean precipitable water W (shown in the parentheses) have been subtracted from the changes in precipitation so that positive values indicate superCC increases and negative, subCC changes. Note that precipitable water increases differ from the oft-quoted number of 7% K in most cases (Fig. S1). This is because the CC scaling is a function of temperature and because the temperature increase is larger up in the troposphere than at the surface, thanks to a decreasing temperature lapse rate (Fig. S2).

Fig. 2.

(A) As in Fig. 1B but for the selected models from the WCRP CMIP3 multimodel dataset. Here the fractional changes of climatological-mean precipitable water (shown within the parentheses in the legends) have been subtracted from each model’s fractional changes of precipitation. (B) As in (A) but for 30–60°N.

In most of the climate models the fractional change in precipitation extremes is larger for a higher percentile of precipitation and asymptotes to certain values at very high percentiles. In the midlatitudes the fractional changes in precipitation are mostly constrained by the precipitable water changes; the majority of curves stay below zero even at very high percentiles. But in the tropics the asymptotic values do not necessarily correspond to the increases in moisture content. In fact, for six out of the 12 climate models examined here, the asymptotic increases in precipitation extremes exceed the CC predictions by more than 2% K. Although the tails of the distributions contain significant statistical uncertainties (as shown in Figs. S3 and S4), such differences warrant a detailed examination into the physical mechanism.

Compared with other models, the Geophysical Fluid Dynamics Laboratory (GFDL) model appears as an outlier because of its very large increase at high percentiles. Excluding this model, the high-resolution version of MIROC shows the largest increase. Although the CMIP3 models consistently underestimate the frequency of heavy precipitation events, MIROC’s precipitation extreme characteristics have been found to be comparable to those of observations (14). It is then useful to examine the physical reason for MIROC’s large change in precipitation extremes.

Decomposition of Precipitation Extreme Changes

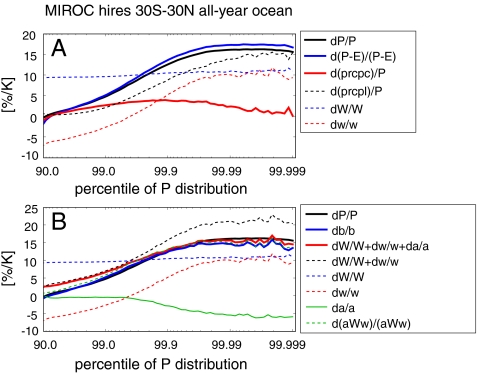
Plotted in Fig. 3 are atmospheric variables related to precipitation extremes in the high-resolution version of MIROC. The variables have been composited with respect to precipitation extremes. All fractional changes are divided by the mean-temperature increase of the spatial domain used for Fig. 3. The target periods are now 2001–2020 and 2081–2100 both from the SRES A1B simulations.

Fig. 3.

(A) Fractional changes in variables composited with respect to precipitation levels corresponding to each CDF value for the high-resolution version of MIROC. This figure focuses on ocean grid points in the 30°S–30°N zonal band for all seasons. Variables analyzed are: precipitation (P), precipitation minus evaporation (P - E), convective precipitation, large-scale condensation, precipitable water (W), and vertical motion at 500 hPa (w). Percentage changes are normalized by the temperature increase in the area in question; we have omitted the denominator dT in the legend. (B) As in (A) but for other variables. The coefficient a is the gross moisture stratification divided by precipitable water, and the coefficient b represents the scaling of (9). See the method for detail.

Because our understanding on precipitation change is mostly derived from the approximated humidity budget (1, 9), we first compare precipitation with precipitation minus evaporation (Fig. 3A). The difference between the two does not appear large.

Large-scale condensation tends to dominate convective precipitation for very rare events as the change in pressure velocity at 500 hPa, ω₅₀₀ = ω(p = 500) becomes larger. The precipitable water change is about 10–11% K, which can be contrasted with the climatological-mean increase of about 9% K. The additional increase in the moisture content mostly takes place above the boundary layer (Fig. S2). The variation in mean-precipitable water may not be an adequate indicator for extreme events (9).

We now quantify the departure from the CC scaling with the following two parameters:

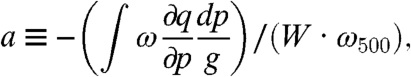[1]

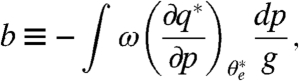[2]

where q is the specific humidity, q^∗ the saturation specific humidity, 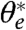the saturation equivalent potential temperature. The integral is taken for the whole atmospheric column.

a simply implies the moisture convergence normalized by precipitable water and midlevel pressure velocity. From the definition, it follows that ΔW/W + Δω₅₀₀/ω₅₀₀ + Δa/a approximates the fractional change in moisture convergence and the fractional change in a, Δa/a represents the component not covered by W or ω₅₀₀. b is the newly proposed scaling (9, 10) and implies the moisture convergence due to atmospheric ascent following the pseudoadiabatic lapse rate.

While b is calculated from the temperature and vertical motion, a requires knowledge of the vertical structure of the moisture field as well. Thus b comes closer to expressing a predictive theory for the rate of change of precipitation extremes with temperature (though it still requires knowledge of the vertical motion field), whereas a is an entirely empirical parameter characterizing the departure from the CC prediction. See the method for detail.

As we will see below, b works well for various models. Nevertheless, a is still useful for decomposing the change in precipitation extremes into ω₅₀₀ amplitude of vertical motion and a, the component that depends on its vertical profile. It is also desirable to examine a because it has been shown to play an important role in the mean precipitation change (15).

Fig. 3B compares the changes including the effects of a and b against extremes in precipitation. At high percentiles precipitation extreme changes surpass the corresponding increase in precipitable water. Combining vertical motion and precipitable water overestimates precipitation extremes.

Only when the vertical profile of moisture convergence is taken into account with Δa/a and Δb/b is it possible to account for the precipitation extreme changes (Fig. 3B). a decreases in a warmed climate because deepening cumulus convection shifts the profile of vertical motion upward (Fig. S5). Such a change in the profile of vertical motion has also been found to be important in the mean circulation change (15). Another contribution to the change in a comes from a slower increase in the vertical derivative of water vapor content than the CC scaling. A similar argument has been made for b (10) but the same argument applies to a because the atmosphere is close to saturation and almost follows a moist adiabatic lapse rate.

The empirical decomposition with Δa/a does marginally better than Δb/b at the very high percentiles but the reverse is true at the lower percentiles. This is rather surprising since the latter is a more direct fit to the moisture budget. Part of the reason for the present results is that the decomposition of the form ΔW/W + Δω₅₀₀/ω₅₀₀ + Δa/a assumes linearity. In Fig. 3B we also show the fractional change in the vertical moisture convergence (denoted by Δ(aWω₅₀₀)/(aWω₅₀₀)), which agrees better with Δb/b. At very high percentiles we find that Δb/b and Δ(aWω₅₀₀)/(aWω₅₀₀) slightly differ from the changes in precipitation, which could be attributed to large standard deviations of composited model variables (S4).

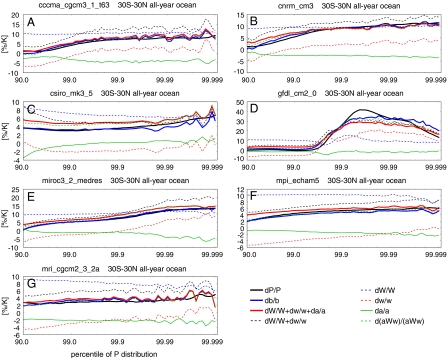
We repeat the present analysis with other IPCC models (Fig. 4). Because of the data availability we present the results from seven models, including the medium-resolution version of MIROC (Fig. 4). As with the high-resolution version of MIROC b gives a better match with the changes in precipitation extremes in IPCC models than changes in precipitable water and midtropospheric vertical motion. Adding Δa/a to ΔW/W + Δω₅₀₀/ω₅₀₀ also yields a reasonable match with the modeled precipitation extremes, except for high percentiles of the GFDL model (gfdl_cm2_0).

Fig. 4.

As in Fig. 3B but for other CMIP3 models. Model names are plotted at the top of each panel.

In the midlatitudes, the precipitation changes tend to be below the increase suggested by the CC relationship and unlike the tropics, very large increases are not identified (Fig. 2B). The fractional change in the midtropospheric vertical motion is small. Despite this, the effect of the vertical profile of atmospheric motion is not negligible (Fig. S6). The scaling b works for MIROC (Fig. S6) and IPCC models (Fig. S7) except for the GFDL model, for which the performance of b is similar to that of precipitable water and midlevel vertical motion.

Likewise, a improves the match of the predicted change with the modeled precipitation extremes.

A key message of Figs. 3 and 4 is that the difference in precipitation extreme changes among models is primarily attributable to variations in the vertical motion. In particular, a decreases in all the models for most of the percentiles, whereas the change in amplitude of midlevel vertical motion varies widely for the tropics, consistent with the findings of ref. 10. In contrast, the change in vertical motion in the extratropics is small (Fig. S7) and thus the precipitable water increases act as a constraint on precipitation extreme changes (Fig. 2B).

Conclusions

Constructing CDFs of precipitation we showed that whereas the precipitable water increase tends to constrain precipitation extreme changes in the midlatitudes, six out of 12 IPCC models exhibit superCC increases for very high percentiles of tropical daily precipitation. Decomposing precipitation extreme changes has revealed that both the amplitude and vertical profile of vertical motion play important roles in the tropics. The newly proposed dynamical scaling (9) can predict the fractional changes in precipitation extremes in MIROC and other IPCC models for both the tropics and midlatitudes, as was shown by (10) with a different method.

Our results are based on daily precipitation CDFs that combine both space and time dimensions. This procedure is essential for the large sample size (Fig. S8) but complicates the interpretation. In fact most of the very rare extreme events are concentrated over a relatively limited area and the results are not representative of the whole domain nor a single grid point. Nevertheless, this does not negate the main conclusion that the CC scaling cannot accurately describe the IPCC model results.

As suggested by the important effect of large-scale precipitation (Fig. 3) and vertical motion (Figs. 3 and 4), some of the extreme events at very high percentiles could be due to tropical storms. Our study did not address how tropical storm-like disturbances in GCMs contribute to precipitation extreme changes. Tropical storms are expected to intensify because the environment is therefore more favorable to them (16–18). It is becoming crucial to understand their future behavior in terms of precipitation extremes.

Materials and Methods

We analyze daily outputs of MIROC (11) for the IPCC 20C3M and SRES A1B simulations. Both the medium-resolution (triangular 42 spectral truncation, approximately 3° in equivalent grid) and high-resolution (triangular 106, approximately 1.1°) versions are employed. There are 20 and 56 layers in the vertical for the medium- and high-resolution versions, respectively. The general characteristics of precipitation extremes in MIROC have been reported elsewhere (19, 20). Cumulus convection is represented by a prognostic Arakawa–Schubert scheme (21) and uses an empirical relative-humidity threshold for deep convection (22), which is part of the reasons for MIROC’s good performance in simulating precipitation extremes (19).

In constructing the space–time CDFs of daily precipitation, we follow refs. (3) and (6). Binning the daily precipitation data both in time and space yields a CDF of precipitation. Latitudinal cosine weighting is not applied. There are 200 bins for the range between 0–1,000 mm/d for Figs. 1 and 2, and 100 bins for the range between 0–400 mm/d for Figs. 3 and 4. The bin size increases linearly with the amplitude of the precipitation of the bin so that the edge value of each bin increases as a quadratic function. The difference in the binning scheme has little impact on the fractional change in precipitation (Figs. S3).

The CDFs for the two periods are inverted and interpolated on common values of percentiles to allow for the calculation of percentage change. We then calculate the mean and standard deviation of other variables conditioned on precipitation extremes. Some examples of the standard deviations are shown in S4. Although the errors are large, the increases for extreme events are as large as, or larger than one standard deviation for large-scale precipitation, precipitable water, and the midlevel vertical motion.

Note that we include nonprecipitating days in the CDFs and that a given percentile c × 100 of a CDF is related to a return period of t d as t = 1/(1 - c). For instance, the 99.973th percentile approximately corresponds to a return period of approximately 3,650 d or 10 yr.

Because we combine both space and time dimensions in creating the CDFs, the sample size is large enough to allow for calculations of extreme events. For example, the count of events exceeding the 99.999 percentile is approximately 1,100 for the tropics (Fig. 3).

In addition to the two versions of MIROC, we examined the selected 10 models from the WCRP CMIP3 multimodel dataset (13). For models other than MIROC, the pressure velocity was obtained by integrating the continuity equation from the surface assuming a rigid bottom. This is only approximate but sufficient for our purposes of analyzing oceanic regions.

The periods used for our analysis are either of the two combinations: 1981–2000 and 2081–2100, or 2001–2021 and 2081–2100. For all IPCC models excluding MIROC, 1981–2000 was used. For MIROC, 1981–2000 was used for Figs. 1 and 2, and for other analyses, 2001–2020 was adopted unless otherwise mentioned. We found little impacts of the choice of analysis periods on the overall results (Figs. S3). We also tested the effect of the grid resolution because our analysis is conducted at the native grid of each model. The grid resolution was found not to have significant influence (Figs. S3) probably because we analyze the fractional change, not the actual intensity of precipitation.

We here elaborate on the definitions of parameters a and b defined in Eqs. 1 and 2. In these equations p is the pressure and g is the acceleration due to gravity, as in the standard meteorological notation. Saturation vapor pressure in q^∗ and 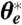is defined with respect to ice when the local temperature is below the melting point.

a is the gross moisture stratification divided by precipitable water (23) and is closely related with gross moist stability. Notice that the sum ΔW/W + Δω₅₀₀/ω₅₀₀ + Δa/a approximately equals the fractional change in the vertical moisture convergence term.

As mentioned in the text the calculation of a requires almost all the knowledge about the humidity budget, and therefore it should not be regarded as a scaling; it is rather a parameter to quantify to what extent the departure from the CC relation can be explained with other effects such as the change in vertical profile of vertical motion, and the slow change in the vertical derivative of specific humidity.

b has been proposed as a scaling for the change in precipitation extremes (9) and tested with IPCC models (10). It denotes the moisture convergence but takes into account the effect of slantwise ascent, which is assumed to follow the pseudoadiabatic lapse rate. It is possible to introduce further simplifications for vertical motion and temperature (9) but we do not introduce them.