Actin polymerization driven mitochondrial transport in mating S. cerevisiae

Abstract

The dynamic microenvironment of cells depends on macromolecular architecture, equilibrium fluctuations, and nonequilibrium forces generated by cytoskeletal proteins. We studied the influence of these factors on the motions of mitochondria in mating S. cerevisiae using Fourier imaging correlation spectroscopy (FICS). Our measurements provide detailed length-scale dependent information about the dynamic behavior of mitochondria. We investigate the influence of the actin cytoskeleton on mitochondrial motion and make comparisons between conditions in which actin network assembly and disassembly is varied either by using disruptive pharmacological agents or mutations that alter the rates of actin polymerization. Under physiological conditions, nonequilibrium dynamics of the actin cytoskeleton leads to 1.5-fold enhancement of the long-time mitochondrial diffusion coefficient and a transient subdiffusive temporal scaling of the mean-square displacement (MSD ∝ τ^α, with α = 2/3). We find that nonequilibrium forces associated with actin polymerization are a predominant factor in driving mitochondrial transport. Moreover, our results lend support to an existing model in which these forces are directly coupled to mitochondrial membrane surfaces.

The intracellular environment is a dynamic multicomponent fluid with relaxations spanning a broad range of length and time scales. As in ordinary fluids, in cells thermally generated inertial forces give rise to stochastic particle motions, which may be characterized by the particle mean-square displacement (MSD). Under many circumstances, thermal diffusion is a primary mechanism of intracellular transport. However, nonequilibrium forces that are generated by protein polymerization, motor proteins, and gradients in thermodynamic potentials can additionally influence particle motion. A central question in modeling cell transport is whether the cytoplasm may be viewed as a simple extension of a complex fluid at equilibrium or if nonequilibrium effects dominate the motions of intracellular species.

For a spatially homogeneous fluid at equilibrium, the MSD scales linearly in time (i.e. MSD ∝ τ^α with α = 1). However, microscopic heterogeneity and viscoelasticity of multicomponent fluids results in “anomalous” particle motion (1–5). In the context of cell dynamics the motion of a macromolecule or larger particle may become hindered by obstacles in its immediate environment, leading to subdiffusive scaling of the MSD (i.e. α < 1), over an appreciable time range (4). For example, the motions of small proteins in bacteria appear to be diffusive (6–8), whereas those of larger particles, such as mRNA-protein clusters in E. coli and yolk granules in yeast, appear to be subdiffusive (2, 3). These differences in the dynamics of intracellular species and host organisms may be reconciled by accounting for the relative size of the mobile particles to a structural length scale of the cytoplasmic environment (9, 10).

A more complex picture of transport can be anticipated if we consider that the cell is host to self-assembling cytoskeletal proteins, such as actin that can also produce physical forces as the polymers grow (11). Actin polymerization is regulated by a core set of proteins, such as the Arp2/3 complex, which functions to nucleate and cross-link growing actin filaments near membrane surfaces (12). Rapid growth of branched networks is known to drive membrane motion forward at a rate of 0.3 μm s^-1. Capping proteins control the extent of network growth and the newly synthesized networks slowly disassemble on the time scale of approximately 6 min by hydrolysis of actin-bound ATP and subsequent γ-phosphase dissociation. This process of actin network assembly and gradual disassembly is the force-generating mechanism for certain intracellular motile events, such as the extension of lamellipodia and the movement of intracellular pathogens (12).

In this paper we address the question of how nonequilibrium forces generated by actin polymerization influence the motions of a specific organelle, the mitochondrion. Mitochondrial motion is often a highly regulated process serving essential biological functions, such as the sorting of mtDNA to daughter cells during mitosis. In the following studies we utilize a molecular genetics approach by comparing mutant cell lines to their wild-type parents. S. cerevisiae is a useful organism for this purpose because of the availability of yeast genetic mutants. In mammalian cells mitochondrial motion depends on both microtubules (MTs) and actin microfilaments (MFs) (13). However, in dividing yeast the polarized movement of mitochondria from a parent cell to its daughter bud requires only an intact actin cytoskeleton (14–16). Subsequent experiments revealed a number of actin-associated proteins that are localized to the mitochondrial membrane and that are required for polarized mitochondrial movement. These and other studies led to the proposal that the mechanism of polarized mitochondrial movement during mitosis involves an Arp2/3 initiated actin network polymerization (16–19). As we discuss below, these considerations suggest that nonequilibrium forces generated by actin are initiated at mitochondrial membrane surfaces rather than occurring randomly throughout the cytoplasm.

To eliminate the polarized movements accompanying cell division, we examined cells in their mating phase (SI Text). By comparing healthy cells to cells with inhibited cytoskeletal activity we isolated the effects of specific protein components on mitochondrial movements. We examined conditions in which the actin and tubulin cytoskeletons were grossly disrupted (using pharmacological agents) in addition to more subtle interferences induced by mutations. We labeled the matrix space of yeast mitochondria using red fluorescent protein and measured their distance-dependent translational mobility using FICS (20). FICS is a high precision optical technique that is sensitive to submicrometer fluctuations of fluorescently labeled species over a broad range of time scales. Using FICS we determined the time correlation functions (TCFs) F(k,τ), which characterize the translational motion of mitochondria as a function of the experimentally adjustable length scale d_G = 0.6–1.2 μm (with wave number k = 2π/d_G). The TFCs are numerically inverted to determine the MSD from which we identify short- and long-time diffusive regimes separated by a transient period of subdiffusive behavior. Both short- and long-time diffusive motions can be related to the microscopic interactions between mitochondria and their local environments.

Results

Mitochondrial Dynamics in Mating S. Cerevisiea are Subdiffusive on Intermediate Time Scales and are Strongly Coupled to the Actin Cytoskeleton, but not to Microtubules.

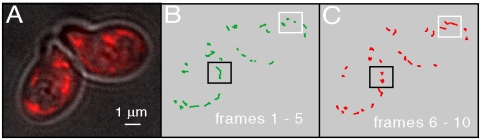
In Fig. 1 we show the results of a digital analysis of sequenced movie images taken from healthy yeast cells. Fig. 1A shows a single composite image in which individual mitochondria (red) can be seen in relation to the outer cell membrane. In Fig. 1B and C we plot the trajectories of mitochondria over a period of five successive frames, with each frame separated by a 20 s interval. It can be seen that the majority of mitochondria are immobilized on the 20 s time scale, whereas a minor subpopulation undergoes submicron displacements. As indicated by the black and white rectangles in Fig. 1B and C after a long intervening period of many tens of seconds, an exchange of population occurs between mobile and immobile subpopulations.

Fig. 1.

(A) Composite fluorescence micrograph of mitochondria in mating yeast cells. (B) and (C) Digital image analysis of sequenced images show that the majority of mitochondria are immobilized on the time scale of successive image frames (20 s/frame).

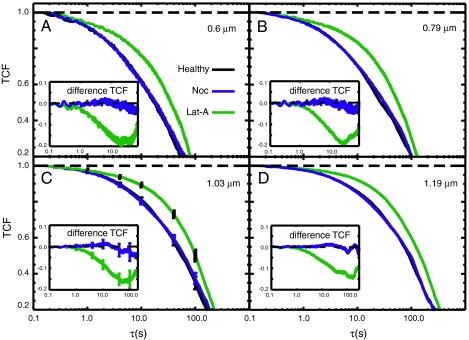
In Fig. 2 we compare the TCFs for mitochondrial fluctuations in healthy cells (black curves) to cells depleted of MTs (blue curves) and to cells depleted of MFs (green curves). Each panel in Fig. 2 represents a specific length scale probed by our measurement (d_G = 0.6, 0.79, 1.03 and 1.19 μm). The rate of decay of the TCF is a direct measure of mitochondrial mobility specific to this length scale (13). We note that the TCFs are multiexponential and span nearly four orders of magnitude in time very similar to those measured in mammalian cells (13). For MT-depleted cells the TCFs are indistinguishable from those of healthy cells indicating that the mobility is unaltered. However, for cells depleted of microfilaments the TCFs decay much more slowly than for those of healthy cells indicating a marked reduction of mitochondrial mobility for all four of the length scales investigated. These data show that mitochondrial dynamics in yeast are sensitive to the integrity of MFs, but not to that of MTs. In panel (C), we include error bars in our decays. We see that the differences between healthy and microfilament-depleted cells are statistically significant, whereas the differences between healthy and microtubule-depleted cells are not.

Fig. 2.

Comparison between TCFs for mitochondrial fluctuations in healthy cells (MYY290, black) and cells depleted of MTs (blue), and cells depleted of MFs (green). Each panel represents the indicated length scale probed by the FICS measurement. In panel (C) we include error bars in our decays. The insets show difference TCFs between drug-treated and healthy cells to emphasize the effects of the cytoskeletal inhibitors.

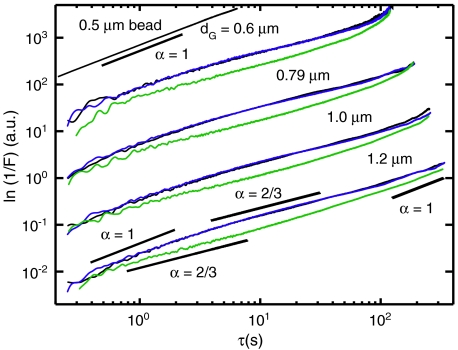
From the measured TCFs, F(k,τ) = F₀ exp[-k²〈Δx²(τ)〉/6] we determined the MSDs [〈Δx²(τ)〉 = 6Dτ^α] according to ln[F₀/F(k,τ)] ∝ 2 ln k + ln 〈Δx²(τ)〉. These functions presented on a log–log plot are proportional to 2 ln k + ln D + α ln τ. Each curve is the sum of two contributions; there is a term that is linear with respect to ln τ with slope α and an offset 2 ln k + ln D. In Fig. 3 we show four sets of curves (displaced vertically by factors of 10) with each set corresponding to one of the experimentally adjustable length scales d_G = 0.6, 0.79, 1.03, and 1.19 μm. These data span three orders of magnitude in time allowing us to distinguish transitions in the temporal scaling behavior. On subsecond time scales the curves appear to scale diffusively as α = 1 followed by a subdiffusive regime with α = 2/3 that persists over many tens of seconds. At very long times (> 50 s) the curves crossover to α = 1 indicating a return to diffusive behavior. The transient subdiffusive scaling of the MSD is consistent with the intermittent mobility apparent from the mitochondrial trajectories. For MT inhibited cells (blue) the behavior is indistinguishable from healthy cells (black) indicating that the dynamics of the local environment in the absence of MTs are unaltered. For cells in which MFs are destabilized (green) the three regimes of temporal scaling remain. However, the time window corresponding to the subdiffusive regime is shifted to shorter times. For the MF destabilized cells the magnitude of the MSD is smaller than healthy cells for all four of the length scales we investigated indicating that the magnitude of forces experienced by mitochondria under F-actin depleted conditions is significantly diminished. The interactions between mitochondria and the local microenvironment that lead to subdiffusive motion are sensitive to the integrity of the actin MFs but not to MTs. To further characterize these interactions we determined from our data the effective diffusion coefficient, 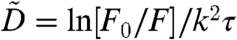, defined over the short- and long-time intervals 0.1–1 s and 70 s, respectively. The values we obtain for the effective diffusion coefficients are listed in SI Text.

Fig. 3.

MSD of mitochondrial fluctuations calculated from the data presented in Fig. 2. Color assignments are the same as in that figure. A control measurement of a 0.5 μm colloid sample in viscous, concentrated sorbitol solution is presented at the top of the figure. Various lines with slopes representing the temporal scaling parameter α are also provided to guide the eye.

Mitochondrial Dynamics are Enhanced in the Actin Mutation ActV159N, and Suppressed in the Deletion Mutation Arc18pΔ of the Arp2/3 Complex.

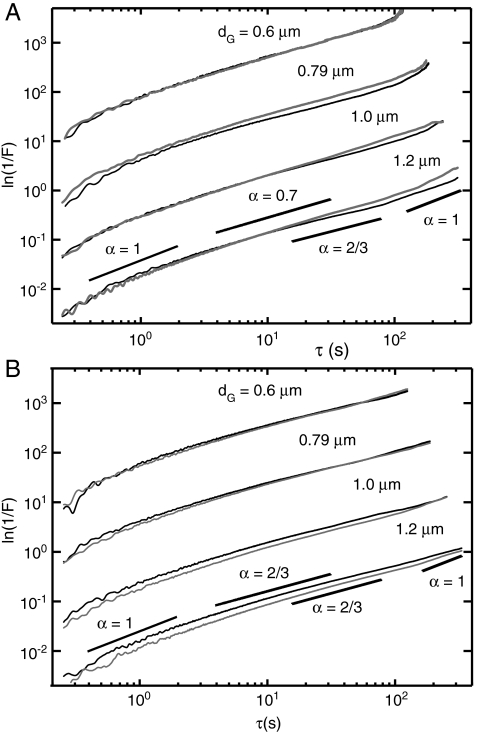
Our observations implicating a direct role of actin polymerization in mitochondrial motion led us to compare measurements of wild-type cells to cells containing mutations of proteins participating in actin assembly. In Fig. 4A we compare the MSD from the actin mutant strain act1-V159N (light gray) to those of its wild-type parent (black), which were measured at the elevated temperature of 36 °C. The MSD for mutant cells exhibit nearly the same temporal scaling behavior with short- and long-time diffusive regimes separated by an intermediate subdiffusive regime. The act1-V159N strain is a temperature sensitive mutation whose cell culture growth rate is suppressed at the elevated temperature of 36 °C. The act1-v159n protein is thought to stabilize F-actin by enhancing the forward polymerization rate. For example, Wen et al. observed in vitro enhanced polymerization rates of yeast act1-v159n protein in the presence of the actin filament nucleation complex Arp2/3 (21). At the elevated temperature of 36 °C we observe an enhancement of the dynamics for act1-V159N in comparison to wild-type mitochondria for d_G≥0.79 μm. This transport enhancement vanishes when we decrease the sample temperature from 36 °C to 22 °C (SI Text). In contrast to our results for drug-treated cells, the act1-V159N cells show no shift in time scale for subdiffusive behavior. Instead, the values for both short- and long-time effective diffusion coefficients are increased at intermediate length scales. We list these values determined from our data in SI Text.

Fig. 4.

(A) Comparison between mitochondrial MSDs for the temperature-sensitive actin mutant strain act1-V159N (DDY1493, gray curves) and its wild-type parent ACT1 (DDY1495, black curves), measured at the nonpermissive temperature 36° C. (B) Similar comparison between MSDs for the deletion mutant strain Arc18pΔ (gray curves) and its wild-type parent BY4741 (ARC18, black curves).

To gain insight into the polymerization process itself as a factor of particle mobility we next asked how molecules that regulate actin polymerization influence mitochondrial transport. One such actin regulating protein, the Arp2/3 complex, initiates rapidly growing filaments of actin that form branches from the sides of existing filaments (12). As a possible mechanism for mitochondrial mobility dendritic actin filaments may exert transient forces on or nearby the mitochondria as the branched network rapidly grows, followed by intervening periods of arrested growth and disassembly. We selected the deletion mutation Arc18pΔ to the ARC18 gene, which expresses a constituent protein of the Arp2/3 complex (22). In Fig. 4B, we compare our results for the mutant Arc18pΔ cells (light gray) to those of the wild-type parent ARC18 (black). For the smallest length scale investigated (d_G = 0.6 μm) the mutant and wild-type parent strains behave nearly identically. However, the mutant Arc18pΔ cells exhibit smaller magnitude displacements at both short and long times for d_G≥0.79 μm. Similar to our findings for the act1-V159N cells the temporal scaling behavior of the Arc18pΔ mutant is the same as its wild-type parent whereas short- and long-time effective diffusion coefficients are decreased at intermediate length scales. These values are reported in SI Text.

Discussion

We have observed the MSD of mitochondria in healthy cells to exhibit three regimes of temporal scaling; short- and long-time diffusion, and an intermediate-time transient subdiffusion. This behavior depends on the structural integrity of MFs but not on MTs. Contrary to the expectation that F-actin would behave simply as obstructions to mitochondrial diffusion, elimination of MFs (using Latrunculin-A) results in the reduction of the overall mobility with an anomalous subdiffusive regime evident at shorter time scales (see Fig. 3). Moreover, mutations known to enhance (or diminish) the nonequilibrium dynamics of actin assembly and disassembly lead to a modest increase (or decrease) in mitochondrial mobility (see Fig. 4).

A possible model to explain the emergence of subdiffusive intracellular transport emphasizes a geometric origin of the local forces that a species experiences. In this picture a mitochondrion undergoes short-time diffusion until it encounters stationary, nonuniformly distributed actin filaments. Subsequent three-dimensional motion on intermediate-time scales is constrained and results in subdiffusive scaling of the MSD. This picture of a random walk in a static heterogeneous distribution of obstacles is consistent with previous conceptions of caging and transient subdiffusive motion in the equilibrium dynamics of complex liquids (2, 9, 23). On long-time scales structural relaxation of the F-actin cage leads to recovery of diffusive scaling of the MSD. Similar three-time-regime behavior of the MSD has been observed in solutions of microspheres suspended in F-actin and transient polymer networks (24, 25), with the long-time structural relaxation governed by the bulk viscosity.

Nonequilibrium effects of actin polymerization can be included in the above picture by allowing the dynamics of the local environment to be modified by the assembly and disassembly of F-actin cages. Here a mitochondrion, which is otherwise free to diffuse, may become temporarily trapped by an out-of-equilibrium particle localization associated with the formation of an F-actin cage. The waiting time for a trapped mitochondrion to return to a mobile state is determined by the lifetime of the unstable cage. Such situations may be modeled using continuous time random walks where the anomalous subdiffusive scaling of the MSD arises from a heavily tailed distribution of waiting times (23). Unlike the first model of “passive” diffusion through a landscape of fixed disordered obstacles the time scale of subdiffusion in the second model depends on “active” assembly and disassembly of actin filaments so that the constraints on particle motion are dynamic.

Although our observations for healthy cells are in qualitative agreement with both the active and passive pictures described above, the decrease in mobility observed upon depletion of F-actin suggests the direct involvement of nonequilibrium forces in the resultant particle mobility such that particle motion is driven by polymerization fluctuations. MacKintosh and Levine showed that the effect of active force-generating elements in filament networks is to introduce nonequilibrium contributions to the power spectrum of displacements at low frequencies, which dominate thermal (equilibrium) contributions (26). In such systems nonequilibrium processes generate motions for which the temporal scaling of the MSD is diffusive yet with an effective diffusion coefficient that is controlled by motor protein activity. In our experiments on MF-depleted cells both short- and long-time effective diffusion coefficients are reduced (see SI Text), indicating the absence of active force-generating elements that are present in healthy cells. The persistence of a subdiffusive regime at shortened time scales in MF-depleted cells might be a reflection of local crowding interactions between mitochondria and intracellular species unrelated to F-actin.

We next discuss the results of our experiments on mutant strains that alter the efficiency of actin polymerization and how these might impact our microscopic picture of anomalous mitochondrial dynamics. Actin filaments form highly dynamic network structures with F-actin tread-milling and Arp2/3-mediated dendritic network assembly known to drive cell motility events (12). Furthermore, there is compelling evidence presented by Pon and coworkers that the Arp2/3 complex localizes to the mitochondrial membrane during cell division in budding yeast and participates in an actin network assembly process that drives mitochondria to the daughter cell (19). Although conditions in the cell cytoplasm of mating yeast are certainly quite different from those of budding yeast, it is possible that components of this machinery are operational in mating cells. This leads us to consider in addition to the passive and active modes of transport discussed above a third possibility that mitochondria are directly coupled by physical connections to the nonequilibrium forces born out by actin polymerization. In this picture Arp2/3 complexes bound to the membrane surfaces of mitochondria nucleate and rapidly grow actin dendritic filaments, which generate force by pushing against nearby macromolecular structures in the cytoplasm. Pseudorandom regeneration of actin network growth, interrupted by pauses of variable duration, is expected to contribute to the overall anomalous dynamics. If such a “direct-coupling” mechanism is valid one might intuitively expect mutations that modify the rates of F-actin polymerization to exhibit proportional changes in mitochondrial mobility. The act1-v159n mutant is known to stabilize F-actin and thereby increase the forward rate of F-actin assembly while decreasing the disassembly rate (21). Our experiments on this mutant show an enhancement of the long-time diffusion coefficient for length scales ≥0.78 μm (see Fig. 4A and SI Text). Conversely, the Arc18pΔ mutant is known to destabilize the Arp2/3 complex leading to partial inhibition of its ability to nucleate and cross-link dendritic actin networks (22). Our measurements on this mutant show a pronounced suppression of both short- and long-time diffusion coefficients for length scales > 0.78 μm (see Fig. 4B and SI Text). In both of the mutants we examined our results appear to be consistent with a direct-coupling mechanism. We emphasize that our observations per se do not prove the validity of a direct-coupling mechanism. It is likely that aspects of passive, active, and direct-coupling mechanisms simultaneously contribute to the overall dynamics. Nevertheless, the results of our experiments on the Act1-v159n and Arc18pΔ mutant strains in combination with previous biochemical studies lend support to the direct-coupling model.

Finally, we speculate on the significance of the value of α, the subdiffusive scaling exponent. It has been suggested that transport by subdiffusive mechanisms may provide advantages to the cell as a means to increase the encounter probability between intracellular species and various targets (2). A subdiffusive particle becomes somewhat localized in its position during the subdiffusive time period resulting in an increased likelihood of contact with a binding partner albeit at a slower association rate. The encounter probability for a subdiffusive particle to find its target of radius a, separated by a distance r, is given by p ≈ (a/r)^3-2/α (2). As pointed out by Golding and Cox a value of the scaling exponent α = 2/3 (as observed in the present work) appears to maximize this effect (2). Mitochondria are well known for their roles in intracellular ATP production, heme,and fatty-acid biosynthesis, and programmed cell death. These functions are highly regulated and must depend on the local interactions between mitochondria and various signaling proteins, substrates, and second messengers. It is therefore interesting to consider that the tens-of-seconds time scale observed for mitochondrial subdiffusion under physiological conditions may indicate a relevant activation time for protein- and lipid-mediated signaling processes.

In this work we have considered how the dynamics of actin influences the movement of a centrally important organelle, the mitochondrion. As suggested by previous studies the effects of nonequilibrium forces due to actin polymerization in the cytoplasm are reflected by the transport properties of mitochondria (4). A possible interpretation is that these nonequilibrium forces distributed throughout the cytoplasm play a predominant role in the motions of all intracellular species of like size. However, we suggest that the cell exerts specific control over the transport of mitochondria by directly coupling its actin assembly machinery to the membrane surfaces of this organelle (19). In addition to the global effects of force-generating cytoskeletal activity, this mechanism of local force generation supplies a means for the cell to regulate subcellular transport. Although our studies are specific to mitochondria in yeast they may provide general insight toward understanding the transport mechanisms of other large intracellular species.

Materials and Methods

Fourier Imaging Correlation Spectroscopy.

We used the FICS technique to quantify the motions of yeast mitochondria in our studies. FICS is a phase-sensitive method to measure the displacements of fluorescently labeled objects as a function of spatial length scale and over a broad distribution of time scales. The approach is an efficient and highly sensitive means to perform uninterrupted data acquisition over extended periods while minimizing the deleterious effects of sample photo degradation, instrument drift, and laboratory noise. The samples were placed at the focal plane of a fluorescence microscope where an excitation grating was generated by intersecting two vertically polarized laser beams (Fig. S2A). The fluorescence signal results from the spatial overlap of the grating with the positions of labeled mitochondrial segments (see Figs. S2B and C). In a typical experiment we collect approximately 524,000 data points at an acquisition frequency of 256 Hz and over a period of approximately 35 min. We repeated our measurements 10–15 times and after comparing them for consistency we averaged them together. Error bars were calculated from the dispersion in the data. Further details are given in SI Text. From the FICS signal we calculate directly the time correlation function (TCF): 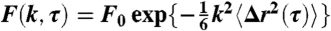where the mean-square displacement 〈Δr²(τ)〉 = 6Dτ^α, D is a generalized diffusion coefficient and α is a temporal scaling exponent.

Yeast Strains and Fluorescent Labeling of Mitochondria.

Cell strains, culturing methods, and labeling techniques are fully described in SI Text.

Video Microscopy and Digital Image Analysis.

The methods used to visually track mitochondria as shown in Fig. 1 are fully described in SI Text.