Summary
Bacterial gene expression depends not only on specific regulations but also directly on bacterial growth, because important global parameters such as the abundance of RNA polymerases and ribosomes are all growth-rate dependent. Understanding these global effects is necessary for a quantitative understanding of gene regulation and for the robust design of synthetic genetic circuits. The observed growth-rate dependence of constitutive gene expression can be explained by a simple model using the measured growth-rate dependence of the relevant cellular parameters. More complex growth dependences for genetic circuits involving activators, repressors and feedback control were analyzed, and salient features were verified experimentally using synthetic circuits. The results suggest a novel feedback mechanism mediated by general growth-dependent effects and not requiring explicit gene regulation, if the expressed protein affects cell growth. This mechanism can lead to growth bistability and promote the acquisition of important physiological functions such as antibiotic resistance and tolerance (persistence).
Keywords: growth rate, constitutive gene expression, gene regulation, genetic circuits, bistability, growth feedback, antibiotics, persister cells
INTRODUCTION
With the emergence of a ‘system-level’ focus in biology, there has been an increasing emphasis on characterizing gene expression and its regulation in a quantitative fashion (Bintu et al., 2005; Golding et al., 2005; Hasty et al., 2002; Kaplan et al., 2008; Kuhlman et al., 2007). Quantitative and semi-quantitative studies have generated new concepts regarding the organization and the dynamic properties of gene regulatory networks, including, e.g., stability of control, robustness of the networks and stochastic heterogeneity of populations (Elowitz et al., 2002; Rao et al., 2002; Shen-Orr et al., 2002), and have led to the design of synthetic genetic circuits (Andrianantoandro et al., 2006; Atkinson et al., 2003; Elowitz and Leibler, 2000; Gardner et al., 2000; Guido et al., 2006). One complication in the quantitative studies of genetic circuits is that these circuits are always coupled to the physiological state of the cell, which, for example, affects the machinery of transcription and translation. As long as the state of the cell remains unchanged, this dependence does not affect the quantification of gene regulation. However, changes in gene expression often reflect changes in the environment, which also affect the state of the cell. In that case the coupling of gene expression to the global state of the cell cannot be ignored. We show in this study that this coupling generates an entire layer of physiologically important global effects on gene expression that has largely been overlooked in quantitative analysis so far. We focus on gene expression in bacteria in balanced exponential growth, for which the effects of environment on the state of the cell are reflected first and foremost by the growth rate.
The growth rate of bacteria can vary wildly, depending on the type or amount of nutrients available in the growth medium. For example, the doubling time of E. coli in exponential batch culture growth ranges easily between ~20 min and several hours. Many parameters of the cells such as their macromolecular composition and the cell size are strongly dependent on the growth conditions (Maaløe, 1979; Neidhardt et al., 1990; Schaechter et al., 1958). For E. coli and Salmonella, in which this dependence has been quantitatively characterized, the results can be expressed miraculously as a dependence on growth rate rather than on the specific growth media themselves: growth experiments with many different media have shown that media that support the same growth rate produce cells with the same macromolecular composition (Maaløe, 1979; Neidhardt et al., 1990; Schaechter et al., 1958). Many parameters of the cell have therefore been characterized quantitatively as functions of the growth rate for E. coli (Bremer and Dennis, 1996), on which we focus in this study.
Many of these growth-rate dependent parameters, e.g. gene and plasmid copy numbers, the abundance of RNA polymerases and ribosomes (Bremer and Dennis, 1996), are known to affect gene expression. Changes in gene expression, which are often accompanied by a change of the growth rate, thus result from a combination of gene regulation and intrinsic global effects due to growth rate. Any quantitative understanding of gene expression therefore requires an understanding of these global effects. Indeed, expression of a large number of proteins is known to exhibit different types of growth-rate dependences (Pedersen et al., 1978). Growth-rate dependent regulation is most notable for the transcription of ribosomal RNA (Haugen et al., 2008), but is also known for ribosomal proteins, where it relies largely on posttranscriptional regulation (Keener and Nomura, 1996), as well as for several non-ribosomal proteins, where it is based on transcriptional mechanisms that appear to be different from the control of ribosomal RNA (Chiaramello and Zyskind, 1989; Husnain and Thomas, 2008). In contrast to these instances of specific growth-rate dependent regulation, the global effects addressed here are expected to affect all genes. Their interplay with specific mechanisms of gene regulation can lead to rather complex behaviors, and it is possible that they play a role in some of the known examples for specific growth-rate dependent regulation.
An obvious starting point to study global growth-rate dependent effects on gene expression is the growth-rate dependence of the expression of an unregulated (constitutively expressed) gene. Indeed, several studies have shown that the expression of a constitutively expressed gene is growth-rate dependent (Liang et al., 1999a; Wanner et al., 1977; Willumsen, 1975). We will show that the observed dependence can be quantitatively explained by a simple model using the known growth rate dependencies of the key cellular parameters without invoking any adjustable free parameters.
We then expand our model to investigate the effect of growth rate on regulated genes and simple genetic circuits to address the following questions: How is the growth-rate dependence of gene expression affected by positive or negative regulation? How should a gene be regulated to exhibit a growth-rate-independent protein concentration? Is the qualitative behavior of a circuit the same at different growth rates? Answers to these questions may also help in the design on synthetic genetic circuits in order to obtain robust performance over a wide range of growth conditions. Experimental results are presented to validate key predictions of the model using simple synthetic genetic circuits.
Finally, we explore cases with global feedback mediated by growth-rate dependent effects: In these situations there is not only an effect of growth rate on gene expression, but the expression level of a protein also has an effect on the growth rate. Circuits of this type can lead to growth bistability. We discuss possible roles these effects may play in metabolic control, antibiotic resistance and tolerance (persistence).
RESULTS
Growth-rate dependence of global cellular parameters
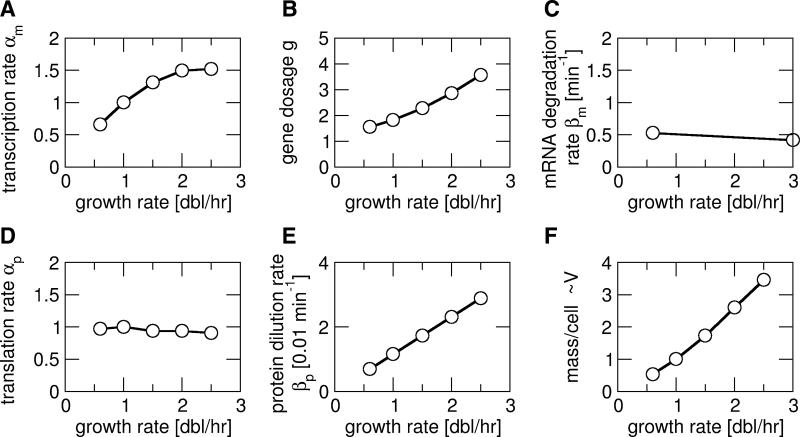
We start by considering the growth-rate dependence of unregulated (constitutive) gene expression, which has been reported experimentally for E. coli in several cases (Liang et al., 1999a; Wanner et al., 1977; Willumsen, 1975). From a bottom-up perspective, it is not clear whether the concentration of a constitutively expressed protein should be expected to increase or decrease at faster growth. On the one hand, faster dilution of the protein by faster growth should reduce its concentration, but on the other hand, the transcription rates are known to be increased at faster growth as well (Liang et al., 1999a). To predict the growth-rate dependence of a constitutively expressed protein, we used a simple model of gene expression and searched the literature for the growth-rate dependence of all relevant parameters (Fig. 1 and Table S1). In our model, the expression level of a protein depends on six parameters, the cellular copy number of the gene (g), the transcription rate per copy of the gene (αm), the mRNA degradation rate (βm), the translation rate per mRNA (αp), the protein degradation rate (βm), and the cell volume (V), all of which may have a dependence on the growth rate (μ). These parameters determine the numbers of mRNA and protein molecules per cell, M = gαm/βm and P=gαmαp/(βm βp), as well as the corresponding concentrations, m=M/V and p=P/V. The quantity of main interest is the resulting concentration of the protein, which is given by
| (1) |
The growth rate dependence of the transcription rate per gene has been characterized for several constitutive promoters (Liang et al., 1999a). They were found to exhibit the same dependence, increasing at slow growth and saturating at fast growth (Fig. 1A). This growth-rate dependence is believed to reflect the availability of RNA polymerase in the cell (Klumpp and Hwa, 2008; Liang et al., 1999a).
Figure 1. Growth-rate dependence of global cellular parameters affecting gene expression.
(A) Transcription rate per gene, (B) gene copy number per cell, (C) mRNA degradation rate, (D) translation rate per mRNA molecule, (E) protein dilution rate due to growth and (F) cell mass, used as a measure for the cell volume V, as functions of the growth rate. All parameters are for constitutively expressed (unregulated) genes. For a description how the data was collected from the literature and for references, see the text and Table S1.
The gene copy number per cell is determined by the dynamics of DNA replication and cell division and has been well characterized (Cooper and Helmstetter, 1968). It is growth rate dependent, because at different growth rates a gene is replicated at different time points in the cell division cycle. At fast growth the gene copy number is further increased due to overlapping rounds of DNA replication. The growth-rate dependence of the gene copy number is calculated using the Cooper-Helmstetter relation (see Table S1) and is plotted in Fig. 1B for a position halfway between the origin and terminus of replication.
The degradation rate of mRNA appears to be rather independent of growth rate, as indicated by studies of the stability of total cellular mRNA (Coffman et al., 1971; Pato and von Meyenburg, 1970) and of specific transcripts such as lacZ (shown in Fig. 1C), bla, and lpp, which all had almost the same lifetime at different growth rates (Liang et al., 1999b; Nilsson et al., 1984). Furthermore, a genome-wide study (Bernstein et al., 2002) found that the lifetimes of most transcripts differed by less than two-fold between growth in minimal and rich medium, with no obvious correlation between the two conditions. The independence of mRNA stability to growth rate may be attributed to the autoregulation of RNase E (Jain et al., 2002); see the Supporting Text.
The growth rate dependence of the translation rate αp has been determined for the lacZ transcript and was found to be approximately constant over a range of growth rates from 0.6-3 doublings/hour (Liang et al., 2000), as shown in Fig. 1D. This finding is surprising, given that the cellular concentration of ribosomes increases strongly with increasing growth rate (Bremer and Dennis, 1996), and is discussed further in the Supporting Text. Here we take the finding for lacZ as typical and assume the translation rate to be growth-rate independent. Finally, if our protein of interest is stable, it is not degraded, but rather diluted out by cell growth and division, so that βp is given by the growth rate μ through βp=μln2 (Fig. 1E).
To predict protein and mRNA concentrations, we also need the growth rate dependence of the cell volume. As a measure of cell volume we use cell mass, which is easily measured by optical density and is commonly used to express measured concentrations. Several studies have shown that cellular mass and volume exhibit the same growth-rate dependence (Donachie and Robinson, 1987; Nanninga and Woldringh, 1985), increasing strongly with increasing growth rate as shown in Fig. 1E (data from Bremer and Dennis, 1996); see also the detailed discussion in the Supporting Text. An alternative normalization for concentrations is per total cellular protein rather than per cell mass. While the two are roughly equivalent, the total cellular protein concentration (per mass) increases slightly at slower growth, so that this normalization leads to a slightly weaker growth rate dependence (see below).
Growth-rate dependence of constitutive gene expression
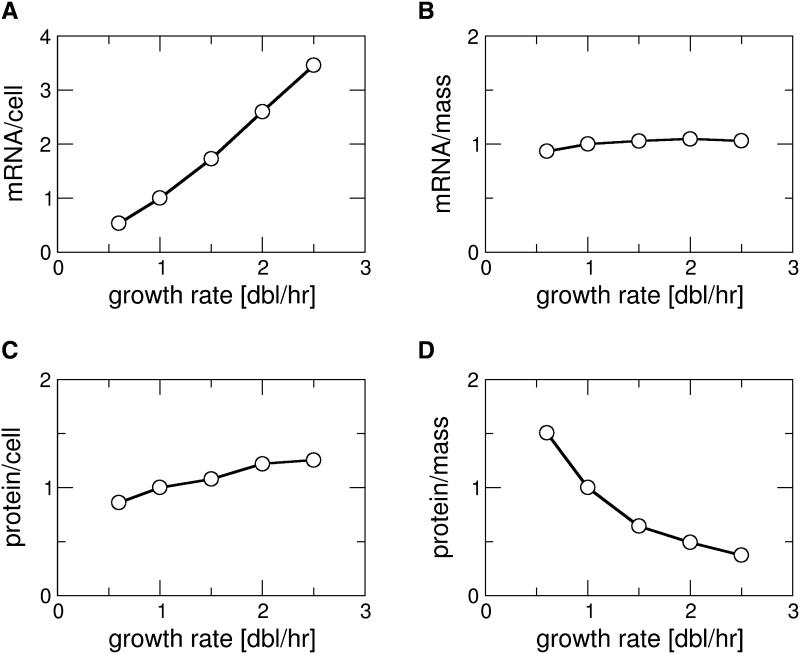
From the growth rate dependence of the global parameters (Fig. 1), we calculated by Eq. (1) the predicted growth rate dependence of the protein and mRNA expression levels for a constitutively expressed gene (Fig. 2A-D). Our results predict that the number of transcripts of such a gene per cell is strongly increased at faster growth (Fig.2A), while the concentration of transcripts is rather independent of growth rate (Fig. 2B). Likewise, the protein copy number per cell is increased at faster growth (Fig. 2C), although less than the number of transcripts, and the protein concentration is decreased at faster growth (Fig. 2D). The decrease of the protein concentration despite an increase of its molecule number per cell reflects the strongly increased cell volume at fast growth.
Figure 2. Calculated growth-rate dependence of constitutive gene expression.
Expression level of a constitutively expressed gene as characterized by the number of mRNA transcripts of that gene per cell (B), its mRNA concentration (C), its number of protein molecules per cell (D), and the protein concentration (D), calculated from the growth rate dependence of the parameters shown in Fig. 1. All curves are normalized to their value at 1 doubling/hour.
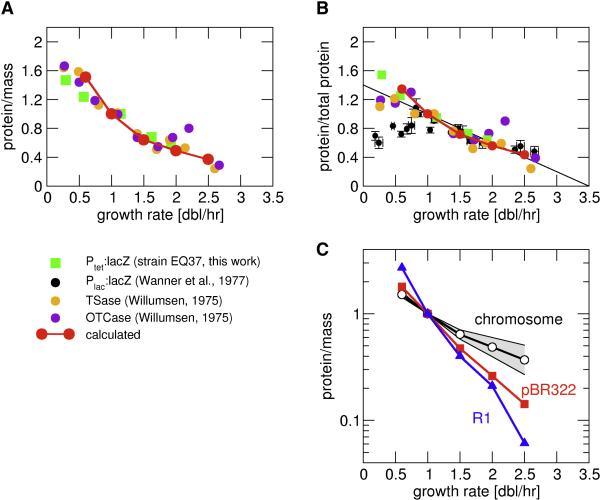
In Fig. 3A and 3B, we compare the calculated growth rate dependence of the concentrations of constitutively expressed proteins with available experimental data. These data are derived by different labs from various E. coli strains, for various genes expressed constitutively because their regulation has been inactivated (by deletion of the regulators or mutations of the operator sites), and for a synthetic promoter-reporter system constructed for this study (green squares). Data in Fig. 3A show concentrations obtained by normalizing to cell mass, while data in Fig. 3B are normalized to total protein. In general, our calculated growth rate dependence (red) agrees very well with the data. Data normalized to total protein however shows a significant spread for very slow growth. The origin of this spread is not clear. We also note that the experimental data for constitutively expressed protein per total protein are well approximated by a linear relation (black line in Fig. 3B). According to this relation, the concentration of such a protein would become zero for a (hypothetical) growth rate of ~3.5 doublings/hour, slightly higher than the highest growth rate that can be attained. The origin of this linear relation is discussed elsewhere (Scott et al., 2009).
Figure 3. Growth-rate dependence of constitutively expressed genes on the chromosome and plasmid.
(A and B) The calculated growth rate dependence of the concentration of a protein encoded by a constitutively expressed gene (red) is compared to experimental data on constitutively expressed genes in various E. coli strains: the orange and purple dots are derived from the activities of tryptophan synthase and ornithine transcarbamylase respectively, from a strain in which their respective regulators were deleted (Willumsen, 1975). The black dots are derived from LacZ expressed from the mutant LacL1 type promoters (Wanner et al., 1977). The green squares are from this work, with LacZ expressed from the synthetic PLTet-O1 promoter in strain EQ37 which contains no TetR. Data in (A) is normalized to total mass as measured by optical density and data in (B) to total protein. All data are plotted relative to their expression levels in cells grown at 1 doubling/hr. (C) Comparison of the calculated protein concentration for genes on the chromosome (shaded grey area, the black line indicates the curve from Fig. 3A), on plasmids pBR322 (red) and R1 (blue).
The gene copy number per cell depends on the position on the chromosome (Bremer and Dennis, 1996; Cooper and Helmstetter, 1968). Fig. 3C indicates the range of growth-rate dependencies for different chromosomal positions: The two boundaries of the grey area indicate the strongest and the weakest growth-rate dependence for chromosomal genes, obtained for genes close to the origin and terminus of DNA replication, respectively. For genes on a plasmid, the gene copy number is given by the plasmid copy number and will in general be different from those for chromosomal genes. For plasmid pBR322, the copy number per cell is slightly increased at faster growth, but much less than for chromosomal genes (Lin-Chao and Bremer, 1986). The copy number of plasmid R1 even decreases at faster growth (Engberg and Nordstrom, 1975), see also Table S1. In both cases, the protein concentration for a plasmid-encoded constitutively expressed gene is predicted to follow a much stronger growth-rate dependence than for chromosomal genes (Fig. 3C).
Simple regulatory elements: activation and repression
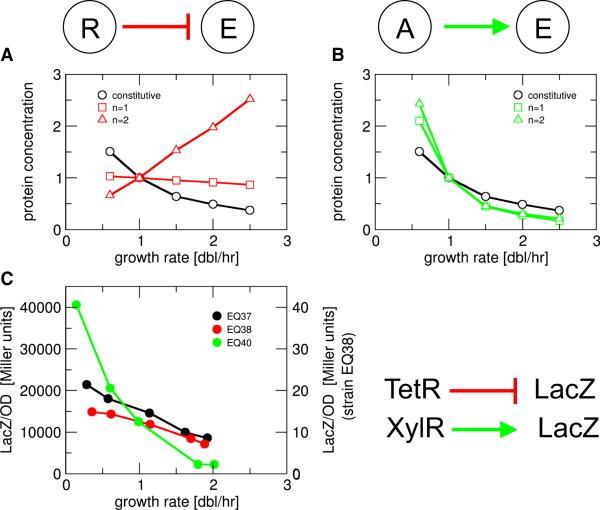
Regulated genes are directly affected by growth rate in the same way as constitutively expressed genes; in addition they are affected by the growth rate dependence of their regulator concentrations. For example, the expression of a protein E that is negatively regulated by a constitutively expressed repressor R (Fig. 4A) is affected by a reduced expression at faster growth due to the direct growth effects discussed above (Fig. 3), and a weakened repression at faster growth due to the growth-rate dependence of the repressor concentration itself. The balance of these two effects is analyzed by expanding the above model of growth-rate dependence to include basic features of gene regulation (Bintu et al., 2005); see Supporting Text. The compounded effect is predicted to depend mainly on the cooperativity of repression, but also on the strength of repression (strengths of the promoter driving the repressor relative to the repression threshold). An example is illustrated in Fig. 4A for strong repression, with a weak, inverse growth rate dependence (red squares) for non-cooperative repression (Hill coefficient n=1), and a strong, positive growth rate dependence (red triangles) for cooperative repression. Weaker repression results in weaker growth rate dependence also in the cooperative case, see Supporting Text.
Figure 4. Growth-rate dependence of simple negative and positive regulation.
Concentration of a protein under (A) negative regulation by a constitutively expressed repressor, and (B) positive regulation by a constitutively expressed activator. The two plots are generated, respectively, by Eq. (S9) and Eq. (S11) in the Supporting Text, for non-cooperative (Hill coefficient n=1, squares) and cooperative regulation (n=2, triangles). Black symbols show the concentration of constitutively expressed protein. The parameters used for the plots are r1/K=10 in (A), and a1/K=0.1 and f=100 in (B). (C) Experimental data for the concentrations of LacZ reporter under constitutive expression (strain EQ37: PLtetO1-lacZ, no tetR, black), repression (strain EQ38: Pcon-tetR, PLTet-O1-lacZ, red) and activation (strain EQ40: PLlac-O1-dnxylR, Pu-lacZ, no lacI, green), showing weaker growth-rate dependence under repression and stronger growth-rate dependence under activation as compared to the constitutive case.
For positive regulation by a constitutively expressed activator A (Fig. 4B), the two effects of growth both tend to decrease the expression level of the target protein E, so that in this case, the target is predicted to always exhibit a stronger inverse growth-rate dependence (green) than a constitutive gene (black).
The above predictions were tested using several synthetic genetic circuits (Table S2) expressing LacZ reporter in strains derived from E. coli MG1655. LacZ activity was assayed during exponential growth in a variety of media which provided a range of growth rates. In strain EQ38, a constitutively expressed repressor (TetR) controls LacZ expression through the synthetic TetR-dependent PLTet-O1 promoter (Lutz and Bujard, 1997). Its LacZ expression (red dots in Fig. 4D) is seen to have a weaker growth-rate dependence than the cogenic strain (EQ37) not containing tetR (black). In strain EQ40, a constitutively expressed activator (dnXylR) controls LacZ expression through the Pu promoter derived from the TOL plasmid of Pseudomonas putida (Perez-Martin and de Lorenzo, 1996). A stronger growth rate dependence (green) than for constitutive expression is seen for this system. The experimental results are in good semi-quantitative agreement with the predictions (compare like-color curves in Fig. 4). Detailed quantitative comparisons require quantitative knowledge of the promoter characteristics (e.g., cooperativity and repression threshold) and will be pursued elsewhere.
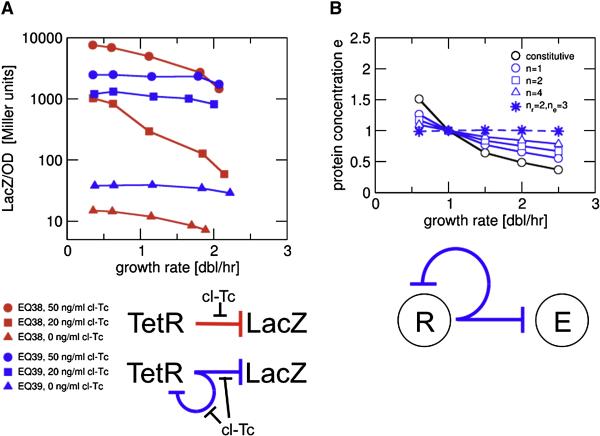
Homeostatic circuits
Although simple repression can result in rather weak growth-rate dependence (Fig. 4C, red dots), significant growth rate dependence of LacZ expression is seen for strain EQ38 (Fig. 5A, red symbols) in the presence of cl-Tc, an inducer of TetR which itself hardly affected growth (Fig. S1). The inducer dependence is complex due to a variety of factors including the inducer-TetR interaction and inducer transport, and is beyond the scope of this study. Here we ask how a gene should be regulated to obtain constant protein concentration over a wide range of growth rates even in the presence of complex growth rate dependent effects. An obvious candidate, proposed long ago (Sompayrac and Maaloe, 1973), is negative autoregulation, a well-known mechanism for homeostasis (Savageau, 1974). Using our model to investigate the expression of a target protein E controlled by a negative autoregulator R, we find very weak growth-rate dependence, in particular for highly cooperative repression (large n); see solid blue curves in Fig. 5B for some examples where both R and E are regulated by the same promoter. If the two genes are expressed by different promoters, it is in principle possible to fine-tune the cooperativity of repression to achieve complete independence to growth effects (dashed blue curve in Fig. 5B); see discussion in the Supporting Text.
Figure 5. Growth-rate dependence of genetic circuits with negative autoregulation.
(A) Experimental data for growth-rate dependence of simple repression (EQ38: Pcon-tetR, PLTet-O1-lacZ, red symbols), and autorepression (EQ39: PLTet-O1-tetR, PLTet-O1-lacZ, blue symbols) in presence of the inducer cl-Tc (circles: 50ng/ml; squares: 20ng/ml; triangles: no inducer). For simple repression, induction results in significant growth-rate dependence. Autorepression exhibits growth rate independent LacZ concentrations which is nevertheless tunable by the inducer level. (B) Our model predicts weak growth-rate dependence for a protein E controlled by an autoregulated repressor R. If E and R are driven by the same promoter (solid lines, from Eq. (S14) with r1/Kr=10), weaker growth rate dependence is obtained by increasing cooperativity (larger Hill coefficient n). Independence of growth rate is predicted for E and R driven by different promoters, whose respective Hill coefficients for repression (ne and nr) satisfy ne=nr+1 (dashed line, from Eq. (S17) with r1/Kr=10 and r1/Ke=10).
The behavior of the negative feedback regulated circuit was tested by replacing the promoter driving tetR in strain EQ38 by the PLTet-O1 promoter. The resulting strain EQ39 exhibited much reduced growth-rate dependence in LacZ expression (Fig. 5A, blue symbols) with or without induction, yet the expression levels clearly depended on the inducer levels. This result shows that negative autoregulation can indeed allow the cell to tune enzyme levels in a growth-rate independent manner.
Bistable circuits
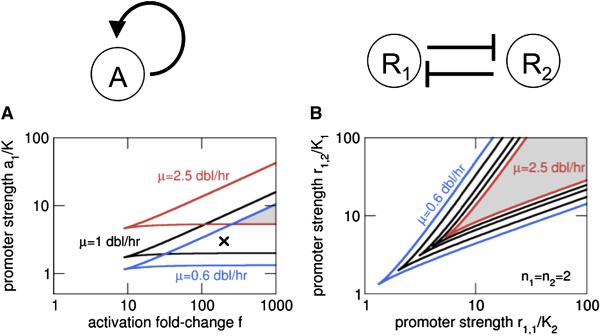
As an example for more complex genetic circuits, we consider bistable circuits, where for some range of the circuit parameters genetically identical cells in a population can exhibit different behaviors, e.g., with a high expression level of a reporter gene in one subpopulation and a low expression level in the other subpopulation. Two such circuit designs have been described in the synthetic biology literature, (i) a single gene controlled by positive autoregulation (Atkinson et al., 2003; Isaacs et al., 2003) and (ii) a ‘toggle switch’ system consisting of two genes which repress each other (Gardner et al., 2000).
The autoactivating circuit is known to exhibit bistability provided that autoactivation is cooperative with a Hill coefficient n>1 (Atkinson et al., 2003; Isaacs et al., 2003). In Fig. 6A, we plot the bistable regimes obtained from our model for different growth rates in the space of two key parameters for this circuit, the promoter strength (a1/K) and the maximal fold-activation (f) of the promoter, for n=2. The bistable regime for each growth rate is contained within the wedge defined by the pair of lines with corresponding color.
Figure 6. Effects of growth rate on bistable genetic circuits.
The parameter ranges for bistability at different growth rates are plotted for (A) the autoactivator and (B) the toggle switch. The lines describe boundaries of the bistable regime, obtained from linear stability analysis of Eq. (S18) for (A) and Eqs. (S19) and (S20) for (B). The grey areas indicate the parameter range for which bistability is obtained over the full range of growth rates considered here (0.6-2.5 dbl/hr).
The results show that the circuit can exhibit qualitatively different behavior at different growth rates: A circuit with parameter values marked by the cross in Fig. 6A will exhibit bistability, i.e., a mixed population of bacteria with either a high or a low level of activator expression, at slow growth (both at 1 and 0.6 doublings per hour) but not at fast growth, where the whole population goes to the low state. The parameter range where bistability persists over a wider range of growth rates can be quite narrow (shaded grey area in Fig. 6A), although it can be expanded within the model by either an increased fold-activation f or higher cooperativity.
For the toggle switch system based on the mutual repression of two genes, the bistable regime predicted by the model depends on the strengths of the two promoters, as plotted in Fig. 6B. We see that the bistable regime for fast growth, although smaller, is entirely contained within the regime for slow growth. Thus unlike the autoactivator case, the toggle switch circuit exhibiting bistability at fast growth is also expected to exhibit bistability at slow growth. Fig. 6B actually pertains to a case where the repressors can provide arbitrarily large degree of repression if expressed high enough. The alternative case with a finite basal expression level produces qualitatively similar behavior as described in the Supporting Text. Consequently, we expect it to be easier to maintain bistability at different growth rates for a toggle switch circuit than an autoactivating circuit.
Feedback through expression-dependent growth rate
So far, we have considered growth-rate dependent effects on genetic circuits, assuming that the output of the circuits would not affect the growth of the cells. While this situation can be mimicked by synthetic circuits expressing moderate amounts of reporter proteins, we note that in many cases, the expression of a target protein will also affect cell growth, if the protein is, e.g., toxic to the cell (inhibiting growth) or relieves a metabolic “bottleneck” (stimulating growth). These cases represent examples of positive and negative feedback through an expression-level-dependent variation of the growth rate, which in turn affects the expression level.
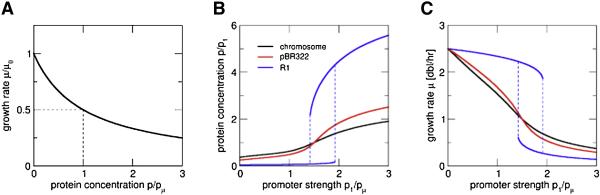
Let us consider the slow-down of growth due to expression of a toxin (an example is HipA, see the discussion below), which we model by a non-cooperative Hill function of the toxin concentration p with threshold pμ (Fig. 7A). For constitutive expression of the toxin, the growth inhibition is expected to increase toxin expression due to the generic growth rate dependent effect discussed above (Fig. 3). This increase will slow down growth further, resulting in positive feedback. Quantitatively, our model predicts a nonlinear relation between the steady state concentration p and the promoter strength (Fig. 7B). Fig. 7C depicts the corresponding predictions on the growth rate. The nonlinearity is seen to be the weakest for a chromosomally encoded toxin (black line) and increases progressively for a toxin gene on the pBR322 plasmid (red line) and on the R1 plasmid (blue line). According to the model, the increasing nonlinearity results from the increasing dependence of constitutive expression on growth rate for the 3 systems (Fig. 3C). Note that the blue lines in Figs. 7B and 7C admit two possible solutions for a range of promoter strengths. This implies occurrence of growth bistability, i.e. the coexistence of two genetically identical subpopulations with different levels of toxin expression and hence growth rate, merely due to a constitutively expressed gene on the R1 plasmid if its promoter strength falls between the two dashed lines. We note that growth-mediated feedback may also work in conjunction with regulatory feedback; see the Supporting Text for an example.
Figure 7. Feedback through growth.
(A) Growth inhibition due to expression of a toxin is described by a Hill function of the toxin concentration p, characterized by a threshold concentration (pμ) for which the growth rate is reduced to half the maximal growth rate (μ0). (B) Toxin concentration (normalized to its concentration at 1 dbl/hr, p1) and (C) growth rate as functions of the promoter strength (characterized by p1 and normalized to pμ), obtained from Eq. (S22). Growth inhibition results in non-linear increase of the toxin concentration, which is steeper for a gene on a pBR322 plasmid (red) than for a gene on the chromosome (black). For a gene on plasmid R1 (blue) with its strong growth-rate dependence (Fig. 3C), there is a region of bistability with two branches, one with high toxin concentration and slow growth and the other with low toxin concentration and fast growth.
DISCUSSION
Genetic circuits are unavoidably coupled to the physiological state of the cell, which is reflected in global cellular parameters such as cell size, gene copy numbers, abundance of RNA polymerases and ribosomes, all of which change when the cell state changes. In this study, we have taken the classic result that these global parameters depend on growth media primarily through the growth rate as an empirical fact (Maaløe, 1979; Schaechter et al., 1958) and explored its consequences by building a simple, parameter-free model of constitutive gene expression that is completely determined by the cellular parameters measured meticulously by different labs in the past 3 decades. The validity of this approach is established through the excellent agreement on the growth rate dependence of constitutive gene expression generated by the model and the experimental results obtained by different labs using different strains of E. coli grown in different media, with different reporter genes expressed by different promoters (Fig. 3A and 3B). Origins of the “universal” nature of the classic result of Schaechter et al. (1958) are addressed in a companion study (Scott et al., 2009), which describes different classes of growth modulation. The growth rate dependent effects studied in this work pertain to ‘nutrient-limited’ growth and should not be applied to growth modulation by, e.g., translational inhibition which results in very different ribosome abundance (Harvey and Koch, 1980) or osmotic stress which changes the mass-volume relation (Cayley and Record, 2004). We also do not exclude the possibility that certain nutrients may not obey the trends discussed here, due e.g., to growth inhibiting effects by toxic intermediate metabolites. Nevertheless, the very robust correlation between growth rate and the cellular parameters documented over the past five decades (Bremer and Dennis, 1996; Maaløe, 1979; Schaechter et al., 1958) lead us to believe that deductions based on these correlations will be equally robust.
The importance of these global growth-dependent effects is illustrated first and foremost by the variable expression level of a constitutively expressed gene: In that case, the resulting protein concentration can differ up to 10-fold between growth in rich and poor medium (Figs. 2 and 3). The predictions of our model for this quantity are in excellent agreement with measured protein concentrations (Fig. 3). Other predictions remain to be tested, including the different growth rate dependence for the expression of genes encoded on the chromosome vs. plasmid (Fig. 3C), and the qualitatively different (i.e., opposing) growth rate dependence of mRNA or protein levels, measured per cell or per cellular mass (Fig. 2).
Growth rate dependences become more complex when gene regulation and feedback are involved. Expansion of our basic model gives precise predictions on the growth rate dependence of regulated genes, by simple repression, activation, as well as including feedback loops. Particularly noteworthy features among these results are the amplification of growth-rate dependence for genes expressed by activators and the suppression of growth-rate dependence for genes controlled by autorepressors. Some of these predictions have been validated at a semi-quantitative level by our experiments using synthetic circuits. Other predictions regarding more complex feedback loops, including regulatory feedback and growth-dependent feedback due to the effect of expressed genes on growth, remain to be tested.
Practical consequences: interpretation of data, circuit modeling and design
Different measures of gene expression have different growth-rate dependence
The existence of global effects on gene expression that reflect the physiological state of the cell has several practical consequences for the analysis of experimental gene expression data in both large-scale expression profiles and in studies of individual circuits, for the design of synthetic genetic circuits, and for circuit modeling. First, our results predict that different measures of the level of gene expression such as the transcription rates, the mRNA concentration and the protein concentration exhibit different growth-rate dependence (Figs. 1 and 2). While these quantities may be considered as equivalent measures of the ‘expression level’ at a fixed growth rate, they are generally not equivalent when data with different growth rates are compared.
Changes in gene expression need not reflect regulation
Second, as even the concentration of a protein product of an unregulated gene is growth-rate dependent, care has to be taken when interpreting data using the expression of a reporter protein. An increased or decreased concentration of the reporter protein in one condition compared to another (e.g., two different growth media, with and without induction, wild-type vs. mutant, etc.), does not necessarily imply the existence of specific regulation, if the growth rate changed between the conditions. The discrepancy will be particularly pronounced for reporter genes on plasmids, where the global growth-rate dependent effects are very strong (Fig. 3C). The effects of growth rate and of regulation can however be disentangled using the results presented here. In particular, this is important when the change in protein concentration is only a few-fold, i.e. of the same order of magnitude as the growth-rate-dependent effects. Large fold-changes in protein concentration on the other hand, are very unlikely to be solely due to growth rate and will therefore typically indicate regulation, but even then growth-rate dependence needs to be taken into account for a quantitative interpretation. Finally, we mention that mRNA abundance is in principle a good candidate measure of gene expression, as mRNA/mass hardly exhibited any growth rate dependence for constitutive expression (Fig. 2B). However, quantification of mRNA (e.g., by qPCR) involves comparison to a “standard”, often taken to be the 16S ribosomal RNA. The latter unfortunately has perhaps the strongest growth rate dependences known (Bremer and Dennis, 1996). Thus care should be taken in the interpretation of these results.
Growth rate effects can change the qualitative behavior of genetic circuits and need to be included in circuit design
The growth rate dependence of gene expression is also an aspect to be taken into account in the design of synthetic genetic circuits. One question of interest is how to design a circuit to make the concentration of an enzyme independent of growth rate (or at least approximately so). We showed that this may be achieved by negative autoregulation (Fig. 5), a strategy which is widely used in bacteria, in particular in the regulation of biosynthetic operons (Shen-Orr et al., 2002; Thieffry et al., 1998).
Furthermore even the qualitative behavior of more complex circuits may be different at different growth rate, as shown by the example of bistability (Fig. 6). In some cases, the growth-rate dependence may be desirable, e.g. to have a switch responding to growth status. In many cases, however, one may be more interested in achieving the same circuit functionality under a wide range of growth conditions, which will impose constraints on the circuit design. For example, in the case of bistability, the toggle switch system will be preferable compared to the autoactivator system.
Growth effects are not accurately described by protein dilution only
Growth-rate dependent effects are not accurately captured by ‘dilution models’ that include only the effect of protein dilution, as is often done in circuit modeling (e.g., Narang and Pilyugin, 2008). Such models are incompatible with the observation that other parameters of gene expression are also growth-rate dependent; they result in approximately correct predictions for the growth-rate dependence of protein concentrations (for growth rates > 0.6 dbl/hr), but not for the amount of protein per cell (Fig. S2 A and B). At slower growth, dilution-models strongly overestimate growth-rate dependent effects (Fig. S2 A); they therefore tend to overemphasize growth-dependent effects such as growth bistability (Fig. S2 C). Finally, we expect dilution-only models to be especially problematic for plasmid-encoded genes that can exhibit very strong growth rate dependencies (Fig. 3C) and for translation-limited growth (Scott et al., 2009).
Possible physiological roles of growth feedback
Feedback through growth-dependent gene expression may be an integral part of metabolic control
Feedback through growth should also play an important role in natural regulatory processes. For example, if growth is limited by the concentration of one specific protein (e.g., because it imports or synthesizes an essential metabolite), there is a built-in negative feedback since a decrease in the concentration of this protein would lead to a slow-down of growth which would in turn increase the protein concentration (Fig. 3) even if the protein is constitutively expressed. A bottleneck enzyme is indeed expected to be effectively constitutive, since it should be expressed at the maximal level, i.e. fully activated or fully derepressed, according to well-designed metabolic control mechanisms. This built-in negative feedback can dampen harmful effects of fluctuations in enzyme levels on growth and compensate against fluctuations in external nutrient levels.
Positive feedback through growth can lead to growth bistability
If a protein is ‘toxic’, i.e., if high concentration of the protein has a detrimental effect on growth, expression of this protein will lead to decreased growth which will further increase its concentration, resulting effectively in a positive feedback even in the absence of specific regulation. Such positive feedback can lead to bistability, i.e., heterogenous subpopulation with different degree of gene expression in genetically identical cells. Here the bistability is reflected not only in gene expression but also in the (very) different growth rates of the subpopulations expressing or not expressing the toxic protein. In Fig. 7, we described an example where this growth bistability is expected to occur for an unregulated gene encoded on a plasmid whose copy number strongly depends on the growth rate.
Growth bistability may underlie persistence
Growth bistability may be a mechanism underlying the phenomenon of persistence, i.e. the tolerance of bactericidal antibiotics in a subpopulation due to an epigenetic (non-mutational) mechanism. Single cell experiments have shown that persistent cells grow slowly and may switch stochastically back to normal growth (Balaban et al., 2004). One known mechanism for slow growth in persistent cells depends on the expression of the toxin HipA (Keren et al., 2004). These observations suggest that persistence may be linked to growth bistability due to a feedback loop through expression level-dependent growth reduction. Of particular interest here is that HipA can induce persistence when expressed constitutively on a high-copy number plasmid (Korch and Hill, 2006). Our analysis suggests that this may be an effect of a strong growth-rate dependence of plasmid copy number (Fig. 7B and 7C), which leads to a strong growth-rate-dependent expression of the plasmid-encoded gene, without the need of invoking any hypothetical cooperative growth inhibition mechanisms, as has been proposed recently (Lou et al., 2008).
Similar type of growth bistability is expected to arise from growth stimulation by the constitutive expression of antibiotic resistance genes in the presence of antibiotics (Scott et al., 2009). The abrupt increase of the growth rate, and thus of bacterial fitness, in the bistable region may provide a driving force promoting the rapid evolution of antibiotic resistance (Walsh, 2000) without the need for elaborate regulation. Nontrivial feedback effects obtained in the absence of genetic regulation is in fact a common theme in all of the growth-dependent effects discussed above. We suggest that these effects may provide an evolutionary expedient mechanism for the development of a rudimentary molecular network for which nonlinear feedback effects are essential. Once a bare network is in place, more elaborate regulatory mechanisms (which are more difficult to arise evolutionarily) may be acquired step-by-step later to fine-tune the system.
METHODS
Model for gene expression
The expression of a gene is modeled by two equations for the mRNA and protein copy number per cell, as described in detail in the Supporting Text. The growth rate dependence of all parameters is taken from the literature as described in Results and summarized in Table S1. Most of the data consists of values for the parameters at a few different growth rates. These were interpolated where necessary to obtain a complete parameter set for the same set of growth rates. The gene copy number for chromosomal genes was calculated according to the Cooper-Helmstetter model for DNA replication (Bremer and Dennis, 1996; Cooper and Helmstetter, 1968).
Model for regulation
A detailed description of the circuits studied here is given in the Supporting Text. In brief, the direct growth rate dependence of a regulated gene, which is the same as for unregulated genes, is described by a function F(μ), given by the concentration of a constitutively expressed protein at a growth rate μ, normalized by its concentration at 1 doubling/hour. The concentration of an unregulated gene is then given by p=p1 F(μ) where p1 is the concentration at 1 doubling/hour. Gene regulation modulates this expression for the protein concentration (e) by a Hill-type regulation function, e=e1 F(μ) R(r) for repression and e=e1 F(μ) A(a) for activation (Bintu et al., 2005). Here e1 is the concentration of the protein at growth rate of 1 doubling/hour, taken at maximal expression (i.e. for full activation or in the absence of repression); r and a are the concentrations of the repressor and activator, respectively. The parameters of the regulation function (R or A), the fold-change f, the Hill coefficient n, and the threshold K, which reflect physical properties of the regulatory elements, are taken to be independent of growth-rate for simple regulatory elements.
Experimental measurement of growth-rate dependent gene expression
All the strains used were derived from E. coli K12 strain MG1655 and the detailed information for making each derivative strain is described in Supplemental Text. The strains and oligonucleotides used are listed in Tables S2 and S3, respectively.
To culture the strains at different growth rates, five defined media were used. They are derived from M63 minimal medium (Miller, 1972) and rich defined medium (RDM) (Neidhardt et al., 1974), supplemented by either glycerol or glucose at 0.5% (w/v) as the primary carbon source. These five media are 1) RDM + glucose; 2) RDM + glycerol; 3) M63 + NH4Cl (20 mM) + glycerol + casamino acids (0.2%); 4) M63+ NH4Cl (20 mM) + glycerol; and 5) M63 + glycerol + glycine (20 mM, the sole nitrogen source). The resulting growth rates range from 0.3 to 2.4 doublings/hr (Fig. S1).
For gene expression measurements, experimental strains were first cultured in LB and then in one of the above 5 media, in glass tubes with vigorous shaking at 37°C. The inducer chloro-tetracycline was added at 20 or 50 ng/ml to some media. After a round of pre-culture growth (5-7 doublings) and another 2-3 doublings in the experimental culture, samples were taken for measurements of OD600 (0.1 to 1), total protein amount, and β-galactosidase activities at 4 points. Growth rates and β-galactosidase expression levels were determined by linear regression as detailed in Supplemental Text.
Supplementary Material
Acknowledgements
We are grateful to Hans Bremer, Patrick Dennis, Mans Ehrenberg, Peter Geiduschek, Carl Gunderson, Po-han Lee, Eduard Mateescu, Atul Narang, Moselio Schaechter, Matthew Scott, Arbel Tadmor, and Lingchong You for discussions during the course of this work. This work was supported by the NSF through the Center for Theoretical Biological Physics (Grant PHY-0822283) and through grant MCB0746581, by the NIH through grant RO1GM77298, and by a fellowship from Deutsche Forschungsgemeinschaft (Grants KL818/1-1 and 1-2, to SK).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- Andrianantoandro E, Basu S, Karig DK, Weiss R. Synthetic biology: new engineering rules for an emerging discipline. Mol Syst Biol. 2006;2:2006.0028. doi: 10.1038/msb4100073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atkinson MR, Savageau MA, Myers JT, Ninfa AJ. Development of genetic circuitry exhibiting toggle switch or oscillatory behavior in Escherichia coli. Cell. 2003;113:597–607. doi: 10.1016/s0092-8674(03)00346-5. [DOI] [PubMed] [Google Scholar]
- Balaban NQ, Merrin J, Chait R, Kowalik L, Leibler S. Bacterial persistence as a phenotypic switch. Science. 2004;305:1622–1625. doi: 10.1126/science.1099390. [DOI] [PubMed] [Google Scholar]
- Bernstein JA, Khodursky AB, Lin PH, Lin-Chao S, Cohen SN. Global analysis of mRNA decay and abundance in Escherichia coli at single-gene resolution using two-color fluorescent DNA microarrays. Proc Natl Acad Sci U S A. 2002;99:9697–9702. doi: 10.1073/pnas.112318199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bintu L, Buchler NE, Garcia HG, Gerland U, Hwa T, Kondev J, Phillips R. Transcriptional regulation by the numbers: models. Curr Opin Genet Dev. 2005;15:116–124. doi: 10.1016/j.gde.2005.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bremer H, Dennis PP. Modulation of chemical composition and other parameters of the cell by growth rate. In: Neidhardt FC, editor. Escherichia coli and Salmonella. ASM Press; Washington D.C.: 1996. pp. 1553–1569. [Google Scholar]
- Cayley S, Record MT. Large changes in cytoplasmic biopolymer concentration with osmolality indicate that macromolecular crowding may regulate protein-DNA interactions and growth rate in osmotically stressed Escherichia coli K-12. Journal of Molecular Recognition. 2004;17:488–496. doi: 10.1002/jmr.695. [DOI] [PubMed] [Google Scholar]
- Chiaramello AE, Zyskind JW. Expression of Escherichia coli dnaA and mioC genes as a function of growth rate. J Bacteriol. 1989;171:4272–4280. doi: 10.1128/jb.171.8.4272-4280.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coffman RL, Norris TE, Koch AL. Chain Elongation Rate of Messenger and Polypeptides in Slowly Growing Escherichia Coli. J Mol Biol. 1971;60:1–19. doi: 10.1016/0022-2836(71)90442-6. [DOI] [PubMed] [Google Scholar]
- Cooper S, Helmstetter CE. Chromosome Replication and Division Cycle of Escherichia Coli B/r. J Mol Biol. 1968;31:519–540. doi: 10.1016/0022-2836(68)90425-7. [DOI] [PubMed] [Google Scholar]
- Donachie WD, Robinson AC. Cell division: Parameter values and the process. In: Neidhardt FC, Ingraham JL, Magasanik B, Low KB, Schaechter M, Umbarger HE, editors. Escherichia coli and Salmonella typhimurium. ASM; Washington DC: 1987. pp. 1578–1592. [Google Scholar]
- Elowitz MB, Leibler S. A synthetic oscillatory network of transcriptional regulators. Nature. 2000;403:335–338. doi: 10.1038/35002125. [DOI] [PubMed] [Google Scholar]
- Elowitz MB, Levine AJ, Siggia ED, Swain PS. Stochastic gene expression in a single cell. Science. 2002;297:1183–1186. doi: 10.1126/science.1070919. [DOI] [PubMed] [Google Scholar]
- Engberg B, Nordstrom K. Replication of R-factor R1 in Escherichia coli K-12 at different growth rates. J Bacteriol. 1975;123:179–186. doi: 10.1128/jb.123.1.179-186.1975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner TS, Cantor CR, Collins JJ. Construction of a genetic toggle switch in Escherichia coli. Nature. 2000;403:339–342. doi: 10.1038/35002131. [DOI] [PubMed] [Google Scholar]
- Golding I, Paulsson J, Zawilski SM, Cox EC. Real-time kinetics of gene activity in individual bacteria. Cell. 2005;123:1025–1036. doi: 10.1016/j.cell.2005.09.031. [DOI] [PubMed] [Google Scholar]
- Guido NJ, Wang X, Adalsteinsson D, McMillen D, Hasty J, Cantor CR, Elston TC, Collins JJ. A bottom-up approach to gene regulation. Nature. 2006;439:856–860. doi: 10.1038/nature04473. [DOI] [PubMed] [Google Scholar]
- Harvey RJ, Koch AL. How partially inhibitory concentrations of chloramphenicol affect the growth of Escherichia coli. Antimicrob Agents Chemother. 1980;18:323–337. doi: 10.1128/aac.18.2.323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasty J, McMillen D, Collins JJ. Engineered gene circuits. Nature. 2002;420:224–230. doi: 10.1038/nature01257. [DOI] [PubMed] [Google Scholar]
- Haugen SP, Ross W, Gourse RL. Advances in bacterial promoter recognition and its control by factors that do not bind DNA. Nat Rev Microbiol. 2008;6:507–519. doi: 10.1038/nrmicro1912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Husnain SI, Thomas MS. The UP element is necessary but not sufficient for growth rate-dependent control of the Escherichia coli guaB promoter. J Bacteriol. 2008;190:2450–2457. doi: 10.1128/JB.01732-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isaacs FJ, Hasty J, Cantor CR, Collins JJ. Prediction and measurement of an autoregulatory genetic module. Proc Natl Acad Sci U S A. 2003;100:7714–7719. doi: 10.1073/pnas.1332628100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jain C, Deana A, Belasco JG. Consequences of RNase E scarcity in Escherichia coli. Mol Microbiol. 2002;43:1053–1064. doi: 10.1046/j.1365-2958.2002.02808.x. [DOI] [PubMed] [Google Scholar]
- Kaplan S, Bren A, Zaslaver A, Dekel E, Alon U. Diverse two-dimensional input functions control bacterial sugar genes. Mol Cell. 2008;29:786–792. doi: 10.1016/j.molcel.2008.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keener J, Nomura M. Regulation of ribosome synthesis. In: Neidhardt FC, editor. Escherichia coli and Salmonella. ASM Press; Washington D.C.: 1996. pp. 1417–1431. [Google Scholar]
- Keren I, Shah D, Spoering A, Kaldalu N, Lewis K. Specialized persister cells and the mechanism of multidrug tolerance in Escherichia coli. J Bacteriol. 2004;186:8172–8180. doi: 10.1128/JB.186.24.8172-8180.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klumpp S, Hwa T. Growth-rate-dependent partitioning of RNA polymerases in bacteria. Proc Natl Acad Sci U S A. 2008;105:20245–20250. doi: 10.1073/pnas.0804953105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korch SB, Hill TM. Ectopic overexpression of wild-type and mutant hipA genes in Escherichia coli: effects on macromolecular synthesis and persister formation. J Bacteriol. 2006;188:3826–3836. doi: 10.1128/JB.01740-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhlman T, Zhang Z, Saier MH, Jr., Hwa T. Combinatorial transcriptional control of the lactose operon of Escherichia coli. Proc Natl Acad Sci U S A. 2007;104:6043–6048. doi: 10.1073/pnas.0606717104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang ST, Bipatnath M, Xu YC, Chen SL, Dennis P, Ehrenberg M, Bremer H. Activities of constitutive promoters in Escherichia coli. J Mol Biol. 1999a;292:19–37. doi: 10.1006/jmbi.1999.3056. [DOI] [PubMed] [Google Scholar]
- Liang ST, Ehrenberg M, Dennis P, Bremer H. Decay of rplN and lacZ mRNA in Escherichia coli. J Mol Biol. 1999b;288:521–538. doi: 10.1006/jmbi.1999.2710. [DOI] [PubMed] [Google Scholar]
- Liang ST, Xu YC, Dennis P, Bremer H. mRNA composition and control of bacterial gene expression. J Bacteriol. 2000;182:3037–3044. doi: 10.1128/jb.182.11.3037-3044.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin-Chao S, Bremer H. Effect of the bacterial growth rate on replication control of plasmid pBR322 in Escherichia coli. Mol Gen Genet. 1986;203:143–149. doi: 10.1007/BF00330395. [DOI] [PubMed] [Google Scholar]
- Lou C, Li Z, Ouyang Q. A molecular model for persister in E. coli. J Theor Biol. 2008;255:205–209. doi: 10.1016/j.jtbi.2008.07.035. [DOI] [PubMed] [Google Scholar]
- Lutz R, Bujard H. Independent and tight regulation of transcriptional units in Escherichia coli via the LacR/O, the TetR/O and AraC/I1-I2 regulatory elements. Nucleic Acids Res. 1997;25:1203–1210. doi: 10.1093/nar/25.6.1203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maaløe O. Regulation of the protein-synthesizing machinery - ribosomes, tRNA, factors, and so on. In: Goldberger RF, editor. Biological regulation and development. Plenum Press; New York: 1979. pp. 487–542. [Google Scholar]
- Miller JH. Experiments in Molecular Genetics. Cold Spring Harbor Laboratory; Cold Spring Harbor, NY: 1972. [Google Scholar]
- Nanninga N, Woldringh CL. Cell growth, genome duplication, and cell division. In: Nanninga N, editor. Molecular cytology of Escherichia coli. Academic Press; London: 1985. pp. 259–318. [Google Scholar]
- Narang A, Pilyugin SS. Bistability of the lac operon during growth of Escherichia coli on lactose and lactose+glucose. Bull Math Biol. 2008;70:1032–1064. doi: 10.1007/s11538-007-9289-7. [DOI] [PubMed] [Google Scholar]
- Neidhardt FC, Bloch PL, Smith DF. Culture medium for enterobacteria. J Bacteriol. 1974;119:736–747. doi: 10.1128/jb.119.3.736-747.1974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neidhardt FC, Ingraham JL, Schaechter M. Physiology of the bacterial cell: a molecular approach. Sinauer; Sunderland: 1990. [Google Scholar]
- Nilsson G, Belasco JG, Cohen SN, von Gabain A. Growth-rate dependent regulation of mRNA stability in Escherichia coli. Nature. 1984;312:75–77. doi: 10.1038/312075a0. [DOI] [PubMed] [Google Scholar]
- Pato ML, von Meyenburg K. Residual RNA Synthesis in Escherichia Coli after Inhibition of Initiation of Transcription by Rifampicin. Cold Spring Harbor Symp Quant Biol. 1970;35:497–504. [Google Scholar]
- Pedersen S, Bloch PL, Reeh S, Neidhardt FC. Patterns of Protein Synthesis in Escherichia Coli. Catalog of Amount of 140 Individual Proteins at Different Growth Rates. Cell. 1978;14:179–190. doi: 10.1016/0092-8674(78)90312-4. [DOI] [PubMed] [Google Scholar]
- Perez-Martin J, de Lorenzo V. In vitro activities of an N-terminal truncated form of XylR, a sigma 54-dependent transcriptional activator of Pseudomonas putida. J Mol Biol. 1996;258:575–587. doi: 10.1006/jmbi.1996.0270. [DOI] [PubMed] [Google Scholar]
- Rao CV, Wolf DM, Arkin AP. Control, exploitation and tolerance of intracellular noise. Nature. 2002;420:231–237. doi: 10.1038/nature01258. [DOI] [PubMed] [Google Scholar]
- Savageau MA. Comparison of classical and autogenous systems of regulation in inducible operons. Nature. 1974;252:546–549. doi: 10.1038/252546a0. [DOI] [PubMed] [Google Scholar]
- Schaechter M, Maaløe O, Kjeldgaard NO. Dependency on medium and temperature of cell size and chemical composition during balanced growth of Salmonella typhimurium. J Gen Microbiol. 1958;19:592–606. doi: 10.1099/00221287-19-3-592. [DOI] [PubMed] [Google Scholar]
- Scott M, Gundersen CW, Mateescu E, Zhang Z, Hwa T. Growth laws and proteome partition dictate the growth dependence and fitness cost of bacterial gene expression. 2009. in submission.
- Shen-Orr SS, Milo R, Mangan S, Alon U. Network motifs in the transcriptional regulation network of Escherichia coli. Nat Genet. 2002;31:64–68. doi: 10.1038/ng881. [DOI] [PubMed] [Google Scholar]
- Sompayrac L, Maaloe O. Autorepressor model for control of DNA replication. Nat New Biol. 1973;241:133–135. doi: 10.1038/newbio241133a0. [DOI] [PubMed] [Google Scholar]
- Thieffry D, Huerta AM, Perez-Rueda E, Collado-Vides J. From specific gene regulation to genomic networks: a global analysis of transcriptional regulation in Escherichia coli. Bioessays. 1998;20:433–440. doi: 10.1002/(SICI)1521-1878(199805)20:5<433::AID-BIES10>3.0.CO;2-2. [DOI] [PubMed] [Google Scholar]
- Walsh C. Molecular mechanisms that confer antibacterial drug resistance. Nature. 2000;406:775–781. doi: 10.1038/35021219. [DOI] [PubMed] [Google Scholar]
- Wanner BL, Kodaira R, Neidhardt FC. Physiological Regulation of a Decontrolled Lac Operon. J Bacteriol. 1977;130:212–222. doi: 10.1128/jb.130.1.212-222.1977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willumsen BM. M. Sc. Thesis. University of Copenhagen; 1975. Expression of constitutive genes in E. coli as function of growth rate. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.