Assessment of dose reconstruction errors in image-guided radiation therapy

Abstract

Dose reconstruction can be used to improve the accuracy of dose evaluation throughout a treatment course. Its working mechanism is based on deformable image registration (DIR). The purpose of this paper is to develop a method to estimate the dose reconstruction error associated with the inaccuracy of DIR algorithms. To reach this goal, we quantified dominant errors in DIR in terms of unbalanced energy (UE), which were compared with the standard displacement error (SDE). Their high similarity, characterized by Pearson correlation coefficient, was verified through nine ‘demons’ registration instances performed within simulated reference frames. Based on the similarity, the dose-warping discrepancy at each voxel was defined as a line integral of the dose gradient within the voxel's neighborhood whose boundary was determined by the voxel's UE value. From this definition, the dose reconstruction error was then calculated at each voxel on nine prostate computed tomography images, obtained from a patient treatment course. The average of the Pearson correlation coefficients between UE and SDE over the simulated registration instances was above 70%. The mean value of the dose reconstruction errors in a target volume was calculated for each of nine treatment fractions. The averaged percentage of these mean values with respect to the prescribed dose on the target volume was 1.68%. These results are consistent with contour-based mean dose error evaluations. This paper has established a relation between a registration error and its induced dose reconstruction discrepancy. It allows an automatic validation method to be developed to estimate the dose accumulation error at each voxel in clinical settings.

1. Introduction

In radiation therapy, it is a well-accepted fact that the clinical effect is proportional to the accumulated dose received by each tumor and normal tissue cell. With the introduction of frequent imaging during the treatment process, such as cone-beam computed tomography (CT) systems (Jaffray et al 2002, Oldham et al 2005, Sykes et al 2005), CT-on-rails systems (Ma and Paskalev 2006, Zhang et al 2007) and proposed on-board magnetic resonance systems (Baldwin et al 2005, Fox et al 2006, Tomas et al 2006) coupled with the use of deformable image registration (DIR), determination of the accumulated dose for arbitrary tissue voxels over a course or fraction of therapy when tissues move with respect to each other is becoming clinically practical (Christensen et al 2001, Foskey et al 2005, Flampouri et al 2005, Schaly et al 2004, Yan et al 1997, 1999). For current DIR algorithms, the displacement vector fields (DVFs) of image registrations, which are used to map the patient dose from one instance of a patient's anatomy (e.g., the time of treatment) to a reference anatomic instance (e.g., the planning image set), are not without error (Wang et al 2005, Li et al 2005, Foskey et al 2005, Webb 2006). The fact that DVFs do not accurately map the motion of each tissue element between anatomic instances results in errors in mapping information, such as dose, between those anatomic instances. The purpose of this paper is to develop a method to automatically assess DVF errors and their potential impact on patient dose reconstruction at other anatomic instances.

Dose reconstruction is becoming an important process in radiation therapy because it can be employed to calculate the total dose delivered in the presence of organ motion and deformation (Bortfeld et al 2004, Keall et al 2003, Siebers et al 2005, Unkelbach and Oelfke 2004). For example, with the known delivered dose at each physical point, three-dimensional (3D) fractionated treatment plans can be updated with different strategies in image-guided radiation therapy, 4D dosimetry assessment can be adjusted through intrafractional dose summation for lung patients and brachytherapy can be combined with external beam radiation therapy to determine the combined dose or biologically effective dose. Furthermore, the quantification of inputs to tissue response models can be improved through use of accumulated dose. The success of these applications largely depends on the accuracy of the dose addition and its underlying DIR.

The accuracy of DIR is compromised by many factors. For example, in a region with low-intensity gradients (e.g., the interior part of a solid organ like the prostate), displacement variations are insensitive to the registration similarity metric used during a registration process. Consequently, registration errors result easily. Meanwhile, the radiation dose distribution can have substantial gradients in this region. As a consequence, the dose-warping error in this region can be significant.

Unfortunately, there is no ground truth for a complete validation of DIR in a clinical setting. For example, whereas contour comparison, a technique often used in the validation of displacement errors around organ boundaries, may provide a gross volumetric dose evaluation (Gordon and Siebers 2007, Lu et al 2006, Rosu et al 2005), it cannot be used to check dose-warping errors at voxels in the interior of an organ or at a place where contours are unable to be delineated. The general lack of a ground truth in DIR makes both the spatial error of DIR and its consequent dosimetric discrepancy in image-guided radiation therapy (IGRT) hard to define and therefore difficult to measure. This paper addresses these two correlated issues in a systematic manner. We present the framework in terms of dose accumulation over multiple treatment fractions, but the methods presented are equally applicable to dose addition over 4D image sets or adding external beam and brachytherapy dose distributions.

In this paper, we will present the definition of voxel-based dose reconstruction error in section 2 and then quantify the relation between the displacement error and the unbalanced energy (UE) of deformable registrations in section 3. In section 4, we substitute the UE into the dose error definition to measure the dose reconstruction errors accumulated over nine treatment fractions. Results are compared with the contour-based mean dose evaluations. Discussion and conclusion are given in the last two sections.

2. Dose reconstruction error

Because of organ motion and setup errors throughout a treatment course, the same physical point may exist at different locations on different treatment images. To assess potential treatment outcome (and enable possible replanning) the dose delivered to each physical point in each fraction must be accumulated to determine the total delivered dose distribution. In this section, we briefly describe the procedure of dose accumulation realized through the aid of DIR (Foskey et al 2005, Lu et al 2006, Schaly et al 2004) and then specify its associated dosimetry error.

2.1. Dose accumulation

Suppose T is a planning image. A physical point p on T moves to $q_0^{(i)}$ on a treatment image S_i. Image registrations are performed from T to each S_i for each treatment session i. For an intensity-based image registration, when the deformation map h_i maximizes a similarity metric M(T(p), S_i(p + h_i(p))), then the physical target $q_0^{(i)}$ satisfies $q_0^{(i)}\approx q_1^{(i)}\equiv p+h_i(p)$. Consequently, the total dose delivered to the point p can be accumulated as

$$D_{\text{total}}(p)=\sum _{i=1,\dots ,N}{D}_i({\mathit{\varphi }}_i\left(p\right))$$ (1)

where N is the number of image sets, and φ_i (p) = p + h_i (p). Because of various factors, h_i is not error free. Registration errors, validated with different approaches such as phantoms (Wang et al 2005, Xiong et al 2006), landmarks (Brock et al 2005, Bharatha et al 2001, Malsch et al 2006), contours (Lu et al 2006, Foskey et al 2005, Gao et al 2006) or simulated reference frames (Wang et al 2005, Zhong et al 2007, Chi et al 2006), have been reported. Compounding the DIR errors, delivered dose distributions are frequently non-uniform, with large dose changes between adjacent voxels, for example, on a beam edge. These scenarios can exaggerate the dosimetric impact of image registration errors. For accurate patient dosimetry, the discrepancy of the cumulative dose needs to be estimated for each clinical case.

2.2. Voxel-based characterization of dose accumulation error

Registration errors at different locations may have different effects on the cumulative dose. Suppose there is an image registration from T to S with a deformation map φ₁. Consider a point p (p ∈ T) is physically moved to q₀ (q₀ ∈ S) between the two time frames, while the image registration map φ₁ generates q₁ = φ₁ (p). The dose-warping error from φ₁ at p is then defined by

$$\delta D^{({\mathit{\varphi }}_1)}(p)=|D^{({\mathit{\varphi }}_1)}(q_1)-D^{({\mathit{\varphi }}_1)}(q_0)|.$$ (2)

To simplify the following discussion, we first assume a one-dimensional dose distribution from q₀ to q₁. The interval Δ(q₁) = [q₀, q₁] is evenly partitioned by the set {r⁽⁰⁾ = q₀, r⁽¹⁾,…, r^(k) = q₁}. Then (2) can be written as

$$\delta D^{({\mathit{\varphi }}_1)}(p)=\left|\sum _{1\le \upsilon \le k}(D^{({\mathit{\varphi }}_1)}(r^{(\upsilon )})-D^{({\mathit{\varphi }}_1)}(r^{(\upsilon -1)}))\right|=\left|{\mathit{\int }}_{\Delta (q_1)}\frac{\partial D^{({\mathit{\varphi }}_1)}}{\partial u}(u)du\right|.$$ (3)

The position of q₀ is unknown; hence, the size of the domain of integration Δ(q₁) ⊂ S cannot be determined. Actually, |Δ(q₁)| comes from the distance between q₀ and q₁, the registration displacement error at p. Thus, to calculate the dose-warping discrepancy defined in (3), the registration error must be quantified.

In the next section, we try to quantify the displacement error at each voxel for a given image registration.

3. Deformable image registration error

In general, the efforts in the validation of deformable registration can be summarized into two categories. One is to measure its spatial discrepancy from a pseudo gold standard such as manually drawn contours, physical phantoms, or numerical simulations. The other is to quantify the physical fidelity of the resultant deformation mappings based on their consistency with the inverse or composition of these mappings or by measuring their Jacobean determinant. The method proposed in this paper will follow the second approach.

3.1. Characterization of deformable image registration error

Tissue deformation can be described as a mechanical process. In solid continuum mechanics, the deformation of soft tissue can be characterized by a set of linear relations between the vectors of the displacements d^e and elastic forces F^e at the vertices of each element e, K^ed^e= F^e, where K^e is the stiffness matrix whose entries contain a Young's modulus as a common factor. If Poisson's ratio in K^e is considered to be constant, the overall elastic force at each node is a summation of the contribution from its neighborhood elements. Consequently, the total elastic force at the node i is $f_i={\sum }_{j\in N{B}_i}{f}_i^{(j)}={\sum }_{j\in N{B}_i}{\sum }_{k=1,\dots ,4}{E}_j{m}_{jk}{d}_k^{(j)}$, where N B_i is the set of elements containing the node i, $d_k^{(j)}$ is the unknown displacement of the kth vertex in element j, E_j is Young's modulus of element j, and E_jm_jk is an entry in the stiffness matrix. While the external forces at the boundary nodes of an anatomy are unknown, at equilibrium the forces at the internal nodes must be null if gravity is ignored. This fact is taken as a basic criterion to judge the quality of DVF derived from an image registration (Zhong et al 2007).

Quantified in a linear finite element framework, the registration errors can be specified as an unbalanced energy (UE), which is defined at tetrahedral element j by

$$\begin{array}{cc}{\delta }_{\mathit{\varphi }}(j)=\sum _{i=1,\dots ,4}\left|d_i^{(j)}{f}_i^{(j)}\right|,& f_i^{(j)}=E_0{\Phi }_{ij}\left(d_1^{(j)},d_2^{(j)},\dots ,d_4^{(j)}\right)\end{array},$$ (4)

where E₀ is a given Young's modulus, and ${\Phi }_{ij}(d_1^{(j)},d_2^{(j)},\dots ,d_4^{(j)})={\sum }_{k=1,2,3,4}{m}_{ik}^{(j)}{d}_k^{(j)}$. From the definition above, δ_φ (j) is proportional to Young's modulus E₀, in this work assumed to be 1 kPa (Sarvazyan et al 1998), constant in the problem domain. Because the representation of the dose-warping error given in section 4.1 depends on δ_φ (j), the exact value of E₀ and its effect on the dose-warping error evaluation will be discussed further in section 5.

To quantify the explicit relation between the UE and the displacement error for a given registration, we need to create a simulation reference frame for their comparison.

3.2. Creation of reference frames

To build a standard displacement error (SDE) to be compared with UE, we first create three sets of simulation frames as references. Suppose that image 0 is a primary image, used for treatment planning, and image i (i = 1, 2, 3) is obtained from three subsequent treatment fractions. To avoid the loss of realism in creating the reference frames, the simulation is focused on the primary organ of interest for this test case, the prostate. The size of these CT images is reduced by cropping the region remote from prostate, leaving a remaining subvolume of 160 × 160 × 35 voxels. The new images cover the region of 15 cm × 15 cm × 10.5 cm around the prostate (see figure 1).

Figure 1.

(a) The primary image for treatment planning; (b) (c) (d) three images obtained in subsequent treatments.

After cropping, 24 points are identified on the planning image. They are selected from three slices showing the prostate at different levels in superior-inferior direction, each having eight points. Among the eight points, four are around prostate and four at bony structures. These points are tracked in subsequent treatment images to form a set of tractable control points for thin-plate spline registration (TPS). With the TPS registration algorithm implemented in VTK (www.vtk.org), we warp the planning image to the treatment image with the corresponding DVF generated. Consequently, the planning image and the warped image, combined with the TPS DVF, may serve as a reference frame to validate another registration algorithm, and the resultant DVF difference is then treated as an SDE. It should be mentioned that the UE is based on the physical property of the tissue deformation. If the SDE is biased, it is not suitable to be compared with the UE. This constraint presents a strong requirement on the fidelity of the simulated deformation for it to serve as a reference frame.

To meet this requirement, some featured points are selected as control points in the TPS interpolations. While the inaccuracy in tracking these control points could partly compromise the objectiveness of the simulation triplets, the TPS algorithm with 12 points around the 4 × 4×4 cm³ prostate region (and 12 located at bony structures) could warp the prostate well to its target, which was validated by tracking a prostatic calcification spot and boundary features of the prostate (Zhong et al 2007).

With the selected tracking pairs, we warp the planning image to each of the three treatment images. Figure 1(a) is the planning image which was warped to three subsequent treatment images (figures 1(b)–(d)). These TPS-warped images are shown in column 1 of figure 2. They serve as targets for Insight Toolkit (ITK) ‘demons’ registrations φ_i (Thirion), which are performed from the planning image (figure 1(a)) to each of these simulated targets ST_i in figure 2. In the ‘demons’ registration, the smoothness of the DVF is determined by its Gaussian kernel filter. The variation of its standard deviation may result in its DVFs having different qualities. To provide more testing cases, the standard deviation of its Gaussian kernel was set to σ = 1.0, 1.3, 2.0, respectively, for each registration φ_i, and their corresponding warped images are shown in columns 2, 3 and 4 of figure 2. Note that while all the images in figure 2 are rigidly aligned well, some distortions of soft tissue and bony structures can be observed, especially for the cases of φ₁, σ = 1.0 and σ = 1.3. These distortions will be illustrated clearly by their SDEs as well as their automatically calculated UE images.

Figure 2.

The first column comprises the three TPS-simulated target images (ST_i); column j (j = 2, 3, 4) comprises the images warped from image 0 to ST_i through ‘demons’ registration φ_i with Gaussian kernel σ_j, σ_j = 1.0, 1.3, 2.0, respectively.

Next the UE of the nine ‘demons’ registrations will be compared by their corresponding SDEs, calculated with respect to the simulated reference frames.

3.3. Evaluation of unbalanced energy

In the last section, four images were employed, one for planning and the others obtained from a patient's treatment course. The DVF from TPS interpolation then served as a reference frame to be compared with the DVF of the ‘demons’ registrations performed in the TPS-simulated framework. The SDE of the ‘demons’ algorithm at voxel i is then defined by

$$\Vert {\overrightarrow{u}}_i^{\text{OFM}}-{\overrightarrow{u}}_i^{\text{TPS}}\Vert =)\stackrel{\_}{{\left(x_i^{\text{OFM}}-x_i^{\text{TPS}}\right)}^2+{\left(y_i^{\text{OFM}}-y_i^{\text{TPS}}\right)}^2+{\left(z_i^{\text{OFM}}-z_i^{\text{TPS}}\right)}^2},$$ (5)

whose distribution over a 3D imaging domain is a standard error image (SEI).

From (5), the SDEs of nine ‘demons’ registrations in figure 2 can be calculated at each voxel. The resultant SEIs are illustrated in figures 3(a)–(c) for the case of the σ = 1.3 in the ‘demons’ algorithm. The UE images (UEI) of the ‘demons’ registrations are shown in figures 3(d)–(f). Recall that there are some distortions observed at the middle part of the image (figure 2, φ₁: σ = 1.3). While it is hard to identify the distortions from the warped images, especially inside the prostate, these errors are clearly illustrated in both the SEIs (figure 3(a)) and the UEIs (figure 3(d)). The similarities between the SDE and the UE for the three registrations are demonstrated in figure 3, and the averaged ratio k between the two types of error representations in the region of the prostate is 0.63 over three registrations φ_i, i = 1, 2, 3, with σ = 1.3.

Figure 3.

Top row: the SDE of the ‘demons’ registrations φ₁, φ₂, φ₃ with Gaussian kernel (σ = 1.0); bottom row: the corresponding UE images.

For the three different qualities of ‘demons’ registrations, it can be observed that when σ = 1, their registration instances are poorly performed (figure 2, column 2), especially for φ₁. This is reflected in their SDEs (figure 4(a)). Their calculated UEIs are shown in the bottom row of figure 4, and the averaged ratio k between SEIs and UEIs over the three registrations is 0.32 in the region of the prostate.

Figure 4.

Top row: the SDE of the ‘demons’ registrations φ₁, φ₂, φ₃ with Gaussian kernel (σ = 2.0); bottom row: the corresponding UE images.

For the three ‘demons’ registrations φ_i, i = 1, 2, 3, with σ = 2.0, their SDEs are shown in the top row of figure 5, and the UE is calculated with the UEI illustrated in the bottom row of figure 5. Their averaged ratio k between SEIs and UEIs is 0.76.

Figure 5.

Top row: the SDE of the ‘demons’ registrations φ₁, φ₂, φ₃ with Gaussian kernel (σ = 2.0); bottom row: the corresponding UE images.

In figures 3–5, some similarities between UEI and SEI can be observed. The TPS registration works well in the region surrogated by the 12 control points (Zhong et al 2007), contrasting to the entire imaging domain. Consequently, in the surrogated region, the SDEs of the ‘demons’ registrations with respect to TPS simulations can faithfully reflect the displacement discrepancy of the ‘demons’ DVF. Out of this region, the fidelity of the TPS displacement references with respect to the physical deformation could be reduced. This result will be supported in the next section by the study which shows that SEI and UEI have a different degree of similarity inside and outside the prostate.

3.4. Similarity between SEI and UEI

A comparison of figures 3-5 suggests that there is a similarity between SEI and UEI. In the UE calculation, when Young's modulus is set to 1 kPa, the mean value of UEIs could be three times higher than that of SEI. To quantify the similarity between the two types of error distributions, we use their Pearson correlation coefficient defined by

$$\tau (\text{SEI},\text{UEI})=\sum \frac{(X(i)-\overline{X})(Y(i)-\overline{Y})}{{\sigma }_X{\sigma }_Y}$$ (6)

where X represents a standard error image and Y represents a UE image. X̄ and Ȳ are their means, and σ_X and σ_Y are their standard deviations, respectively.

Recalling that in the TPS interpolations, the prostate is surrogated by 12 points, the TPS warping simulations are more objective or have higher fidelity in the region of the prostate than in any other place. This observation suggests that the similarity between SEI and UEI should be maximized in the region of prostate. To demonstrate this point, we generate a bitmap mask of the prostate derived from its contour in its treatment plan, and then calculate the correlation coefficients of SEI and UEI within the prostate as well as in the whole image domain. The calculated τ values for the three pairs of SEI and UEI are shown in table 1.

Table 1.

The means of SEI and UEI for different ‘demons’ registrations are calculated over the prostate as well as the whole image domain.

	φ1		φ2		φ3
τ (SEI, UEI)	Prostate	Image	Prostate	Image	Prostate	Image
σ = 1.0	0.882	0.212	0.718	0.481	0.638	0.490
σ = 1.3	0.776	0.552	0.770	0.573	0.659	0.548
σ = 2.0	0.729	0.422	0.525	0.235	0.512	0.354

The results in table 1 show a high similarity between the two kinds of error representations, especially inside the prostate. This parallel results from the high fidelity of the TPS warping at the prostate. From table 1, the registrations with σ_i = 1.3 in general have a high similarity between the UE and the SDE, whereas the least similarity over the entire imaging domain appears in the case of the registration φ₁, σ = 1.0.

4. Evaluation of dose reconstruction error in clinical settings

The correlation coefficient values in table 1 illustrate a high similarity between registration displacement error and UE. Consequently, we can make a linear approximation to the relation between the two types of error representations. This approximation allows the size of the domain of integration Δ(q₁) defined in section 2 to be quantified by δ_φ(p), theUE of φ at p.

4.1. Measurable dose reconstruction error in clinic

In clinical cases, image registration for IGRT is performed in 3D imaging domains. Suppose Δ(q₁) is defined as a cube of the side length 2kδ_φ(p) with the center q₁ = φ(p). The physical target q₀ of p, represented as q₀ = φ₀(p), is then located within Δ(q₁). From the simulation in the previous section, the coefficient k, estimated as the ratio between the mean of SEIs and the mean of UEIs, is about 0.32–0.76, while its exact value for clinical registrations may require further investigations.

Similar to (3), the discrepancy of the 3D dose reconstruction can be expressed as

$$\delta D^{(\mathit{\varphi })}(p)={\mathit{\int }}_l\frac{\partial D^{(\mathit{\varphi })}}{\partial l}(s)\text{d}s$$ (7)

where the line integral path l is an interval from q₀ = φ₀(p) to q₁ = φ(p), which satisfies |l| = |kδ_φ(p)|. From the definition of Δ(q₁), it can be seen that l ⊂ Δ(q₁), though the exact direction of l is still unknown. To address this issue, (7) is converted to δD^(φ)(p) = g^(φ),^l)(s₀)|kδ_φ(p)| based on the integral mean value theorem, where g^(φ,l)(s₀) is the mean value of $\frac{\partial D^{(\mathit{\varphi })}}{\partial l}(s)$ on l. An approximation of g^(φ,l)(s₀) is calculated as the average g̃(φ, Δ(q₁)) of the means of $\frac{\partial D^{(\mathit{\varphi })}}{\partial x},\frac{\partial D^{(\mathit{\varphi })}}{\partial y},\frac{\partial D^{(\mathit{\varphi })}}{\partial z}$ over Δ(q₁). Consequently, (7) is written as

$$\delta D^{(\mathit{\varphi })}(p)=\stackrel{\sim }{g}(\mathit{\varphi },\Delta (q_1))|k{\delta }_{\mathit{\varphi }}(p)|.$$ (8)

For the implementation convenience, Δ(q₁) is translated to a local domain Ω = [0, M, 0, M, 0, M] such that any point {x, y, z} in Δ(q₁) is shifted to {x − x(q₁) + M/2, y − y(q₁) + M/2, z − z(q₁) + M/2} where M is set to 48 mm. With the large value of M, Ω is able to cover the translated Δ(q₁) for any given q₁. The translated domain is employed for calculating the mean of all the dose gradients in Δ(q₁) for each q₁. Next, we will demonstrate that the definition of (8) is comparable to a contour-based dose error evaluation.

4.2. Contour-based evaluation of dose reconstruction error

For the validation of DIR, mathematical simulation is often employed as a reference frame. Its advantage is that when an image registration is performed on the pair of the referenced source and target images, its DVF can be compared with the referenced mapping voxel by voxel. The mathematical simulation could be derived from a finite element simulation or another registration result. However, these simulations are still limited in their fidelity to a physical deformation, which may prevent its service as an objective reference frame. For example, within the TPS-simulation frame described in section 3, the ‘demons’ registrations may have different realism when they are evaluated inside or outside the prostate. This possibility is consistent with the high similarity (correlation coefficient) between SEI and UEI when the region for their comparison is restricted within the prostate volume instead of the whole imaging domain.

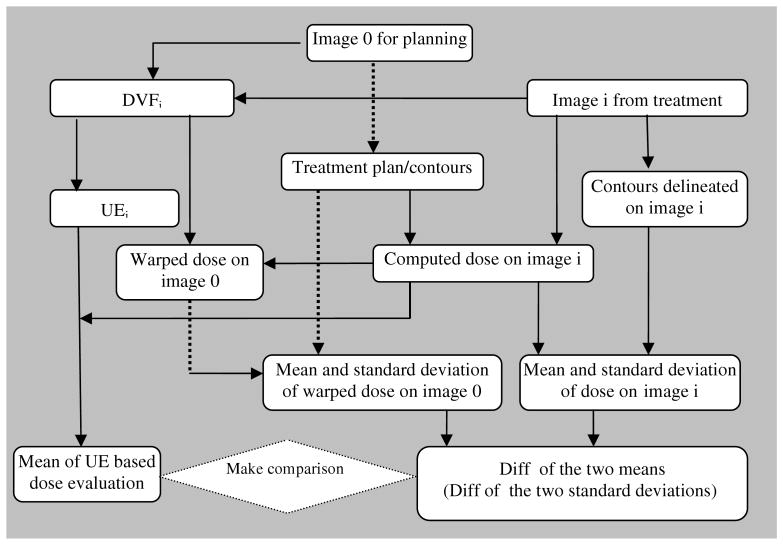
To avoid errors potentially introduced from any inaccurate simulation frame, we next employ a contour-based evaluation approach to demonstrate that the definition of (8) can characterize the dose accumulation error. Ten fractionated CT images are used in this study. The primary image is named as image 0, used for treatment planning. Images 1-9 are obtained in the subsequent treatments. The error in the accumulated dose resulting from the warping operation will be evaluated as follows (figure 6).

Figure 6.

A procedure to compare the UE-based dose accumulation error with contour-based evaluation.

An IMRT treatment plan is first developed on image 0 with contours delineated by an experienced physician. The dose grid size is 4 × 4 × 4 mm³, and the planning dose is calculated and denoted by D⁰. The primary CT image in the IMRT plan is then replaced by each of the nine treatment CT images, respectively, while the beam settings are unchanged. With an updated Image i, i = 1,…, 9, the dose distribution Dⁱ is calculated as the delivered dose for fraction i. On each of the nine treatment images, the physician delineates prostate contours and expands them 10 mm on each direction to form target contours, the same way as the planning target volume (PTV) was generated for treatment planning. These contours drawn on image i, i = 0, 1,…, 9, is named target contour i and denoted by Cⁱ. Using these contours Cⁱ, we can measure the mean ε(Dⁱ, Cⁱ), and standard deviation σ(Dⁱ, Cⁱ) of the delivered doses Dⁱ inside the contour Cⁱ, i = 1,…, 9.

Next, we make DIRs from the planning image to the treatment image i (i = 1,…, 9), again using ITK ‘demons’ algorithm. The standard deviation of its Gaussian kernel is set to σ = 1.3. Using the DVFs generated from these registrations, we warp the dose distribution Dⁱ back to the planning image based on the procedure described in section 2. The reconstructed dose distributions are named as w(Dⁱ), and consequently the mean ε(w(Dⁱ), C⁰) and standard deviation σ(w(Dⁱ), C⁰) of the warped dose w(Dⁱ) located in the contour C⁰ can be calculated.

4.3. Results of contour-based evaluation

Figure 7(a) shows the DVHs of the doses delivered in the first three fractions and measured in Cⁱ, i = 1, 2, 3. Since C¹ is more closely aligned to C⁰ than C² and C³, the DVHs in figure 7(a) show that fraction one has a better dose coverage over Cⁱ than any other fraction. In figure 7(b), the delivered doses are warped back to the planning image and measured in C⁰. Note that the warping resultant dose is not expected to be equal to the planned dose. Instead, a high-fidelity warping should keep a similar DVH distribution between the delivered dose and the warped dose. In figures 7(a) and (b), it can be observed that the DVH of fraction one has a large variation before and after the dose warping, which means that the dose of fraction one is poorly warped.

Figure 7.

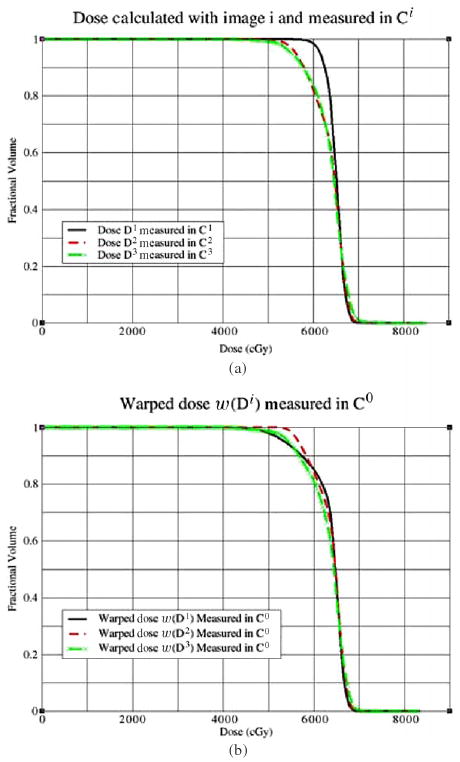
(a) Dose calculated with Image i, i = 1, 2, 3, is measured in its corresponding Cⁱ; (b) dose calculated on image i is warped back to the planning image and measured in C⁰.

Although a treatment plan, such as the hypothetical plan used for this study, is usually delivered over 28 fractions, we only have nine acquired CT images in this study. For each image, the mean of the delivered doses measured in Cⁱ and the mean of the warped doses measured in C⁰ are compared in figure 8(a). Their corresponding standard deviations are shown in figure 8(b). The largest discrepancy between the two criteria occurs at images 1 and 8. While the mean dose of image 3 has the largest deviation from the planned dose, its warping operation has a high fidelity.

Figure 8.

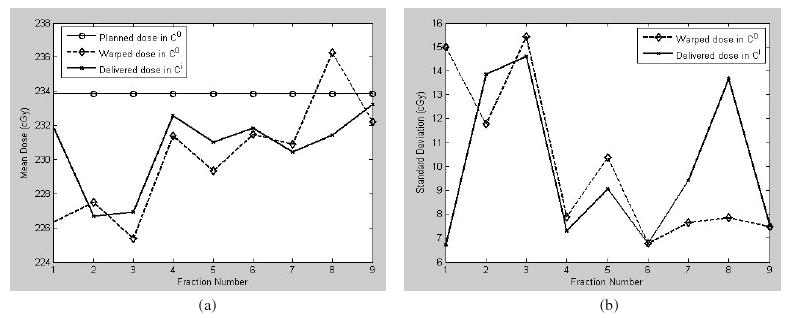
The doses (cGy) calculated from the nine treatment images are measured in Cⁱ, and their warped doses are measured in C⁰. Their means are illustrated in (a), and their standard deviations are shown in (b).

The mean and standard deviation of the dose distributions from the above calculation have quantified the dose delivered to each given anatomic structure, especially the treatment volume. Their changes before and after warping should be limited to a small range for an ideal warping operation. Here, the dose delivered to each physical point is assumed to be invariant in the dose-warping operation. Consequently, the mean and standard deviation of the delivered dose in a physical domain should not change if the dose warping is committed to the physical deformation. Otherwise, their changes, defined as

$$E_{\epsilon }^i=\left|\epsilon (w(D^i),C^0)-\epsilon (D^i,C^i)\right|,\text{and}{E}_{\sigma }^i=\left|\sigma (w(D^i),C^0)-\sigma (D^i,C^i)\right|,$$ (9)

respectively, could reflect the quality of the dose-warping performance. The explicit values of $E_{\epsilon }^i$ and $E_{\sigma }^i$ over the nine warping operations are listed in table 2.

Table 2.

The dose reconstructions errors from ‘demons’ with σ = 1.3 are evaluated with different criteria.

(cGy)	w1	w2	w3	w4	w5	w6	w7	w8	w9
δφi	2.9	1.2	0.6	1.0	1.4	1.4	1.2	2.4	2.0
ε̃(Di,φi)	6.4	3.9	2.0	2.8	4.1	3.6	2.8	5.3	4.5
$E_{\epsilon }^i$	5.5	0.82	1.58	1.21	1.70	0.38	0.46	4.85	1.01
$E_{\sigma }^i$	8.29	2.07	0.82	0.57	1.31	0.01	1.74	5.82	0.03

4.4. UE-based evaluation of dose accumulation error

After the contour-based evaluation in table 2, we next turn to the UE to calculate the UE-based dose-warping errors. We create a mesh consisting of 132 K nodes and 780 K tetrahedrons, covering the whole image domain (46 × 46 × 27 cm³). The displacements of each node are obtained from the interpolation of its corresponding DVF. Because the mesh consists of a large number of elements, its global stiffness matrix may contain up to 396 K × 396 K entries. It is impossible to create such a large matrix to hold all the entries. Actually, for a 3D linear tetrahedral mesh, each row in its stiffness matrix contains only about 24 nonzero entries, where each node is assumed to have, at most, 24 adjacent nodes. This specification allows the sparse matrix to be written as a 50 MB array during the assembling process. With the code implemented in C++, the resultant program can be executed on a desktop computer.

For the nine ‘demons’ registrations φ_i which are from image 0 to image i, the UE δ_φi is calculated from its definition in equation (4). Figure 9(a) is image 1 and (b) is the output image from image 0 warped by φ₁. The obvious distortions detected from the two images are in the rectum and at the anterior of the prostate. These distortions are clearly demonstrated as the registration error in the term of UE in figure 9(c).

Figure 9.

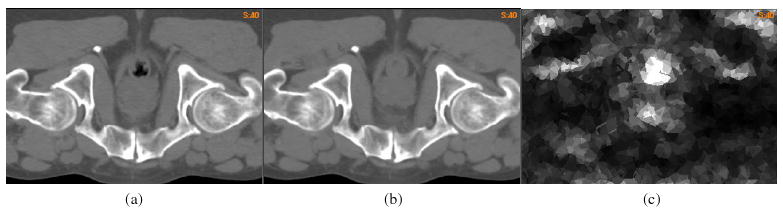
(a) Image 1 obtained from fraction one, (b) the output image of the registration φ₁ from image 0 to image 1 and (c) the UE δ_φ1 of the registration φ₁.

To get the UE-based dose error evaluation δD^(φ_i)(p), the dose gradient ∇Dⁱ, i = 1,…, 9, is calculated and averaged over the registration error domain Δ(q₁). The averaged value is multiplied by the corresponding kδ_φi (p) to get the dose-warping discrepancy δD^(φ_i)(p) at the voxel p.

The voxel-based dose error estimate can be used for further dosimetry analysis. For example, the potential maximum dose at a point p can be calculated as D^(φ_i)(p) + δD^(φ_i)(p) and incorporated with contour-based dose evaluations. The potential minimum dose at p can be similarly evaluated. In figure 10(a), the PTV contour (thick) is illustrated on the planning image, and the thin curves are the 90% isodose warped from the delivered dose D^(φ_i) at fraction 1. In figures 10(b) and (c), the warped-dose distribution is corrected by adding and subtracting the dose-warping discrepancy δD^(φ_i)(p) at each point p, respectively, to estimate the potential maximum or minimum of the delivered dose. Consequently, the 90% isodose curves (thin) are enlarged (maximum dose) or shrunk (minimum dose), with the obvious differences illustrated by the PTV contour in figures 10(b) and (c).

Figure 10.

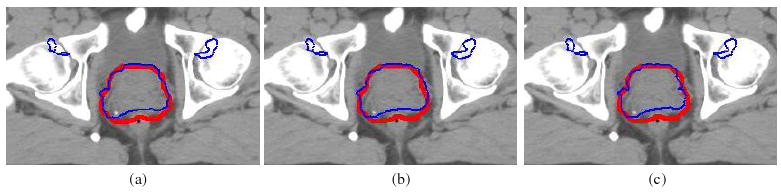
(a) PTV (thick) versus the 90% warped isodose (thin), PTV (thick) versus the 90% warped isodose (b) added or (c) subtracted by the UE-based dose-warping error (thin).

When the UE-based dose discrepancy δD^(φ_i)(p) is calculated within the PTV contour C⁰, we get its mean dose error ε̃_{(Dⁱ, φi)}, which can be compared with $E_{\epsilon }^i$ and $E_{\sigma }^i$. Their consistency will be demonstrated through the nine warping operations.

4.5. Comparison between two types of evaluations

Before making numerical comparison between the two types of dose-warping evaluations presented, respectively, in sections 4.3 and 4.4, we first study their theoretical relationship. From its definition, we know that $E_{\epsilon }^i$ is the difference between the mean of the warped dose on the C⁰ and the mean of the delivered dose on Cⁱ, i = 1,…, 9, i.e.,

$$E_{\epsilon }^i=\left|\frac{1}{\Vert {\Delta }_{C^0}\Vert }\sum _{p\in {\Delta }_{C^0}}({\mathit{\varphi }}_i^{-1}(D^i))(p)-\frac{1}{\Vert {\Delta }_{C^i}\Vert }\sum _{q\in {\Delta }_{C^i}}{D}^i(q)\right|,$$

where ‖ΔC⁰‖ represents the volume of the target contour C⁰ on the planning image, and ‖ΔCⁱ‖ represents the region bounded by the contour Cⁱ in the ith CT image. Suppose the true physical deformation map for the ith image is denoted by ${\mathit{\varphi }}_0^{(\mathit{\text{i}})}$. If the target volume in C⁰ is preserved during the physical deformation and the manually drawn contours are accurate, then $\Vert {\Delta }_{C^0}\Vert =\Vert {\mathit{\varphi }}_0^{(i)}({\Delta }_{C^0})\Vert =\Vert {\Delta }_{C^i}\Vert$. From the notations used previously, suppose $q_0^{(i)}={\mathit{\varphi }}_0^{(i)}(p)$ and $q_1^{(i)}={\mathit{\varphi }}_i(p)$, where the point p ∈ T, ${\mathit{\varphi }}_0^{(\mathit{\text{i}})}$ and φ_i represent the physical deformation and the DVF mapping of the ith image registration, respectively. Then, from the dose-warping approach specified in section 2, we have

$$\begin{array}{l}{E}_{\epsilon }^i=\left|\frac{1}{\Vert {\Delta }_{C^0}\Vert }\sum _{p\in {\Delta }_{C^0}}({\mathit{\varphi }}_i^{-1}(D^i))(p)-\frac{1}{\Vert {\mathit{\varphi }}_0^{(i)}({\Delta }_{C^0})\Vert }\sum _{q_0^{(i)}\in {\mathit{\varphi }}_0^{(i)}({\Delta }_{C^0})}{D}^i(q_0^{(i)})\right|\\ \le \frac{1}{\Vert {\Delta }_{C^0}\Vert }\sum _{p\in {\Delta }_{C^0}}\left|D^i(q_1^{(i)})-D^i(q_0^{(i)})\right|.\end{array}$$ (10)

When the unknown right-hand side of (10) is approximated by ε̃_(Dⁱ,φi), an average of δD^(φ_i)(p) over the volume of C⁰, it is expected that

$$E_{\epsilon }^i\le {\stackrel{\sim }{\epsilon }}_{(D^i,{\mathit{\varphi }}_i)}.$$ (11)

This inequality provides an additional criterion to estimate the lower bound of k in equation (8) for clinical settings. In addition, the values on both sides of (11) should tend to zero if the DIR is accurate.

Table 2 lists theUE δ_φi, the UE-based dose error evaluation ε̃_(Dⁱ,φi), and the contour-based discrepancy evaluations of means and standard deviations measured in C⁰ for the nine dose-warping operations. In this treatment plan, the prescribed dose is 234 cGy per fraction to 100% of the PTV volume. For the registrations between these clinical images, the parameter k in (8) is set to 0.54, which is at the middle of the range (0.32–0.76) derived from the TPS simulations in section 3.3. The average ratio of ε̃_(Dⁱ,φi) to the prescribed dose on C⁰ over the nine fractions is 1.68% whereas the average ratio for $E_{\epsilon }^i$ is 0.9%. This result is consistent with the inequality of (11).

The results in table 2 are plotted as figure 11. It can be observed that the UE-based dose-warping discrepancy in general is consistent with the contour-based evaluations of mean and standard deviation (figure 11(a)). The largest warping discrepancies at fractions 1 and 8 can be identified from both the evaluation criteria.

Figure 11.

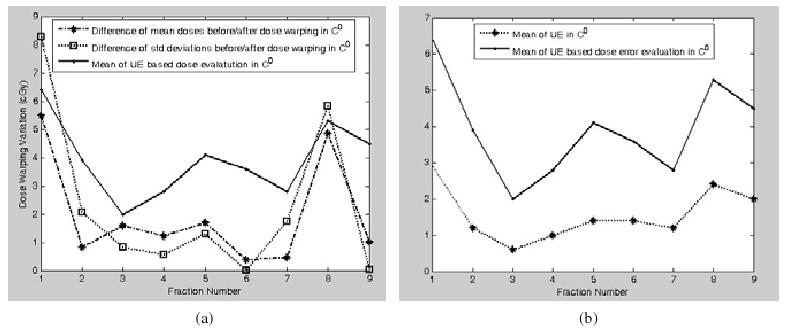
(a) Dose-warping errors of nine fractions are represented as the differences of mean doses, the differences of standard deviations before and after dose warping, and the means of UE-based evaluation (8) in target contour 0; (b) the relation between the UE and the UE-based dose evaluation in the target contour C⁰ is illustrated.

Considering that ε̃_(Dⁱ,φi) and $E_{\epsilon }^i$ are two different error indicators, their difference is not expected to be constant for all the instances. They satisfy only the relation of $E_{\epsilon }^i\le {\stackrel{\sim }{\epsilon }}_{(D^i,{\mathit{\varphi }}_i)}$, demonstrated in figure 11(a). The UE and its corresponding dose error evaluation are illustrated in figure 11(b). There is no surprise that the image registration error is exaggerated when it is combined with dose distributions.

5. Discussion

Dose reconstruction is used to add the delivered dose distributions according to the physical deformation of the tissue. Usually the physical deformation cannot be measured directly. Deformable image registration may provide an approximate solution, but the accuracy of the approximation at each point is still unknown. Because of the lack of a general method to measure the displacement error of the approximation, the concept of UE was proposed and developed in our previous work (Zhong et al 2007) to quantify the local inconsistency of the DVF mapping, which may directly contribute to the displacement error.

In this paper, we have exploited the quantitative relation between UE and SDE. The similarities of their 3D distributions characterized by Pearson correlation coefficient are calculated within simulated reference frames. Their high similarities suggest that SDE can be linearly approximated by UE with the linear coefficient k quantifiable with simulated reference frames. The exact value of k, which is dependent on the absolute value of UE, is proportional to Young's modulus of the underlying mechanical model. When Young's modulus is set to one, the range of k is between 0.32 and 0.76 in our simulated reference frames. While differences in the values of k exist, they are generally in the same range, and therefore the resultant UE-based dose error assessment is able to serve as a reference. However, for clinical applications, the exact value of k associated with a given Young's modulus may need further investigation.

When the discrepancy of a given DIR at a point p is approximated by its UE, the dose-warping error at p can be calculated as the product of the mean of the dose gradients over its local registration error domain and the UE-based estimate of the registration displacement error. Different from the contour-based evaluation of the dose-warping errors, which calculates the differences of means or standard deviations between the delivered dose and its warped dose at an anatomic level, the UE-based dose-warping evaluations can be performed at individual voxels. The two different error indicators derived from nine registration instances satisfy equation (11), as expected.

To calculate the UE-based dose-warping discrepancy, the mean of dose gradients over the integral path l is substituted by their mean in the voxel's registration error domain. This approximation therefore gives each voxel only an averaged dose-error estimate. In addition, the accuracy of the dose-warping evaluation may depend on the factors of the parameter k, Young's modulus and mesh grid resolution. In this paper, Young's modulus E₀ of the underlying mechanical model is set to 1 kPa, a low bound for soft tissue used in the literature (Sarvazyan et al 1998, Greenleaf et al 2003). This value could be different from the accurate modulus of each organ in the images. However, if we use the same Young's modulus in the models for all of the registration instances, the resultant k values should be equivalent to each other because k is proportional to E₀. Consequently, the linear coefficient k obtained from the registration between simulated reference frames (section 3) can be used as a reference in the calculation of dose-warping errors in clinical settings (section 4).

6. Conclusion

Dose reconstruction is fundamental to IGRT, and its quality depends on the underlying DIR. In this paper, the correlation between the registration displacement errors and their UE has been established and validated within TPS-simulated reference frames. Their similarity reaches 88%. While the similarity could vary among different registration instances, it provides a method to understand and estimate the registration error in general and could be used in various clinical applications. The advantage of the UE-based assessment is that it can be automatically performed at each voxel without the need for knowledge of the ground truth in tissue deformation.

With this relation, the dose reconstruction discrepancy induced from the deformable registration error can be defined and calculated at each voxel. Although this method requires further investigation, the initial results from the validation of nine clinical registration instances show that the UE-based assessments of the dose reconstruction discrepancies are generally consistent with the contour-based mean dose evaluations.