One factor underlies individual differences in auditory informational masking within and across age groups

Abstract

Masked threshold for a pure-tone signal can be substantially elevated whenever the listener is uncertain about the spectral or temporal properties of the masker, an effect referred to as auditory informational masking. Individual differences in the effect are large, with young children being most susceptible. When masker uncertainty is introduced by randomizing the frequencies of a multitone masker on each presentation, the function relating a child's pure-tone signal threshold to the number of masker components is found to be substantially elevated above that of most adults. The age effect and the individual differences among adults are not well understood, though a difference in the shapes of the masking functions suggests that different detection strategies may be involved. The present study reports results from a principal components analysis of informational masking functions obtained from 38 normal-hearing children ranging in age from 4 to 16 years and 46 normal-hearing adults ranging in age from 19 to 38 years. The premise underlying the analysis is that if different detection strategies are involved, they should add independent sources of variance to the masking functions. Hence, more than one principal component (PC) should be required to account for a substantial proportion of the variance in these functions. The results, instead, supported the operation of a single underlying strategy with all but 17% of the variance accounted for by the first PC within and across age groups. An analysis of variance on the first two PCs showed that only the first changed with age, and a cluster analysis of the masking functions showed complete separation of clusters along this PC for all but 1 listener. The results are taken to suggest that large individual differences in informational masking at all ages reflect differences in the extent to which masker uncertainty adds variance to the decision variable of an otherwise optimal decision strategy.

It seems a common observation that young children are more easily distracted than adults by novel or unexpected noises occurring in their surroundings. In the classroom and in other settings requiring selective listening, such noises can be especially disruptive because they interfere with the processing of relevant acoustic signals. Informational masking is the term often used in the psychoacoustics literature to describe this type of interference. By definition informational masking is the elevation in signal threshold resulting from masker novelty or uncertainty (Watson, Kelly, & Wroton, 1976). The elevations in threshold can be quite large. When masker uncertainty is introduced by varying the frequencies and levels of masker components at random on each presentation, the amount of informational masking of a pure-tone signal can be as much as 50 dB for well-trained adult listeners (Neff & Callaghan, 1987, 1988; Neff & Green, 1987; Oh & Lutfi, 1998). For preschool-age children performing in very similar conditions it can be in excess of 70 dB (Oh, Wightman, & Lutfi, 2001).

The reason for such sizable effects and for children's apparent greater susceptibility to informational masking is not well understood. Unlike more commonly studied forms of masking involving fixed-frequency or broadband noise maskers, the amount of informational masking is not simply related to energetic factors, as would be predicted by traditional filter models of the auditory periphery (see Fletcher, 1940; Patterson, 1976). Large amounts of informational masking are observed when there is little or no masker energy in close temporal or spectral proximity to the signal. And, while energetic factors generally predict a monotonically increasing amount of masking with increasing number of masker components, informational masking often varies nonmonotonically with the number of masker components, first increasing and then decreasing as the number of components exceeds 10–20 (Neff & Green, 1987; Oh & Lutfi, 1998).

By far the greatest challenge for understanding, however, is the enormous variation in the amount of informational masking that is observed from one individual to the next. Neff and Dethlefs (1995) reported masked thresholds spanning a range of 59 dB across 49 adult listeners who, over the course of several studies, participated in similar conditions involving the detection of a 1.0-kHz tone in the presence of random-frequency multitone maskers. Oh et al. (2001) noted similar variability among 8 preschool children, reporting informational masking for the preschool children to be on average 20 dB greater than that for 8 adults obtained under identical conditions. Similar adult–child differences have also been reported in the masking effectiveness of a single random-frequency distractor tone (Allen & Wightman, 1995). The magnitude of these differences can be appreciated by comparing them with findings from traditional tone-in-noise masking studies, where the range of masked thresholds for adults rarely exceeds a few decibels (Patterson, Nimmo-Smith, Weber, & Milroy, 1982) and where masked thresholds of children are only a few decibels greater on average than those of adults (Oh et al., 2001; Wightman & Allen, 1992).

In addition to the differences in the overall magnitude of the effect, there are also clear individual differences with regard to the shapes of the informational masking functions. Neff, Dethlefs, and Jesteadt (1993) identified two groups of listeners on the basis of the shape of their masking functions. The so-called high-threshold group exhibited the characteristic nonmonotonicity of masking with increasing number of masker components. The low-threshold group showed a monotonically increasing function that asymptoted at the level of masking produced by an equal-energy broadband noise (also see Oh & Lutfi, 1998). Oh et al. (2001) noted similar differences in the shape of the masking functions for preschoolers and adults. They identify all 8 of their preschool-age children as high-threshold listeners, and all but 3 of their 8 adults as low-threshold listeners.

Understanding individual differences in informational masking is likely a key to understanding informational masking and the reason why children appear to be particularly susceptible to this type of interference. Yet, with the exception of the few studies noted above, there has been little consideration of specific factors that might contribute to the individual differences. The fundamental question has been whether such large individual differences imply the use of qualitatively different detection strategies by listeners. This possibility was implied early on by Watson et al. (1976) and appears to be favored by Neff and Dethlefs (1995). Neff and Dethlefs suggest that the shape of the masking function for low-threshold listeners is consistent with the strategy of detecting an energy increment at the output of an auditory filter centered on the signal, as is given by the traditional view. They suggest, however, that the nonmonotonicity in the function for high-threshold listeners reflects a different process, one in which the listener identifies the signal as the one component in the complex having the maximum level. In support of this view they noted that in the region of the nonmonotonicity the level of the signal at threshold is often close to the level of individual masker components. Although appearing to favor this view, Neff and Dethlefs also noted that their listeners failed to cluster at different performance levels, a result that might have been expected if different detection strategies had been involved. Oh and Lutfi (1998) have more strongly questioned the need to infer different detection strategies. They have pointed to predictions of a model that has had some success in accounting for past results of informational masking studies (see Lutfi, 1993). Like traditional energy detection models, the component relative entropy (CoRE) model assumes that detection is based on the energy output of an auditory filter centered at the signal frequency. Unlike traditional models, it allows for the possibility that additional filter outputs contribute to the decision when maskers are uncertain. The number and frequency range of the additional filters are presumed to vary from one individual to the next, but in each case the effect is to elevate threshold by adding variance to the energy detection process. In this way the model attempts to account for individual differences within the context of a single detection strategy.

To date there is no compelling evidence to rule out either view. The argument favoring different detection strategies is based largely on the difference in the shape of the masking functions for high- and low-threshold listeners. But the available data are insufficient to rule out the possibility that a single detection strategy might account for the differences in shape. In their seminal study identifying these two groups, Neff et al. (1993) reported data from only 4 adults in each group and gave only the average masking functions of the listeners within each group. Oh and Lutfi (1998) reported individual masking functions from 11 adult listeners, and although the CoRE model provided reasonably good fits to these functions, only 2 of the listeners could be identified as low-threshold listeners. Current data are also inadequate to evaluate whether the apparent greater susceptibility of children to informational masking is due to different detection strategies adopted by children relative to most adults. Oh et al. (2001) reported individual masking functions from only 8 preschoolers, and these functions were far too variable in shape to warrant conclusions regarding differences in detection strategies without additional data from both children and adults.

The goal of the present study, therefore, was twofold: to provide more extensive documentation of individual differences in informational masking, including adult–child differences, than has been provided by past studies, and to evaluate two divergent views of the factors responsible for these differences. For this purpose we analyzed complete masking functions from 84 listeners ranging in age from 4 to 38 years who performed under nearly identical conditions. Without focusing on specific detection strategies, we tested the possibility of one or more detection strategies by using a principal components analysis (PCA) to evaluate whether the variance in the masking functions arises from one or more underlying sources. PCA is a statistical analysis that is often used in cases where one wishes to represent the underlying structure of a highly variable set of correlated measures (for specific applications in psychoacoustics see Kistler & Wightman, 1992; Pols, van der Kamp, & Plomp, 1969; Zahorian & Rothenberg, 1981). The goal is to represent measures (individual masking functions in the present case) as a weighted sum of a small number of underlying basis functions, each representing an independent source of variance contributing to the total variance among measures.¹ The principal components (PCs), the collections of weights associated with each basis function, are then used to evaluate the relative importance of different factors in describing the total variance across measures.

In applying PCA to the question of multiple detection strategies, our premise is that qualitatively different detection strategies should add largely independent sources of variance to the masking functions and so should require multiple PCs to account for the variance in these functions. The premise is justified by the primary argument made in favor of multiple detection strategies—that different detection strategies should produce differently shaped masking functions. It is also justified in that there would be little practical value in positing multiple detection strategies that accounted for the same sources of variance—that is, that made identical predictions for the data. Hence, if adult–child differences result from real differences in the detection strategies adopted by children and adults, then at least two PCs should be required to account for these differences, one for children and the other for adults. On the other hand, if children and adults employ the same detection strategy, but merely with different degrees of efficiency, then the variance in the masking functions both within and between age groups should be well described by a single PC.

Method

Listeners

All listeners had normal hearing with pure-tone air conduction thresholds less than 15 dB HL (American National Standards Institute, 1989) at the octave frequencies from 250 to 4000 Hz. The listeners were divided into five groups on the basis of their age and details of the procedure in which their data were collected. Details of each group are as follows and are summarized in Table 1.

Table 1. Summary of Listener Groups.

		No.	Ages	Gender
Group	Description	Listeners	(Yrs.)	(M/F)	Procedure
1	Adult (A2IFC)	30a	19–38	6/24	Adaptive 2IFC
2	Adult (staircase)	16b	19–30	3/13	Cued staircase
3	Late school age	16a	11–16	6/10	Cued staircase
4	Early school age	12a	6–10	5/7	Cued staircase
5	Preschoolers	10b	4–5	7/3	Cued staircase

^aIncludes 11 listeners from Oh and Lutfi (1998).

^bIncludes 8 listeners from Oh, Wightman, and Lutfi (2001).

Group 1: Adults (A2IFC)

The 30 listeners in this group ranged in age from 19 to 38 years; 6 were males and 24 were females. All were students at the University of Wisconsin, Madison, and all were paid an hourly rate for their participation. The data from 11 of these listeners were taken from the study of Oh and Lutfi (1998). The data from the remaining 19 listeners were collected under identical conditions, though these listeners received somewhat less practice before data collection: a few dozen trials on each condition versus hundreds of trials for the Oh and Lutfi listeners. Comparison of the mean and range of thresholds from these listeners revealed no clear effect of practice. Signal thresholds for this group were obtained using an adaptive two-interval, forced-choice (A2IFC) procedure, the details of which are described in the Procedure section.

Group 2: Adults (staircase)

The 16 listeners of this group ranged in age from 19 to 30 years; 3 were males and 13 were females. All were employees or students of the University of Wisconsin, Madison, and all were paid at an hourly rate for their participation in the study. Half of these listeners were from the study of Oh et al. (2001), and the remaining half were run in conditions identical to those of that study. No practice was given except for a few trials to ensure that listeners understood the task. This group of adult listeners differed primarily from the Group 1 adults in that signal thresholds were obtained using a cued staircase procedure rather than an A2IFC procedure. Specific details of the cued-staircase procedure are given in the Procedure section. All other procedural differences were quite minor, involving differences in headphones, feedback display, and response collection (see published studies for specific details).

Group 3: Late school-age children

The 16 listeners of this group were aged 11 to 16 years; 6 were males and 10 were females. They were recruited by way of advertisements posted in the Waisman Center, where the research was conducted; hence, many were from families of employees of the Waisman Center. All conditions for this group, including details regarding listener recruitment, payment, and data collection, were identical to those of the Group 2 adults.

Group 4: Early school-age children

The 12 listeners of this group were aged 6 to 10 years; 5 were males and 7 were females. All conditions for this group, including details regarding listener recruitment, payment, and data collection, were identical to those of Groups 2 and 3.

Group 5: Preschoolers

The 10 listeners of this group were aged 4 to 5 years; 7 were males and 3 were females. All listeners of this group were recruited from the Waisman Early Childhood Program, a local preschool program specializing in the teaching of children under the age of 6 years. Eight of these listeners participated in the study of Oh et al. (2001), and the data obtained in that study are used here. All conditions of this group, except for payment, were identical to those of Groups 2, 3, and 4. Instead of cash payment, listeners in this group received coupons that could be redeemed for gifts.

Stimuli

The stimuli were the same for all listeners (see Oh & Lutfi, 1998; Oh et al., 2001). The maskers were multitone complexes for which the frequencies, amplitudes, and phases of individual components varied at random on each presentation. The distribution of component frequencies was uniform over the range of 0.1–10 kHz and excluded the frequencies between 920 and 1080 Hz, the distribution of component amplitudes was Rayleigh, and the distribution of component phases was rectangular. These stochastic properties were selected so that as the number of masker components increased, the multitone maskers would begin to approximate random samples of Gaussian noise, band-pass filtered between 0.1 and 10 kHz, and band rejected between 920 and 1080 Hz. The number of masker components, m, was fixed within blocks of trials but varied across blocks (m = 2, 10, 20, 40, 200, 906, 3,667), the last of these values representing a true 370-msec burst of the filtered Gaussian noise. For m < 3,667, the multitone maskers were created by sampling m frequencies at random from the Fast-Fourier Transforms (FFTs) of Gaussian noise samples. The sampling was done so that no two neighboring frequencies were separated by less than 11 Hz. The multitone masker was then synthesized by means of inverse-FFT of the m randomly selected components. Average total power of the maskers was kept constant at 60 dB SPL regardless of the number of masker components. The signal was a 1000-Hz pure tone. The signal and maskers were gated on and off together with 10-msec, cos² onset/offset ramps for a total duration of 370 msec. All stimuli were computer generated using 16-bit, digital-to-analog conversion (Tucker Davis Technologies DD1) at a sampling rate of 44.1 kHz. Stimuli were presented monaurally through Sennheiser Model HD-520 (Group 1) or HD-414 (Groups 2–5) headphones to individual listeners seated in a double-walled IAC sound-attenuation chamber.

Procedure

Signal thresholds in quiet and in the presence of maskers were obtained using different psychophysical procedures for Group 1 and Groups 2–5:

Adaptive 2IFC (Group 1)

On each trial, two of the random multitone maskers were presented to listeners separated by a 500-msec silent interval. The signal occurred with equal a priori probability in the first or second interval. Listeners indicated by keypress which one of the two intervals they believed contained the signal on each trial. Visual feedback was presented after each response indicating whether the response was correct or incorrect. For two successive correct responses the signal was stepped down in level, and for each incorrect response it was stepped up in level. The initial step size was 4 dB, but was reduced to 2 dB after the third reversal in level. This adaptive procedure converges on the signal level corresponding to the 70.7% point of the psychometric function (Levitt, 1971). A single trial block consisted of a total of 12 level reversals. A single threshold estimate was taken as the average of the last 8 reversal levels. Threshold for each condition was the average of five such threshold estimates obtained from five consecutive trial blocks. Prior to each block of trials the listener was reminded of the signal by having it presented in isolation.

Cued-staircase (Groups 2–5)

The cued-staircase procedure differed from the A2IFC procedure in two respects. First, the listener was reminded of the signal by having it presented it in isolation prior to each trial, rather than merely having it presented prior to each block. Second, the level of signal on each trial was predetermined for each block and did not depend on the listener's response. The starting level was always clearly audible. For the first four trials it was reduced in 8-dB steps, then for the next four trials it was increased in 8-dB steps so as to return to the starting level. This up–down pattern was repeated five times for each trial block. Listeners completed three or more trial blocks for each condition yielding at least 15 trials each for the highest and lowest signal levels, and 30 trials for each intermediate signal level. A logistic function relating percentage of correct responses to signal level was fit to the data for each listener and each condition using a maximum-likelihood criterion (see Allen & Wightman, 1994). The signal level corresponding to the 75% correct point of the logistic function was taken as the threshold for the signal.

Results

Individual Differences in the Masking Functions

Figure 1 summarizes the individual differences in the masking functions obtained for the two groups of adult listeners run in the two different psychophysical procedures. Total masking is expressed as the mean difference in the estimates of masked threshold and quiet threshold in decibels. Error bars indicate 1 SD on either side of the mean. The rightmost point of each function is the total masking produced by the broadband noise (m = 3,667). The dashed curves in each panel represent the masking functions from the “best” and “worst” performing listeners from each group. The data are typical of those reported by Neff and coworkers (Neff & Callaghan, 1988; Neff & Dethlefs, 1995; Neff et al., 1993). Although the amount of masking produced by the broadband noise differed little across individuals, the masking functions for individual adults differed substantially from one another. For the majority of adult listeners the masking functions were nonmonotonic; as the number of masker components increased the total masking first increased and then decreased. For listeners with the lowest masked thresholds the functions appeared monotonic; the amount of masking increased with the number of masker components and eventually asymptoted at a value equal to the amount of masking produced by the broadband noise masker. Neff and Dethlefs reported measures of dispersion across adult listeners for conditions most comparable to those of our Group 1 listeners (see their Table 1), and though they did not obtain complete masking functions for most listeners, their measures compare favorably with ours. Both studies show a progression of increasing variability with decreasing number of masker components. For their 2-component masker Neff and Dethlefs reported a range in masked thresholds for 28 listeners of 59 dB and a standard deviation of 17 dB. For Group 1 listeners our corresponding values for range and standard deviation are 51 and 16 dB. For the broadband noise condition Neff and Dethlefs reported a range and standard deviation of 9 and 2 dB, whereas our corresponding Group 1 values are 15 and 4 dB. Slightly less variability would be expected for Neff and Dethlefs's broadband noise condition since these authors did not band-reject filter around the signal frequency, as was done in the present study (see Patterson, 1976). The pattern of results for Group 2 adults is also comparable to that of Group 1 adults with the exception that average thresholds for 2- and 10-component maskers are lower. Better performance in some conditions is, perhaps, to be expected since the cued-staircase procedure affords many more opportunities to hear the signal in isolation and in the presence of maskers. As noted in the Method section, however, Group 2 listeners also received no practice.

Figure 1.

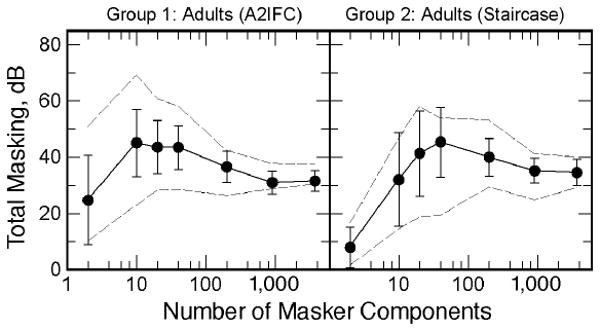
The average total masking (circles) is plotted as a function of the number of masker components for Group 1 (A2IFC) and Group 2 (staircase) adults. Error bars indicate 1 SD on either side of the mean. The rightmost point in each panel gives the amount of masking produced by a broadband Gaussian noise excluding the frequencies between 920 and 1080 Hz. The dashed curves give the data from the individual listeners having on average the highest and the lowest masked thresholds within their group.

Figure 2 summarizes the individual differences in the masking functions for children and adults obtained using the same (cued-staircase) procedure. As before, masked thresholds in broadband noise differed little across individuals. The masking functions for individuals, however, differed substantially both within and across groups. With regard to the effect of age, there was both a replication of earlier results and an important new result. The inclusion of additional listeners to the preschool and adult age groups has not changed the original conclusion reached by Oh et al. (2001)—on average the preschoolers (Group 5) appeared to perform significantly more poorly than adults under identical conditions (Group 2). The new result is that the adult–child differences persist well into the school years with the range of individual differences being greatest during the early school years. Note, in particular, that within the early school-age children the range extended from the best performance of adults to the worst performance of preschoolers. Performance for the late school-age children appears to have been slightly better on average than that for the early school-age group, but the difference is not likely significant given the range of individual differences. Though the youngest member of the early school-age group (age 6 years) gave the worst performance, this performance was essentially matched by one of the oldest members of the late school-age group (age 13.5 years). Two of the younger children (ages 8 and 10 years) also gave the best performance of all school-age children.

Figure 2.

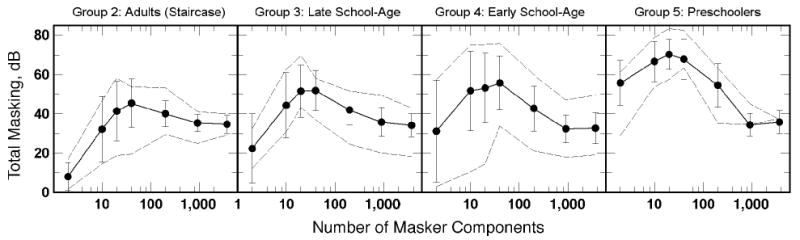
Same as Figure 1 but comparing masking functions for Groups 2–5.

PCA of the Masking Functions

To evaluate the possibility of multiple detection strategies, PCA was applied to determine the relative contribution of independent sources of variance to the shapes of the masking functions. The shape of each function was determined by expressing masked thresholds for each listener relative to the broadband noise masked threshold for that listener, as a difference in decibels. With regard to Figures 1 and 2 this merely has the effect of shifting all functions down so that each has a common intercept of 0 dB at m = 3,667 (broadband noise condition). Normalizing the masking functions in this way eliminates small variations in the intercept due to individual differences in quiet thresholds, and is in keeping with Neff and Dethlefs's (1995) practice of using masked thresholds rather than amount of masking to distinguish among listener groups.² Let M denote the difference in decibels between the masked threshold for the multitone masker and the masked threshold for the broadband noise. Furthermore, let m_l represent the vector of these values corresponding to the normalized masking function for the lth listener. The estimate of m_l resulting from the PCA is then given by

$${\widehat{\mathbf{\text{m}}}}_l={\mathbf{\text{Cw}}}_l+\overline{\mathbf{\text{m}}},$$ (1)

where the matrix C gives the basis functions (represented by discrete values), the column vector w_l gives the PC weights, and m̄ is the mean normalized masking function averaged across listeners. Here the basis function for a given PC is a vector of values representing deviations in decibels from the mean normalized masking function.³ There are six basis functions altogether (given by the columns of C) each having six values (given by the rows of C) corresponding to the six multitone masker conditions. The first basis function (first column of C) is for first PC, the second basis function (second column of C) is for the second basis function, and so forth. The vector w_l gives the weights listener l gives to the six basis functions. Hence, for listener l the normalized masked threshold for the ith multitone masker is given by

$$\begin{array}{cc}{M}_{li}=\sum _k\left(C_{ik}{w}_{lk}\right)-{\overline{M}}_i& k=1,2,\dots ,B,\end{array}$$

where B = 6 is the number of basis functions. In practice, the basis functions are derived from the covariance matrix K, whose entries are the covariances associated with each possible pair of normalized masked thresholds in m_l. Specifically, for i, j th pair the covariance is

$$\begin{array}{cc}{K}_{ij}=\left(1/N\right)\sum _l\left(M_{li}-{\overline{M}}_i\right)\left(M_{lj}-{\overline{M}}_j\right),& i,j=1,2,\dots ,T\end{array}$$ (2)

where N is the number of listeners for each analysis and T = 6 is the number of normalized masked thresholds.

Two PCAs were performed. The first was intended to evaluate the age effect and so included only the adults and children who performed in identical conditions (Groups 2–5, staircase procedure). The second was intended to evaluate whether the factor or factors contributing to the differences across age groups are likely to be the same as those contributing to the differences across individual adults. For this purpose a PCA was performed on the separate group of adults (Group 1, A2IFC procedure). Table 2 summarizes the results of both PCAs in terms of the percent of variance accounted for by each PC in the shapes of the masking functions. The results are nearly identical, with both PCAs identifying a single component with most of the variance in the masking functions. Overall, the first principal component (PC-1) accounts for 83% of the variance, the second (PC-2) 9%, and the remaining four PCs taken together less than 9%. As a check, we also performed the PCAs on the masking functions without subtracting the amount of masking by the broadband noise. The results differed very little. As to be expected, the proportion of variance accounted for by PC-1 decreased slightly and that of PC-2 increased slightly, but the first two basis functions were essentially identical to those resulting from the analysis of the shapes of the masking functions.

Table 2.

Percentage of Variance Accounted for in the Masking Functions for Each PC for Separate Analyses Performed on Groups 2–5 (Staircase Procedure, Adults and Children) and on Group 1 (A2IFC, Adults Only)

	% Variance Accounted for
Principal Component	Groups 2–5 Analysis	Group 1 Analysis
1	82.8	83.1
2	9.3	8.8
3	3.8	3.5
4	1.9	2.7
5	1.6	1.3
6	0.6	0.6

The top panel of Figure 3 shows the basis functions corresponding to PC-1 (continuous curve) and PC-2 (dashed curve) for both PCAs. In each case the first basis function decreases monotonically with increasing number of masker components, whereas the second basis function first increases and then decreases slightly as the number of masker components exceeds 20–30. To obtain the predicted masking function for a given listener the basis functions are scaled by the listener's PC weights and then added to the mean normalized masking function m̄ (dotted line in Figure 3). The bottom panel of Figure 3 shows the breakdown of the variance accounted for by each PC for each number of masker components. Note that the variance in the data (dotted curve) is by far the greatest for maskers comprising 40 or less components. Here, PC-1 never accounts for less than 71% of the variance, whereas PC-2 never accounts for more than 14% of the variance. PC-2 accounts for a slightly greater proportion of the variance than PC-1 for maskers comprising 200 or more components. For these maskers, however, the variance across listeners is quite small.

Figure 3.

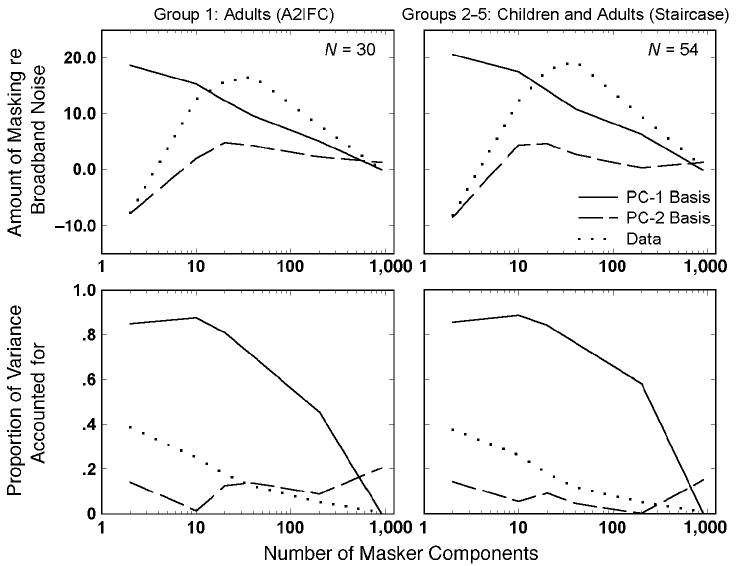
Top panels: Basis functions corresponding to PC-1 (continuous curve) and PC-2 (dashed curve) from PCA of the shapes of the individual masking functions for Group 1 (left) and Groups 2–5 (right) analyses. The dotted line gives the mean data across all listeners. Bottom panel: The proportion of variance accounted for by PC-1 (continuous curve) and PC-2 (dashed curve) plotted as a function of the number of masker components. The dotted line gives the proportion of the total variance in the data attributed to the variance in the data associated with each number m of masker components.

Figure 3 makes clear the remarkable similarity of the results of the two PCAs. Indeed, the basis functions describing differences across age are essentially identical to those describing individual differences within the independent group of adults. This outcome, together with the predominance of PC-1 in accounting for the variance in masking functions, suggests that a single factor contributes to differences both within and across age groups. To further evaluate this statement two subsequent analyses were performed. The first was an analysis of variance (ANOVA) of the PCs from the Groups 2–5 analysis. For PC-1 alone to account for the differences across age groups there should be a significant interaction between PC and age group such that PC-1 varies systematically with age whereas PC-2 remains constant. As predicted, the interaction was significant [F(3,50) = 11.14, p < .0001]; PC-1 weights decreased significantly with age [F(3,50) = 18.38, p < .0001], whereas PC-2 weights did not [F(3,50) = 0.563, p < .642]. Figure 4 shows the mean of the two PCs for each age group with error bars. The second analysis was a K-means cluster analysis of the individual masking functions from all groups. Cluster analysis is a statistical procedure that is used to identify similarities among individual members of a set of measures (masking functions in this case). It does this by grouping the measures in such a way that the variance within groups (clusters) is minimized at the same time that the variance between groups is maximized (see Hartigan, 1975). If differences in the masking functions are to be described by PC-1 alone, then clusters resulting from the analysis should separate along PC-1 but overlap substantially along PC-2. We constrained the analysis to yield no more than three clusters on the basis of the precedent established by Neff and Dethlefs (1995; listeners were placed in high-, intermediate-, and low-threshold groups). The results are shown in Figure 5. Here PC-1 is plotted against PC-2 for each listener participating in the study, with the three clusters represented by different symbol types. As can be seen, cluster membership does indeed separate along PC-1 with little relation to PC-2. The degree of separation is such that for all but 1 listener it is possible to identify cluster membership simply by knowing the listener's PC-1 weight.

Figure 4.

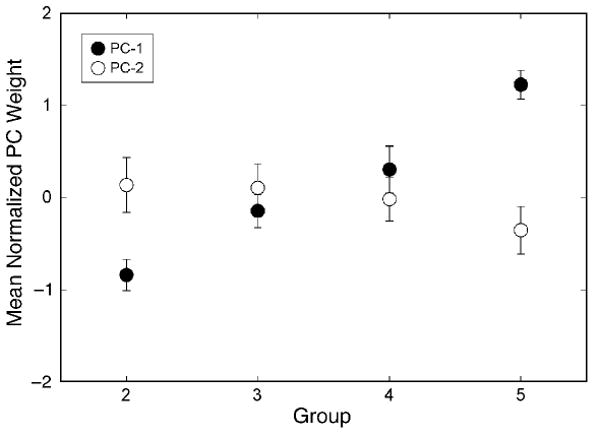
Means and standard errors for PC-1 (filled circles) and PC-2 (unfilled circles) weights within Groups 2–5.

Figure 5.

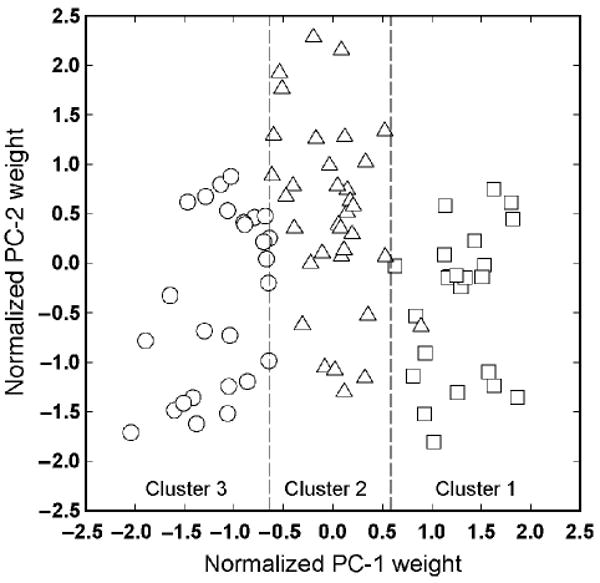
Comparison of PC weights to results of a K-means cluster analysis of individual masking functions from Groups 1–5. Each listener's data is represented in PC space with clusters designated by different symbols. Note clusters separate on PC-1.

Predictions of the CoRE Model

The results of the foregoing analyses suggest that a single factor can account for individual differences in the masking functions both within and across age groups. In this section we offer an interpretation of what this factor might be. As noted earlier the CoRE model (Lutfi, 1993) would account for all individual differences in terms of differences in the degree to which maskers add variance to the decision variable of an optimal detection strategy. Oh and Lutfi (1998) have given a complete development of the model's predictions for the present task, which we review here: Briefly, the listener is assumed to monitor the level output L₀ of an auditory filter centered on the signal at 1.0 kHz (an optimal detection strategy). The inability to ignore maskers is represented by the monitoring of additional filters, whose level outputs are effectively independent of the signal filter output and independent of one another. The number of these additional filters, n, and the frequency range over which they are monitored, W, are the two free parameters of the model. In formal terms, the listener's decision rule is

$$\mathit{\text{Respond signal iff}}{L}_0+\sum _{i=1}^n{L}_i>\beta ,\mathit{\text{else respond no signal}},$$ (3)

where β is a response criterion. Here, the two terms to the left of the inequality identify two potential sources of masking. The first is energy based and is caused by masker components falling within the same auditory filter as the signal. The second is informational and is caused by masker components falling outside the signal filter. Without further assumptions, the decision rule leads to the prediction that the total masking will be the decibel sum of informational and energetic components,

$$\begin{array}{ll}\mathit{\text{Total Masking}}=& \mathit{\text{Energetic}}(E)\\ & +\mathit{\text{Informational}}(I)\text{in dB}.\end{array}$$ (4)

In practice, the amount of energetic masking E is computed using a traditional filter model (see Oh & Lutfi, 1998, for specific details). The amount of informational masking is derived analytically from the decision rule and is given by

$$\mathbf{I}\approx \sqrt{n}{\mathbf{\sigma }}_L,$$ (5)

where σ_L is the standard deviation across all maskers in the output level (in decibels) of a monitored filter. According to the model, therefore, it is the variance of components falling within monitored filters, not the number of components falling in these filters, that determines the amount of informational masking. In this way the model's predictions for informational masking differ fundamentally from its predictions for energetic masking.

The value of σ_L is computed directly from the power spectra of the maskers and is affected by the frequency range—the free parameter W—over which the computation is performed (again see Oh & Lutfi, 1998, for specific details). Figure 6 shows for different values of W how σ_L varies with the number of masker components. Here, as in Oh and Lutfi, only the upper value of W is varied since σ_L changes significantly only with the inclusion of higher frequency auditory filters.⁴ Note that whereas energetic masking increases monotonically with the number of masker components, σ_L does not. Rather, σ_L reaches its maximum value somewhere between 10–30 masker components. According to the model, then, the nonmonotonicity of masking is due exclusively to the informational component of the prediction for total masking. Also, because the energetic component is assumed, in practice, to be the same for all listeners, the informational component is responsible for all individual differences according to the model.

Figure 6.

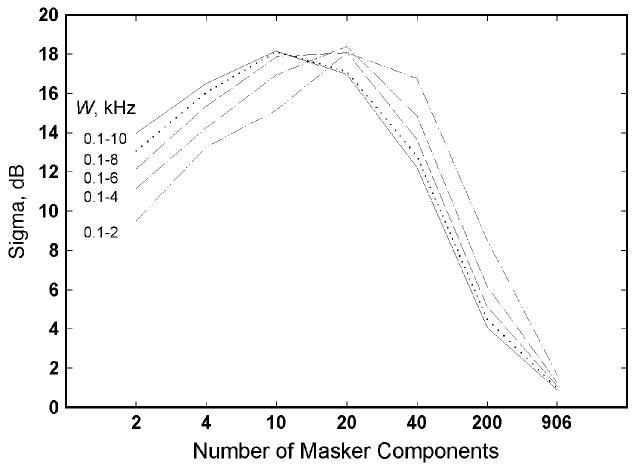
Estimated values of σ_L are plotted as a function of number of masker components m and free parameter W.

The predictions of the model were fit to the data by selecting values of n and W independently for each listener so as to minimize the total rms error in decibels between the obtained and predicted amounts of masking. In the special case of n = 1 predictions were based on the output of the single auditory filter centered at the signal frequency, as in the traditional filter model. Overall the fits accounted for 82% of the total variance in the data, very nearly equal to the total variance accounted for by PC-1. The large number of listeners precludes showing the individual fits for each listener; however, individual fits were reported by Oh and Lutfi (1998) and Oh et al. (2001) for a subset of the listeners comprising Groups 1, 2, and 5. These fits are quite representative of the group as a whole. Figure 7 plots the PC-1 and PC-2 weights relative to the best-fitting values of n and W for each listener. Here, it can be seen that the estimated number of monitored filters n is highly correlated with PC-1, whereas W is little correlated with either PC. The age effect is also evident in that the preschoolers (small black circles) have both the highest values of n and the highest PC-1 weights, whereas the comparable Group 2 adults (triangles) have the smallest values of n and the lowest PC-1 weights.

Figure 7.

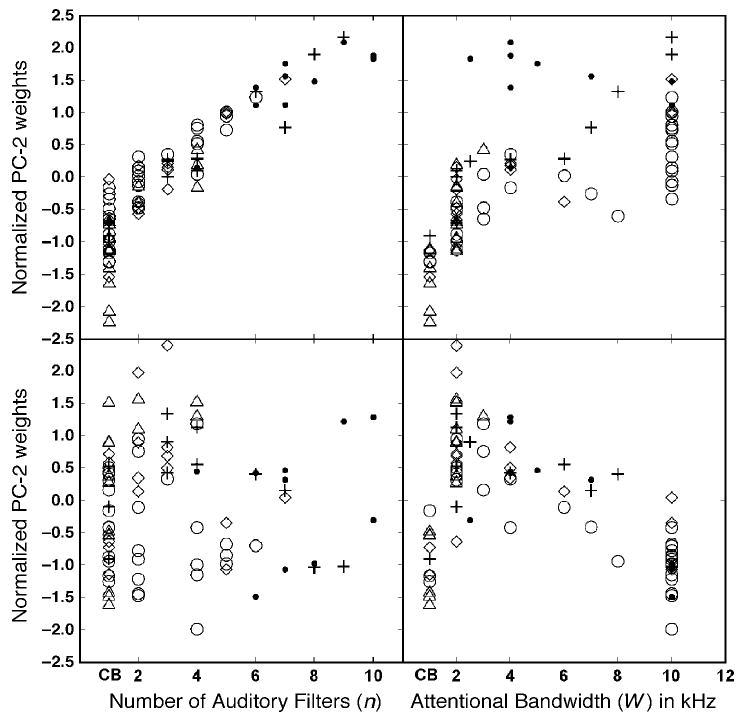
Scatterplot of the normalized PC-1 and PC-2 weights against CoRE model parameters n and W for Group 1 adults (unfilled circles), Group 2 adults (triangles), Group 3 late school-age children (diamonds), Group 4 early school-age children (crosses), and Group 5 preschoolers (small filled circles).

Discussion

The results of the present study replicate those of earlier studies showing large individual differences, both within and across age groups, in the masking of a pure-tone signal by random-frequency multitone maskers. At the one extreme, high-threshold listeners show nonmonotonic masking functions, with the amount of masking in every case exceeding that of the broadband noise. At the other extreme, low-threshold listeners show monotonic or nearly monotonic functions, with the amount of masking rarely exceeding that of the noise. With regard to the interpretation of these differences there are two new results. The first is that all but 17% of the variance in the shape of the masking functions is accounted for by a single PC. This result indicates that most of the observed differences among individuals, including differences between children and adults, can likely be accounted for in terms of the influence of a single perceptual factor, and that interpretations invoking multiple detection strategies are likely unnecessary. The conclusion is based on the premise that different detection strategies should have qualitatively different effects on the masking functions. There would be little practical reason to propose different detection strategies if this were not true. Further evidence against multiple detection strategies is provided by the results of an ANOVA on the PCs showing that only PC-1 changes with age, by results of a cluster analysis on the masking functions showing complete separation along PC-1, and by the predictions of the CoRE model accounting for the same proportion of variance as the PCAs.

The second new result is that the group detection advantage of adults over children appears to continue well into the school years, with the range of individual differences appearing to be greatest during the early school years. With regard to range, some of the school-age children of this study performed as poorly as the worst performing preschoolers, whereas other school-age children performed as well as the best performing adults. Though no clear age trend was observed across listeners within the school-age groups, the performance of the late school-age children overall tended to be more adult-like. This suggests a transition period where for many children the random noise typical of everyday listening may become less of a distraction. Other reports have also suggested the onset of schooling as a point of transition, these reports involving more basic auditory abilities such as frequency discrimination (Allen, Wightman, Kistler, & Dolan, 1989) and spectral pattern discrimination (Allen & Wightman, 1992). It is difficult to say what factors might underlie the transition at this age. It may be that schooling plays a crucial role in the development of normal auditory abilities after age 6, or it may be that the natural development of auditory abilities after age 6 is one reason that this age is chosen to begin schooling. Although the present study sheds no additional light on this question, it does at least suggest that the generally greater amounts of informational masking observed in children before age 6 are not due to substantial qualitative differences in the way these children process acoustic information relative to adults.

This raises the question as to what factor, other than processing strategy, might be responsible for individual differences in informational masking. The modeling results suggest that that factor is the extent to which auditory filters, other than the one centered on the signal, contribute variance to the decision variable of an otherwise optimal detection strategy. According to this interpretation, differences among individuals relate primarily to the number n of independent auditory filters that influence the detection process, with the frequency range of auditory filters W having a smaller secondary effect. The success of the model raises the question as to how specific values of n and W for individual listeners should be interpreted. In the simplest sense, these values represent estimates of the extent to which individual listeners are capable of “focusing in” on the signal to the exclusion of maskers. One should not, however, read too much meaning into their values since they represent only very crude measures of how listeners distribute their attention across frequency. This is particularly true of W, which has a relatively small effect on the predicted shape of the masking function, as evident from Figure 7. If the goal is specifically to evaluate listener attention to different frequencies, there are means of obtaining more accurate measures (see Berg, 1989; Lutfi, 1995; Richards & Zhu, 1994).

Finally, we should address the issue as to what extent the energetic component of masking might also have contributed to the difference between preschoolers and adults, and to individual differences overall. In applying the CoRE model, we have assumed the energetic component to be the same for all listeners, but this is certainly incorrect. Oh and Lutfi (1998) have discussed the difficulties associated with obtaining precise estimates of energetic masking in these conditions. One means of evaluation is to compare masked thresholds for broadband noise where informational masking is believed to be minimal (see Neff & Dethlefs, 1995; Neff et al., 1993; Oh & Lutfi, 1998). Individual differences in this case are quite small, but they may not be reflective of individual differences in energetic masking by tones. Though there are problems associated with obtaining precise estimates of energetic masking in these conditions, in many applications one merely wishes to identify specific conditions wherein masking is predominantly informational. This is true in studies involving young children, where complete masking functions may be difficult or impossible to obtain (see Wightman & Allen, 1992). The present data suggest that if one requires a “pure” measure of informational masking, it is best not to use 10–20 component maskers where informational masking is believed to be greatest (see Neff & Dethlefs, 1995) but rather to use 2–4 component maskers where energetic masking is estimated to be the smallest. For 2–4 component maskers, PC-1, which is identified with the informational component of masking, accounts for roughly 90% of the variance where the variance among individuals happens to be the greatest.