What have we learned from mathematical models of defibrillation and postshock arrhythmogenesis? Application of bidomain simulations

Understanding how electric current delivered to the heart in order to terminate lethal arrhythmias traverses myocardial structures and interacts with wavefronts of fibrillation has been challenging researchers for many years. Of particular importance is insight into the mechanisms by which the shock fails. Reinitiation of fibrillation is related not only to the effect of the shock on the electrical state of the myocardium but also to the intrinsic properties of the tissue that lead to destabilization of postshock activations and their degradation into electric turbulence. The complexity of the relationships and dependencies to be teased out and dissected in this quest have been staggering. Historically, overwhelming electrical artifacts prevented researchers from recording during, as well as shortly after, the shock. A breakthrough in mapping cardiac activity associated with defibrillation occurred during the last decade of the 20th century with the introduction of potentiometric dyes, which allowed continuous recording of activity before, during, and after the shock.

At the same time, the theoretical electrophysiology community adopted a novel modeling methodology, termed the bidomain model. The bidomain model¹ is a continuum representation of the myocardium that takes into consideration current distribution resulting from a particular characteristic of cardiac tissue: the fact that the two spaces composing the myocardium—intracellular and extracellular—both are anisotropic but to a different degree. Thus, the myocardium is characterized with “unequal anisotropy ratios.” Because the bidomain model accounts for current flow in the interstitium, it instantly became a powerful modeling tool in the study of stimulation of cardiac tissue (with an eye on defibrillation), where current delivered in the extracellular space finds its way across the membranes of cardiac cells. The first significant achievement of this new approach was the study of the passive (i.e., ionic currents are not accounted for) shock-induced change in transmembrane potential following a strong unipolar stimulus. Bidomain simulations by Sepulveda et al² demonstrated that tissue response in the vicinity of a strong unipolar stimulus involved simultaneous occurrence of positive (depolarizing) and negative (hyperpolarizing) effects in close proximity. This finding of “virtual electrodes” was in stark contrast with the established view that tissue responses should only be depolarizing (hyperpolarizing) if the stimulus was cathodal (anodal). Subsequent optical mapping studies convincingly confirmed these theoretical predictions.³ Virtual electrode polarization has since been documented in experiments and simulations involving various stimulus configurations.

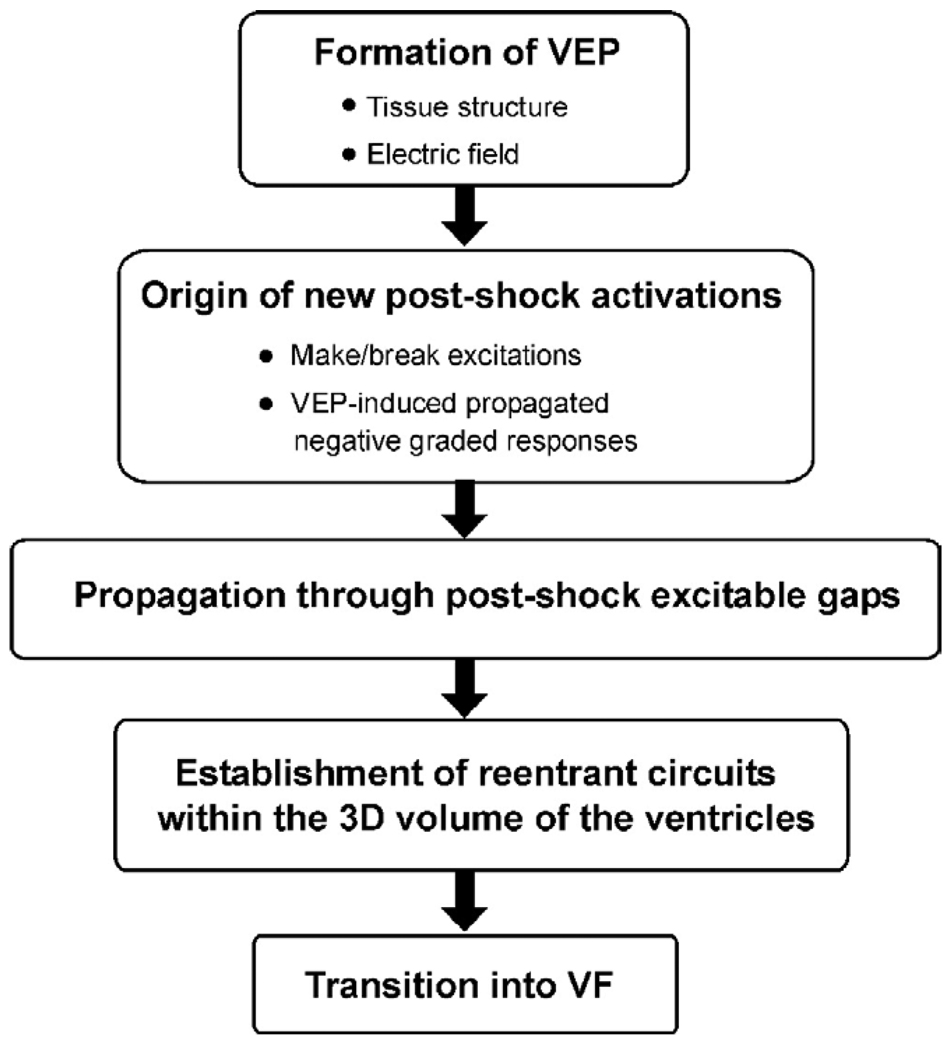
The next big contribution of passive bidomain modeling (bidomain modeling contributions are outlined in Figure 1) was the detailed analysis of virtual electrode polarization etiology and its dependence on cardiac tissue structure and the configuration of the applied field. Both were shown to be major determinants of the shape, location, polarity, and intensity of shock-induced polarization.⁴ In particular, theoretical considerations led to the recognition of two types of virtual electrode polarization: (1) “surface virtual electrode polarization,” which penetrates the ventricular wall over a few cell layers, due to current redistribution near the boundaries separating myocardium from blood cavity or surrounding bath; and (2) “bulk virtual electrode polarization” throughout the ventricular wall.⁵ Analysis of the bidomain equations revealed that a necessary condition for the existence of the bulk virtual electrode polarization is unequal anisotropy in the myocardium. Sufficient conditions include either spatial nonuniformity in applied electric field or nonuniformity in tissue architecture, such as fiber curvature, fiber rotation, fiber branching, and anastomosis, and local changes in tissue conductivity due to resistive heterogeneities.

Figure 1.

Schematic of major contributions, made by bidomain simulations, to the current understanding of defibrillation and shock-induced arrhythmogenesis. 3D = three-dimensional; VEP = virtual electrode polarization; VF = ventricular fibrillation.

How do cells respond to externally imposed changes in their transmembrane potential, such as those predicted by the bidomain model? The cellular response to shock-induced virtual electrode polarization depends on its magnitude and polarity, as well as on the electrophysiologic state of the cell at the time of shock delivery. Action potential duration can be either extended (by positive virtual electrode polarization) or shortened (by negative virtual electrode polarization) to a degree that depends on virtual electrode polarization magnitude and shock timing, with strong negative virtual electrode polarization completely abolishing (de-exciting) the action potential and thus creating postshock excitable areas in the virtual anode regions. Two-dimensional (myocardial sheet) simulations with the bidomain model that incorporated for the first time ionic fluxes through cell membranes (active bidomain modeling) resulted in recognition of the importance of the distribution of transmembrane potential established by the shock to the origin of postshock activations (Figure 1). Roth⁶ demonstrated that the close proximity of a de-excited region and a virtual cathode could result in excitation at shock end (termed “break” excitation, i.e., at the break of the shock). The virtual cathode serves as an electrical stimulus eliciting a regenerative depolarization and a propagating wave in the newly created excitable area. Break excitations arise at the borders between oppositely polarized regions, provided the transmembrane potential gradient across the border spans the threshold for regenerative depolarization. The finding of break excitations, combined with the fact that positive virtual electrode polarization can result in regenerative depolarization in regions where tissue is at or near diastole (“make” excitation; takes place at the onset of the shock), provided the necessary framework for understanding how a defibrillation shock results in the development of new postshock activations. Additional insight that arose from bidomain considerations and virtual electrode polarization concepts was the recognition that some postshock activations could originate much later than the end of the shock (Figure 1). These activations were termed virtual electrode polarization-induced propagated graded responses⁷ and were shown to occur in regions of intermediate virtual electrode polarization magnitude. Although the spatial gradient in transmembrane potential at the borders between oppositely polarized regions is again the stimulus that elicits the postshock activation, this occurs at an instant much later than shock-end, when the mildly negatively polarized region repolarizes enough to “pick up” the stimulus. Such delayed activations have been proposed as a mechanism for the isoelectric window, the electrically quiescent period sometimes observed after a not-so-strong shock.

The outcome of a defibrillation shock (a success or a failure in terminating the wavefronts of fibrillation) depends crucially on propagation of newly formed postshock excitations through shock-induced excitable areas (Figure 1). The shock succeeds in extinguishing fibrillatory wavefronts and not initiating new reentry if the excitations manage to traverse the excitable areas before the rest of the myocardium recovers from shock-induced depolarization. Active bidomain simulations in two dimensions⁸ demonstrated that the latency in onset of these excitations, their propagation velocity through excitable gaps, and shock-induced extension of refractoriness in depolarized areas determine how quickly postshock activity subsides following successful shocks. Vulnerability and defibrillation failure also can stem from shock-induced virtual electrode polarization. The onset of a break excitation is associated with formation of a (virtual electrode polarization-induced) phase singularity⁹; it forms at a point along the boundary between shock-induced depolarization and de-excitation and is independent of the preshock state of the myocardium. If these phase singularities survive, thus allowing development of a spiraling wavefront, the shock results in (re)initiation of reentrant arrhythmia. The establishment of a reentrant arrhythmia in the ventricles thus strongly depends on the anatomic features and geometric asymmetries of the cardiac chambers, which significantly affect three-dimensional (3D) global postshock propagation.

Further inquiry into the 3D mechanisms governing the failure of defibrillation has been hampered by the inability of current experimental techniques to resolve, with sufficient accuracy, electrical behavior confined to the depth of the ventricles during and after the shock. Mapping the entire epicardial surface of the ventricles, the current state of the art in optical imaging, does not reveal the global 3D activity that follows the shock because activations can propagate intramurally, without a signature on the epicardial surface. Most importantly, as discussed earlier, there is a dramatic difference between the magnitude and pattern of shock-induced virtual electrode polarization in the surface layers and in the depth of the myocardium. Such differences in virtual electrode polarization could result in different electrophysiologic behavior on the surfaces and in depth, with midmyocardial postshock activity remaining confined to the depth of the ventricular wall and detached from surface postshock behavior for stretches of time. A major break-through in understanding these mechanisms again came from bidomain simulations, this time in 3D (Figure 1).

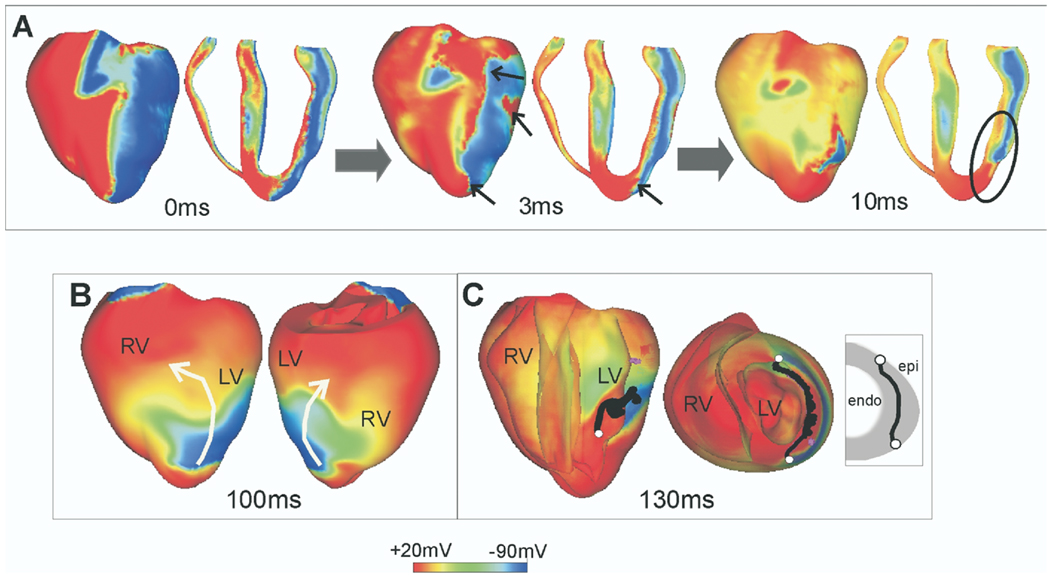
The quest to unravel how shocks could succeed in terminating fibrillation or how they could reinstate arrhythmia has also driven the technologic aspects of computer simulations of 3D bidomain activity. In order to be able to simulate postshock arrhythmogenesis in the ventricles, computational research has managed to overcome tremendous difficulties associated with obtaining solutions of very large systems of unknowns, involving stiff equations and computational meshes of irregular geometry. The results are fascinating.¹⁰ First, active bidomain simulations of activity in the 3D ventricles demonstrated that understanding of shock-induced phenomena acquired in earlier, simpler bidomain studies, such as the causes of the specific pattern of virtual electrode polarization and how the postshock activations originate, remains valid in the 3D ventricles. Furthermore, these simulations revealed the importance of accounting for the geometry of the ventricular chambers in the quest to understand generation of postshock arrhythmias (Figure 2). The difference in the thickness of the ventricular walls ultimately is manifested as a preferential location of the postshock excitable area. These simulations showed that the postshock excitable areas were always located in the thick left ventricle and septum, but never in the thin right ventricle (Figure 2A). In addition, the location of the postshock excitable area determines the types of postshock reentrant circuits (Figure 2B). One can speculate that identifying the location of the main postshock excitable area is important for improving clinical defibrillation efficacy because eradication of the area can be specifically targeted by auxiliary small-magnitude shocks, resulting in a dramatic decrease in defibrillation threshold.

Figure 2.

Postshock transmembrane potentials in the rabbit ventricles. Time is counted from the end of the shock. A: Virtual electrode polarization at shock-end and activity at 3 and 10 ms postshock, demonstrating break excitations (small arrows) and propagation through the postshock excitable areas (encircled region). B: Shock-induced arrhythmia in the rabbit ventricles. White arrows indicate the direction of propagation of the reentrant waves. C: Postshock scroll-wave filaments (shown in black). The ends of the filaments are shown in white and are in touch with the same surface, the epicardium (U-type filaments). Inset shows schematic of filament location. LV = left ventricle; RV = right ventricle.

Results from bidomain simulations have provided important insights into how 3D postshock reentrant circuits established soon after a failed shock further degrade into ventricular fibrillation (Figure 1).¹¹ The location and type of postshock scroll-wave filaments (Figure 2C) play important roles in this process. As demonstrated by the simulations, transitions between the various types of filaments (I, U, and O) are very frequent at the early stages of postshock activity (first 200–250 ms). U-type filaments (filament whose two ends are in contact with the same [endocardial or epicardial] surface), such as the one shown in Figure 2C, often dominate postshock reentrant activity in the left ventricle.

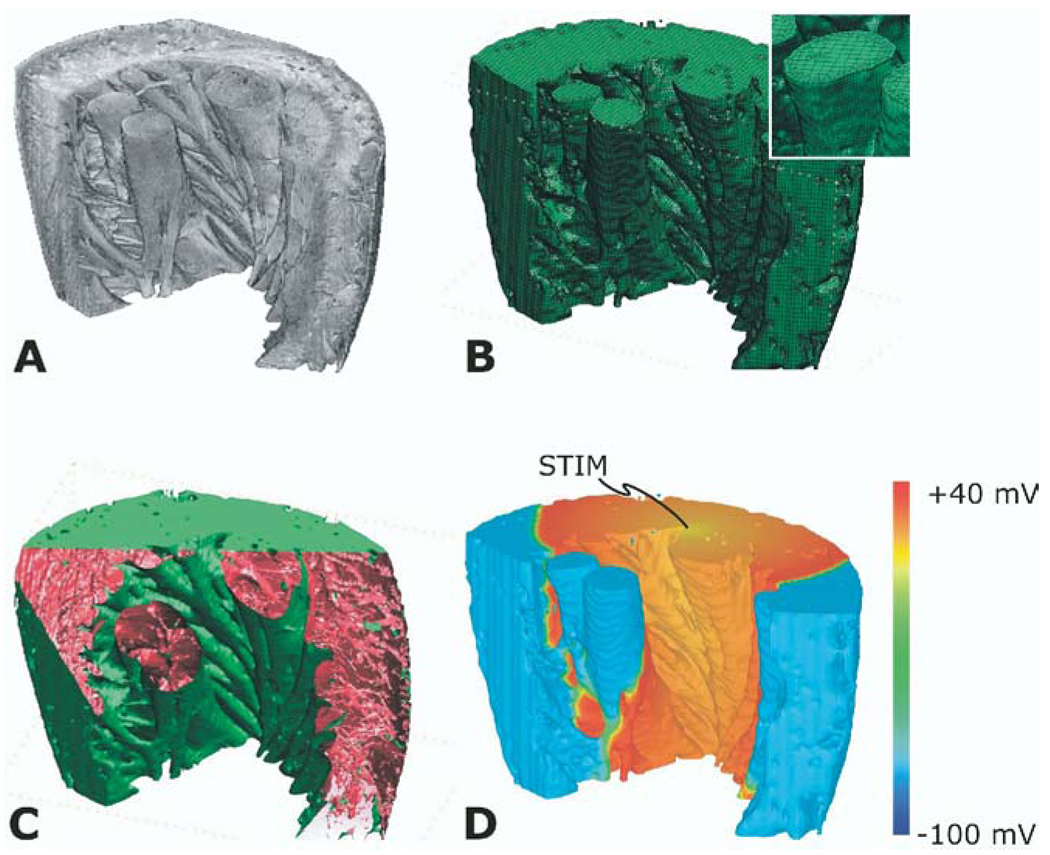
This short exposé on the achievements of bidomain modeling clearly demonstrates the importance of using simulation tools as we attempt to (1) unravel the mechanisms by which lethal arrhythmias arise and (2) learn how to best terminate them. Given the fact that we now are capable of simulating the 3D activity in the ventricles, as shown in Figure 2, where do we go from here? What will be the new frontier in defibrillation and shock-induced arrhythmogenesis that will be tackled by simulations in the near future? We believe that the set of questions remaining to be addressed in this field include issues regarding the involvement of features of cardiac structure that have been ignored in the “one heart fits all” approach used in the studies leading to the present state of knowledge. Figure 3 illustrates our view of the future through an example of a paced activation in a left ventricular wedge from the rabbit heart.¹² Cardiac geometry could be acquired from high-resolution magnetic resonance imaging (MRI) data or histologic sectioning; the computational mesh then is generated by gray-level thresholding followed by an octree-based meshing technique. In Figure 3, a cut through the mesh exposes the presence of structural (micro)heterogeneities, such as blood vessels and collagen septa. A paced propagation through the wedge model, in which the myocardium is represented as a bidomain, is also shown; it demonstrates the feasibility of this approach for studying the role of cardiac (micro)structure in arrhythmogenesis and defibrillation. Simulations in cardiac electrophysiology clearly are on the way to an exciting future.

Figure 3.

Reconstruction of a left ventricular wedge from the rabbit heart. A: Segmented magnetic resonance imaging stack. B: Computational mesh (inset shows mesh detail). C: Presence of structural heterogeneities, such as blood vessels and collagen septa. D: Propagation of a paced activation in the bidomain wedge. The location of the pacing stimulus is on the top surface of the wedge.