Learning and liking an artificial musical system: Effects of set size and repeated exposure

Abstract

We report an investigation of humans' musical learning ability using a novel musical system. We designed an artificial musical system based on the Bohlen-Pierce scale, a scale very different from Western music. Melodies were composed from chord progressions in the new scale by applying the rules of a finite-state grammar. After exposing participants to sets of melodies, we conducted listening tests to assess learning, including recognition tests, generalization tests, and subjective preference ratings. In Experiment 1, participants were presented with 15 melodies 27 times each. Forced choice results showed that participants were able to recognize previously encountered melodies and generalize their knowledge to new melodies, suggesting internalization of the musical grammar.

Preference ratings showed no differentiation among familiar, new, and ungrammatical melodies. In Experiment 2, participants were given 10 melodies 40 times each. Results showed superior recognition but unsuccessful generalization. Additionally, preference ratings were significantly higher for familiar melodies. Results from the two experiments suggest that humans can internalize the grammatical structure of a new musical system following exposure to a sufficiently large set size of melodies, but musical preference results from repeated exposure to a small number of items. This dissociation between grammar learning and preference will be further discussed.

The human knowledge of melody and harmony

Music we encounter every day is composed of sequentially and simultaneously presented pitches. While sequential pitches give rise to melody, simultaneous pitches give rise to harmony. Together, melody and harmony are viewed as the horizontal and vertical organizational dimensions in music.

Various studies in the field of music perception and cognition have shown that humans have reliable but implicit knowledge of both melody and harmony. Melodies that end with unexpected or incongruous notes elicit electrophysiological responses such as an enhanced Late Positive Component (Besson & Faïta, 1995); this LPC was observed in both musicians and nonmusicians but their precise amplitude and latency depended on training. Behavioural results from the probe tone paradigm (Krumhansl, 1990) also showed decreased goodness-of-fit ratings for unexpected notes within a melodic context.

In the vertical dimension, when perceiving chord progressions that violate the principles of traditional Western harmony, e.g. when a chord progression resolves to a chord other than the one that is most commonly used given the context (such as the tonic), the listener's expectation is violated. This kind of expectation violation has been observed empirically using reaction time methodologies (Bharucha & Stoeckig, 1986). Harmonic priming studies (Bharucha & Stoeckig, 1986; Bigand et al., 1999) have shown that humans are slower to respond to chords that were unexpected given the global harmonic context. These effects have been observed in phoneme identification (Bigand et al., 2001), timbre discrimination (Tillmann et al., 2006), consonance detection (Bigand et al., 1999), and asynchrony detection tasks (Tillmann & Bharucha, 2002), and although musically untrained listeners tended to be slower to respond to chords overall, similar patterns of results were observed regardless of musical training, suggesting that these kinds of knowledge in the typical progressions of musical harmony were implicitly learned, possibly from repeated cultural exposure to music composed according to prototypical chord progressions. Electrophysiological studies investigating harmonic knowledge (Koelsch et al., 2000) have observed an Early Anterior Negativity (ERAN, or EAN) and a Late Negativity or N5 during the neural processing of unexpected harmonies. These effects are observed in musicians and nonmusicians alike (Koelsch et al., 2000; Loui et al., 2005), again suggesting that these kinds of musical knowledge may be acquired independently of explicit musical training.

The source of musical knowledge — cross-cultural and developmental approaches

The aforementioned studies conclusively demonstrate musical knowledge, in the form of expectations for probable pitches in melodies and chords in harmony. These results have led researchers to ask about the source of knowledge in melody and harmony. One way to compare these results is to look at cross-cultural experiments in music cognition. Castellano, Bharucha, and Krumhansl (1984) have looked at tonal hierarchies of music from North India, showing that participants rate frequently-occurring tones in melodies as being more fitting in a non-Western musical context. Krumhansl et al. (2000) have also shown similar sensitivity to musical frequencies in North Sami Yoiks of Finland. These results demonstrate that individuals develop knowledge and expectations for music depending on long-term cultural exposure to their musical system.

Another approach to the source of musical knowledge is via developmental methods. Schellenberg & Trehub (1996) observed preferences for consonant intervals in infants as young as six months of age, suggesting an importance for low-integer, simple frequency ratios in music. Trainor and Trehub (1994) also found sensitivity to key membership in children as young as 5 years and implied harmony in children as young as 7 years. This pattern of results suggests that key membership is acquired before implied harmony. These developmental constraints of perception seem to shape the common patterns of musical systems.

While some aspects of harmonic knowledge may result from neurobiological properties of the auditory system (Tramo, 2001), certain features of harmony may also be learned via exposure within one's culture. In particular, the previously mentioned developmental studies suggest that key membership and especially implied harmony may be acquirable relatively late in life. Cross-cultural studies also suggest that our expectation for frequently occurring pitches in melodies may be learnable. As musical systems of some other cultures, such as Indian and Afro-Cuban music, seem to rely less on chord progressions compared to Western harmony, our expectation for prototypical chord progressions might also be learned via exposure to the relative frequencies and probabilities of sounds in the environment.

In investigating the acquisition of harmony, one approach that has yet to be explored is the use of artificial musical systems. An artificial musical system is useful because participants have no prior knowledge of the system, including the pitches that it contains, as well as its typical melodic and harmonic structures. Thus we can create a novel musical environment where we give subjects controlled exposure to the musical system and then assess the kinds of knowledge they can acquire from any exposure which would be only given in the experiment. Artificial system studies such as the present experiments stem from a literature in language acquisition, where researchers have long made use of artificial linguistic systems to investigate the human sources of knowledge in language.

Studies in implicit learning and music acquisition

While studies in artificial musical systems are as yet relatively novel, the learning of artificial systems has been explored in the context of language acquisition. Experiments in statistical learning have shown that after a brief exposure period to an artificial language, humans as young as eight-month-olds are sensitive to the transitional probabilities of one syllable following another (Saffran et al., 1996; Aslin et al., 1998), and this has been posited as being useful in acquiring music as well as language (Huron, 2006). Some research has addressed the learning of tone sequences (Saffran et al., 1999), interleaved melodies (Creel et al., 2004), timbre sequences (Tillmann & McAdams, 2004), serialist music (Dienes & Longuet-Higgins, 2004) and nonlocal musical rules (Kuhn & Dienes, 2005; 2007), showing that humans are able to recognize melodies that followed certain musical rules following exposure to sequences of tones.

In the present study we investigate the acquisition of harmony and melody using a statistical learning approach. We developed artificial musical grammars based on a microtonal tuning system. The artificial grammars consist of chord progressions in a non-Western scale, from which we compose melodies. Thus the new musical grammars include both vertical and horizontal dimensions of music, and while they are designed to follow some principles of existing musical systems, they are completely new in the sense that the participants of our studies have not heard any music composed using these materials.

A new musical system

In the equal-tempered Western chromatic scale, frequencies are defined as the following:

$$\text{Frequency}(\text{Hz})=\text{k}\ast 2^{\text{n}/12}$$

where n is the number of steps along the chromatic scale, and k is a constant and typically equals 440Hz.

For the following experiments we used the Bohlen-Pierce scale, a microtonal tuning system based on 13 logarithmically even divisions of a tritave, which is a 3:1 ratio in frequency. The tones in one tritave of the Bohlen-Pierce scale are defined as:

$$\text{Frequency}(\text{Hz})=\text{k}\ast 3^{\text{n}/13}$$

where n is the number of steps along the tritave scale, and k is a constant which equals 220Hz.

Based on this scale, it was possible to define chords using pitches with frequencies that were approximately related to each other in low- integer ratios, which are relatively consonant psychoacoustically One “major” chord in this new system is defined as a set of three pitches with frequencies that approximate a 3:5:7 ratio within three cycles of the scale (see Krumhansl, 1987, for a derivation of chords in the Bohlen-Pierce scale). We composed two chord progressions consisting of four major chords in the Bohlen-Pierce scale, with three pitches in each chord. The two chord progressions consisted of identical chords, but were reversed in temporal order relative to each other. These two chord progressions formed the bases of the grammatical rules which we used to form the stimuli of the present study. Two sets of melodies were generated from each of the two chord progressions by applying rules according to a finite-state grammar. In a finite-state grammar, each note in each chord was treated as a node in the system. Each node could either repeat itself or lead to another node which was either in the same chord or in the next chord. Thus each chord progression was a grammar with four states (each chord being a state), and three possible items (pitches) in each state. Each chord was equally likely to repeat itself and to move forward to the next chord, and each chord consisted of three equally likely pitches. Thus, the transitional probability between successive chords was 0.5 and the probability of occurrence of each pitch in any chord was 0.33, so that the transitional probability between any two pitches in the musical system was 0.5 × 0.33 = 0.167. For example, two possible melodies from Grammar I (which were used in the experiments) are below:

6 4 7 7 7 6 10 10

and 10 10 4 7 3 6 6 10

where each integer plugs into n in the equation F = 220*3ˆ(n/13) to make the frequency of one note.

By applying these rules in the fashion of a finite-state grammar, we composed sets of melodies from the above chord progressions. One of the two chord progressions (Grammar I) was used to test the learning of the musical system, whereas the other chord progression (Grammar II) was used to as a control to generate foil melodies as incorrect answers in listening recognition and generalization tests. The chord progression named Grammar II was the same as Grammar I except the chords were in reverse order — that is, Grammar I and Grammar II are retrogrades (reversals) of each other. Thus the two chord progressions are mathematically similar in every respect except for the transitional probabilities between chords. Figure 2a illustrates a chord progression as a finite-state grammar, whereas Figure 2b provides one example of using a grammar to generate a melody.

Figure 2.

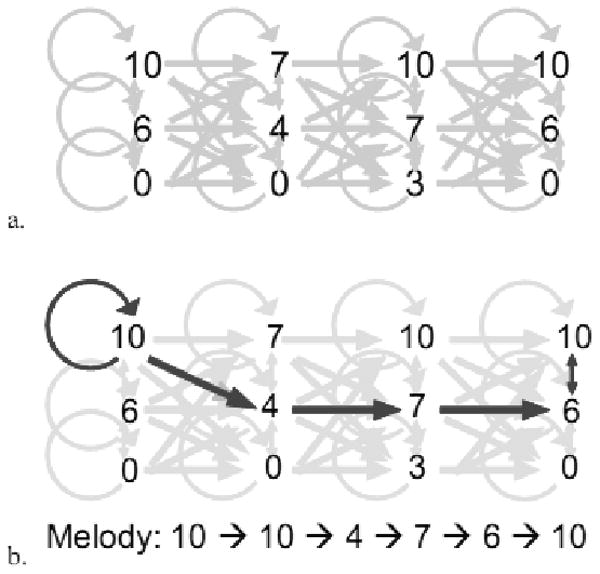
a. A finite-state grammar diagram illustrating the possible ways to compose melody from harmony. b. An illustration of applying a finite-state grammar as a set of rules to compose one melody based on the finite-state grammar. Dark arrows illustrate the paths taken, whereas light arrows illustrate other possible paths that are legal in the grammar. One resultant melody is shown at the bottom of the figure. Other melodies can be constructed by following a pathway specified by any combination of arrows connecting nodes in the grammar.

Each melody was composed according to one of the two grammars. Taken together, this artificial musical system adheres to many of Lerdahl and Jackendoff's rules for a generative theory of tonal music (Lerdahl & Jackendoff, 1983). For example, the musical grammars are parsable, groupable, hierarchical, and statistically predictable. This makes the system viable as a new compositional tool, yet capable of generating melodies that are unfamiliar to all participants of our studies. The musical grammars described here can support investigations not only in music cognition, but also in grammar learning more generally. Materials constituting the finite-state grammars are such that the items themselves (the tones) are non-rehearsable in the sense that one cannot easily designate a verbal label to each individual tone. Most artificial grammar studies to date have used grammatical items such as letter strings (Reber, 1989; Gomez & Schvaneveldt, 1994) and verbal syllables (Saffran et al., 1996). The items in those artificial grammars are relatively easy to rehearse verbally, as they have a clear mental representation as items by being easy to pronounce or visualize. Unlike existing artificial grammar studies, new musical grammars force the cognitive system to represent items in a non-linguistic manner, thus minimizing the possibility of rote memorization of the items of an artificial grammar through covert verbalization or visual rehearsal of its exemplars. In addition to grammar learning, experiments in artificial musical systems may be useful for future investigations in cognitive science on topics such as the use of prototypes and exemplars in category learning (Zaki et al., 2003; Minda & Smith, 2001), where melodies in the new musical system can be treated as exemplars of a category and cognitive factors underlying category learning and discrimination can be examined (Zaki et al., 2003).

Research questions

To investigate knowledge acquisition in the new musical system, we employ a statistical learning approach where participants are given exposure to a set of melodies generated from an underlying chord progression, and subsequently tested for knowledge using the melodies. In particular, we use the artificial musical grammar as a tool to answer the following questions:

1. Can participants recognize melodies (grammatical items) they had heard?

2. Can they generalize their knowledge of the harmonic grammar towards new melodies?

3. Can they learn to form preferences for any aspect of the musical grammar?

To address questions 1 and 2, we employ two-alternative forced choice tests of recognition and generalization, where participants hear old and new melodies in both grammars, and are asked to choose the more familiar melody. Question 3 is addressed using a subjective preference rating task, where participants rate their preference of each melody after hearing it. Previously we have reported two experiments in which five and 400 melodies were presented to participants respectively (Loui et al., 2007). In one experiment, five melodies were presented for 25 minutes with 100 repetitions per melody. Recognition tests indicated that participants were at ceiling levels of accuracy in recognizing previously-encountered melodies, but generalization tests revealed that they were unable to generalize their knowledge to new items of the same grammar. Preference ratings, however, showed that participants formed an increased preference for previously encountered items. In another experiment, 400 melodies were presented non-repeatedly for 30 minutes. In addition to performing above chance for recognition tests, participants now also performed above chance in generalization tests, suggesting that after limited exposure to the melodies in the new scale, humans were able to infer the harmonic grammar underlying the melodies. These results are indicative of a rapid learning system in the human brain that can infer different kinds of knowledge based on its input. Knowledge of the underlying structure can be learned when given a large number of exemplars, whereas preference can be changed when given repeated exposure. These results suggest a double dissociation between grammar learning strategies and preference formation in the human brain.

Here we present two further experiments in which we manipulate the set size of melodies presented during exposure. Two experiments are presented in which the overall duration of exposure to melodies remain the same (30 minutes overall), but the number of melodies presented during the exposure phase differ. In the first experiment, 15 melodies are presented repeatedly for 27 repetitions, whereas in the second experiment, 10 melodies are presented for 40 repetitions, so that the overall duration of exposure was the same. Based on previous results (Loui et al., 2007) showing grammar learning when given large numbers of exemplars and preference change when given repeated exposure, we expect that performance on generalization tasks would be better in Experiment 1 whereas preference change would be more significant in Experiment 2.

Experiment 1

Method

• Participants

12 undergraduate students from the University of California at Berkeley participated in this study in return for course credit. Participants were recruited based on having normal hearing and five or more years of musical training. Four males and eight females participated, with an average age of 20 (range: 18 – 22) and an average of nine years of musical experience (range: 5 – 16) in various instruments including piano, violin, cello, double bass, guitar, trumpet, horn, percussion, and voice. All participants reported having normal hearing. Four of the participants reported having absolute pitch (an unusually high rate given the incidence of absolute pitch in the population — see Levitin & Rogers, 2004), but the results from participants who reported having absolute pitch did not differ from those who reported no absolute pitch, and as a result, data from these participants were included in the analysis. Informed consent was obtained from each participant prior to the start of the experiment.

• Stimuli & Materials

The experiment was conducted in a sound-attenuated chamber using a Dell PC and AKAI headphones. All stimuli were generated and presented using Max/MSP 4.6 (Zicarelli, 1998) at an approximate level of 70dB. Melodies were automatically generated in Max/MSP based on the finite-state grammar as described in the section entitled “A new musical system”. Sound examples in the new musical system are available at http://cnmat.berkeley.edu/.

• Procedure

Each experiment was conducted in four phases:

1. Exposure: 15 melodies were presented in random order to each participant, over the course of 30 minutes. Each melody contained eight notes of 500ms each, so that the duration of each melody was four seconds. Each note was a pure tone between 220Hz and 660Hz with a duration of 500ms, including envelope rise and fall times of 5ms each. The inter-onset interval between two notes in a melody was 500ms, and the silent pause between two melodies was 500ms long. Each melody was presented 27 times over 30 minutes of exposure. During the exposure phase participants were instructed to listen passively to the music without any specific attempt to analyze what was heard; no further information was given about the nature of the music. To alleviate boredom participants were provided with coloured pencils and paper and instructed to draw as a distracter task.

2. Forced choice recognition test: Each participant was given ten recognition trials. In each trial, participants were presented with two melodies sequentially. One of the melodies was from the set of 15 melodies presented during exposure. The other melody was generated from another grammar, which was derived from the retrograde of the chord progression that formed the exposure grammar. Participants were required to choose the melody that sounded more familiar to them.

3. Forced choice generalization test: Each participant was given ten generalization trials. In each trial participants heard two melodies, neither of which had been presented during the exposure period. One of the melodies was generated from the same chord progression as the exposure grammar, whereas the other melody was generated from another grammar derived from the retrograde chord progression. Participants were required to choose the melody that sounded more familiar to them.

4. Preference ratings: The preference ratings test included 20 trials for each participant. Each trial consisted of one melody being presented, followed by the participant's preference rating. Participants were to rate their preference of each melody on the scale of 1 to 7 (where 7 is best and 1 is worst). Three kinds of melodies could be presented in any trial: old melodies (from the exposure set), new melodies in the exposure grammar (but not from the exposure set), and new melodies in another grammar. Out of the 20 trials in this phase, melodies from ten trials were from the exposure grammar and the other ten were from the foil grammar. Five of the ten trials in the exposure grammar were old items (i.e. melodies presented during exposure), whereas the other five were new melodies that were not used during exposure.

• Data analysis

Data was grouped across subjects. In the two-alternative forced choice tests of recognition and generalization, participants' responses were scored as correct if they identified the melody that was generated from their grammar as being more familiar. (Since the foil was always in another grammar, it was possible to use generalization strategies to perform the recognition task, but one could not perform the generalization task based on rote recognition of a previously encountered melody.)

In the affect ratings tests, each participant's ratings were averaged for each of the three groups of melodies: old melodies in the same grammar, new melodies in the same grammar, and new melodies in a different grammar.

Results

Recognition scores were analyzed using a two-tailed t-test comparing recognition scores for each subject (in percent correct) relative to the chance level of 50%. Forced-choice tests of recognition yielded above-chance performance for recognition of melodies (t(11) = 5.17, p < 0.01, see Fig. 3), confirming that participants recognized melodies that had been presented in the exposure phase.

Figure 3.

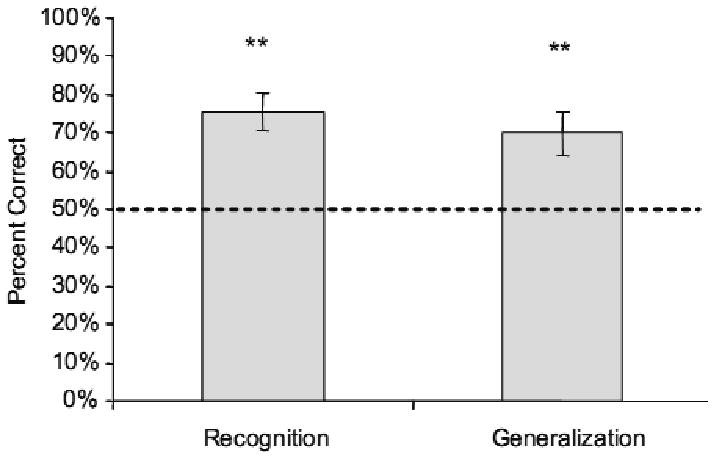
Experiment 1 forced choice results plotted as percent correct in recognition and generalization trials. Average across 12 participants. For all figures, ** = p < 0.01; error bars indicate between-subject standard errors. Dashed line indicates chance levels of performance.

Generalization scores were analyzed in the same manner as recognition scores, using a two-tailed t-test comparing subjects' recognition scores against the chance level of 50%. Participants significantly generalized their familiarity to the new instances of the same grammar (t(11) = 3.46, p < 0.01). Figure 3 shows results from the recognition and generalization tasks following exposure to 15 melodies. The significantly above-chance performance in both recognition and generalization tests suggest that participants were not only able to recognize the rote items that they had heard, but could also learn the underlying structure of their given musical grammar after a half-hour exposure to 15 melodies repeating 27 times each.

Preference ratings were assessed in an Analysis of Variance (ANOVA) comparing participants' average ratings for the three groups of melodies: old melodies from the exposure grammar, new melodies from the exposure grammar, and melodies from the alternate grammar. No significant differences were observed among ratings for old, new, and other-grammar melodies (F(2,33) = 0.96, n. s.). Figure 4 plots the average preference ratings across participants for this experiment, showing similar ratings across all three groups of melodies. Results from the preference portion of the present listening tests suggest that exposure to 27 repetitions of 15 melodies did not lead to significant changes in preference.

Figure 4.

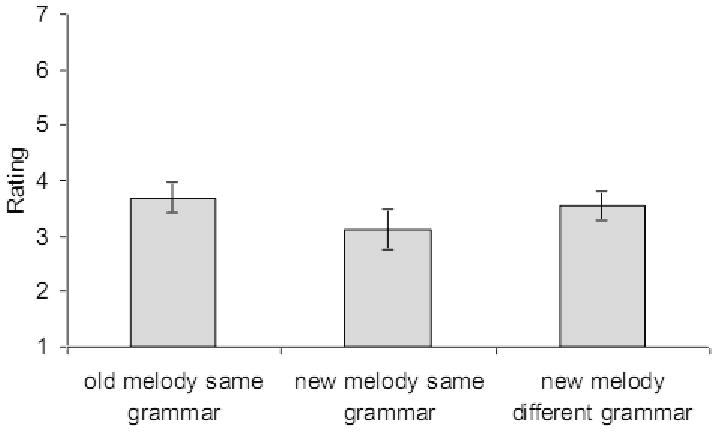
Experiment 1 preference ratings results plotted as average ratings across 12 subjects for old melodies in the same grammar, new melodies in the same grammar, and new melodies in another grammar.

Conclusion

After a 30-minute period of exposure to 15 melodies, participants were above chance at recognizing previously-encountered melodies. In addition, participants significantly identified new melodies generated from the same grammar as being more familiar than melodies from another grammar, suggesting that they learned the underlying grammar that generated the melodies. This suggests that when given limited exposure to a sufficiently large set of exemplars of a musical grammar, the human brain could rapidly infer structure within music.

Preference ratings showed no significant differences between conditions. Thus the melodies that participants had previously encountered, which the forced choice tests had shown that participants could recognize, did not influence their musical preferences.

One possible explanation for this null result was that two conflicting effects were at work against each other, where participants differed between two strategies used: forming unconscious preferences for previously-exposed items, and consciously recognizing familiar items and thus rating them as less preferable. This view represents a tension between the implicit system of affect formation and the explicit system of recognition (Bornstein, 1989; Peretz et al., 1998), and would predict drastic individual differences in ratings for different types of melodies resulting in a null effect overall. To address this possibility, an analysis of individual participants' ratings for each condition was conducted. Results did not show any distinctive tendency for participants to prefer new melodies over familiar ones; rather, each participant tended to give similar ratings to all melodies regardless of grammaticality or prior exposure. While it was possible that the artificial musical sounds we used were simply too impoverished to induce a change in affective response, our hypothesis was that the current exposure parameters (15 melodies repeating 27 times each) were insufficient to cause changes in preference. Based on previous observations of preference increase following repeated exposure to a smaller number of melodies (Loui et al., 2007), we expect that exposure to more repeating melodies, for the same overall period of time, may lead to change in preference.

Experiment 2

In Experiment 1, it was shown that following a half-hour of exposure to 15 melodies repeating 27 times each, participants could recognize previously heard melodies as well as identify new melodies in the same grammar. This suggests fairly fast learning of musical grammars. However, when the task was to rate their preferences for melodies, participants' preference ratings among familiar, grammatical, and ungrammatical melodies were similar. This was unexpected based on results from previous literature using familiar and unfamiliar melodies (Meyer, 1903; Peretz et al., 1998) as well as patchwork compositions (Tan et al., 2006) which had shown that repeated exposure to unfamiliar melodies would lead to some increased liking of the melodies. While it was possible that the observed lack of change in preference ratings was due to the unemotional stimuli used in Experiment 1, it was previously observed that highly repetitive exposure to a small set of melodies (five melodies repeated 100 times each) generated from the same artificial musical system used in Experiment 1 of the present study led to increased liking as evidenced by increased preference ratings for familiar items (Loui et al., 2007). Thus it would seem that by increasing the number of repetitions in the next experiment, it may be possible to induce preference change for familiar and/or grammatical melodies.

In Experiment 2, the number of melodies presented during the exposure phase was decreased from 15 to 10, while the exposure period remained the same such that participants were presented with more repetitions of each melody compared with Experiment 1. Instead of 15 melodies being presented for 27 times each, 10 melodies were presented for 40 times each in the following experiment. All other experimental procedures were the same as Experiment 1.

Method

• Participants

12 university undergraduates from the University of California at Berkeley were recruited using the same criteria as Experiment 1. Participants included 3 males and 9 females in the age range of 18 to 24 years (average = 20 years) who had an average of 7 years of musical training (range = 5 to 11 years) in various instruments including piano, cello, flute, piccolo, clarinet, and voice. All participants reported having normal hearing, and one participant reported having absolute pitch. None of the participants in Experiment 2 had previously participated in Experiment 1.

• Stimuli, Materials

All stimuli and materials were the same as Experiment 1. Procedures were the same as Experiment 1 except only 10 melodies were used. These ten melodies were randomly selected out of the 15 from Experiment 1.

• Procedure

Experiments included the four phases identical to Experiment 1: Exposure, forced choice recognition test, forced choice generalization test, and preference ratings test. The only difference between Experiment 2 and Experiment 1 was in the exposure phase: 10 melodies were presented in random order to each participant, over the course of 30 minutes. Each melody was presented 40 times during the course of 30 minutes of exposure.

• Data analysis

Recognition and generalization scores were compared against chance, whereas average preference ratings were compared across the three types of melodies in the same manner as in Experiment 1.

Results

Participants performed significantly above chance in the two-alternative forced choice recognition test (t(11) = 20.1, p < 0.01), yielding near-ceiling levels of performance (average = 91% correct; SE = 2%).

Generalization tests, however, yielded only chance levels of performance (average = 49% correct; SE = 5%; t(11) = 0.16, n. s.). Thus, participants did not generalize their knowledge to new melodies in the grammar. Figure 5 shows recognition and generalization results from Experiment 2.

Figure 5.

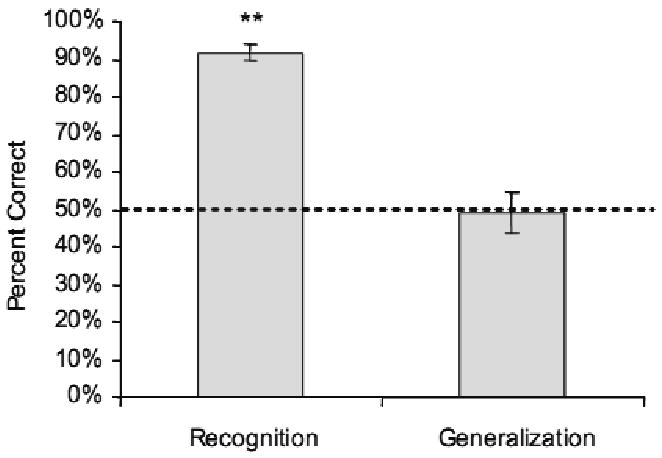
Experiment 2 forced choice results.

In preference rating tests, ratings for old melodies were rated as more preferable than new melodies in either grammar (old melodies same grammar: average = 4.33, SE = 0.32; new melodies same grammar: average = 3.65, SE = 0.27; different grammar: average = 3.65, SE = 0.26). An omnibus analysis of variance comparing ratings with the fixed factor of melody type (old melodies same grammar, new melodies same grammar, different grammar) and the random factor of individual subjects showed a significant effect of melody type (F(2,22) = 17.4, p < 0.001). In addition, paired samples t-tests showed that ratings for old melodies in the same grammar were significantly different from ratings for the other two groups of melodies (old versus new melodies in the same grammar: t(11) = 4.76, p = 0.001; old melodies versus melodies in the other grammar: t(11) = 4.31, p = 0.001), whereas ratings for new melodies in the same grammar were undifferentiated from ratings for melodies in the other grammar (t(11) = 0.011, p = 0.99.) Figure 6 summarizes results from the preference ratings for Experiment 2.

Figure 6.

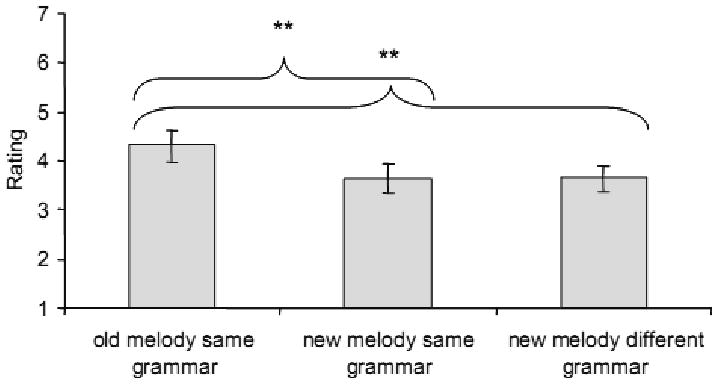
Experiment 2 preference ratings results.

Conclusion

When exposed to 10 melodies in a new musical grammar repeating 40 times each, participants unambiguously recognized melodies they had heard before, but did not generalize their knowledge to new instances of the same grammar. This suggests that participants were engaging in rote memorization of the smaller number of melodic exemplars, rather than learning a generalized form of the grammar. Old melodies in the same grammar were rated as more preferable than new melodies in the same grammar or new melodies in a different grammar, suggesting that repeated listening to melodies can result in changes in preference.

Comparing Experiment 2 to Experiment 1, we note that decreasing the number of exposure melodies from 15 to 10 led to increased recognition rate but decreased performance in generalization. However, with the increase in number of repetitions for each melody, participants rated familiar melodies as more preferable. The increased exposure to each melody resulted in increased preference for familiar items, replicating the Mere Exposure Effect (Zajonc, 1968) in the domain of music (Peretz et al., 1998) and in accordance with a previous study using artificial musical systems where few melodies were presented repeatedly (Loui et al., 2007).

General discussion

The present study investigated the learning and liking of a new musical grammar following a half-hour period of exposure to melodies in a new musical system. Specifically, the two experiments reported here investigate effects of the input on learning versus liking. While both experiments used the same musical grammar, Experiment 1 involved presenting more melodies fewer times each, whereas Experiment 2 presented a smaller set size of melodies with more repetitions. Experiment 1 showed that participants recognized melodies they had heard, and could generalize their knowledge to new melodies composed in the same grammar. In this experiment, no effects of preference change were observed. In Experiment 2 participants' showed superior recognition but chance levels of generalization, coupled with increased ratings for previously-heard melodies.

The forced choice results here suggest that large numbers of melodies lead to an internalization of grammatical rules, whereas repeated presentation of fewer melodies may result in rote memorization. This interpretation is consistent with the proposed distinction between two mechanisms of learning and memory, a Simple Recurrent Network (SRN) and a fixed memory buffer (Kuhn & Dienes, 2007), each of which may account for some aspects of musical knowledge, learning, and enjoyment. Investigating the acquisition of artificial musical systems may provide new insight into existing debates in cognitive science about grammar and category learning. More specifically, models of category learning have fallen under two families: prototype-based models (e.g. Minda & Smith, 2001) which state that the categorization space is characterized by central points, or prototypes, around which objects of a category may cluster; another family of models is exemplar-based (e.g. Zaki et al., 2003), where a category is defined by the set of exemplary items in space. Because it is not clear that participants inferred a prototype from melodies they heard, whereas each melody is clearly an exemplar of its underlying grammar, these results appear to be consistent with an exemplar-based model of categorization. However, the learning documented in this study closely resembles a system which continuously monitors conditional or transitional probabilities between tones to build an updated representation of the statistical structure we identify as grammar. Thus, a Bayesian learning framework may be at work in acquiring new musical structures (Tenenbaum & Griffiths, 2001). Future studies will attempt to tease apart these models of learning by analyzing the high-order statistics within specific melodies that cause success or failure in learning.

Preference ratings revealed that previously heard melodies were more preferable than new melodies, suggesting that repeated exposure to an unfamiliar musical system could influence musical preference. This is similar to the classic Mere Exposure Effect (Zajonc, 1968) as well as seminal studies in the psychology of music (Meyer, 1903) which demonstrate increased preference following repeated exposure in music and other domains. It is interesting to speculate on why such a small change in the input could result in a completely different pattern of results. Perhaps the ratio of repetitions to different melodies in the exposure stream might have triggered the use of different listening strategies in participants. Specifically, a shifting of attention between the repetitions and variability might be enhancing the size of the effects in the directions observed here. Nonetheless, our present claim is not in having discovered exactly how many repetitions are necessary before significant preference change, or precisely how many exemplars are necessary before seeing generalization, especially as these numbers may change depending on duration, prior familiarity, and other aspects of the input. Rather, we emphasize the pattern of results here: more variability leads to grammar learning, whereas more repetition leads to preference change. This may operate at an unconscious level (Bornstein & D'Agostino, 1992; Bornstein & D'Agostino, 1994), leading to larger observed Mere Exposure Effects in subliminally presented stimuli (Bornstein & D'Agostino, 1992).

Taken together, these experiments show that given limited exposure to a novel musical system, humans can exhibit rapid statistical learning to develop expectations that conform to the musical grammar. Increasing the number of exemplars of the musical grammar may a) help to enhance sensitivity to the underlying statistics of a grammar; and b) aid learners in generalizing the acquired statistics to novel instances. On the other hand, preference for melodies seems to be driven by repeated exposure, rather than variability in the exposure set. These results suggest a dissociation between musical preference and grammatical knowledge; preference may be a result of recognition and familiarity. It is interesting that while a clear preference increase was observed in Experiment 2 for old melodies, this preference did not generalize to new melodies in the same grammar. This raises important questions about the generalizability of preferences. Past studies on the Mere Exposure Effect have observed generalization of preferences to previously-unencountered items of a similar structure (Zajonc, 2001); it remains to be seen whether more extensive exposure — over multiple days such as in one's cultural exposure to common-practice music, would lead to the generalization of preferences. While the Mere Exposure Effect is probably only one of many important factors that predict musical preference, future work could address the contribution of exposure towards emotion in music, especially with regard to Meyer's (1956) model of expectancy violation and arousal, and Berlyne's (1971) model relating stimulus novelty and complexity to hedonic value in aesthetics. Currently we are conducting follow-up studies to further examine these links between familiarity, grammar, and preference.

We believe that artificial musical systems offer a new approach for music perception and cognition, and can also be applied more generally to the psychology of learning. Musical knowledge, in particular as it is quantifiable in the formation of musical expectations, has been posited as distinguishable between schematic and veridical expectations (Justus & Bharucha, 2001). Schematic expectations were considered to be reflective of a long-term knowledge of musical rules, whereas veridical expectations were a result of memory for specific instances of music (Justus & Bharucha, 2001). Huron (2006) posits a third type of expectation: dynamic adaptive expectation, which allows the short-term memory to integrate a new experience of music into a novel musical schema. The present experiments make use of dynamic adaptive expectations and are consistent with the view that expectations can be rapidly learned from a novel musical experience. Similar studies conducted on participants without formal musical training suggest that nonmusicians behave similarly as musicians in the learning and liking of new musical grammars (Loui et al., in review); thus these effects probably do not result from formal musical education, but from an implicit learning mechanism similar to that proposed by the statistical learning theory in language (Saffran et al., 1996). Ongoing work also uses Event-Related Potentials to study the perception of this new musical system; results may help characterize neural mechanisms underlying the learning and liking of new sounds.

Figure 1.

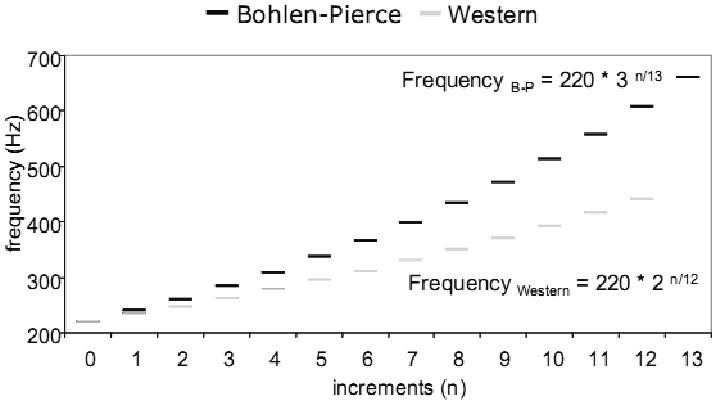
Frequencies along the Bohlen-Pierce scale and the equal-tempered Western chromatic scale.