Abstract
Previous studies indicate that visual working memory performance increases with age in childhood but it is not clear why. One main hypothesis has been that younger children are less efficient in their attention, specifically less able to exclude irrelevant items from working memory to make room for relevant items. We examined this hypothesis by measuring visual working memory capacity under a continuum of 5 attention conditions. A recognition advantage was found for items to be attended as opposed to ignored. The size of this attention-related effect was adult-like in young children with small arrays, suggesting that their attention processes are efficient even though their working memory capacity is smaller than that of older children and adults. With a larger working memory load, this efficiency in young children is compromised. The efficiency of attention cannot be the sole explanation for the capacity difference.
Working memory is the set of several active memory representations concurrently guiding behavior. It is now well-known that the capacity of working memory, broadly defined, increases with age in childhood. It is not yet clear, though, which aspects of working memory account for this increasing capacity (for reviews, see Cowan & Alloway, in press; Reznick, in press). Perhaps the most fundamental distinction that can be drawn is between the storage function of working memory and the processes that affect how working memory is used. Working memory capacity has traditionally been considered as the result of storage and processing together (Baddeley & Hitch, 1974; Daneman & Carpenter, 1980). A performance difference could result from developmental change in processing. For example, in the recall of verbal lists, many researchers have pointed to the increase with age in the speed and proficiency of covert verbal rehearsal as an important factor in working memory development (e.g., Flavell, Beach, & Chinsky, 1966; Henry, 1991; Hulme & Tordoff, 1989; Kail & Ferrer, 2007; Ornstein & Naus, 1978). Aside from this instance, though, there is a great deal of uncertainty regarding the basis of working memory development and whether it stems from storage and/or processing changes.
Research on Visual Working Memory and Attention
Recent research on working memory has made extensive use of a procedure that minimizes the role of verbal processes and tests memory for a set of visual objects (Luck & Vogel, 1997). On the basis of this type of procedure, some researchers have argued that individual differences in capacity depend on the ability to filter out irrelevant items so as to fill working memory with relevant items (e.g., McNabb & Klingberg, 2008; Vogel, McCollough, & Machizawa, 2005), a view that is popular in the field (e.g., Kane, Bleckley, Conway, & Engle, 2001). On each trial of the Luck and Vogel procedure, an array of visual objects is presented and, after a short retention interval, a probe appears to test memory for this array. It has been shown that this kind of memory representation is not maintained verbally even in adults, inasmuch as the suppression of verbal rehearsal has little effect on performance (Morey & Cowan, 2004). In the version of the task that we use in the present article, the probe consists of a single object that is identical to the array object that was in the same location or differs from it in color. The task is basically to indicate whether the probe differs in color from its counterpart in the array, though we elicit further details from our participants. Adults typically can carry out this working memory task well if there are no more than 4 objects (with declining performance as the array set size increases), but children in the early elementary school years recall substantially fewer objects than adults (Cowan et al., 2005; Cowan, Naveh-Benjamin, Kilb, & Saults, 2006; Riggs, McTaggart, Simpson, & Freeman, 2006). It is not known why this developmental difference occurs.
The utility of the Luck and Vogel (1997) procedure is that it involves a simple task that has been well-researched in adults. Two studies have shown a close convergence between behavioral measures of working memory load in this type of task and activity in specific areas within the posterior parietal cortex (Todd & Marois, 2004; Xu & Chun, 2006). Considerable research has been conducted to determine whether individuals differ in the number of objects that can be kept in working memory at once, or in the ability to limit the access of irrelevant, potentially distracting objects to working memory. Such objects could displace some of the relevant objects in working memory. The results of these adult studies, however, have been mixed.
This research on the reason for the capacity limit has been based on arrays with more than one type of object. For example, Vogel et al. (2005) required that participants attend to the orientations of bars presented in one color, but not another. The dependent measure was an event-related potential index of working memory load. It showed that low-span individuals’ brains included the irrelevant items in the working memory load; 2 relevant plus 2 irrelevant objects caused as much load as 4 relevant objects. In contrast, high-span individuals’ brains responded as if the irrelevant objects did not count toward the working memory load. A similar result was obtained by McNab and Klingberg (2008) using a brain imaging technique. These studies have suggested that the ability to select relevant objects and filter out irrelevant ones is the primary basis of individual differences in working memory, in keeping with some investigators who have used very different procedures (e.g., Kane et al., 2001).
In contrast to these findings, though, other work with the Luck and Vogel (1997) type of procedure suggests that individual differences can arise from differences in storage capacity rather than differences in filtering out irrelevant items. Todd and Marois (2005) found individual differences in brain responses for arrays that did not include any distracters. Cowan, Fristoe et al. (2006) found individual differences in both the Luck and Vogel (1997) type of task and also a task that required filtering out a stimulus sequence in one modality while focusing attention on a stimulus sequence in another modality. Both tasks predicted intelligence in adults, but both of them picked up considerable unique variance in intelligence, indicating that storage capacity is an important component of individual differences in cognition.
Rationale for the Present Developmental Study
Another study leading to a similar conclusion (Gold et al., 2006) was the closest precursor to the present study. Gold et al. compared behavioral responses in adults diagnosed with schizophrenia to those of normal control participants using a task in which the arrays included two types of objects (e.g., circles and bars). The probe on a particular trial was an array duplicating only one type of object (e.g., circles). On most trials (e.g., in one experiment, 75%), the probe was a type of object that the participant had been led to expect. However, on a minority of trials (e.g., in one experiment, 25%), the probe was the other type of object. It was therefore possible to test both filtering capability and the storage function of working memory. First, the measure of filtering capability was the estimate of items retained from the expected (usually-tested) set minus those retained from the unexpected (not-usually-tested) set. For example, if a participant successfully attended to circles and ignored bars, then many more circles than bars should be retained in working memory and performance should be a lot higher when the probe was the set of circles than when it was the set of bars. Second, the measure of storage was the sum of the estimates of the number of items retained in working memory on usually-tested and not-usually-tested probe trials (e.g., circles plus bars). This indicates how many items are in working memory, regardless of how many of the available slots were taken up with the expected versus the unexpected shape.
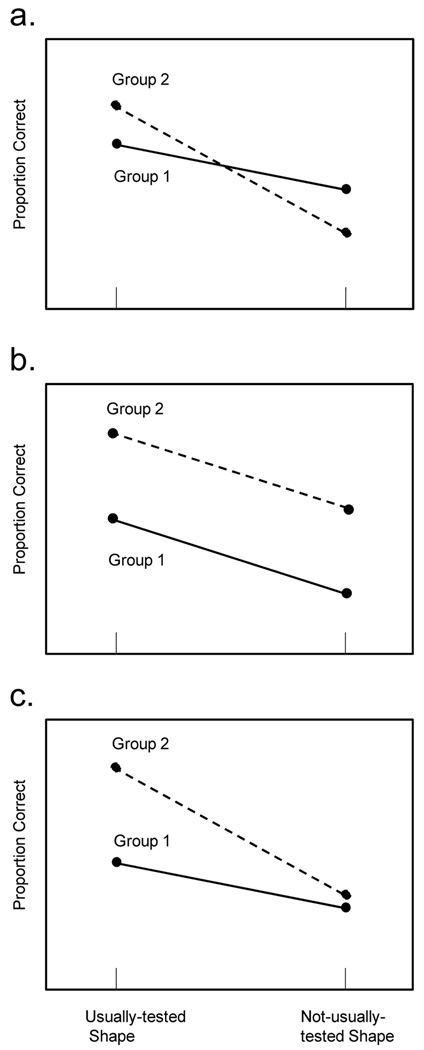
Figure 1 illustrates three different possible outcomes of this type of experiment, with any two participant groups. (The outcomes are based on a measure of the number of items in working memory that will be explained shortly.) In Figure 1a, the outcome is what would be expected if the groups differed only in the ability to select relevant items. The working memory advantage for the usually-tested items over the not-usually-tested items is greater in Group 2 than in Group 1, indicating that filtering ability is better in Group 2. The groups have the same overall amount in working memory (summing across the two conditions) but Group 2 allocates more of that capacity to the more relevant items. In Figure 1b, the outcome is what would be expected if the groups differed only in working memory capacity. The advantage of usually-tested over not-usually-tested items does not differ between the groups, but Group 2 recalls more items overall. Finally, in Figure 1c, the outcome is what would be expected if both factors contribute to the results. Group 2 recalls more items overall (producing a level difference), but also differentiates between usually-tested and not-usually-tested items better than Group 1 (producing a slope difference). The surprising finding of Gold et al. (2006) was that individuals with schizophrenia filtered out not-usually-tested items about as well as the control group, but simply included fewer items in working memory, conforming to the pattern shown in Figure 1b.
Figure 1.
Theoretical functions indicating the pattern of mean capacities to be expected for a less-advanced and a more-advanced group of participants (Groups 1 and 2) when attention is divided unevenly among items of two different shapes in an array to be retained in working memory. a. Expectation if the groups differ in the ability to filter out items of the not-usually-tested shape and fill working memory with usually-tested items. b. Expectation if the groups differ in the total capacity but not in filtering. c. Expectation if both factors operate together.
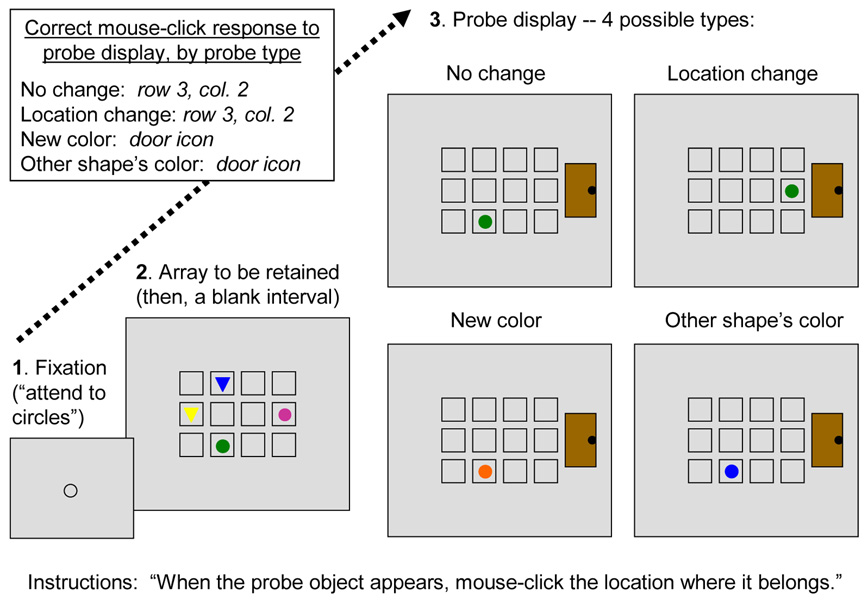
We adapted this method in several ways to examine the basis of the developmental increase in performance on the Luck and Vogel (1997) type of task. Our procedure is illustrated in Figure 2. We included two shapes, circles and triangles, in some arrays, with a different color for each object in the array. The subsequent probe was a single object (as in, e.g., Wheeler & Treisman, 2002). This probe was either identical to the item at the same location in the array or it was different in color (in one of three ways, as shown in the figure). The probe never differed in shape from the array object in the same location. To make the task interesting for children, the cover story was that the colored shapes represented “children” in a classroom and the task was to indicate with a mouse click where the probe child belonged: in the “seat” in which the probe was shown if the probe was identical to the array item in that location, in a different seat in the “classroom” if there was such a location containing an item identical to the probe or, otherwise, out the “door”. In the primary scoring method, both other-seat and out-the-door responses were coded as detection of a change. The results were used to estimate the number of array objects encoded into a participant’s working memory, k, according to a commonly-used formula (Cowan, 2001; Cowan et al., 2005) that takes into account guessing. The formula is derived from the assumption that if the array item corresponding to the probe is one of k items in working memory when the probe arrives, the participant will know if the probe changed color or not; otherwise, the participant will guess.
Figure 2.
Main events occurring in each experimental trial. (1) The fixation object reminded the participant where to look and what shape was to be attended. In trial blocks in which either shape could be tested equally often, a "+ " appeared instead. (2) A brief array of objects appeared (4 or 6 objects total; half circles and half triangles, except on 1-shape trial blocks). A blank retention interval followed. (3) The probe display, one of four types as shown, appeared until a mouse click response was made. Directions and correct responses are shown in the figure.
To gain a detailed understanding of the role of attention in the task, we used a continuum of 5 attention conditions (presented in 4 types of trial block). The 5 conditions in the order of diminishing attention to the object in the shape that was tested were 1-shape, 100%, 80%, 50%, and 20%. These conditions came from different trial blocks except that the 80% and 20% conditions came from the same trial block. Participants were instructed to pay attention to objects of one of the two shapes, except in the 50% condition, in which objects of both shapes were to be attended equally. The task was to remember the color and location of each colored shape that was to be attended. In 1-shape trial blocks, an array included all objects of the same shape so no filtering was needed. In 100% trial blocks, half of the array objects on each trial were the attended shape and half were the other shape. However, the probe always corresponded to an object in the assigned, attended shape so filtering was fully warranted. The 80%-20% trial blocks had the same mixture of shapes as in the 100% trial blocks but, on 20% of the trials, the probe was an item of the shape that was to be ignored according to the instructions. The task was to attend to the shape that was probed 80% of the time and ignore the shape that was probed only rarely, 20% of the time. Critically, the 80%-attended and 20%-unattended trials were scored separately. These instructions and presentation probabilities were meant to provoke a strategy of filtering out the less-relevant, 20%-probed shape most of the time (yet, with attention potentially divided, unevenly, between the shapes). Last, in the 50%-50% trial blocks, attention was to be divided evenly between items in the two shapes. Half of the trials had a circle probe and the other half had triangle probe and performance was collapsed across these trials. This condition should produce results intermediate between the 80% and 20% conditions as attention is shared evenly between shapes.
According to a theory in which the ability to control attention is what develops, it would be expected that the mean k across conditions will not differ between groups but that the effects of attention will be larger in more mature groups. In contrast, the expectation of a storage growth theory of working memory development is that there will be a larger mean k value for more mature participants in every attention condition, but with essentially the same magnitude of attention effects at every age group. A hybrid theory also is possible, with both higher mean k values and larger attention effects in more mature participants.
Most of the conditions were run with arrays of either 2 circles and 2 triangles or 3 circles and 3 triangles, and the attention instructions for the trial block were intended to influence the relative allocation of attention to one shape versus the other. Pilot data suggested that our youngest group was at about the lowest age at which the task could be carried out, and that the two set sizes we used were, respectively, challenging for the younger participants (2 items per shape) and challenging even for the older participants (3 items per shape).
In the 1-shape condition, however, there were 2, 3, 4, or 6 items of one shape and none of the other shape. Including only relevant objects and including supra-capacity set sizes is traditional in this line of research stemming from Luck and Vogel (1997). We included the 1-shape condition with these array set sizes as a benchmark for comparison with prior child developmental studies of visual working memory capacity (Cowan et al., 2005; Cowan, Fristoe et al., 2006; Riggs et al., 2006). Also, the k estimate sometimes is found to decline from its peak with increasing set sizes, possibly because the encoding process becomes less efficient with too many items to be encoded at once. The array set sizes in the 1-shape condition allow a comparison across age groups in terms of how important this encoding problem is. It also is possible to use this condition to check the storage cost of dividing attention between two shapes. For example, if there is no cost of dividing attention between two shapes, the k value on 50% trials with 4 (or 6) objects in all, added across circles and triangles, should approximate the k value on 1-shape trials with 4 (or 6) objects. If there is a cost of dividing attention, the k value on 50% trials should be smaller than that.
Finally, the different types of changes that could occur between the array and the probe (as shown in Figure 2) were meant to examine in detail what information was included in the working memory representation of the array in each age group. It is possible to detect that a new color has appeared in the array on the basis of a feature memory, but it requires the binding between the color and location to detect that the probe appears in a color that was present at a different location in the array. Previous work showed that, in comparison to adults, children in the early elementary school years have a deficit in this bound information relative to feature information (Cowan, Naveh-Benjamin et al., 2006). There has been debate regarding whether binding in working memory requires attention beyond that required to place objects in working memory in the first place; recent results suggest not (Allen, Baddeley, & Hitch, 2006; Cowan, Naveh-Benjamin et al., 2006). That being the case, it is of interest to see whether the ability to notice a change in the binding of color to location is enhanced when the probe appears in a color that was originally used for a color of the non-attended shape.
Method
Participants
N=30 per age group, including children in Grades 1–2 (7–8 years old) and Grades 6–7 (12–13 years old), and college students.
Apparatus and Stimuli
The computer monitor was located in a private, sound-attenuated booth. Figure 2 shows the stimulus arrangement. The possible colors for circles and triangles included black, white, red, blue, yellow, green, orange, purple, brown, and pink. Within each array, no color was used for more than one object. Shapes were displayed inside an 8.19 cm (horizontal) × 6.72 cm (vertical) rectangle, comprising a 4 × 3 arrangement of 1.77-cm-wide squares. Each shape was sized to fit inside a 0.57 cm box. On the probe screen only, a 1.38 × 2.35 cm door appeared to the right of the grid.
Procedure
Our procedure (Figure 2) was engaging for children. The cover story was that the array objects (circles and triangles) represented children in a classroom (grid). The probe object was always presented in the same location as an array object of that same shape, but not necessarily of that same color. The task was to use the mouse to click on the place where this probe object belonged: in the same place as it was shown, in a different place on the grid, or nowhere on the grid. In the latter case, the participant was to click on the door icon, sending the “child” out of the room.
Each participant was assigned a shape (circle or triangle) to be attended throughout the session, although trial blocks differed in attention instructions. On each trial, an unfilled shape on the computer screen for 1000 ms reminded the participant what shape (circles or triangles) to attend throughout the trial block; or '+' indicated that attention should be divided between both shapes. This signal was replaced by an array of objects for 500 ms, then a 1500-ms blank screen, and then a grid that included the probe object and door icon. These remained until the participant indicated by mouse click where the probe object belonged.
There were 4 blocks of trials that yielded 5 conditions that fit along a continuum in terms of the necessary amount of attention to the tested stimuli. As summarized in Table 1a, the 5 conditions were 1-shape, 100%, 80%, 50%, and 20%. This last condition came from the same trial block as the 80% trials. Descriptions of the trial blocks are as follows.
Table 1.
| Table 1a. Features of each attention condition. | |||||
|---|---|---|---|---|---|
| Attention Condition | |||||
| Experimental Feature | 1-shape | 100% | 80% | 50% | 20% |
| Attention Trial Block | 1-shape | 100% | 80%–20% | 50% | 80%–20% |
| No. of Attended-shape Items | 2,3,4, or 6 | 2 or 3 | 2 or 3 | 4 or 6a | 2 or 3 |
| No. of Ignored-shape Items | 0 | 2 or 3b | 2 or 3b | 0 | 2 or 3b |
| No. of Shapes present | 1 | 2 | 2 | 2 | 2 |
| Probe typesc | 1–3 | 1–4 | 1–4 | 1–4 | 1–4 |
| Table 1b Features of each probe type. | ||||
|---|---|---|---|---|
| Probe Type | ||||
| 1. No | 2. New | 3. Location | 4. Other shape's | |
| Probe Feature | change | color | change | color |
| Probe’s color in array? | yes | no | yes | yes |
| Probe’s color in probe’s | ||||
| shape in array? | yes | no | yes | no |
| Probe identical to array | ||||
| item in that location? | yes | no | no | noa |
| Correct Response | same | out | specific | out |
| loc | diff loc | |||
| Acceptable response | same | any diff | any diff | any diff |
| for k analysis | loc | loc or out | loc or out | loc or out |
| Table 1c Trials per participant in each combination of attention condition and probe type. | |||||
| Attention Condition | |||||
|---|---|---|---|---|---|
| Probe Type | 1-shape | 100% | 80% | 50% | 20% |
| 1. No change | 32 | 30 | 32 | 24 | 8 |
| 2. New color | 16 | 10 | 16 | 8 | 4 |
| 3. Location Change | 16 | 10 | 16 | 8 | 4 |
| 4. Other shape's color | 0 | 10 | 16 | 8 | 4 |
Note. No. = number.
Attention divided between both shapes, equally represented in array
Same number of attended and ignored items
These probe type numbers refer to Table 1b.
Note. loc = array location, diff = different, out = the out door icon
The probe is the same shape as the array item at its location but the color is from an item elsewhere in the array of the other shape.
(1) In 1-shape trial blocks, an array included 2, 3, 4, or 6 objects of the same shape. In half of the trials, the probe object was an item from the array in its correct location (no-change trials). On one quarter of the trials, it was an item from elsewhere in the array (location-change trials) and, on the remaining quarter, it was an item that had not appeared in the array (new-color trials).
(2) In 100% trial blocks, half of the array objects on each trial were the attended shape and half were the other shape (2 of each or 3 of each). However, the probe always was in the assigned, attended shape. In half of the trials, the probe was an item from the array in its correct location (i.e., no-change trials). Probes in the remaining trials were evenly divided among three types: those identical to an item of that shape elsewhere in the array (i.e., location-change trials), those of a color found in an object of the unattended shape but with the probe itself in the attended shape (other shape’s color trials not found in the previous trial block), and those of a color not found anywhere in the array (i.e., new-color trials). In the latter two cases, the correct answer was the door icon.
(3) The 80%-20% trial blocks had the same conditions as in the 100% trial blocks except that, on 20% of the trials, the probe was in the shape that was to be ignored (as was the array item that had occupied that location). The probe types were otherwise the same for the 80% attended-shape and 20% ignored-shape trials. For each probed shape, no-change probes occurred on only 40% of the trials, to allow enough of each type of change trial even in the rare, 20% trials.
(4) In the 50%-50% trial blocks, 50% of the trials had a probe in the location of a circle in the array and 50% had a probe in the location of a triangle. The numbers of change- and no-change trials were distributed as in the 100% condition. Attention was to be divided between the two shapes and performance was collapsed across shapes in the analyses.
The trial blocks were run in the order listed in 1–4 above except that a second block of 1-shape trials occurred last. The numbers of trials in each trial block were set in a manner that allowed adequate trials of each type, including those that had to occur only rarely (in the 20% condition). Table 1b summarizes the characteristics of each probe type and, completing the summarization of the design, Table 1c indicates how many trials of each probe type occurred in each attention condition. Each trial block was preceded by 8 to 13 practice trials of its type (roughly proportional to the number of trial types within the trial block) which, unlike test trials, included accuracy feedback.
Data Analysis
For the analyses that included all 5 attention conditions, only trial types that existed for each condition were included. This excluded 1-shape trials with 4 or 6 objects, so that all included trials had 2 or 3 objects in the tested shape. It also excluded “other shape’s color” trials in the other trial blocks; these, of course, could not occur in 1-shape blocks. The two change trial types that contributed to the analyses (location change and new color) were equally weighted in the means. To examine capacity for detecting whether the object in the probed location had changed, same-location responses were labeled no-change judgments, whereas both the other-grid-location and door-icon responses were labeled new-probe judgments.
In the derivation of capacity for the probed shape, k (Cowan et al., 2005), we considered hits to equal the proportion correct judgment that the probe was new (not in the array) and false alarms, the proportion incorrect judgment that the probe was new. Assume k objects of the probed shape are encoded into working memory and, if the probe object is in working memory, the response will be correct. If the probe object is not in working memory, the participant presumably guesses "new" with probability g. Thus, for a set of A objects of the shape matching the probe, hits=k/A+(1−k/A)g and false alarms=(1−k/A)g. Combining these functions, k=A(hits-false alarms).
Results
Baseline Capacity: Results of the 1-Shape Condition
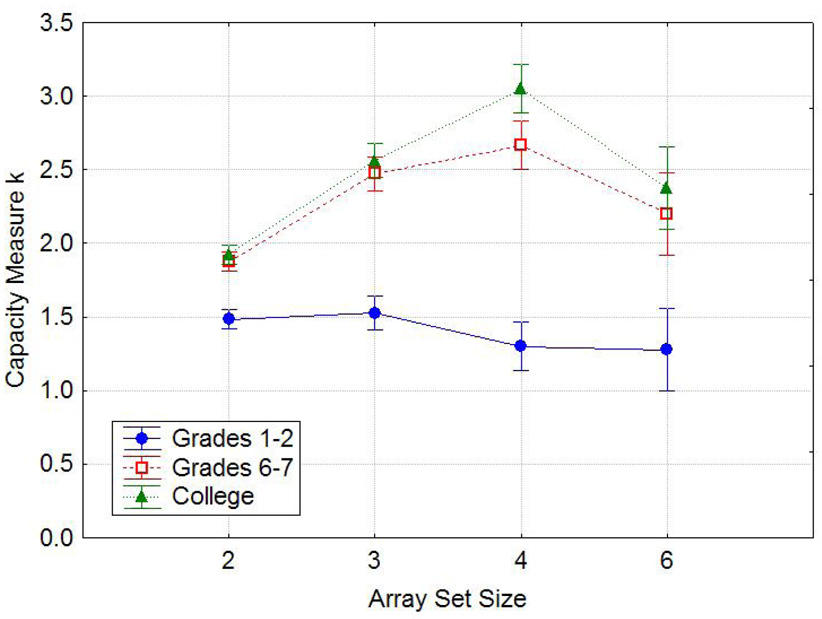
Figure 3 shows performance in each age group across array set sizes in the 1-shape condition. This condition yielded an effect of age group F(2,87)=27.40, p<0.001, ηp2=0.39 and of array set size (3,261)=8.01, p<0.001, ηp2=0.08, as well as an interaction of these two variables, F(6,261)=3.20, p<0.01, ηp2=0.07. A clear, monotonic effect of age group can be seen. Also, for each age group, the capacity estimates peaked at a certain array set size and then declined again at an even higher set size. Although this decline suggests that there was some inefficiency in encoding of the stimuli when the set size greatly exceeded the capacity, this inefficiency in encoding was no more severe for the young children than for the older children or adults. In particular, it can be seen that the drop from the peak k is, if anything, smallest in the youngest group and largest in the oldest group. When only the older two groups were included in the analysis, there was no significant effect of age group or interaction including that factor.
Figure 3.
The mean capacity measure k for each age group in 1-shape trial blocks, as a function of the number of items in the array. Error bars are standard errors.
Effects of Attention Condition
Overall analyses
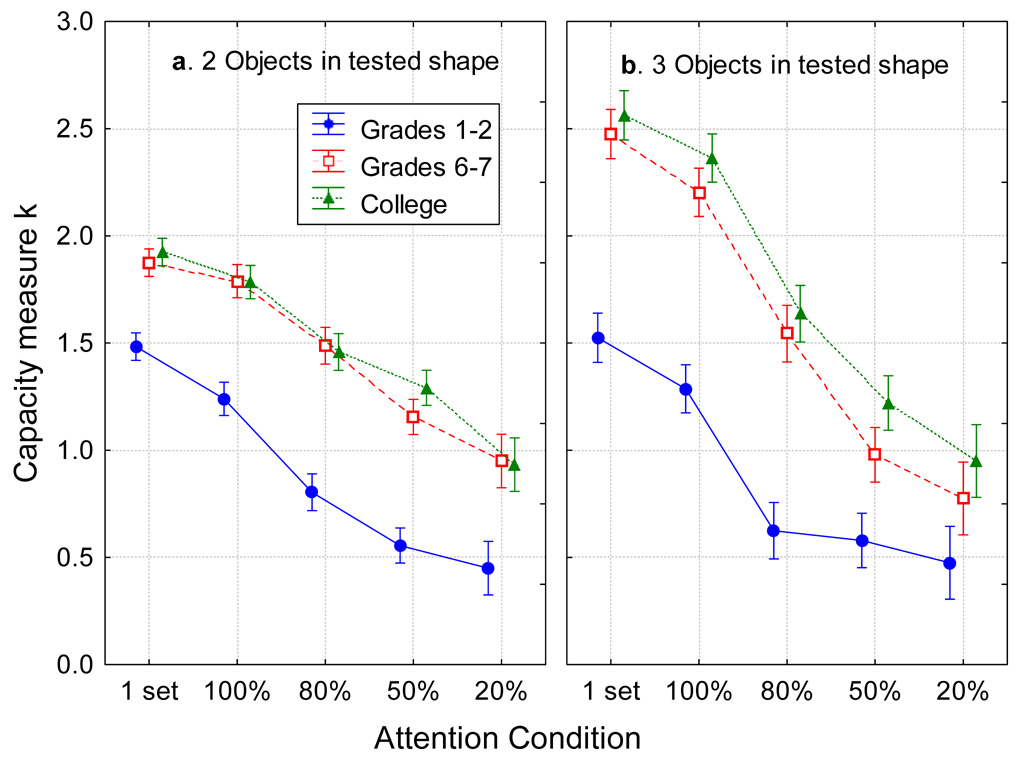
In ANOVAs of the capacities, the index of capacity increase is a main effect of age group, and the index of an increase in the efficiency of attention is an attention condition × age group interaction. The results of such analyses (below) indicate that, although capacity increased markedly with age in childhood, attention was adult-like for arrays with 2 objects of the tested shape (Figure 4a), but not completely so for arrays with 3 objects of the tested shape (Figure 4b). Specifically, with only 2 items of the tested shape there was no significant interaction between attention condition and age group, F(8,348)=0.86, p=0.55, ηp2=0.02. There was a large advantage of older children (M=1.52) and adults (M=1.61) over younger children (M=0.90), pooled SEM=0.06, F(2,87)=33.70, p<0.001, indicating a working memory difference that did not depend on the attention condition. With 3 items of the tested shape, however, there was an interaction between attention condition and age group, F(8,348)=2.40, p<0.05, ηp2=0.05. The advantage of older children and adults over younger children was large for strongly-attended objects but shrank as the strength of attention to the objects decreased. This may suggest more efficient allocation of attention by adults. Another possibility is that there was a floor effect for divided-attention conditions in young children though, below, we will rule out that interpretation for a subset of the data.
Figure 4.
The mean capacity measure k in each age group as a function of the attention condition. Within each panel, moving rightward, conditions reflect diminishing amounts of attention to be paid to the tested object. a. Arrays with 2 items in the tested shape. b. Arrays with 3 items in the tested shape. This capacity measure is based on combining responses to indicate if the probe matched the array item presented in that location, or differed from it. Error bars are standard errors.
Overall, there was again a large advantage of older children (M=1.60) and adults (M=1.75) over younger children (M=0.90), pooled SEM=0.09, F(2,87)=26.78, p<0.001. In a combined analysis, the difference between the pattern of results in these two array sizes produced a three-way interaction of array size, attention condition, and age group, F(8,348)=2.68, p<0.01, ηp2=0.06. In short, participants in all age groups allocated their attention in accord with instructions, provided that the working memory load was small, in which case the results were analogous to the capacity-growth prediction as illustrated in Figure 1b. When the working memory load was larger, though, young children were less adept at controlling attention and the results were analogous to the two-factor, capacity plus attentional control growth situation illustrated in Figure 1c. Similar results were obtained in an analysis in which the 1-shape trial blocks were excluded so that all probe types could be included.
Further analyses of the deployment of attention and capacity
A further test of the above conclusion is whether, in the 80%-20% trial blocks, participants of each age group retained objects corresponding to the expected shape (tested 80% of the time) in greater number than the other (20%-tested) shape. Post-hoc Newman-Keuls analyses indicated that this was the case for the older two age groups, for arrays with 2 objects and with 3 objects of the tested shape, p<0.001 in each case. For the two array sizes, respectively, the older children filled 39% and 33% of their capacity with the less-often-tested shape, and adults similarly filled 39% and 37% of their capacity with the less-often-tested shape. In Grade 1–2 children, however, this effect was significant for arrays with 2 objects of the tested shape, p<0.01, but not 3 objects, p=0.609. For these array sizes, respectively, these young children filled 36% versus 43% of their capacities with the less-often-tested shape. So, although young children's ability to attend to a 100% consistent cue extended to 3 objects of the tested shape, the ability to distribute attention unequally over two shapes with different test probabilities tended to break down for that set size.
It can be shown that young children’s low capacity in comparison to adults was not the result of poor filtering, in any trial block. To demonstrate this, we compared k values on 80% trials in adults to the sum of k values on 80% and 20% trials in young children. This slants the comparison in favor of the young children by giving them credit for knowledge of items of either shape, whereas adults are only given credit for items that were of the shape to be attended most closely. In an ANOVA of these two age groups with the array set size as a within-participant factor, there was only a main effect of age group, F(1,58)=5.39, p<0.05, ηp2=0.09. The mean k value for adults on 80% trials only (M=1.55) was larger than the young children’s mean sum of k values on 80% plus 20% trials (M=1.18), pooled SEM = 0.11. This result indicates that poor filtering on the part of young children cannot explain their lower storage capacity (although that could play some role).
Two additional analyses were carried out to determine whether there was a storage cost of dividing attention between two shapes or filtering out one shape. In one analysis, the responses for 1-shape trials with 4 and 6 objects were compared to the 50%-50% trial blocks; the latter had the same number of objects in all, but divided between two shapes. Given that the k value in the latter case was calculated on the basis of the tested shape only, doubling this value yields an estimate of how many items were held in working memory in this condition, and the doubled values were used in the analysis. It included age group as a between-participant factor and two within-participant factors, trial block (1-shape or 50%-50%) and array set size (4 or 6 items in all). This analysis yielded no significant effects involving the trial block. Another analysis was conducted in which the k values for 80% and 20% trials were added together to yield the capacity on 80% - 20% trial blocks, and that summed capacity was compared to the capacity in the 1-shape trial blocks. With the same factors as in the previous analysis, this analysis also yielded no significant effects involving the trial block. (For all such effects in both analyses, ηp2 ≤ 0.04.) These analyses thus yield no evidence for any age group that there was a storage cost of dividing attention or of filtering out one shape, which strengthens the inference that there were storage capacity differences across age groups.
Analysis by the Type of Probe
The distribution of responses across types of probe was similar across attention conditions, as shown by the accuracy for all experimental conditions in Table 2 and, for illustrative purposes, by the detailed breakdown of responses for the 100% condition in Table 3. These tables show that the largest age effects in proportion correct occurred for location-change and no-change trials. Those trial types may be developmentally difficult because the probe items were not new objects, as in the remaining trial types; they required binding of objects to array locations (cf. Cowan, Naveh-Benjamin et al., 2006).
Table 2.
Mean Accuracy in All Conditions
| Tested | Condition | Grades | SD | Grades | SD | College | SD |
|---|---|---|---|---|---|---|---|
| Set | 1–2 | 6–7 | |||||
| Size | |||||||
| 1-Shape Trial Blocks | |||||||
| 2 | Location Change | 0.62 | 0.24 | 0.93 | 0.15 | 0.92 | 0.18 |
| New Color | 0.87 | 0.17 | 0.95 | 0.12 | 0.98 | 0.08 | |
| No Change | 0.84 | 0.25 | 0.96 | 0.07 | 0.98 | 0.06 | |
| 3 | Location Change | 0.47 | 0.23 | 0.79 | 0.23 | 0.77 | 0.24 |
| New Color | 0.74 | 0.21 | 0.92 | 0.15 | 0.88 | 0.16 | |
| No Change | 0.65 | 0.25 | 0.86 | 0.14 | 0.92 | 0.12 | |
| 4 | Location Change | 0.30 | 0.26 | 0.58 | 0.30 | 0.67 | 0.27 |
| New Color | 0.72 | 0.28 | 0.82 | 0.22 | 0.87 | 0.14 | |
| No Change | 0.47 | 0.26 | 0.76 | 0.20 | 0.83 | 0.16 | |
| 6 | Location Change | 0.15 | 0.19 | 0.35 | 0.31 | 0.39 | 0.28 |
| New Color | 0.68 | 0.24 | 0.68 | 0.29 | 0.68 | 0.24 | |
| No Change | 0.37 | 0.19 | 0.52 | 0.21 | 0.54 | 0.19 | |
| 100% Trial Block | |||||||
| 2 | Location Change | 0.61 | 0.31 | 0.88 | 0.19 | 0.91 | 0.17 |
| New Color | 0.85 | 0.17 | 0.95 | 0.10 | 0.91 | 0.14 | |
| No Change | 0.73 | 0.28 | 0.94 | 0.08 | 0.95 | 0.09 | |
| Other Shape's | 0.77 | 0.26 | 0.92 | 0.17 | 0.88 | 0.21 | |
| Color | |||||||
| 3 | Location Change | 0.36 | 0.28 | 0.73 | 0.29 | 0.79 | 0.25 |
| New Color | 0.77 | 0.22 | 0.85 | 0.19 | 0.90 | 0.13 | |
| No Change | q | 0.22 | 0.78 | 0.17 | 0.84 | 0.17 | |
| Other Shape's | 0.65 | 0.26 | 0.85 | 0.18 | 0.84 | 0.20 | |
| Color | |||||||
| 80% Trials (Within 80%–20% Trial Blocks) | |||||||
| 2 | Location Change | 0.34 | 0.19 | 0.69 | 0.22 | 0.68 | 0.24 |
| New Color | 0.83 | 0.17 | 0.85 | 0.17 | 0.89 | 0.14 | |
| No Change | 0.52 | 0.25 | 0.82 | 0.16 | 0.79 | 0.16 | |
| Other Shape's | 0.65 | 0.21 | 0.76 | 0.22 | 0.68 | 0.29 | |
| Color | |||||||
| 3 | Location Change | 0.18 | 0.16 | 0.48 | 0.31 | 0.45 | 0.24 |
| New Color | 0.72 | 0.26 | 0.80 | 0.18 | 0.83 | 0.18 | |
| No Change | 0.35 | 0.24 | 0.61 | 0.25 | 0.66 | 0.18 | |
| Other Shape's | 0.69 | 0.23 | 0.69 | 0.20 | 0.62 | 0.27 | |
| Color | |||||||
| 50% (Divided Attention) Trial Blocks | |||||||
| 2 | Location Change | 0.24 | 0.25 | 0.56 | 0.31 | 0.61 | 0.31 |
| New Color | 0.71 | 0.33 | 0.84 | 0.23 | 0.93 | 0.15 | |
| No Change | 0.41 | 0.21 | 0.72 | 0.18 | 0.73 | 0.19 | |
| Other Shape's | 0.56 | 0.32 | 0.69 | 0.24 | 0.62 | 0.31 | |
| Color | |||||||
| 3 | Location Change | 0.17 | 0.21 | 0.37 | 0.29 | 0.33 | 0.20 |
| New Color | 0.72 | 0.32 | 0.76 | 0.26 | 0.73 | 0.30 | |
| No Change | 0.31 | 0.22 | 0.46 | 0.21 | 0.54 | 0.17 | |
| Other Shape's | 0.52 | 0.29 | 0.58 | 0.27 | 0.65 | 0.30 | |
| Color | |||||||
| 20% Trials (Within 80%–20% Trial Blocks) | |||||||
| 2 | Location Change | 0.17 | 0.27 | 0.50 | 0.44 | 0.63 | 0.41 |
| New Color | 0.65 | 0.37 | 0.78 | 0.39 | 0.85 | 0.23 | |
| No Change | 0.38 | 0.29 | 0.57 | 0.31 | 0.61 | 0.31 | |
| Other Shape's | 0.55 | 0.38 | 0.80 | 0.31 | 0.55 | 0.40 | |
| Color | |||||||
| 3 | Location Change | 0.22 | 0.31 | 0.27 | 0.34 | 0.33 | 0.36 |
| New Color | 0.80 | 0.31 | 0.72 | 0.39 | 0.68 | 0.33 | |
| No Change | 0.23 | 0.24 | 0.38 | 0.31 | 0.51 | 0.29 | |
| Other Shape's | 0.62 | 0.43 | 0.65 | 0.30 | 0.62 | 0.36 | |
| Color | |||||||
Note. For location changes, responses were counted as correct in this table only if the correct location was indicated.
Table 3.
Breakdown of Performance by Response Types for the 100% Condition
| Response Type | |||||
|---|---|---|---|---|---|
| Trial | Age | "No | "Location | "Out (door | Proportion |
| Type | Group | change" | change" | Icon)" | correct |
| 2 objects in tested shape | |||||
| Location | Grades 1–2 | 0.15 | 0.72 | 0.13 | 0.61 |
| change | Grades 6–7 | 0.06 | 0.91 | 0.03 | 0.88 |
| College | 0.05 | 0.91 | 0.03 | 0.91 | |
| New | Grades 1–2 | 0.07 | 0.07 | 0.85 | 0.85 |
| color | Grades 6–7 | 0.03 | 0.02 | 0.95 | 0.95 |
| College | 0.06 | 0.03 | 0.91 | 0.91 | |
| No | Grades 1–2 | 0.73 | 0.12 | 0.14 | 0.73 |
| change | Grades 6–7 | 0.94 | 0.02 | 0.04 | 0.94 |
| College | 0.95 | 0.02 | 0.03 | 0.95 | |
| Other | Grades 1–2 | 0.10 | 0.13 | 0.77 | 0.77 |
| shape's | Grades 6–7 | 0.03 | 0.05 | 0.92 | 0.92 |
| color | College | 0.04 | 0.08 | 0.88 | 0.88 |
| 3 objects in tested shape | |||||
| Location | Grades 1–2 | 0.13 | 0.49 | 0.39 | 0.36 |
| change | Grades 6–7 | 0.06 | 0.80 | 0.14 | 0.73 |
| College | 0.07 | 0.83 | 0.09 | 0.79 | |
| New | Grades 1–2 | 0.09 | 0.14 | 0.77 | 0.77 |
| color | Grades 6–7 | 0.04 | 0.11 | 0.85 | 0.85 |
| College | 0.04 | 0.06 | 0.90 | 0.90 | |
| No | Grades 1–2 | 0.54 | 0.16 | 0.30 | 0.54 |
| change | Grades 6–7 | 0.78 | 0.06 | 0.16 | 0.78 |
| College | 0.84 | 0.05 | 0.10 | 0.84 | |
| Other | Grades 1–2 | 0.17 | 0.18 | 0.65 | 0.65 |
| shape's | Grades 6–7 | 0.07 | 0.08 | 0.85 | 0.85 |
| color | College | 0.07 | 0.09 | 0.84 | 0.84 |
Note. For location changes, responses were counted as correct in this table only if the correct location was indicated. The distribution of responses was similar for other attention conditions, though overall levels varied.
This pattern of results just described held for trials with both 2 and 3 items in the tested shape, with slight differences between them. The pattern was confirmed in two analyses of the proportion correct that produced similar results. One analysis included all of the attention conditions but excluded trials in which the probe was in a color that had occurred with an object of the other shape, inasmuch as these trials were not found in 1-shape trials. The statistical results were similar in another analysis that included all types of probe but, in order to do so, excluded the 1-shape condition. This more informative analysis will be reported. It produced an interaction of probe type × age group, F(6, 261)=7.94, p<0.001, ηp2=0.15. There also was a three-way interaction of probe type × age group × array size, F(6, 261)=2.68, p<.05, ηp2=0.06. In both array sizes, there was a large developmental difference in trials with location changes. For arrays with 2 items in the tested shape, the proportions correct for the three age groups, respectively, were .34, .66, and .71; for 3 items in the tested shape, the proportions were .23, .46, and .37. There also was a large developmental difference in trials with no change (2 items in the tested shape, .51, .76, & .77; 3 items, .36, .56, & .64). There was less developmental change for trials in which the probe was in a new color (2 items in the tested shape, 76, .86, & .89; 3 items, .75, .78, & .78). Interestingly, performance showed relatively little developmental change when the probe was in a color that had belonged to an object of the other shape (2 items in the tested shape, .63, .79, & .68; 3 items, .62, .69, & .68).
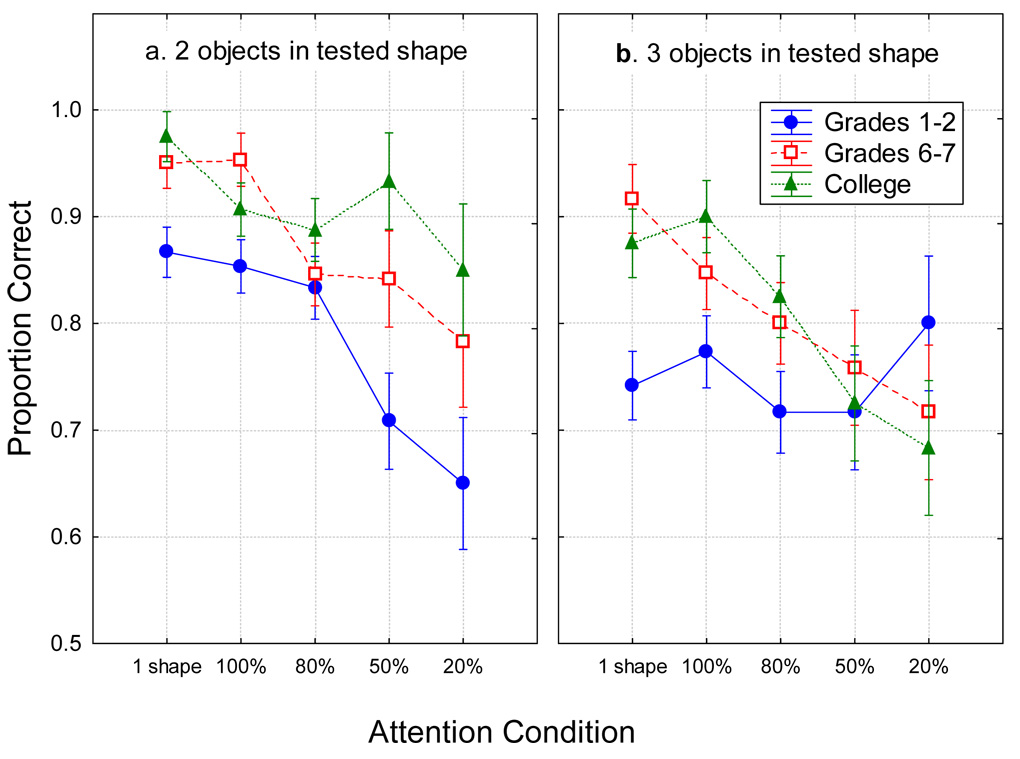
To explore this pattern further, separate analyses were carried out for each probe type. These yielded main effects of age group for location-change trials, no-change trials, and other shape’s color trials. There was no main effect of age group for the trials with a probe of a new color. For those trials, however, there was a very informative interaction of the attention condition and the array set size. This analysis was re-run with all five attention conditions and was again significant, F(6, 261)=4.43, p<0.001, ηp2=0.09. As shown in Figure 5, the children in Grades 1–2 showed a very different pattern of performance across attention conditions with the smaller versus larger arrays. For the smaller arrays (2 items of the tested shape), they filtered out the less-relevant items as well as older participants did. For the larger arrays (3 items of the tested shape), however, their response pattern was much flatter across attention conditions. This finding reinforces the premise advanced above, that young children’s attentional filtering ability is impaired when the working memory load surpasses their capacity by a certain amount. A similar interaction of smaller magnitude was obtained in the analysis of location-change trials, but not for the other probe types.
Figure 5.
The mean proportion correct for new-color probes in each age group as a function of the attention condition. Within each panel, moving rightward, conditions reflect diminishing amounts of attention to be paid to the tested object. a. Arrays with 2 items in the tested shape. b. Arrays with 3 items in the tested shape. Error bars are standard errors.
Discussion
The present study examines developmental changes in visual working memory in a task in which, in some trial blocks, objects of one shape are much more often tested than objects of another shape, making filtering of information necessary in order to allow good overall performance. Some related adult studies have advocated that such filtering is a major basis of observed individual differences in working memory capacity (e.g., McNabb & Klingberg, 2008; Vogel et al., 2005). These studies do not directly question the suggestion that each individual may have a fixed number of working memory slots that can be filled with visual objects, a suggestion that receives strong support from several recent adult studies (Awh, Barton, & Vogel, 2007; Rouder et al., 2008; Zhang & Luck, 2008). They do, however, question whether differences in the number of slots comprise an important source of individual differences in visual working memory, instead emphasizing filtering capability. In contrast, other studies have suggested that the number of slots could be at least as important as filtering for individual differences in working memory capacity (Cowan, Fristoe et al., 2006; Gold et al., 2006; Todd & Marois, 2005). The present study brings this debate to the developmental arena.
Younger children recalled considerably less than older children or adults (Figure 3) but, for displays with only 4 objects in all, the age effect did not depend on the attention condition (Figure 4a). For displays of 6 objects, the older children and adults were far superior to younger children during full attention but lost some, but not all, of that superiority for items that were not supposed to receive full attention (Figure 4b). These results, taken together, suggest that the age difference in capacity is fundamental (cf. Cowan et al., 2005) and that the age difference in attentional filtering may be only a consequence of a memory load that is large compared to participants' working memory capacity. Given that, for small arrays, young children filtered out irrelevant items in a manner similar to adults (Figure 4a), a basic ability of selective attention thus may be adult-like at an age considerably younger than was previously assumed (Plude, Enns, & Brodeur, 1994; Rueda, Posner, & Rothbart, 2005).
Several auxiliary results further support the hypothesis that there is an age group difference in storage capacity in addition to the age group difference in filtering out irrelevant items when the working memory load is high relative to the capacity. First, although there was a dropoff from the peak capacity as the memory load increased beyond the peak in the 1-shape condition and this dropoff might reflect a breakdown in the use of attention for encoding, the dropoff was no more severe in younger children than in older children or adults (Figure 3). Second, filtering cannot explain the age difference in capacity in that the capacity of adults for 80% trials was larger than for young children in the sum of 80% and 20% trials. Third, an analysis of the trials in which the probe was a new color resulted in a striking interaction, shown in Figure 5, indicating distinct filtering in all age groups when there were 2 items in the tested shape, but only in the older two groups when there were 3 items in the tested shape.
Although it still could be argued that there was a greater cost of filtering for storage in the youngest group, this possibility is made improbable by the finding that there was no observable cost of filtering in either group. In particular, the k value for 1-shape trials was not significantly different from the k value for 80% plus 20%, or different from twice the 50% value.
Because working memory capacity was smaller in young children than in older participants, young children's working memory maintenance of objects from 6-object arrays would have diverted attention away from object selection more often than in older participants. We think the reason why a relatively large working memory load compromised young children's selective attention is that attention sometimes must be shared between selection and maintenance of objects in working memory. An attention cue to a location in an array differentially assists admission of the object at that location into working memory (Gold et al., 2006; Schmidt et al., 2002), and attention also helps keep selected representations active in working memory (Cowan & Morey, 2007; Lepsien & Nobre, 2007; Raye et al., 2007). Given that it takes time to admit objects to working memory (Woodman & Vogel, 2005), as they get admitted there is a decrease in the resources available to determine which additional objects to admit. The result is an increasing chance of admitting less-relevant objects at the expense of more-relevant ones (Makovski & Jiang, 2007). The strain on selective attention with 6-object arrays would be most severe for participants with the lowest working memory capacity, the young children.
We do not know why working memory capacity increases markedly during the elementary school years. One possibility is that older participants have more attentional resources that can be devoted to maintenance of the visual array items. Clearly, attention does develop in the age range we are investigating (for a review see Rueda et al., 2005). Although we cannot entirely rule out this sort of account on the basis of our data, we can place important constraints on it. The current theoretical accounts in which attentional resources are used to support capacity specifically emphasize the use of attention to filter out or inhibit irrelevant information, and individual differences in that function (e.g., Kane et al., 2007; McNab & Klingberg, 2008; Vogel et al., 2005). However, any such superiority in attentional resources in the present study cannot explain the age group difference in capacity; at least, not completely. Given that the sum of k values for 80% and 20% trials in young children was smaller than adults’ k value for 80% trials alone, even perfect filtering would not have brought the young children up to the adult level of working memory storage.
There are several alternative conceptions of what could cause an increase in storage capacity across age groups. There could be a basic speedup in neural function with age (Kail & Ferrer, 2007) affecting how many representations can be kept active in the brain concurrently (Lisman & Idiart, 1995; Tiitinen et al., 1993), or there could be more specific maturation of dedicated working memory storage mechanisms, such as those that have recently been identified in the inferior parietal cortex using functional magnetic resonance imaging (Todd & Marois, 2004; Xu & Chun, 2006).
One clue to understanding age differences in capacity is that the trial types that produced the largest age differences were those in which the probe items were in fact in the array but not necessarily in the same location, i.e., the distinction between location-change versus no-change trials. This requires object-location binding (cf. Cowan, Naveh-Benjamin et al., 2006). Apparently, it is easier to bind the shape and color features than it is to bind the color and location features. Thus, there was only a small developmental difference on trials in which the probe color belonged to an array object of the other shape, and therefore in which memory for the color-shape binding can contribute to knowledge of the color-location binding (inasmuch as the probe never differed in shape from the array object in the same location). This finding reinforces other research suggesting that location cues play a special role in working memory encoding (Treisman & Zhang, 2006).
Additional research is needed to confirm the basis of the effects that we have obtained. For example, the ability to filter out n unexpected (not-usually-tested) items was only tested in the presence of n expected (usually-tested) items. Our load interpretation leads to the general notion that it should be easier for children to filter out a certain number of unexpected items in the presence 2 rather than 3 expected items because the latter case involves a higher working memory load; but we cannot verify that prediction, inasmuch as we did not independently vary the number of expected and unexpected items in the array.
Our finding of what appears to be a genuine age difference in storage capacity (e.g., Figure 4a), and our finding that children carried out sophisticated control of attention when working memory demands were minimized, can help shape information-processing-based concepts of cognitive development. They tend to support theories in which age differences exist in both the storage and the processing functions of attention (e.g., Cowan, Fristoe et al., 2006; Gavens & Barrouillet, 2004; Pascual-Leone, 2005) as opposed to approaches in which the age differences are attributed largely or entirely to increases in processing efficiency (e.g., Case, Kurland, & Goldberg, 1982; Kail & Ferrer, 2007).
The present study leads toward a better understanding of the relation between working memory and attention, which can improve educational instruction and neuropsychological diagnoses and treatments. The results suggest that overloading children’s working memory can lead to inefficient attention. This point seems consistent with the observation that it is low-span individuals who report mind-wandering when they are trying to concentrate (Kane et al., 2007), and with the finding that young children in the classroom who are considered inattentive often are the same ones who cannot recall instructions (Gathercole, Lamont, & Alloway, 2006). Many of what have been termed attention deficits actually could reflect working memory deficits. It is therefore understandable that a recent, successful regimen for the treatment of attention deficit disorders in children has emphasized working memory training (Klingberg, 2006). This treatment might be fine-tuned by emphasizing the first array size at which the child's selective attention falters. In general, children’s attention to relevant information could be improved by minimizing irrelevant objects or information cluttering working memory.
Acknowledgment
We acknowledge Grant NIH-R01-HD21338. We thank Melissa Knipe, Caleb O’Brien, and Timothy Ricker for assistance; J.S. Saults and Jeremy Wolfe for comments.
Contributor Information
Nelson Cowan, University of Missouri.
Candice C. Morey, Washington University
Angela M. AuBuchon, University of Missouri
Christopher E. Zwilling, University of Missouri
Amanda L. Gilchrist, University of Missouri
References
- Allen RJ, Baddeley AD, Hitch GJ. Is the Binding of Visual Features in Working Memory Resource-Demanding? Journal of Experimental Psychology: General. 2006;135:298–313. doi: 10.1037/0096-3445.135.2.298. [DOI] [PubMed] [Google Scholar]
- Awh E, Barton B, Vogel EK. Visual working memory represents a fixed number of items regardless of complexity. Psychological Science. 2007;18:622–628. doi: 10.1111/j.1467-9280.2007.01949.x. [DOI] [PubMed] [Google Scholar]
- Baddeley AD, Hitch G. Working memory. In: Bower GH, editor. The psychology of learning and motivation. Vol. 8. New York: Academic Press; 1974. pp. 47–89. [Google Scholar]
- Case R, Kurland DM, Goldberg J. Operational efficiency and the growth of short-term memory span. Journal of Experimental Child Psychology. 1982;33:386–404. [Google Scholar]
- Cowan N, Alloway T. The development of working memory. In: Courage M, Cowan N, editors. The development of memory in infancy and childhood. Hove, East Sussex, UK: Psychology Press; (in press) [Google Scholar]
- Cowan N, Elliott EM, Saults JS, Morey CC, Mattox S, Hismjatullina A, Conway ARA. On the capacity of attention: Its estimation and its role in working memory and cognitive aptitudes. Cognitive Psychology. 2005;51:42–100. doi: 10.1016/j.cogpsych.2004.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N. The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behavioral and Brain Sciences. 2001;24:87–185. doi: 10.1017/s0140525x01003922. [DOI] [PubMed] [Google Scholar]
- Cowan N, Fristoe NM, Elliott EM, Brunner RP, Saults JS. Scope of attention, control of attention, and intelligence in children and adults. Memory & Cognition. 2006;34:1754–1768. doi: 10.3758/bf03195936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N, Morey CC. How can dual-task working memory retention limits be investigated? Psychological Science. 2007;18:686–688. doi: 10.1111/j.1467-9280.2007.01960.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N, Naveh-Benjamin M, Kilb A, Saults JS. Life-Span development of visual working memory: When is feature binding difficult? Developmental Psychology. 2006;42:1089–1102. doi: 10.1037/0012-1649.42.6.1089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daneman M, Carpenter PA. Individual differences in working memory and reading. Journal of Verbal Learning & Verbal Behavior. 1980;19:450–466. [Google Scholar]
- Flavell JH, Beach DH, Chinsky JM. Spontaneous verbal rehearsal in a memory task as a function of age. Child Development. 1966;37:283–299. [PubMed] [Google Scholar]
- Gathercole SE, Lamont E, Alloway TP. Working memory in the classroom. In: Pickering SJ, editor. Working memory and education. San Diego: Academic Press; 2006. [Google Scholar]
- Gavens N, Barrouillet P. Delays of retention, processing efficiency, and attentional resources in working memory span development. Journal of Memory and Language. 2004;51:644–657. [Google Scholar]
- Gold JM, Fuller RL, Robinson BM, McMahon RP, Braun EL, Luck SJ. Intact attentional control of working memory encoding in schizophrenia. J. Abnormal Psychology. 2006;115:658–673. doi: 10.1037/0021-843X.115.4.658. [DOI] [PubMed] [Google Scholar]
- Henry LA. The effects of word length and phonemic similarity in young children's short-term memory. Quarterly Journal of Experimental Psychology. 1991;43A:35–52. [Google Scholar]
- Hulme C, Tordoff V. Working memory development: The effects of speech rate, word length, and acoustic similarity on serial recall. Journal of Experimental Child Psychology. 1989;47:72–87. [Google Scholar]
- Kail RV, Ferrer E. Processing speed in childhood and adolescence: Longitudinal models for examining developmental change. Child Development. 2007;78:1760–1770. doi: 10.1111/j.1467-8624.2007.01088.x. [DOI] [PubMed] [Google Scholar]
- Kane MJ, Bleckley MK, Conway ARA, Engle RW. A controlled-attention Attention view of working-memory capacity. Journal of Experimental Psychology: General. 2001;130:169–183. doi: 10.1037//0096-3445.130.2.169. [DOI] [PubMed] [Google Scholar]
- Kane MJ, Brown LH, McVay JC, Silvia PJ, Myin-Germeys I, Kwapil TR. For whom the mind wanders, and when: An experience-sampling study of working memory and executive control in daily life. Psychological Science. 2007;18:614–621. doi: 10.1111/j.1467-9280.2007.01948.x. [DOI] [PubMed] [Google Scholar]
- Klingberg T, Fernell E, Olesen PJ, Johnson M, Gustafsson P, Dahlstrom K, et al. Computerized training of working memory in children with ADHD – A randomized, controlled trial. Journal of the American Academy of Child and Adolescent Psychiatry. 2005;44:177–186. doi: 10.1097/00004583-200502000-00010. [DOI] [PubMed] [Google Scholar]
- Lepsien J, Nobre AC. Attentional modulation of object representations in working memory. Cerebral Cortex. 2007;17:2072–2083. doi: 10.1093/cercor/bhl116. [DOI] [PubMed] [Google Scholar]
- Lisman JE, Idiart MAP. Storage of 7 + 2 short-term memories in oscillatory subcycles. Science. 1995;267:1512–1515. doi: 10.1126/science.7878473. [DOI] [PubMed] [Google Scholar]
- Luck SJ, Vogel EK. The capacity of visual working memory for features and conjunctions. Nature. 1997;390:279–281. doi: 10.1038/36846. [DOI] [PubMed] [Google Scholar]
- Makovski T, Jiang YV. Distributing versus focusing attention in visual short-term memory. Psychonomic Bulletin & Review. 2007;14:1072–1078. doi: 10.3758/bf03193093. [DOI] [PubMed] [Google Scholar]
- McNab F, Klingberg T. Prefrontal cortex and basal ganglia control access to working memory. Nature Neuroscience. 2008;11:103–107. doi: 10.1038/nn2024. [DOI] [PubMed] [Google Scholar]
- Morey CC, Cowan N. When visual and verbal memories compete: Evidence of cross-domain limits in working memory. Psychonomic Bulletin & Review. 2004;11:296–301. doi: 10.3758/bf03196573. [DOI] [PubMed] [Google Scholar]
- Ornstein PA, Naus MJ. Rehearsal processes in children's memory. In: Ornstein PA, editor. Memory development in children. Hillsdale, NJ: Erlbaum; 1978. pp. 69–99. [Google Scholar]
- Pascual-Leone J. A neoPiagetian view of developmental intelligence. In: Wilhelm O, Engle RW, editors. Understanding and measuring intelligence. London: Sage; 2005. pp. 177–201. [Google Scholar]
- Plude DJ, Enns JT, Brodeur D. The development of selective attention: A life-span overview. Acta Psychologica. 1994;86:227–272. doi: 10.1016/0001-6918(94)90004-3. [DOI] [PubMed] [Google Scholar]
- Rabinowicz T. In: The differentiate maturation of the human cerebral cortex. Falkner F, Tanner JM, editors. Human Growth, V. 3: Neurobiology and Nutrition. NY: Plenum Press; 1980. pp. 97–123. [Google Scholar]
- Raye CL, Johnson MK, Mitchell KJ, Greene EJ, Johnson MR. Refreshing: A minimal executive function. Cortex. 2007;43:135–145. doi: 10.1016/s0010-9452(08)70451-9. [DOI] [PubMed] [Google Scholar]
- Reznick JS. Working memory in infants and toddlers. In: Courage M, Cowan N, editors. The development of memory in infancy and childhood. Hove, East Sussex UK: Psychology Press; in press. [Google Scholar]
- Riggs KJ, McTaggart J, Simpson A, Freeman RPJ. Changes in the capacity of visual working memory in 5- to 10-year-olds. Journal of Experimental Child Psychology. 2006;95:18–26. doi: 10.1016/j.jecp.2006.03.009. [DOI] [PubMed] [Google Scholar]
- Rouder JN, Morey RD, Cowan N, Zwilling CE, Morey CC, Pratte MS. An assessment of fixed-capacity models of visual working memory. Proceedings of the National Academy of Sciences (PNAS) 2008;105:5975–5979. doi: 10.1073/pnas.0711295105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rueda MR, Posner MI, Rothbart MK. The Development of Executive Attention: Contributions to the Emergence of Self-Regulation. Developmental Neuropsychology. 2005;28:573–594. doi: 10.1207/s15326942dn2802_2. [DOI] [PubMed] [Google Scholar]
- Schmidt BK, Vogel EK, Woodman GF, Luck SJ. Voluntary and automatic attentional control of visual working memory. Perception & Psychophysics. 2002;64:754–763. doi: 10.3758/bf03194742. [DOI] [PubMed] [Google Scholar]
- Tiitinen H, Sinkkonen J, Reinikainen K, Alho K, Lavikainen J, Näätänen R. Selective attention enhances the auditory 40-Hz transient response in humans. Nature. 1993;364:59–60. doi: 10.1038/364059a0. [DOI] [PubMed] [Google Scholar]
- Todd JJ, Marois R. Capacity limit of visual short-term memory in human posterior parietal cortex. Nature. 2004;428:751–754. doi: 10.1038/nature02466. [DOI] [PubMed] [Google Scholar]
- Todd JJ, Marois R. Posterior parietal cortex activity predicts individual differences in visual short-term memory capacity. Cognitive, Affective, & Behavioral Neuroscience. 2005;5:144–155. doi: 10.3758/cabn.5.2.144. [DOI] [PubMed] [Google Scholar]
- Treisman A, Zhang W. Location and binding in visual working memory. Memory & Cognition. 2006;34:1704–1719. doi: 10.3758/bf03195932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogel EK, McCollough AW, Machizawa MG. Neural measures reveal individual differences in controlling access to working memory. Nature. 2005;438:500–503. doi: 10.1038/nature04171. [DOI] [PubMed] [Google Scholar]
- Wheeler ME, Treisman AM. Binding in short-term visual memory. Journal of Experimental Psychology: General. 2002;131:48–64. doi: 10.1037//0096-3445.131.1.48. [DOI] [PubMed] [Google Scholar]
- Woodman GF, Vogel EK. Fractionating working memory: Consolidation and maintenance are independent processes. Psychological Science. 2005;16:106–113. doi: 10.1111/j.0956-7976.2005.00790.x. [DOI] [PubMed] [Google Scholar]
- Xu Y, Chun MM. Dissociable neural mechanisms supporting visual short-term memory for objects. Nature. 2006;440:91–95. doi: 10.1038/nature04262. [DOI] [PubMed] [Google Scholar]
- Zhang W, Luck SJ. Discrete fixed-resolution representations in visual working memory. Nature. 2008:xxx. doi: 10.1038/nature06860. [DOI] [PMC free article] [PubMed] [Google Scholar]