Abstract
Spike-frequency adaptation causes reduced spiking during prolonged stimulation, but the full impact of adaptation on neural coding is far more complex, especially if one takes into account the diversity of biophysical mechanisms mediating adaptation and the different ways in which neural information can be encoded. Here, we show that adaptation has opposite effects depending on the neural coding strategy and the biophysical mechanism responsible for adaptation. Under noisy conditions, calcium-activated K+ current (IAHP) improved efficient spike-rate coding at the expense of spike-time coding by regularizing the spike train elicited by slow or constant inputs; noise power was increased at high frequencies but reduced at low frequencies, consistent with noise shaping that improves coding of low- frequency signals. In contrast, voltage-activated M-type K+ current (IM) improved spike-time coding at the expense of spike-rate coding by stopping the neuron from spiking repetitively to slow inputs so that it could generate isolated, well timed spikes in response to fast inputs. Using dynamical systems analysis, we demonstrate how IAHP minimizes perturbation of the interspike interval caused by high- frequency noise, whereas IM minimizes disruption of spike-timing accuracy caused by repetitive spiking. The dichotomous outcomes are related directly to the distinct activation requirements for IAHP and IM, which in turn dictate whether those currents mediate negative feedback onto spiking or membrane potential. Thus, based on their distinct activation properties, IAHP implements noise shaping that improves spike-rate coding of low-frequency signals, whereas IM implements high-pass filtering that improves spike-time coding of high- frequency signals.
Keywords: interspike interval correlation, noise shaping, ROC analysis, spike-timing reliability, neural code, noise
Introduction
Adaptation is ubiquitous in the nervous system and can improve neural coding (Barlow, 1961; Sharpee et al., 2006; Wark et al., 2007). However, adaptation occurs through several mechanisms and neural information is encoded in various ways, which opens up the possibility that different forms of adaptation may have disparate effects on neural information depending on how that information is encoded. Here, we focus on adaptation of neuronal responsiveness, i.e., spike-frequency adaptation or accommodation. This adaptation is typically ascribed to the voltage-activated M-type K+ current (IM) or the calcium-activated K+ current (IAHP) (Madison and Nicoll, 1984; Schwindt et al., 1988; Storm, 1990), although it can occur through other mechanisms such as sodium-activated K+ current (Schwindt et al., 1989) or cumulative Na+ channel inactivation (Fleidervish et al., 1996). One critical distinction is whether adaptation is spike dependent or spike independent. IAHP responsible for the medium-duration afterhyperpolarization is mediated by apamin-sensitive SK channels (Villalobos et al., 2004) that are activated predominantly by Ca2+ arriving via high-voltage-activated Ca2+ channels or by Ca2+ released from intracellular stores, both of which rely on spike generation (Williams et al., 1997; Bowden et al., 2001; Yamada et al., 2004; Goldberg and Wilson, 2005); activation of IAHP is therefore spike dependent. In contrast, IM mediated by KCNQ channels (Wang et al., 1998) can be activated at voltages below spike threshold (Adams et al., 1982; Halliwell and Adams, 1982; Gutfreund et al., 1995; Wang and McKinnon, 1995; Wang et al., 1998); activation of IM is therefore largely spike-independent.
Neural information can be encoded in diverse ways (Perkel and Bullock, 1968). Known coding strategies used by single neurons can be divided approximately into rate codes and temporal codes, but these terms have been used inconsistently and are prone confusion (Dayan and Abbott, 2001). To distinguish our usage, we refer to spike-rate coding and spike-time coding. In spike-rate coding, the number of spikes within a time window or the reciprocal of a single interspike interval (ISI) (1/ISI = instantaneous rate) correlates with some stimulus attribute; in this case, ISIs must be shorter than the minimum time scale of the stimulus, as explained by the Nyquist theorem (Theunissen and Miller, 1995; Rieke et al., 1997). In spike-time coding, the fine temporal structure of the spike train (i.e., spike timing) sparsely encodes information about the temporal structure of the stimulus; in this case, ISIs are longer than the minimum period of the stimulus and simply reflect the interval between suprathreshold stimulus upstrokes (Oswald et al., 2007). Reliable spike timing confers good spike-time coding whereas reliable ISIs confer good spike-rate coding.
Based on their distinct activation properties, we hypothesized that IM and IAHP have different effects depending on how information is encoded. Using a minimal model amenable to dynamical systems analysis as well as a more biophysically realistic multicompartmental model, we demonstrate that these two forms of adaptation do indeed have opposite effects depending on the neural coding strategy. The dynamical mechanisms through which this occurs are explained.
Materials and Methods
Morris-Lecar model and simulations.
All data presented in the main study are based on simulations in a modified Morris-Lecar model (Morris and Lecar, 1981; Rinzel and Ermentrout, 1998; Prescott et al., 2006) described by the following:
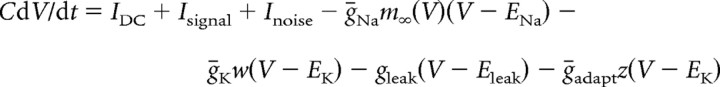 |
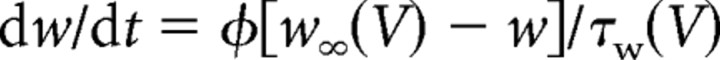 |
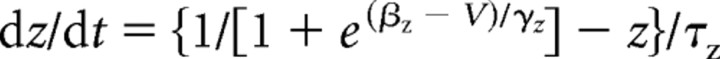 |
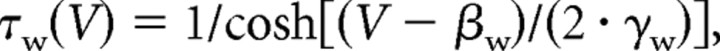 |
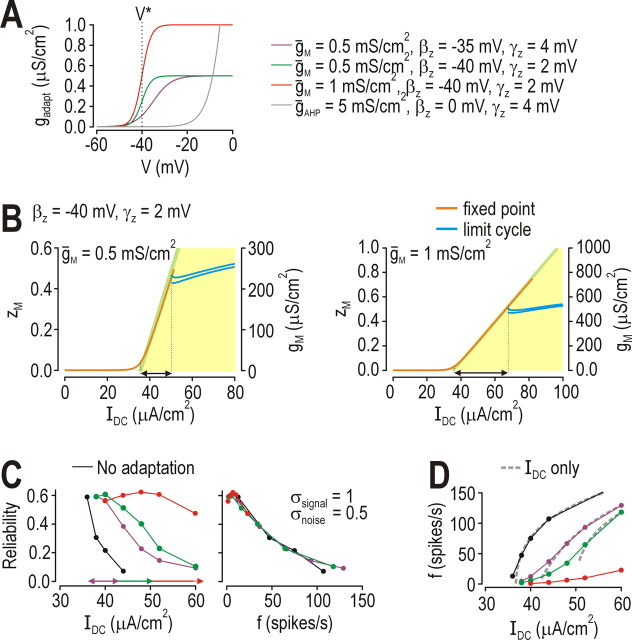
with C = 2 μF/cm2, ḡNa = 20 mS/cm2, ENa = 50 mV, ḡK = 20 mS/cm2, EK = −100 mV, gleak = 2 mS/cm2, Eleak= −70 mV, φ = 0.15, βm = −1.2 mV, γm = 18 mV, βw = 0 mV, and γw = 10 mV. Magnitude of gleak was set to replicate the low-conductance state characteristic of in vitro conditions (compare with parameters in Prescott et al., 2006). Adaptation was modeled after the formalism described by Ermentrout (1998) [see also Prescott et al. (2006)]. Parameters for IM were ḡadapt = ḡM = 0.5 mS/cm2, τz = 100 ms, βz = −35 mV, and γz = 4 mV unless otherwise indicated. Parameters for IAHP were ḡadapt = ḡAHP = 5 mS/cm2 (or 10 mS/cm2 for open squares in Fig. 4F), τz = 100 ms, βz = 0 mV, γz = 4 mV. The critical difference is the voltage at half-maximal activation (controlled by βz): when βz = −35 mV, the left tail of the activation curve extends below spike threshold (thus allowing IM to be activated at subthreshold voltages), whereas when βz = 0 mV, the activation curve is shifted to more depolarized potentials and does not extend below threshold (meaning IAHP is activated only during spikes) (see Introduction). In reality, IAHP is activated by calcium influx driven by suprathreshold depolarization but, technically, it is unnecessary to explicitly include this additional step, which would necessarily increase the dimensionality of our model and compromise our ability to apply dynamical systems analysis (see below); calcium-dependent activation of IAHP was explicitly modeled in the multicompartmental model described in supplemental data, available at www.jneurosci.org. Equations were integrated numerically in XPPAUT (Ermentrout, 2002) using the Euler method with a time step of 0.1 ms.
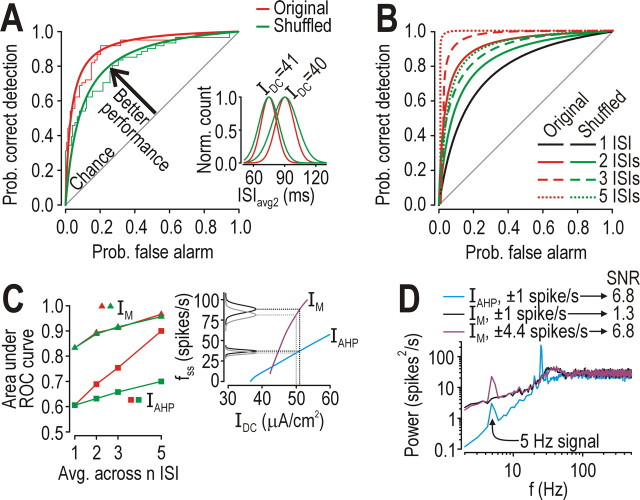
Figure 4.
Effects of adaptation on spike-rate coding. A, Inset shows that a negative ISI correlation causes narrowing of the distribution of ISIavg2 (i.e., running average of two consecutive ISIs) plotted here as normalized counts per bin fitted with a Gaussian curve. σnoise = 0.5 μA/cm2 in A–D. Recall that ISI distribution was much narrower in the neuron with IAHP even without averaging (Fig. 2B). Narrower distributions overlap less, making it easier for an ideal observer to discriminate ISIs associated with subtly different IDC (i.e., on the order of 1 SD of Inoise) as shown here using ROC analysis (see Results). Thick lines show fitted curves (y = x/(a + bx) where a + b = 1). B, Averaging across multiple ISIs improved performance, especially when ISIs were correlated: five uncorrelated (shuffled) ISIs needed to be averaged to achieve the same performance as averaging two correlated ISIs. C, In neuron with IAHP, averaging across correlated ISIs rapidly improved discriminability of responses to 50 versus 51 μA/cm2 with σnoise = 0.5 μA/cm2; performance is reported as area under the ROC curve, which varies from 0.5–1.0 (chance to perfect, respectively). Without averaging, neuron with IM performed better than neuron with IM but only by firing at much higher rates (inset). D, A 5 Hz sine wave stimulus whose amplitude was adjusted to give ± 1 spike/s modulation around a 25 spikes/s baseline was clearly encoded in the neuron with IAHP (SNR = 6.8) but not in the neuron with IM (SNR = 1.3). Applying the same amplitude sine wave in both neurons caused 4.4 spikes/s modulation in the neuron with IAHP (because of its steeper f–I curve) but, despite increasing the signal, the SNR only reached 6.8 because of the strong noise. SNR was calculated as the ratio of power at 5Hz for the response with the 5 Hz signal vs without that signal but with equivalent noise.
The modified Morris-Lecar model is ideal for certain analyses (see below), but building such a simple model requires that one makes several simplifying assumptions (e.g., regarding calcium-dependent activation of IAHP; see above). To confirm that these assumptions did not compromise our results, all key analyses were repeated in a more biophysically realistic, multicompartmental, conductance-based model described in the legend of supplemental Figure 1, available at www.jneurosci.org as supplemental material.
Stimulation.
Constant stimulation was controlled by IDC. Dynamics signals and noise were modeled as Ornstein-Uhlenbeck processes (Uhlenbeck and Ornstein, 1930),
where Isignal(noise) is the random variable, τsignal(noise) is a time constant controlling the rate of drift back toward zero mean (τ = 0 ms → white noise; τ > 0 ms → colored noise), N(t) is normally distributed (zero mean, unit variance) noise source that is scaled by D/, where D controls noise amplitude (Tuckwell, 1988; Destexhe et al., 2001). The scaling factor D/ accounts for effects of the time step on the amplitude of Isignal(noise) fluctuations and is reported in the text as σsignal(noise) where σ = D/. The variance of Isignal(noise) equals σ2τ/2 (see Gillespie, 1996). τsignal(noise) was 5 ms in all cases unless otherwise indicated.
Autocorrelation and power spectral analysis.
Autocorrelation was used to compare an ISI sequence {Ij} against a lagged version of itself. The ISI serial correlation coefficient was defined as ρj =  IiIi+j −
IiIi+j − 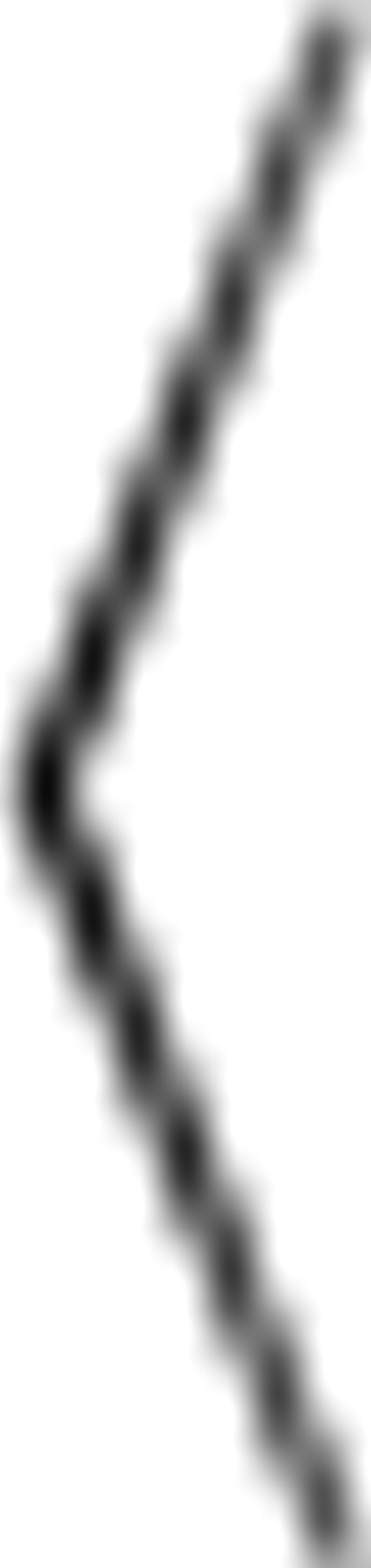 Ii
Ii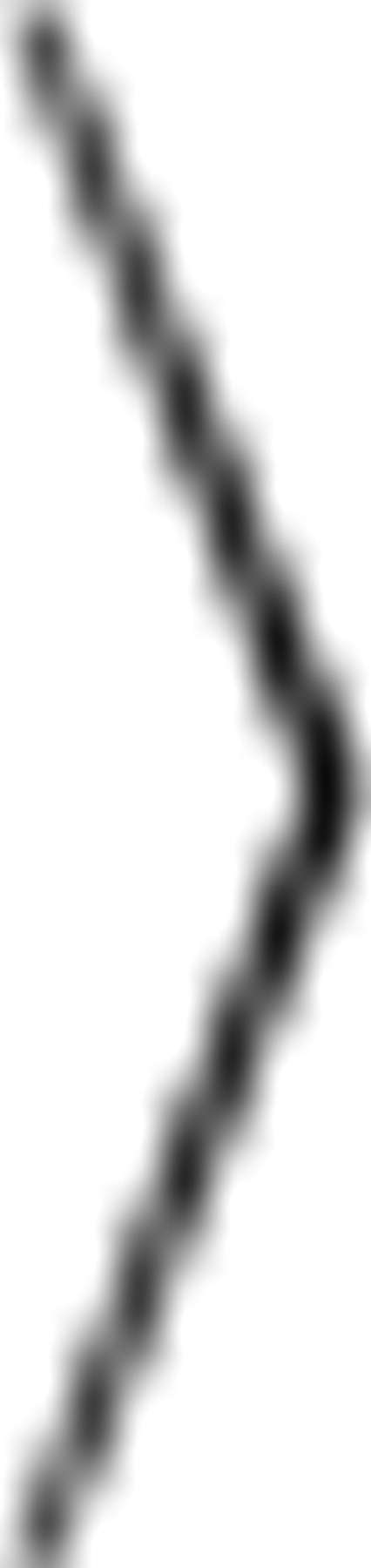 2
2
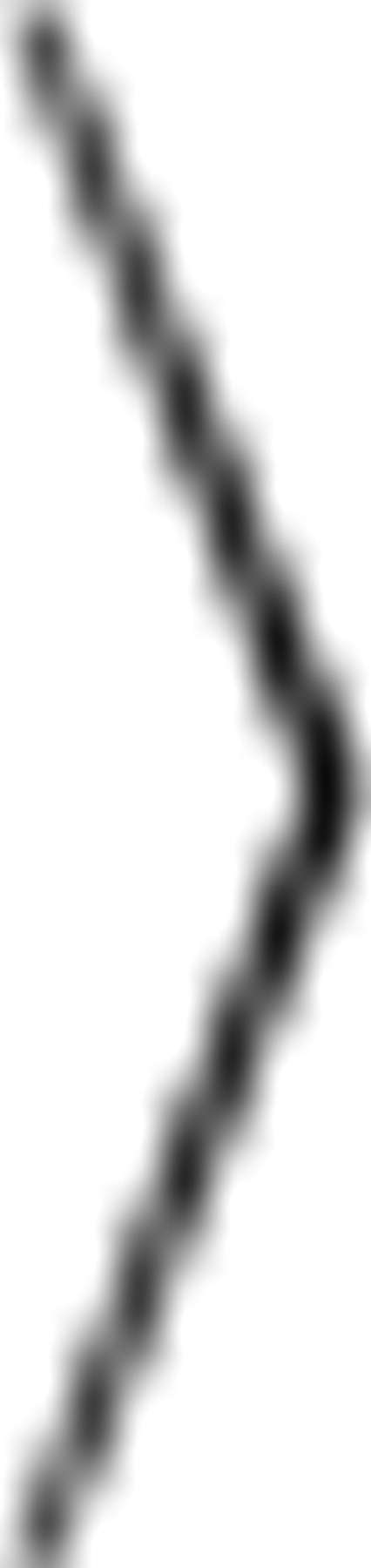 /
/ 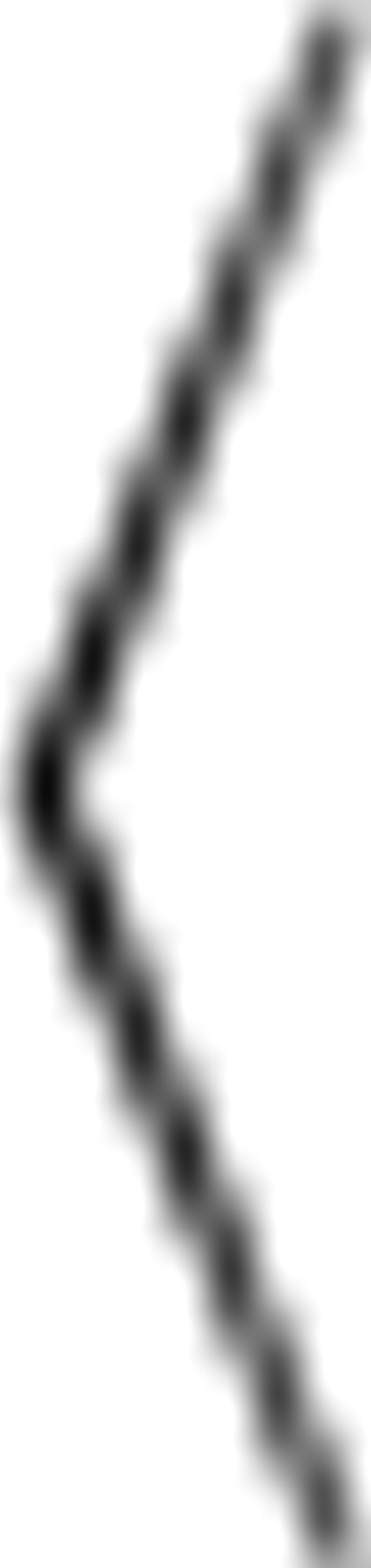 IiIi −
IiIi − 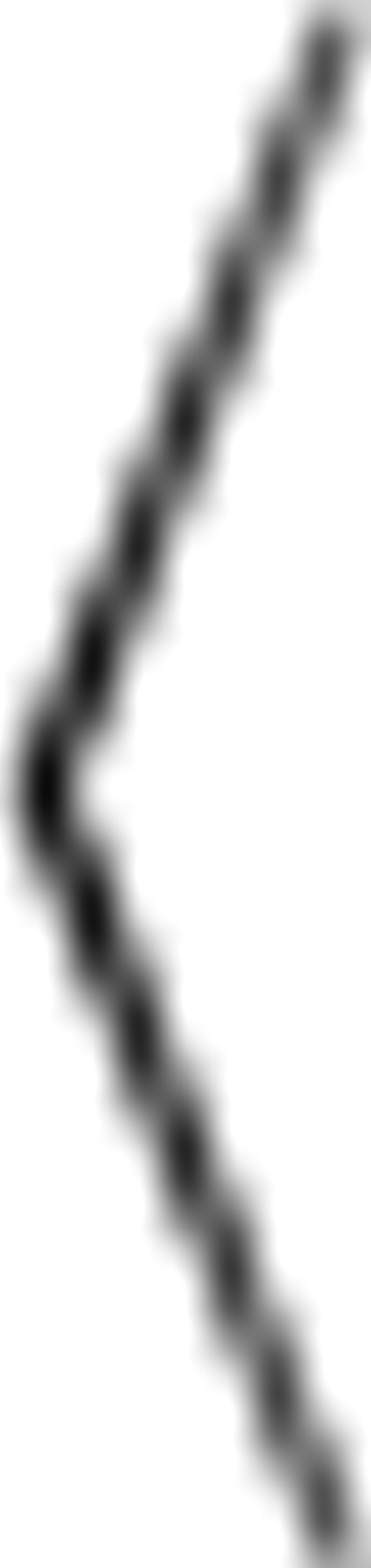 Ii
Ii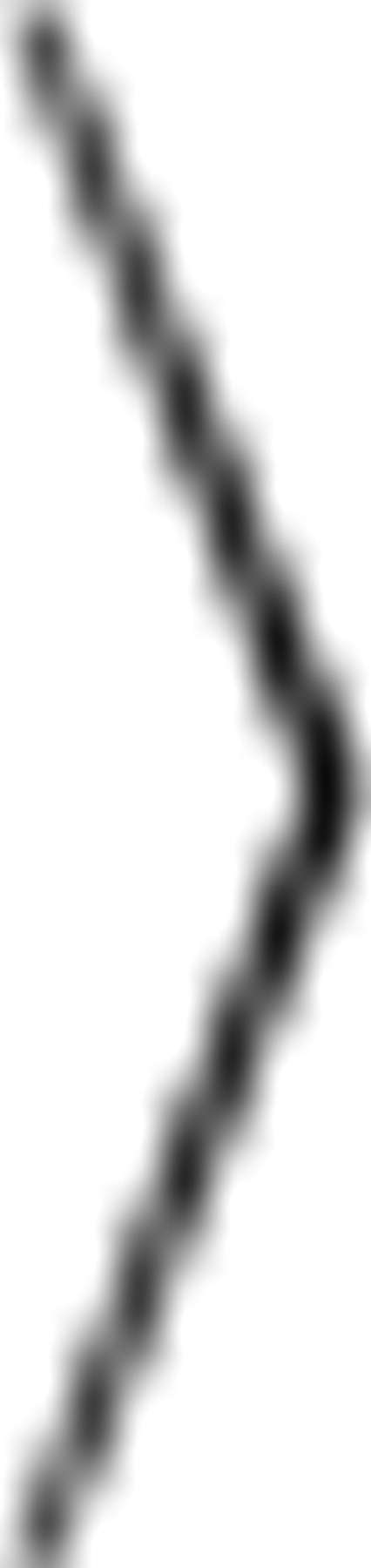 2
2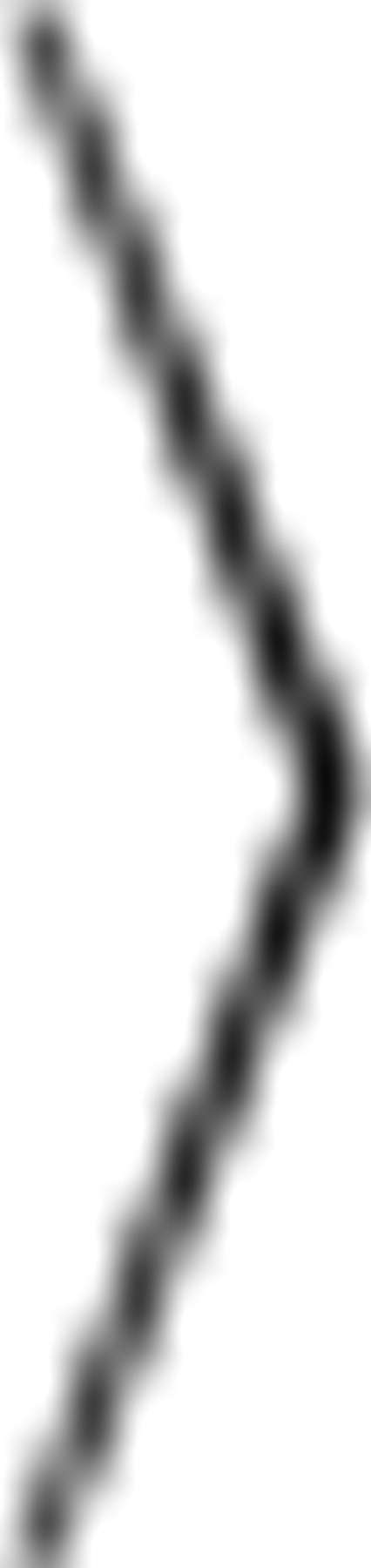 where
where 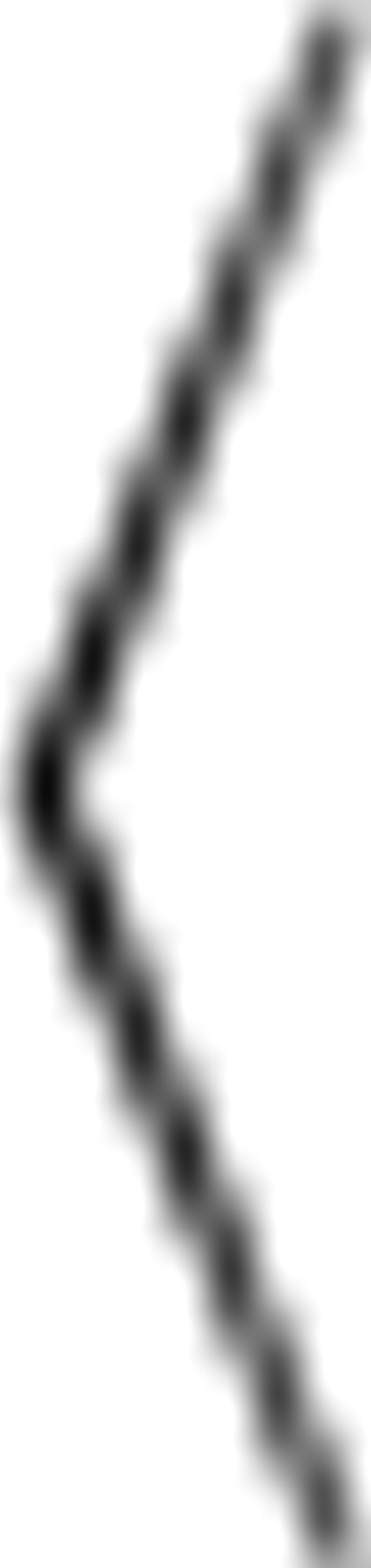 …
… denotes averaging across index i and j is the lag. Consecutive ISIs have a lag of 1. Power spectra were measured using routines provided by Gabbiani and Koch (1998).
denotes averaging across index i and j is the lag. Consecutive ISIs have a lag of 1. Power spectra were measured using routines provided by Gabbiani and Koch (1998).
ROC analysis.
Receiver operating characteristic (ROC) analysis was used to answer how well an ideal observer can discriminate between two stimuli on the basis of differences in firing rate (Green and Swets, 1966; Gabbiani and Koch, 1998). The decision rule is simply whether rate < threshold (→ IDC x) or rate > threshold (→ IDC y). We plot the probability of correct detection against the probability of false alarm over a range of different threshold values. The further the ROC curve lies above the diagonal (which represents chance performance; probability of false alarm = probability of correct detection), the better one is able to discriminate between the two stimuli. Firing rate was measured from the reciprocal of single ISIs or from the running average of two or more ISIs from the original or shuffled ISI sequence. Shuffling means that ISIs were re-ordered randomly to destroy whatever correlations existed in the originally ordered sequence.
Spike-timing reliability.
Our measurement of spike-timing reliability was motivated by the concept of spike-triggered averaging. Here, instead of using the spike to trigger sweeps of the preceding stimulus, we used spikes to trigger sweeps from separate responses to the same stimulus. Specifically, the neuron was stimulated with signal alone (i.e., without noise) on the first trial and then with signal plus noise on subsequent trials; the signal remained the same but noise varied from trial to trial. Spikes at time t in the first “reference” trial (without noise) were used to trigger voltage sweeps at t ± Δt in subsequent “test” trials (with noise). Spikes in the triggered sweeps were detected and their timing relative to reference spikes was recorded. The resulting histogram of triggered spike times relative to reference spikes provides information on the impact of noise: the width of the distribution reflects the reduced precision (jitter) caused by noise while area under the curve (after normalization by the number of reference spikes) reflects the reduced reliability caused by noise. We controlled for coincident spikes occurring by chance, which varies with firing rate (de la Rocha et al., 2007), by shuffling the ISI sequence of the reference trial and repeating the analysis. Subtracting this “baseline” from the uncorrected cumulative probability distribution gave a corrected probability distribution with a peak <1 (see Fig. 4D) that is referred to as reliability in subsequent plots.
Bifurcation and phase plane analyses.
We chose to investigate effects of adaptation using a modified Morris-Lecar model because such a model is ideally suited for dynamical systems analysis, which can be used to rigorously characterize the effects of adaptation on neuronal spiking, as explained below. Because adaptation develops slowly relative to other variables, z (which controls adaptation; see above) can be treated as constant over some time window (in other words, z is treated as a parameter), which allows the model to be reduced from three-dimensional (3D) to two-dimensional (2D). Unlike more complex models, behavior of the 2D model can be explained entirely by the interaction between the fast activation variable V and a slower recovery variable w; that interaction can be visualized on a phase plane. Nullclines represent areas in phase space where a given variable remains constant, i.e., V′ = 0 along the V-nullcline and w′ = 0 along the w-nullcline. How the nullclines intersect (i.e., whether the intersection is stable or unstable) determines whether the system evolves toward a fixed point or toward a limit cycle (i.e., subthreshold membrane potential or repetitive spiking, respectively). To determine the effects of certain parameters, the parameter of interest (e.g., z in the 2D model) can be continuously varied to determine its effects on the system's behavior including, most importantly, abrupt transitions (i.e., bifurcations) between quiescence and repetitive spiking. Simulations in the 3D model (with z treated as a variable) can then be compared with simulations in the 2D model to see the effects of adaptation. See Rinzel and Ermentrout (1998) for a more detailed discussion of these methods in the context of neuronal excitability or Strogatz (1998) for an in-depth explanation.
Results
Effects of adaptation on firing rate
Computational modeling in a Morris-Lecar-type model showed that IM could terminate spiking elicited by constant stimulation (IDC) whereas IAHP only reduced firing rate (Fig. 1A). This translated into distinct modulation of the f–IDC curve (Fig. 1B): IM had a predominantly subtractive effect, shifting the curve to the right, which corresponds to increasing the current threshold for sustained spiking or I*; IAHP had a purely divisive effect, reducing the slope of the curve at low firing rates, notwithstanding saturation effects at high firing rates. Furthermore, gAHP had pulsatile kinetics, increasing abruptly during each spike and decreasing slowly between spikes because its activation is spike dependent; in contrast, gM remained relatively constant throughout the ISI since it remains activated at subthreshold voltages (Fig. 1A). The activation time constants (τz) of IAHP and IM influence the kinetics of conductance changes (see below), but τz was set equal for all simulations in the Morris-Lecar model (see Materials and Methods).
Figure 1.
Effects of adaptation on firing rate. A, Sample responses to constant stimulation (IDC in μA/cm2 indicated on left). Top traces show voltage response. Bottom traces show gM or gAHP; notice the difference in kinetics and specifically that gAHP is pulsatile because of its spike-dependent activation. For IDC = 40 μA/cm2, time-averaged conductance was slightly less for gM than for gAHP although the former terminated spiking whereas the latter did not; thus, maintenance of outward current (possible only with spike-independent adaptation mechanisms) is critical for allowing adaptation to terminate repetitive spiking. B, IM had a predominantly subtractive effect on the steady-state f–IDC curve, whereas IAHP had a divisive effect on the initial slope of the steady-state f–IDC curve.
Simulations were repeated in a multicompartmental, conductance-based model to test whether IM and IAHP had effects comparable with those described above for the Morris-Lecar model. As expected, IM and IAHP had the same effects in the more biophysically realistic model (supplemental Fig. 1, available at www.jneurosci.org as supplemental material), thus demonstrating that simplifications inherent in our Morris-Lecar model (see Materials and Methods) did not compromise the applicability of our results to biophysically realistic conditions.
Effects of adaptation on other spike-train statistics
Because noise is another ubiquitous feature of the nervous system with myriad effects on coding (Calvin and Stevens, 1968), our next step was to characterize how different forms of adaptation impact spike trains generated under realistically noisy conditions. Noise disrupted the regularity of spiking much more in the neuron with IM than in the neuron with IAHP (Fig. 2A). Closer analysis revealed that, for a given steady-state firing rate (fss), the ISI distribution for the neuron with IAHP was symmetrical and narrow compared with that for the neuron with IM or no adaptation (Fig. 2B). Over a range of fss, IAHP caused a large reduction in the coefficient of variation of the ISI (CVISI) whereas IM caused only a modest reduction compared with the model without adaptation (Fig. 2C). Additionally, in the neuron with IAHP, a long ISI was typically followed by a short ISI, and vice versa (Fig. 2D). This was quantified by autocorrelation, which revealed a strong negative correlation between immediately consecutive ISIs (lag j = 1) in the neuron with IAHP, but not in other neurons (Fig. 2E,F). The negative ISI correlation caused by IAHP has been noted previously (Wang, 1998) but its functional consequences were not investigated, although other work has shown that a negative ISI correlation improves coding of low-frequency signals through noise shaping (Chacron et al., 2001, 2004, 2005). Effects of IAHP are also comparable with those of “threshold fatigue” (Chacron et al., 2007).
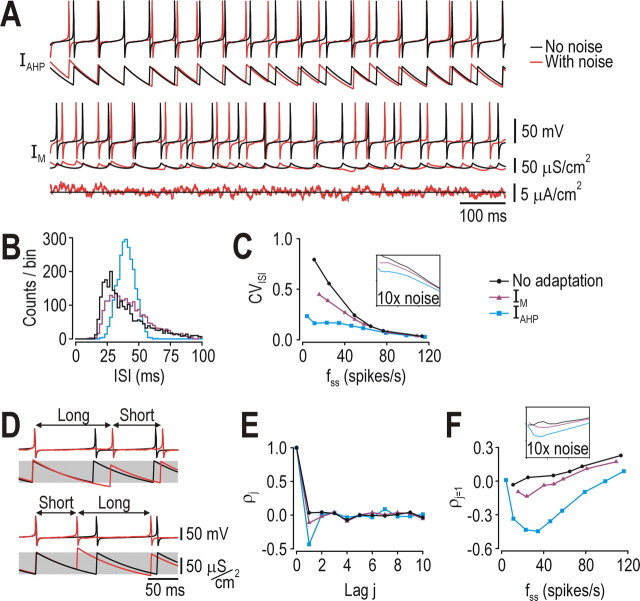
Figure 2.
Effects of adaptation on other spike-train statistics. A, Responses to stimulation with and without weak noise (σnoise = 0.5 μA/cm2) simulated as an Ornstein-Uhlenbeck process (see Materials and Methods). Spiking in the neuron with IM was noticeably less regular than spiking in the neuron with IAHP. Both neurons spiked at ∼25 spikes/s when stimulated with IDC = 43 μA/cm2; this is the stimulus intensity at which the f-I curves cross (see also Fig. 1B) and was therefore chosen as the comparison point for subsequent panels. The neuron without adaptation (data not shown here) was stimulated with IDC = 37 μA/cm2 in order for it to spike at ∼25 spikes/s. B, ISI distribution was noticeably skewed and much wider with IM or no adaptation than with IAHP. C, Coefficient of variation of the interspike interval (CVISI = SDISI/AvgISI) was least in the neuron with IAHP for all firing rates. The same trends existed when noise amplitude was increased 10× (inset). D, Sample responses showing a long ISI followed by a short ISI, and vice versa, which is typical in a neuron with IAHP and results from gAHP trying to remain within its preferred operating range (gray shading). E, F, Autocorrelation confirmed that IAHP caused a strong negative correlation between immediately consecutive ISIs (lag j = 1) over a broad range of firing rates. That correlation was absent without adaptation, and was very modest with IM. With faster spiking, ρj=1 became positive because of positive correlations within the stimulus itself. The same trends existed when noise amplitude was increased 10× (inset).
To further investigate noise shaping, we analyzed the power spectrum of the spike train. Regularity of spiking in the neuron with IAHP was manifested as reduced power at low frequencies and increased power near fss when compared with the power spectra for IM or no adaptation (Fig. 3A). This reshaping of the power spectrum constitutes noise shaping (Shin, 2001) and is known to improve coding of signals comprising frequencies where noise power is reduced (Chacron et al., 2001; Mar et al., 1999) (see below). The more realistic conductance-based model with different forms of adaptation exhibited exactly the same response properties (supplemental Fig. 2, available at www.jneurosci.org as supplemental material). Destroying the negative ISI correlation by shuffling the ISI sequence changed the power spectrum of the neuron with IAHP as predicted (Chacron et al., 2004), although the power at low frequencies was still less than in the neuron with IM or no adaptation (Fig. 3B). Thus, although the negative ISI correlation contributed to noise shaping, the power spectrum was also shaped by other effects of IAHP, most likely by its enhancement of the refractory period (Franklin and Bair, 1995). To test this, we varied post-spike refractoriness by varying the adaptation time constant (τz): a faster time constant allows gadapt to vary more (i.e., cause greater refractoriness immediately following a spike) than a slower time constant (Fig. 3C, inset). As predicted for the neuron with IAHP, increasing refractoriness (shortening τz) caused greater power reduction at low frequencies, whereas decreasing refractoriness (lengthening τz) caused less power reduction compared with baseline (Fig. 3C). In contrast, varying τz in the neuron with IM caused little change in the power spectrum (Fig. 3D), consistent with the observation that gM tends to remain relatively constant throughout the ISI (Fig. 3D, inset).
Figure 3.
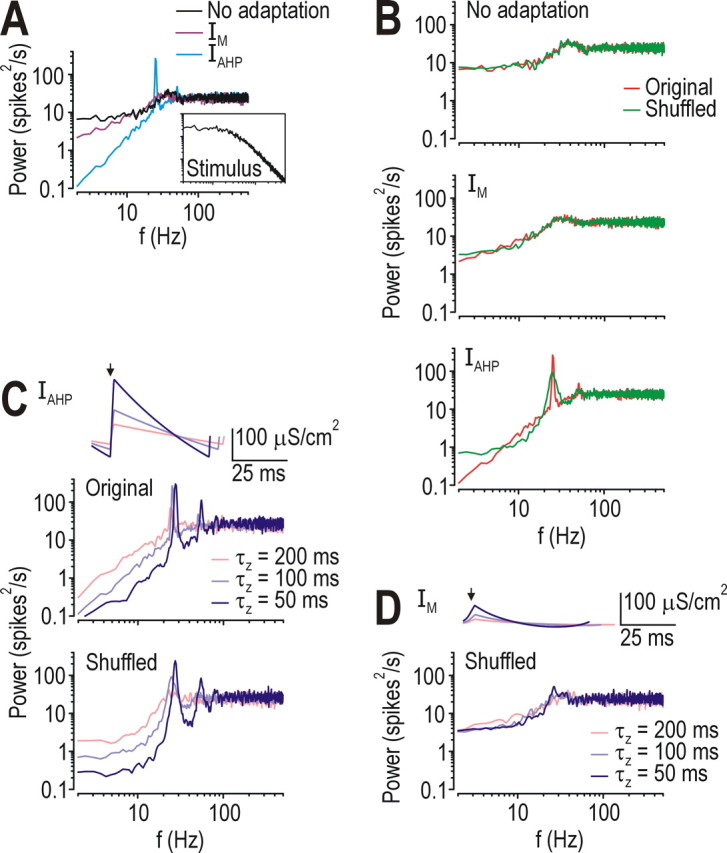
Effects of negative ISI correlation and refractoriness on power spectra. A, Power spectral analysis of the spike train showed that IAHP reduced noise power at low frequencies. Inset shows power spectrum of stimulus over same frequency range. B, Destroying the ISI correlation by shuffling the ISI sequence affected only the power spectrum of the neuron with IAHP, consistent with the lack of ISI correlation in other neurons (see also Fig. 2). Despite shuffling, power at low frequencies was still less in the neuron with IAHP than in other neurons. C, Shortening the IAHP time constant τz caused increased post-spike refractoriness (because of the larger increase in gAHP; see inset), which translated into reduced power at low frequencies according to the power spectrum. Lengthening τz had the opposite effect. Comparing power spectra from the original and shuffled ISI sequences (top and bottom panels, respectively) shows that negative ISI correlations and refractoriness had distinct effects on the shape of the spectrum. Arrow in inset here and in D show timing of spike onset. D, Because gM remains activated at subthreshold potentials, it remains relatively constant throughout the ISI (inset; compare with C); consequently, varying τz had little effect on refractoriness or on the shape of the power spectrum in the neuron with IM.
Based on these results, we conclude that IM contributes relatively constant outward current that increases I* but has only modest effects on other spike train statistics. In contrast, IAHP varies during individual ISIs and across consecutive ISIs, which causes post-spike refractoriness and negative ISI correlations, respectively. This “spike-history dependence” allows IAHP to regularize the spike train, which has important consequences for spike-rate coding, as explained below.
Effects of adaptation on spike-rate coding
As shown in Figure 2B, the ISI distribution was narrower in the neuron with IAHP than in other neurons, consistent with IAHP causing regularization of the spike train (see above). Averaging across two or more consecutive ISIs caused further narrowing of the averaged ISI distribution, especially if those ISIs were negatively correlated (Fig. 4A, inset). Reducing overlap of ISI distributions associated with different IDC improves the ability of an ideal observer to infer IDC from firing rate. This can be shown by receiver operating characteristic (ROC) analysis wherein probability of correctly identifying IDC is plotted against the probability of incorrectly identifying IDC as different thresholds are used to separate the ISI distributions (Fig. 4A). The further the ROC curve extends away from the diagonal, the better the performance or discriminability relative to chance. In the example in Figure 4B, five uncorrelated ISIs needed to be averaged to achieve the same performance achieved by averaging two correlated ISIs, while averaging five correlated ISIs allowed near-perfect distinction between subtly different IDC (i.e., on the order of 1 SD of Inoise). By reducing the variability of individual ISIs and by introducing a negative ISI correlation that enhanced the reduction in ISI variability achieved by averaging across ISIs, IAHP allowed excellent spike-rate coding at low firing rates; indeed, when firing rate was averaged across 5 unshuffled ISIs, the neuron with IAHP achieved nearly the same performance as the neuron with IM (Fig. 4C). The neuron with IM performed better than the neuron with IAHP when firing rate was averaged over <5 ISIs, but only because of the high firing rate in the former. In other words, the neuron with IM (and the neuron without adaptation; data not shown) relied on widely separated peaks (i.e., large differences in firing rate) to separate the ISI distributions associated with different IDC, whereas the neuron with IAHP relied on narrow distributions (i.e., reduced ISI variability) (Fig. 4C, inset).
To further illustrate the last point and to also consider encoding of nonconstant stimuli, we applied a 5 Hz sine wave stimulus whose amplitude was either the same in the neuron with IM or IAHP, or was reduced in the former so that firing rate modulation caused by the sine wave stimulus was the same in both neurons. With equivalent stimulation, the signal-to-noise ratio (SNR) was 6.8 in both neurons, but, with equivalent modulation of firing rate, the SNR dropped to only 1.3 in the neuron with IM (Fig. 4D). The high SNR in the neuron with IAHP was therefore the result of reduced noise rather than enhanced signal. It is precisely this noise reduction that allows a neuron with IAHP to accurately encode constant or low-frequency inputs with small changes in firing rate.
Effects of adaptation on spike-time coding
The same noise reduction that benefits efficient spike-rate coding of slow signals is liable to impair spike-time coding of fast signals. For example, inserting an extra “noise” spike in a neuron with IAHP could disrupt, over the next several hundred milliseconds, the timing of spikes elicited by the signal; that disruption was minimal in the neuron with IM (Fig. 5A). This disruption was even more evident when continuous noise was superimposed on the signal (Fig. 5B). To quantify the reliability of spike timing, we compared the timing of spikes elicited with noise (Fig. 5C, red rasters) with the timing of reference spikes elicited without noise (black raster); histograms in Figure 5C show timing of triggered spikes (red) relative to reference spikes (black). Cumulative probability of a triggered spike increased as spikes were counted at increasing times relative to reference spikes (Fig. 5D, top), but so too did the chance of randomly coincident spikes as determined by repeating the analysis after shuffling the reference spike train (Fig. 5D, middle); subtracting the latter cumulative probability distribution from the former gave a corrected distribution (Fig. 5D, bottom) whose peak height is a metric of spike-timing reliability.
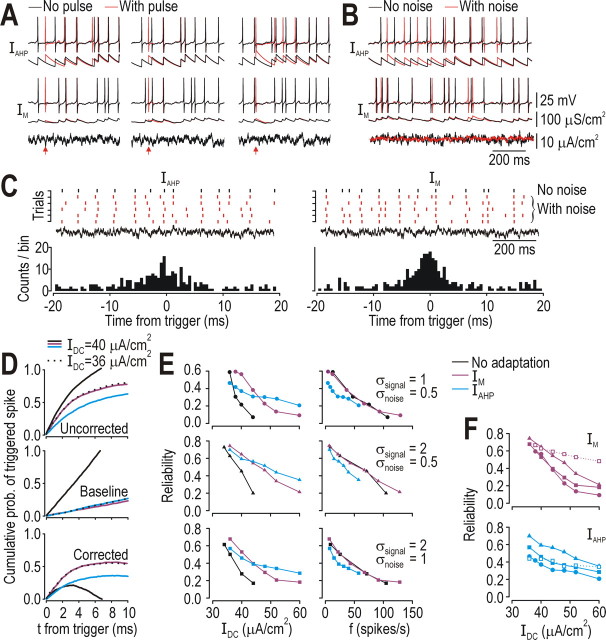
Figure 5.
Effects of adaptation on spike-time coding. A, In neuron with IAHP, timing of “signal” spikes (elicited by signal of interest) could be disrupted for several hundred milliseconds by “noise” spikes (elicited by pulses indicated by red arrows); degree of disruption depended on timing of noise spikes (compare panels). By comparison, noise spikes caused minimal disruption in neuron with IM. B, The same effects were seen more dramatically when continuous noise (σnoise = 0.5 μA/cm2) was superimposed on a dynamic signal (σsignal = 1 μA/cm2). C, Rasters (top) show spike times in neuron stimulated by signal with or without noise that varied across trials (red and black spikes, respectively). Black reference spikes were used to trigger voltage sweeps from trials with noise; timing of spikes in those triggered sweeps were compared with timing of reference spikes, as shown in the histogram. D, In top panel, cumulative probability of triggered spikes is plotted against ±t relative to reference spikes. Middle panel shows same analysis after shuffling the reference spike train, which provides a necessary control for coincident spikes based on chance (which varies with spike rate) rather than response to a common dynamic signal. Bottom panel shows corrected measure (top panel minus middle panel). Corrected curves consistently exhibited a peak beyond which the probability of triggered spikes increased more because of chance coincidence than because of elicitation by a common signal. Maximal cumulative probability of triggered spike (i.e., peak of corrected curves) is denoted reliability and plotted in E and F for different signal-to-noise ratios (σ in μA/cm2). For a given firing rate, neuron with IM or no adaptation exhibited the same reliability whereas neuron with IAHP consistently exhibited lower reliability. Increasing ḡM to a value that prevented the neuron from firing repetitively to IDC as high as 70 μA/cm2 improved reliability for IDC <70 μA/cm2 (compare open squares with filled squares), whereas increasing ḡAHP did not uniformly improve reliability.
All neurons in Figure 5D were stimulated with a constant offset (IDC) plus a dynamic signal (σsignal = 1 μA/cm2). Neurons with IM and IAHP both responded at ∼12 spikes/s to 40 μA/cm2 IDC, but the former exhibited higher reliability that was equivalent to that in the neuron without adaptation stimulated with 36 μA/cm2 (which also spiked at ∼12 spikes/s). Given the increase in I* caused by IM (Fig. 1B), 40 and 36 μA/cm2 are just below I* for neurons with IM or no adaptation, respectively (Fig. 1B); therefore, the dynamic signal was solely responsible for eliciting spikes under those stimulus conditions. In contrast, 40 μA/cm2 stimulation in the neuron without adaptation (which is well above I*) drove fast but unreliable spiking. These comparisons suggest that spike-time coding is improved by responding selectively to stimulus fluctuations (i.e., by operating in the subthreshold or perithreshold regimen rather than in the suprathreshold regimen), which is consistent with previous investigations (Gutkin et al., 2003; Prescott et al., 2006) and the inverse relationship between spike-timing reliability and spike rate (Tang et al., 1999). Reliability of responses to different IDC and SNR is summarized in Figure 5E. Similar results were found in the more realistic model (supplemental Fig. 3, available at www.jneurosci.org as supplemental material). As predicted, neurons with IAHP performed worse than neurons with IM or no adaptation when reliability was compared at the same firing rate. When ḡM was increased to prevent repetitive spiking for all IDC < 70 μA/cm2, reliability remained high across a broad range of IDC; in contrast, increasing ḡAHP worsened reliability at low IDC while causing only marginal improvements at high IDC (Fig. 5F; see below).
Effects of combining both forms of adaptation
If IAHP improves spike-rate coding at the expense of spike-time coding, and IM improves spike-time coding at the expense of spike-rate coding, what happens when both forms of adaptation co-occur? We tested this by adding both forms of adaptation to a single cell and repeating the analysis described above (supplemental Fig. 4, available at www.jneurosci.org as supplemental material). IM continued to function to prevent repetitive spiking driven by constant or slow inputs, thus encouraging fast stimulus fluctuations to elicit isolated, well timed spikes for IDC < I*; under those conditions, IAHP had no effect on the reliability of fluctuation-driven spiking. For IDC > I*, IAHP reduced reliability at a given firing rate but extended the range of IDC over which reliability remained high (because of the reduction in firing rate caused by IAHP). For spiking driven by slow or constant inputs, IAHP continued to function to regularize the spike train, thus improving spike-rate coding; IM had no significant effect other than increasing I* and thereby shifting the stimulus range over which spike-rate coding occurs. In short, benefits of IAHP and IM do not simply cancel out; instead, effects of one or the other form of adaptation predominate depending on the operating regimen (i.e., perithreshold vs suprathreshold). Thus, combining IAHP and IM produces net benefit for both spike-rate and spike-time coding.
Effects of adaptation dynamics on spike initiation
Data presented thus far indicate that IAHP improves spike-rate coding whereas IM seems to improve spike-time coding (see below). Our next goal, therefore, was to determine how these two forms of adaptation produce their dichotomous effects. Spike-rate coding requires the neuron to spike repetitively at a rate proportional to IDC or other slow signals (where “slow” must be judged relative to the ISI) and is improved by reducing ISI variability (see Fig. 4). IAHP reduced ISI variability in two ways: on a spike-by-spike basis, by increasing the refractory period after each spike, and across spikes, by causing a negative ISI correlation (see Figs. 2,3). Spike-time coding, however, benefits from the neuron not spiking repetitively in response to IDC, lest the timing of spikes elicited by fast signals be corrupted by repetitive spiking associated with slow signals. Maintained activation of IM at subthreshold potentials can prevent repetitive spiking, thereby allowing the neuron to spike selectively in response to those signals that drive voltage changes that are too fast for IM to cancel out (see below). The functional importance of kinetic differences between gM and gAHP (see Fig. 1) is clear: sustained activation of gM below threshold helps prevent repetitive spiking whereas the pulsatile kinetics of gAHP help enforce the regularity of repetitive spiking.
To explore these issues further, we used bifurcation analysis to demonstrate how differences in the activation properties of IM and IAHP affect spiking. A bifurcation refers to an abrupt, qualitative change in the behavior of the system (e.g., transition between quiescence and repetitive spiking) as a parameter (e.g., IDC or gadapt) is varied. Our Morris-Lecar model is three-dimensional because it has conductances that operate on three time scales. Since gM and gAHP are slower than conductances responsible for spike generation, the model can be reduced from 3D to 2D by treating z (which controls activation of gadapt) as a parameter (see Materials and Methods). Bifurcation diagrams in Figure 6A,B were generated by systematically varying z in the 2D model to determine how strong IM and IAHP must be to terminate spiking for a given IDC. In turn, simulations in the 3D model (i.e., with z treated as a variable) revealed how strongly IM and IAHP were activated, and whether that was sufficient to terminate repetitive spiking; results of those simulations are superimposed in black on the bifurcation diagrams. With weak stimulation, IM activated strongly enough to drive the system through the bifurcation and terminate spiking (Fig. 6A, left panel); with strong stimulation, IM was not sufficiently activated and repetitive spiking persisted (Fig. 6A, right panel). In contrast, IAHP activated strongly enough to force the system through the bifurcation at both stimulus intensities, but, instead of stopping the neuron from spiking, the system invariably drifted back across the bifurcation as IAHP waned during the ISI (Fig. 6B).
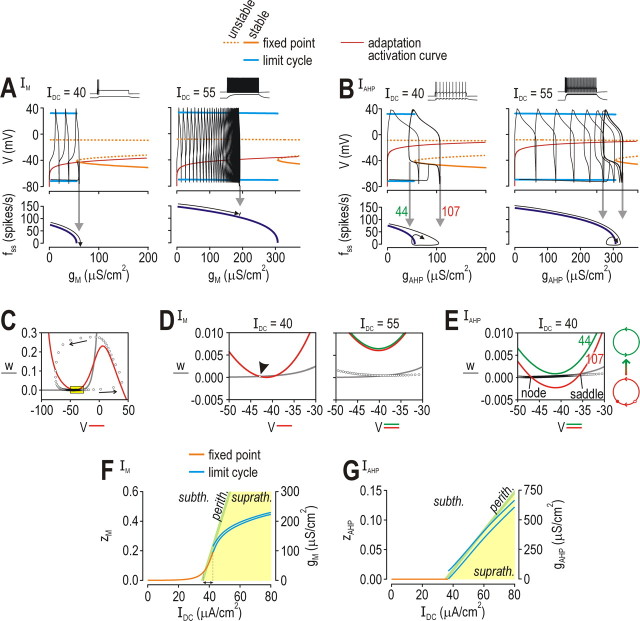
Figure 6.
Dynamical changes in strength of adaptation and their consequences for spiking. Strength of adaptation[IM (A), IAHP (B)] was systematically varied in the 2D model (with z treated as a bifurcation parameter; gadapt = ḡz) to determine the strength of adaptation required to prevent repetitive spiking. Bifurcation diagrams (top) show voltage at the fixed point (i.e., subthreshold voltage) and at the max/min of the limit cycle (i.e., spike). Voltage dependency of z is represented by a thin red line, which intercepts the stable fixed point (solid orange line) only in the neuron with IM, and only for weak stimulation (left panel of A). This predicts that the neuron with IM will stop spiking when stimulated weakly, but will continue spiking when stimulated more strongly, whereas the neuron with IAHP will never stop spiking on account of adaptation. Simulations in 3D model (with z treated as a variable) are superimposed in black and confirmed our prediction. Notice that gAHP increased high enough to force the system through its bifurcation but waned during the ISI, thus allowing the system to drift back across the bifurcation (B), unlike gM, which stabilized at a constant (or nearly constant) value (A). Bottom panels show steady-state firing rate (fss) as a function of gadapt; f can be extrapolated based on how high gadapt increases in the 3D model simulations (gray arrows). C, Typical phase plane showing fast activation variable V plotted against slower recovery variable w. V-nullcline (color) and w-nullcline (gray) show where V′ and w′ = 0, respectively. Circles show V and w at each time point over the course of one spike. Yellow boxed region is shown enlarged in D and E. D, With weak stimulation (left), neuron with IM settled at the intersection between the V- and w-nullclines (arrowhead). With stronger stimulation (right), neuron spiked repetitively because nullclines did not intersect. V-nullcline is shown for maximum (red) and minimum (green) activation of gM during steady-state spiking; the difference is negligible because fluctuation in gM is small (see A). E, In contrast, V- and w-nullclines intersected when gAHP was strongly activated (red), but not when it was weakly activated (green); strengths of gAHP correspond to labels on left panel of B. Large red and green circles on right show diagram representation of refractory and excitable conditions, respectively. (F, G) For these bifurcation diagrams, IDC was systematically varied in the 3D model; unstable solutions are not shown. Colored regions show conditions below I* (subth., white), above I* (suprath., yellow), or within 1 SD of I* (perith., green) based on Isignal fluctuations when σsignal = 1 μA/cm2 (SD = 1.6 μA/cm2). I* was determined by simulations in the 2D model in which z was held constant at different values while IDC was systematically varied to determine at the lowest IDC at which the neuron spiked repetitively. F, IM produced sustained outward current that offset increases in IDC so that the neuron operated in the perithreshold regimen over a relatively broad range of IDC (arrow). G, IAHP did not increase until IDC exceeded I*; thereafter, fluctuations in gM straddled I*, consistent with analysis in B and E.
According to the above analysis, IAHP forced the system to straddle its bifurcation whereas IM caused the system to operate on one or the other side of that bifurcation depending on IDC. The consequences of this are evident on the V-w phase plane, which shows the interaction between V (voltage) and w (activation of IK,dr) (Fig. 6C–E). In the neuron with IM, the V- and w-nullclines either intersected (and thus prevented repetitive spiking for IDC < I*) or did not intersect (and thus allowed repetitive spiking for IDC > I*) (Fig. 6D). In the neuron with IAHP, however, phase plane geometry changed over the course of the ISI: V- and w-nullclines intersected early in the ISI (thus making the neuron refractory while gAHP was strong), but they did not intersect later in the ISI (once gAHP had waned) (Fig. 6E). Using the 3D model, IDC was systematically varied to determine the stimulus ranges in which the neuron operated in these different regimes. The neuron with IM stabilized its voltage just below threshold over a reasonably broad range of IDC (Fig. 6F); this corresponds to sustained, subthreshold activation of IM preventing repetitive spiking, as in the left panel of Figure 6D. In contrast, the neuron with IAHP could not stabilize its voltage in this perithreshold regimen and instead straddled threshold (Fig. 6G), as in Figure 6E.
Effects of operating regimen on neural coding
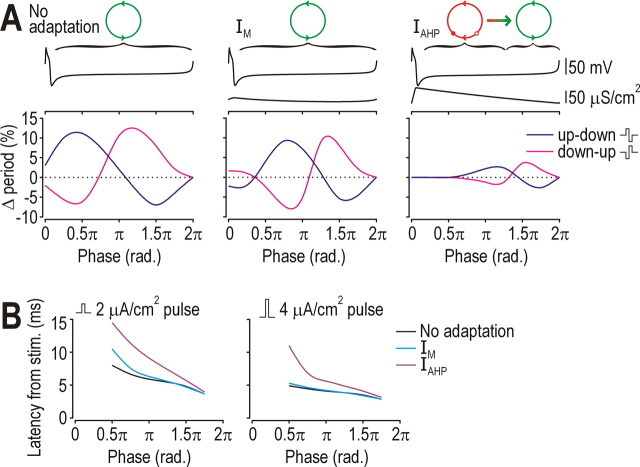
Analysis described above showed that IAHP caused transient post-spike refractoriness whereas that relative refractory period was completely absent from neurons with IM or those without adaptation. To measure how this refractoriness impacted spike-rate coding, we applied a “noise” pulse at different phases of the ISI and measured disruption of the ISI (Fig. 7A). In all cells, the pulse could shorten or lengthen the ISI (i.e., advance or delay the next spike) depending on the phase at which the pulse occurred. However, maximal disruption was far smaller in the cell with IAHP than in other cells, and there was little or no disruption if the pulse occurred in the first half of the ISI (Fig. 7A, right panel), during which strong activation of IAHP makes the neuron refractory (see above). Thus, in the neuron with IAHP, effects of high-frequency noise were actively minimized during much of the ISI, leaving a relatively short interval during which effects of noise could accumulate and affect timing of the next spike. To investigate how adaptation dynamics impact spike-time coding, we applied a “stimulus” pulse at different phases of the ISI and measured the influence of phase on latency between the pulse and the spike (Fig. 7B). As expected, pulses applied earlier in the ISI elicited spikes with longer latencies in all cells, although that effect was most pronounced in the neuron with IAHP. This is a natural consequence of the noise reduction mechanism described above: the same mechanism that reduces effects of “noise” on the ISI will reduce responsiveness to fast “signals.”
Figure 7.
Effects of refractoriness on spike-rate coding and spike-time coding. A, To investigate effects of refractoriness on spike-rate coding, a biphasic “noise” pulse was applied at different phases of the ISI. The 0.5 μA/cm2 pulse comprised a 5-ms-long up phase and a 5-ms-long down phase (therefore giving 0 μA/cm2 mean) and was tested in both orientations (up-down and down-up). IDC was adjusted to elicit 10 spikes/s in each neuron. Bottom graphs show percentage change in ISI caused by the pulse. ISIs in the neuron with IAHP (right) were disrupted much less than in other cells and were unaffected by pulses applied early in the ISI, when the neuron was refractory. Top traces show voltage and gadapt during one ISI. Circles are diagram representations of each dynamical condition, as explained in Figure 6E. B, To investigate effects of refractoriness on spike-time coding, a monophasic “signal” pulse (amplitude indicated on figure) was applied at different phases and latency from stimulus onset to the spike was measured. Latency was much more sensitive to phase in the neuron with IAHP, and was longer at all phases than in other neurons.
Unlike the transient refractoriness caused by IAHP, IM could stabilize voltage below threshold and thus terminate spiking driven by IDC (see above). This ability to place the neuron in a perithreshold operating regimen depends on how strongly IM is activated below threshold; therefore, to investigate how operation in the perithreshold regimen affects spike-time coding, we varied the strength and activation properties of IM (Fig. 8A) to change the range of IDC over which the neuron operates in the perithreshold regimen. Increasing subthreshold activation of IM caused the predicted widening of the range of perithreshold operation (Fig. 8B). Expanding the range of perithreshold operation allowed spike timing reliability to be maintained at a high level over an increasing broad range of IDC (Fig. 8C, left panel), but it did not affect the relationship between reliability and firing rate (Fig. 8C, right panel), consistent with Figure 5E. Figure 8D shows that increasingly strong subthreshold activation of IM caused progressively larger shifts in I* (dashed curves), but the neuron was nonetheless able to spike at low rates (solid curves) because average voltage remained so close to threshold (see Fig. 8B) that even weak dynamic stimulation caused fluctuation-driven spiking. It is precisely these fluctuation-driven spikes that are so reliable; thus, IM improves spike-time coding by encouraging the neuron to operate in the perithreshold regimen in which spikes are generated by fast stimulus fluctuations.
Figure 8.
Effects of perithreshold operation on spike-time coding. A, Maximal conductance (ḡM) and voltage dependency (βz and γz) were varied to adjust how strongly IM was activated at voltages below threshold. Voltage threshold (V*) can vary but its approximate value is indicated on the graph. B, Increasing subthreshold activation of IM extended the range of IDC over which the neuron operated in the perithreshold regimen, as indicated by arrows. Arrows are shown again on left panel of C, together with arrow from Figure 6F. Bifurcation diagrams shown here were generated as explained in Figure 6F,G. C, Extension of the range of perithreshold operation demonstrated in B was paralleled by an extension of the range of IDC over which spike-timing reliability remained high (left); relationship between reliability and firing rate remained unchanged (right), consistent with results in Figure 5E. D, Increasing subthreshold activation of IM resulted in increased shifting of I*, which is seen most clearly when comparing f–I curves generated by constant stimulation (dashed gray curves). Notice also that increased activation of IM caused dashed curves to become discontinuous, i.e., curves did not extend to 0 spikes/s; the implications of this are discussed in Figure 9. Inclusion of high-frequency noise/signal caused fluctuation-driven spiking that was manifested on f–I curves as a leftward tail (solid curves).
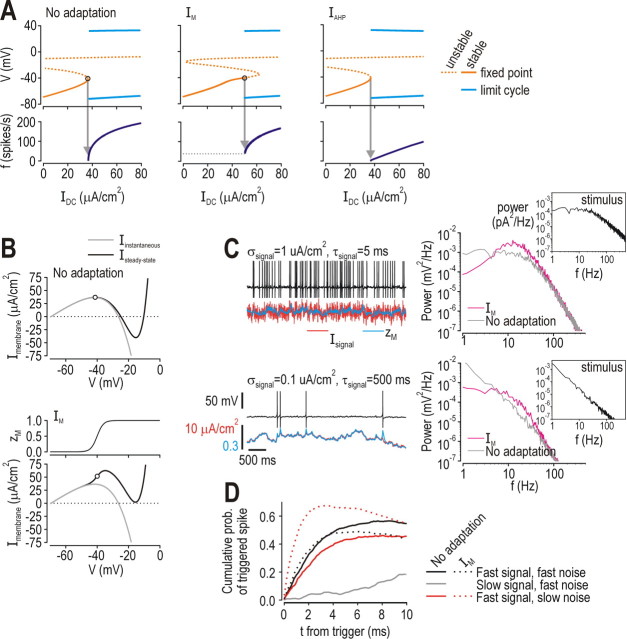
Our final step was to demonstrate how IM encourages reliable fluctuation-driven spiking. Figure 8D reveals that not only does subthreshold activation of IM cause a shift in I*, it also causes the f–IDC curve to become discontinuous, meaning spiking driven by constant input cannot be maintained below a certain rate. This switch from continuous to discontinuous f–IDC curve reflects conversion of the neuron from class 1 to class 2 according to Hodgkin's classification of intrinsic excitability (Hodgkin, 1948). This conversion is also evident from bifurcation analysis in which IDC was systematically varied in the 3D model (Fig. 9A) and from the shape of the steady-state I–V curve (Fig. 9B) (Rinzel and Ermentrout, 1998). In the neuron without adaptation, spike threshold corresponds to the peak of the steady-state I–V curve, which means net steady-state current becomes inward as IDC exceeds I* (Fig. 9B, top); this is similarly true in the neuron with IAHP (data not shown). In contrast, subthreshold activation of IM means that steady-state current is outward at threshold (Fig. 9B, bottom). In the latter case, fast-activating inward current must outrun slow-activating IM in order for spikes to be generated (this is the basis for spike generation through a Hopf bifurcation in class 2 neurons); in the former case, no such time-dependent competition occurs between inward and outward current because steady-state current is inward (this is the basis for spike generation through a saddle-nose on invariant circle or SNIC bifurcation). See Prescott et al. (2008a) for additional details on the dynamics of spike initiation in class 1 and 2 neurons.
Figure 9.
Effects of IM on spike initiating dynamics. A, Top panels shown bifurcation diagrams generated by varying IDC in the 3D model (i.e., with z treated as a parameter). Diagrams show voltage at the fixed point (i.e., subthreshold voltage) and at the max/min of the limit cycle (i.e., spike). Neuron with IM initiated spikes through a Hopf bifurcation whereas the neuron without adaptation or the one with IAHP initiated spikes through a saddle-node on invariant circle or SNIC bifurcation (see Results). Bottom panels show corresponding f–I curves. Notice that f–I curve for neuron with IM is discontinuous, which is consistent with the distinct bifurcation mechanism in this cell. For all data on this figure, ḡM = 0.5 mS/cm2, βz = −40 mV, and γz = 2 mV. B, Unlike neuron without adaptation (top) or with IAHP (data not shown), steady-state I–V curve from neuron with IM had a positive slope at threshold (bottom), meaning steady-state current was outward because of subthreshold activation of IM. Circles indicate threshold as determined in A. Iinstantaneous = INa + Ileak; Isteady-state = INa + Ileak + IK + Iadapt. C, Sample traces show voltage (black) and activation of IM (zM, blue) in response to Isignal (red). Fast-varying Isignal (top) elicited many more spikes than slow-varying Isignal (bottom) despite equivalent IDC and Isignal having equivalent SD (see Materials and Methods). Power spectra on right confirmed that IM attenuated voltage changes driven by low-frequency input. Insets show power spectra of stimuli. D, Reliability of spike timing is shown after correction based on the methodology explained in Figure 5D. In neuron without adaptation (solid lines), spiking driven by slow signal was severely disrupted by fast noise (gray), while spiking driven by fast signal was disrupted more by slow noise (red) than by fast noise (black). In contrast, neuron with IM (dotted lines) did not respond to slow signal, and the spiking driven by fast signal was disrupted less by slow noise (red) than it was by fast noise (black). Parameters for fast and slow signals were as in C; SNR was 0.5 in all cases. IDC was 36 μA/cm2 for neuron without adaptation and 44 μA/cm2 for neuron with IM to give ∼12 spikes/s in both based on fast signal/fast noise stimulation.
For purposes here, the important point is that subthreshold activation of IM causes the neuron to spike selectively in response to those stimulus fluctuations that cause voltage to change faster than IM can counteract; this selectivity depends on IM activation kinetics relative to stimulus kinetics. To illustrate this, Figure 9C shows that many more spikes were generated when activation of IM (blue trace) could not keep up with fast Isignal fluctuations (red trace) than when Isignal fluctuations were slow enough that activation of IM could keep up (compare top and bottom panels). Power spectral analysis of voltage responses confirmed that IM reduced voltage changes driven by low-frequency input (Fig. 9C, right). As shown previously (Mainen and Sejnowski, 1995), slow signals drive unreliable spiking (Fig. 9D, gray curve); it is, therefore, significant that slow signals were prevented from driving (unreliable) spiking in the neuron with IM (see above). In fact, for the neuron without adaptation, reliability of spiking driven by fast signals was degraded more by slow noise than by fast noise (compare solid red and black curves on Fig. 9D); the opposite was true for the neuron with IM (dotted curves on Fig. 9D). Overall, these results show how IM implements a high-pass filter that prevents the neuron from generating unreliable spikes to slow signals; this obviously compromises the ability of a neuron with IM to encode slow signals with a spike-rate code, but it clearly improves encoding of fast signals using a spike-time code.
Discussion
Results of this study indicate that spike-frequency adaptation has opposite effects on neural coding depending on the biophysical mechanism responsible for adaptation. Adaptation mediated by IAHP implements noise shaping that improves spike-rate coding of constant or low-frequency signals, but which compromises spike-time coding. Conversely, adaptation mediated by IM implements high-pass filtering that improves spike-time coding of high-frequency signals, but which compromises spike-rate coding. Despite their opposite effects, coexistence of IAHP and IM within a single neuron produces net benefit for both spike-rate and spike-time coding, although which form of adaptation has the predominant effect depends on the neuron's preferred coding strategy as reflected by its operating regimen.
We propose that spike-rate coding is best achieved when the neuron fires repetitively (or oscillates, to use dynamics terminology) at a rate proportional to a constant or low-frequency signal. To accurately encode the signal amplitude with as few spikes as possible, variability of the ISI (oscillation period) should be minimized; recall that instantaneous firing rate is the reciprocal of the ISI. Spike-time coding, however, is best achieved when the neuron generates well timed, isolated spikes; by “isolated” we mean that the generation of one spike is independent from the preceding spike. Fluctuation-driven spikes produced when the neuron is operating in the perithreshold regimen are generated independently of one another, whereas spikes generated as part of an ongoing oscillation are not generated independently since the oscillation period dictates the time of the next spike based on time since the last spike. Furthermore, if the neuron is oscillating (spiking repetitively), the timing of a spike elicited by a rapid stimulus upstroke is confounded by the phase of the oscillation during which that stimulus occurs (Fig. 7). Thus, spike-time coding is improved when IM causes the neuron to operate in the perithreshold regimen (by discouraging repetitive spiking and encouraging fluctuation-driven spiking), whereas spike-rate coding is improved when IAHP regularizes the repetitive spiking associated with operation in the suprathreshold regimen (by reducing the effects of noise on ISI variability).
IM and IAHP thus work toward antithetical goals, namely, discouraging or encouraging regular spiking, respectively. Achieving these different goals relies on the distinct activation properties of each current. As outlined in the Introduction, IAHP is activated during the spike, which leads to its pulsatile kinetics: gAHP increases abruptly after each spike, but because its activation cannot be sustained, gAHP invariably decreases until the next spike occurs. Pulsatile kinetics would be reduced if IAHP was significantly activated via Ca2+ channels activated at subthreshold voltages or if Ca2+ kinetics were particularly slow, either of which can occur in some neurons (Pineda et al., 1999; Wolfart and Roeper, 2002); indeed, unlike IAHP, sodium-activated potassium channels are activated via persistent sodium currents activated at subthreshold potentials (Schwindt et al., 1989; Sanchez-Vives et al., 2000) and would therefore be predicted to have effects more like IM (see below). In any case, activation of IAHP is spike dependent and pulsatile in most neurons, including pyramidal neurons whose medium-duration AHP is mediated by SK channels (Schwindt et al., 1988;Villalobos et al., 2004). Previous experimental studies have shown that IAHP affects the slope of the f–I curve (Lorenzon and Foehring, 1992; Schwindt et al., 1988; Miles et al., 2005) and the regularity of spiking (Miles et al., 2005), consistent with our results (Figs. 1, 2). By comparison, IM has been shown to terminate repetitive spiking (Cole and Nicoll, 1983) and to subtractively modulate the f–I curve (Alaburda et al., 2002) (Fig. 1), while its involvement in phenomena like subthreshold resonance (Hu et al., 2002; Prescott et al., 2008b) attests to the functional significance of its activation at subthreshold voltages.
The distinct activation properties of IAHP and IM explain the different effects of these two forms of adaptation (see Fig. 6). As firing rate increases, so too will spike-dependent activation of IAHP, which means IAHP will increase high enough to force the system through its SNIC bifurcation (notwithstanding saturation effects). This would terminate spiking were it not for the fact that activation of IAHP invariably wanes during the ISI, eventually allowing another spike to occur, but not without influencing when that spike occurs relative to the last spike (which serves to reduce the effects of noise on ISI variability) (Fig. 7A). Time-averaged voltage is not linearly related to firing rate (Holt and Koch, 1997) (data not shown), with the effect that voltage-dependent activation of IM does not keep pace with increases in firing rate; consequently, IM may fail to force the system through the SNIC bifurcation depending on stimulus intensity. However, when IM is activated strongly enough to force the system through the bifurcation, its sustained activation prevents the system from drifting back across that bifurcation, thus ensuring sustained termination of repetitive spiking driven by slow input and, instead, selectively allowing spikes driven by fast stimulus fluctuations (see below). In short, these two forms of adaptation encourage the neuron to operate in very different regimes: IAHP encourages regular, repetitive spiking whose rate is proportional to how much IDC exceeds I* whereas IM modulates I* so that that neuron operates in the perithreshold regimen in which well timed spikes are elicited independently by fast stimulus fluctuations.
Furthermore, although both IAHP and IM modulate neuronal excitability through a negative feedback mechanism, that feedback targets different aspects of responsiveness. Spike-dependent activation of IAHP means that IAHP mediates feedback directly onto firing rate; effects include reducing average firing rate as well as reducing the variability of firing rate via post-spike refractoriness and negative ISI correlations. These effects benefit spike-rate coding, as already explained, and may explain effects of IAHP on firing rate gain modulation by noise (Higgs et al., 2006) insofar as increasingly strong noise will more readily overcome the noise reduction mechanism implemented by IAHP (Fig. 7A). However, subthreshold voltage-dependent activation of IM means that IM mediates feedback onto membrane potential. Because IM has relatively slow kinetics, its feedback implements a high-pass filter (Benda et al., 2005) that minimizes voltage changes caused by low- frequency signals, thereby accentuating the capacity of high-frequency signals to drive rapid voltage changes that elicit well timed spikes (Fig. 9). This has obvious benefits for spike-time coding, consistent with previously reported effects of sustained outward currents on spike-timing reliability (Schreiber et al., 2004; Billimoria et al., 2006; Prescott et al., 2006). Similarly, spike-independent activation of the sodium-dependent potassium current (see above) is consistent with the ability of that current to decorrelate the spiking response to temporally correlated input (Wang et al., 2003).
To conclude, detailed quantitative analysis reveals that adaptation mediated by different currents has opposite effects depending on the neural code: IAHP improves spike-rate coding at the expense of spike-time coding, whereas IM improves spike-time coding at the expense of spike-rate coding. These dichotomous effects arise from the distinct activation properties of IAHP and IM, as revealed by dynamical systems analysis of our simple model. Investigating how adaptation impacts neural dynamics and, in turn, how neural dynamics impact neural coding represents a useful stepwise approach for relating biophysical mechanisms with neural coding. Overall, these results clearly indicate that spike-frequency adaptation is not a generic process, and that greater care should be taken in identifying the type of adaptation and its specific effects.
Footnotes
This work was supported by the Howard Hughes Medical Institute (T.J.S.) and by a postdoctoral fellowship from the Human Frontier Science Program (S.A.P.). We thank L. Maler, B. N. Lundstrom, and M. Bonjean for their comments on this manuscript.
References
- Adams PR, Brown DA, Constanti A. M-currents and other potassium currents in bullfrog sympathetic neurones. J Physiol. 1982;330:537–572. doi: 10.1113/jphysiol.1982.sp014357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alaburda A, Perrier JF, Hounsgaard J. An M-like outward current regulates the excitability of spinal motoneurones in the adult turtle. J Physiol. 2002;540:875–881. doi: 10.1113/jphysiol.2001.015982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barlow HB. Possible principles underlying the transformation of sensory messages. In: Rosenblith W, editor. Sensory communication. Cambridge, MA: MIT; 1961. [Google Scholar]
- Benda J, Longtin A, Maler L. Spike-frequency adaptation separates transient communication signals from background oscillations. J Neurosci. 2005;25:2312–2321. doi: 10.1523/JNEUROSCI.4795-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Billimoria CP, DiCaprio RA, Birmingham JT, Abbott LF, Marder E. Neuromodulation of spike-timing precision in sensory neurons. J Neurosci. 2006;26:5910–5919. doi: 10.1523/JNEUROSCI.4659-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowden SE, Fletcher S, Loane DJ, Marrion NV. Somatic colocalization of rat SK1 and D class (Ca(v)1.2) L-type calcium channels in rat CA1 hippocampal pyramidal neurons. J Neurosci. 2001;21(RC175) doi: 10.1523/JNEUROSCI.21-20-j0006.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calvin WH, Stevens CF. Synaptic noise and other sources of randomness in motoneuron interspike intervals. J Neurophysiol. 1968;31:574–587. doi: 10.1152/jn.1968.31.4.574. [DOI] [PubMed] [Google Scholar]
- Chacron MJ, Longtin A, Maler L. Negative interspike interval correlations increase the neuronal capacity for encoding time-dependent stimuli. J Neurosci. 2001;21:5328–5343. doi: 10.1523/JNEUROSCI.21-14-05328.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chacron MJ, Lindner B, Longtin A. A Noise shaping by interval correlations increases information transfer. Phys Rev Lett. 2004;92 doi: 10.1103/PhysRevLett.92.080601. 080601. [DOI] [PubMed] [Google Scholar]
- Chacron MJ, Maler L, Bastian J. Electroreceptor neuron dynamics shape information transmission. Nat Neurosci. 2005;8:673–678. doi: 10.1038/nn1433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chacron MJ, Lindner B, Longtin A. Threshold fatigue and information transfer. J Comput Neurosci. 2007;23:301–311. doi: 10.1007/s10827-007-0033-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole AE, Nicoll RA. Acetylcholine mediates a slow synaptic potential in hippocampal pyramidal cells. Science. 1983;221:1299–1301. doi: 10.1126/science.6612345. [DOI] [PubMed] [Google Scholar]
- Dayan P, Abbott LF. Theoretical neuroscience. Cambridge, MA: MIT; 2001. [Google Scholar]
- de la Rocha J, Doiron B, Shea-Brown E, Josić K, Reyes A. Correlation between neural spike trains increases with firing rate. Nature. 2007;448:802–806. doi: 10.1038/nature06028. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Rudolph M, Fellous JM, Sejnowski TJ. Fluctuating synaptic conductances recreate in vivo-like activity in neocortical neurons. Neuroscience. 2001;107:13–24. doi: 10.1016/s0306-4522(01)00344-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ermentrout B. Linearization of F-I curves by adaptation. Neural Comput. 1998;10:1721–1729. doi: 10.1162/089976698300017106. [DOI] [PubMed] [Google Scholar]
- Ermentrout B. Simulating, analyzing, and animating dynamical systems: a guide to XPPAUT for researchers and students. Philadelphia: SIAM; 2002. [Google Scholar]
- Fleidervish IA, Friedman A, Gutnick MJ. Slow inavtivation of Na+ current and slow cumulative spike adaptation in mouse and guinea-pig neocortical neurones in slices. J Physiol. 1996;493:83–97. doi: 10.1113/jphysiol.1996.sp021366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franklin J, Bair W. The effect of a refractory period on the power spectrum of neuronal discharge. SIAM J Appl Math. 1995;55:1074–1093. [Google Scholar]
- Gabbiani F, Koch C. Principles of spike train analysis. In: Koch C, Segev I, editors. Methods in neuronal modeling. Cambridge, MA: MIT; 1998. pp. 313–360. [Google Scholar]
- Gillespie DT. The mathematics of brownian motion and johnson noise. Am J Phys. 1996;64:225–240. [Google Scholar]
- Goldberg JA, Wilson CJ. Control of spontaneous firing patterns by the selective coupling of calcium currents to calcium-activated potassium currents in striatal cholinergic interneurons. J Neurosci. 2005;25:10230–10238. doi: 10.1523/JNEUROSCI.2734-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green D, Swets J. Signal detection theory and psychophysics. New York: Wiley; 1966. [Google Scholar]
- Gutfreund Y, Yarom Y, Segev I. Subthreshold oscillations and resonant frequency in guinea-pig cortical neurons: physiology and modelling. J Physiol. 1995;483:621–640. doi: 10.1113/jphysiol.1995.sp020611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutkin B, Ermentrout GB, Rudolph M. Spike generating dynamics and the conditions for spike-time precision in cortical neurons. J Comput Neurosci. 2003;15:91–103. doi: 10.1023/a:1024426903582. [DOI] [PubMed] [Google Scholar]
- Halliwell JV, Adams PR. Voltage-clamp analysis of muscarinic excitation in hippocampal neurons. Brain Res. 1982;250:71–92. doi: 10.1016/0006-8993(82)90954-4. [DOI] [PubMed] [Google Scholar]
- Higgs MH, Slee SJ, Spain WJ. Diversity of gain modulation by noise in neocortical neurons: regulation by the slow afterhyperpolarization conductance. J Neurosci. 2006;26:8787–8799. doi: 10.1523/JNEUROSCI.1792-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin AL. The local electric changes associated with repetitive action in a non-medullated axon. J Physiol. 1948;107:165–181. doi: 10.1113/jphysiol.1948.sp004260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holt GR, Koch C. Shunting inhibition does not have a divisive effect on firing rates. Neural Comput. 1997;9:1001–1013. doi: 10.1162/neco.1997.9.5.1001. [DOI] [PubMed] [Google Scholar]
- Hu H, Vervaeke K, Storm JF. Two forms of electrical resonance at theta frequencies, generated by M-current, h-current and persistent Na+ current in rat hippocampal pyramidal cells. J Physiol. 2002;545:783–805. doi: 10.1113/jphysiol.2002.029249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorenzon NM, Foehring RC. Relationship between repetitive firing and afterhyperpolarizations in human neocortical neurons. J Neurophysiol. 1992;67:350–363. doi: 10.1152/jn.1992.67.2.350. [DOI] [PubMed] [Google Scholar]
- Madison DV, Nicoll RA. Control of the repetitive discharge of rat CA1 pyramidal neurones in vitro. J Physiol. 1984;354:319–331. doi: 10.1113/jphysiol.1984.sp015378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mainen ZF, Sejnowski TJ. Reliability of spike timing in neocortical neurons. Science. 1995;268:1503–1506. doi: 10.1126/science.7770778. [DOI] [PubMed] [Google Scholar]
- Mar DJ, Chow CC, Gerstner W, Adams RW, Collins JJ. Noise shaping in populations of coupled model neurons. Proc Natl Acad Sci U S A. 1999;96:10450–10455. doi: 10.1073/pnas.96.18.10450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miles GB, Dai Y, Brownstone RM. Mechanisms underlying the early phase of spike frequency adaptation in mouse spinal motoneurones. J Physiol. 2005;566:519–532. doi: 10.1113/jphysiol.2005.086033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris C, Lecar H. Voltage oscillations in the barnacle giant muscle fiber. Biophys J. 1981;35:193–213. doi: 10.1016/S0006-3495(81)84782-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oswald AM, Doiron B, Maler L. Interval coding. I. Burst interspike intervals as indicators of stimulus intensity. J Neurophysiol. 2007;97:2731–2743. doi: 10.1152/jn.00987.2006. [DOI] [PubMed] [Google Scholar]
- Perkel DH, Bullock TH. Neural coding. Neurosci Res Prog Sum. 1968;3:405–527. [Google Scholar]
- Pineda JC, Galarraga E, Foehring RC. Different Ca2+ source for slow AHP in completely adapting and repetitive firing pyramidal neurons. Neuroreport. 1999;10:1951–1956. doi: 10.1097/00001756-199906230-00029. [DOI] [PubMed] [Google Scholar]
- Prescott SA, Ratté S, De Koninck Y, Sejnowski TJ. Nonlinear interaction between shunting and adaptation controls a switch between integration and coincidence detection in pyramidal neurons. J Neurosci. 2006;26:9084–9097. doi: 10.1523/JNEUROSCI.1388-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prescott SA, De Koninck Y, Sejnowski TJ. Biophysical basis for three distinct dynamical mechanisms of action potential initiation. PLoS Computational Biology. 2008a;4:e1000198. doi: 10.1371/journal.pcbi.1000198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prescott SA, Ratté S, De Koninck Y, Sejnowski TJ. Pyramidal neurons switch from integrators in vitro to resonators under in vivo-like conditions. J Neurophysiol. 2008b doi: 10.1152/jn.90634.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rieke F, Warland D, de Ruyter van Steveninck RR, Bialek W. Spikes: exploring the neural code. Cambridge, MA: MIT; 1997. [Google Scholar]
- Rinzel J, Ermentrout GB. Analysis of neural excitability and oscillations. In: Koch C, Segev I, editors. Methods in neuronal modeling: from ions to networks. Cambridge, MA: MIT; 1998. pp. 251–291. [Google Scholar]
- Sanchez-Vives MV, Nowak LG, McCormick DA. Cellular mechanisms of long-lasting adaptation in visual cortical neurons in vitro. J Neurosci. 2000;20:4286–4299. doi: 10.1523/JNEUROSCI.20-11-04286.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schreiber S, Fellous JM, Tiesinga P, Sejnowski TJ. Influence of ionic conductances on spike timing reliability of cortical neurons for suprathreshold rhythmic inputs. J Neurophysiol. 2004;91:194–205. doi: 10.1152/jn.00556.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwindt PC, Spain WJ, Crill WE. Long-lasting reduction of excitability by a sodium-dependent potassium current in cat neocortical neurons. J Neurophysiol. 1989;61:233–244. doi: 10.1152/jn.1989.61.2.233. [DOI] [PubMed] [Google Scholar]
- Schwindt PC, Spain WJ, Foehring RC, Stafstrom CE, Chubb MC, Crill WE. Multiple potassium conductances and their functions in neurons from cat sensorimotor cortex in vitro. J Neurophysiol. 1988;59:424–449. doi: 10.1152/jn.1988.59.2.424. [DOI] [PubMed] [Google Scholar]
- Sharpee TO, Sugihara H, Kurgansky AV, Rebrik SP, Stryker MP, Miller KD. Adaptive filtering enhances information transmission in visual cortex. Nature. 2006;439:936–942. doi: 10.1038/nature04519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shin J. Adaptation in spiking neurons based on the noise shaping neural coding hypothesis. Neural Netw. 2001;14:907–919. doi: 10.1016/s0893-6080(01)00077-6. [DOI] [PubMed] [Google Scholar]
- Storm JF. Potassium currents in hippocampal pyramidal cells. Prog Brain Res. 1990;83:161–187. doi: 10.1016/s0079-6123(08)61248-0. [DOI] [PubMed] [Google Scholar]
- Strogatz SH. Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering. Don Mills, ON, Canada: Addison-Wesley; 1998. [Google Scholar]
- Tang AC, Wolfe J, Bartels AM. Cholinergic modulation of spiking timing and spike rate. Neurocomputing. 1999;26–27:293–298. [Google Scholar]
- Theunissen F, Miller JP. Temporal encoding in nervous systems: a rigorous definition. J Comput Neurosci. 1995;2:149–162. doi: 10.1007/BF00961885. [DOI] [PubMed] [Google Scholar]
- Tuckwell HC. Introduction to theoretical neurobiology: vol. 2. nonlinear and stochastic theories. New York: Cambridge UP; 1988. [Google Scholar]
- Uhlenbeck GE, Ornstein LS. On the theory of brownian motion. Phys Rev. 1930;36:823–841. [Google Scholar]
- Villalobos C, Shakkottai VG, Chandy KG, Michelhaugh SK, Andrade R. SKCa channels mediate the medium but not the slow calcium-activated afterhyperpolarization in cortical neurons. J Neurosci. 2004;24:3537–3542. doi: 10.1523/JNEUROSCI.0380-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang HS, McKinnon D. Potassium currents in rat prevertebral and paravertebral sympathetic neurones: control of firing properties. J Physiol. 1995;485:319–335. doi: 10.1113/jphysiol.1995.sp020732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang HS, Pan Z, Shi W, Brown BS, Wymore RS, Cohen IS, Dixon JE, McKinnon D. KCNQ2 and KCNQ3 potassium channel subunits: molecular correlates of the M-channel. Science. 1998;282:1890–1893. doi: 10.1126/science.282.5395.1890. [DOI] [PubMed] [Google Scholar]
- Wang XJ. Calcium coding and adaptive temporal computation in cortical pyramidal neurons. J Neurophysiol. 1998;79:1549–1566. doi: 10.1152/jn.1998.79.3.1549. [DOI] [PubMed] [Google Scholar]
- Wang XJ, Liu Y, Sanchez-Vives MV, McCormick DA. Adaptation and temporal decorrelation by single neurons in the primary visual cortex. J Neurophysiol. 2003;89:3279–3293. doi: 10.1152/jn.00242.2003. [DOI] [PubMed] [Google Scholar]
- Wark B, Lundstrom BN, Fairhall A. Sensory adaptation. Curr Opin Neurobiol. 2007;17:423–429. doi: 10.1016/j.conb.2007.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams S, Serafin M, Mühlethaler M, Bernheim L. Distinct contributions of high- and low-voltage-activated calcium currents to afterhyperpolarizations in cholinergic nucleus basalis neurons of the guinea pig. J Neurosci. 1997;17:7307–7315. doi: 10.1523/JNEUROSCI.17-19-07307.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfart J, Roeper J. Selective coupling of T-type calcium channels to SK potassium channels prevents intrinsic bursting in dopaminergic midbrain neurons. J Neurosci. 2002;22:3404–3413. doi: 10.1523/JNEUROSCI.22-09-03404.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamada S, Takechi H, Kanchiku I, Kita T, Kato N. Small-conductance Ca2+-dependent K+ channels are the target of spike-induced Ca2+ release in a feedback regulation of pyramidal cell excitability. J Neurophysiol. 2004;91:2322–2329. doi: 10.1152/jn.01049.2003. [DOI] [PubMed] [Google Scholar]