Joint modeling of self-rated health and changes in physical functioning

Abstract

Self-rated health is an important indicator of future morbidity and mortality. Past research has indicated that self-rated health is related to both levels of and changes in physical functioning. However, no previous study has jointly modeled longitudinal functional status and self-rated health trajectories. We propose a joint model for self-rated health and physical functioning that describes the relationship between perceptions of health and the rate of change of physical functioning or disability. Our joint model uses a non-homogeneous Markov process for discrete physical functioning states and connects this to a logistic regression model for “healthy” versus “unhealthy” self-rated health through parameters of the physical functioning model. We use simulation studies to establish finite sample properties of our estimators and show that this model is robust to misspecification of the functional form of the relationship between self-rated health and rate of change of physical functioning. We also show that our joint model performs better than an empirical model based on observed changes in functional status. We apply our joint model to data from the Cardiovascular Health Study (CHS), a large, multi-center, longitudinal study of older adults. Our analysis indicates that self-rated health is associated both with level of functioning as indicated by difficulty with activities of daily living (ADL) and instrumental activities of daily living (IADL), and the risk of increasing difficulty with ADLs and IADLs.

1 INTRODUCTION

Subjective assessments of health have become increasingly important to the evaluation of the health experience. Self-rated health has been shown to be associated with morbidity and mortality, independent of other potential explanatory factors such as hospital visits, body mass index, and cognitive functioning (Idler and Benyamini 1997; Benyamini and Idler 1999; Miller and Wolinsky 2007). This measure is sensitive to changes in health and strongly predictive of future health outcomes. A great deal of research has, therefore, focused on identifying factors that drive self-rated health.

Previous research has identified a relationship between level of disability and self-rated health, especially in older adults (Liang et al. 2007; Shooshtari et al. 2007). Moreover, self-rated health has been shown to be connected both to current level of functioning and to change in functioning (Ferraro et al. 1997; Bailis et al. 2003). This may be because self-rated health is associated with the level of objective health and an individual's ability to adapt to change (Leinonen et al. 2001). Careful modeling of the relationship between physical disability and self-rated health is necessary to elucidate the factors influencing an individual's perceptions of health.

Studies of longitudinal changes in functioning and their effect on self-rated health have most often used binary indicators of functional status trajectories to summarize changes in functioning (e.g. Bailis et al. (2003); Shooshtari et al. (2007)). For instance, subjects are described as stable versus declining or improving. Although these studies have identified a relationship between self-rated health and physical functioning, they are limited by this relatively imprecise measure of change. Liang et al. (2007) also note the high degree of within-subject variability in functional status, with physical functioning fluctuating from day to day. On this basis, Liang et al. (2007) construct a model for self-rated health using age and dummy variables representing a variety of functional status trajectories as predictors. Trajectories considered include “minimal decrement” and “early onset of decline”. Although this approach addresses the association between self-rated health and trends in physical functioning, it is limited by relatively coarse measures of change in functional status. As an alternative, we propose a joint model to study the relationship between self-rated health and changes in physical functioning, simultaneously estimating parameters of the functional status model and their association with self-rated health.

A number of previous studies of functional status in older adults have used multi-state models, particularly Markov processes, to investigate longitudinal trajectories of functional status and disability (Beckett et al. 1996; Izmirlian et al. 2000; Peres et al. 2005; Pan et al. 2007). These models are frequently used in biomedical studies of multi-state diseases because of their applicability to a broad range of disease and observational schemes (see e.g. Klein et al. (1984); Kalbfleisch and Lawless (1985); Kay (1986); Gentleman et al. (1994); Perez-Ocon et al. (2001)). Markov processes are particularly useful for addressing the interval censored nature of functional status data since the exact transition times between physical functioning states are rarely known.

The rate of transition among functional disability states is strongly age-dependent. It has been previously noted that decline in physical functioning is non-linear with respect to age with older subjects experiencing more rapid decline than younger subjects (Beckett et al. 1996; Peres et al. 2005). Increased rates of functional decline may be attributable to loss of the ability to maintain physiologic homeostasis as subjects age (Strawbridge et al. 1992). However, previous multi-state models for functional status in the elderly have only addressed this by stratifying the cohort into large age groups, such as over or under 80 years of age, and modeling non-age dependent transition rates within these strata We implement a non-homogeneous Markov process model for the functional status process which allows for smooth age related variations in transition rates across the age range.

We connect our functional status model to self-rated health by including parameters of the multi-state model for functional status as covariates in our self-rated health model. For example, temporal trends in self-rated health may depend on the rate of transition to states of greater functional disability from our Markov process model. By including functional status level, age, and risk of transition to states of more impaired functional status in a model for self-rated health we can make inference about how they impact health perceptions.

Previous research on joint models has focused on the case in which the trajectory of a continuous marker influences a discrete disease process (see e.g. Tsiatis and Davidian (2004)). The objective of these models is to use the continuous measure to describe or predict time to some disease event. By contrast, our joint model will investigate the relationship between the rate of change of a discrete disease process, functional status, and a binary indicator of self-rated health. The joint modeling allows us to simultaneously estimate the rate of change of one process and assess its impact on state occupancies in the other process.

The structure of this manuscript is as follows. In Section 2, we propose a framework for carrying out joint modeling of functional status and self-rated health as a function of both covariates, current level of physical functioning and temporal trends in functioning. We propose an estimation method for this model in Section 3. In Section 4, we present a simulation study to investigate properties of our joint model. We then apply our method to the Cardiovascular Health Study (CHS) cohort of older adults to investigate the association between longitudinal changes in functional status and self-rated health.

2 JOINT MODELING OF SELF-RATED HEALTH AND MULTI-STATE DISEASE PROCESSES

Let m denote the number of subjects in the study and n_k denote the number of observation times for the k^th subject. The time of the i^th observation for subject k is denoted u_ki, and at time u_ki we observe the subject's functional status, denoted X(u_ki), with realized value x_ki, a discrete value in 1, … , r. For ease of presentation, we suppress the subscript relating to subject and express number of observations, observation time and functional status simply as n, u_i, and X(u_i) respectively. The vector of functional status measurements over time is denoted X. In the application presented in Section 4 we focus on the case where X(u_i) is a measure of functional status. However, the methods developed below could be applied to any multi-state disease process.

Functional status is assumed to follow a first-order continuous time discrete state Markov process with transition probabilities

$${\left\{\mathbf{p}(u_{i-1},u_i)\right\}}_{x_{i-1},x_i}=p_{x_{i-1},x_i}(u_{i-1},u_i)\doteq P\{X\left(u_i\right)=x_i\mid X\left(u_{i-1}\right)=x_{i-1}\}$$

and transition intensities

$${\left\{\mathbf{q}\left(u_i\right)\right\}}_{x_{i-1},x_i}=q_{x_{i-1},x_i}\left(u_i\right),$$

defined as, q_ab(u) = lim_Δu→0 p_ab(u, u + Δu)/Δu, a ≠ b and q_aa(u) = −Σ_b≠a q_ab(u) (Cox and Miller (1965)).

We address non-homogeneity of the process via the time transformation approach of Hubbard et al. (2008). Specifically, we assume that

$$\mathbf{p}(u_{i-1},u_i)=\exp \left({\mathbf{q}}_0(h(u_i;\theta )-h(u_{i-1};\theta ))\right)\doteq \underset{s=0}{\overset{\infty }{\Sigma }}{\left({\mathbf{q}}_0(h(u_i;\theta )-h(u_{i-1};\theta ))\right)}^s∕s!,$$

where q₀ denotes a baseline transition matrix, and θ denotes the parameters of the time transformation function, h(u; θ). Under this model, transition intensities are time-dependent on the original time scale, but we assume that there exists an alternative time-scale on which the process is homogeneous. The time transformation function represents an alternative time-scale for the process and hence must be positive and non-decreasing, that is, h(u; θ) > 0 and dh(u; θ)/du > 0 for all u > 0. This method of modeling non-homogeneous disease processes has been shown to fit the data well even if the assumption of homogeneity on the alternative time scale, h(u; θ) is not met (Hubbard et al. 2008).

Let Y = (Y (u₁), … , Y (u_n))′ be a vector of health outcomes with probability mass or density function P (Y (u_i)|η(C(u_i); β)), where C(u_i) = (C₁(u_i), … ,C_p(u_i))′ is a vector of risk factors associated with the measure of health under study and β are parameters relating these factors to the health outcome. Let η(.; .) denote a link function which is assumed known. We model η(C(u_i); β) = C′(u_i)β. Thus, η(C(u_i); β) links the disease process to the subjective health model.

Elements of C(u_i) may include current or past functional status (X), measures of progression of the functional status process, such as the probability of transition to severe disability, and demographics or other covariates. This model allows us to assess the extent to which current health assessments depend on both current or past functional status and rates of change in functional status. That is, we assume self-rated health is dependent on some function, η(.; .), of current functional status, covariates, and parameters describing the rate of change in physical functioning.

The joint likelihood of functional status and self-rated health is

$$\begin{array}{cc}\hfill P& (\mathit{X},\mathit{Y}\mid \beta ,\psi )\hfill \\ \hfill & =P(\mathit{Y}\mid \mathit{X},\beta ,\psi )P(\mathit{X}\mid \psi )\hfill \\ \hfill & =\left\{\prod _{i=1}^{n}P(Y\left(u_i\right)\mid \eta (\mathit{C}\left(u_i\right);\beta ),\psi )\right\}\times \left\{P(X\left(u_1\right)=x_1)\prod _{i=2}^{n}P(X\left(u_i\right)=x_i\mid X\left(u_{i-1}\right)=x_{i-1},\psi )\right\}\hfill \\ \hfill & =\left\{\prod _{i=1}^{n}P(Y\left(u_i\right)\mid \eta (\mathit{C}\left(u_i\right);\beta ),\psi )\right\}\times \left\{P(X\left(u_1\right)=x_1)\prod _{i=2}^n{p}_{x_{i-1},x_i}(u_{i-1},u_i)\right\},\hfill \end{array}$$

where ψ denotes the functionally independent elements of the baseline transition intensity matrix and parameters of the time transformation. The first term in the joint likelihood represents the contribution of the self-rated health likelihood. The remaining terms represent the contribution of the disease process likelihood. We note that the above formulation assumes a non-homogeneous Markov model for the disease process. Moreover, it assumes that self-rated health observations are conditionally independent given the disease process “history.”

In our application, we focus on a binary outcome. In this case, we consider health assessments that arise from a binomial distribution with probability P(Y (u_i)|η(C(u_i); β)) and use a logistic link function which gives rise to

$$P(Y\left(u_i\right)=1\mid \eta (\mathit{C}\left(u_i\right);\beta ))=\frac{\exp \left({\mathit{C}}^{\prime }\left(u_i\right)\beta \right)}{1+\exp \left({\mathit{C}}^{\prime }\left(u_i\right)\beta \right)}.$$ (1)

The log-likelihood in this example is

$$\log P(\mathit{X},\mathit{Y}\mid \beta ,\psi )=K+\underset{i=2}{\overset{n}{\Sigma }}\log p_{x_{i-1},x_i}(u_{i-1},u_i)+\left(\underset{i-1}{\overset{n}{\Sigma }}Y\left(u_i\right){\mathit{C}}^{\prime }\left(u_i\right)\beta -\log (1+\exp \left({\mathit{C}}^{\prime }\left(u_i\right)\beta \right))\right),$$ (2)

where K = log P(X(u₁) = x₁) is a nuisance parameter. Although we apply our methods to binary measures of health, our methods can be easily extended to a wide class of distributions and link functions.

The identifiability of parameters in the joint model will depend on the specific time transformation function and functional form of the elements of ψ occurring in C(u). We discuss identifiability within our specific application of the joint model in which h(u; θ) = uθ^u and C(u_i) contains a transition probability from the functional status model, p_xi,2(u_i, u_i + 5), in Appendix A. Identifiability of the models presented in the simulation and the case study can be established following arguments similar to those presented in Appendix A.

3 MAXIMUM LIKELIHOOD ESTIMATION

We implement numerical maximization of the likelihood using the Fisher scoring algorithm, a quasi-Newton method first proposed for estimation of continuous time Markov process models by Kalbfleisch and Lawless (1985). One advantage of this maximization method is that it only requires the first derivatives of the log-likelihood with respect to the model parameters.

We focus on the case in which the self-rated health model depends on parameters of the functional status process model and undertake joint maximization of the functional status and self-rated health likelihoods. Thus, we consider derivatives of the log-likelihood with respect to functional status model parameters, ψ, and self-rated health model parameters, β. In symbols, we derive

$$\frac{\partial \log P(\mathit{X},\mathit{Y}\mid \beta ,\psi )}{\partial {\psi }_k}=\underset{i=2}{\overset{n}{\Sigma }}\frac{\partial \log p_{x_{i-1},x_i}(u_{i-1},u_i)}{\partial {\psi }_k}+\underset{i=1}{\overset{n}{\Sigma }}\frac{\partial \log P(Y\left(u_i\right)\mid \eta (C\left(u_i\right);\beta ))}{\partial {\psi }_k}$$ (3)

and

$$\begin{array}{cc}\hfill \frac{\partial \log P(\mathit{X},\mathit{Y}\mid \beta ,\psi )}{\partial {\beta }_k}& =\underset{i=2}{\overset{n}{\Sigma }}\frac{\partial \log p_{x_{i-1},x_i}(u_{i-1},u_i)}{\partial {\beta }_k}+\underset{i=1}{\overset{n}{\Sigma }}\frac{\partial \log P(Y\left(u_i\right)\mid \eta (\mathit{C}\left(u_i\right);\beta ))}{\partial {\beta }_k}\hfill \\ \hfill & =\underset{i=1}{\overset{n}{\Sigma }}\frac{\partial \log P(Y\left(u_i\right)\mid \eta (\mathit{C}\left(u_i\right);\beta ))}{\partial {\beta }_k}.\hfill \end{array}$$ (4)

Complete expressions for partial derivatives occurring in the score functions, equations (5) and (6), are available in Appendix B.

We note that if the self-rated health model depends only on functional status and not on parameters of the functional status model, then equation (5) is independent of the self-rated health model parameters and we can carry out separate estimation for parameters of the functional status and self-rated health models. In particular, the estimation of the physical functioning process can be carried out using a numerical maximization method such as the Fisher scoring algorithm. Estimation of the self-rated health model, on the other hand, may allow for explicit formulae for estimators of β. This is the case, for example, when considering a normal model for self-rated health and the identity link. When explicit solutions are, however, not available, we can also use numerical maximization via the Fisher scoring algorithm or another maximization algorithm, such as the iteratively reweighted least squares approach employed in the generalized linear models framework, to obtain estimates of β. In all applications presented in Section 4 the Fisher scoring algorithm is used to obtain parameter estimates

Variance estimates are based on the inverse expected information. We define the expected information for the joint model as

$$I\left(\varphi \right)=E\left[\left(\frac{\partial \log P(\mathit{X},\mathbf{Y}\mid \beta ,\psi )}{\partial \varphi }\right){\left(\frac{\partial \log P(\mathit{X},\mathbf{Y}\mid \beta ,\psi )}{\partial \varphi }\right)}^{\prime }\right],$$

where ϕ = (ψ′, β′)′. We estimate the variance of model parameters using an estimate of the inverse expected information, Î⁻¹(ϕ̂), where

$$\widehat{I}\left(\widehat{\varphi }\right)=\underset{k=1}{\overset{m}{\Sigma }}\underset{i=2}{\overset{n_k}{\Sigma }}\left[\left({\phantom{\mid }\frac{\partial \log P(X\left(u_{\mathit{ki}}\right),Y\left(u_{\mathit{ki}}\right)\mid \beta ,\psi )}{\partial \varphi }\mid }_{\widehat{\varphi }}\right){\left({\phantom{\mid }\frac{\partial \log P(X\left(u_{\mathit{ki}}\right),Y\left(u_{\mathit{ki}}\right)\mid \beta ,\psi )}{\partial \varphi }\mid }_{\widehat{\varphi }}\right)}^{\prime }\right].$$

In many cases we may not be directly interested in model parameters such as the baseline transition intensities but we may be interested in derived quantities such as transition probabilities or average time to first occurrence of disability. In this case variances can be computed using the delta method.

4 APPLICATIONS

4.1 Simulation study

We conducted a simulation study to assess bias, efficiency, and confidence interval coverage probabilities for maximum likelihood estimators of the model parameters. Functional status data, X, were simulated from a five-state process with one absorbing state. In this model, state one is an absorbing state representing death, and states two through five represent increasing levels of physical functioning. Health state data, Y, were simulated from a Bernoulli distribution with probability of state one, representing good health, dependent on current functional status level, age, and probability of being in functional status level two in five years. Here Y is an indicator of good self-rated health that depends on the probability of transitioning to a state representing the most severe level of functional disability.

Specifically, functional status data were simulated from a time-transformed homogeneous process with

$${\mathbf{q}}_0=\left(\begin{array}{ccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0.4\hfill & \hfill -1.1\hfill & \hfill 0.4\hfill & \hfill 0.2\hfill & \hfill 0.1\hfill \\ \hfill 0.2\hfill & \hfill 0.4\hfill & \hfill -1.2\hfill & \hfill 0.4\hfill & \hfill 0.2\hfill \\ \hfill 0.1\hfill & \hfill 0.2\hfill & \hfill 0.4\hfill & \hfill -1.1\hfill & \hfill 0.4\hfill \\ \hfill 0.05\hfill & \hfill 0.1\hfill & \hfill 0.2\hfill & \hfill 0.4\hfill & \hfill -0.75\hfill \end{array}\right).$$

We investigated the performance of models using two different time transformation functions: a power time transformation function, h₁(u; θ) = uθ^u, with θ = 1.1 and a more complex function, h₂(u; θ) = u(1 + θ₁ exp(u − θ₂)/(1 + exp(u − θ₂))) with θ₁ = 1 and θ₂ = 5. The first function represents a process in which the rate of transition between all states is increasing with respect to time. In previous research we have found this to be a good model for studies of functional status transitions in elderly subjects (Hubbard 2007). The second function represents a process in which the rate of transition increases in the early part of the observation period, reaching a maximum at u = 5.729, after which the process slows.

Probability of good self-rated health was based on a logistic model of functional status, transition probability, and time,

$$P(Y\left(u_i\right)=1\mid u_i,X\left(u_i\right),\beta )=\frac{\exp \left(\eta (\mathit{C}\left(u_i\right);\beta )\right)}{1+\exp \left(\eta (\mathit{C}\left(u_i\right);\beta )\right)},$$

where

$$\eta (\mathit{C}\left(u_i\right);\beta )={\beta }_0{p}_{x_i,2}(u_i,u_i+5)+{\beta }_1{u}_i+{\beta }_{2}1(X\left(u_i\right)=3)+{\beta }_{3}1(X\left(u_i\right)=4)+{\beta }_{4}1(X\left(u_i\right)=5).$$

In our simulations, we let β = (−0.1, −0.5, 1, 1, 1)′. Self-rated health is undefined for dead subjects (X(u) = 1). Thus, subjects who die during the observation period contribute to the self-rated health portion of the likelihood only up to the last observation prior to death. Our model for simulated self-rated health data represents a case in which good self-rated health is less likely among subjects who are older or have higher probability of being in a state of severe disability in five years (state 2) and higher among subjects with less disability (states 3, 4, or 5). This structure for the disability process and self-rated health model was selected to mirror the general structure of our real data from the Cardiovascular Health Study. We note that, because p_xi,2(u_i, u_i + 5) arises from our Markov model for the functional status process, we need not observe a subject at time u_i + 5 in order to include this probability in our model for good self-rated health.

Data were simulated for varying numbers of subjects and observations. We report estimated biases, standard errors, 95% confidence interval coverage probabilities, and empirical standard errors for β̂₀ computed across simulations based on 1000 simulations per sample size. We focus on properties of our estimation method for β̂₀ because this parameter is of greatest interest in our joint model. It represents the effect of the rate of change of functional status on self-rated health. Results for other parameters in the joint model are presented in Appendix C.

Results for β̂₀ are presented in Table 7. In the model using time transformation function h₁(u; θ), we observe low bias for all sample sizes and that bias decreases for both larger numbers of subjects and larger numbers of observations per subject. Decreases in bias are somewhat more marked when we increase the number of subjects as compared to more modest decreases when the number of observations per subject is increased. Model based standard errors are underestimated across the range of sample sizes investigated relative to empirical standard errors leading to depressed confidence interval coverage probabilities. However, as the number of subjects is increased from 100 to 500 the percent underestimation of standard errors decreases. For instance, in simulations with five observations per subject the percent underestimation of standard errors decreases from 20.3% for a sample size of 100 subjects to 5.7% in simulations with a sample size of 500 subjects. This suggests that a large cohort is needed in order for asymptotic standard error estimates and confidence intervals based on asymptotic normality of the estimators to be appropriate.

For the second time transformation function investigated, we have restricted attention to sample sizes with at least ten observations per subject. This was done because a longer course of observation is necessary in order to estimate θ in this more complex function. A shorter course of observation results in a relatively flat likelihood which is difficult to maximize using numerical methods. Similar to results when using h₁(u; θ), bias is low and decreases as sample sizes increases with asymptotic standard errors slightly underestimating true standard errors. However, this underestimation is more modest and decreases with increasing sample size. Confidence interval coverage probabilities are depressed by this underestimation for smaller sample sizes but approach nominal levels for larger sample sizes at which underestimation of standard errors is about 4%.

We carried out a second simulation study to compare the improvement in model fit associated with using a joint model as compared to simpler models in which self-rated health depends only on current functional status or the observed history of changes in functional status. Data were simulated from a five-state process as described above using h₁(u; θ) in which self-rated health depends on the probability of transition to the state corresponding to severe disability. Because this simulation study focuses on misspecification of η(C(u_i); β) and not on misspecification of h(u; θ) we present results for only one time transformation function.

To investigate the impact of misspecifying the functional form of the relationship between self-rated health and functional status we fit both the true model and misspecified models. Specifically, we compare the following four models:

$$\begin{array}{cc}\hfill \mathrm{M}1:\eta (\mathit{C}\left(u_i\right);\beta )& ={\beta }_1{u}_i+{\beta }_{2}1(X\left(u_i\right)=3)+{\beta }_{3}1(X\left(u_i\right)=4)+{\beta }_{4}1(X\left(u_i\right)=5)\hfill \\ \hfill \mathrm{M}2:\eta (\mathit{C}\left(u_i\right);\beta )& ={\beta }_{0}1(X\left(u_i\right)<X\left(u_{i-1}\right))+{\beta }_1{u}_i+{\beta }_{2}1(X\left(u_i\right)=3)+{\beta }_{3}1(X\left(u_i\right)=4)+{\beta }_{4}1(X\left(u_i\right)=5)\hfill \\ \hfill \mathrm{M}3:\eta (\mathit{C}\left(u_i\right);\beta )& ={\beta }_0{q}_{x_i,2}\left(u_i\right)+{\beta }_1{u}_i+{\beta }_{2}1(X\left(u_i\right)=3)+{\beta }_{3}1(X\left(u_i\right)=4)+{\beta }_{4}1(X\left(u_i\right)=5)\hfill \\ \hfill \mathrm{M}4:\eta (\mathit{C}\left(u_i\right);\beta )& ={\beta }_0{p}_{x_i,2}(u_i,u_i+5)+{\beta }_1{u}_i+{\beta }_{2}1(X\left(u_i\right)=3)+{\beta }_{3}1(X\left(u_i\right)=4)+{\beta }_{4}1(X\left(u_i\right)=5).\hfill \end{array}$$

Note that in all cases data are simulated from M4. In M1, the probability of good self-rated health is assumed to depend only on current disability state and age. This is the true model in the case where β₀ = 0. In M2, we included an additional covariate in the self-rated health model, 1(X(u_i) < X(u_i−1)), which is an indicator function representing an observed decline in functional status. This is similar to previous studies that have classified subjects as “stable” versus “declining” on the basis of observed changes in physical functioning and used this as a predictor in models for self-rated health (Bailis et al. 2003; Shooshtari et al. 2007). M3 and M4 include estimates of the rate and probability, respectively, of the decline in functional ability arising from the functional status model. However, in M3 we use a misspecified form based on the transition rate while the true model, M4, depends on the probability of transition to state two.

Models were fit to 1000 simulated data sets consisting of data for 250 subjects with 8 observations per subject. Eight observations were used to mirror the structure of the CHS data. We varied the strength of the parameter associated with the transition probability, β₀, from zero, representing no dependence, to −0.5, representing stronger dependence, of self-rated health on probability of transition to the most severe level of functional impairment. We thus investigated the effect of model misspecification under varying degrees of dependence of health outcomes on the probability of transition. Model performance was summarized using the Bayesian Information Criterion, defined as BIC = −2 log L(ψ̂, β̂) + p log(N), where $N={\Sigma }_{i=1}^m{n}_i$, p is the number of model parameters and L(ψ̂, β̂) is the joint likelihood, based on X and Y, evaluated at the maximum likelihood estimates ψ̂ and β̂. Results are presented in Table 2.

Table 2.

Mean (Standard Deviation) of differences between BIC for each model and the BIC of the true model for joint functional status and self-rated health models computed across 1000 simulated data sets. The true model is M4 when β₀ ≠ 0 and M1 when β₀ = 0.

	β0
	0	−0.25	−0.5
M1	–	22.67 (10.63)	76.28 (17.81)
M2	6.48 (1.42)	27.52 (10.34)	78.16 (17.53)
M3	6.47 (1.39)	9.06 (6.06)	14.68 (7.69)
M4	6.48 (1.33)	–	–

When self-rated health is independent of rates of change in functioning (β₀ = 0) the true model containing only information on the current level of functional status provides the best model fit. In this scenario, all three models including measures of change in functional status perform almost identically. When β₀ < 0, the joint probability model including the probability of transition, M4, provides the best model fit. However, the misspecified model including the rate, M3, rather than the probability of transition to the highest level of disability, achieves substantially improved fit relative to the model using observed declines in self-rated health. The model including observed changes in self-rated health, M2, provides no improvement in fit over the model including only current functional status.

4.2 Joint modeling of functional status and self-rated health in older adults

We investigated the association between functional status and self-rated health in the Cardiovascular Health Study (CHS) cohort of older adults. CHS is a community based longitudinal study of adults aged 65 or older. Subjects at four study centers were recruited from Medicare eligibility rolls and participated in yearly clinic visits at which they were assessed for a variety of cardiovascular health outcomes as well as contributing factors. The CHS study population is comprised of two cohorts, an initial cohort (n = 5201) for whom data collection began in 1990 and a second cohort consisting entirely of African-Americans (n = 687) initiated three years later. In our analysis we have pooled data from the two cohorts, using the date of a subject's first study visit as baseline and adjusting for race in analyses. A complete description of the CHS study design and sampling scheme has been published by Fried et al. (1991).

Subjects were evaluated at up to nine follow-up study visits and continue to be followed for occurrence of cardiovascular events or death and to be assessed for self-rated health. The mean number of assessments available for subjects, including follow-up visits and ascertainment of death, was 7.5. Although study visits were scheduled at approximately one-year intervals, follow-ups varied from a minimum elapsed time between observations of 1 month to a maximum of 8 years.

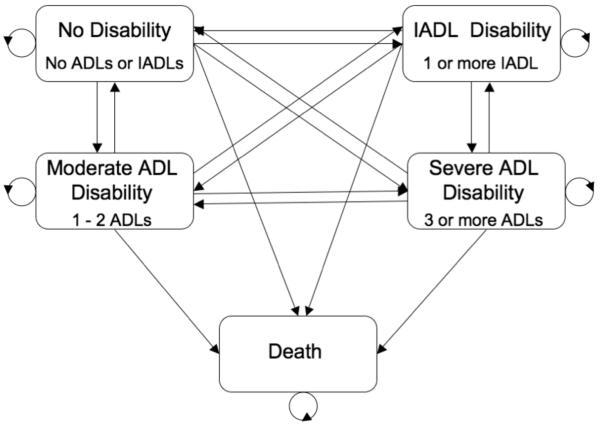
We defined functional status using a five-state variable based on activities of daily living (ADLs) and instrumental activities of daily living (IADLs). ADL and IADL scores represent the number of domains of self-care which the subject has difficulty completing. ADLs represent fundamental daily tasks necessary for self-care such as dressing, eating, and bathing, while IADLs represent more complex tasks necessary for functional independence such as shopping, using a telephone, and doing light housework. We use ADLs and IADLs to classify subjects into functional status levels as follows: no difficulties with any ADLs or IADLs, difficulty with one or more IADL, difficulty with one or two ADLs, difficulty with three or more ADLs, and death. This classification system allows us to distinguish subjects with no disability, those with mild disability as indicated by difficulties with IADLs only, and those with more serious disability as indicated by difficulty with ADLs. This classification system has been used in several previous studies of functional status in older adults (Mor et al. 1994; Anderson et al. 1998; Porell and Wiltiades 2001; Fonda et al. 2002). Figure 1 summarizes states and transitions in this model. The observed number of transitions between physical functioning states at successive study visits is presented in Table 3.

Figure 1.

Functional disability states and allowed transitions in our functional status model.

Table 3.

Observed number of transition between states defined by level of functional disability at successive follow-up visits.

	None	IADL	Mild ADL	Severe ADL	Death
None	21206	2999	1608	201	649
IADL	2456	2985	1305	191	423
Mild ADL	940	966	2166	504	367
Severe ADL	58	65	269	537	268

Self-rated health was reported by subjects as “excellent”, “very good”, “good”, “fair”, or “poor”. We dichotomize subjects into “healthy” for those reporting self-rated health as excellent, very good or good and “unhealthy” for those reporting their health to be fair or poor. This provides a simple and easily interpretable indication of subjective health. Manor et al. (2000) and Ferraro and Wilmoth (2000) found that this dichotomous assessment of subjective health was strongly associated with morbidity and mortality. This dichotomization of self-rated health was previously used for the CHS cohort by Diehr et al. (2001). In the CHS cohort, subjects described their health as “excellent”, “very good”, or “good” in 74.5% of follow-up assessments. Baseline demographics for subjects stratified by baseline subjective health state are presented in Table 4.

Table 4.

Baseline demographic characteristics for 5888 CHS subjects stratified by self-rated health at baseline.

		Healthy (n = 4388)	Unhealthy (n = 1500)
Age Mean (SD)		72.6 (5.52)	73.55 (5.83)
Male N (%)		1902 (43.35)	593 (39.53)
Non-white race N (%)		554 (12.63)	409 (27.27)
High school education N (%)		3350 (76.50)	789 (52.88)
Functional status
	No disability N (%)	3542 (80.72)	735 (49.00)
	IADL disability N (%)	662 (15.09)	469 (31.27)
	Mild ADL disability N (%)	170 (3.87)	246 (16.40)
	Severe ADL disability N (%)	14 (0.32)	50 (3.33)

Longitudinal self-rated health and functional status trajectories for a sample of four CHS subjects are presented in Figure 2. These trajectories show the volatility of functional status and suggest that, in general, subjects with greater functional impairment tend to report unhealthy self-rated health more often. However, the timing of the relationship between functional status and self-rated health is unclear with some subjects reporting unhealthy self-rated health just prior to a transition to greater impairment and others reporting unhealthy self-rated health following a transition to greater impairment.

Figure 2.

Trajectories of self-rated health and difficulties in ADLs and IADLs for four CHS subjects. Solid lines represent ADL/IADL trajectories; dashed lines represent self-rated health trajectories. Right-hand axis gives self-rated health states. Left hand axis gives level of functional disability.

We investigate the effect of variations in functional status over time on self-rated health by using our joint model for the association between self-rated health, difficulties with ADLs and IADLs, and temporal trends in difficulties with ADLs and IADLs after adjusting for the effects of baseline characteristics. This model allows us to separate the effect of current functional status from that due to longitudinal trends in functional status. We model transitions between functional status levels using the time-transformed Markov process model. We investigate performance of models using the two time transformation functions presented in Section 4.1 to account for non-homogeneity of transition rates. We incorporate the effect of temporal trends in functional status via the probability of experiencing severe ADL disability in five years.

We model self-rated health using three approaches. In the first approach, referred to as the “demographics-only” model, self-rated health is assumed to depend only on age, gender, race, and level of education. In the second model, referred to as the “functional status” model, we include additionally the current functional status level. Finally, in the third model, referred to as the “increasing disability” model, we incorporate the probability of being in the severe ADL disability state in five years. Let Y (u_i) represent self-rated health for subject i at age u_i, Y (u_i) = 1 represent healthy self-rated health, and W_i = (W_i1, … , W_i3)′ represent covariates associated with self-rated health. We use the logistic link function, P(Y (u_i) = 1|X(u_i), W_i, β)) = exp(η(C(u_i); β))/(1 + exp(η(C(u_i); β))) to connect self-rated health to functional status, functional status trajectory, and other covariates. Our three models for self-rated health can then be expressed as

$$\begin{array}{cc}\hfill \text{Demographics-only}:\eta (\mathit{C}\left(u_i\right);\beta )& ={\beta }_0+{\beta }_1{u}_i+{\beta }_2{W}_{i1}+{\beta }_3{W}_{i2}+{\beta }_4{W}_{i3}\hfill \\ \hfill \text{Functional status}:\eta (\mathit{C}\left(u_i\right);\beta )& ={\beta }_0+{\beta }_1{u}_i+{\beta }_2{W}_{i1}+{\beta }_3{W}_{i2}+{\beta }_4{W}_{i3}+{\beta }_{5}1(X\left(u_i\right)=2)\hfill \\ \hfill & +{\beta }_{6}1(X\left(u_i\right)=3)+{\beta }_{7}1(X\left(u_i\right)=4)\hfill \\ \hfill \text{Increasing disability}:\eta (\mathit{C}\left(u_i\right);\beta )& ={\beta }_0+{\beta }_1{u}_i+{\beta }_2{W}_{i1}+{\beta }_3{W}_{i2}+{\beta }_4{W}_{i3}+{\beta }_{5}1(X\left(u_i\right)=2)\hfill \\ \hfill & +{\beta }_{6}1(X\left(u_i\right)=3)+{\beta }_{7}1(X\left(u_i\right)=4)+{\beta }_8{p}_{x_i,2}(u_i,u_i+5),\hfill \end{array}$$

where W_i1 is an indicator of male gender, W_i2 is an indicator of non-white race, and W_i3 is an indicator of having completed a high school education for subject i. MLEs for parameters of the functional status and self-rated health models were obtained via the Fisher scoring algorithm implemented in C. Other statistical analyses for the CHS data were carried out using R 2.2.0.

In all three models, using the time transformation h₁(u; θ) resulted in better model fit evaluated using BIC than did use of h₂(u; θ). We therefore present the results of the better fitting model below. Results from the model using h₂(u; θ) are presented in Appendix D. Inference on parameters in the self-rated health model were similar for the two time transformation functions. However, standard errors for model parameters were generally larger when using h₂(u; θ) resulting in a lack of statistical significance for the model parameter associated with the probability of transition to poorest functional status. Estimates for parameters in the self-rated health portion of models using h₁(u; θ) are presented in Table 5. Reported effects are exponentiated regression coefficients and can be interpreted as multiplicative effects on odds of healthy self-rated health. Because we use a non-homogeneous disease process model, the probability of transition among functional status levels is dependent upon both the current state and the age of the subject. In all three models, odds of healthy self-rated health were statistically significantly lower, on average, for older subjects and those of non-white race. Having completed high school was significantly associated with increased odds of healthy self-rated health. Males were significantly less likely to report healthy self-rated health in the functional status and increasing disability models but were significantly more likely in the demographics-only model. This discrepancy is likely due to an association between functional status and gender. This association confounds the relationship between gender and self-rated health.

Table 5.

Maximum likelihood estimates for self-rated health model parameters and 95% confidence intervals (CI). Reference group for functional status is no disability.

		Demographics-only		Functional Status		Increasing Disability
		OR	95%CI	OR	95%CI	OR	95%CI
Probability of severe ADL disability						0.925	(0.894,0.957)
Functional status level
	Severe ADL Disability			0.099	(0.087,0.112)	0.126	(0.107,0.149)
	Moderate ADL Disability			0.201	(0.188,0.215)	0.245	(0.220,0.273)
	IADL Disability			0.296	(0.279,0.315)	0.325	(0.302,0.348)
Age		0.956	(0.952,0.960)	0.984	(0.980,0.988)	0.980	(0.976,0.985)
Male		1.100	(1.049,1.153)	0.885	(0.841,0.931)	0.887	(0.843,0.933)
Non-white race		0.536	(0.504,0.570)	0.574	(0.538,0.613)	0.576	(0.539,0.615)
High school education		2.126	(2.024,2.233)	2.113	(2.007,2.226)	2.109	(2.003,2.222)

In models including current functional status level, healthy self-rated health was strongly negatively associated with all levels of disability relative to subjects with no disability. Additionally, our analysis indicated that an increase in the probability of severe ADL disability is associated with a statistically significant decrease in odds of healthy self-rated health after adjusting for the effect of current functional status, age and other covariates.

We used BIC to compare the performance of these models for self-rated health (Table 6). Relative to the demographics-only model, both the functional status model and the increasing disability model achieved improved model fit. The best model fit was achieved by the increasing disability model. A likelihood ratio test of the improvement in model fit associated with including functional status and probability of decline in functional status in our model for self-rated health indicated a highly statistically significant improvement in model fit relative to the demographics-only model. We define the likelihood ratio as

$$-2(\log L_0({\widehat{\psi }}_0,{\widehat{\beta }}_0)-\log L(\widehat{\psi },\widehat{\beta }))\stackrel{.}{\sim }{\chi }^2\left(k\right),$$

where L₀(ψ̂₀, β̂₀) is the joint likelihood based on X and Y, evaluated at the maximum likelihood estimates ψ̂₀, β̂₀ in the demographics only model and L(ψ̂, β̂) is the joint likelihood evaluated at the maximum likelihood estimates ψ̂, β̂ in the alternative model and k is the number of extra parameters needed for the alternative model.

Table 6.

BIC and results of likelihood ratio test comparing the demographics-only model to models including functional status level (functional status) and probability of difficulty with more than one ADL or IADL within the next five years (increasing disability).

	BIC	χ2	df	p
Demographics-only	117404.4	-	-	-
Functional status	113819.8	3616.84	3	<0.0001
Increasing disability	113811.0	3636.37	4	<0.0001

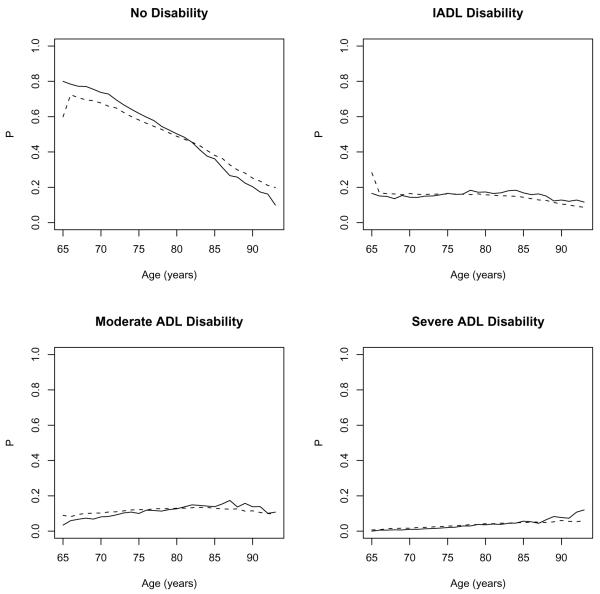
We investigated model fit for our time-transformed Markov model for functional status by comparing the expected and observed proportions of subjects in each physical functioning state (Figure 3). To compute the observed proportion of subjects in each state, subjects' ages were rounded to the nearest whole year and the proportion in each state was computed for each whole year age. Gentleman et al. (1994) discusses the use of empirical and predicted state occupancies to assess goodness–of–fit for Markov process models. Expected state occupancies were computed using our increasing disability model. However, we note that all three models produced extremely similar estimates for the parameters of the functional status process. Estimates for model parameters from the functional status model based on our increasing disability model are presented in Appendix E. The predicted proportion of subjects in each state agrees well with observed proportions in the CHS cohort. The proportion of subjects with no disability appears to be underestimated for subjects under 80 years of age and over-estimated for older subjects. Estimates for other states agree very closely with observed proportions across the entire observed age range.

Figure 3.

Observed (solid) and expected (dashed) proportion (P) of subjects in each of four physical functioning states. Expected proportions based on a non-homogeneous Markov model of functional status in the CHS cohort.

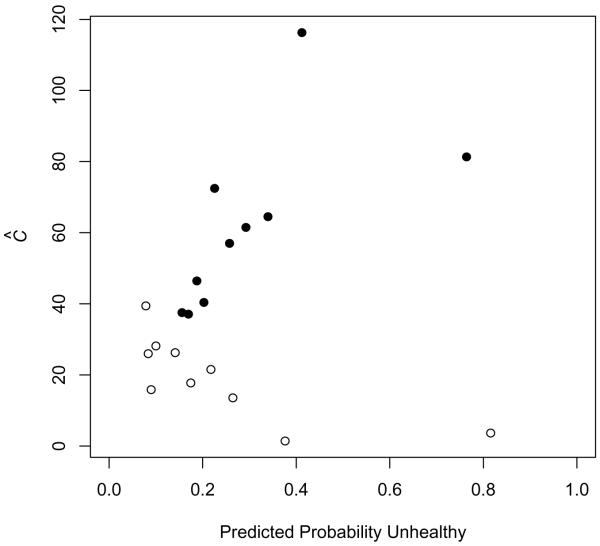
We evaluated the goodness-of-fit of our model for self-rated health using the Hosmer and Lemeshow decile-of-risk (Hosmer and Lemeshow 1980). We divided observations into 10 groups of approximately equal size, denoted J₁, … , J₁₀, on the basis of predicted probability of healthy self-rated health. We then compared the observed number of subjects with healthy self-rated health within each group to the expected number based on predicted probabilities from our model. We express goodness-of-fit for group J_j as

$${\widehat{C}}_j=\frac{{\left(n_{1j}-{\Sigma }_{r\in J_j}{\widehat{\pi }}_r\right)}^2}{{\Sigma }_{r\in J_j}{\widehat{\pi }}_r\left({\Sigma }_{r\in J_j}1-{\widehat{\pi }}_r\right)},$$

where n_1j is the number of subjects with healthy self-rated health in group j and π̂_r is the predicted probability of the r^th subject in group J_j. For a model that fits well, π̂_r will be close to one for healthy subjects and close to zero for unhealthy subjects. Thus, Σ_r∈Jjπ̂_r will be close to the number of unhealthy subjects in group J_j and Ĉ_j will be small. We plot Ĉ versus deciles of predicted probability for the increasing disability model and the demographics-only model in Figure 4. There is closer agreement between expected and observed number of subjects reporting healthy self-rated health for the increasing disability model for almost all ten deciles. Notably, for predicted probabilities in excess of 0.2, the increasing disability model performs increasingly well while the demographics-only model performs substantially worse.

Figure 4.

Comparison of expected and observed probability of healthy self-rated health using Hosmer and Lemeshow's decile of risk statistic, Ĉ, for increasing disability model (empty dots) and demographics-only model (filled dots).

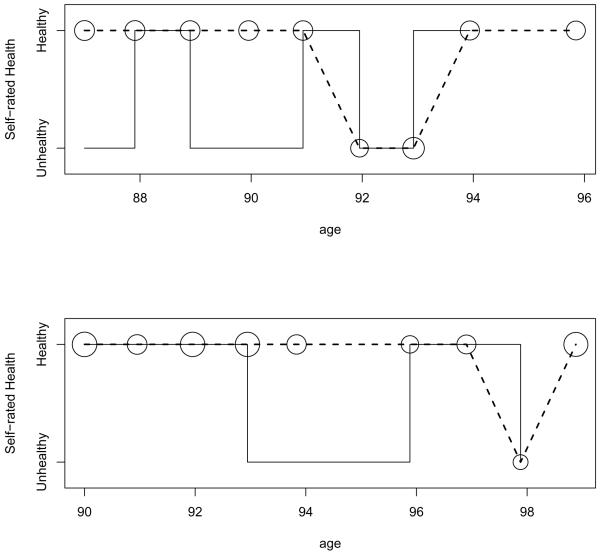
Our joint model can be used to predict future self-rated health. In Figure 5, we illustrate one-step ahead prediction using our joint model. In this example, we predict self-rated health at each observation point using information on covariates, functional status, and the probability of transition to severe ADL disability from the previous observation. For the two subjects illustrated in this example the final self-rated health evaluation was not available. However, we have used our increasing disability model to estimate the probability of healthy self-rated health. In both cases, our model correctly predicts self-rated health at all but one observation point. Our model also predicts unhealthy self-rated health for both subjects at their next observation.

Figure 5.

Observed and predicted self-rated health for two subjects from the CHS cohort. Solid line segments represent observed self-rated health state, predicted probability of healthy self-rated health is dashed. Circles indicate the self-rated health state with the highest predicted probability at each observation with the radius of the circle representing the strength of the prediction.

5 DISCUSSION

In this article we proposed a joint model for functional status and self-rated health to describe the longitudinal relationship between perceptions of health and trends in physical functioning. Our joint model allows us to incorporate information about temporal trends in functional status into the description and prediction of self-rated health. Prior studies have indicated that physical functioning is strongly related to subjective health assessments. However, few of these studies have investigated the relationship between the rate of change of physical functioning and perceptions of health. Application of our joint model suggests that demographic characteristics, functional status, and rate of change of functional status may all influence self-rated health in the CHS cohort of older adults.

Simulation studies indicated that parameter estimates from our joint model have low bias. However, standard errors and confidence intervals based on the asymptotic distribution of the MLEs are only appropriate for large cohorts. Our simulations indicated that the joint model performs better than a model based on observed changes in functional status when self-rated health is dependent on the risk of decline in functioning. We also found that the joint model is relatively insensitive to misspecification of the functional form of the relationship between self-rated health and the rate of change in functional status.

In our joint models we have not addressed the possibility of non-random missingness in the CHS data. Subjects with poorer self-rated health or greater disability may be less likely to attend follow-up visits resulting in data that are not missing at random. By conditioning on functional status at the previous observation and other covariates, our longitudinal model mitigates the impact of missing data to some extent. Specifically, functional status will be missing at random and parameter estimates will be valid if missingness is independent of current functional status after conditioning on functional status at the previous observation. Similarly, self-rated health will be missing at random if missingness can be predicted by age or other covariates.

In our model for the CHS data we have investigated only one measure of longitudinal change in functional status, the probability of severe disability in five years. This measure was selected because previous studies have found an association between declines in functional status and self-rated health (Ferraro et al. 1997; Bailis et al. 2003; Liang et al. 2007; Shooshtari et al. 2007) and five years was selected as a clinically relevant time-frame. However, other measures of decline such as the probability of any disability or death might also be associated with self-rated health. In general, multiple such measures cannot be included in a single model because they are highly correlated leading to model instability. However, model selection using BIC or other measures of model fit could be undertaken to identify the most predictive measure of change in functional status. Additionally, if no time-frame of greatest clinical relevance is known a priori, the instantaneous rate of change in functional status could be used as an alternative to the probability of transition.

The basic non-homogeneous functional status model proposed in this research could be extended in several ways. We have focused on modeling age-dependent transition intensities via a transformation of the time-scale. This transformation can be made dependent not only on time but other measures such as gender, race, or frailty. This allows for the estimation of transition rates that vary across subjects according to demographics or other measures of health. However, if some variables are believed to act on both transition rates in the Markov process model and self-rated health, care must be taken to ensure that the model is identifiable if the same variables are introduced in both stages of the model.

Some authors have suggested that poor self-rated health is in fact a cause of future declines in cognitive and physical functioning (Ferraro et al. 1997; Idler et al. 2000). Although we have not investigated the reciprocal relationship between self-rated health and functional status, the statistical methods described above could be employed to investigate this relationship as well.

Our model relies on parametric assumptions about the distribution of self-rated health. If these parametric assumptions do not hold, parameter estimates and variances for the joint model may not be appropriate. An alternative to fully specifying the likelihood for the self-rated health model is to use a quasi-likelihood approach, specifying only the first two moments of the distribution of self-rated health and using these in expressions for the score function and information.

We also have assumed that functional status data follow a first-order Markov process. In the case of the CHS functional status data, we have focused on the effect of age on the rate of transition between physical functioning states. This reflects a belief that age or time since the process origin exerts the most important temporal effect on transition rates. However, if the history of the functional status process is more relevant to the rate of transition between states then semi-Markov process models would be more appropriate. In future research we plan to investigate alternative stochastic process models for aging and disability.

7 Appendix

Appendix A: Identifiability of parameters in the joint model

Below we address identifiability using an example of a joint model in which η(C(u_i); β) = βp_xi,2(u_i, u_i + 5). This example is similar to one of the models fit to the data from the Cardiovascular Health Study in Section 4.2 with the addition of other covariates as elements of C(u_i).

Under the above example, the joint likelihood is given by

$$\begin{array}{cc}\hfill & L(\psi ,\beta )\hfill \\ \hfill & \propto \frac{\exp \left(\beta p_{x_1,2}(u_1,u_1+5)\right)}{1+\exp \left(\beta p_{x_1,2}(u_1,u_1+5)\right)}\prod _{i=2}^n\frac{\exp \left(\beta p_{x_i,2}(u_i,u_i+5)\right)}{1+\exp \left(\beta p_{x_i,2}(u_i,u_i+5)\right)}{\left\{\mathbf{p}(u_{i-1},u_i)\right\}}_{x_{i-1},x_i}.\hfill \end{array}$$

Note that in the above expression we utilize p_xi,2(u_i, u_i+5) as the function of ψ that connects the self-rated health and physical functioning models.

Assume this model is non-identifiable. Then there exist ψ′ and β′ such that L(ψ, β) = L(ψ′, β′). Let k = β′/β. Then

$$\begin{array}{cc}\hfill L({\psi }^{\prime },{\beta }^{\prime })\propto & \frac{\exp \left({\beta }^{\prime }{p}_{x_1,2}^{\prime }(u_1,u_1+5)\right)}{1+\exp \left({\beta }^{\prime }{p}_{x_1,2}^{\prime }(u_1,u_1+5)\right)}\prod _{i=2}^n\frac{\exp \left({\beta }^{\prime }{p}_{x_i,2}^{\prime }(u_i,u_i+5)\right)}{1+\exp \left({\beta }^{\prime }{x}_{x_i,2}^{\prime }(u_i,u_i+5)\right)}{\left\{{\mathbf{p}}^{\prime }(u_{i-1},u_i)\right\}}_{x_{i-1},x_i},\hfill \\ \hfill \propto & \frac{\exp \left(k\beta p_{x_1,2}^{\prime }(u_1,u_1+5)\right)}{1+\exp \left(k\beta p_{x_1,2}^{\prime }(u_1,u_1+5)\right)}\prod _{i=2}^n\frac{\exp \left(k\beta p_{x_i,2}^{\prime }(u_i,u_i+5)\right)}{1+\exp \left(k\beta p_{x_i,2}^{\prime }(u_i,u_i+5)\right)}{\left\{{\mathbf{p}}^{\prime }(u_{i-1},u_i)\right\}}_{x_{i-1},x_i}.\hfill \end{array}$$

This will be equal to L(ψ, β) only if ${\mathit{kp}}_{x_i,2}^{\prime }(u_i,u_i+5))=p_{x_i,2}(u_i,u_i+5))$ and {p′(u_i−1, u_i)}_xi−1,xi = {p(u_i−1, u_i)}_xi−1,xi, ∀i = 1, 2, … n. However, if ${\mathit{kp}}_{x_i,2}^{\prime }(u_i,u_i+5))=p_{x_i,2}(u_i,u_i+5))$ then {p′(u_i−1, u_i)}_xi−1,xi ≠ {p(u_i−1, u_i)}_xi−1,xi when x_i = 2. We therefore conclude that model parameters are identifiable.

Appendix B: Analytical expression for partial derivatives occurring in the score function

For a single subject observed at times u₁, … , u_n the contribution to the score function for the joint model is

$$\frac{\partial \log P(\mathit{X},\mathit{Y}\mid \beta ,\psi )}{\partial {\psi }_r}=\underset{i=2}{\overset{n}{\Sigma }}\frac{\partial \log p_{x_{i-1},x_i}(u_{i-1},u_i)}{\partial {\psi }_r}+\underset{i=1}{\overset{n}{\Sigma }}\frac{\partial \log P(Y\left(u_i\right)\mid \eta (\mathit{C}\left(u_i\right);\beta ))}{\partial {\psi }_r}$$ (5)

and

$$\frac{\partial \log P(\mathit{X},\mathit{Y}\mid \beta ,\psi )}{\partial {\beta }_l}=\underset{i=1}{\overset{n}{\Sigma }}\frac{\partial \log P(Y\left(u_i\right)\mid \eta (\mathit{C}\left(u_i\right);\beta ))}{\partial {\beta }_l}.$$ (6)

The first portion of equation (1) arises from the multi-state functional status model, while the second part of equation (1) and equation (2) arise from the self-rated health model. Below we give expressions for the partial derivatives occurring in the score function.

The portion of the score function arising from the Markov process model for functional status can be rewritten as

$$\underset{i=2}{\overset{n}{\Sigma }}\frac{\partial \log p_{x_{i-1},x_i}(u_{i-1},u_i)}{\partial {\psi }_r}=\underset{i=2}{\overset{n}{\Sigma }}\frac{1}{p_{x_{i-1}{x}_i}(h\left(u_i\right)-h\left(u_{i-1}\right))}\frac{\partial }{\partial {\psi }_r}{p}_{x_{i-1}{x}_i}(h\left(u_i\right)-h\left(u_{i-1}\right)).$$

If ψ_r is an element of q₀ then the vector of first derivatives of p(h(u_i)−h(u_i−1)) is available via the eigen decomposition. Let A be the matrix of eigenvectors of q₀ and D = diag(λ₁, … , λ_s) the matrix with the eigenvalues of q₀ on the diagonal.

$$\begin{array}{cc}\hfill \frac{\partial }{\partial {\psi }_r}\mathbf{p}(u_{i-1},u_i)& =\frac{\partial }{\partial {\psi }_r}{e}^{{\mathbf{q}}_0(h\left(u_i\right)-h\left(u_{i-1}\right))}\hfill \\ \hfill & =\frac{\partial }{\partial {\psi }_r}\underset{s=0}{\overset{\infty }{\Sigma }}\frac{{\mathbf{q}}_0^s{(h\left(u_i\right)-h\left(u_{i-1}\right))}^s}{s!}\hfill \\ \hfill & =\underset{s=0}{\overset{\infty }{\Sigma }}\underset{l=0}{\overset{s-1}{\Sigma }}{\mathbf{q}}_0^l\frac{\partial {\mathbf{q}}_0}{\partial {\psi }_r}{\mathbf{q}}_0^{s-1-l}\frac{{(h\left(u_i\right)-h\left(u_{i-1}\right))}^s}{s!}\hfill \\ \hfill & =\underset{s=0}{\overset{\infty }{\Sigma }}\underset{l=0}{\overset{s-1}{\Sigma }}{\mathbf{AD}}^l{\mathbf{A}}^{-1}\frac{\partial {\mathbf{q}}_0}{\partial {\psi }_r}{\mathbf{AD}}^{s-1-l}{\mathbf{A}}^{-1}\frac{{(h\left(u_i\right)-h\left(u_{i-1}\right))}^s}{s!}\hfill \\ \hfill & =\mathbf{A}\left(\underset{s=0}{\overset{\infty }{\Sigma }}\underset{l=0}{\overset{s-1}{\Sigma }}{\mathbf{D}}^l{\mathbf{A}}^{-1}\frac{\partial {\mathbf{q}}_0}{\partial {\psi }_r}{\mathbf{AD}}^{s-1-l}\frac{(h\left(u_i\right)-h\left(u_{i-1}\right)s)}{s!}\right){\mathbf{A}}^{-1}\hfill \\ \hfill & ={\mathbf{AV}}_r{\mathbf{A}}^{-1}.\hfill \end{array}$$

Let ${\mathbf{G}}_r={\mathbf{A}}^{-1}\frac{\partial {\mathbf{q}}_0}{\partial {\psi }_r}\mathbf{A}$ with jk^th element $g_{\mathit{jk}}^{\left(r\right)}$. The jk^th element of the matrix V_r is

$$\begin{array}{cc}\hfill V_{\mathit{jk}}^{\left(r\right)}& =g_{\mathit{jk}}^{\left(r\right)}\underset{s=0}{\overset{\infty }{\Sigma }}\underset{l=0}{\overset{s-1}{\Sigma }}{\lambda }_j^l{\lambda }_k^{s-1-l}\frac{{(h\left(u_i\right)-h\left(u_{i-1}\right))}^s}{s!}\hfill \\ \hfill & =g_{\mathit{jk}}^{\left(r\right)}\frac{e^{{\lambda }_j(h\left(u_i\right)-h\left(u_{i-1}\right))}-e^{{\lambda }_k(h\left(u_i\right)-h\left(u_{i-1}\right))}}{{\lambda }_j-{\lambda }_k},j\ne k\hfill \\ \hfill V_{\mathit{jk}}^{\left(r\right)}& =g_{\mathit{jk}}^{\left(r\right)}\underset{s=0}{\overset{\infty }{\Sigma }}\underset{l=0}{\overset{s-1}{\Sigma }}{\lambda }_j^{s-1}\frac{{(h\left(u_i\right)-h\left(u_{i-1}\right))}^s}{s!}\hfill \\ \hfill & =g_{\mathit{jk}}^{\left(r\right)}(h\left(u_i\right)-h\left(u_{i-1}\right))e^{{\lambda }_j(h\left(u_i\right)-h\left(u_{i-1}\right))},j=k.\hfill \end{array}$$

For ψ_r an element of θ then

$$\begin{array}{cc}\hfill \frac{\partial }{\partial {\psi }_r}\mathbf{p}(u_{i-1},u_i)& =\frac{\partial }{\partial {\psi }_r}{e}^{{\mathbf{q}}_0(h(u_i;\theta )-h(u_{i-1};\theta ))}\hfill \\ \hfill & =\left(\frac{\partial h(u_i;\theta )}{\partial {\psi }_r}-\frac{\partial h(u_{i-1};\theta )}{\partial {\psi }_r}\right){\mathbf{q}}_0\mathbf{p}(u_{i-1},u_i).\hfill \end{array}$$

We present partial derivatives for the portion of the score arising from the self-rated health model assuming the binomial model presented in Section 2. The form of the derivatives with respect to ψ depend on the function of transition intensities or probabilities included in the self-rated health model. As an example, we present the case where the l^th covariate in the self-rated health model proposed in equation (1) is the probability of transition to state a in an elapsed time of Δu, C_l(u_i) = p_xi,a(u_i, u_i + Δu). Then,

$$\frac{\partial \log P(Y\left(u_i\right)\mid \eta (\mathit{C}\left(u_i\right);\beta ))}{\partial {\psi }_r}={\beta }_l\frac{\partial p_{x_i,a}(u_i,u_i+\Delta u)}{\partial {\psi }_r}(Y\left(u_i\right)-p(Y\left(u_i\right)\mid \eta (\mathit{C}\left(u_i\right);\beta ))).$$

In the binary/logistic model, the partial derivatives with respect to self-rated health model parameters β are given by

$$\frac{\partial \log P(Y\left(u_i\right)\mid \eta (\mathit{C}\left(u_i\right);\beta ))}{\partial {\beta }_k}=C_k\left(u_i\right)(Y\left(u_i\right)-p(Y\left(u_i\right)\mid \eta \mathit{C}\left(u_i\right);\beta ))).$$

Appendix C: Simulation study results for parameters in the joint model

Table 1.

Bias, empirical standard errors (ESE), model based standard errors (ASE), and 95% confidence interval coverage probabilities (CP) for maximum likelihood estimates of model parameters from joint modeling of simulated functional status and self-rated health data using h₁(u; θ).

Number Subjects	Number Obs.	q12				q13				q14
		Bias	ESE	ASE	CP	Bias	ESE	ASE	CP	Bias	ESE	ASE	CP
100	5	0.0458	0.3012	0.1849	95.9	0.0184	0.2405	0.1404	97.1	0.0060	0.1158	0.1105	96.6
100	10	0.0137	0.1724	0.1271	95.5	−0.0001	0.1327	0.0996	97.0	0.0056	0.0685	0.0757	95.3
100	20	0.0105	0.1910	0.1174	94.6	0.0009	0.1169	0.0956	96.7	0.0017	0.0701	0.0713	95.8
250	5	0.0011	0.1071	0.1022	94.1	0.0033	0.0814	0.0764	95.8	0.0008	0.0543	0.0545	95.9
250	10	0.0030	0.0782	0.0766	95.3	−0.0002	0.0598	0.0599	96.2	0.0037	0.0430	0.0438	95.0
250	20	−0.0014	0.0714	0.0701	95.5	−0.0048	0.0552	0.0560	96.7	0.0015	0.0421	0.0412	95.2
500	5	0.0038	0.0710	0.0722	95.6	−0.0007	0.0539	0.0533	96.3	0.0031	0.0396	0.0383	95.3
500	10	−0.0044	0.0532	0.0532	95.0	0.0006	0.0415	0.0417	95.6	0.0031	0.0305	0.0305	95.2
500	20	0.0009	0.0500	0.0498	94.5	−0.0006	0.0397	0.0398	96.8	0.0013	0.0298	0.0292	95.5
		q15				q21				q23
100	5	0.0101	0.0742	0.0646	94.8	0.0308	0.2135	0.1776	94.7	0.0266	0.2313	0.1990	96.5
100	10	0.0038	0.0702	0.0429	95.4	0.0126	0.1341	0.1280	95.7	0.0216	0.1493	0.1501	96.7
100	20	0.0021	0.0571	0.0397	93.9	−0.0015	0.1174	0.1156	96.6	0.0215	0.1443	0.1417	96.4
250	5	0.0007	0.0322	0.0323	94.8	0.0038	0.1072	0.1034	95.5	0.0130	0.1174	0.1171	96.1
250	10	−0.0012	0.0241	0.0247	96.4	−0.0015	0.0775	0.0771	95.2	0.0103	0.0914	0.0903	95.2
250	20	−0.0012	0.0222	0.0232	96.7	−0.0050	0.0703	0.0707	94.6	0.0094	0.0829	0.0846	95.6
500	5	−0.0010	0.0221	0.0223	95.9	0.0013	0.0712	0.0724	95.0	0.0115	0.0812	0.0819	94.7
500	10	−0.0008	0.0173	0.0174	95.4	−0.0012	0.0558	0.0542	95.1	0.0048	0.0613	0.0629	96.5
500	20	−0.0003	0.0171	0.0165	96.0	−0.0001	0.0523	0.0504	94.3	0.0089	0.0596	0.0597	94.4
		q24				q25				q31
100	5	0.0113	0.1486	0.1430	96.4	0.0055	0.0785	0.0842	94.4	0.0092	0.1408	0.1368	96.2
100	10	−0.0063	0.1072	0.1063	97.3	0.0015	0.0599	0.0609	95.4	0.0023	0.1095	0.1049	96.4
100	20	−0.0009	0.1018	0.1023	96.5	−0.0024	0.0567	0.0567	95.0	0.0029	0.0998	0.0987	96.6
250	5	−0.0024	0.0781	0.0806	98.0	0.0015	0.0471	0.0476	96.1	0.0001	0.0793	0.0786	96.8
250	10	−0.0063	0.0609	0.0640	97.8	−0.0008	0.0368	0.0366	96.4	0.0010	0.0638	0.0629	96.3
250	20	−0.0089	0.0576	0.0606	98.3	−0.0008	0.0352	0.0345	95.6	−0.0012	0.0595	0.0592	97.0
500	5	−0.0041	0.0559	0.0561	97.3	0.0007	0.0321	0.0331	96.7	0.0011	0.0550	0.0551	96.5
500	10	−0.0024	0.0436	0.0450	97.3	0.0012	0.0250	0.0260	95.9	0.0012	0.0432	0.0439	95.9
500	20	−0.0034	0.0425	0.0432	96.6	−0.0010	0.0243	0.0245	96.0	−0.0001	0.0409	0.0421	97.0
		q32				q34				q35
100	5	0.0312	0.2044	0.2035	97.3	0.0456	0.2017	0.2013	97.4	−0.0007	0.1169	0.1120	96.7
100	10	0.0278	0.1638	0.1557	96.3	0.0256	0.1586	0.1502	95.9	0.0014	0.0852	0.0841	96.1
100	20	0.0215	0.1512	0.1461	96.0	0.0247	0.1480	0.1416	95.8	0.0017	0.0774	0.0784	96.8
250	5	0.0144	0.1186	0.1193	95.8	0.0122	0.1184	0.1148	95.1	0.0014	0.0698	0.0662	96.2
250	10	0.0063	0.0929	0.0923	95.2	0.0137	0.0911	0.0897	95.2	0.0007	0.0522	0.0510	96.0
250	20	0.0067	0.0836	0.0870	96.0	0.0073	0.0837	0.0835	95.6	−0.0007	0.0492	0.0475	95.2
500	5	0.0100	0.0827	0.0831	95.5	0.0100	0.0812	0.0802	95.2	0.0038	0.0455	0.0468	95.4
500	10	0.0048	0.0626	0.0646	95.6	0.0023	0.0620	0.0618	95.0	0.0021	0.0357	0.0358	96.1
500	20	0.0063	0.0595	0.0615	95.7	0.0090	0.0583	0.0591	94.1	0.0004	0.0347	0.0336	94.6
		q41				q42				q43
100	5	0.0093	0.1170	0.1260	95.2	0.0129	0.2089	0.1649	96.9	0.0681	0.3535	0.2211	96.1
100	10	0.0005	0.0822	0.0904	95.8	0.0004	0.1847	0.1228	96.9	0.0449	0.2746	0.1659	95.5
100	20	0.0024	0.0774	0.0811	95.6	0.0003	0.1372	0.1150	96.9	0.0282	0.2099	0.1515	95.8
250	5	0.0034	0.0572	0.0602	96.5	0.0016	0.0998	0.0862	96.8	0.0086	0.1302	0.1182	95.9
250	10	0.0023	0.0486	0.0486	95.1	−0.0054	0.0682	0.0694	98.0	0.0091	0.0913	0.0934	96.1
250	20	−0.0013	0.0481	0.0461	95.6	−0.0067	0.0608	0.0664	98.5	0.0066	0.0900	0.0879	94.5
500	5	0.0011	0.0413	0.0410	96.2	−0.0039	0.0565	0.0595	97.5	0.0114	0.0823	0.0830	94.7
500	10	−0.0003	0.0330	0.0338	96.8	−0.0035	0.0465	0.0487	97.8	0.0034	0.0661	0.0648	95.7
500	20	0.0008	0.0329	0.0328	95.2	−0.0023	0.0456	0.0472	97.9	0.0041	0.0623	0.0619	94.7
Number Subjects	Number Obs.	q45				θ				β0
		Bias	ESE	ASE	CP	Bias	ESE	ASE	CP	Bias	ESE	ASE	CP
100	5	0.0458	0.3318	0.1650	94.2	0.0114	0.0828	0.0835	95.0	0.0228	0.1277	0.1018	92.9
100	10	0.0136	0.2097	0.1147	94.3	0.0050	0.0358	0.0349	94.6	0.0101	0.0782	0.0728	94.6
100	20	0.0058	0.1354	0.1020	95.8	0.0048	0.0249	0.0245	95.7	0.0059	0.0779	0.0701	94.2
250	5	0.0051	0.1108	0.0928	94.6	0.0050	0.0526	0.0508	93.9	0.0063	0.0587	0.0512	92.6
250	10	0.0020	0.0677	0.0682	94.8	0.0021	0.0215	0.0215	95.3	0.0035	0.0434	0.0428	95.8
250	20	−0.0006	0.0616	0.0621	95.8	0.0023	0.0152	0.0151	94.5	0.0026	0.0449	0.0422	93.8
500	5	0.0025	0.0645	0.0651	95.2	0.0009	0.0341	0.0354	96.6	0.0029	0.0366	0.0345	94.4
500	10	0.0005	0.0493	0.0480	95.0	0.0008	0.0155	0.0151	95.7	0.0030	0.0323	0.0300	92.4
500	20	0.0007	0.0442	0.0439	95.1	0.0007	0.0107	0.0106	93.9	−0.0007	0.0314	0.0294	93.3
		β1				β2				β3
100	5	−0.0054	0.4359	0.4035	93.6	−0.0132	0.3974	0.3849	95.2	−0.0138	0.3801	0.3651	94.5
100	10	−0.0205	0.3455	0.3559	95.6	−0.0265	0.3358	0.3418	95.8	−0.0214	0.3105	0.3260	95.1
100	20	−0.0091	0.3543	0.3510	95.6	−0.0007	0.3408	0.3370	95.0	−0.0176	0.3306	0.3225	94.3
250	5	−0.0055	0.2630	0.2518	93.8	−0.0119	0.2449	0.2397	94.6	−0.0048	0.2357	0.2270	94.1
250	10	−0.0090	0.2280	0.2233	93.7	−0.0061	0.2135	0.2143	96.1	−0.0175	0.2049	0.2043	94.5
250	20	−0.0119	0.2197	0.2200	95.2	−0.0078	0.2092	0.2113	95.6	−0.0114	0.2029	0.2018	94.8
500	5	−0.0085	0.1749	0.1772	95.6	−0.0020	0.1702	0.1687	95.0	−0.0051	0.1574	0.1595	96.0
500	10	−0.0081	0.1621	0.1572	94.1	−0.0120	0.1545	0.1509	94.5	−0.0069	0.1482	0.1440	94.1
500	20	0.0018	0.1539	0.1547	94.9	0.0040	0.1476	0.1487	95.4	0.0014	0.1430	0.1420	94.7
		β4
100	5	−0.0011	0.1317	0.1112	91.7
100	10	0.0058	0.0659	0.0663	95.0
100	20	0.0079	0.0637	0.0613	93.9
250	5	0.0030	0.0722	0.0669	93.5
250	10	0.0033	0.0421	0.0411	94.4
250	20	0.0040	0.0372	0.0378	96.2
500	5	−0.0012	0.0504	0.0462	93.1
500	10	0.0017	0.0297	0.0290	93.9
500	20	0.0004	0.0261	0.0265	95.9

Table 2.

Bias, empirical standard errors (ESE), model based standard errors (ASE), and 95% confidence interval coverage probabilities (CP) for maximum likelihood estimates of model parameters from joint modeling of simulated functional status and self-rated health data using h₂(u; θ).

Number Subjects	Number Obs.	q12				q13				q14
		Bias	ESE	ASE	CP	Bias	ESE	ASE	CP	Bias	ESE	ASE	CP
100	10	0.0080	0.1905	0.1181	95.2	−0.0037	0.1422	0.0926	97.5	−0.0012	0.0606	0.0694	96.7
100	20	−0.0020	0.1093	0.1072	94.9	−0.0016	0.0849	0.0850	97.3	0.0003	0.0600	0.0627	96.2
250	10	−0.0056	0.0704	0.0708	95.9	0.0007	0.0564	0.0559	96.9	0.0002	0.0437	0.0407	94.7
250	20	−0.0010	0.0679	0.0674	94.7	−0.0009	0.0530	0.0531	96.8	−0.0005	0.0383	0.0386	96.1
500	10	−0.0012	0.0500	0.0498	94.8	−0.0012	0.0381	0.0391	96.9	0.0007	0.0294	0.0287	95.4
500	20	−0.0005	0.0489	0.0472	94.1	−0.0002	0.0369	0.0373	96.2	0.0017	0.0270	0.0275	95.8
		q15				q21				q23
100	10	0.0002	0.0607	0.0405	95.6	−0.0112	0.1147	0.1156	96.1	0.0128	0.1371	0.1368	96.5
100	20	−0.0002	0.0344	0.0360	94.5	−0.0018	0.1122	0.1092	95.6	0.0161	0.1289	0.1298	95.8
250	10	−0.0012	0.0234	0.0237	96.0	−0.0022	0.0726	0.0722	94.5	0.0066	0.0832	0.0835	96.0
250	20	−0.0008	0.0223	0.0222	95.2	−0.0019	0.0703	0.0685	95.9	0.0074	0.0794	0.0798	94.9
500	10	0.0003	0.0170	0.0168	95.6	−0.0005	0.0504	0.0508	95.3	0.0059	0.0580	0.0584	95.0
500	20	0.0004	0.0161	0.0158	95.1	0.0004	0.0489	0.0481	94.9	0.0018	0.0545	0.0553	96.1
		q24				q25				q31
100	10	−0.0055	0.0945	0.0969	97.4	−0.0019	0.0572	0.0568	95.6	−0.0005	0.0962	0.0953	96.7
100	20	−0.0027	0.0938	0.0927	96.3	0.0016	0.0532	0.0539	95.7	−0.0058	0.0901	0.0901	96.9
250	10	−0.0037	0.0586	0.0600	97.7	−0.0021	0.0350	0.0349	96.1	−0.0021	0.0577	0.0588	96.9
250	20	−0.0034	0.0542	0.0572	98.2	−0.0003	0.0337	0.0332	96.0	−0.0011	0.0566	0.0561	96.3
500	10	−0.0021	0.0422	0.0422	96.7	−0.0012	0.0251	0.0247	96.5	−0.0001	0.0418	0.0413	95.5
500	20	−0.0020	0.0391	0.0403	96.8	−0.0014	0.0240	0.0232	96.0	−0.0013	0.0393	0.0393	95.7
		q32				q34				q35
100	10	0.0099	0.1400	0.1403	96.6	0.0109	0.1414	0.1352	94.6	−0.0015	0.0758	0.0782	97.0
100	20	0.0262	0.1398	0.1353	95.1	0.0150	0.1310	0.1287	96.1	−0.0023	0.0765	0.0732	96.5
250	10	0.0094	0.0856	0.0863	95.7	0.0041	0.0863	0.0826	94.5	0.0009	0.0482	0.0483	96.1
250	20	0.0075	0.0800	0.0823	96.0	0.0066	0.0792	0.0786	95.1	0.0003	0.0487	0.0455	95.1
500	10	0.0043	0.0569	0.0600	96.0	0.0009	0.0576	0.0574	94.9	0.0012	0.0342	0.0339	94.4
500	20	0.0032	0.0552	0.0572	95.5	0.0041	0.0569	0.0551	94.0	0.0007	0.0316	0.0320	95.5
		q41				q42				q43
100	10	−0.0000	0.0720	0.0761	97.0	−0.0081	0.1089	0.1063	97.6	0.0181	0.1792	0.1439	95.8
100	20	0.0078	0.0976	0.0753	95.3	−0.0038	0.1148	0.1068	96.8	0.0269	0.2008	0.1404	94.4
250	10	−0.0012	0.0454	0.0452	95.5	−0.0044	0.0642	0.0650	97.6	0.0058	0.0870	0.0869	96.2
250	20	0.0010	0.0440	0.0437	95.1	−0.0051	0.0599	0.0623	97.8	0.0039	0.0817	0.0827	95.6
500	10	0.0008	0.0317	0.0321	96.9	−0.0031	0.0445	0.0458	97.2	0.0024	0.0586	0.0606	96.7
500	20	0.0008	0.0296	0.0308	96.2	−0.0015	0.0424	0.0441	97.2	0.0056	0.0586	0.0583	95.2
Number Subjects	Number Obs.	q45				θ1				θ2
		Bias	ESE	ASE	CP	Bias	ESE	ASE	CP	Bias	ESE	ASE	CP
100	10	−0.0037	0.1531	0.1033	94.8	0.3357	0.9172	0.8810	96.3	0.0659	0.8650	0.8194	96.7
100	20	0.0023	0.1290	0.0974	93.8	0.1359	0.3671	0.3745	94.7	0.1639	0.8712	0.5396	91.5
250	10	−0.0047	0.0651	0.0635	95.0	0.1008	0.2613	0.2607	94.3	0.0255	0.5209	0.4712	95.5
250	20	−0.0018	0.0606	0.0601	95.8	0.0449	0.1986	0.1947	94.4	−0.0079	0.3961	0.3288	94.8
500	10	−0.0009	0.0443	0.0448	95.3	0.0345	0.1584	0.1652	95.9	0.0277	0.3246	0.3286	94.8
500	20	0.0007	0.0422	0.0423	95.0	0.0187	0.1381	0.1325	94.4	0.0131	0.2462	0.2308	93.3
		β0				β1				β2
100	10	0.0104	0.0989	0.0724	93.9	−0.0049	0.3575	0.3481	94.4	−0.0189	0.3314	0.3319	95.3
100	20	0.0020	0.0755	0.0695	94.5	−0.0160	0.3386	0.3421	96.0	−0.0028	0.3196	0.3260	94.7
250	10	0.0028	0.0476	0.0433	93.2	−0.0007	0.2263	0.2193	94.6	0.0018	0.2152	0.2091	94.8
250	20	0.0006	0.0424	0.0430	95.5	0.0038	0.2148	0.2153	95.2	0.0051	0.2047	0.2050	95.5
500	10	0.0003	0.0300	0.0301	95.5	0.0039	0.1501	0.1547	96.4	−0.0048	0.1452	0.1476	96.2
500	20	0.0015	0.0312	0.0300	94.3	−0.0088	0.1549	0.1517	94.6	−0.0065	0.1421	0.1446	95.0
		β3				β4
100	10	−0.0169	0.3119	0.3154	95.6	0.0101	0.0680	0.0641	94.9
100	20	−0.0235	0.3124	0.3094	95.5	0.0099	0.0581	0.0564	94.5
250	10	−0.0063	0.2002	0.1980	94.6	0.0036	0.0431	0.0392	93.1
250	20	0.0003	0.1869	0.1939	95.7	0.0008	0.0354	0.0349	94.7
500	10	0.0015	0.1393	0.1398	95.9	0.0015	0.0296	0.0274	93.2
500	20	−0.0095	0.1371	0.1368	94.6	0.0025	0.0260	0.0245	93.2

Appendix D: Results of analysis of CHS data using alternative time transformation function

Results of analyses of the CHS data using joint models with the time transformation function h₂(u; θ) are presented below. BIC for these models was lower than that for models using h₁(u; θ). However, these models did provide an indication that a maximum may exist in the CHS data beyond which the rate of evolution of the functional status process decreases. Specifically, the estimated time transformation function from the increasing disability model corresponds to a process that is decreasing for subjects over 85 years of age. Because only 12% of observations occur in this range, it is likely that the extra complexity of the model could not be justified by improved model fit for these observations. The increased complexity of this model also results in very imprecise estimates for some transition rates, specifically the transition rate from no disability to severe ADL disability and from severe ADL disability to IADL disability, due to the small number of transitions of this kind observed in the data (Table 1).

Table 1.

Bias, empirical standard errors (ESE), model based standard errors (ASE), and 95% confidence interval coverage probabilities (CP).

Number Subjects	Number Observations	h1(u; θ)				h2(u; θ)
		Bias	ESE	ASE	95% CP	Bias	ESE	ASE	95% CP
100	5	0.0228	0.1277	0.1018	92.9	-	-	-	-
100	10	0.0101	0.0782	0.0728	94.6	0.0104	0.0989	0.0724	93.9
100	20	0.0059	0.0779	0.0701	94.2	0.0020	0.0755	0.0695	94.5
250	5	0.0063	0.0587	0.0512	92.6	-	-	-	-
250	10	0.0035	0.0434	0.0428	95.8	0.0028	0.0476	0.0433	93.2
250	20	0.0026	0.0449	0.0422	93.8	0.0006	0.0424	0.0430	95.5
500	5	0.0029	0.0366	0.0345	94.4	-	-	-	-
500	10	0.0030	0.0323	0.0300	92.4	0.0003	0.0300	0.0301	95.5
500	20	−0.0007	0.0314	0.0294	93.3	0.0015	0.0312	0.0300	94.3

Inference based on this model is similar to that for the model using h₁(u; θ). However, in this case the functional status model provides a better model fit than the increasing disability model, and the effect of probability of severe ADL disability is non-significant. Other parameter estimates in the self-rated health model give rise to similar inference as that reported under h₁(u; θ).

Table 1.

Maximum likelihood estimates for transition intensities and time transformation parameter with 95% confidence intervals (CI) from joint model for activities of daily living and self-rated health for CHS data. Estimates are based on the “increasing disability” model using h₂(u; θ).

	Estimate	(CI)
No disability → IADL disability	0.182	(0.174,0.191)
No disability → moderate ADL disability	0.065	(0.059,0.072)
No disability → severe ADL disability	0.000	(0,Inf)
No disability → death	0.016	(0.014,0.019)
IADL disability → no disability	0.516	(0.491,0.542)
IADL disability → moderate ADL disability	0.406	(0.377,0.438)
IADL disability → severe ADL disability	0.005	(0.001,0.047)
IADL disability → death	0.055	(0.047,0.065)
Moderate ADL disability → no disability	0.180	(0.160,0.204)
Moderate ADL disability → IADL disability	0.425	(0.391,0.462)
Moderate ADL disability → severe ADL disability	0.222	(0.199,0.247)
Moderate ADL disability → death	0.051	(0.040,0.065)
Severe ADL disability → no disability	0.003	(0.000,0.456)
Severe ADL disability → IADL disability	0.003	(0.000,360.508)
Severe ADL disability → moderate ADL disability	0.415	(0.361,0.477)
Severe ADL disability → death	0.241	(0.211,0.275)
θ1	0.133	(0.112,0.158)
θ2	22.215	(21.870,22.565)

Table 2.

Maximum likelihood estimates for self-rated health model parameters and 95% confidence intervals (CI). Reference group for functional status is no disability.

		Demographics-only		Functional Status		Increasing Disability
		OR	95%CI	OR	95%CI	OR	95%CI
Probability of severe ADL disability						0.967	(0.92,1.017)
Functional status level
	IADL Disability			0.296	(0.279,0.315)	0.307	(0.284,0.332)
	Moderate ADL Disability			0.201	(0.188,0.215)	0.217	(0.190,0.248)
	Severe ADL Disability			0.099	(0.087,0.112)	0.109	(0.089,0.134)
Age		0.956	(0.952,0.960)	0.984	(0.980,0.988)	0.983	(0.979,0.988)
Male		1.100	(1.049,1.153)	0.885	(0.841,0.931)	0.885	(0.842,0.931)
Non-white race		0.536	(0.504,0.570)	0.574	(0.538,0.613)	0.575	(0.538,0.614)
High school education		2.126	(2.024,2.233)	2.113	(2.007,2.226)	2.112	(2.005,2.224)

Table 3.

BIC and results of likelihood ratio test comparing the demographics-only model to models including functional status level (functional status) and probability of difficulty with more than one ADL or IADL within the next five years (increasing disability).

	BIC	χ2	df	p
Demographics-only	117616.1	-	-
Functional status	114031.5	3616.84	3	<0.0001
Decline in functional status	114040.5	3618.51	4	<0.0001

Appendix E: Parameter estimates for the functional status model for CHS data

Table 1.

Maximum likelihood estimates for transition intensities and time transformation parameter with 95% confidence intervals (CI) from joint model for activities of daily living and self-rated health for CHS data. Estimates are based on the “increasing disability” model using h₁(u; θ).

	Estimate	(CI)
No disability → IADL disability	0.119	(0.111,0.128)
No disability → moderate ADL disability	0.043	(0.038,0.048)
No disability → severe ADL disability	0.000	(0.000,0.008)
No disability → death	0.012	(0.01,0.013)
IADL disability → no disability	0.334	(0.311,0.359)
IADL disability → moderate ADL disability	0.261	(0.238,0.286)
IADL disability → severe ADL disability	0.003	(0.000,0.027)
IADL disability → death	0.038	(0.032,0.044)
Moderate ADL disability → no disability	0.116	(0.102,0.132)
Moderate ADL disability → IADL disability	0.276	(0.25,0.305)
Moderate ADL disability → severe ADL disability	0.137	(0.121,0.156)
Moderate ADL disability → death	0.035	(0.028,0.043)
Severe ADL disability → no disability	0.003	(0.000,0.123)
Severe ADL disability → IADL disability	0.002	(0.000,22.198)
Severe ADL disability → moderate ADL disability	0.264	(0.226,0.307)
Severe ADL disability → death	0.146	(0.125,0.171)
θ	1.021	(1.018,1.023)