Efficient Correction of Inhomogeneous Static Magnetic Field-Induced Distortion in Echo Planar Imaging

Abstract

Single-shot Echo Planar Imaging (EPI) is one of the most efficient magnetic resonance imaging (MRI) acquisition schemes, producing relatively high-definition images in 100 ms or less. These qualities make it desirable for Diffusion Tensor Imaging (DTI), functional MRI (fMRI), and Dynamic Susceptibility Contrast MRI (DSC-MRI). However, EPI suffers from severe spatial and intensity distortion due to B₀ field inhomogeneity induced by magnetic susceptibility variations. Anatomically accurate, undistorted images are essential for relating DTI and fMRI images with anatomical MRI scans, and for spatial registration with other modalities. We present here a fast, robust, and accurate procedure for correcting EPI images from such spatial and intensity distortions. The method involves acquisition of scans with opposite phase encoding polarities, resulting in opposite spatial distortion patterns, and alignment of the resulting images using a fast nonlinear registration procedure. We show that this method, requiring minimal additional scan time, provides superior accuracy relative to the more commonly used, and more time consuming, field mapping approach. This method is also highly computationally efficient, allowing for direct ‘real-time’ implementation on the MRI scanner. We further demonstrate that the proposed method can be used to recover dropouts in gradient echo (BOLD and DSC-MRI) EPI images.

INTRODUCTION

Spatial and intensity distortion in EPI images due to inhomogeneous static magnetic fields is a well-known phenomenon (Haacke et al., 1999; Bernstein et al., 2004a). Apart from scanner imperfections and Maxwell fields (Weisskoff et al., 1993; Jezzard and Clare, 1999), static field inhomogeneity will arise from the subject itself due to its magnetization (the magnetic response of the subject to the applied field) and the different magnetic environments found in different molecules. Spatial and intensity distortion follow since tissue localization is determined by the transverse phase of the nuclear spins under applied linear gradient fields, and the spins’ rate of precession is proportional to the local field. In particular, the degree of local distortion is proportional to the local magnetic field inhomogeneity. Distortion is most pronounced in the phase-encoded direction in rectilinear, or blipped, Echo Planar Imaging (EPI) (Mansfield, 1977; Pykett and Rzedzian, 1987; Jezzard and Clare, 1999) because of the relatively long time between sampling points in that direction, compared to the readout direction, during which there can be substantial change in phase accumulation due to the field inhomogeneity. Increasing the main field strength or the time to acquire a frequency-encoded line will proportionally increase the distortion. Also, since image or signal intensity is proportional to the spin density, intensity distortion will be proportional to the local compression or expansion. All this pertains to both gradient-echo EPI, as used in BOLD fMRI, and spin-echo EPI. In gradient-echo EPI, however, there are two additional significant problems: the well-known through-plane dropout that occurs for tissue in regions of susceptibility change, and the hitherto largely unaddressed problem of in-plane dephasing (discussed further below), which occurs whether there is local tissue compression or expansion in the image, but can be severe in the case of compression or ‘spin bunching’.

The magnetic field inhomogeneity a priori is unknown: it depends on the applied magnetic field, the magnetic susceptibilities within the subject, the geometry of the subject, and its orientation with respect to the external field; it can not be accurately modeled for or shimmed away in advance, but will be smooth within any region of constant susceptibility. The susceptibility of the magnetically linear and isotropic brain is essentially due to water, which is weakly diamagnetic, and the magnetization-induced magnetic field variation within the brain will mainly be governed by the brain’s interface with air, which has essentially zero-susceptibility.

Because of its ultra-fast imaging speed and relatively good image definition, blipped EPI is the pulse sequence of choice for diffusion (Mori, 2007) and perfusion imaging (Bernstein et al., 2004b), BOLD fMRI (Buxton, 2009), cardiac (Bhat et al., 2009), and abdominal imaging (Low et al., 2009). However, inhomogeneous static magnetic field-induced distortions in, for example, a 3T scan can easily be a centimeter or more near an air-tissue boundary, e.g., near the sinuses. This can lead to ~10 or more voxels’ worth of tissue being bunched into a single image voxel. The effect of the distortion artifact can therefore be severe, and has seriously impacted the utility of EPI.

There have been several attempts over the years to obtain distortion-free EPI images in a robust and efficient way. The unwarping method most commonly used is ‘field map’-based (Jezzard and Balaban, 1995). In this method, the back-ground magnetic field inhomogeneity, or field map, ΔB(r⃗), is determined from the phase difference between a pair of conventional (undistorted) complex gradient echo images acquired using different echo times, where, for each complex image data set I, the phase map is given by ϕ = tan⁻¹(Im(I)/Re(I)). In both conventional and echo train gradient echo imaging, in contrast to spin echo imaging, the resonant nuclear spins will continue to accrue transverse phase throughout the MRI acquisition due to background magnetic field inhomogeneities, and the resulting complex image will acquire a phase term exp(−iγΔB(r⃗)T_E), where γ is the gyromagnetic ratio and T_E is the echo time. If two complex gradient echo images are obtained using slightly different echo times, then B₁ (radiofrequency pulse) phase errors can be eliminated and the phase difference Δϕ between the two images gives the field inhomogeneity: Δϕ(r⃗) = −γΔB(r⃗)ΔT_E, where ΔT_E is the difference in echo times. Knowing ΔB(r⃗), the distortion can be calculated from Eq. 3 below.

Note that a full EPI image of the human brain takes only a few seconds, while acquiring a phase map (by conventional gradient-echo imaging so as to be anatomically geometrically correct) requires several minutes. This increases the chance of subject motion during the scan, which can lead to large errors in the resulting field map. Furthermore, the phase maps require phase unwrapping, and tend to be very noisy where image intensity in the amplitude image is low. The phase maps are also problematic near tissue edges and in regions of high variation in the background magnetic field (Zeng and Constable, 2002; Andersson et al., 2003; Li et al., 2007). Thus, use of unregularized phase maps produces rather poor images.

MRI images can also be unwarped based on the point spread function (PSF). Since an acquired image is given by the convolution of the ‘true’ image with the PSF of the imaging system, the displacement field that maps the recorded image back to the true, undistorted, geometry, is incorporated in the PSF. The PSF approach to unwarping EPI images (Robson et al., 1997; Zeng and Constable, 2002) is more robust to noise and high gradients in the background field, and potentially quite accurate, but requires relatively long scan times—taking several minutes for a full brain volume. It involves many (32 or more) single-shot EPI scans per slice, where, for each such scan, a preparatory constant-time phase-encoding gradient (along ŷ) is applied prior to data acquisition, with the gradient amplitude varying from scan to scan. The full set of preparatory gradients essentially constitutes a new set of k_y-points per data point acquired in the data sampling window, and enables an image of the PSF to be made for each voxel. The displacement field can then be calculated as the barycenter of the PSF. The PSF mapping technique has been optimized and combined with parallel imaging (Zaitsev et al., 2004; Speck et al., 2008) for reliable and faster distortion correction at high field strengths.

A promising and efficient method for correcting geometric distortion (and N/2 ghosting), a kind of simplified PSF method using an EPI field map, is Phase Labeling for Additional Coordinate Encoding (PLACE) (Xiang and Ye, 2007). This requires two EPI acquisitions, where the preparatory phase-encoding gradient areas for the acquisitions differ only by an amount equal to that of one or two normal phase encoding ‘blips’. The extra preparatory phase-encoding gradient causes a linear phase difference between the complex images in undistorted space, which need not exceed 2π across the FOV—obviating phase unwrapping. Thus, knowing the phase difference between the distorted complex EPI images for any voxel, the correct location for that voxel follows from the known linear phase difference in undistorted space. Post-processing is very fast, involving expansion and heavy smoothing of the complex images.

Another promising method employs Two Reduced Acquisitions Interleaved (TRAIL) (Priest et al., 2004, 2006, 2008). In the acquired images, blurring and distortion in the phase-encode direction are reduced by a factor of 2. Distortion correction, however, does require phase unwrapping, and the SNR is reduced by $\sqrt{2}$.

A very different approach (Morgan et al., 2004), using the reversed gradient method (Chang and Fitzpatrick, 1992), attempts to calculate the local distortions directly from magnitude EPI images. The reversed gradient method exploits the fact that if the phase-encoding gradients are reversed in polarity, i.e., if k-space in traversed in the opposite direction along the phase-encoding axis, then the distortions will be precisely reversed. The undistorted, anatomically correct image is then midway between the two oppositely-distorted images. The problem, however, is that one still has an integral equation to solve: the distortion of neighboring voxels around a voxel impacts the distortion of that voxel. The method employed to solve this relies on detection of compatible edges in both distorted images, and performing line integrals. The main limitations of this method are the requirement to identify boundaries for matching, and the use of 1-D unwarping, resulting in streaking or discontinuities in the frequency encoding and slice selection directions.

An alternative implementation of the reversed gradient method by Andersson et al. (2003) involves fitting for a smoothly-varying 3-D displacement field using discrete cosine basis functions. The resolution of the displacement field is limited by the highest frequency component of the DCT.

The method proposed here is similar in spirit to the approach of Andersson et al. (2003). It is computationally very efficient; full sub-voxel resolution is implicit in that the displacement field element at each voxel is explicitly determined.

METHODS

Human Subjects

The MRI scanning performed in this experiment was approved by the Institutional Review Board. All subjects provided informed written consent prior to scanning.

Image Acquisition

For the examples presented here, spin-echo EPI images and phase maps were acquired at both 1.5T and 3T. A 3T T₁-weighted structural image was also acquired for direct geometric comparison. Additionally, gradient-echo EPI images were acquired at 3T, together with a corresponding pair of spin-echo EPI images. Though implicit, below we explicitly give voxel sizes as this is the scale at which displacement field elements are calculated.

1.5T data were acquired on a General Electric Signa EXCITE HDx 1.5T scanner with an 8-channel phased-array head coil. The two single shot spin-echo EPI sequences were acquired with k-space matrix size 96 × 96, field of view (FOV) 24 cm (acquired or Fourier voxel size, i.e., the resolution, along both readout and phase-encoded axes equal to 2.5 mm; both corresponding reconstructed image voxel sizes equal to 1.875 mm), 47 axial slices of thickness 2.5 mm, and T_E 80.4 ms. One set of EPI images was collected with forward phase-encoding polarity, and the other set with reversed phase-encoding polarity. Two phase map scans (Jezzard and Balaban, 1995) were also acquired for use with FSL’s error correction tools (Smith et al., 2004), using conventional gradient-echo pulse sequences with k-space matrix size 128 × 128, FOV 24 cm (both acquired voxel size and reconstructed image voxel size along both readout and phase-encoded axes equal to 1.875 mm), 47 axial slices of thickness 2.5 mm, T_E 4 ms and 6.3 ms, respectively, and T_R 1,000 ms.

3T data were acquired on a General Electric Signa EXCITE HDx 3.0T scanner with an 8-channel phased-array head coil. The T₁-weighted 3D structural scan was acquired with k-space matrix size 256 × 192 (standard ADNI protocol (Jack et al., 2008)), FOV 24 cm (acquired voxel size along readout and phase-encoded axes equal to 0.9375 mm and 1.25 mm, respectively; both corresponding reconstructed image voxel sizes equal to 0.9375 mm), 166 slices of thickness 1.2mm, T_E 2.8 ms, T_R 6.5 ms, T_I 600 ms, flip angle 8°, and bandwidth 31.25 kHz. The forward and reverse phase-encoded spin-echo EPI sequences were acquired with k-space matrix size 96 × 96, FOV 24 cm (acquired voxel size along both readout and phase-encoded axes equal to 2.5 mm; both corresponding reconstructed image voxel sizes equal to 1.875 mm), 47 axial slices of thickness 2.5 mm, and T_E 83 ms. Two phase map scans were also acquired as described above. Additionally, a pair of forward and reverse phase-encoded gradient-echo EPI scans was acquired with k-space matrix size 64 × 64, FOV 22 cm (both acquired voxel size and reconstructed image voxel size along both readout and phase-encoded axes equal to 3.4375 mm), 32 axial slices of thickness 4 mm, and T_E 30 ms. For use in correcting these gradient-echo EPI scans, a corresponding pair of forward and reverse phase-encoded spin-echo EPI scans was acquired with T_E 100 ms, but otherwise with the same parameters as the gradient-echo EPI acquisition. The T_E can be less than 100 ms; a large value simply ensures high contrast between CSF (bright with a long T₂) and tissue.

Field Map Error Correction

Ppge4, a script provided by the UCSD Center for Functional Magnetic Resonance Imaging designed to facilitate the unwarping of GE DICOM images, was used to perform field map error correction. Ppge4 serves as a front end for FSL’s PRELUDE and FUGUE programs which correct the B₀ distortion using a phase map from each of two conventional gradient-echo images (acquired with different echo times) to calculate the field inhomogeneity map.

Unwarping Cost Function

The pair of oppositely distorted spin-echo EPI images will be corrected—such that both corrected images will be essentially identical—without the use of basis functions, by searching for the displacement in the phase encoding direction at each voxel that brings about the match of the images. This will be done by setting up a least-squares cost function that explicitly depends on all the voxel displacements. The numerical task is then to efficiently minimize this function—a task which will greatly be facilitated by going through a hierarchy of image smoothings.

Spatial distortion can be expressed in terms of the field inhomogeneity, pulse sequence timings, and the applied phase-encoding gradient, or dimensionlessly as a ratio of bandwidths. Let x̂ be the readout axis, ŷ the phase-encoding axis, and ẑ the slice-select axis. Let G be the average phase encoding gradient amplitude during each phase encoding period τ, and Δt_y ≡ t_esp the echo spacing, or equivalently the length of time between the start of each frequency-encoding or readout line (t_esp = N_xΔt_x + τ, where N_x is the number of readout sampling points, each separated by the dwell time Δt_x). If ΔB(x, y, z) is the inhomogeneity in the magnetic field, then, ignoring the more than two-orders of magnitude smaller shifts along the slice-select and readout directions, the signal emanating from real-space location (x, y, z) will be shifted to (x, y + δy, z), where (Jezzard and Balaban, 1995; Li et al., 2007)

$$\delta y(x,y,z)=(t_{esp}/\tau )\frac{\mathrm{\Delta }B(x,y,z)}{G}.$$ (1)

Note that this ŷ-displacement is a function of x, y, and z. If L_y is the FOV along the phase-encoding axis, and there are N_y phase-encoding steps, then Δy = L_y/N_y is the voxel dimension along ŷ, and the shift in units of pixels is the dimensionless quantity

$$u(x,y,z)=\frac{\delta y}{\mathrm{\Delta }y}.$$ (2)

Let the phase-encoding k-space step size be Δk_y. The discrete Fourier transform (DFT) pair Δy and Δk_y is related by ΔyΔk_y = 1/N_y. Note that Δk_y = γ̶Gτ = γ̶G′ Δt_y, where γ̶ = γ/(2π), γ the gyromagnetic ratio for the hydrogen nucleus, and G′ ≡ Gτ/t_esp is an effective phase-encoding gradient. Similarly, the time-frequency DFT pair for the phase-encoding axis is related by Δν_ppΔt_y = 1/N_y, where Δν_pp is the bandwidth per pixel (in Hz) across the phase-encoding FOV. Through the Larmor equation, the spatial distribution of the static background field inhomogeneity can be expressed in Hz as Δν_B = γ̶ΔB(x, y, z) (Jezzard and Clare, 1999). Hence, the pixel shift can be written as

$$u=\frac{\mathrm{\Delta }{\nu }_B}{\mathrm{\Delta }{\nu }_{pp}},$$ (3)

which is proportional to t_esp. Hereinafter, x, y, and z will refer to undistorted voxel-space, so that an imaged voxel that should be at voxel location (x, y, z), under an inhomogeneous field will instead be at voxel location (x, y + u, z). The image intensity will be proportional to the spin density, so if distortion leads to local compression the signal will be higher by the amount of compression. I.e., suppressing x and z, it will be scaled by the Jacobian J of the transformation y → y′ = y + u(y):

$$J=1+\frac{\partial u(y)}{\partial y}=1+T_{pe}\text{γ̶}\frac{\partial \mathrm{\Delta }B(y)}{\partial y},$$ (4)

where T_pe = N_yt_esp is the phase-encoding acquisition time, i.e., the time to traverse k-space along ŷ. If the phase-encoding gradient is reversed, i.e., k-space is traversed in the opposite direction along the phase-encoding axis, and a second image acquired, the signal emanating from location (x, y, z) this time will be shifted to (x, y − u, z), and tissue that was compressed in the forward image will now be expanded.

Using this information, a merit or cost function can be constructed to encapsulate the problem. That is, if there are N voxels, where the center of voxel i in the undistorted image is indexed by the voxel integers r⃗_i = (x_i, y_i, z_i, then the correct displacement field u(r⃗) ≡ {u_i = u(x_i, y_i, z_i);i = 1,…,N}, giving for each i the location of (x_i, y_i, z_i) in the distorted images, can be found as the minimizing vector of variables of a suitable cost function. To be specific, let I₁ denote the forward gradient EPI image, acquired traversing k-space in the positive ŷ-direction, and I₂ the oppositely-distorted reverse gradient image acquired traversing in the negative ŷ-direction. Let I denote the true undistorted image. The center of voxel i will have intensity I(x_i, y_i, z_i). In the forward image I₁, this will show up at voxel location (x_i, y_i + u_i, z_i), and at (x_i, y_i − u_i, z_i) in the reverse image, I₂. The problem is to identify corresponding locations in both forward and reverse images where the intensities are related by scaling as a result of local volume compression in one and expansion in the other.

In image I, let the neighboring voxel on the +ŷ side of voxel i be denoted ip, and im on the −ŷ side. Let the displacements of their centers, giving their voxel coordinates in the forward image, be u_ip and u_im, respectively. Then

$$I({\overrightarrow{r}}_i)=J_{1i}{I}_1({\overrightarrow{r}}_i+u_i\widehat{y})=J_{2i}{I}_2({\overrightarrow{r}}_i-u_i\widehat{y}),$$ (5)

where J_1i and J_2i are estimated from a discrete version of Eq. 4 (in voxel space):

$$J_{1i}=1+\frac{u_{ip}-u_{im}}{2},$$ (6)

,

$$J_{2i}=1-\frac{u_{ip}-u_{im}}{2}.$$ (7)

. Thus, one can construct a useful convex merit function from

$$\begin{array}{l}f(u_1,\dots ,u_N)=\hfill \\ \frac{1}{N}{\displaystyle \sum _{i=1}^N{\left[J_{1i}{I}_1({\overrightarrow{r}}_i+u_i\widehat{y})-J_{2i}{I}_2({\overrightarrow{r}}_i-u_i\widehat{y})\right]}^2,}\hfill \end{array}$$ (8)

which vanishes by design when all displacements correctly unwarp both images to make each identical to the true undistorted image. That is, when the correct displacement field is found, the undistorted image I is given for all voxels i by Eq. 5. The system must be constrained and regularized to keep the deformation field u(r⃗) smooth. As noted above, the magnetic field within the brain will vary smoothly, but Eq. 3 does not imply y′ is a monotonic function of y: depending on ΔB, for a given pulse sequence fold-over is possible. But if, say, in the forward image there is fold-over at (x, y + u, z), there will be magnification (or expansion) in the reverse image at (x, y − u, z), where u is the true displacement. The formulation of the problem in Eq. 8 precludes correct modeling of fold-over (where the Jacobians would become negative); it assumes a one-to-one mapping from the true undistorted image to the forward (and reverse) image, though in principle mappings that are non-injective (many-to-one) are possible. However, given the forward and reverse images, regularizing Eq. 8 (see Eq. 9 below) will allow for a smooth deformation field to be found that will be accurate outside of regions of fold-over, and keep small fold-over regions (which at any location may occur only in one image) well behaved. In other words, when the system is sufficiently regularized, the deformation field will remain single valued and smooth; correct matching outside any region of fold-over will be possible, and the smoothness constraint will maintain a well-defined deformation field within any small region of fold-over. If fold-over occurs at a voxel, the Jacobian will become negative there for an under-constrained system. In practice, we have found that fold-over is insignificant in the brain, even at 3T. That is, the corrected forward and reverse images invariably look practically identical.

The interface of a region of one susceptibility with a region of a different susceptibility causes local field variation when an external field is applied. The magnetic field of MRI interest at any point is the component parallel to the main field. Though this field will vary smoothly within a region of uniform susceptibility, it need not vary smoothly when traversing a boundary into a region of different susceptibility—there is refraction of the magnetic field lines at the interface: Maxwell’s equation ∇⃗ · B⃗ = 0 requires only that the magnetic field component normal to the interface be continuous across it. In the head, this refraction only happens when the other medium is air and, to a much lesser extent, bone, and in both cases there is essentially no MRI signal, in the former because the proton density is practically zero, in the latter because of very fast transverse relaxation compared to soft tissue. Thus, though discontinuities in the magnetic field variation will exist in the head, they are irrelevant. Hence, it is reasonable to look for a smoothly varying displacement field.

A smooth deformation field can be obtained by controlling the sum of the squares of the gradients of the displacements at each voxel. One can also add a term constraining the amplitude of the displacements. Hence, including the driving term Eq. 8, a suitable cost function f is

$$\begin{array}{l}f(u_1,\dots ,u_N)=\hfill \\ \begin{array}{ccc}& & \frac{1}{N}{\displaystyle \sum _{i=1}^N{\left[J_{1i}{I}_1({\overrightarrow{r}}_i+u_i\widehat{y})-J_{2i}{I}_2({\overrightarrow{r}}_i-u_i\widehat{y})\right]}^2+}\end{array}\hfill \\ \begin{array}{ccc}& & {\lambda }_1{\displaystyle \sum _{i=1}^N{u}_i^2+{\lambda }_2{\displaystyle \sum _{i=1}^N{\left[{\overrightarrow{\nabla }}_i{u}_i\right]}^2,}}\end{array}\hfill \end{array}$$ (9)

where λ₁ and λ₂ are regularization parameters of the model that control the quality of the unwarping—they will generally have a range of valid values, but that range depends on the scale of intensities. In practice, the unwarping has been quite robust to variations in λ₁ and λ₂. With the 1.5T images in this study, where intensities ranged from 0 to 8k (arbitrary scale), we used λ₁ = 0 and λ₂ = 10⁴. (Originally the 3T images ranged from 0 to 31k, and were rescaled to conform to the scale of the 1.5T images, so the values of λ₁ and λ₂ used at 1.5T were also used at 3T.)

There are many possible variations on this cost function. E.g., higher powers could be used, or the smoothing term could be appended to explicitly take into account neighboring displacements, e.g., in the notation of Eq. 6, the term [(u_ip − u_i)² + (u_i − u_im)²] could be added, though in practice it behaves similarly to the gradient term.

Cost Function Minimization

If each oppositely distorted image is heavily smoothed (blurred), e.g., by convolving with an isotropic Gaussian kernel of standard deviation ≃3–4 mm, they will look rather similar, even though the unsmoothed images may have relative internal deformations on the order of a cm. The 3T images, being more severely distorted, will generally benefit from higher initial smoothing. The similarity can be exploited to get around the myriad local minima on the path toward the global minimum of f. In other words, given a current estimate of {u_i}, which can be initialized to all zeros, sufficient smoothing will allow the global minimum location to be accessible, if not visible, unobscured by local hills and troughs in a landscape of N-dimensions. Having reached that point, one has a very good estimate for the new global minimum for images with less smoothing. Iterating over decreasing levels of smoothing, all the way to the native resolution, allows the displacement field gradually to accumulate large displacements.

The minimization carried out at any level of image smoothing will be done most expeditiously if as much gradient information as possible is taken into account—conjugate directions in a second-order Newton’s method (Gershenfeld, 1999); a first-order Newton’s method using conjugate gradients is stable and accurate, but slow. At the other extreme is steepest descent, where only the steepest gradient direction is used, requiring the next step to be orthogonal. The high smoothing and overall similarity of the images means a second-order Taylor expansion of f is a reasonable approximation—with enough smoothing one is in a concave basin of attraction. So one can perturb the quadratic form approximation for f around the current best estimate u⃗ = (u₁, u₂,…, u_N) of the system displacement vector, and one has a large, sparse, symmetric linear algebra problem:

$$\mathbf{H}(\overrightarrow{u})\cdot \overrightarrow{\upsilon }=-\overrightarrow{g}(\overrightarrow{u}),$$ (10)

where H (u⃗) is the Hessian of f at u⃗, g⃗(u⃗) is the gradient of f at u⃗ and the unknown quantity υ⃗ = (υ₁, υ₂,…, υ_N) is the displacement around u⃗) that nudges f toward the new global minimum u⃗ + υ⃗) at the new (finer) level of smoothing. The sparseness results from the coupling only of neighboring voxels through the derivative terms in H—the smoothing term couples nearest neighbors, and those terms involving the Jacobians will couple second-neighbors. There exist several efficient iterative methods for finding the solution υ⃗ of Eq. 10, e.g., conjugate gradients squared (CGS), generalized minimal residuals (GMRES), and biconjugate gradients stabilized method (Bi-CGSTAB) (van der Vorst, 1992, 2003). All results presented here were obtained using Bi-CGSTAB.

It should be noted that the displacements u⃗ (Eq. 2) are not restricted to integral voxel values, but, since intensities are well defined for all subvoxel locations through sinc interpolation (Hajnal et al., 1995), can indeed be real numbers.

In summary, distortion-correction is carried out as follows: (0) initialize the displacement field u⃗ to zero, and the standard deviation of the smoothing kernel to 3.5–4 mm; (1) smooth the original forward and reverse images; (2) set up the Hessian (u⃗) and gradient g⃗(u⃗) for the current net displacement field; (3) register the smooth images, i.e., calculate the refinement υ⃗ to the deformation field by solving Eq. 10; (4) update the deformation field: u⃗ = u⃗+υ⃗; (5) decrease the width of the smoothing kernel by 0.25–0.5 mm. Repeat (1)–(5) until there is no smoothing.

RESULTS AND DISCUSSION

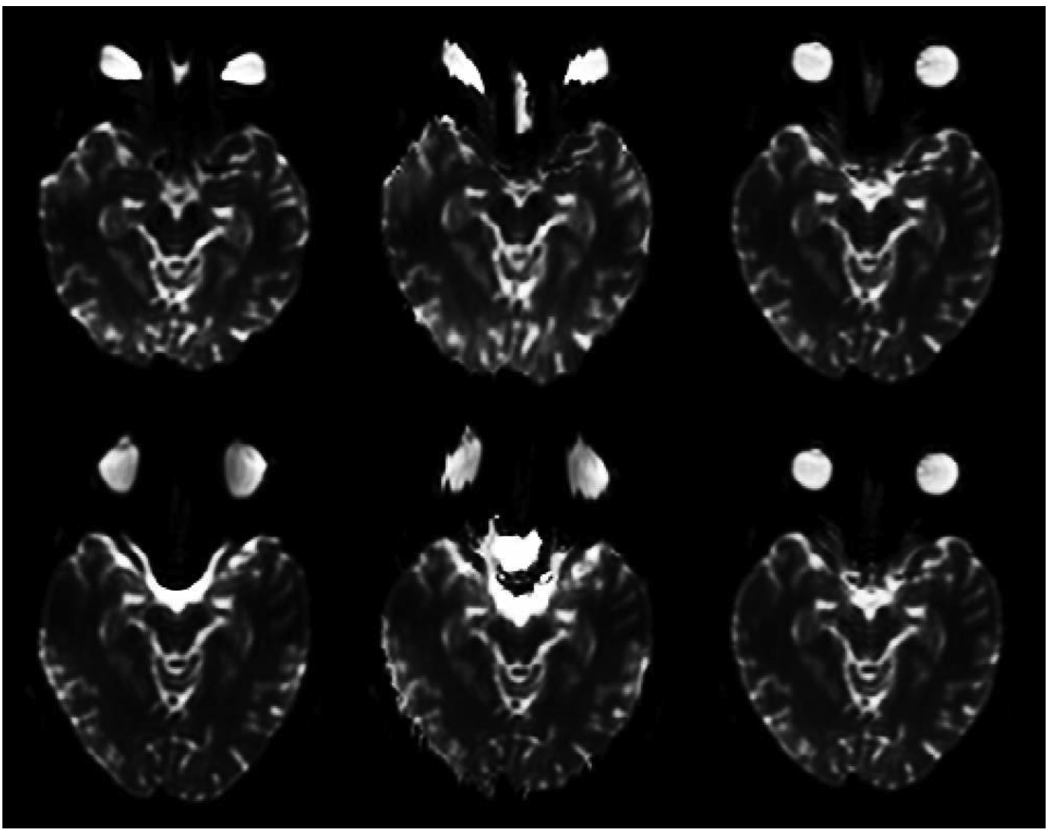
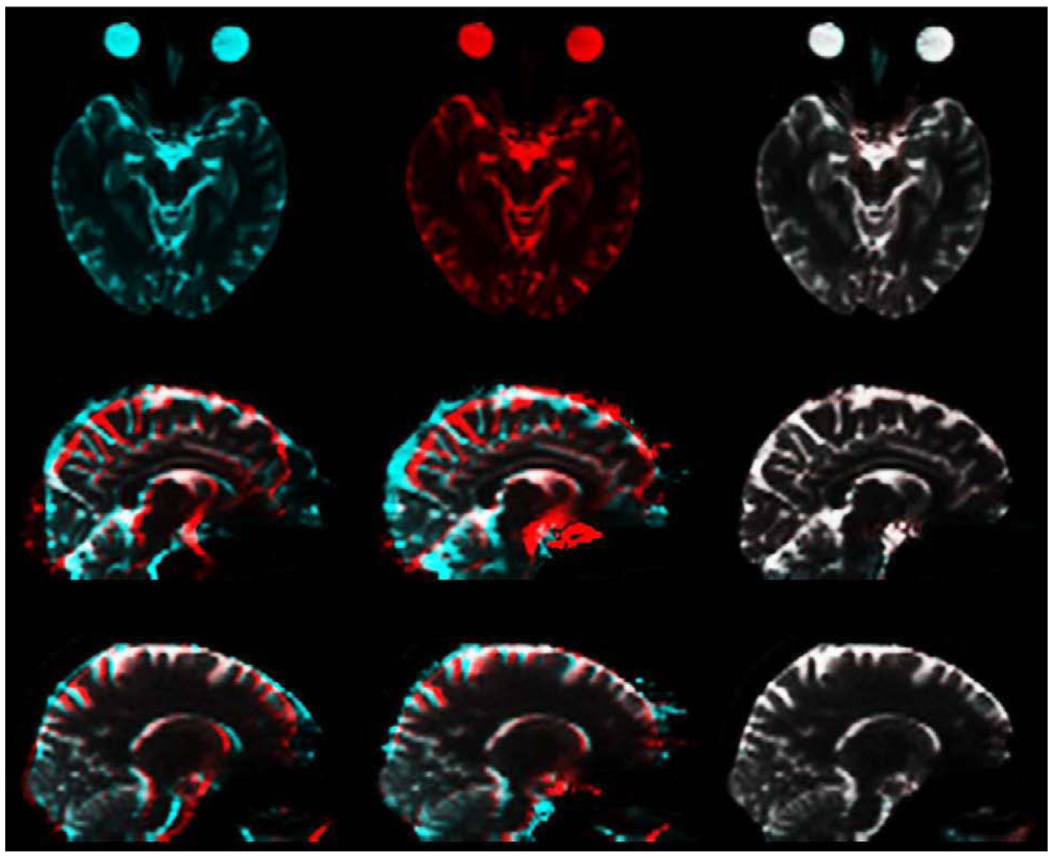
Blipped EPI scans were acquired at 1.5T and 3T, with a T₁-weighted structural scan also acquired at 3T, as described above. 3T EPI images are shown in Fig. 1: the top and bottom frames on the left hand side are axial slices from the forward and reverse images; the middle column shows the same images corrected by the standard field map method; and on the right are the same images after correction using the method presented here. To highlight the degree of mismatch in the uncorrected images and the accuracy of the current method, Fig. 2 employs complementary color overlays of the forward and reverse images. The top row again shows the corrections of the 3T images shown on the right hand side of Fig. 1, the upper one cyan and the lower one red. Their color addition is shown on the top right of Fig. 2: white implies a good match, i.e., the forward and reverse corrections are identical and so must equal the true undistorted image. The middle row in Fig. 2 shows 3T forward (red) and reverse (cyan) sagittal images: uncorrected on the left hand side, field map corrected in the middle, and corrected as described here on the right hand side. The bottom row is arrayed the same way for a similar slice but at 1.5T. Mismatch in the uncorrected images is significantly greater at 3T, particularly in the occipital and frontal lobes and the brain stem. Sulci are clearly misaligned. As can be seen in the middle sagittal panes in the bottom two rows in Fig. 2, the field map method substantially improves the misalignment at the front and back of the brain, but the interior is at best only partially corrected in places, even at 1.5T.

Figure 1.

Forward (top) and reverse (bottom) spin-echo EPI at 3T. Left: uncorrected. Middle: field map corrected. Right: corrected as described here.

Figure 2.

Complementary color comparison of forward and reverse spin-echo EPI. Top row shows 3T axial images corrected as described here: forward (red), reverse (cyan), and on the right their color-overlay sum (red+cyan=white). Middle row shows 3T sagittal color-overlay sum: left, uncorrected forward (red) and reverse (cyan); center, field map corrected forward and reverse; right, forward and reverse corrected as described here. Bottom row: same as middle row for a similar sagittal plane, but at 1.5T.

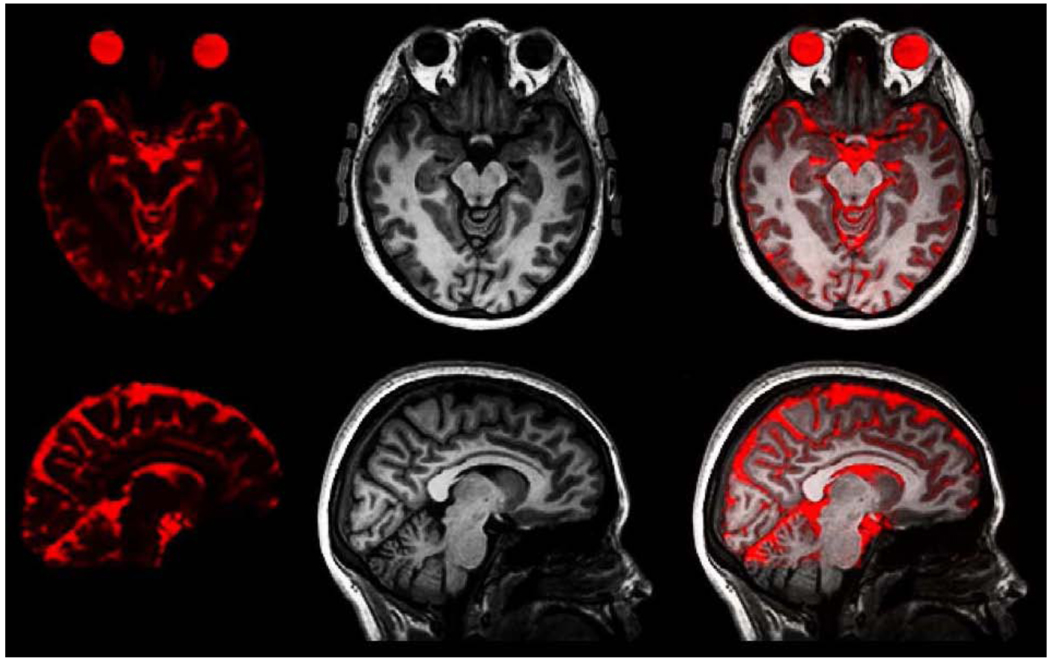
The lack of color in the panes on the right hand side in Fig. 2 implies that the corrected forward and corrected reverse images are practically identical, even at 3T. This also implies that they both equate to the true undistorted EPI image, and in principle could be averaged for higher SNR. Fig. 3 shows the excellent agreement of the average corrected 3T EPI image with the 3T T₁-structural, to which it has been rigid-body registered using mutual information (Leventon and Grimson, 1998): the front and back of the head are anatomically correct, and even the internal sulci are correctly aligned.

Figure 3.

Corrected spin-echo EPI compared with T₁-weighted structural scan. Left: axial and sagittal views of the average forward and reverse corrected 3T EPI. Middle: 3T T₁-weighted structural. Right: overlay of corrected EPI on structural.

PLACE (Xiang and Ye, 2007), using EPI readouts, is a promising method for measuring the phase map. The conventional phase map method, however, apart from the inherent difficulty in unwrapping the phase, where a binary decision must be made at each voxel, still requires the acquisition of two phase images at two different echo times. This can add minutes to scan times, and the longer the scan the greater the chance of motion corrupting the data. In contrast, the present method requires an additional EPI volume; the full acquisition can be implemented as an integrated sequence, with reversed phase encoding direction, in a single series. The correction procedure has been implemented in a way that allows it to be automatically applied after image reconstruction on the scanner, thus enabling integration into standard clinical workflow, taking less than a minute for a 3T pair of image volumes with 128 × 128 × 47 voxels (as a single process, single thread, on an Intel “Core i7” 2.67 GHz processor with 8 GB RAM). The displacement field, once calculated, can, for example, be applied to a subsequent series of diffusion-weighted images. Indeed, the current method has been applied to a large number of diffusion-weighted images (Hagler et al., 2009; McDonald et al., 2008), without needing any parameter adjustment. These time-series data sets were acquired with a spin-echo EPI pulse sequence for T₂ contrast, where loci of signal dephasing reveal white matter tracts. To correctly identify the white matter tracts, the images need to be registered to structural T₁ images, and this is facilitated using the B₀-unwarping described here. Note that image distortion in the DW volumes caused by eddy currents was corrected for separately; the displacement field calculated only from the initial forward and reverse b=0 images can then be applied to each DW scan. Since the displacement field is calculated from images which are close in time (about 2 seconds apart), motion is a minor issue in its estimation. Any relative displacement that may have occurred due to motion for subsequent frames in the DW time series can be corrected for by rigid-body registration of these images to the initial b=0 image of the same phase-encoding polarity. Such displacement, however, will generally produce a change in the distortion pattern: if motion is severe, a new displacement field would need to be calculated. It is also possible to apply real-time motion correction procedures (van der Kouwe et al., 2006; White et al., 2009) when acquiring a time-series of images so that the output images are already aligned with the b=0 image.

Geometric distortion in EPI, whether spin-echo or gradient echo, results from background gradients in the magnetic field. Assuming the same bandwidths are used, the distortion is identical in both cases, almost entirely in the phase encoding direction, and is due to the in-plane inhomogeneous static magnetic field gradient along the phase-encoding axis. There is a concomitant enhancement or diminution of image intensity directly proportional to the degree of local bunching or distension of spins.

In spin-echo EPI, phase dispersion due to any background magnetic field gradients, whether in-plane or through-plane, will be recovered at the spin echo; where background gradients are present, there will be just a very slight blurring resulting from the narrower echo peak. In gradient echo EPI, however, where there is continued dephasing throughout the echo train, background gradients can have profound effects on signal intensity, distinctly different for in-plane and through-plane. For through-plane (ẑ) gradients, there is signal loss due to phase dispersion; for linear variation of the background magnetic field ΔB across a voxel of through-plane extent Δz, it is given by sinc(Δϕ_z), where, in real space coordinates, Δϕ_z = γΔzT_E∂ΔB/∂z, with T_E the echo time and γ the gyromagnetic ratio (Zhao et al., 2005; Li et al., 2007). This in principle can be calculated by using Eq. 1 and Eq. 2 to estimate ∂ΔB/∂z from the z-gradient of the smooth three-dimensional y-displacement field u(x, y, z), with the latter determined by correcting corresponding spin-echo EPI forward and reverse images as described here (care being taken when going between real-space and voxel space: if ∂u/∂z is determined in voxel space, as was done for ∂u/∂y above, then Δϕ_z = γG(τ/t_esp)ΔyT_E∂u/∂z ). In practice, however, correcting for a low signal would mean also scaling up the noise; there would still be low SNR. For complete signal loss, the only recourse with magnitude images would be to reduce T_E or slice thickness so as to reduce dephasing.

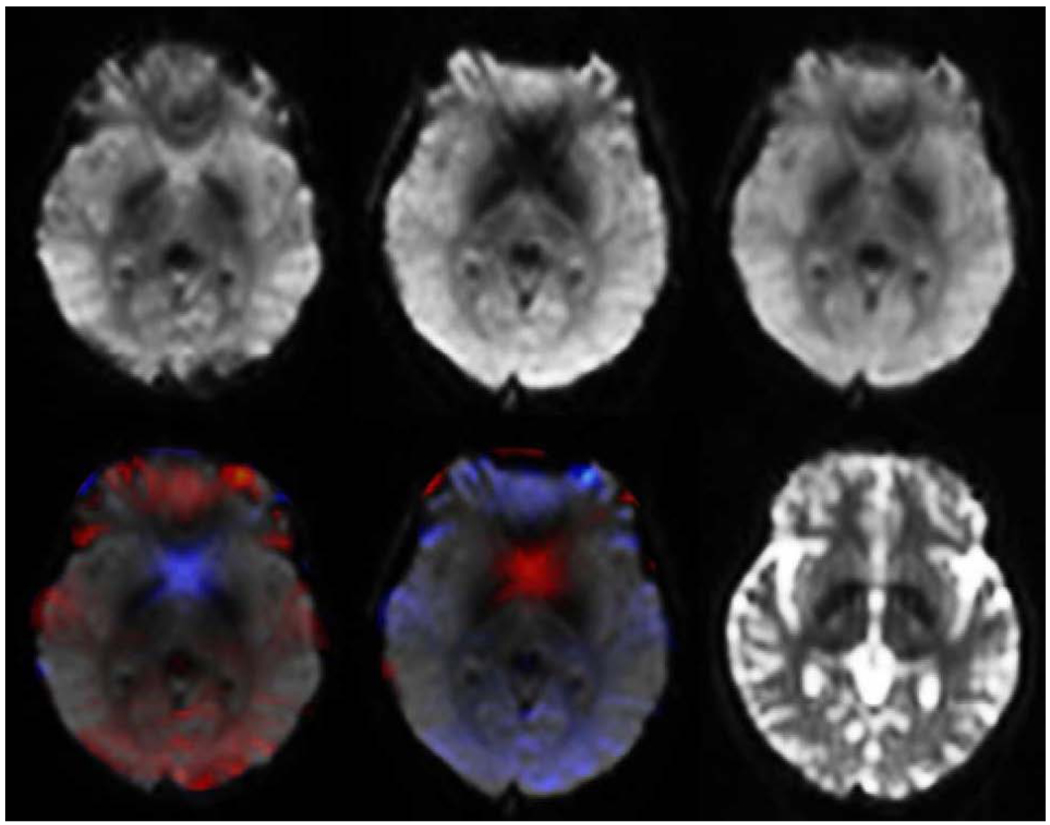
The effect of in-plane dephasing due to background field gradients along the phase-encoding direction can be even more severe, but with forward and reverse gradient-echo EPI, any signal loss can largely be recovered. An example is shown in Fig. 4.

Figure 4.

Axial slices from 3T gradient echo EPI, corrected using the displacement field calculated from spin echo EPI, showing complementary in-plane signal dropout patterns. Top row L to R: forward; reverse; root mean square of forward and reverse. Bottom row L to R: forward overlain with Jacobian of displacement field; reverse overlain with Jacobian of inverse displacement field; identical slice from average corrected forward and reverse spin echo EPI. For the overlays, red and blue indicate regions from which tissue was recorded as compressed or expanded, respectively, in the uncorrected images. Red thus indicates regions of recoverable dephasing dropout due to spin bunching.

In a region of compression in the forward gradient image, say, the imaged intensity in a voxel comes from a broader region of actual tissue: the entire phase variation across that broader region, due to the change in net magnetic field throughout the volume, contributes to an attenuation of the recorded voxel image intensity, and the greater the phase variation the greater the attenuation. Conversely, only a small piece of the same tissue region contributes to a specific imaged voxel in the reverse gradient image. There will therefore be substantially less dephasing per imaged voxel, and correspondingly less signal loss. As with spin-echo EPI, one still has geometric scaling of intensity, but with gradient echo EPI it is of a relatively dephased intensity (signal intensification due to geometric compression and signal diminution due to dephasing go hand in hand).

In through-plane dephasing, signal loss results from dephasing across only the slice thickness of a voxel. In in-plane dephasing, however, because of the distortions resulting in many voxels-worth of tissue being imaged into a single voxel, the dephasing effect can be far more severe, yet in this case it can largely, and easily, be rectified.

Because of nonuniform signal loss due to dephasing, the B₀-unwarping algorithm described here is not applicable directly to gradient-echo EPI forward and reverse images. However, if a corresponding pair of spin-echo EPI images is acquired, the correct unwarping displacement field can be found from them and then applied to the gradient-echo images. Voxels will be correctly shifted in space, but their intensities will not be accurate in regions where the susceptibility-induced magnetic field varies, e.g., the blue and red regions in Fig. 4. Geometrically-corrected forward and reverse gradient-echo EPI images can be combined, as in Fig. 4, to produce an image superior to either individually: by taking the voxel-wise maximum of both (or equivalently, locally taking the image for which the Jacobian of the displacement field is greater than 1), thus minimizing the effect of dephasing at any voxel; or by forming the root-mean-square of the forward and reverse images to produce an overall less noisy image.

Gradient-echo EPI is used for BOLD fMRI, which relies on $T_2^{*}$-contrast (Kwong et al., 1992), and DSC-MRI, which is commonly used to measure perfusion in stroke and tumors (Ostergaard et al., 2000; Zaharchuk, 2007; Marstrand et al., 2001; Carroll et al., 2008). To minimize the impact of in-plane dephasing in BOLD fMRI and $T_2^{*}$-weighted DSC-MRI, either forward or reverse phase-encoded imaging can be used, depending on which one expands the region of interest in the image. If a sampling frequency of several seconds is not an issue, however, a $T_2^{*}$ image, or time-course series of images, with minimal in-plane signal loss could be made as described here from a corrected pair, or corrected series of pairs, of forward and reverse gradient-echo EPI images, but with an effectively doubled T_R. When combined with shimming (Wilson et al., 2002), signal loss can be minimized further.

CONCLUSION

Spatial distortion in spin-echo and gradient-echo EPI, and additionally signal loss in the latter, have restricted the utility of this fast MRI acquisition scheme. For example, spatial distortion degrades the accuracy of registration of fMRI and DTI data with conventional structural MRI acquisitions, while signal loss in gradient echo DSC-MRI scans may be mistaken for loss of perfusion. The method presented here for unwarping EPI images, however, is sufficiently fast, robust, and accurate that it can be implemented in a clinical workflow to produce anatomically correct images, which can then directly be compared with images from other modalities. In addition, we have shown how to recover signal in regions of dropout, which is particularly important in and near the orbitofrontal and inferotemporal cortices.