Abstract
To reduce the access times of an endoscopy department, we developed an iterative combination of Discrete Event simulation and Integer Linear Programming. We developed the method in the Endoscopy Department of the Academic Medical Center in Amsterdam and compared different scenarios to reduce the access times for the department. The results show that by a more effective allocation of the current capacity, all procedure types will meet their corresponding performance targets in contrast to the current situation. This improvement can be accomplished without requiring additional equipment and staff. Currently, our recommendations are implemented.
Keywords: Access time, Waiting lists, Diagnostic department, Gastroenterology, Discrete event simulation, Integer linear programming
Introduction
Background
Long access times1 are a major problem in hospitals around the world. Not only patients requiring urgent attention want to be seen as soon as possible, also patients with an appointment expect to be seen at a short notice. If we can develop cost-effective solutions to reduce access times, budgets do not have to be increased. Such solutions would increase efficiency in the use of available resources rather than requiring investment in additional equipment and staff.
Our problem concerned the long access times in the endoscopy department of the Academic Medical Center (AMC) in Amsterdam. In the endoscopy department, various procedure types had to be performed with different durations and different urgency levels with corresponding access time targets. Therefore, we needed a method to evaluate the performance of a weekly master schedule in terms of access times for each procedure type. To schedule additional hours for poor performing procedure types, we had to take the complex scheduling environment of the endoscopy department into account. The various procedure types had to be performed in a suitably equipped procedure room by an available, specialized physician.
Literature review
Both Marcus [1] as well as Zamir and Rex [2] described qualitative methods to improve the efficiency of an endoscopy department. Shoaib et al. [3] and Baron et al. [4] tackle the access time problem from the demand side and both conclude that a quarter of the number of colonoscopies performed are unnecessary when compared to the guidelines. Implementing the guidelines would reduce the access times for diagnostic colonoscopy. Our study presents a quantitative approach to reduce access times.
Various quantitative methods are available to improve the efficiency of available resources. Gupta and Denton [5] described the difficulties in appointment scheduling in health care. More specific, the literature describing methods to reduce waiting/access times or improving resource utilization at outpatient departments (see for example [6–9]) or diagnostic departments (see for example [10–12]) is extensive. However, these methods are not sufficient to solve our complete problem of the endoscopy department, because the complex scheduling problem was not addressed in these papers.
Apart from literature about reducing waiting/access times or improving resource utilization at outpatient departments or diagnostic departments, we also searched for comparable problems and mathematical methods in other hospital departments and found two related topics: the nurse scheduling problem and operating room scheduling. Several articles deal with the scheduling of nurses – Cheang et al. provide an overview of nurse scheduling articles [13]. Sherali et al. describe how to schedule residents [14, 15] and Day et al. describe the scheduling of trainees [16]. However, in these articles the future demand is assumed to be known, which is different from our research. Centeno et al. [17] first predict the future demand for nursing staff of an emergency department with simulation and use that as input for an ILP to optimize the shifts. Although Centeno et al. use a combination of simulation and ILP, a few important differences with our study need to be mentioned. Firstly, in an emergency department the aim is to minimize waiting times in minutes in stead of access times in days, so the demand can not be scheduled and patients have to be treated in order of urgency and arrival. The second difference is that Centeno et al. do not distinguish different skills for the nursing staff which will be necessary for scheduling the specialized physicians of an endoscopy department in most teaching hospitals. The third difference is that the rooms in the emergency department are not scheduled explicitly while we have to deal with different procedure rooms as a constraint in the scheduling problem. Lastly, simulation and ILP are not used iteratively, which was necessary in our situation (see the methods section).
A topic which also has similarities with our research is operating room scheduling. A lot of articles are about maximizing the number of operations planned given e.g. a maximum risk on overtime [18–20]. A second subtopic is the operating room scheduling with restrictions on intensive care beds [21–23]. Unfortunately, none of these studies incorporated Discrete Event simulation to deal with the stochastic behavior of the system. These methods were not applicable to our situation, as Discrete Event simulation was necessary to solve our problem (see the Modeling section).
Summarizing, we found no articles in which both access time targets as well as various procedure types, specialized physicians and different procedure rooms are modeled simultaneously.
Research question
The purpose of our study was to answer the question: Is it possible to develop a mathematical method to reduce the access times for an endoscopy department in a teaching hospital?
We developed an iterative combination of Discrete Event simulation and Integer Linear Programming and applied this method in the endoscopy department of the Academic Medical Centre (AMC) in Amsterdam, The Netherlands. The result was a weekly master schedule that minimized the number of hours while meeting access time targets as well as taking into account equipment and physician–related constraints for each procedure type.
Problem analyses
Introduction of the AMC endoscopy department
To develop our mathematical method, we studied the endoscopy department of the AMC, particularly the procedures performed by the gastroenterologists. A gastroenterological (GE) endoscopy is a procedure to examine the upper or lower gastrointestinal tract. When combined with radiology, it also allows examination of the bile ducts. Furthermore, many different types of procedures (gastroscopy, colonoscopy and sigmoidoscopy to name some) assist diagnosis and treatment.
At the start of our study in August 2007, the access times for several procedure types were on average 12 weeks. In December 2007, these access times increased to on average 15 weeks. In this period, the endoscopy-GE department was staffed by 10 gastroenterologists and 6 resident-physicians. In 2006, these physicians performed over 9,000 endoscopic procedures in six different procedure rooms including trials of novel therapy and research.
The procedures were performed on outpatients (77%) and inpatients (23%). In addition to the inpatients from the AMC also patients from neighboring, general hospitals transported by an ambulance to the AMC were regarded as inpatients.
Endoscopic procedures
Endoscopic procedures differ with respect to (1) required equipment – e.g. a specific type of scope, X-ray machine or not, ultrasound equipment or not –, (2) duration and (3) urgency level. Patients were usually rated as semi-urgent or elective, but specific patients could also be urgent. Table 1 lists the access time targets set by the endoscopy department for these different urgency levels.
Table 1.
Urgency levels with access time target
| Urgency level | Access time target |
|---|---|
| Urgent | 100% within 24 h |
| Semi-urgent | 95% within one week |
| Elective | 95% within three weeks |
In general, the department considered the Endoscopic Retrograde CholangioPancreatography (ERCP), the Endoscopic UltraSound (EUS) and the dilatation of the esophagus (Oesdil) procedures to be semi-urgent. Additionally, Colonoscopy and general GE-procedures were considered to be elective procedures. These general GE-procedures were further subdivided based on scheduled duration times of 15 and 30 min. The average and standard deviation of the weekly demand of procedures in 2006, the duration, the default urgency level and the percentage of urgent procedures are listed in Table 2.
Table 2.
Weekly demand of procedures, duration, default urgency level and urgent percentage
| Procedure type | Average weekly number of procedures in 2006 (st. dev.) | Scheduled duration (minutes) | Default urgency level | Percentage of urgent procedures |
|---|---|---|---|---|
| ERCP | 18.4 (4.2) | 60 | Semi-urgent | 21% |
| EUS | 14.7 (4.3) | 45 | Semi-urgent | 4% |
| Oesdil | 10.1 (3.4) | 30 | Semi-urgent | 8% |
| Colonoscopy | 35.6 (6.0) | 60 | Elective | 9% |
| GE15 | 55.7 (8.7) | 15 | Elective | 24% |
| GE30 | 8.9 (2.6) | 30 | Elective | 32% |
| Feeding tube | 13.0 (3.9) | 30 | n.a. | 100% |
| Research | 21.3 (5.0) | 15–60 | Varying | 0% |
Available resources
Each procedure required one gastroenterologist and preferably two nurses. The nurses were trained to assist every endoscopic procedure. Not all gastroenterologists performed all endoscopic procedures, for example ERCP and EUS procedures required a specialized physician.
A pre-assessment room was available for preparation of patients for several procedures. The six different procedure rooms did not have the same equipment, so a procedure could not be scheduled in an arbitrary procedure room. For example, one room was equipped with X-ray technology required for ERCP and one room was equipped with ultrasound equipment for EUS. Besides the scheduled closures of the procedure rooms including nine public holidays and seven training days, occasional closures – due to illness, holidays and conference attendance of physicians – occurred frequently. Due to these occasional closures 9% of the yearly capacity could not be used. The public holidays were known in advance, the training days are spread evenly over the year and the occasional closures were randomly distributed over the year. Another relevant room of the endoscopy-GE unit was a recovery room with a maximum capacity of 10 patients. Here, patients recovered from anesthesia.
Patient scheduling
The scheduled operational time of the procedure rooms was six hours per day, divided into time slots. The department uses a weekly master schedule with a fixed number of dedicated time slots for each procedure type. Research and urgent procedures did not use dedicated time slots but instead dedicated time periods were scheduled to allocate these procedures. In the weekly master schedule, the time slots of each procedure type were scheduled in a procedure room with the required equipment and a dedicated physician specialized in the corresponding procedure type.
The time slots were differentiated in length depending on the corresponding procedure type. Particularly, one GE-timeslot could either be used by one 30 min procedure or two 15 min procedures. Both elective and semi-urgent patients were scheduled in an available, suitable timeslot. A timeslot was suitable if it was dedicated to the corresponding procedure type and a timeslot may be suitable for more than one procedure type. If a timeslot for an elective patient was not occupied a week before, the timeslot was also available for other procedures – so called soft blocks. Eight percent of the scheduled patients called to reschedule their appointment.
On Monday, Wednesday and Friday one procedure room was completely dedicated to urgent procedures and additionally on Tuesday and Thursday afternoon. If an urgent patient could not be planned within regular urgent time the same day, the patient was double-booked. These double-bookings often resulted in both overtime for physicians and nurses as well as extra waiting time for patients. The maximum percentage of double-bookings was set by the management of the endoscopy unit to limit the unscheduled overtime by physicians and nurses. Although double-bookings were only one of the many factors that effect overtime, on the tactical decision level it was the most significant factor. To ensure the total overtime limit would not be exceeded, the maximum percentage of double-bookings was fixed on 3%. We assumed the management of the department was able to specify the overbooking target level correctly to ensure the total overtime limit would not be exceeded.
Modeling
The appropriate mathematical method(s)
To evaluate whether or not the access time targets will be met and the percentage of double-bookings will not exceed 3% of the total number of procedures, a time-dependent and dynamic mathematical method is needed. Additionally, the fluctuating number of referrals and occasional closures of procedure rooms required the mathematical method to be stochastic.
If the access time targets are not met, additional hours have to be scheduled. Due to the limited availability and usability of the procedure rooms and the specialized physicians, this scheduling problem is too complex to solve manually. Therefore, we need a method to determine a new feasible weekly master schedule taken all constraints into account.
Dynamic, stochastic problem
Both queuing theory as well as computer simulation is an applicable mathematical method to solve dynamic, stochastic problems. In the following part of this section, we explain why queuing theory is not applicable to solve our specific problem.
At the start of our study, each endoscopic procedure had dedicated time slots so we could analyze the access times for each type separately. The ERCP is best suitable to evaluate the applicability of a queuing model, because the daily number of time slots available for ERCP was fixed: namely, five time slots. Except on Wednesday, when the specific procedure room was scheduled to be closed. We needed to model these scheduled closures because patients do arrive on Wednesday. Next to the scheduled closures, the ERCP procedure room was occasionally closed approximately 10 days per year.
Most queuing models assume the number of referrals to fit a Poison distribution. Because this was the case in the endoscopy department of AMC, we selected the formulas used by D’Antone [24] to handle the scheduled and occasional closures of procedure rooms. These formulas are suitable to calculate the waiting times for priority models with deterministic service times. Unfortunately, we were not able to model the closures of the ERCP room correctly with these formulas, because when applying priority queuing, the number of closures is Poison distributed, so both the number and the specific day within a year are random. Therefore, the fixed closures on Wednesday could not be modeled according to practice. Unfortunately, the randomly distributed closures have a large effect on the average access time so priority queuing did not lead to a valid model.
Therefore, we used computer simulation to evaluate the performance of the weekly master schedule in terms of access times and double-bookings. We found Discrete Event simulation best suitable to model our complex situation. Several other types of computer simulation are applied to patient logistics within hospitals to deal with the stochastic behavior [25, 26]: (1) Monte Carlo simulation, (2) System Dynamics and (3) Agent Based simulation. We will explain why these types of simulation are not applicable to our situation. Monte Carlo simulation is static so not applicable to our problem due to the time-dependent rescheduling of appointments. With System Dynamics, no detailed modeling of the scheduling rules is possible. This type of simulation is best applicable for macroscopic, strategic modeling [27]. Agent based simulation is used to model dynamic interaction between floating entities (e.g. patients). In our case, time-dependent interaction between patients is relevant, but dynamic interaction is not.
We build the Discrete Event simulation model using MedModel Professional Version 7. We applied Welch method [28] to decide upon the warm-up period of three months. The run length (excluding warm-up period) was set on one year and we determined the required number of replications to obtain a 3% half-width for the 95% confidence interval of the target percentage of the access time target. Therefore, we ran the model for 30 replications per scenario. The access time targets are met if the average value exceeds the target percentage of the access time target for each procedure.
To validate our simulation model, we studied the endoscopy-GE unit of the AMC. We compared the average access time of our model to the historical output data of the actual system. The first time we validated with 2006 data, the validation was not successful. We identified the main cause for this was that the assumption an elective patient would be scheduled in the first available timeslot was not justified. This appeared not to be the case in practice for three different reasons: (1) Patients can have preferences about their appointment, (2) medical or procedural reasons can require delays and (3) some patients need to be seen by a specific physician. This is all modeled together by a varying minimal delay in the appointment for semi-urgent and elective patients. We calibrated this delay in appointment with 2005 data and successfully validated the simulation model using 2006 data. The difference between the average access times of the model and the actual system, was within 15%.
Scheduling problem
If the access time targets are not met, a new feasible weekly schedule is needed including the required additional hours indicated by the simulation model. Linear programming is capable to solve this type of scheduling problem. As the decision variables must be integer values, Integer Linear Programming (ILP) is required to solve our specific scheduling problem.
The basic ILP-model for a teaching hospital is described in the Appendix. We did not incorporate the nursing staff in our ILP-model because the availability of nurses was very flexible and if the number of nurses was insufficient, a single nurse was scheduled in a procedure room.
We implemented the ILP-models in AIMMS and solved them using CPLEX 11.
Iterative combination of discrete event simulation and ILP
If one or more of the access time targets are not met, the number of hours used in the simulation model cannot be increased without applying the ILP-model to make sure the physician and procedure room constraints will be met. Therefore, an iterative combination of Discrete Event simulation and ILP was necessary.
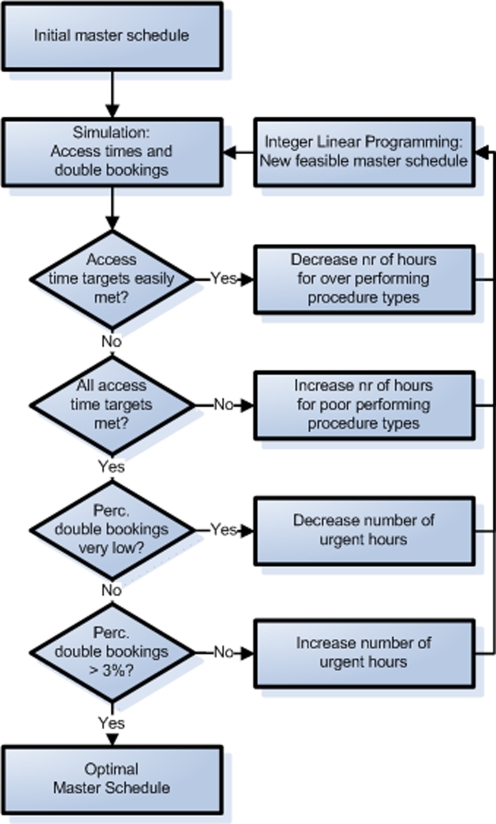
The iterative process started with evaluating the performance in terms of access times and double-bookings of the current weekly schedule (Fig. 1). For the well performing procedure types, the minimum number of weekly hours was reduced and for the poor performing procedure types, the minimum number of weekly hours was increased. The new required hours were scheduled by the ILP model to determine a feasible weekly master schedule. Subsequently, we evaluated the performance of the new master schedule with the simulation model. This iterative procedure continued until the minimum weekly number of hours required to meet the access time target for each procedure type was determined.
Fig. 1.
Iterative combination of Discrete Event simulation and ILP
We used the same iterative procedure to determine the minimum number of hours for urgent patients to make sure the percentage of double-booking would not exceed 3%. Note that the percentage of double bookings mainly depends on the number of urgent hours but indirectly also on the number of elective hours due to the soft blocks.
The result of this iterative process is a feasible, weekly master schedule taking all relevant constraints into account, including the access time targets and the double-booking limitation.
If no feasible master schedule is possible, one can increase the availability of the procedure rooms and/or the physicians. The availability can be increased by extending the opening/working hours and/or increasing the usability of procedure rooms and physicians. To decide how to increase the availability and/or usability, the most logical way is to select the most cost-effective way to obtain a feasible master schedule.
Results
We used our iterative method to evaluate the performance of various scenarios for the endoscopy-GE unit of the AMC. We started with the current situation and determined both the minimum weekly number of hours required to meet the access time target for each procedure type as well as the minimum number of hours for urgent patients so the percentage of double-bookings would not exceed 3% of the total number of procedures. We called this first alternative scenario the “performance target” scenario.
Table 3 shows the service level – the percentage of patients seen within the corresponding number of days – for each procedure. For research patients, no performance target was specified. The current situation required 144.5 h per week and the target scenario 143.5 h.
Table 3.
Service level per procedure type
| Procedure type | Current situation (standard deviation) | Performance target scenario (standard deviation) |
|---|---|---|
| ERCP | 99% (2%) | 99% (5%) |
| EUS | 94% (2%) | 95% (1%) |
| Oesdil | 81% (5%) | 96% (1%) |
| Colonoscopy | 19% (3%) | 95% (4%) |
| GE15 | 84% (21%) | 97% (7%) |
| GE30 | 77% (27%) | 95% (11%) |
Surprisingly, the “performance target” scenario required one hour less than the current situation. The reason for this is that the required number of hours for urgent patients can be reduced by almost 50% without significantly increasing the number of double-bookings. These hours can be used for Oesdil, Colonoscopy and general GE procedures to help these procedure types meet their performance targets.
We also experimented with various configurations to not only make sure that all procedures meet their corresponding performance targets but also minimize the total number of hours required.
All additional alternative scenarios took the access times target, double-bookings and procedure room and physician constraints into account. Therefore, we compared these scenarios with respect to the minimum weekly number of hours required in the first alternative scenario, the target scenario.
The additional alternative scenarios were the following:
We incorporated a backup system for physicians in the ILP-model to reduce the number of occasional closures. The backup system will make sure that if the dedicated physician is absent, a backup physician will take over the shift. At the start of our study, the occasional closures were 9% of the yearly capacity. With a backup system we expect this percentage to drop drastically. To evaluate the effect of the occasional closures, we experimented with 2% occasional closures. The backup system does not require additional investments but may be hard to implement. Therefore, it is important to quantify the expected reduction in required hours before implementation. If the reduction is small, the implementation may not be worth the trouble but a large reduction will be.
For the elective procedure types (general GE procedures and Colonoscopy), an extra urgency level – semi-urgent – was introduced to reduce the number of urgent procedures. Note that all urgent procedures have to be performed within 24 h. To deal with the fluctuating daily number of urgent procedures, a lot of spare capacity has to be dedicated to urgent procedures. Semi-urgent procedures can be equally scheduled during the week and therefore require less spare capacity. We scheduled the semi-urgent procedures in dedicated time slots, which will be available for urgent patients if these time slots are still empty. The physicians predicted that approximately 20% of the urgent procedures were in fact semi-urgent. Implementing this idea is relatively straightforward requiring no additional equipment and staff.
Pooling the time slots of different procedures may reduce the minimum weekly number of hours required to meet the access time target for each procedure [29]. Especially, for the semi-urgent procedures a relatively large reduction in required hours was to be expected. Unfortunately, these procedures (ERCP, EUS and Oesdil) require different equipment and/or specialized physicians. Therefore, we could only experiment with pooling general GE and Colonoscopy procedures. Indeed, these procedures have the same access time target, require the same equipment and the same physicians are specialized in both types. Pooling the two procedure types is easy to accomplish and makes the scheduling of patients easier.
Another potential improvement is to increase the flexibility of the available resources – in our case, procedure rooms and physicians. Increasing the usability of the procedure rooms – by adding equipment – may reduce the minimum required weekly number of hours, because more procedures are allowed to be scheduled in the corresponding rooms. This could also result in extra pooling possibilities as described in the previous scenario. Another way to increase the usability of the available resources is to increase the number of procedures a physician is specialized in. These non-recurrent investments may be more cost-effective than a structural extension of the opening/working hours of procedure rooms and physicians.
We expected that an additional X-ray machine would be the most cost-effective investment. This alteration allows semi-urgent GE and Colonoscopy procedures and Oesdil procedures to be pooled. Because the investment in an additional X-ray is considerable, the reduction of required hours has to substantial.
-
5.
The final scenario was a combination of the promising alternative configurations. This combination scenario included a backup system for physicians, semi-urgent general GE and Colonoscopy procedures, pooled time slots for general GE and Colonoscopy procedures. We did not include an additional X-ray machine because this only saves half an hour compared with the first additional scenario (see Table 4) and therefore, will not be a cost-effective solution.
Table 4.
Minimum required weekly number of hours per alternative scenario
| Alternative scenario | Required hours per week |
|---|---|
| 0. Performance target | 143.5 |
| 1. Backup system for physicians | 129.0 |
| 2. Semi-urgent general GE and Colonoscopy | 142.5 |
| 3. Pooling general GE and Colonoscopy | 143.0 |
| 4. Additional X-ray machine | 142.0 |
| 5. Combination scenario | 128.5 |
Discussion
Answer to our research question
We successfully developed a mathematical method to reduce the access times for an endoscopy department and applied an iterative combination of Discrete Event simulation and Integer Linear Programming to our AMC case study. The results show that by a more effective division of the current number of hours, all procedure types will meet their corresponding performance targets. Specifically, almost 50% of the urgent hours can be assigned to Oesdil, Colonoscopy and general GE procedures without significantly increasing the number of double-bookings. This reduction of the access times can be achieved by improving efficiency in the use of available resources rather than investing in additional equipment and staff.
The introduction of the semi-urgency level for urgent general GE and Colonoscopy procedures may lead to more efficient use of the urgent hours. Unfortunately, the results show that it will not lead to a large reduction in the minimum required weekly number of hours for the AMC endoscopy department. If the percentage of urgent patients actually being semi-urgent would increase to more than 20%, this scenario will be more beneficial.
A backup system for physicians will reduce the number of occasional closures. The results show that the weekly required number of hours will decrease by 10% if the occasional closures drop from 9% to 2%. Although physicians have to take over shifts and, therefore, work more hours, the backup system will still save capacity – on average six hours per week. Additionally, the weekly capacity will be more stable, which on itself will reduce the access times.
Pooling general GE and Colonoscopy procedures does not lead to a large reduction of the required number of hours. Unfortunately, with the current physician and procedure room constraints, only two elective procedure types could be pooled. The utilization rate for both procedures types was already high because the elective performance target is not stringent. Therefore, pooling does not lead to a significantly higher utilization rate and consequently, does not save much capacity.
Pooling the semi-urgent general GE and Colonoscopy procedures and Oesdil procedures saves only half-an-hour per week compared to the scenario with semi-urgency for general GE and Colonoscopy procedures. This reduction does not justify the investment in a new X-ray machine. The reason for the small reduction is that semi-urgent general GE and Colonoscopy procedures are often scheduled in empty time slots due to rescheduled appointments. Additionally, both types of procedures have a limited number of semi-urgent patients (only 5–6% of the total number of general GE and Colonoscopy procedures). Therefore, the absolute reduction is small.
Limitations and further research
Some patients need to be seen by a specific physician. In the AMC case this is due to research related specialization of physicians within one procedure type. Another reason could be that patients prefer their own physician, but the management of the AMC endoscopy department decided not to take this into account. A minimal delay in appointment was implemented to implicitly model the doctor-patient relationship (also see the methods section).
Currently, our recommendations are being implemented. Especially, the proposed backup system for physicians to reduce the number of occasional closures – due to illness of physicians and nurses, holidays and conference attendance by physicians – may be hard to implement. However, the physicians’ increased awareness of the major effect of this reduction on the access times – shown by our numerical results – will contribute to a successful implementation.
We did not incorporate the daily process in our study. Therefore, we were not able to check if the increased utilization rate would not lead to unacceptable high waiting time for patients in the waiting room. Additionally, we could not check whether or not the available numbers of scopes and the capacity of the recovery room were sufficient.
Also, the weekly schedule is optimized for the endoscopy department. We did not consider other related departments. Therefore, we could not analyze the effect of combining the endoscopy procedure with other appointments. Vermeulen et al. [30] illustrated the trade-off between the percentage of combination-appointments and the utilization rate of a department’s resources.
Conclusions
Our final recommendations to the AMC endoscopy department were to implement the backup system for physicians, the introduction of semi-urgency for general GE and Colonoscopy procedures and to pool these procedure types. Although, the effect of the latter two interventions is not large, no investments are necessary to accomplish them and a small reduction is still better than no reduction at all.
From the results obtained in our case study, we conclude that the described combination between Discrete Event simulation and ILP – if possible with the specified resources – will lead to a feasible, weekly master schedule that takes all constraints into account. This weekly master schedule does not only ensure that the access time targets and double-booking limitation will be met, but also takes into account the limited availability and usability of both procedure rooms as well as physicians.
The iterative mathematical method is not only applicable to the AMC endoscopy department but also for other teaching hospitals with comparable performance targets and double-booking limitation. In addition, many other hospitals also have to deal with the complex scheduling environment of an endoscopy department due to various equipped procedure rooms and specialized physicians.
In summary we conclude that the described mathematical method is a cost-effective way to reduce the access times of an endoscopy department. This is an addition to the available mathematical methods to reduce the access times of an outpatient or diagnostic department and to optimize operating room schedules.
Acknowledgements
The authors are grateful to C. Ponsioen, E. Ouburg, B. Wagner, M. van Haaster, J. Bergman and M. van den Bergh of the endoscopy-GHE department at the AMC for their collaboration during the project. The authors would also like to thank H. Greuter of the Team Innovation and Process Management at the AMC for his contribution to the study and E. Hans and P. VanBerkel of the University of Twente for the supervision of B. Overbeek and J. de Wit.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Appendix
| Indices | |
| a | Attendant-physician: experienced gastroenterologist. |
| d | Resident-physician: physician who is learning on the job. |
| r | Room: the available procedure room with specific equipment. |
| Furthermore, one dummy room – supervisor – is created. See constraint (c). | |
| s | Shift: every working day consists of a morning and afternoon shift. |
| t | Type of procedure. |
| Parameters | |
| AttAvailas | = 1 if attendant-physician a is available during shift s |
| = 0 otherwise | |
| AttShiftsa | The (maximum) number of shifts attendant-physician a works in the endoscopy-GE department |
| AttPosat | = 1 if procedure type t can be done by attendant-physician a |
| = 0 otherwise | |
| ResAvailds | = 1 if resident-physician d is available during shift s |
| = 0 otherwise | |
| ResShiftsd | The (maximum) number of shifts resident-physician d works in the endoscopy-GE department |
| ResPosdt | =1 if procedure type t can be done by resident- physician d |
| = 0 otherwise | |
| Demandt | Demand for procedures of type t. |
| Durt | Duration of one patient of procedure type t. |
| MaxLengths | Maximal length of shift s. Normally 3.5 h for morning shifts and 3 h for afternoon shifts. |
| RoomPosrt | = 1 if procedure type t can be done in room r |
| = 0 otherwise | |
| M | Sufficient large number |
| Decision Variables | |
| Xstr | Number of patients of type t in shift s in room r |
| Attasr | = 1 if attendant a planned in room r in shift s |
| = 0 otherwise | |
| Residdsr | = 1 if resident d planned in room r in shift s |
| = 0 otherwise | |
Objective function
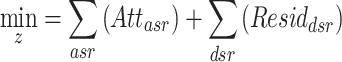 |
Subject to
| (a) |
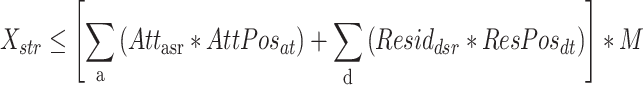
|
|
| (b) |
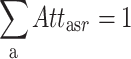
|
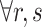
|
| (c) |
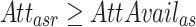
|
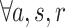
|
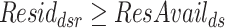
|
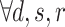
|
|
| (d) |
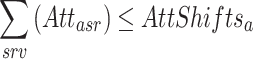
|
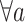
|
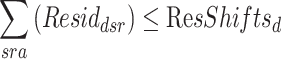
|
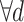
|
|
| (e) |
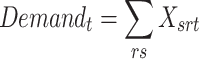
|
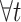
|
| (f) |
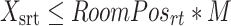
|
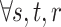
|
| (g) |
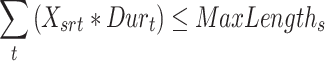
|
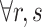
|
Clarification of constraints:
For each procedure type an attendant- or a resident-physician is needed to perform the procedures.
An attendant-physician must be present to supervise.
Both attendant- and resident-physicians can only be planned on shifts where they are available.
The time spent by different attendant- and resident-physicians is bound to a maximum.
Demand must be met for each procedure type t.
A procedure type can be done in one or more procedure rooms.
The length of each shift s may not exceed its maximum duration.
Footnotes
The access time of a patient is the number of days between referral and the actual appointment.
References
- 1.Marcus SN. Efficiency in endoscopy centers. Gastrointest Endosc. 2006;64(5):765–767. doi: 10.1016/j.gie.2006.07.028. [DOI] [PubMed] [Google Scholar]
- 2.Zamir S, Rex DK. An initial investigation of efficiency in endoscopy delivery. Am J of Gastroenterol. 2002;97(8):1968–1972. doi: 10.1111/j.1572-0241.2002.05909.x. [DOI] [PubMed] [Google Scholar]
- 3.Shoaib A, Hamade A, Zia A, Basnyat PS, Taffinder N. Why wait for a colonoscopy? An easy cure. Colorectal Dis. 2006;8(6):480–3. doi: 10.1111/j.1463-1318.2005.00922.x. [DOI] [PubMed] [Google Scholar]
- 4.Baron TH, Kimery BD, Sorbi D, Gorkis LC, Leighton JA, Fleischer DE. Strategies to address increased demand for colonoscopy: Guidelines in an open endoscopy practice. Clin Gastroenterol and Hepatol. 2004;2(2):178–82. doi: 10.1016/S1542-3565(03)00317-3. [DOI] [PubMed] [Google Scholar]
- 5.Gupta D, Denton B. Appointment scheduling in health care: challenges and opportunities. IIE Trans. 2008;40(9):800–819. doi: 10.1080/07408170802165880. [DOI] [Google Scholar]
- 6.Cayirli T, Veral E. Outpatient-scheduling in health care: A review of the literature. Prod and Oper Manag. 2003;12:519–549. [Google Scholar]
- 7.Murray M, Berwick DM. Advanced access: reducing waiting and delays in primary care. JAMA. 2003;289(8):1035–1040. doi: 10.1001/jama.289.8.1035. [DOI] [PubMed] [Google Scholar]
- 8.Thomas SJ, Williams MV, Burnet NG, Baker CR. How much surplus capacity is required to maintain low waiting times? Clin Oncol. 2001;13:23–28. doi: 10.1053/clon.2001.9210. [DOI] [PubMed] [Google Scholar]
- 9.Elkhuizen SG, Das SF, Bakker PJM, Hontelez JAM. Using computer simulation to reduce access time for outpatient departments. Qual and Saf in Health Care. 2007;16:382–386. doi: 10.1136/qshc.2006.021568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Walter SD. A comparison of appointment schedules in a hospital radiology department. Br J of Prev and Soc Med. 1973;27:160–167. doi: 10.1136/jech.27.3.160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Patrick J, Puterman ML. Improving resource utilization for diagnostic services through flexible inpatient scheduling: a method for improving resource utilization. J of Oper Res Soc. 2007;58:235–245. [Google Scholar]
- 12.Kolisch R, Sickinger S. Providing radiology health care services to stochastic demand of different customer classes. OR Spectr. 2008;30:375–395. doi: 10.1007/s00291-007-0116-1. [DOI] [Google Scholar]
- 13.Cheang B, Li H, Lim A, Rodrigues B. Nurse rostering problems–a bibliographic survey. Eur J of Oper Res. 2003;151:447–460. doi: 10.1016/S0377-2217(03)00021-3. [DOI] [Google Scholar]
- 14.Sherali HD, Rahamahi MH, Saifee QJ. Hospital resident scheduling problem. Prod Plan and Control. 2002;13:220–233. doi: 10.1080/09537280110069667. [DOI] [Google Scholar]
- 15.Day TE, Napoli JT, Kuo PC. Scheduling the resident 80-hour work week: an operations research algorithm. Cur Surg. 2006;63:136–141. doi: 10.1016/j.cursur.2005.12.001. [DOI] [PubMed] [Google Scholar]
- 16.Beliën J, Demeulemeester E. Scheduling trainees at a hospital department using a branch-and-price approach. Eur J of Oper Res. 2005;175:258–278. doi: 10.1016/j.ejor.2005.04.028. [DOI] [Google Scholar]
- 17.Centeno MKA, Giachetti R, Linn R, Ismail AM. A simulation-ILP based tool for scheduling ER staff. Proc of 2003 Winter Simul Conf. 2003;2:1930–1938. [Google Scholar]
- 18.Marcon E, Kharraja S, Simonnet G. The operating theatre planning by the followup of the risk of no realization. Int J Prod Econ. 2003;85:83–90. doi: 10.1016/S0925-5273(03)00088-4. [DOI] [Google Scholar]
- 19.Jebali A, Hadj Alouane AB, Ladet P. Operating room scheduling. Int J Prod Econ. 2005;99:52–62. doi: 10.1016/j.ijpe.2004.12.006. [DOI] [Google Scholar]
- 20.Guinet A, Chaabane S. Operating theatre planning. Int J Prod Econ. 2003;85:69–81. doi: 10.1016/S0925-5273(03)00087-2. [DOI] [Google Scholar]
- 21.van Oostrum JM, van Houdenhoven M, Hurink JL, Hans EW, Wullink G, Kazemier G. A master surgical scheduling approach for cyclic scheduling in operating room departments. OR Spectr. 2008;30:355–374. doi: 10.1007/s00291-006-0068-x. [DOI] [Google Scholar]
- 22.Santibáñez P, Begen M, Atkins D. Surgical block scheduling in a system of hospitals: an application to resource and wait list management in a British Columbia health authority. Health Care Manag Sci. 2006;10:269–282. doi: 10.1007/s10729-007-9019-6. [DOI] [PubMed] [Google Scholar]
- 23.Vissers JMH, Adan IJBF, Bekkers JA. Patient mix optimization in tactical cardiothoracic surgery planning: a case study. IMA J of Manag Math. 2005;16:281–304. doi: 10.1093/imaman/dpi023. [DOI] [Google Scholar]
- 24.D’Antone I. Pipeline length optimization in a digital asynchronous trigger controller. Nucl Instrum and Methods in Phys Res A. 2000;451:439–448. doi: 10.1016/S0168-9002(00)00325-9. [DOI] [Google Scholar]
- 25.Brailsford SC (2007) Tutorial: advances and challenges in healthcare simulation modelling. In: Henderson SG, Biller B, Hsieh M-H, Shortle J, Tew JD, Barton RR (eds) Proceedings of the 2007 Winter Simulation Conference. J. W. Marriott Hotel, Washington, D.C., pp 1436–1448
- 26.Brennan A, Chick SE, Davies R. A taxonomy of model structures for economic evaluation of health technologies. Health Econ. 2006;15:1295–1310. doi: 10.1002/hec.1148. [DOI] [PubMed] [Google Scholar]
- 27.Rauner MS, Schaffhauser-Linzatti M-M. Impact of international in-patient payment strategies on health technology management: a system-dynamics-model for Austria. Socio-Econ Plann Sci. 2002;36(3):133–154. [Google Scholar]
- 28.Welch PD. On the problem of the initial transient in steady-state simulation. Yorktown Heights, NY: IBM Watson Research Center; 1981. [Google Scholar]
- 29.Joustra PE, van der Sluis E, Van Dijk NM (2009) To Pool or not to pool in hospitals: a theoretical and practical comparison for a radiotherapy outpatient department. Ann of Oper Res (in press)
- 30.Vermeulen IB, Bohte SM, Elkhuizen SG, Bakker PJM, La Poutré H (2008) Decentralized online scheduling of combination-appointments in hospitals. Proceedings of ICAPS-2008, the International Conference on Automated Planning and Scheduling, Sydney, Australia September 14–18, 2008. pp 372–379, AAAI Press