Abstract
When enumerating small sets of elements nonverbally, human infants often show a set-size limitation whereby they are unable to represent sets larger than three elements. This finding has been interpreted as evidence that infants spontaneously represent small numbers with an object-file system instead of an analog magnitude system (Feigenson, Spelke, and Dehaene, 2004). In contrast, non-human animals and adult humans have been shown to rely on analog magnitudes for representing both small and large numbers (Brannon & Terrace, 1998; Cantlon & Brannon, 2007; Cordes et al., 2001). Here we demonstrate that, like adults and non-human animals, children as young as three years of age spontaneously employ analog magnitude representations to enumerate both small and large sets. Moreover, we show that children spontaneously attend to numerical value in lieu of cumulative surface area. These findings provide evidence of young children’s greater sensitivity to number relative to other quantities and demonstrate continuity in the process they spontaneously recruit to judge small and large values.
Introduction
A puzzling phenomenon in developmental studies of numerical cognition is that infants discriminate large numerosities (i.e., ≥ 4) that differ by at least a 1:2 ratio when cumulative surface area, element size, or cumulative perimeter are not available as cues (e.g., Brannon, Abbott, & Lutz, 2004; Cordes & Brannon, 2008; Lipton & Spelke, 2003; Xu, 2003; Xu & Spelke, 2000; Xu, Spelke, & Goodard, 2005) but they fail to discriminate small numerosities (i.e., < 4) under similar conditions (e.g., Clearfield & Mix, 1999; Feigenson, Carey, & Spelke, 2002; Lipton & Spelke, 2004; Wood & Spelke, 2005; Xu, 2003; Xu, Spelke, & Goodard, 2005; but see Feigenson 2005; Feigenson & Carey, 2003; Jordan & Brannon, 2006; Cordes & Brannon, in press A). Further, there is evidence that infants’ quantitative representations of small sets are incompatible with their representations of large sets (e.g., Feigenson, Carey, & Hauser, 2000; Feigenson et al., 2002; Feigenson & Carey, 2005; Lipton & Spelke, 2004; Wood & Spelke, 2005; Xu, 2003; but see Wynn, Bloom, and Chiang, 2002; Cordes & Brannon, in press A, under revision). These and other findings have led researchers to propose that infants spontaneously represent small and large numerical values in qualitatively different ways (e.g., Feigenson, Dehaene, & Spelke, 2004; but see Gelman & Butterworth, 2005).
When presented with small sets of objects, infants appear to employ an object-based attention mechanism that is domain-general and represents individual objects as discrete tokens in working memory (e.g., Leslie, Xu, Tremoulet, & Scholl, 1998; Uller, Carey, Huntley-Fenner, & Klatt, 1999; Trick & Pylyshyn, 1994). The main signature of this system is that there is an upper limit to the number of objects that can be represented, usually around four. In addition, recent studies suggest that feature information, such as surface area, can be bound to the discrete mental tokens that represent individual objects, thereby accounting for infants’ biases to attend to cumulative surface area instead of number for small sets (Feigenson et al., 2002). While this representational format is not inherently quantitative, it can be used, to judge quantity through one-to-one comparison of objects and object features, including comparisons of cumulative surface area (Feigenson et al., 2002).
A second mechanism, the analog magnitude mechanism, is thought to underlie infants’ numerical representations of large sets (e.g., Dehaene, 1992; Gallistel & Gelman, 1992, 2000). The behavioral signatures of the analog system include the numerical distance effect, in which the speed and accuracy of judgment increase with the difference between numerical values, and the numerical magnitude effect, wherein speed and accuracy decrease with number (e.g., Moyer & Landauer, 1967). The combination of the distance and magnitude effects results in ratio-dependent discrimination or, Weber’s law. Unlike discrimination of small sets, infants’ discrimination of large sets such as 8 vs. 12, 8 vs. 16, and 16 vs. 32 obeys Weber’s law: 6-month-old infants can discriminate 8 vs. 16 or 16 vs. 32 but not 8 vs. 12 (Lipton & Spelke, 2003; Xu & Spelke, 2000). This pattern of discrimination fits with the characteristics of an analog numerical representation mechanism which represents quantities as continuous, noisy mental magnitudes that are scaled to the number of items in a set (Gallistel & Gelman, 1992). The analog magnitude mechanism differs from the object-file system not only in its behavioral signatures, but also in that it is a purely quantitative mechanism.
In contrast to findings from studies with human infants, adults and non-human animals appear to represent small and large numerical values within the analog magnitude system. Cordes and colleagues (2001) demonstrated that adults’ nonverbal estimates of symbolic numbers can exhibit numerical magnitude and distance effects within the small number range that continue seamlessly into the large number range. Similarly, non-human primates exhibit fluid numerical distance and magnitude effects throughout the small and large number ranges on nonverbal numerical comparison tasks (Brannon & Terrace, 1998; Cantlon & Brannon, 2007). These studies provide evidence that adults and non-human primates rely on a single, coherent analog numerical continuum to judge numerical quantity. A central issue for developmental psychologists concerns the circumstances under which these two different numerical representation systems (analog magnitude and object file) are recruited by infants and children to solve numerical problems.
Recent studies have increasingly emphasized the importance of the object-file system in the initial development of numerical concepts. For example, some evidence suggests that young children spontaneously rely on object-file representations rather than analog magnitudes to acquire initial knowledge of the verbal counting system (e.g., Le Corre & Carey, 2007). Although several prior studies have demonstrated that young children can use an analog magnitude mechanism during non-verbal numerical processing (e.g., Barth, Lamont, Lipton, & Spelke, 2005; Brannon & Van de Walle, 2001; Gelman & Meck, 1983; Huntley-Fenner, 2001; Huntley-Fenner & Cannon, 2000), all of these studies simultaneously tested small and large numerical values and some have argued that the presence of large values may inhibit spontaneous quantity representation via the object-file system (e.g., Feigenson et al., 2002). Further, these prior studies either verbally or through their reward structure instructed children to attend to number and ignore non-numerical features. Thus it is unclear from these prior studies of young children’s numerical abilities whether they can spontaneously represent small sets in an analog magnitude format, like adults and non-human animals, or instead rely on an object-file format, like human infants.
Finally, recent studies have suggested that number may be less salient to developing humans than spatial dimensions, such as cumulative surface area, for small sets of objects. Some evidence suggests that infants fail to successfully discriminate number for small sets when non-numerical dimensions, such as cumulative surface area, are controlled (Lipton and Spelke, 2004; Wood & Spelke, 2005; Xu, 2003; but see Feigenson, 2005; Feigenson & Carey, 2003; Cordes & Brannon, 2008, in press; Jordan & Brannon, 2006; Kobayashi et al. 2005) and, in other studies, infants and preschool children have exhibited biases to attend to spatial dimensions instead of number when presented with small sets of objects (e.g., Clearfield & Mix, 1999 e.g., Clearfield & Mix, 2001; Feigenson, Carey, & Spelke, 2002; Rousselle, Palmers, & Noel, 2004; but see Cordes and Brannon, in press; Suriyakham, L.W., Ehrlich, S.B. & Levine, S.C., submitted). These studies raise questions regarding the timing of sensitivity to numerical value versus spatial extent over development.
In this study, we ask 1) whether the analog magnitude system operates over small and large values alike in young children and 2) whether young children are biased to attend to the numerical value or spatial extent of a set of items. If the ability to represent the entire range of numerical values as a coherent, unitary continuum develops early and, if numerical value is a cognitively primitive dimension over development, we would expect children to spontaneously base their decisions on numerical values and to represent these values in an analog magnitude format.
We tested children with a matching task in which they matched a sample stimulus to one of two choice stimuli. On most trials, the cumulative surface area of the elements was confounded with the numerical value of the elements. However, children were occasionally presented with trials in which number and surface area were pitted against each other to determine which dimension they would spontaneously use as a basis for matching. Additionally, as described earlier, the analog magnitude system predicts that performance should be modulated by numerical ratio. In the first experiment, we tested a group of children with only small numerical values (<5) to determine whether a numerical ratio effect emerges in the small number range. In the second experiment, we tested children with both small and large numerical values at equal numerical ratios to determine whether performance is comparable for small and large numerical values at equal ratios.
Experiment 1
Method
Subjects
Participants were fifteen 3- to 4-year-old children (Mean age = 3.5, SD = .33) and twelve 4- to 5-year-old (Mean age = 4.7, SD = .39). Seven children who failed to complete at least 45 trials or failed to perform above chance (50%) accuracy on Standard trials were excluded from the sample. Although previous cognitive studies of preschool children have reported similar drop-out rates (e.g., Gershkoff-Stowe, Connell, & Smith, 2006; Ristic, Friesen, & Kingstone, 2002), the somewhat high drop-out rate for this study is likely due to the fact, described in Task & Procedure, that children were not explicitly instructed on which dimension to base their decisions. Instead, they were simply told to ‘match’ the stimuli. The lack of explicit instructions, though potentially frustrating to the children, allowed us to assess the dimension to which children would spontaneously attend.
Task & Procedure
Children were tested on a delayed match-to-sample task in which a sample stimulus was presented on a computer screen. A response to the sample resulted in a 1-s delay followed by the presentation of two test stimuli. The child was then allowed to touch either choice stimulus.
On Standard trials (Figure 1a), one of the test stimuli matched the sample in number and cumulative surface area (match) and the second test stimulus differed from the sample on both dimensions (non-match). The difference in magnitude between the match and non-match in terms of both number and surface area are described in the Stimuli section. Correct responses were rewarded with a sticker and computer-generated positive visual and auditory feedback. Incorrect responses resulted in computer-generated negative visual and auditory feedback and no sticker. On Probe trials (Figure 1b), one of the two test stimuli matched the sample in number but not in cumulative surface area (number match) and the second test stimulus matched in cumulative surface area but not in number (cumulative surface area match). On Probe trials, children were rewarded with a sticker and positive visual and auditory feedback regardless of which choice stimulus they selected. Thus children were free to base their decisions on either number or cumulative surface area.
Figure 1.
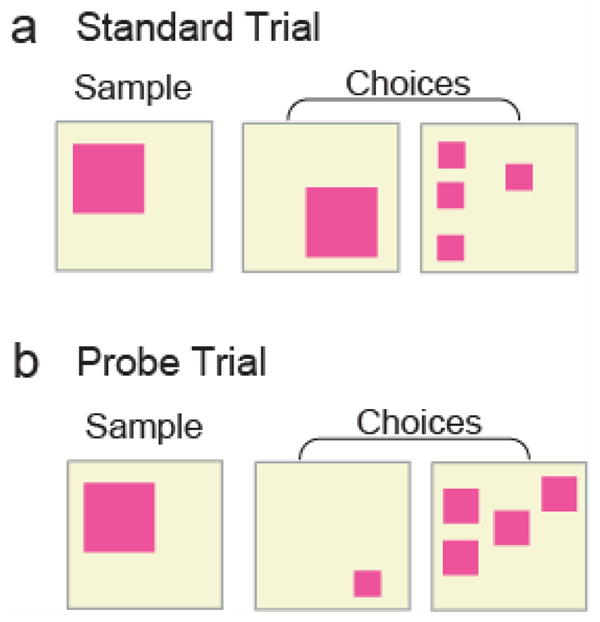
Illustration of stimuli used in the matching task. On Standard trials (a), one of the choice stimuli matched the sample exactly, in both number and cumulative surface area, whereas the other choice stimulus did not match in either number or cumulative surface area. On Probe trials (b), one choice stimulus matched the sample in number, but not in cumulative surface area, whereas the other choice stimulus matched the sample in cumulative surface area, but not in number.
Prior to testing, children were given a five-trial demonstration of the task. The only instruction that children were given about the objective of the task was to look at the sample stimulus, to remember it, and then, when presented with the two choice stimuli, to “Choose the box that matches the one you just saw.” Thus children were given no instruction as to which stimulus dimension they should use to select a match.
Each test session began with ten Standard trials. Probe trials were presented pseudo-randomly with the constraint that at least two Standard trials separated each Probe trial. Each child was tested on between 45 and 80 trials. Probe trials comprised approximately 30% of the total trials in a session.
Stimuli
Element shape (square) and color (red) were constant and element position was randomly varied across the sample and choice stimuli on both Standard and Probe trials. For both Standard and Probe trials, the numerical values of the sample and choice stimuli consisted of all pairwise combinations of the values 1 to 4 and the values for cumulative surface area (in pixels) were all pairwise combinations of 1200, 2400, 3600, 4800, 6000, and 7200, presented with equal frequency. For numerical values, the ratios tested ranged from 0.25 to 0.75 and for cumulative surface area values, the ratios tested ranged from 0.17 to 0.83. This resulted in an equal average ratio between the ranges of numerical and cumulative surface area values (Means = 0.5). This set of values was used to define the numerical and cumulative surface area relationships among stimuli on the Standard and Probe trials. On Standard trials, the match was identical to the sample in terms of both the number and cumulative surface area of the sets while the match and non-match differed in terms of both the number and cumulative surface area of the sets. In contrast, on Probe trials, the match and non-match each were identical to the sample in one dimension (either the number or cumulative surface area of the set) and differed from the sample in the other dimension.
Results and Discussion
Overall, children in both age groups performed significantly above chance during Standard trials when number and cumulative surface area were confounded (One-sample t-tests; 3–4 years: Mean = 80%, t(14) = 8.60, p < .0001; 4–5 years: Mean = 85%, t(11) = 9.93, p < .0001). On Probe trials, when number and cumulative surface area predicted different choices, children in both ages groups exhibited a strong bias to select the numerical match over the cumulative surface area match (One-sample t-tests; 3–4 years: Mean = 70%, t(14) = 5.10, p < .001; 4–5 years: Mean = 77%, t(11) = 7.53, p < .0001).
Children responded rapidly on this matching task; the average RT to make a choice between the two stimuli was 1.6 s (SE = .09) for 3-year-old children and 1.5 s (SE = .09) for 4-year-old children. The rapid rate with which children responded makes it unlikely that they were verbally counting to match stimuli in this task (Geary & Brown, 1991; Landauer, 1962).
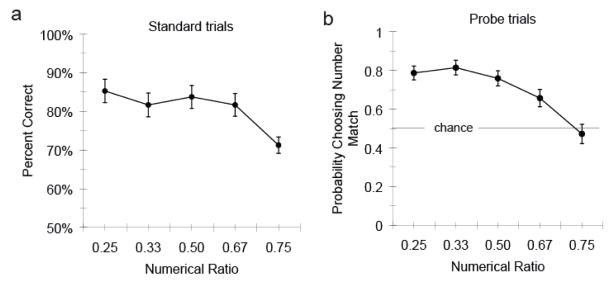
To investigate the relationship between age and the quantitative strategies that children relied on to perform this task, we performed a 2 × 2 × 5 Repeated Measures ANOVA for Age (3–4 or 4–5 years) × Trial Type (Standard or Probe) × Numerical Ratio (0.25, 0.33, 0.5, 0.67, 0.75) with the dependent variable of response percentage1. Response percentage refers to accuracy on Standard trials since there is only one correct choice whereas on Probe trials, it represents the probability of choosing either the number match or the cumulative surface area match since both choices are technically correct. This analysis revealed significant main effects of Trial Type (F(1,50) = 9.14, p < .005) and Numerical Ratio (F(4, 100) = 20.12, p < .0001) and an interaction between Trial Type and Numerical Ratio (F(4,200) = 4.78, p < .01). No other main effects or interactions were significant. Figure 2 shows children’s accuracy as a function of numerical ratio for Standard (a) and Probe trials (b) collapsed across the two age groups.
Figure 2.
Children’s performance on the Standard trials in Experiment 1 as a function of numerical ratio (a) and the probability with which children selected the numerical match during Probe trials as a function of the numerical ratio (b).
The main effect of Trial Type in the ANOVA was due to children’s greater accuracy at choosing the correct match during Standard trials, when number and cumulative surface area were confounded (Mean = 82%) compared to the probability with which they chose the numerical match on Probe trials, when number and cumulative surface area predicted different choices (Mean = 73%; Fisher’s LSD post hoc tests: p < .05). The main effect of Numerical Ratio was due to a higher probability of choosing the numerical match on numerical ratios of 0.25, 0.33, and 0.5 than ratios of 0.67 or 0.75 (Fisher’s LSD post hoc tests; all p’s < .05). The interaction between Trial Type and Numerical Ratio resulted from a greater effect of Numerical Ratio on children’s performance during Probe trials than on Standard trials. However, children exhibited a significant numerical ratio effect within each of these trial types (Simple regression; Standard trials: F(1, 133) = 7.66, p < .01; Probe trials: F(1, 133) = 30.91, p < .001). The lack of an interaction between Age and any of the remaining variables indicates that the same patterns held across both age groups.
Finally, we investigated the effect of cumulative surface area differences on children’s choices on Standard and Probe trials. We conducted an ANOVA of Age, Trial Type, and Cumulative Surface Area Ratio. The only significant effect in this analysis was a main effect of Trial Type (F(1,36) = 5.60, p < .05) due to that fact that children’s probability of selecting the correct match on Standard trials (.81) was significantly greater than the probability with which they selected the cumulative surface area match on Probe trials (.30). Surprisingly, we found no main effect of Cumulative Surface Area Ratio on young children’s performance (F(6, 216) = 1.15, p = .34) and no interactions. The lack of a main effect of Cumulative Surface Area ratio and the lack of an interaction between Trial Type and Cumulative Surface Area Ratio indicate that the difference in cumulative area between the two choices had little effect on children’s decisions on Standard or Probe trials.
Despite the fact that differences in cumulative surface area values did not affect children’s performance, their performance was not equivalent on Standard and Probe trials. The significantly higher probability of choosing the correct match on Standard trials (.81) compared to the probability of choosing the number match on Probe trials (.70) indicates that de-confounding number from cumulative surface area did, in fact, negatively impact children’s numerical judgments. Children were significantly better at choosing the numerical match when number and surface area were confounded on Standard trials than when they were in conflict on Probe trials. However, the ratio between the cumulative surface area values of the choices did not modulate performance and thus children’s judgments were not overtly affected by relative differences in cumulative surface area. Note that this was not because cumulative surface area was more difficult to discriminate than numerical value; the mean cumulative surface area ratio in this experiment was 2:1 and was equated with the mean ratio for numerical values. Furthermore, the range of cumulative surface area values tested was comparable to the range that can be discriminated by human infants (e.g., Clearfield & Mix, 1999).
The lack of a significant ratio effect for cumulative surface area suggests that children were not explicitly comparing cumulative surface area values during their matching decisions. Yet, relative differences between cumulative surface area values may have implicitly influenced children’s performance. One piece of evidence that supports this claim is that there was a marginally non-significant interaction between Cumulative Surface Area Ratio and Trial Type wherein children were less likely to select the cumulative surface area match with increasing cumulative surface area ratio only on Probe trials (F(6,216) = 1.90, p = .08). Additionally, the correlation between cumulative surface area ratio and performance on Probe trials was significant (r = 0.88, p < .01). Yet, despite evidence that children processed the cumulative surface area values, they never exhibited a bias to select the cumulative surface area match at any ratio during Probe trials.
Experiment 2
In Experiment 1, we demonstrated that when tested with a small range of numerical values, young children 1) show ratio-dependent performance within the small number range and 2) preferentially attend to the numerical value of the stimuli rather than the cumulative surface area of the elements in this paradigm. In Experiment 2 we investigated whether children’s performance in this small number range is qualitatively similar to their performance in the large number range. Using the same paradigm from Experiment 1, we tested 3- to 4-year-old children with both small and large numerical values at each of three numerical ratios: 0.25, 0.5, and 0.67.
Subjects
Participants were eleven 3- to 4-year-old children (Mean age = 3.43, SD = .3). Two children who failed to complete at least 45 trials or failed to perform above 56% accuracy on Standard trials were excluded from the sample.
Task & Procedure
The task and procedure was identical to that of Experiment 1.
Stimuli
Stimuli were constructed with the same parameters as Experiment 1. However, in this experiment we tested numerical values for the two choice stimuli at the following numerical ratios: 0.25 (1 vs. 4, 2 vs. 8, 3 vs. 12), 0.5 (1 vs. 2, 2 vs. 4, 4 vs. 8, 6 vs. 12), 0.67 (2 vs. 3, 4 vs. 6), and 0.75 (9 vs. 12). Cumulative surface area values were 1600, 2400, 4800, and 9600 pixels and were tested in ratios of 0.17, 0.25, 0.33, 0.5, and 0.67.
Results & Discussion
As in Experiment 1, 3- to 4-year-old children performed significantly above chance on Standard trials (One-sample t-tests vs. chance (50%); Mean = 77%, t(14) = 7.21, p < .0001). Also consistent with Experiment 1, children were biased overall to select the numerical match over the cumulative surface area match on Probe trials, when number and cumulative surface area were in conflict (One-sample t-tests vs. chance (50%); Mean = 58%, t(14) = 3.08, p < .05). Finally, the children in Experiment 2 responded at a similarly rapid pace to the children in Experiment 1: the average RT to make a choice between the two stimuli was 1.7 s (SE = .3).
We conducted a 2 × 4 Repeated Measures ANOVA for Trial Type (Standard or Probe) × Numerical Ratio (0.25, 0.5, 0.67, 0.75) with the dependent variable of response percentage. This analysis yielded a main effect of Trial Type (F(1,20) = 22.75, p < .001), a main effect of Numerical Ratio (F(3, 60) = 27.22, p < .0001), and an interaction between Trial Type and Numerical Ratio (F(3, 30) = 10.55, p < .0001). Fisher’s LSD posthoc tests on our main effects revealed that children’s performance on Standard trials was significantly higher than the percentage of Probe trials for which they selected the numerical match (77% vs. 58%, p < .001). Thus as in Experiment 1, children were more likely to select a numerical match when number was confounded with surface area than when number was pitted against surface area. Both experiments indicate that redundant quantitative information from number and surface area improves quantity discrimination in children.
Also similar to Experiment 1, children were more affected by Numerical Ratio during Probe trials than Standard trials and there was again a significant effect of Numerical Ratio for both trial types (Simple regression; Standard trials: F(1,108) = 4.76, p < .05; Probe trials: F(1, 108) = 53.77, p < .0001). On Probe trials, children’s bias to select the numerical match over the cumulative surface area match decreased as numerical ratio increased. In other words, children were less likely to base their matching choices on number when the numerical values were difficult to discriminate. Yet, children rarely exhibited a bias to match based on surface area instead of number, even at the most difficult numerical ratios: of the 10 number pairs tested, children exhibited a tendency to match based on cumulative surface area only for one pair (pair 9 vs. 12; t(11) = 3.02, p < .05). Children’s propensity to use numerical value over surface area as the basis for matching given equal relative differences along these two dimensions is thus clearly established. However, children may base their decisions on cumulative surface area when numerical values are too difficult to discriminate.
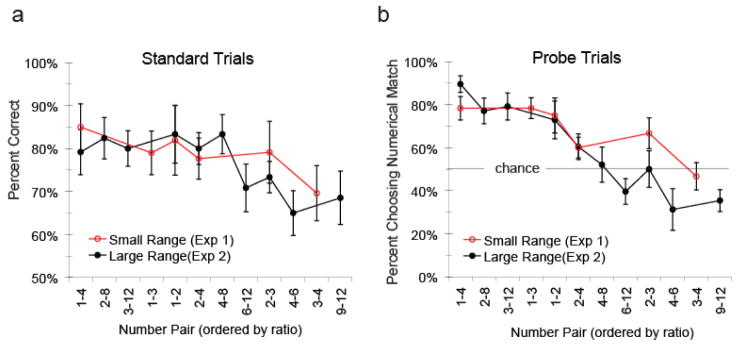
Next, we compared children’s performance on the numerical pairs within each of the three ratios in which both small and large numerical comparisons were tested: 0.25, 0.5, and 0.67. At a 0.25 ratio, children were tested with the pairs 1 vs. 4, 2 vs. 8, and 3 vs. 12. There were no significant differences in children’s performance among these pairs (all p’s > .09). The numerical pairs 1 vs. 2, 2 vs. 4, 4 vs. 8, and 6 vs. 12, were tested for the 0.5 ratio. Children’s performance on the 1 vs. 2 pair was significantly higher than the 4 vs. 8 and 6 vs. 12 pairs. However, upon further investigation, we found that this effect was driven entirely by 1vs. 2 trials in which the sample stimulus consisted of 1 element: children’s performance on 1 vs. 2 trials in which the sample stimulus consisted of 2 elements was not significantly different from their performance on the 4 vs. 8 pair (t(10) = 0.92, p = .38) or 6 vs. 12 pair (t(10) = 1.52, p = .16). Thus children found it easier to remember a sample when it contained 1 element as opposed to 2, 4, 6, 8, or 12 elements but, apart from this difference, they performed similarly on small and large numerical pairs at a 0.5 ratio. Lastly, there was no significant difference between children’s performance on the numerical pairs 2 vs. 3 and 4 vs. 6 at the 0.67 ratio (t(10) = 1.49, p = .17). Thus our general finding is that, consistent with the properties of the analog magnitude system, children’s performance is constant when numerical ratio is constant. Figure 3 illustrates the results of Experiments 1 and 2 for each number pair, ranked from least difficult to most difficult ratio.
Figure 3.
Children’s accuracy on Standard trials during Experiment 1 (open circles) and Experiment 2 (closed circles) for each number pair ordered along the x-axis by numerical ratio (a). The percentage of Probe trials on which children selected the numerical match for each number pair, ordered by ratio for Experiment 1 and Experiment 2 (b).
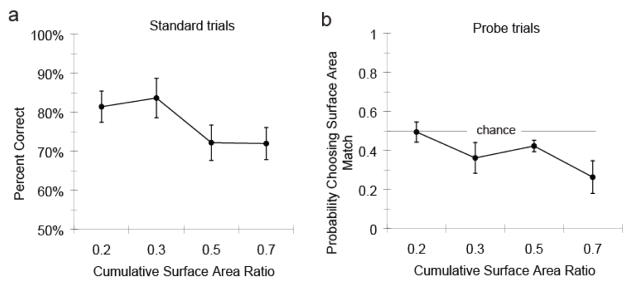
Finally, we analyzed children’s performance as a function of the cumulative surface area ratio between the choice stimuli (Figure 4). An ANOVA of Trial Type (Standard or Probe) × Cumulative Surface Area Ratio revealed a main effect of Trial Type (F(1,20) = 10.50, p < .01), no main effect of Cumulative Surface Area Ratio (F(3,60) = 1,68, p = .18), and an interaction between Trial Type and Cumulative Surface Area Ratio (F(3, 60) = 3.73, p < .05). Children were significantly biased to select the numerical match over the cumulative surface area match at the two most difficult cumulative surface area ratios (ratios 0.5 & 0.7; p’s < .05) and showed a non-significant trend toward a numerical bias at the third finest ratio (ratio 0.4; p = .09). When the difference in cumulative surface are values between the two options was relatively easy to detect (a .3 ratio in cumulative surface area), children performed at chance (ratio 0.3; p = .91). Thus, children never exhibited a significant bias to select the cumulative surface area match at any cumulative surface area ratio. Addionally, children showed a decreasing impact of cumulative surface area on their performance as cumulative surface area discrimination increased in difficulty on Probe trials (Figure 4b). These data are consistent with studies of adults and young children showing bidirectional interference among quantitative dimensions such as number and cumulative surface area in the sense that children represented the numerical values of the stimuli but, the suppressed dimension (cumulative surface area) interfered (Hurewitz & Gelman, 2006; Rousselle & Noel, 2008).
Figure 4.
Children’s accuracy on Standard trials in Experiment 2 as a function of the cumulative surface area ratio (a) and the probability with which children selected the cumulative surface area match during Probe trials (b).
General Discussion
The results of these two experiments suggest that by 3–4 years of age children are biased to attend to the numerosity of an array rather than its cumulative surface area and they spontaneously recruit an analog magnitude system to represent the numerosity of small and large numbers of objects alike. We discuss the implications of each of these two findings in turn.
In both experiments, children as young as three years of age spontaneously represented the numerical value of sets of objects, even though attending to number was not necessary to successfully perform this task. Children could have made successful matches and received positive feedback by relying on the cumulative surface area of the elements alone. The fact that children did not spontaneously base their matching decisions on cumulative surface area is striking given claims that the representation of cumulative surface area is more primary and develops earlier than the representation of number (e.g., Clearfield & Mix, 1999; Newcombe, 2002; Mix, Huttenlocher, & Levine, 2002; Mix, Levine, & Huttenlocher, 1997; Rousselle, Palmers, & Noel, 2004). Yet, this is not to say that children did not represent cumulative surface area in our study.
Children exhibited clear interference effects from the cumulative surface area dimension in their numerical judgments. These interference effects are analogous to those reported for adults and older children and support the conclusion that representations of multiple quantitative dimensions occur automatically (e.g., Hurewitz, Gelman, & Schnitzer, 2006; Rousselle & Noel, 2008). Our study extends these findings by demonstrating that the automaticity of cumulative surface area and numerical representation develops by at least 3 years of age. Moreover, at this young age, children’s explicit responses can be spontaneously dominated by the numerical dimension. The data also demonstrate that young children base their decisions on cumulative surface area when number is too difficult to discriminate. A similar result was obtained by Gelman (1972) who found that children spontaneously attend to number over length and density in a conservation-like task.
The second main finding was that children’s judgments of small sets were modulated by numerical ratio to the same degree as large sets. The numerical ratio effect is a hallmark of analog magnitude representations, not of object-file representations (see Gelman and Gallistel, 2000; Feigenson, Dehaene, & Spelke, 2004 for reviews). Therefore, our results suggest that by three years of age, children represent the numerical quantity of small sets via an analog magnitude mechanism. Previous studies with younger children have reported that children make numerical judgments of small sets by invoking an object-file mechanism (e.g., Feigenson, Carey, & Hauser, 2000; Feigenson et al., 2002; Feigenson & Carey, 2005; Lipton & Spelke, 2004; Wood & Spelke, 2005; Xu, 2003). Although infants and children may simultaneously possess both an object-file and an analog magnitude system for judging quantity, our study suggests that unlike infants, 3-year-old children spontaneously represent both small and large values as analog magnitudes. Three-year-old children therefore show continuity in their representations of numerical values much like adults and nonhuman animals.
Taken together, our findings from young children raise the issue of why a cognitive change might occur between infancy and early childhood in the cognitive mechanisms underlying numerical judgments. One possibility is that as children learn language, particularly numerical language, they are more likely to attend to number as a relevant dimension of a stimulus (e.g., Brannon & Van de Walle, 2001; Cantlon, Fink, Safford, & Brannon, 2007; Mix, 1999). Number differs from other quantitative dimensions in that there are specific linguistic terms that refer to each interval along a numerical continuum; there is no linguistic parallel of the numerical counting sequence for cumulative surface area. Experience using the verbal counting system may make number a more salient dimension for children and result in the more widespread recruitment of the inherently quantitative analog system that applies to all the values in their counting range. In fact, children within the age range tested in the current study are typically familiar with the verbal counting sequence and some of the counting principles that emerge from it (e.g., Gelman & Gallistel, 1978; Le Corre & Carey, 2007; Wynn, 1992). Counting experience may render nonverbal numerical representations more robust.
A second possibility is that there is no cognitive change between infancy and early childhood – recent work by our lab has suggested that number is in fact much more salient and discriminable to the young infant than previously thought (Brannon, Abbot, & Lutz, 2004; Cordes & Brannon, 2008, in press A, in press B) and that young infants are capable of comparing small and large numerical values under some conditions, presumably by relying on analog magnitude representations (Cordes and Brannon, in press B). Thus, it may be the case that children are biased to attend to the numerical properties of a set throughout development and to represent the entire range of numerical values as analog magnitudes. Children’s use of a single representational system for both small and large quantities is consistent with studies demonstrating that, when making quantity judgments, adults spontaneously invoke a coherent analog magnitude continuum rather than representing small values via an object-file system (e.g., Cordes, Gelman, Gallistel, & Whalen, 2001). These data are also consistent with evidence that non-human primates rely on analog magnitude representations for small and large numbers alike (e.g., Brannon & Terrace, 1998; Cantlon & Brannon, 2006, 2007).
We recently conducted a study parallel to the current study with non-human primates (who obviously lack language) and found that they also spontaneously recruited the analog system for small and large numbers and attended to number over cumulative surface area (Cantlon & Brannon, 2007). Like children, monkeys showed an overall bias to attend to number over cumulative surface area and a numerical ratio effect in both the small and large number ranges. Moreover, we showed that a monkey who had never been trained to represent numerical values was strongly biased to match stimuli based on number over cumulative surface area despite her complete lack of experience with numerical judgments. Thus our previous data from non-human primates parallel our current data from human children and demonstrate that linguistic experience is not required for spontaneous analog numerical representation in the small number range. The observation of these parallel behavioral signatures during quantity judgments by young children and non-human primates reinforces our overarching conclusion that number is cognitively primitive and is psychologically represented by a single, coherent numerical continuum.
Acknowledgments
We thank Maggie Vogel and Emily Hopkins for help preparing this manuscript. We are also grateful to Kerry Jordan, Melissa Libertus, and Sara Cordes for comments on this manuscript. This research was supported by an NSF CAREER award and McDonnell Scholar Award to EMB and an NRSA postdoctoral fellowship to JFC.
Footnotes
Analyses are based exclusively on response percentage since there is no correct or incorrect choice on Probe trials, rendering response time difficult to interpret.
References
- Balakrishnan JD, Ashby FG. Subitizing: Magical Numbers or Mere Superstition? Psychol Res. 1992;54(2):80–90. doi: 10.1007/BF00937136. [DOI] [PubMed] [Google Scholar]
- Barth H, La Mont K, Lipton J, Spelke ES. Abstract Number and Arithmetic in Preschool Children. Proceedings of the National Academy of Sciences of the United States of America. 2005;102(39):14116–14121. doi: 10.1073/pnas.0505512102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brannon EM. The Independence of Language and Mathematical Reasoning. Proceedings of the National Academy of Sciences of the United States of America. 2005;102(9):3177–3178. doi: 10.1073/pnas.0500328102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brannon EM, Abbott S, Lutz D. Number Bias for the Discrimination of Large Visual Sets in Infancy. Cognition. 2004;93:B59–B68. doi: 10.1016/j.cognition.2004.01.004. [DOI] [PubMed] [Google Scholar]
- Brannon EM, Terrace HS. Ordering of the numerosities 1–9 by monkeys. Science. 1998;282:746–749. doi: 10.1126/science.282.5389.746. [DOI] [PubMed] [Google Scholar]
- Brannon EM, Van De Walle GA. The Development of Ordinal Numerical Competence in Young Children. Cognitive Psychology. 2001;43(1):53–81. doi: 10.1006/cogp.2001.0756. [DOI] [PubMed] [Google Scholar]
- Cantlon JF, Brannon EM. The effect of heterogeneity on numerical ordering in rhesus monkeys. Infancy. 2006;9 (2):173–189. [Google Scholar]
- Cantlon JF, Brannon EM. How much does number matter to a monkey? Journal of Experimental Psychology: Animal Behavior Processes. 2007;33(1):32–41. doi: 10.1037/0097-7403.33.1.32. [DOI] [PubMed] [Google Scholar]
- Cantlon JF, Fink R, Safford K, Brannon EM. Heterogeneity impairs numerical matching but not numerical ordering in preschool children. Developmental Science. 2007;10(4):431–440. doi: 10.1111/j.1467-7687.2007.00597.x. [DOI] [PubMed] [Google Scholar]
- Clearfield M, Mix K. Number Versus Contour Length in Infants’ Discrimination of Small Visual Sets. Psychological Science. 1999;10(5):408–411. [Google Scholar]
- Cordes S, Brannon EM. The difficulties of representing continuous extent in infancy: representing number is just easier. 2008 doi: 10.1111/j.1467-8624.2007.01137.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordes S, Brannon EM. The relative salience of discrete and continuous quantities in infants. Developmental Science. doi: 10.1111/j.1467-7687.2008.00781.x. (in press A) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordes S, Brannon EM. Quantitative competencies in infancy. Developmental Science. 11(6) doi: 10.1111/j.1467-7687.2008.00770.x. (in press B) [DOI] [PubMed] [Google Scholar]
- Cordes S, Brannon EM. Discrimination of small from large numbers in 7-month old infants (under revision) [Google Scholar]
- Cordes S, Gelman R, Gallistel C, Whalen J. Variability Signatures Distinguish Verbal from Nonverbal Counting for Both Large and Small Numbers. Psychonomic Bulletin & Review. 2001;8(4):698–707. doi: 10.3758/bf03196206. [DOI] [PubMed] [Google Scholar]
- Dehaene S. Varieties of numerical abilities. Cognition. 1992;44(1):1–42. doi: 10.1016/0010-0277(92)90049-n. [DOI] [PubMed] [Google Scholar]
- Feigenson L. A double dissociation in infants’ representation of object arrays. Cognition. 2005;95:B37–B48. doi: 10.1016/j.cognition.2004.07.006. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Carey S, Spelke E. Infants’ Discrimination of Number vs. Continuous Extent. Cognitive Psychology. 2002;44(1):33–66. doi: 10.1006/cogp.2001.0760. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Carey S, Hauser M. The Representations Underlying Infants’ Choice of More: Object Files Versus Analog Magnitudes. Psychological Science. 2002;13(2):150–156. doi: 10.1111/1467-9280.00427. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Carey S. Tracking individuals via object-files: Evidence from infants’ manual search. Developmental Science. 2003;6:568–584. [Google Scholar]
- Feigenson L, Carey S. On the limits of infants’ quantification of small object arrays. Cognition. 2005;97:295–313. doi: 10.1016/j.cognition.2004.09.010. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Dehaene S, Spelke E. Core Systems of Number. Trends in Cognitive Sciences. 2004;8(7):307–314. doi: 10.1016/j.tics.2004.05.002. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, Gelman R. Preverbal and Verbal Counting and Computation. Cognition. 1992;44(1–2):43–74. doi: 10.1016/0010-0277(92)90050-r. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, Gelman R. Non-Verbal Numerical Cognition: From Reals to Integers. Trends in Cognitive Sciences. 2000;4(2):59–65. doi: 10.1016/s1364-6613(99)01424-2. [DOI] [PubMed] [Google Scholar]
- Geary DC, Brown SC. Cognitive addition: Strategy choice and speed-of-processing differences in gifted, normal, and mathematically disabled children. Developmental Psychology. 1991;27(3):398–406. [Google Scholar]
- Gelman R. Logical capacity of very young children: Number invariance rules. Child Development. 1972;43:75–90. [Google Scholar]
- Gelman R, Meck E. Preschoolers Counting - Principles before Skill. Cognition. 1983;13(3):343–359. doi: 10.1016/0010-0277(83)90014-8. [DOI] [PubMed] [Google Scholar]
- Gelman R, Butterworth B. Number and Language: How Are They Related? Trends in Cognitive Sciences. 2005;9(1):6–10. doi: 10.1016/j.tics.2004.11.004. [DOI] [PubMed] [Google Scholar]
- Gershkoff-Stowe L, Connell B, Smith L. Priming overgeneralizations in two- and four-year-old children. Journal of Child Language. 2006;33:461–486. doi: 10.1017/s0305000906007562. [DOI] [PubMed] [Google Scholar]
- Huntley-Fenner G, Cannon E. Preschoolers’ Magnitude Comparisons Are Mediated by a Preverbal Analog Mechanism. Psychological Science. 2000;11(2):147–152. doi: 10.1111/1467-9280.00230. [DOI] [PubMed] [Google Scholar]
- Huntley-Fenner G. Children’s Understanding of Number Is Similar to Adults’ and Rats’: Numerical Estimation by 5–7-Year-Olds. Cognition. 2001;78(3):B27–B40. doi: 10.1016/s0010-0277(00)00122-0. [DOI] [PubMed] [Google Scholar]
- Hurewitz F, Gelman R, Schnitzer B. Sometimes area counts more than number. Proceedings of the National Academy of Sciences of the United States of America. 2006;103(51):19599–19604. doi: 10.1073/pnas.0609485103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan KE, Brannon EM. The multisensory representation of number in infancy. Proceedings of the National Academy of Sciences. 2006;103:3486–3489. doi: 10.1073/pnas.0508107103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klahr D. A Production System for Counting, Subitizing and Adding. In: Chase WG, editor. Visual Information Processing. New York: Academic Press; 1973. [Google Scholar]
- Kobayashi T, Hiraki K, Hasegawa T. Auditory-visual intermodal matching of small numerosities in 6-month-old infants. Developmental Science. 2005;8(5):409–419. doi: 10.1111/j.1467-7687.2005.00429.x. [DOI] [PubMed] [Google Scholar]
- Landauer TK. Rate of implicit speech. Perceptual and Motor Skills. 1962;15:646. doi: 10.2466/pms.1962.15.3.646. [DOI] [PubMed] [Google Scholar]
- Le Corre M, Carey S. One, two, thee, four, nothing more: An investigation of the conceptual sources of the verbal counting principles. Cognition. 2007;105(2):395–438. doi: 10.1016/j.cognition.2006.10.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leslie A, Xu F, Tremoulet P, Scholl B. Indexing and the Object Concept: Developing ‘What’ and ‘Where’ Systems. Trends in Cognitive Science. 1998;2(1):10–18. doi: 10.1016/s1364-6613(97)01113-3. [DOI] [PubMed] [Google Scholar]
- Lipton J, Spelke E. Origins of Number Sense: Large-Number Discrimination in Human Infants. Psychological Science. 2003;14(5):396–401. doi: 10.1111/1467-9280.01453. [DOI] [PubMed] [Google Scholar]
- Lipton J, Spelke E. Discrimination of Large and Small Numerosities by Human Infants. Infancy. 2004;5(3):271–290. [Google Scholar]
- Mandler G, Shebo B. Subitizing: An Analysis of Its Component Processes. Journal of Experimental Psychology: General. 1982;111:1–22. doi: 10.1037//0096-3445.111.1.1. [DOI] [PubMed] [Google Scholar]
- Meck WH, Church RM. A Mode Control Model of Counting and Timing Processes. Journal of Experimental Psychology-Animal Behavior Processes. 1983;9(3):320–334. [PubMed] [Google Scholar]
- Mix K, Levine S, Huttenlocher J. Numerical Abstraction in Infants: Another Look. Developmental Psychology. 1997;33(3):423–428. doi: 10.1037//0012-1649.33.3.423. [DOI] [PubMed] [Google Scholar]
- Mix K. Similarity and Numerical Equivalence: Appearances Count. Cognitive Development. 1999;14(2):269–297. [Google Scholar]
- Mix K, Huttenlocher J, Levine S. Multiple Cues for Quantification in Infancy: Is Number One of Them? Psychological Bulletin. 2002;128(2):278–294. doi: 10.1037/0033-2909.128.2.278. [DOI] [PubMed] [Google Scholar]
- Moyer RS, Landaeur TK. Time Required for Judgements of Numerical Inequality. Nature. 1967;215:1519–1520. doi: 10.1038/2151519a0. [DOI] [PubMed] [Google Scholar]
- Newcombe N. The Nativist-Empiricist Controversy in the Context of Recent Research on Spatial and Quantitative Development. Psychological Science. 2002;13(5):395–401. doi: 10.1111/1467-9280.00471. [DOI] [PubMed] [Google Scholar]
- Ristic J, Friesen CK, Kingstone A. Are eyes special? It depends on how you look at it. Psychonomic Bulletin & Review. 2002;9(3):507–513. doi: 10.3758/bf03196306. [DOI] [PubMed] [Google Scholar]
- Rousselle L, Noel MP. The development of automatic numerosity processing in preschoolers: Evidence for numerosity-perceptual interference. Developmental Psychology. 2008;44 (2):544–560. doi: 10.1037/0012-1649.44.2.544. [DOI] [PubMed] [Google Scholar]
- Rousselle L, Palmers E, Noel MP. Magnitude comparison in preschoolers: What counts? Influence of perceptual variables. Journal of Experimental Child Psychology. 2004;87:57–84. doi: 10.1016/j.jecp.2003.10.005. [DOI] [PubMed] [Google Scholar]
- Suriyakham LW, Ehrlich SB, Levine SC. Infants’ sensitivity to quantity: Number, amount, or both? (submitted) [Google Scholar]
- Trick LM. The role of working memory in spatial enumeration: Patterns of selective interference in subitizing and counting. Psychonomic Bulletin & Review. 2005;12(4):675–681. doi: 10.3758/bf03196757. [DOI] [PubMed] [Google Scholar]
- Trick LM, Pylyshyn ZW. Why Are Small and Large Numbers Enumerated Differently - a Limited-Capacity Preattentive Stage in Vision. Psychological Review. 1994;101(1):80–102. doi: 10.1037/0033-295x.101.1.80. [DOI] [PubMed] [Google Scholar]
- Uller C, Carey S, Huntley-Fenner G, Klatt L. What Representations Might Underlie Infant Numerical Knowledge? Cognitive Development. 1999;14(1):1–36. [Google Scholar]
- Whalen J, Gallistel CR, Gelman R. Nonverbal Counting in Humans: The Psychophysics of Number Representation. Psychological Science. 1999;10(2):130–137. [Google Scholar]
- Wood JN, Spelke ES. Infants’ enumeration of actions: numerical discrimination and its signature limits. Developmental Science. 2005;8(2):173–181. doi: 10.1111/j.1467-7687.2005.00404.x. [DOI] [PubMed] [Google Scholar]
- Wynn K. Children’s acquisition of the number words and the counting system. Cognitive Psychology. 1992;24:220–251. [Google Scholar]
- Wynn K, Bloom P, Chiang W. Enumeration of Collective Entities by 5-Month-Old Infants. Cognition. 2002;83(3):B55–B62. doi: 10.1016/s0010-0277(02)00008-2. [DOI] [PubMed] [Google Scholar]
- Xu F, Spelke E. Large Number Discrimination in 6-Month-Old Infants. Cognition. 2000;74(1):B1–B11. doi: 10.1016/s0010-0277(99)00066-9. [DOI] [PubMed] [Google Scholar]
- Xu F. Numerosity Discrimination in Infants: Evidence for Two Systems of Representations. Cognition. 2003;89(1):B15–B25. doi: 10.1016/s0010-0277(03)00050-7. [DOI] [PubMed] [Google Scholar]
- Xu F, Spelke E, Goddard S. Number Sense in Human Infants. Developmental Science. 2005;8(1):88–101. doi: 10.1111/j.1467-7687.2005.00395.x. [DOI] [PubMed] [Google Scholar]