Cortical Layer-dependent Arterial Blood Volume Changes: Improved Spatial Specificity relative to BOLD fMRI

Abstract

The spatial specificity of functional hemodynamic responses was examined by simultaneous mapping of BOLD changes and quantitative changes in cerebral arterial blood volume (ΔCBV_a) across the cortical depth in cats (n = 7) during 40-s visual stimulation. Studies were performed at 9.4 T using the recently-developed, non-invasive magnetization transfer (MT)-varied gradient-echo (GE) fMRI technique to separate signals from MT-independent arterial blood and MT-dependent tissue. The highest conventional BOLD signal changes occurred at the cortical surface, where large pial veins exist, whereas the highest CBV_a changes occurred in the middle of the cortex, where T₁-weighted images show a hyperintense layer. In the middle cortical region, the average BOLD change (echo time = 20 ms) was 1.16 ± 0.45% during stimulation and −0.59 ± 0.31% during the post-stimulus period, while the average ΔCBV_a was 0.33 ± 0.02 ml/ 100g during stimulation and −0.08 ± 0.12 ml/ 100g post-stimulus (post-stimulus ΔCBV_a is not statistically significant). Time-dependencies of the ΔCBV_a cortical profiles show a slightly higher signal at the cortical surface during initial 10 sec, followed by highest responses in the middle of cortex during the remainder of the stimulus; this observation is similar to total CBV responses previously measured during visual stimulation in cats with a susceptibility contrast agent. Our findings demonstrate the value of non-invasive and quantitative ΔCBV_a measurement in high-resolution MT-varied GE fMRI studies, where spatial specificity is better localized to sites of neural activity as compared with conventional GE BOLD changes.

Introduction

Most functional MRI studies have been performed using conventional blood oxygenation level-dependent (BOLD) methodology (Ogawa et al., 1990) with a spatial resolution of several millimeters. One crucial question is whether the area of activity indicated by BOLD fMRI fully corresponds with the actual site of neural activation. To examine the specificity of fMRI signals, the cortical layer model can be used. The cerebral cortex consists of six cellular layers between the pial surface and the underlying white matter, with the layers running parallel to the pial surface. The middle cortical layer in sensory areas, layer IV, contains granular cells, and has a direct input from the thalamus by thalamo-cortical projections. Moreover, layer IV has the highest density of capillary mesh and synapses, and during sensory stimulation it has the highest metabolic rate and blood flow change (Woolsey et al., 1996).

The commonly used gradient-echo (GE) BOLD technique produces signals sensitive to deoxyhemoglobin changes, resulting in signal changes heavily weighted by baseline venous blood volumes. Therefore, the highest GE BOLD signal changes often appear in areas with large veins, which can be far away from neural activation sites. For example, the highest conventional GE BOLD signal changes in cats (Zhao et al., 2006; Zhao et al., 2004), monkeys (Goense and Logothetis, 2006) and humans (Ress et al., 2007; Truong and Song, 2009) occur at the surface of the visual cortex, not in the middle cortical layer. To reduce these large vessel contributions to fMRI, the spin-echo (SE) BOLD technique at high magnetic fields has been proposed; this approach suppresses the extravascular contribution of large vessels and minimizes the intravascular venous signals by setting the echo time > T₂ of blood (Duong et al., 2003; Kim and Ugurbil, 2003; Lee et al., 1999; Yacoub et al., 2003; Zhao et al., 2004). In the cortical layer model, the highest SE BOLD signals are found within the cortex, not at the surface of the cortex (Zhao et al., 2004), indicating that SE BOLD improves the spatial specificity to sites of neural activity. Since BOLD signals are related to a mismatch between cerebral blood flow (CBF) and oxygen consumption changes, its spatial response should be broader than that of CBF. In fact, the profiles of SE BOLD signals across the cortex show that the signal difference between different cortical layers is quite small (Zhao et al., 2006). Thus, it is important to use different fMRI methodologies, each relying on a single physiological parameter, to examine the intrinsic spatial specificity of hemodynamic responses and to interpret BOLD data.

Single physiological parameter-based fMRI includes arterial spin labeling (ASL) for measuring CBF, and the susceptibility contrast agent method for detecting total cerebral blood volume (CBV_t) change. The highest CBF and CBV_t responses occur in the middle of the cortex and their profiles across the cortex are sharper than those from SE BOLD (Jin and Kim, 2008a; Zhao et al., 2006), indicating that CBF and CBV responses possess greater specificity for neuronal active sites. However, CBF-based fMRI provides poor sensitivity and temporal resolution, and CBV_t-based fMRI requires contrast agent injection. Based on our total and arterial CBV studies in the rat somatosensory cortex, the increased change in CBV during neural activation originates mainly from arterial rather than venous blood volume changes (Kim et al., 2007). This finding suggests that cerebral arterial blood volume (CBV_a) changes may specifically occur in the middle cortical layer, the site of neural activation, in a manner similar to what occurs with total CBV changes; validation of this possibility requires further study.

In this study, we applied the magnetization transfer (MT)-varied fMRI technique (Kim et al., 2008) to simultaneously measure stimulus-induced CBV_a changes (units of ml/ 100g) and BOLD responses across the visual cortical layers in cats in an effort to evaluate the spatial specificity of functional CBV_a changes (ΔCBV_a). CBV_a represents blood volume within arterial vessels of all sizes, and includes a portion of capillaries before water exchange occurs. For ΔCBV_a measurements, the MT-varied GE fMRI method is technically simple and provides a higher temporal resolution as compared with both the MOdulation of TIssue and VEssel (MOTIVE) technique with MT-varied ASL (Kim and Kim, 2005) and the Look-Locker echo planar imaging (EPI) technique with ASL (Brookes et al., 2007). We selected the cat visual cortex model to compare data previously obtained in our laboratory by other fMRI techniques. The stimulus-induced R₂^* changes at varied MT level and ΔCBV_a were measured during stimulation and post-stimulation periods. We found that time-dependencies of CBV_a changes across the cortex are similar to our previous CBV_t findings, and that MT-varied GE fMRI technique is useful for obtaining quantitative CBV_a changes non-invasively with high resolution.

Materials and methods

Theoretical background for ΔCBV_a measurement

It is assumed that an imaging voxel consists of three compartments: intravascular arterial blood, extravascular tissue, and intravascular venous blood. MT effects in the extravascular tissue are dependent on the duration, power, and off-resonance frequency of long radiofrequency (RF) pulses. However, the arterial blood pool has minimal MT effect when the RF coil geometry is configured such that there is an inflow of fresh blood spins not affected by the MT-inducing pulse (as for certain coil geometries). Capillary water freely exchanges with tissue water, and this upstream exchange could generate the same MT effects in venous blood as in tissue. Therefore, we consider the extravascular tissue and intravascular venous blood pools together as one compartment. Thus, the signal in an imaging voxel would originate from two compartments: MT-dependent tissue and MT-independent arterial blood. Signal intensity in the presence of MT at steady state (S_ss,MT) can thus be expressed as

$$S_{\mathit{\text{SS}},\mathit{\text{MT}}}=(1-{\nu }_a)·S_{\mathit{\text{ss}},\mathit{\text{MT}}}^{\mathit{\text{tissue}}}+{\nu }_a·S_0^{\mathit{\text{artery}}}$$ [1]

where ν_a is the fraction of arterial blood spins (% units); $S_{\mathit{\text{ss}},\mathit{\text{MT}}}^{\mathit{\text{tissue}}}$ is the signal intensity of the tissue compartment with MT effect; and $S_0^{\mathit{\text{artery}}}$ is the signal intensity of the arterial blood compartment without the MT effect. For a gradient echo with a flip angle θ and a short repetition time (TR), $S_{\mathit{\text{ss}},\mathit{\text{MT}}}^{\mathit{\text{tissue}}}$ can be expressed as

$$S_{\mathit{\text{ss}},\mathit{\text{MT}}}^{\mathit{\text{tissue}}}=\frac{M_0·(M_{\mathit{\text{MT}}}/M_0)·(1-e^{-R_{1,\mathit{\text{tissue}}}·\mathit{\text{TR}}})}{1-(M_{\mathit{\text{MT}}}/M_0)·\text{cos}\theta ·e^{-R_{1,\mathit{\text{tissue}}}·\mathit{\text{TR}}}}·\text{sin}\theta ·e^{-R_{2,\mathit{\text{tissue}}}^{*}·\mathit{\text{TE}}},$$ [2]

and the arterial blood signal can be expressed as

$$S_0^{\mathit{\text{artery}}}=M_0·\text{sin}\theta ·e^{-R_{2,\mathit{\text{artery}}}^{*}·\mathit{\text{TE}}},$$ [3]

where M₀ and M_MT are the magnetization without and with MT effects at a fully-relaxed condition, respectively; R₁ is the longitudinal relaxation rate; and R₂^* is the effective transverse relaxation rate. The contribution of venous blood signals at high fields is minimal due to its short T₂^*. In order to assume fully relaxed magnetization in arterial blood (Eq. [3]), the TR should be long enough to allow fresh arterial blood to fill the arterial vasculature (e.g., TR of 1 s; see the MRI Acquisition section). It should be noted that the theory reported in our previous paper (Kim et al., 2008) assumed the fully-relaxed condition for the tissue pool (i.e., TR is long) using a spin-echo sequence (θ = 90° for the excitation pulse).

Since ν_a is very small (~1%), the signal intensity can be normalized to S₀ $S_0(\approx M_0·\text{sin}\theta ·e^{-R_{2,\mathit{\text{tissue}}}^{*}·\mathit{\text{TE}}})$, and the fully-relaxed signal in the absence of MT can be described as

$$S_{\mathit{\text{ss}},\mathit{\text{MT}}}/S_0\approx S_{\mathit{\text{ss}},\mathit{\text{MT}}}^{\mathit{\text{tissue}}}/S_0=\frac{(M_{\mathit{\text{MT}}}/M_0)·(1-e^{-R_{1,\mathit{\text{tissue}}}·\mathit{\text{TR}}})}{1-(M_{\mathit{\text{MT}}}/M_0)·\text{cos}\theta ·e^{-R_{1,\mathit{\text{tissue}}}·\mathit{\text{TR}}}},$$ [4]

During neural stimulation, we assume no changes in arterial blood oxygenation, venous blood volume and tissue MT level, and we expect i) a very small increase in tissue ${T_2}^{*}(=1/R_{2,\mathit{\text{tissue}}}^{*})$; ii) an increase in arterial blood volume; and iii) a corresponding decrease in tissue volume. Even though venous blood T₂^* will change during stimulation, intravascular venous blood signal will be minimal due to the short T₂^* at 9.4 T and is also closely dependent on MT effects. Thus, any remaining venous signal induced by blood T₂^* changes will not be considered as a separate term in our theoretical description. Signal intensity during neural stimulation follows as

$$S_{\mathit{\text{ss}},\mathit{\text{MT}}}^{\mathit{\text{stim}}}=(1-{\nu }_a-\mathrm{\Delta }{\nu }_a)·S_{\mathit{\text{ss}},\mathit{\text{MT}}}^{\mathit{\text{tissue}}}·e^{-\mathrm{\Delta }{R}_{2,\mathit{\text{tissue}}}^{*}·\mathit{\text{TE}}}+({\nu }_a+\mathrm{\Delta }{\nu }_a)·S_0^{\mathit{\text{artery}}}.$$ [5]

The stimulus-induced signal change in the presence of MT normalized to S₀ is

$$\begin{array}{cc}\mathrm{\Delta }{S}_{\mathit{\text{ss}},\mathit{\text{MT}}}/S_0\hfill & =[(1-{\nu }_a-\mathrm{\Delta }{\nu }_a)·e^{-\mathrm{\Delta }{R}_{2,\mathit{\text{tissue}}}^{*}·\mathit{\text{TE}}}-(1-{\nu }_a)]·(S_{\mathit{\text{ss}},\mathit{\text{MT}}}^{\mathit{\text{tissue}}}/S_0)+\mathrm{\Delta }{\nu }_a·e^{-(R_{2,\mathit{\text{artery}}}^{*}-R_{2,\mathit{\text{tissue}}}^{*})·\mathit{\text{TE}}}\hfill \\ \hfill & \approx -(\mathrm{\Delta }{\nu }_a+\mathrm{\Delta }{R}_{2,\mathit{\text{tissue}}}^{*}·\mathit{\text{TE}})·(S_{\mathit{\text{ss}},\mathit{\text{MT}}}/S_0)+\mathrm{\Delta }{\nu }_a·e^{-(R_{2,\mathit{\text{artery}}}^{*}-R_{2,\mathit{\text{tissue}}}^{*})·\mathit{\text{TE}}}\hfill \end{array}$$ [6]

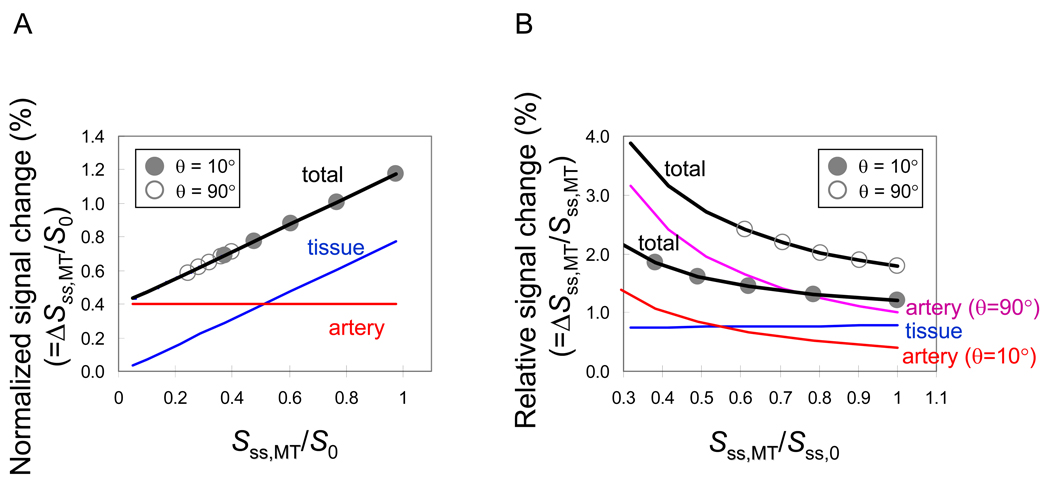
Contribution from the tissue (first term) and arterial blood (second term) to fMRI signal changes are shown schematically in Fig. 1A. A linear fit of ΔS_ss,MT / S₀ versus the normalized baseline signal S_ss,MT / S₀ yields an intercept of $\mathrm{\Delta }{\nu }_a·e^{-(R_{2,\mathit{\text{artery}}}^{*}-R_{2,\mathit{\text{tissue}}}^{*})·\mathit{\text{TE}}}$, and a slope of $-\mathrm{\Delta }{\nu }_a-\mathrm{\Delta }{R}_{2,\mathit{\text{tissue}}}^{*}·\mathit{\text{TE}}$. Since R₂ of blood and tissue are similar at 9.4 T (i.e., ~25 s⁻¹), we expect that $R_{2,\mathit{\text{tissue}}}^{*}$ is similar to $R_{2,\mathit{\text{artery}}}^{*}$. Therefore, the intercept obtained at 9.4 T is Δν_a, which can be easily converted to ΔCBV_a (units of ml blood/g tissue) by multiplying the tissue-to-blood partition coefficient of 0.9 ml/g.

Fig. 1.

Schematic diagrams of MT-varied GE fMRI signals. To visualize the effect of flip angle to functional BOLD fMRI, signal changes were simulated with Eq. [1] – Eq. [6] with two flip angles (θ) = 10° (closed symbols) and 90° (open symbols). See texts for other parameters. The total signal is the sum of the signal from the tissue and arterial blood components. (a) The normalized signal change of tissue has a linear dependence on MT level (blue line), while that from the artery is independent of MT (red line). When ΔS_ss,MT / S₀ is linearly fitted against the normalized baseline signal, S_ss,MT / S₀ (black line), an intercept yields Δν_a. The smaller flip angle, θ = 10° provides a greater dynamic range for linear fitting than data obtained with the larger flip angle, θ = 90°. (b) Percentage signal changes (S_ss,MT / S_ss,MT) (black lines with closed circle symbols for θ = 10° and open circle symbols for θ = 90°) are non-linearly increased with MT levels because percentage signals of MT-independent Δν_a (red line for θ= 10 and purple line for θ= 90°) increased with MT, while the percentage change of tissue signals (blue line) is independent of MT. The larger flip angle induces greater saturation of the steady-state tissue signals, increasing the relative Δν_a contribution to the fMRI signal; the contribution of arterial blood signals with θ = 90° (purple line) is higher than with θ = 10° (red line).

In fMRI studies, BOLD signal changes are usually expressed as the relative percentage signal change (ΔS_ss,MT / S_ss,MT), instead of as the normalized signal changes (ΔS_ss,MT / S₀) (see Eq. [6]). The relative percentage fMRI signal changes with MT effects can be written as

$$\mathrm{\Delta }{S}_{\mathit{\text{ss}},\mathit{\text{MT}}}/S_{\mathit{\text{ss}},\mathit{\text{MT}}}=(-\mathrm{\Delta }{\nu }_a-\mathrm{\Delta }{R}_{2,\mathit{\text{tissue}}}^{*}·\mathit{\text{TE}})+\mathrm{\Delta }{\nu }_a·(S_0/S_{\mathit{\text{ss}},\mathit{\text{MT}}})$$ [7]

The first term in Eq. 7 is the MT-dependent tissue contribution while the second term is the MT-independent arterial blood contribution. Relative change of tissue signal is constant with MT, while the arterial blood contribution increases with MT effects (see Fig. 1B). Therefore, taking into consideration the two MT levels, MT₁ and MT₂, CBV_a-weighted signal changes can also be estimated as,

$$\frac{\mathrm{\Delta }{S}_{\mathit{\text{ss}},{\mathit{\text{MT}}}_1}}{S_{\mathit{\text{ss}},{\mathit{\text{MT}}}_1}}-\frac{\mathrm{\Delta }{S}_{\mathit{\text{ss}},{\mathit{\text{MT}}}_2}}{S_{\mathit{\text{ss}},{\mathit{\text{MT}}}_2}}\approx \mathrm{\Delta }{\nu }_a·(S_0/S_{\mathit{\text{ss}},{\mathit{\text{MT}}}_1}-S_0/S_{\mathit{\text{ss}},{\mathit{\text{MT}}}_2})$$ [8]

Here S₀ can be acquired with a long TR, or obtained from the first image (which doesn’t affected by any saturation) acquired for fMRI studies with a short TR. When the TR is long or the flip angle is small, the signal at steady state without MT (S_ss,0) is close to S₀ (see Eq. [4]). It should be emphasized that the contribution of MT-independent cerebrospinal fluid (CSF) signal is ignored here. Thus, tissue pixels without CSF contamination should be analyzed for determining ΔCBV_a.

Simulation of MT-dependent fMRI responses

To evaluate effects of flip angle on ΔCBV_a measurements, arterial and tissue signal changes induced by stimulation were calculated with Eq. [1] – Eq. [6] using the following parameters: TR = 1 s; ν_a = 1 %; Δν_a = 0.4 %; R_1,tissue = 0.5 s⁻¹; $R_{2,\mathit{\text{tissue}}}^{*}=R_{2,\mathit{\text{artery}}}^{*}=50{\mathrm{s}}^{-1};\mathrm{\Delta }{R}_{2,\mathit{\text{tissue}}}^{*}=-0.6{\mathrm{s}}^{-1}$; TE = 20 ms; M_MT/M₀ = 1, 0.9, 0.8, 0.7 and 0.6; and flip angle (θ) = 10° and 90°.

Animal preparation and stimulation

With the approval from the University of Pittsburgh Institutional Animal Care and Use Committee, we performed seven studies using five adolescent cats weighing 1.1–2.0 kg; two of these cats were studied twice, with at least a week between studies. Details of animal preparation were described previously (Zhao et al, 2006). In short, cats were initially anesthetized with an intramuscular injection of a ketamine (15 mg/kg) and xylazine (2 mg/kg) cocktail. The cats were orally intubated and mechanically ventilated. A catheter was placed at either the cephalic vein or the femoral vein to allow infusion of supplemental fluids (1.25 ml/kg/hr of 2.5% – 5% glucose in saline) with pancuronium bromide (0.15 – 0.2 mg/kg/hr). Ophthalmic solution was dropped into the eyes, and the appropriate contact lenses were inserted. The head was fixed with a homemade head frame with bite and ear bars. The animals were then anesthetized with 1.0 – 1.1% isoflurane in air supplemented with O₂ to attain a total O₂ level of ~30% throughout the experiments. End-tidal CO₂ was maintained in the range of 3.5–3.8% by adjusting ventilation volume and rate. Rectal temperature was maintained at 38.5 ± 0.5 °C with a feedback hot water circulator.

For 40-s long visual stimulation, binocular, full-field, black and white square-wave moving gratings (spatial frequency of 0.15 cycles/degree and temporal frequency of 2 cycles/s) were presented onto a screen using a video projector (NEC, model MT1055; resolution 1040×890). Luminance of white color was adjusted to 29 cd/m². A stationary grating pattern was presented during the control period.

MRI Acquisition

Images were acquired at 9.4T (magnet bore size = 31-cm diameter), with a Unity INOVA console (Varian, Palo Alto, CA, USA); a 12-cm inner diameter actively-shielded gradient coil with a maximal strength of 400 mT/m and a rise time of 130 µs; and a 1.5-cm diameter surface coil. Magnetic field homogeneity was manually optimized using a slab twice the imaging slice thickness. Preliminary multi-slice GE BOLD fMRI was performed in the visual cortical area. Then, one 2-mm thick coronal slice was selected for MT-varied GE fMRI studies. High-resolution T₁-weighted anatomical images (matrix size of 128 × 128) were obtained at the same slice to identify brain structures by the two-segmented turbo-FLASH technique with an inversion time of 1.4 s.

fMRI data was acquired with a single-shot GE EPI technique with slice thickness = 2 mm; matrix size = 64 × 64; field of view = 2.0 × 2.0 cm²; flip angle = 20 – 30° ; TR = 1 s, which consisted of an 880-ms off-resonance MT pulse duration, 20 ms delay, and 100-ms slice excitation and data acquisition; and TE = 20 ms. The 880-ms long MT RF pulses were applied at +5000 Hz offset relative to water to guarantee irradiation of macromolecular protons, without direct saturation of water protons (Zhou J et al., 2005). Although the MT-induced signal may not reach steady state during a single ~0.9-s MT period, the relatively short 0.1-s acquisition time allowed virtually continuous MT during the fMRI studies, ensuring steady-state MT conditions. The power level of the MT-inducing RF pulse was adjusted to achieve intensities in the visual cortical area (S_ss,MT) of 1, ~0.7 and ~0.4 of the steady-state signal without MT (S_ss,0), corresponding to B₁ field strengths of 0, ~0.03 and ~0.05 gauss, respectively. MT ratios in the steady-state condition (MTR_ss) calculated as (1− S_ss,MT/S_ss,0) were 0, ~0.3 and ~0.6. Note that this differs from the conventional MT ratio in the fully-relaxed condition (MTR) of (1− S_MT/S₀).

For fMRI studies, each run consisted of 50 pre-stimulation, 40 stimulation and 100 post-stimulation images for each MT level. This procedure was repeated ~ 20 times for data average. For normalization purposes, fully-relaxed images (S₀) were also acquired with the same aforementioned parameters, except TR = 6 s.

General data analysis

We performed data analysis using STIMULATE, a graphical user interface-based fMRI analysis software package (Strupp, 1996) and in-house Matlab® routines (Mathworks, Natick, MA). For each study, all runs from identical conditions were averaged. The first 10 s of pre-stimulation data were excluded to ensure that the steady-state condition was met. The baseline images included data acquired 40 s before simulation, while the stimulation images included data acquired between 7 s and 40 s after stimulation onset. Individual results were averaged and group data are reported as mean ± SD. Statistical significance was determined by repeated measure ANOVA tests and student’s t-tests.

Generating fMRI maps

fMRI maps in each MT level were generated from the baseline and the stimulation images with 2D Gaussian smoothing (kernel size = 3×3, sigma = 0.5). For pixels with P-values < 0.05, percentage signal changes (ΔS_ss,MT/S_ss,MT) were calculated as the stimulus-induced signal changes divided by the baseline signals. For calculating ΔCBV_a maps, only active pixels in all MT levels were selected. To avoid CSF-containing regions, pixels with an MTR_ss (calculated by highest MT vs. no MT) less than 2 standard deviations from the mean MTR_ss calculated for the middle cortical regions of interest (ROI) (mostly tissue pixels; see below) were excluded from the ΔCBV_a calculations. The normalized stimulus-induced signal changes (ΔS_ss,MT/S₀) were linearly fitted against corresponding normalized baseline signals (S_ss,MT /S₀) (see Eq. [6]). Standard errors of intercepts were calculated by the linear regression analysis (Devore, 1990). Pixels with an intercept divided by standard error of ≥ 0.7 were selected to convert intercepts to absolute CBV_a changes (units of ml blood/g tissue) by multiplying 0.9 ml/g.

Quantitative ROI analysis

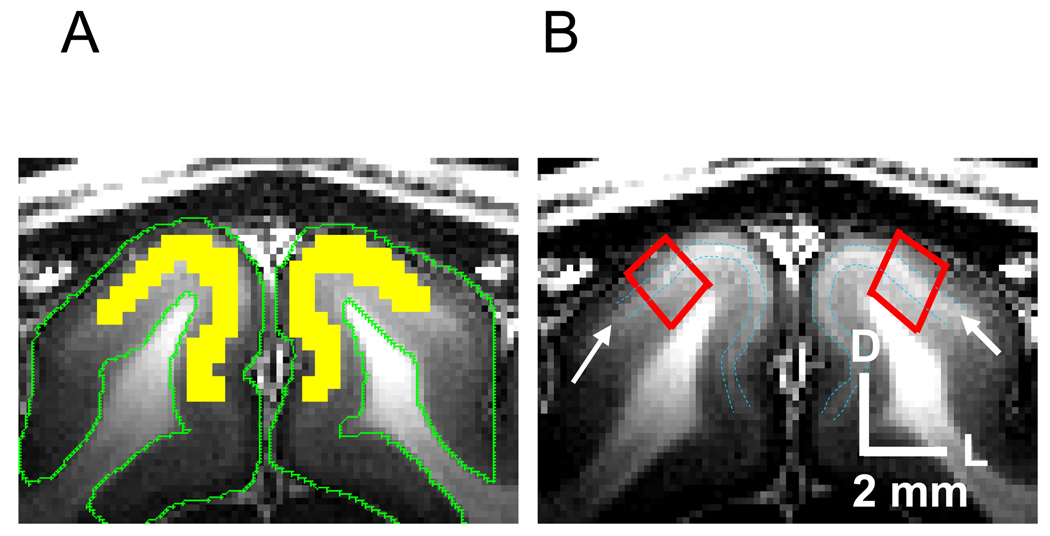
Quantitative analysis was performed on each ROI without any spatial smoothing, regardless of statistical criteria for activation. ROIs were chosen in the visual cortical area, based on high-resolution T₁-weighted anatomical images. For ΔR₂^* and time course analysis, the middle cortical ROI (yellow area in Fig. 2A) was determined along the white band within cortical area in T₁-weighted images (see blue dashed contours pointed by arrow marks in Fig. 2B), which is likely to be the stripe of myelin-rich Gennari, similar to observations in the human visual cortex (Barbier et al., 2002). These blue dashed line contours of the stripe were overlaid on ΔCBV_a maps for the approximation of layer IV. All pixel signals within the ROI were averaged at each time point and each study, and fMRI time courses were then obtained in each MTR_ss. Averaged ΔR₂^* values for the stimulation condition were calculated as ln$(S_{\mathit{\text{ss}},\mathit{\text{MT}}}^{\mathit{\text{stim}}}/S_{\mathit{\text{ss,MT}}})/\text{TE})$ in each MTR_ss. Also, ΔCBV_a time course of each study was calculated from time courses with three MT levels (see Eq. [6]).

Fig. 2.

Selection of regions of interest. (a) The middle cortical ROI is delineated by yellow, which was determined along the white band within the cortical area in T₁-weighted images, likely the stripe of myelin-rich Gennari. These bands were manually traced for comparison with arterial blood volume change maps (blue dashed lines pointed by arrow marks in Fig. 2B). Green contours: gray matter. (b) Two quadrangular ROIs within visual area 18 were defined for the cortical depth analysis from the surface of cortex to the white matter. D: dorsal, L: lateral

Cortical depth profile analysis was performed in area 18 within the visual cortex, as described previously (Zhao et al., 2006). To generate a signal profile in the cortical depth dimension, two quadrangular ROIs were selected from the surface of the cortex to the gray/white matter boundary based on T₁-weighted anatomical images in each animal (Fig. 2B). Data were then spatially interpolated with the linear nearest-neighbor resampling method to 11 pixels, resulting in an average depth resolution of 163 µm. Since the clear contrast, likely layer IV, within the cortex due to myelin-rich contribution was detected in the same slice thickness of T₁-weighted anatomical image (Fig. 2B), depth variations of cortical layers within the 2-mm thick slice appeared to be relatively small. The signals at the same relative cortical depth were averaged along the surface dimension. Three cortical profiles of fMRI were generated for each MT level from the ROIs, and plotted as the distance from the cortical surface. Profiles of ΔCBV_a were calculated from the intercept of linear fit to fMRI profiles of all three MT levels at each cortical depth point. Cortical layer locations were approximately assigned based on relative distances of those layers in area 18 (Payne and Peters, 2002) and the profile of T₁-weighted image. To examine time-dependencies of the cortical profile, the cortical depth profiles were calculated as every 10-s time period from stimulation onset

Results

Simulation of MT-dependent fMRI Responses

Figure 1 shows the plots of functional signal changes normalized to S₀ and percentage signal changes normalized to baseline (S_ss,MT) at each MT level. MR signal intensity (S_ss,MT) at steady state closely depends on the flip angle, TR, and MT level (see Eq. [4]). Increasing the flip angle with a relatively short TR (e.g., 1 s), leads to a decrease in the steady-state signal intensity; thus, with a larger flip angle, the absolute signal change induced by tissue ΔR₂^* diminishes (Fig. 1A). Normalized signal changes (ΔS_ss,MT/S₀) using a smaller flip angle have a greater dynamic range over a given range of MT power levels (θ = 10° vs. = 90° in Fig. 1A), resulting in an improved linear fit. At the same time though, signals using a smaller flip angle (below the Ernst angle) also have a lower SNR due to smaller transverse magnetization (sinθ terms in Eq. [2] and Eq. [3]). Thus, optimization of both SNR and dynamic range requires adjustment of the flip angle. Larger flip angle excitation pulses reduce more tissue signal intensity with MT, but percentage signal changes (signal changes divided by baseline signal intensities (ΔS_ss,MT/S_ss,MT)) of tissue remain constant. Percentage changes of arterial blood signals increase with the reduction of tissue signals because the fixed arterial blood signals are divided by the reduced total signal intensity. Thus, when TR is short relative to T₁, the relative contribution of ΔCBV_a to fMRI percentage signal changes increases with the excitation flip angle (θ = 10° vs. θ = 90° at TR = 1.0 s in Fig. 1B).

MT-dependent fMRI: BOLD and ΔCBV_a Maps

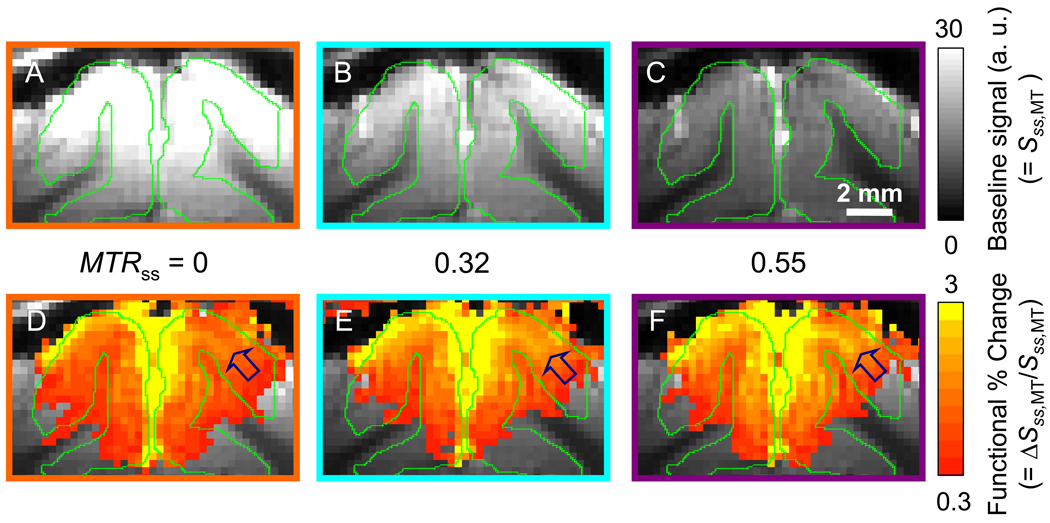
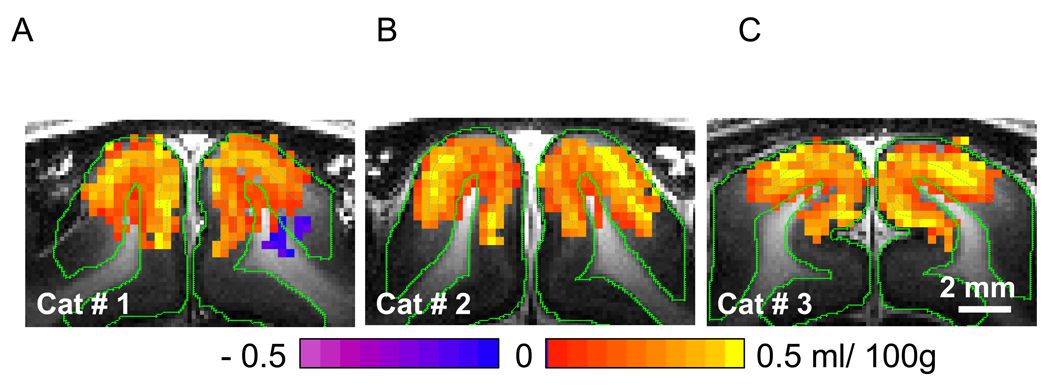
As expected, increases in MT levels corresponded with decreases in, baseline EPI signals (S_ss,MT) (Fig. 3A–C: left to right). Cortical surface regions and sulci, such as those found between the two hemispheres, appeared bright in high MT images (Fig. 3C) due to the small MT effect in CSF. Stimulus-induced fMRI signal changes were observed in the visual area; interestingly, percentage signal changes (ΔS_ss,MT/S_ss,MT) increased with MTR_ss, as shown in color maps (Fig. 3D–F: left to right). In conventional GE-BOLD fMRI (i.e. without MT, MTR_ss = 0), the highest percentage signal changes occurred at the surface of the cortex, where large draining veins are located (Fig. 3D). As the MT level increased, percentage signal changes of the intra-cortical regions increased (see arrow marks in Fig. 3D–F), while cortical surface signals remained unaltered. By pixel-wise fitting ΔS_ss,MT/S₀ vs. S_ss,MT/S₀, ΔCBV_a maps were obtained (Fig. 4). The highest CBV_a changes (yellow pixels) were detected in the middle of the cortex, which is similar to total CBV responses measured with a susceptibility contrast agent (Zhao et al., 2006), and matched well with blue dashed contours from white bands in T₁-weighted images, which are likely to be layer IV (Fig. 4).

Fig. 3.

MT-varied baseline images (a–c) and GE fMRI maps (d–f). (a–c) Baseline signals (S_ss,MT) decreased with an increase of MT level, as expected. (d–f) Percentage signal changes (ΔS_ss,MT/S_ss,MT) corresponding to visual stimulation increased with MTR_ss. The highest percentage signal changes occurred at the surface, but did not increased with MT. Percentage signal changes at the middle of the cortex, indicated by arrows, increased with MT.

Fig. 4.

ΔCBV_a maps of three animals. Data from the animal shown in Fig. 3 is shown in panel A (Cat #1). Red/yellow pixels represent increases in ΔCBV_a, and blue/purple pixels indicate negative changes. The peaks of ΔCBV_a responses matched well with the white bands within the cortex in T₁-weighted images (blue dashed contours), likely to be layer IV. The negative response was not detected in most studies.

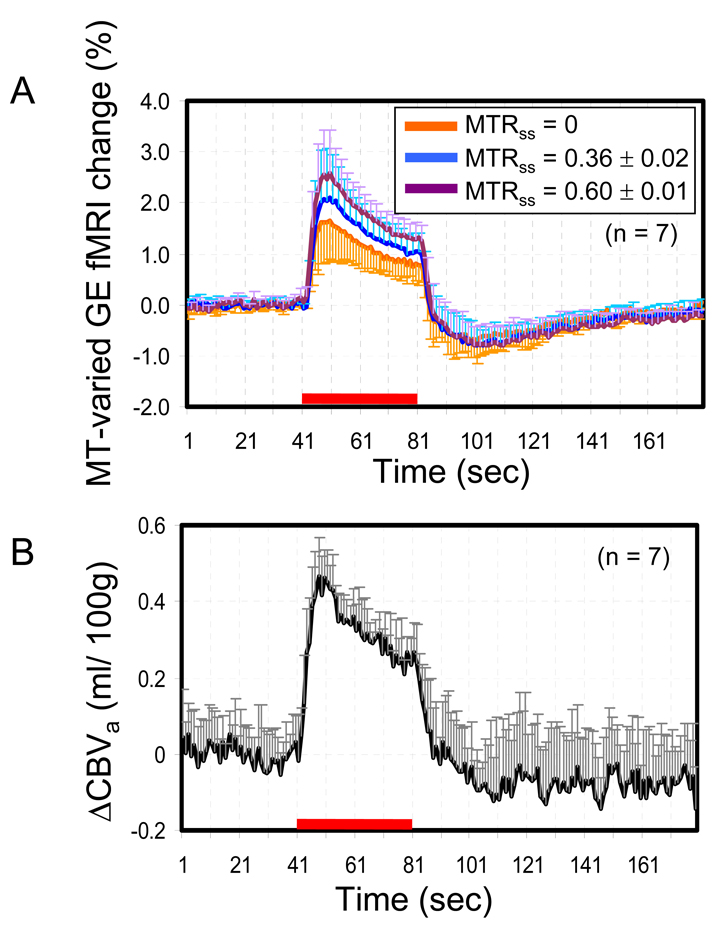
BOLD and ΔCBV_a Time Courses

Figure 5A shows the fMRI percentage time courses obtained from the middle cortical ROI (yellow ROI in Fig. 2A). Following the stimulus onset, fMRI signals increased, and then slowly decreased during the stimulation period. After the stimulus offset, undershoots were consistently observed. Positive changes during stimulation increased with MTR_ss, as also seen in the fMRI maps (Fig. 3D–F), while post-stimulus undershoots were similar among data acquired in three MT levels. Average ΔR₂^* values (n = 7) were −0.58 ± 0.22, −0.74 ± 0.25 and −0.91 ± 0.20 s⁻¹ during stimulation, and 0.30 ± 0.15, 0.34 ± 0.15 and 0.35 ± 0.17 s⁻¹ during the 11 – 40 s period after stimulus offset at MTR_ss = 0, 0.36 ± 0.02 and 0.60 ± 0.01, respectively. ΔR₂^* values obtained at different MT levels were statistically different during stimulation (repeated measure ANOVA test; F(2,12) = 152.24, post-hoc test; all p < 0.001), but not significantly different during the post-stimulation period (repeated measure ANOVA test; F(2,12) = 1,214, post-hoc test; all p > 0.05).

Fig. 5.

MT-varied GE fMRI (a) and ΔCBV_a time courses (b) obtained from the middle cortical ROI. The red bar indicates the stimulation period. Error bars: SD. Error bars of MTR_ss = 0.36 and 0.6 are show every 2 s for better visualization.

Time courses for ΔCBV_a were successfully calculated from three fMRI responses with different MT levels (Fig. 5B). The average stimulus-induced ΔCBV_a was 0.33 ± 0.02 ml/ 100g (n = 7). During post-stimulus periods, slightly decreased ΔCBV_a was observed with large variations (−0.08 ± 0.12 ml/100g, n = 7), but the average post-stimulus undershoot did not return to the pre-stimulus baseline level when BOLD signals returned to baseline. To determine the detectability of ΔCBV_a, a contrast-to-noise ratio (CNR) from the middle cortical ROI was calculated. CNR was calculated by dividing the stimulus-induced change by the temporal standard deviation of pre-stimulus baseline signals. The CNR was 3.97 ± 0.81 (n = 7) for ΔCBV_a, and 11.81 ± 5.94, 13.65 ± 5.60 and 13.58 ± 2.78 (n = 7) at MTR_ss = 0, 0.36 ± 0.02 and 0.60 ±0.01, respectively. This indicates that fMRI with MT slightly increases the detectability.

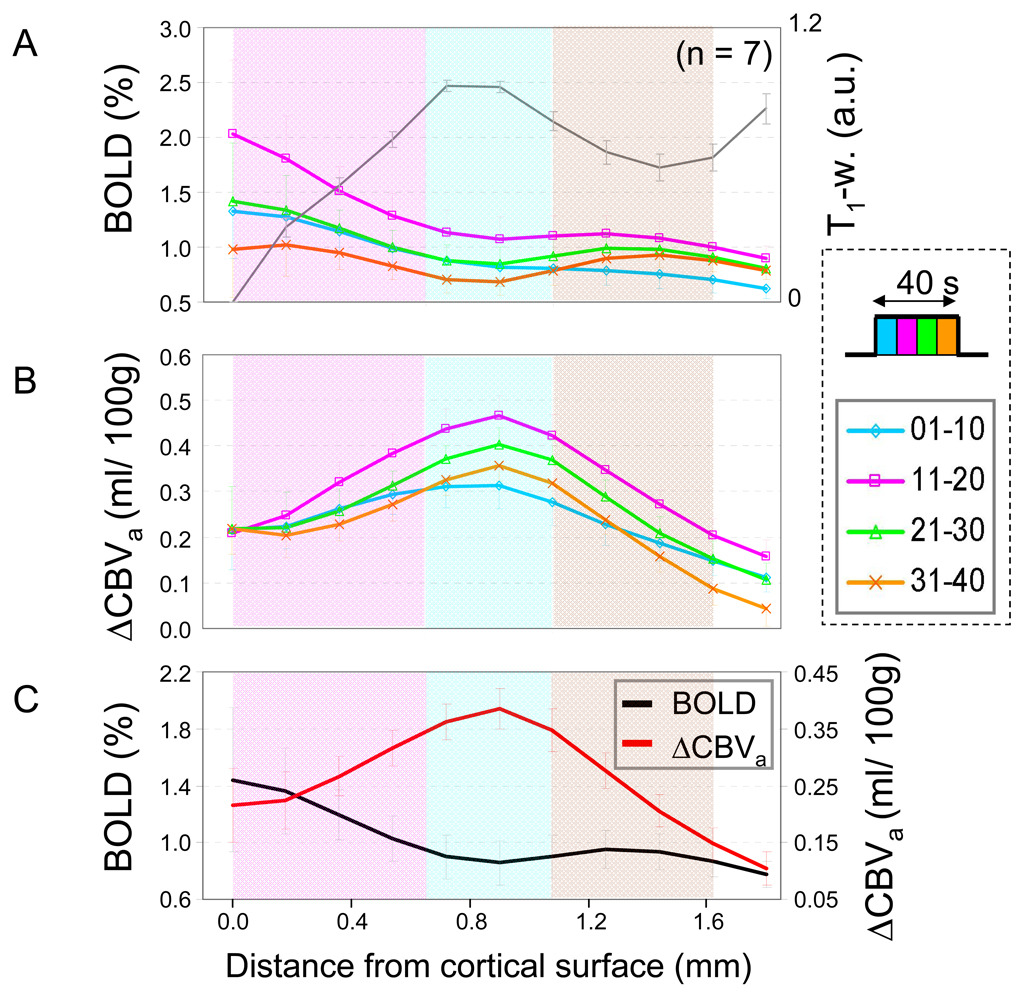
Time-dependence of Cortical Depth Profiles

Cortical depth profiles were determined within two quadrangular ROIs shown in Figure. 2B, and plotted as a function of depth from the surface of cortex (Fig. 6). To observe spatiotemporal responses, cortical profiles were plotted for every 10-s time period during stimulation for conventional GE BOLD (without MT effects) (Fig. 6A) and ΔCBV_a (Fig. 6B). Cortical profiles obtained during the entire 40-s stimulation period were plotted for conventional GE BOLD without MT (black line in Fig. 6C) and ΔCBV_a (red line in Fig. 6C). Overall, the highest BOLD signal responses were obtained in the superficial cortical area, while the highest ΔCBV_a changes were detected in the middle cortical layer. These observations are similar to our previous GE-BOLD and total CBV findings (Jin and Kim, 2008a; Zhao et al., 2006). Dynamically, BOLD responses were less in the initial 10-s period than in the second 10-s period because of the delayed hemodynamic response after stimulation onset, and then decreased during the stimulation period (Fig. 6A). Initially, the ΔCBV_a response was slightly higher at the cortical surface; then, the highest ΔCBV_a responses were obtained from the middle of the cortex during the remainder of the stimulation periods, but with reduced overall responses (Fig. 6B). These ΔCBV_a findings agree well with dynamic total CBV responses (Jin and Kim, 2008a), indicating that CBV changes mostly originate from arterial vessels.

Fig. 6.

Average cortical depth profiles of GE BOLD fMRI (without MT) and ΔCBV_a generated from the quadrangular ROIs in each animal. The surface of the cortex is zero. Approximate cortical layer locations were determined by relative distances of those layers in area 18 (Payne and Peters, 2002) and the profile of T₁-weighted image (gray line in panel A; a.u. = arbitrary units); layer IV should be located in the region between ~0.65 mm and ~1.08 mm from the surface of the cortex (blue color band). Supra-(layer II–III) and infra-granular layers (layer V–VI) are indicated by pink and purple color-bands, respectively. It is known that layer IV has highest capillary density, and during stimulation it has highest increases in neural activity, metabolism and blood flow. (a and b) Cortical depth profiles were calculated at every 10-s time period from stimulation onset to examine time-dependencies of the cortical profile. (c) BOLD and ΔCBV_a profiles were obtained from the entire 40-s stimulation period. The largest BOLD change is located at the surface of the cortex, while the highest ΔCBV_a change is observed at the middle of the cortex. Error bars: SEM.

Discussion

We have successfully obtained functional CBV_a change maps from fMRI using multiple MT levels. The highest functional CBV_a changes were observed at the middle of the cortex, unlike conventional BOLD fMRI. Thus, the MT-varied GE fMRI method can be used to improve spatial specificity of fMRI. Our GE BOLD observations in the cat visual cortex appear to be different from rat forepaw stimulation studies at high magnetic fields. Both statistical and percentage changes were highest at the cortical surface in our cat study. However, in rat somatosensory studies, the highest statistical changes were localized in the middle cortical layer (Duong et al., 2000; Silva and Koretsky, 2002; Silva et al., 2007; Van Camp et al., 2006), but the highest BOLD percentage changes were detected along the cortical surface (Duong et al., 2000; Silva and Koretsky, 2002). Mismatch between statistical and percentage changes in rat data can be explained by the fact that pixels at the cortical surface have low SNR due to short T₂^* of venous blood (i.e., reduction of signal change even if the same percentage change occurs) and large fluctuations due to vessel and CSF pulsations, consequently reducing statistical significances. This mismatch does not apply to the cat visual cortex data because of the large functional signal changes in pial vessels induced by large activation volume. When the activation volume is small, such as in the rat forelimb area, blood from the neighboring non-activated region will effectively dilute stimulus-induced deoxyhemoglobin changes in draining veins. On the other hand, full-field visual stimulation, as what was used in this current study, activates the entire visual cortex and so, blood containing stimulus-induced deoxyhemoglobin changes travels far downstream without dilution, inducing large BOLD signal changes in the cortical surface. Thus, to examine signal properties of large pial vessels versus middle cortical layer, the stimulation paradigms that induce large brain volumes are preferable.

Technical considerations of ΔCBV_a quantification with MT-varied GE fMRI

To determine ΔCBV_a from MT-varied GE fMRI, we assumed that (i) intravascular venous blood contribution is minimal, and (ii) arterial oxygenation level change is negligible. (i) When capillary water freely exchanges with tissue water, the MT effect in venous blood is similar to that of tissue. The conditions of virtually-continuous MT during fMRI studies may ensure enough time for a free exchange between tissue and capillary water. Then, MT-insensitive arterial signal changes can be separated from MT-sensitive venous signal changes within the vasculature. Even if the aforementioned assumption is not valid (capillary water does not completely exchange with tissue water), the contribution of any remaining venous blood signal to quantification of ΔCBV_a is minimal due to the very short T₂ of venous blood at 9.4 T (Kim et al., 2008). However, at low magnetic fields, if the capillary water does not freely exchange with tissue water, then venous blood may contribute to the intercept in ΔS_ss,MT / S₀ vs. S_ss,MT / S₀ because of the significant intravascular venous signals. (ii) When the arterial blood oxygenation change (ΔY_a) is significant, then the intercept in Eq. [6] has two terms with arterial blood volume (Δν_a) and arterial R₂^* changes $(\mathrm{\Delta }{R}_{2,\mathit{\text{artery}}}^{*})$. The intercept will be $\mathrm{\Delta }{\nu }_a·e^{-(R_{2,\mathit{\text{artery}}}^{*}+\mathrm{\Delta }{R}_{2,\mathit{\text{artery}}}^{*}-R_{2,\mathit{\text{tissue}}}^{*})·\mathit{\text{TE}}}+{\nu }_a·e^{-(R_{2,\mathit{\text{artery}}}^{*}-R_{2,\mathit{\text{tissue}}}^{*})·\mathit{\text{TE}}}·(e^{-\mathrm{\Delta }{R}_{2,\mathit{\text{artery}}}^{*}·\mathit{\text{TE}}}-1)$. We assumed that $R_2^{*}$ values of tissue and artery are similar at 9.4 T, and $\mathrm{\Delta }{R}_{2,\mathit{\text{artery}}}^{*}$ is zero. If $R_{2,\mathit{\text{artery}}}^{*}>R_{2,\mathit{\text{tissue}}}^{*}$, then Δν_a would be overestimated by the term of difference between $R_{2,\mathit{\text{artery}}}^{*}$ and $R_{2,\mathit{\text{tissue}}}^{*}$. In our laboratory, we observed a small increase in oxygen saturation levels in pial arteries in rats during somatosensory stimulation (Vazquez et al., 2009). If $\mathrm{\Delta }{R}_{2,\mathit{\text{artery}}}^{*}$ is significant, then Δν_a calculated without considering arterial oxygenation increases would be underestimated. Since we do not know the exact arterial blood R₂^* values and changes, it is difficult to estimate precise errors of Δν_a. Further systematic studies are necessary to evaluate this issue.

CSF contribution to ΔCBV_a measurements

We did not consider the contribution of CSF in our model. Since CSF has a minimal MT effect (Pike et al., 1992; Wolff et al., 1991), a change in this MT-insensitive CSF component appears as the intercept from the linear fit of ΔS_ss,MT / S₀ vs. S_ss,MT / S₀. To remove the CSF contribution from the ΔCBV_a maps, we excluded the pixels with an MTR_ss less than 2 standard deviations from the average MTR_ss calculated for the middle cortical ROI (see Fig. 4). Intercepts from the excluded pixels are shown in Figure 7A. Pixels with negative intercepts mostly localized to the surface of the cortex, where CSF exists. Figure 7B shows a pixel-wise plot of negative intercepts versus relative MTR_ss., calculated as the pixel MTR_ss divided by averaged MTR_ss of the middle cortical ROI. Pixels having larger negative intercept values correlated with lower relative MTR_ss (i.e., these pixels have a larger CSF partial volume fraction). These negative intercepts can be explained by decreases in CSF volume fraction during activation. When the average fMRI signal change was computed from pixels with negative intercepts, it was 2.83 ± 1.00, 2.44 ± 1.02 and 2.13 ± 0.95% at MTR_ss = 0, 0.19 ± 0.02 and 0.33 ± 0.03, respectively (n = 7). These decreased fMRI responses with increases in MTR are consistent with motor activation studies in humans (Zhang et al., 1997). Partial-volume contribution of MT-insensitive CSF is common in human fMRI data collected at relatively low spatial resolution. Thus, a stimulus-induced decrease in CSF volume induces the apparent fMRI signal decrease associated with a MT increase. Therefore, for accurate ΔCBV_a measurements from MT-varied GE fMRI, CSF contamination should be eliminated. This potential problem could be solved by a using high spatial resolution such as used in our study, or by nulling CSF with the fluid attenuated inversion recovery (FLAIR) technique (Donahue et al., 2006).

Fig. 7.

Effect of CSF contributions to ΔCBV_a. (a) Intercept maps were calculated for pixels in which MTR_ss is below 2 standard deviation of the mean MTR_ss in the middle cortical ROI. (b) A plot of the intercept vs. relative MTR_ss, which was calculated by dividing the pixel MTR_ss value by the averaged MTR_ss value of the middle cortical ROI (= 0.60 ± 0.04, n = 7). Each point indicates each negative intercept pixel, and different symbols indicate the different animals. Pixels with larger negative intercepts have the lower relative MTR_ss values (i.e. a smaller MT effects), indicating the larger CSF partial volume fraction.

Simplified ΔCBV_a-weighted fMRI method

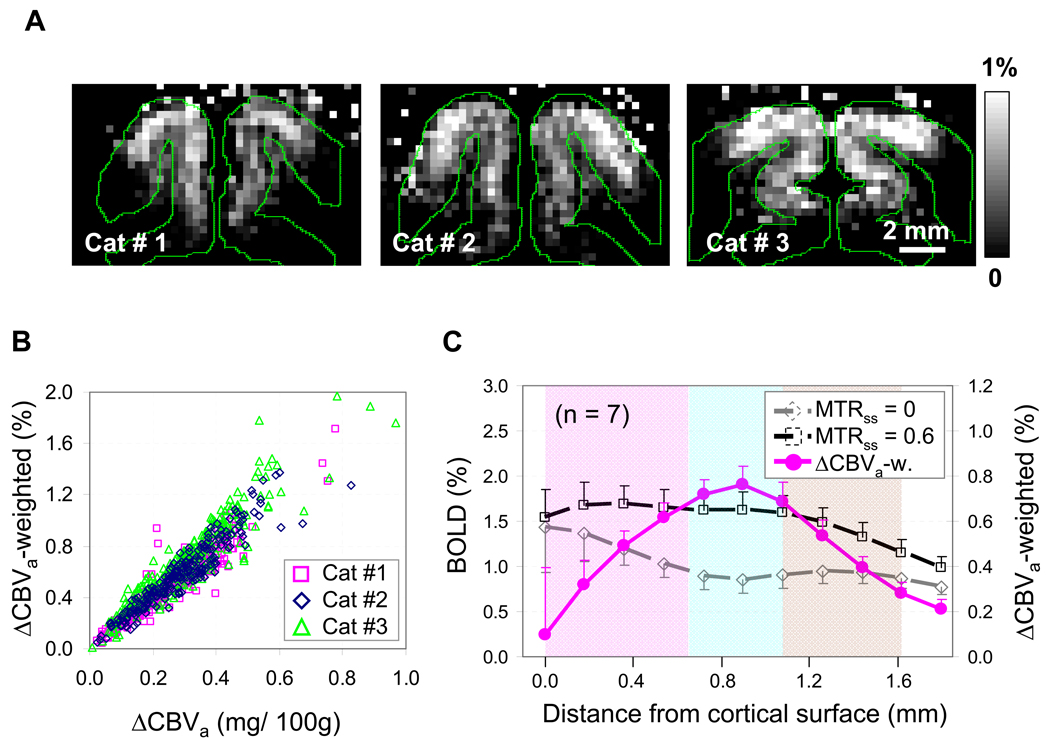
In order to utilize MT-varied GE fMRI for routine studies, we propose to obtain ΔCBV_a-weighted information from data with and without MT effects (see Eq. [8]). ΔCBV_a-weighted maps were calculated by simple pixel-wise subtraction of percentage signal changes with no MT (MTR_ss = 0) from those with high MT fMRI (MTR_ss = 0.6) (Fig. 8A). ΔCBV_a–weighted maps from three cats show the highest changes in the middle of the cortex (Fig. 8A), and match well with quantitative ΔCBV_a maps in Figure 4. These pixel-wise ΔCBV_a–weighted values determined from data with two MT levels highly correlated with quantified ΔCBV_a values obtained by a linear fit to data with three MT levels (R = 0.95 ± 0.01, n = 7) (Fig. 8B). This indicates that ΔCBV_a-weighted fMRI with two MT levels is a good alternative to ΔCBV_a measurement because of its simplicity. Although ΔCBV_a-weighted fMRI does not provide a quantitative value, it is easy to detect ΔCBV_a contrast.

Fig. 8.

ΔCBV_a-weighted fMRI signals determined by a simplified method. (a) ΔCBV_a-weighted maps were calculated by the difference between GE fMRI percentage maps with MTR_ss = 0 and MTR_ss = 0.6 using Eq. [8]. The maps are from the same three animals (Cats #1 – #3) as seen in Fig. 4. The largest responses were observed at the middle of the cortex. (b) Pixel-wise ΔCBV_a–weighted signal intensity, determined by the subtraction method, is plotted against quantitative ΔCBV_a determined by the linear fit method. Comparisons from three cats shown in panel A are presented. The average pixel-wise correlation coefficient between the two values was 0.95 ± 0.01 (n = 7). This indicates that ΔCBV_a-weighted fMRI with two MT levels provides a good alternative to quantitative ΔCBV_a measurements. (c) Cortical profiles of fMRI percentage signal changes of MTR_ss = 0 and MTR_ss = 0.6, and ΔCBV_a–weighted responses (n = 7). The fMRI percentage signal changes at the middle of the cortex increased with MT effect, while those at the surface of the cortex did not changed. As a result, the profiles of ΔCBV_a-weighted signals exhibit the highest response at the middle of the cortex. The blue color band presents approximate layer IV.

To further evaluate ΔCBV_a-weighted signals, cortical depth profiles were calculated from fMRI percentage signal changes with and without MT effects (black squared symbols from MTR_ss = 0.6 and gray diamond symbols from MTR_ss = 0 in Fig. 8C). BOLD percentage changes at the middle cortical area were enhanced with MT, while the largest BOLD percentage changes at the surface of the cortex were not changed with MT. Thus, the highest ΔCBV_a-weighted signal was observed in the middle cortical area (pink closed circles in Fig. 8C). This observation indicates that ΔCBV_a-weighted fMRI can improve the spatial specificity relative to BOLD fMRI.

Comparison with other functional CBV techniques

Functional CBV measurements with endogenous contrasts have been shown by i) arterial spin labeling with varied MT effect (i.e., modulation of tissue and vessel signal, MOTIVE) (Kim et al., 2007) and LL-EPI (Brookes et al., 2007); ii) vascular space occupancy (VASO); and iii) apparent diffusion coefficient (ADC). (i) The MOTIVE and LL-EPI techniques have been used to determine absolute baseline CBV_a and its functional change. However, these approaches with arterial spin labeling have poor temporal resolution compared to our current method of GE fMRI with varied MT, and MOTIVE also requires two RF coils: one for arterial spin labeling and the other for MT and data collection. (ii) The VASO technique nulls blood signals by selecting an appropriate inversion recovery time using the difference in T₁ values between blood and tissue (Lu et al., 2003). The VASO technique is sensitive to total CBV change, rather than only ΔCBV_a. When a relatively short repetition time (e.g. TR = ~3 s) is used for fMRI applications, the sensitivity of VASO is reduced because tissue water signal is closer to zero at the blood nulling points with shorter TRs. In this case, the sensitivity for CBV change is very low. Furthermore, the quantification of absolute or relative CBV changes is difficult. (iii) The CBV-weighted fMRI signal can be also obtained from diffusion-weighted fMRI studies with b values of 200–300 s/mm² (Jin et al., 2006; Truong and Song, 2009). Functional ADC changes with small b-values are heavily weighted by ΔCBV_a when the intravascular BOLD contribution is minimized at a sufficiently long TE at high fields or at a very short TE at any magnetic fields. The highest ADC changes were observed in the middle of the cortex in humans and animals (Jin et al., 2006; Truong and Song, 2009). This qualitative ADC technique has high temporal resolution, but poor sensitivity. Overall, the MT-varied GE fMRI technique used in our studies provides simplicity, high temporal resolution, and high sensitivity for the quantification of ΔCBV_a.

The MT-varied GE fMRI technique can be applicable to human studies for improving spatial specificity and for quantifying spatiotemporal arterial blood volume changes. The MT-varied GE fMRI approach is straightforward, and does not require any exogenous contrast agents. Since conventional T₂^*-weighted EPI can be used, the temporal resolution is not limited by the imaging technique, but by the physiological requirement that TR is greater than the transit time of the arterial blood from the outside imaging slab to the pre-capillaries. One concern is the power deposition due to MT-inducing pulses when short TR is used at high magnetic fields. Another potential problem is the requirement of MT-inducing RF pulses and the need of at least two separate experiments with different MT levels. This limits the application to reproducible, block-design fMRI studies. Thus, the MT-varied GE fMRI technique is unlikely suitable to event-related fMRI studies for localization of cognitive functions when dynamic changes in neural activity (e.g., habituation) occur. This problem may be solved by using single-MT fMRI acquired with a very short echo time, in which MT enhances relative CBV_a contribution, while short TE reduces BOLD contribution.

Functional ΔCBV_a vs. CBV changes measured with other techniques

The CBV_a change of 0.33 ml/100g during cat visual stimulation in this study is similar to the 0.34 ml/100g value found in our previous rat somatosensory stimulation studies measured by MOTIVE (Kim et al., 2007). Based on our total blood volume measurements with a contrast agent in the same animal model, we found the average relative CBV change to be ~8%, when averaged across the middle cortical layer (Zhao et al., 2006). If baseline total CBV of the cat visual cortex is assumed to be ~5 ml/100g, then the absolute change of total CBV is ~0.40 ml/100g. This suggests that the total CBV change during activation is dominated by ΔCBV_a, which is consistent with the observation in the rat somatosensory cortex (Kim et al., 2007). The CNR value is closely depend on spatial resolution and the number of measurement for average; thus, it cannot be directly compared between the different measurements. When the CNR of GE-BOLD was compared, the CNR of CBV_t with a contrast agent is about four times higher than that of ΔCBV_a (CNR of CBV_t / CNR of GE-BOLD = 1.5 (Zhao et al., 2006) and CNR of ΔCBV_a / CNR of GE-BOLD = 0.34 here).

Functional CBV_a change peaked at ~0.9 mm from the surface of the cortex, where layer IV is located (Fig. 6). This observation is consistent with previous CBV measurements in the same cat model measured using a contrast agent (Zhao et al., 2006), VASO (Jin and Kim, 2008b) and ADC (Jin et al., 2006). Dynamically, the CBV_a response in the initial 10-s period had a relatively large change at the upper cortical layer, which decreased for later time periods, while it has a relatively small change at the middle cortical layer, which increased for later time periods. Thus, at later time periods, improved functional localization to the middle of cortex was observed. This is consistent with time-dependencies of total CBV cortical profiles in the same animal model (Jin and Kim, 2008a). It is not surprising to detect similar time-dependent observations between arterial and total CBV changes, since the total CBV change mostly originated from a change in arterial CBV. Full-width of half-maximum (FWHM) of CBV_a response across the cortex is ~1.5 mm, which is wider than that of contrast agent studies (~0.9 mm with BOLD correction, (Zhao et al., 2006)), showing less localization to the middle cortical layer.

Post-stimulus undershoot was observed in our BOLD fMRI studies (see Fig. 5A), but it was not significant in the ΔCBV_a responses. The slightly decreased but insignificant ΔCBV_a after stimulus offset had large error bars and did not returned to the pre-stimulus baseline. This may be caused by inter-subject variations and baseline drift effects (Bandettini et al., 1993; Smith et al., 1999). In our previous CBF and total CBV studies (Jin and Kim, 2008a), small, but significant post-stimulus undershoots were observed after a 60-s long visual stimulation. The slightly different post-stimulus undershoots between arterial and total CBV changes can be partly due to the different stimulus duration, thus requiring further systematic studies in the same animals.

Conclusion

We have obtained ΔCBV_a maps from T₂^*-weighted fMRI with varied-MT effects. The highest ΔCBV_a changes were detected at the middle of the cortex, while the highest BOLD changes were observed at the surface of the cortex. This indicates that the ΔCBV_a measurement technique improves functional spatial specificity compared with conventional GE BOLD fMRI. This simple, non-invasive MT-varied GE fMRI technique is an excellent approach for high-resolution studies, and may be applicable to human subjects.