The Correspondence Between Equilibrium Biphasic and Triphasic Material Properties in Mixture Models of Articular Cartilage

Abstract

Mixture models have been successfully used to describe the response of articular cartilage to various loading conditions. Mow and co-workers [1980, J. Biomech. Eng. 102, 73–84] formulated a mixture model of articular cartilage where the collagen-proteoglycan matrix is modeled as an intrinsically incompressible porous-permeable solid matrix, and the interstitial fluid is modeled as an incompressible fluid. Lai and co-workers [1991, J. Biomech. Eng. 113, 245–258] proposed a triphasic model of articular cartilage as an extension of their biphasic theory, where negatively charged proteoglycans are modeled to be fixed to the solid matrix, and monovalent ions in the interstitial fluid are modeled as additional fluid phases. Since both models co-exist in the cartilage literature, it is useful to show how the measured properties of articular cartilage (the confined and unconfined compressive and tensile moduli, the compressive and tensile Poisson’s ratios, and the shear modulus) relate to both theories. In this study, closed-form expressions are presented that relate biphasic and triphasic material properties in tension, compression and shear. These expressions are then compared to experimental findings in the literature to provide greater insight into the measured properties of articular cartilage as a function of bathing solutions salt concentrations and proteoglycan fixed-charge density.

Introduction

Mixture models have been successfully used to describe the response of articular cartilage to various loading conditions. In their classical study, Mow, Lai and co-workers (1980) formulated a mixture model of articular cartilage where the collagen-proteoglycan matrix is modeled as an intrinsically incompressible porous-permeable solid matrix, and the interstitial fluid is modeled as an incompressible fluid. This biphasic model has been able to describe the response of articular cartilage in confined compression creep, stress-relaxation, and dynamic loading (Mow et al., 1980; Lee et al., 1981; Soltz and Ateshian, 1998, 2000b). By incorporating the tension-compression nonlinearity of the solid matrix into this biphasic framework, the model has been able to describe the response of cartilage in unconfined compression as well (Cohen et al., 1998; Soulhat et al., 1999; Soltz and Ateshian, 2000a). However, the negatively-charged proteoglycans in articular cartilage produce an osmotic pressure which swells the tissue and contributes to its compressive stiffness (Maroudas, 1979; Eisenberg and Grodzinsky, 1985; Lai et al., 1991; Schwartz et al., 1994; Buschmann and Grodzinsky, 1995; Kovach, 1996; Khalsa and Eisenberg, 1997; Basser et al., 1998; Narmoneva et al., 1999, 2001; Bursac et al., 2000). Proteoglycans are also responsible for various electromechanical effects such as streaming potentials and currents (Frank and Grodzinsky, 1987a,b) and reduced tissue permeability (Maroudas, 1979; Gu et al., 1993). Lai and co-workers (1991) proposed a triphasic model of articular cartilage as an extension of their biphasic theory, where proteoglycans are modeled as a negative charge density fixed to the solid matrix and monovalent ions in the interstitial fluid modeled as additional fluid phases. This model was later extended to incorporate multiple polyvalent ions by Gu et al. (1998).

Despite the fact that the triphasic model of cartilage provides a more accurate description of the tissue composition and mechano-electrochemical response, the biphasic model continues to be used in the literature because of its ability to successfully describe the response of cartilage to various loading conditions. Since both models are likely to co-exist in the cartilage literature, it is useful to show how the measured properties of articular cartilage (the confined and unconfined compressive and tensile moduli and the compressive and tensile Poisson’s ratios) relate to both theories. To date, the correspondence between the two models has been typically presented in numerical examples requiring the solution of nonlinear equations. In this study, closed-form expression are presented that relate biphasic and triphasic material properties, which are then analyzed to provide greater insight into the measured properties of articular cartilage as a function of proteoglycan fixed-charge density, under various bathing solutions salt concentrations.

Model Formulation

This presentation specializes the formulation of Gu et al. (1998) to the case of a solid phase, and three fluid phases consisting of the solvent (water) and two solutes (anion and cation) representative of sodium and chloride ions. The balance of linear momentum for the entire mixture, and the balance of momentum for the fluid phases, under quasi-static conditions, are given by

$$\text{div}\mathbf{\sigma }=\mathbf{0}$$ (1)

$$-{\rho }^{\alpha }\text{grad}{\stackrel{\sim }{\mu }}^{\alpha }+\sum _{\beta }{f}_{\alpha \beta }({\mathbf{v}}^{\beta }-{\mathbf{v}}^{\alpha })=\mathbf{0},\alpha \ne s$$ (2)

where summations are performed over the solid, water, and ion phases (α,β= s,w,+,−) with exceptions as specified. In these expressions, σ is the total stress in the mixture, ρ^α is the apparent density of phase α, v^α is its velocity, μ̃^α is its electrochemical potential, and f_αβ is the diffusive drag coefficient between phases α and β. If the diffusive drag between anions and cations, and between ions and the solid matrix are neglected (f₊₋ ≈ f_s+ ≈ f_s− ≈ 0), the remaining diffusive drag coefficients relate to the ion diffusivities D⁺,D⁻ and interstitial fluid permeability k through (Gu et al., 1993)

$$D^{-}=\frac{{\varphi }^{w}R\theta c^{-}}{f_{w-}},D^{+}=\frac{{\varphi }^{w}R\theta c^{+}}{f_{w+}},\text{and}k=\frac{{\varphi }^{w^2}}{f_{ws}},$$ (3)

where R is the universal gas constant, θ is the absolute temperature, and ϕ^w is the water volumetric fraction (tissue porosity). The concentrations c^α (moles of solute per unit solvent volume) are related to apparent densities through

$$c^{\alpha }={\rho }^{\alpha }/{\varphi }^w{M}_{\alpha },$$ (4)

where M_α is the molecular weight. The balance of mass for the entire mixture and the balance of mass for the individual phases are given by

$$\sum _{\beta }\text{div}({\varphi }^{\beta }{\mathbf{v}}^{\beta })=0,$$ (5)

$$\frac{\partial {\rho }^{\alpha }}{\partial t}+\text{div}({\rho }^{\alpha }{\mathbf{v}}^{\alpha })=0.$$ (6)

Equation (5) derives from Eq.(6) under the assumption of mixture saturation and intrinsic incompressibility of the solid and fluid phases. The volumetric fraction ϕ^α is related to the true density ${\rho }_T^{\alpha }$ of phase α through ${\varphi }^{\alpha }={\rho }^{\alpha }/{\rho }_T^{\alpha }$. It is generally assumed that the ion phases are dilute so that their volumetric fractions are negligibly small, ϕ^+,ϕ⁻ ≪ 1. The constitutive relations for the total mixture stress and the electrochemical potentials of the fluid phases are

$$\mathbf{\sigma }=-p\mathbf{I}+2\mu \mathbf{E}+\sum _{i=1}^3{\lambda }_1\{{\mathbf{A}}_i:\mathbf{E}\}({\mathbf{A}}_i:\mathbf{E}){\mathbf{A}}_i+{\lambda }_2({\mathbf{A}}_i:\mathbf{E})(\mathbf{I}-{\mathbf{A}}_i),$$ (7)

$${\stackrel{\sim }{\mu }}^{\alpha }={\mu }_0^{\alpha }(\theta )+\frac{p}{{\rho }_T^{\alpha }}+z_{\alpha }\frac{F_c\psi }{M_{\alpha }}+\frac{R\theta }{M_{\alpha }}ln{a}^{\alpha },$$ (8)

where p is the interstitial fluid pressure (inclusive of osmotic effects), λ₁, λ_2, μ are elastic constants within a cubic symmetry framework, E is the small strain tensor (E= (gradu + grad^T u)/2 where u is the solid matrix displacement and v^s= ∂u/∂t), and A _i= a _i ⊗a _i (a _i · a _j = δ_ij) are texture tensors as described in our earlier study (Soltz and Ateshian, 2000a). The texture directions a _i correspond with the direction parallel to local split lines (i = 1), perpendicular to local split lines (i = 2), and normal to the articular surface (i = 3). According to the conewise linear elasticity (CLE) theory of Curnier et al. (1995), if the solid matrix response differs in tension and compression, then λ₁ {A _i:E} = λ_±1 depending whether the normal strain component A _i: E along the texture direction a _i is positive or negative. The reference chemical potential ${\mu }_0^{\alpha }(\theta )$ depends on temperature only, whereas z_α is the charge valence and a^α is the activity of phase α, F _c is Faraday’s constant, and ψ is the electrical potential in the mixture. For a fluid mixture with water as the solvent and ions as the solutes in a dilute solution, the electrochemical potentials can be further reduced to

$${\stackrel{\sim }{\mu }}^w={\mu }_0^w(\theta )+\frac{1}{{\rho }_T^w}\left[p-R\theta \mathrm{\Phi }(c^{+}+c^{-})\right],$$ (9)

$${\stackrel{\sim }{\mu }}^{+}={\mu }_0^{+}(\theta )+\frac{F_c\psi }{M_{+}}+\frac{R\theta }{M_{+}}ln{\gamma }_{+}{c}^{+},$$ (10)

$${\stackrel{\sim }{\mu }}^{-}={\mu }_0^{-}(\theta )-\frac{F_c\psi }{M_{-}}+\frac{R\theta }{M_{-}}ln{\gamma }_{-}{c}^{-},$$ (11)

where Φ is the osmotic coefficient of the solution and γ₊,γ₋ are the activity coefficients of the ions. Finally, the electroneutrality condition is given by

$$\sum _{\beta }{z}_{\beta }{c}^{\beta }=c^{+}-c^{-}-c^F=0,$$ (12)

where z_w= 0 (neutral solvent), z₊ = 1, z₋ = −1 (monovalent ions), and z_sc^s≡ −c^F where c ^F is the charge density of proteoglycans fixed to the solid phase. Combining this equation with the balance of mass equations yields the current condition

$$\text{div}{\mathbf{I}}_e=\text{div}\left({\varphi }^w{F}_c\sum _{\alpha }{z}_{\alpha }{c}^{\alpha }{\mathbf{v}}^{\alpha }\right)=0.$$ (13)

From the balance of mass for the solid matrix, and the mixture saturation condition Σ_β ϕ^β ≈ ϕ^s+ ϕ^w= 1, it is also possible to relate the proteoglycan fixed charge density c ^F and the interstitial water volume fraction ϕ^w to their respective reference values $c_r^F$ and ${\varphi }_r^w$ in the absence of solid matrix dilatation,

$$c^F\approx c_r^F\left(1-\frac{\text{tr}\mathbf{E}}{{\varphi }_r^w}\right),{\varphi }^w\approx {\varphi }_r^w+(1-{\varphi }_r^w)\text{tr}\mathbf{E}.$$ (14)

These governing equations must be solved subject to appropriate boundary conditions. At any interface between a triphasic material and its surroundings, defined on the solid matrix by a unit normal n, the continuity of fluid and ion fluxes and solid velocity normal to the interface, the total traction, and the fluid and ion electrochemical potentials must be satisfied (Hou et al., 1989; Lai et al., 1991; Sun et al., 1999; Ateshian et al., 2003):

$$\left[[{\rho }^{\alpha }({\mathbf{v}}^{\alpha }-{\mathbf{v}}^s)]\right]·\mathbf{n}=0,\left[[{\mathbf{v}}^s]\right]·\mathbf{n}=0,$$ (15)

$$\left[[\mathbf{\sigma }]\right]\mathbf{n}=\mathbf{0},\left[[{\stackrel{\sim }{\mu }}^{\alpha }]\right]=0,\alpha \ne s.$$ (16)

The triphasic model can be reduced to the biphasic model by dropping the ion phases (ρ⁺ = ρ⁻ = 0, f_w+ = f_w− = 0) and letting the reference fixed charge density reduce to zero, $c_r^F=0$.

Equilibrium Response Under Uniaxial Loading

The objective of this study is to relate the triphasic material properties λ_±1, λ_2, μ, k to what might be determined from experimental measurements of the confined and unconfined compressive and tensile moduli, and the torsional or shear modulus. Because the biphasic theory can always be deduced as a special case of the triphasic theory, the analysis focuses on the latter. All of these loading configurations can be analyzed under axisymmetric conditions using a cylindrical coordinate system. All problems consider a cylindrical cartilage specimen of radius r₀ and height h, with its axis aligned along the z–coordinate. A zero-current (open-circuit) condition is assumed in all cases, representative of most experimental configurations reported in the literature. The specimen is placed in a well-mixed bathing solution of sodium chloride of homogeneous concentration c^*, with ambient pressure p^* and electric potential ψ^* (it is common to set p^*= 0 and ψ^* = 0). It is also assumed that the material properties are homogeneous and that solid matrix strains remain sufficiently small.

In this section, the steady-state response to loading is analyzed to extract the equilibrium properties of the tissue. Thus v^β = 0 for all phases and the remaining unknowns are the solid matrix displacement u, the ion concentrations c⁺,c⁻, the interstitial fluid pressure p, and the electric potential ψ.

Uniaxial Loading with Lateral Confinement

In confined compression or tension under equilibrium conditions, the shear strain components are equal to zero, and the normal strains are given by E _rr = E_θθ = 0 and E _zz= constant. The applied equal and opposite stress at the two ends of the cylindrical specimen is given by σ_a. Satisfying the jump conditions of Eq.(16) yields the relations

$$c^{-}=\frac{-c^F+\sqrt{c^{F^2}+{\left(2\frac{{\gamma }_{\pm }^{\ast }}{{\gamma }_{\pm }}{c}^{\ast }\right)}^2}}{2},c^{+}=\frac{c^F+\sqrt{c^{F^2}+{\left(2\frac{{\gamma }_{\pm }^{\ast }}{{\gamma }_{\pm }}{c}^{\ast }\right)}^2}}{2},$$ (17)

$$p-p^{\ast }=R\theta \left[\mathrm{\Phi }\sqrt{c^{F^2}+{\left(2\frac{{\gamma }_{\pm }^{\ast }}{{\gamma }_{\pm }}{c}^{\ast }\right)}^2}-2{\mathrm{\Phi }}^{\ast }{c}^{\ast }\right],\psi -{\psi }^{\ast }=\frac{R\theta }{2F_c}ln\frac{{\gamma }_{+}^{\ast }{\gamma }_{-}{c}^{-}}{{\gamma }_{+}{\gamma }_{-}^{\ast }{c}^{+}},$$ (18)

$$E_{zz}=\frac{R\theta \left[\mathrm{\Phi }\sqrt{c^{F^2}+{\left(2\frac{{\gamma }_{\pm }^{\ast }}{{\gamma }_{\pm }}{c}^{\ast }\right)}^2}-2{\mathrm{\Phi }}^{\ast }{c}^{\ast }\right]+{\sigma }_a}{H_A\{E_{zz}\}},c^F=c_r^F\left(1-\frac{E_{zz}}{{\varphi }_r^w}\right),$$ (19)

where γ_± = γ₊γ_−, and the aggregate modulus H_A {E_zz} depends on the sign of the strain,

$$H_A\{E_{zz}\}=\{\begin{array}{ll}{H}_{-A}={\lambda }_{-1}+2\mu \hfill & E_{zz}<0\hfill \\ H_{+A}={\lambda }_{+1}+2\mu \hfill & E_{zz}>0\hfill \end{array}.$$ (20)

Substituting Eq.(19)₂ into Eq.(19)₁ yields a quadratic equation in the strain E_zz which can be solved in closed-form, though the expression is too cumbersome to present here. Performing a Taylor series expansion of the radical for small strains about zero yields the approximate relation

$$E_{zz}\approx \frac{{\sigma }_a+\pi }{H_A\{E_{zz}\}+\mathrm{\Pi }}.$$ (21)

where

$$\pi =R\theta \left[\mathrm{\Phi }\sqrt{c_r^{F^2}+{\left(2\frac{{\gamma }_{\pm }^{\ast }}{{\gamma }_{\pm }}{c}^{\ast }\right)}^2}-2{\mathrm{\Phi }}^{\ast }{c}^{\ast }\right],$$ (22)

$$\mathrm{\Pi }=\frac{R\theta \mathrm{\Phi }{c}_r^{F^2}}{{\varphi }_r^w\sqrt{c_r^{F^2}+4{\left(\frac{{\gamma }_{\pm }^{\ast }}{{\gamma }_{\pm }}{c}^{\ast }\right)}^2}}.$$ (23)

In these expressions π is the osmotic pressure in the tissue and Π is (the negative of) the rate of change of the osmotic pressure with dilatation (tr E), both evaluated in the limit of zero dilatation. To get the free-swelling strain $E_{zz}^0$, which represents the swelling of the tissue in response to the osmotic pressure difference given by Eq.(18)₁ or Eq.(22), it suffices to let σ_a = 0 and H_A {E _zz} = H_+A in Eq.(21) since the swelling strain is tensile,

$$E_{zz}^0\approx \frac{\pi }{H_{+A}+\mathrm{\Pi }}.$$ (24)

To get the effective confined (aggregate) modulus of the specimen, which represents the modulus measured experimentally from the slope of the stress-strain response, Eq.(21) is rearranged and differentiated to yield

$$H_A^{\mathit{eff}}\{E_{zz}\}\equiv \frac{\partial {\sigma }_a}{\partial E_{zz}}=H_A\{E_{zz}\}+\mathrm{\Pi }.$$ (25)

Note that the effective aggregate modulus is dependent upon the sign of E _zz, yielding different values in tension and compression.

In the biphasic theory, the effect of the fixed charge density of the proteoglycans is not explicitly included. Hence, $c_r^F=0,E_{zz}^0=0$, Π = 0, and $H_A^{\mathit{eff}}\{E_{zz}\}=H_A^{\mathit{biphasic}}\{E_{zz}\}$. Therefore, when modeling the tissue with the biphasic theory, the measured tissue modulus is attributed entirely to the solid matrix, whereas in the triphasic theory the measured modulus has contributions from the solid matrix and from the rate of change of the osmotic pressure with dilatation, Π (Lai et al., 1991). The biphasic and triphasic aggregate moduli do not represent the same physical quantity; they are related through

$$H_A^{\mathit{eff}}\{E_{zz}\}=H_A^{\mathit{biphasic}}\{E_{zz}\}=H_A\{E_{zz}\}+\mathrm{\Pi },$$ (26)

where H_A {E _zz} = H_±A represents triphasic properties.

Unconfined Uniaxial Loading

The next equilibrium loading configuration to be considered is unconfined uniaxial tensile or compressive loading (traction-free lateral boundary). In this case, E _rr= E_θθ = constant, E _zz = constant, and from the interface jump conditions of Eq.(16) the relations that need to be satisfied are of the same form as Eqs.(17)–(18), as well as

$$H_A\{E_{rr}\}{E}_{rr}+{\lambda }_2(E_{rr}+E_{zz})-R\theta \left[\mathrm{\Phi }\sqrt{c^{F^2}+{\left(2\frac{{\gamma }_{\pm }^{\ast }}{{\gamma }_{\pm }}{c}^{\ast }\right)}^2}-2{\mathrm{\Phi }}^{\ast }{c}^{\ast }\right]=0,$$ (27)

$$2{\lambda }_2{E}_{rr}+H_A\{E_{zz}\}{E}_{zz}-R\theta \left[\mathrm{\Phi }\sqrt{c^{F^2}+{\left(2\frac{{\gamma }_{\pm }^{\ast }}{{\gamma }_{\pm }}{c}^{\ast }\right)}^2}-2{\mathrm{\Phi }}^{\ast }{c}^{\ast }\right]={\sigma }_a,$$ (28)

where

$$c^F=c_r^F\left(1-\frac{2E_{rr}+E_{zz}}{{\varphi }_r^w}\right).$$ (29)

Given the Taylor series expansion

$$\sqrt{c^{F^2}+{\left(2\frac{{\gamma }_{\pm }^{\ast }}{{\gamma }_{\pm }}{c}^{\ast }\right)}^2}\approx \sqrt{c_r^{F^2}+{\left(2\frac{{\gamma }_{\pm }^{\ast }}{{\gamma }_{\pm }}{c}^{\ast }\right)}^2}-(2E_{rr}+E_{zz})\frac{c_r^{F^2}}{{\varphi }_r^w\sqrt{c_r^{F^2}+{\left(2\frac{{\gamma }_{\pm }^{\ast }}{{\gamma }_{\pm }}{c}^{\ast }\right)}^2}},$$

these equations can be solved for the strain components as a function of the applied stress,

$$E_{rr}\approx \frac{(H_A\{E_{zz}\}-{\lambda }_2)\pi -({\lambda }_2+\mathrm{\Pi }){\sigma }_a}{(H_A\{E_{rr}\}+{\lambda }_2+2\mathrm{\Pi })(H_A\{E_{zz}\}+\mathrm{\Pi })-2{({\lambda }_2+\mathrm{\Pi })}^2},$$ (30)

$$E_{zz}\approx \frac{(H_A\{E_{rr}\}-{\lambda }_2)\pi +(H_A\{E_{rr}\}+{\lambda }_2+2\mathrm{\Pi }){\sigma }_a}{(H_A\{E_{rr}\}+{\lambda }_2+2\mathrm{\Pi })(H_A\{E_{zz}\}+\mathrm{\Pi })-2{({\lambda }_2+\mathrm{\Pi })}^2},$$ (31)

and they can be rearranged and differentiated to yield the effective Young’s modulus and Poisson’s ratio,

$$E_Y^{\mathit{eff}}\equiv \frac{\partial {\sigma }_a}{\partial E_{zz}}\approx H_A\{E_{zz}\}+\mathrm{\Pi }-\frac{2{({\lambda }_2+\mathrm{\Pi })}^2}{H_A\{E_{rr}\}+{\lambda }_2+2\mathrm{\Pi }},$$ (32)

$${\nu }^{\mathit{eff}}\equiv -\frac{\partial E_{rr}}{\partial E_{zz}}\approx \frac{{\lambda }_2+\mathrm{\Pi }}{H_A\{E_{rr}\}+{\lambda }_2+2\mathrm{\Pi }}.$$ (33)

To get the free-swelling strain $E_{rr}^0=E_{zz}^0$, let σ_a= 0, H_A {E_rr} = H_+A and H_A {E _zz} = H_+A in Eqs.(30)–(31),

$$E_{rr}^0=E_{zz}^0\approx \frac{\pi }{(H_{+A}+\mathrm{\Pi })+2({\lambda }_2+\mathrm{\Pi })}.$$ (34)

The biphasic Young’s modulus and Poisson’s ratio can be obtained from Eqs.(32)–(33) by letting $c_r^F=0$ (or equivalently, Π = 0). Thus it can be noticed that in addition to Eq.(26), it is possible to establish the relation

$${\lambda }_2^{\mathit{eff}}={\lambda }_2^{\mathit{biphasic}}={\lambda }_2+\mathrm{\Pi },$$ (35)

such that

$$E_Y^{\mathit{eff}}\{E_{rr},E_{zz}\}=H_A^{\mathit{eff}}\{E_{zz}\}-\frac{2{\lambda }_2^{{eff}^2}}{H_A^{\mathit{eff}}\{E_{rr}\}+{\lambda }_2^{\mathit{eff}}},$$ (36)

$${\nu }^{\mathit{eff}}\{E_{rr}\}=\frac{{\lambda }_2^{\mathit{eff}}}{H_A^{\mathit{eff}}\{E_{rr}\}+{\lambda }_2^{\mathit{eff}}}.$$ (37)

Note that in general E _rr and E _zz will have opposite signs in this loading configuration, so that $H_A^{\mathit{eff}}\{E_{rr}\}$ will not be the same as $H_A^{\mathit{eff}}\{E_{zz}\}$. These results also indicate that Young’s modulus and Poisson’s ratio differ in tension and compression.

Torsion

The last equilibrium loading configuration considered here is torsion of an unconfined cylinder. The initial state can be given by the solution for unconfined loading described above, upon which a torsional displacement is superposed. In this case, the state of strain is supplemented by the non-zero shear strain component E_θz = αr/2, while the stress is supplemented by the non-zero shear stress-component σ_θz= 2μE_θz= αμr according to Eq.(22), where α is the torsional angle per unit length. Since the shear stress component is not influenced by the fixed-charge density and osmotic pressure, it is found that the effective shear modulus is equal to μ and remains the same in both triphasic and biphasic theories,

$${\mu }^{\mathit{eff}}={\mu }^{\mathit{biphasic}}=\mu .$$ (38)

Results

The expressions derived above for the free-swelling strains in confined and unconfined configurations, and for π,Π, $H_A^{\mathit{eff}},E_Y^{\mathit{eff}}$, ν^eff and μ^eff, are presented in closed-form and are therefore straightforward to evaluate for any choice of intrinsic material properties. For illustration purposes, plots are generated using representative values for the temperature (θ), water volumetric content ( ${\varphi }_r^w$) and intrinsic material properties of the triphasic theory (H_±A, λ_2, μ): θ = 20°C=293K, ${\varphi }_r^w=0.8$, H_+A= 6 MPa, H_−A= 0.2 MPa, and λ₂= 0.1 MPa. The external bath concentration c^* is varied from 0.001 M to 2 M, with 0.15 M representing physiological conditions. (While the general framework of the triphasic theory allows for H_±A, λ_2, μ to be functions of their ionic environment, and thus vary with c^*, they are assumed to remain constant in this study.) The reference fixed charge density, $c_r^F$, is varied from 0 to 0.4 mEq/ml, with the typical range for normal articular cartilage being 0.05–0.2 mEq/ml (Maroudas, 1979). In SI units the universal gas constant is R= 8.314 J/K.Mole; to use the above formulas, c^* should be converted to units of Mole/m³ and $c_r^F$ to Eq/m³. In all plots, it is assumed that Φ = Φ^* = 1 and ${\gamma }_{\pm }^{\ast }/{\gamma }_{\pm }=1$, representing ideal physicochemical conditions; deviations of these coefficients from unity are described, for example, by Maroudas (1979) and Buschmann and Grodzinsky (1995).

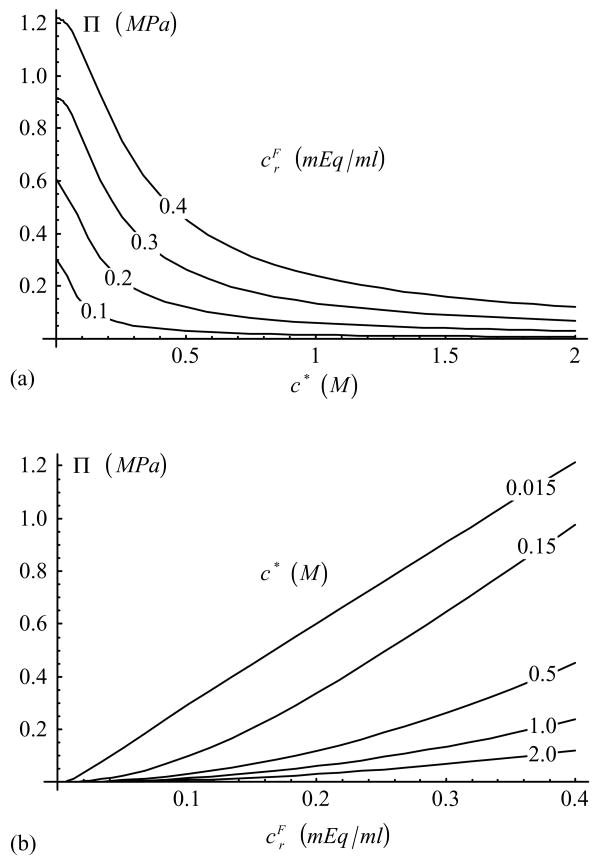
The rate of change of osmotic pressure with dilatation, Π in Eq.(23), is shown in Figure 1. In confined compression, the effective modulus, $H_{-A}^{\mathit{eff}}$, is given by Eq.(26) with H_A {E _zz} = H_−A, and can be deduced from the response of Π by the simple addition of the constant H_−A; similarly for the effective aggregate modulus in tension $H_{+A}^{\mathit{eff}}=H_{+A}+\mathrm{\Pi }$ and the “off-diagonal” effective modulus ${\lambda }_2^{\mathit{eff}}={\lambda }_2+\mathrm{\Pi }$. The free-swelling strain $E_{zz}^0$ in the laterally confined configuration, Eq.(24), is presented in Figure 2.

Figure 1.

Rate of change of osmotic pressure with dilatation, Π, as a function of (a) c^* and (b) $c_r^F$ [Eq.(23)]. $H_{\pm A}^{\mathit{eff}}=H_{\pm A}+\mathrm{\Pi }$ and ${\lambda }_2^{\mathit{eff}}={\lambda }_2+\mathrm{\Pi }$ can be obtained by offsetting the response of Π with the appropriate constant.

Figure 2.

Free-swelling strain, $E_{zz}^0$, in laterally confined configuration, as a function of (a) c^* and (b) $c_r^F$ [Eq.(24)].

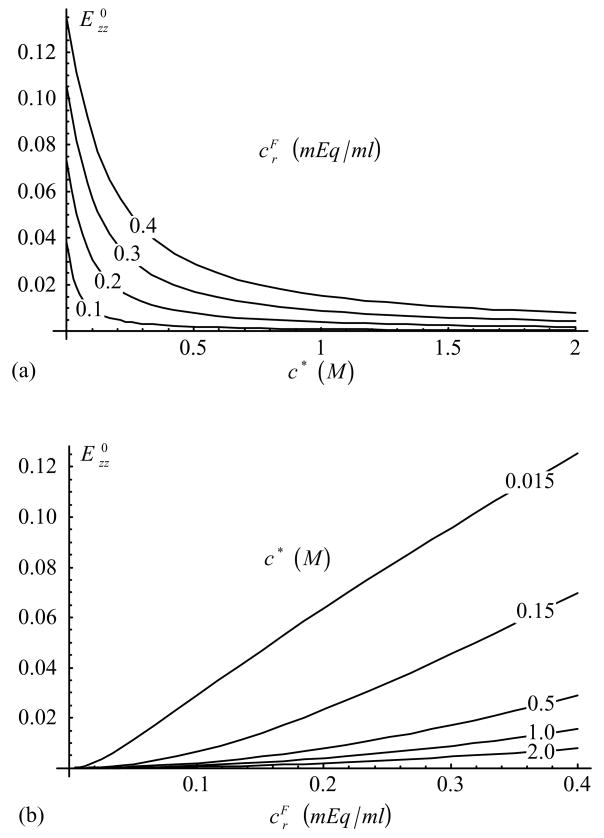
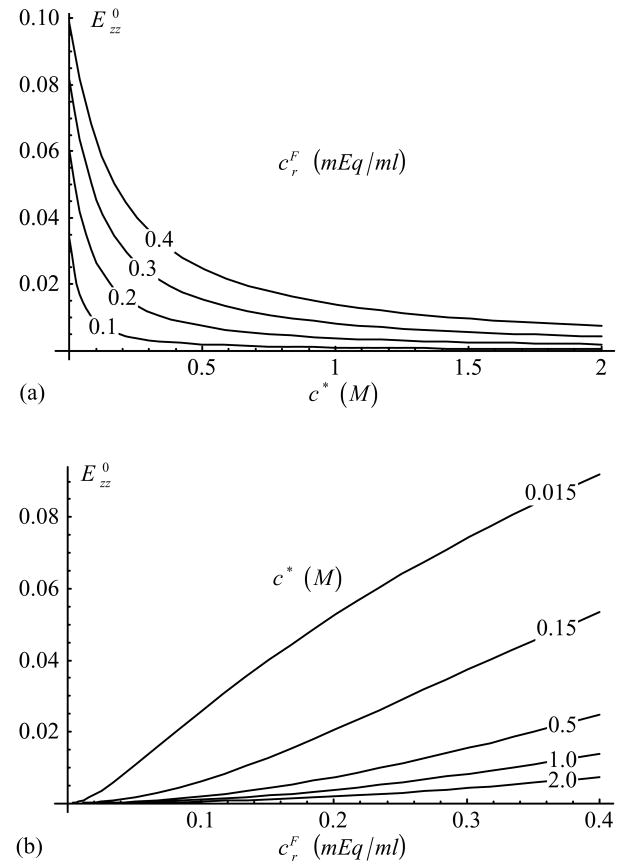
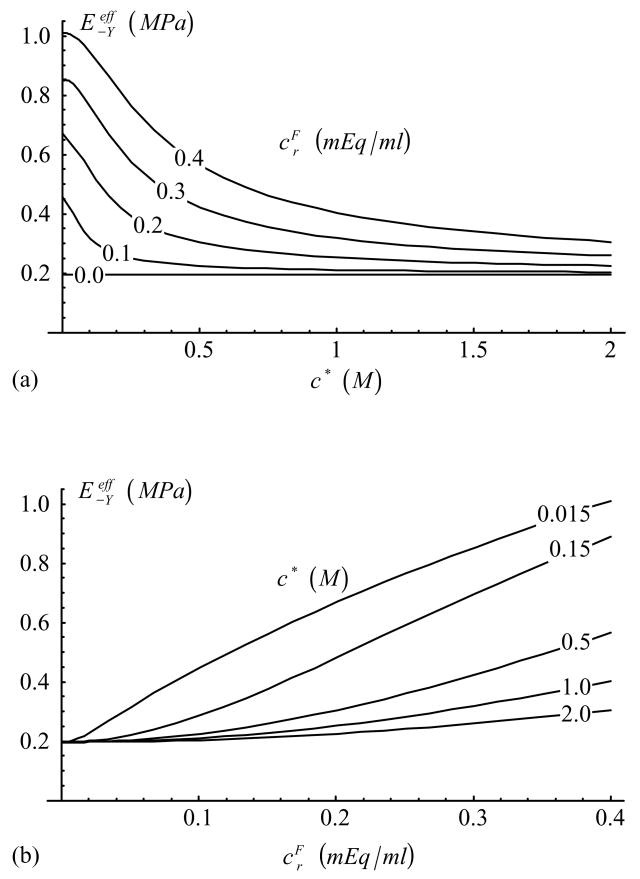
In the unconfined configuration, the free swelling axial strain, $E_{zz}^0$ from Eq.(34), is presented in Figure 3. The effective Young’s modulus, Eq.(36), is provided in Figure 4 for compression ( $E_{-Y}^{\mathit{eff}}$, with $H_A^{\mathit{eff}}\{E_{zz}\}=H_{-A}+\mathrm{\Pi }$ and $H_A^{\mathit{eff}}\{E_{rr}\}=H_{+A}+\mathrm{\Pi }$). In tension ( $E_{+Y}^{\mathit{eff}}$, with $H_A^{\mathit{eff}}\{E_{zz}\}=H_{+A}+\mathrm{\Pi }$ and $H_A^{\mathit{eff}}\{E_{rr}\}=H_{-A}+\mathrm{\Pi }$), the Young’s modulus is found to remain almost constant, at $E_{+Y}^{\mathit{eff}}\approx 6\text{MPa}$, for all values of c^* and $c_r^F$. Corresponding effective Poisson’s ratios, Eq.(37), are provided in Figure 5 in compression (with $H_A^{\mathit{eff}}\{E_{rr}\}=H_{+A}+\mathrm{\Pi }$) and Figure 6 in tension (with $H_A^{\mathit{eff}}\{E_{rr}\}=H_{-A}+\mathrm{\Pi }$).

Figure 3.

Axial strain, $E_{zz}^0$, in unconfined free swelling configuration, as a function of (a) c^* and (b) $c_r^F$ [Eq.(34)].

Figure 4.

Effective Young’s modulus in compression, $E_{-Y}^{\mathit{eff}}$, as a function of (a) c^* and (b) $c_r^F$ [Eq.(36), with $H_A^{\mathit{eff}}\{E_{zz}\}=H_{-A}+\mathrm{\Pi }$ and $H_A^{\mathit{eff}}\{E_{rr}\}=H_{+A}+\mathrm{\Pi }$)].

Figure 5.

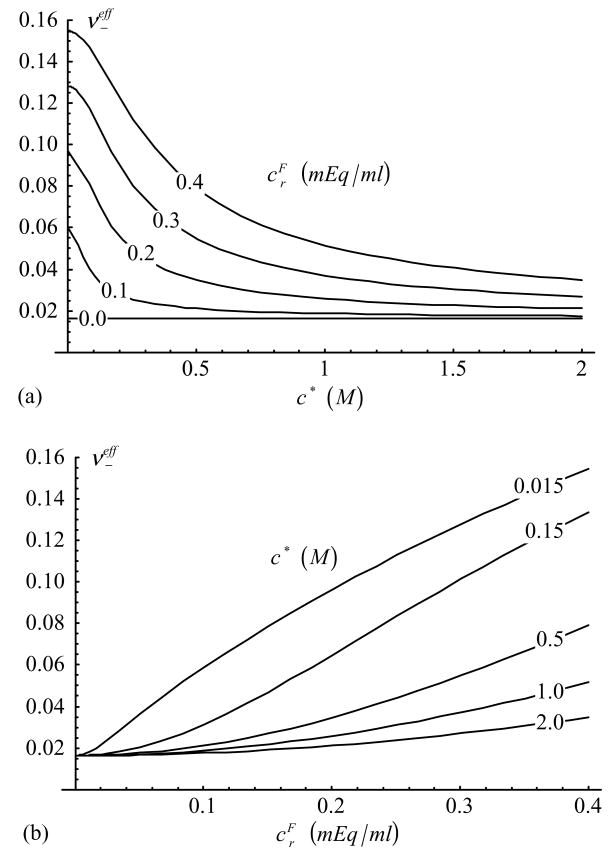
Effective Poisson’s ratio in compression, ${\nu }_{-}^{\mathit{eff}}$, as a function of (a) c^* and (b) $c_r^F$ [Eq.(37), with $H_A^{\mathit{eff}}\{E_{rr}\}=H_{+A}+\mathrm{\Pi }$)].

Figure 6.

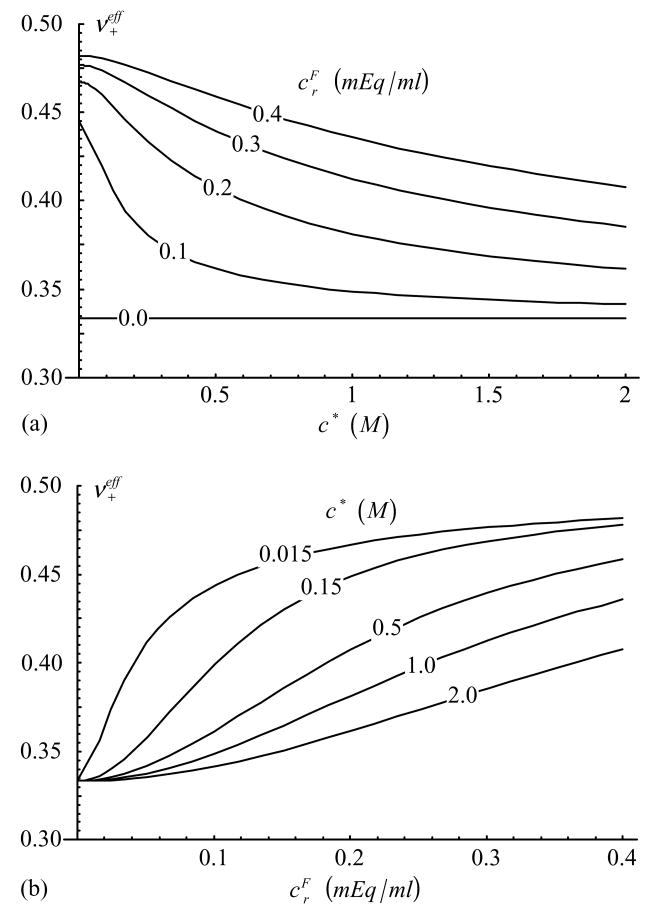
Effective Poisson’s ratio in tension, ${\nu }_{+}^{\mathit{eff}}$, as a function of (a) c^* and (b) $c_r^F$ [Eq.(37), with $H_A^{\mathit{eff}}\{E_{rr}\}=H_{-A}+\mathrm{\Pi }$)].

Discussion

The objective of this study was to formulate closed-form expressions for the equivalence of biphasic and triphasic equilibrium properties. Biphasic properties also represent effective, or measured, equilibrium properties typically reported in the literature. Many studies have shown that the equilibrium properties of articular cartilage depend on the bathing solution concentration as well as the fixed charge density in the tissue as described below. This dependence becomes explicit in the triphasic theory of Lai et al. (1991) and the results of this study provide straightforward formulas that express this dependence.

As expected from the earlier work of Lai et al. (1991), the formulas for the equilibrium moduli, $H_A^{\mathit{eff}},{\lambda }_2^{\mathit{eff}},E_Y^{\mathit{eff}}$, and Poisson’s ratio, ν^eff, depend not on the osmotic pressure π but on the rate of change of osmotic pressure with dilatation, Π; Eq.(23) can also be inferred directly from equation (2) of Narmoneva et al. (2001). Indeed, if the osmotic pressure in cartilage were to remain constant with even small changes in strain, it would not contribute to the stiffness of the tissue. In contrast, the swelling strains in confined and unconfined configurations depend on both π and Π.

Examining the response of Π in Figure 1, it is noted that this modulus decreases with increasing bathing solution salt concentration and increases with fixed-charge density. According to Eq.(26) the effective confined compression aggregate modulus, $H_{-A}^{\mathit{eff}}$, is obtained by simply adding the constant value H_−A to Π. The resulting response is in good agreement with the experimental data for articular cartilage in Figure 8 of the study by Eisenberg and Grodzinsky (1985), for the functional dependence of the aggregate modulus on salt concentration. The corresponding free-swelling strain predicted in Figure 2 also agrees with Figure 11 of these authors. The dependence of $H_{-A}^{\mathit{eff}}$ on proteoglycan content, and thus fixed charge density, has been verified in many experimental studies as well (e.g., Kempson et al., 1970; Mow et al., 1990; LeRoux et al., 2000; Rivers et al., 2000; Chen et al., 2001); for example, the experimental behavior observed in Figure 10A of Chen et al. (2001) is consistent with the response shown in Figure 1b of the current study.

The aggregate modulus in tension, $H_{+A}^{\mathit{eff}}$, is similarly predicted to depend on Π, and is thus a function of salt concentration and fixed charge density. In practice this property cannot be measured directly because it is predicated on a uniaxial tensile elongation with no lateral contraction, which is not experimentally feasible under general conditions. Consequently, there is no experimental study against which the theoretical expression for $H_{+A}^{\mathit{eff}}$ can be compared. It should be noted however that Narmoneva et al. (2001) inferred the value of H_+A by fitting experimental data to theory and found that this parameter was dependent on salt concentration; as mentioned above, the current analysis assumes that the intrinsic triphasic properties (such as H_+A) are constant, as a first approximation.

The value of ${\lambda }_2^{\mathit{eff}}$ is similarly obtained by adding the constant value λ₂ to Π (Figure 1), according to Eq.(35), where λ₂ < H_−A (Soltz and Ateshian, 2000a). To our knowledge, this theoretical relationship has not been described previously. Khalsa and Eisenberg (1997) performed experimental measurements of $H_{-A}^{\mathit{eff}}$ and ${\lambda }_2^{\mathit{eff}}$ in confined compression (see Figure 3 of their study) and found that they both decrease with increasing salt concentration, as predicted by the triphasic model expression derived in this study. Moreover, according to Eqs.(26)&(35), the difference $H_{-A}^{\mathit{eff}}-{\lambda }_2^{\mathit{eff}}=H_{-A}-{\lambda }_2$ is expected to remain independent of salt concentration (and fixed charge density, assuming that H_−A, λ₂ are indeed constant), which is reasonably well supported by Figure 3 of Khalsa and Eisenberg.

These authors also calculated the shear modulus from their experimental measurements, assuming standard theoretical relationships from linear isotropic elasticity, and found that the shear modulus remained constant at various salt concentrations (their Figure 4B). Though the current cubic symmetry formulation does not establish a relationship between μ and λ₂, it is nevertheless interesting that their conclusion regarding the shear modulus is in agreement with Eq.(38), which also finds that this parameter is independent of salt concentration. It should be noted that a later study by the same group (Bursac et al., 2000) did not confirm this earlier finding. Conversely, some experimental studies have shown that the shear modulus of articular cartilage decreases with loss of proteoglycans (Zhu et al., 1993; LeRoux et al., 2000), which is not predicted from the simple expression of Eq.(38). However, most of these experimental studies have involved degradative mechanisms of cartilage which may potentially have altered the properties of the collagen matrix.

The free-swelling strain in unconfined conditions (Figure 3) behaves similarly to the strain under laterally confined conditions (Figure 2), though it exhibits slightly smaller magnitudes. The theoretical dependence on salt concentration demonstrated in the model is in good agreement with various experimental studies (Maroudas, 1976; Myers et al., 1984; Setton et al., 1998; Narmoneva et al., 1999; Chahine et al., 2002b); for example, Figure 3a compares favorably with Figure 3 of Setton et al. (1998), where the stretch ratio is used as a measure of strain.

The dependence of Young’s modulus on Π is slightly more complex than in the case of the aggregate modulus, as shown in Eq.(32). According to theory, $E_Y^{\mathit{eff}}\le H_A^{\mathit{eff}}$ and these two measured properties can be equal to each other only when Π=0 and λ₂ = 0, conditions which are unlikely to happen in cartilage in general. The response of Young’s modulus in compression (Figure 4) is consistent with the compressive aggregate modulus, decreasing in magnitude with increasing salt concentration and decreasing fixed charge density. Our recent experimental results on the equilibrium response of articular cartilage in unconfined compression (Chahine et al., 2002b) confirm the theoretical finding of Figure 4a, showing a decrease in $E_{-Y}^{\mathit{eff}}$ with increasing salt concentration. However, in tension, the current theoretical model predicts very little dependence of $E_{+Y}^{\mathit{eff}}$ on salt concentration or fixed charge density. This can be seen from the formula of Eq.(32) with the proper substitution made for the tensile response,

$$E_{+Y}^{\mathit{eff}}\approx H_{+A}+\mathrm{\Pi }-\frac{2{({\lambda }_2+\mathrm{\Pi })}^2}{H_{-A}+{\lambda }_2+2\mathrm{\Pi }}.$$ (39)

In this expression, when Π ≫ H_−A, λ₂ (i.e., for low values of c^* and high values of $c_r^F$), it is found that $E_{+Y}^{\mathit{eff}}\approx H_{+A}$, whereas when Π ≪ H_−A, λ₂ (for high values of c^* and low values of $c_r^F$) this relation yields $E_{+Y}^{\mathit{eff}}\approx H_{+A}-2{\lambda }_2^2/(H_{-A}+{\lambda }_2)$, and since H_−A,λ₂ ≪ H_+A this expression also reduces to $E_{+Y}^{\mathit{eff}}\approx H_{+A}$. Consequently the theoretical model is unable to predict any significant dependence of the tensile Young’s modulus on salt concentration or fixed charge density, despite experimental indications that such a dependence does exist (Grodzinsky et al., 1981; Myers et al., 1984; Chahine et al., 2002b).

This study also establishes, for the first time to our knowledge, an expression for the dependence of the effective Poisson’s ratio on salt concentration and fixed charge density, Eq.(33). Conveniently, the dependence of ν^eff on $H_A^{\mathit{eff}}$ and ${\lambda }_2^{\mathit{eff}}$ maintains the same general form as in a linear elastic or biphasic-CLE cubic symmetry framework (Soltz and Ateshian, 2000), as shown in Eq.(37). Note that in a cubic symmetry framework, as in isotropic symmetry, the upper bound on ν^eff is 0.5; higher values of Poisson’s ratio can be achieved in an orthotropic symmetry framework, as shown in our recent study (Wang et al., 2003). The dependence of the compressive Poisson’s ratio, ${\nu }_{-}^{\mathit{eff}}$, on salt concentration and fixed charge density is shown in Figure 5, demonstrating that this parameter decreases with increasing c^* and decreasing $c_r^F$. The dependence on salt concentration agrees with the calculations of Khalsa and Eisenberg (1997) based on their experimental results for $H_{-A}^{\mathit{eff}},{\lambda }_2^{\mathit{eff}}$ (their Figure 4A), and with the direct measurements of Poisson’s ratio as a function of c^* in our recent study (Chahine et al., 2002a). The tensile Poisson’s ratio, ${\nu }_{+}^{\mathit{eff}}$, exhibits a similar trend (Figure 6) with respect to variations in c^* and $c_r^F$, and the dependence on c^* is also confirmed in our recent study (Chahine et al., 2002a). Furthermore, Poisson’s ratio in tension is significantly greater than in compression according to the model (Figure 5 and Figure 6) as supported by direct measurements of Poisson’s ratio reported in the literature (Woo et al., 1979; Jurvelin et al. 1997, Wong et al. 2000, Elliott et al., Chahine et al., 2002a).

An important prediction of the current model stems from the initial free swelling state of the tissue. Since the strain in the solid matrix is tensile in this initial configuration, the aggregate and Young’s moduli employ H_A {E _zz} = H_+A according to Eqs.(20), (25) and (32). Thus, as long as the applied compressive strain on the tissue is smaller in magnitude than the tensile swelling strain, the solid matrix remains in tension and the equilibrium modulus measured from such a compressive test would be equal to the tensile modulus of the solid matrix (e.g., on the order of 6 MPa for the representative properties used in this study). Only when the applied compressive strain magnitude exceeds the free swelling strain would the effective modulus reduce to the typical compressive properties, e.g., on the order of 0.5 MPa. This theoretical prediction, which may initially seem at odds with literature results, is in fact supported by our recent experimental studies where compressive strains of small magnitudes were applied relative to a free-swelling state, in an unconfined compression experiment (Chahine et al., 2002b); the initial Young’s modulus measured at 2% compression was as high as 9 MPa under hypotonic conditions, but reduced to 0.4 MPa under compressive strains of 10% or greater. This strain-softening effect, which was also noted to a smaller extent by Schinagl et al. (1997), Bursac et al. (1999, 2000), and Wang et al. (2003), will be addressed in greater detail in a future study. These results also suggest that the tensile modulus of cartilage is strain-dependent (rather than the constant modulus used in this study), as modeled for example by Li et al. (1999).

In summary, this study presents a series of simple formulas which relate biphasic and triphasic properties within a framework of cubic symmetry and a bilinear response in tension-compression. These expressions are derived from the nonlinear triphasic theory equations of Lai et al. (1991), coupled with the conewise linear elasticity theory of Curnier et al. (1995), using Taylor series expansions about the condition of zero strain. They help to explain why the equilibrium biphasic properties reported in the literature depend on the bathing solution salt concentration, the fixed charge density within the tissue, and the tensile or compressive nature of the strain. The theoretical behavior predicted from these expressions is shown to agree, at least qualitatively, with most experimental findings reported in the articular cartilage literature for the dependence of the equilibrium moduli, Poisson’s ratios, and swelling strains on bathing solution salt concentration. However the model in its current form does not predict the experimentally observed dependence of the tensile modulus on salt concentration. The experimentally observed dependence of the compressive modulus of cartilage on fixed charge density is well predicted by the expression presented here. The current study uses the theoretical model of the triphasic theory of Lai et al. (1991) and includes tension-compression nonlinearity of the solid matrix, as also described in our recent study (Ateshian et al., 2003). It offers newly derived formulas for the dependence of the tensile and compressive Young’s modulus and Poisson’s ratio, as well as the off-diagonal modulus, on proteoglycan fixed charge density and bathing solution salt concentration. This mathematical framework complements other models in the literature which have also examined the relationship between osmotic pressure and the equilibrium response of cartilage (Schwartz et al., 1994; Buschmann and Grodzinsky, 1995; Kovach, 1996; Basser et al., 1998; Narmoneva et al., 1999, 2001; Bursac et al., 2000). In future studies it will be shown that the transient response of biphasic and triphasic materials can also be related through the expressions derived here.