Two-Stage Capture Employing Active Transport Enables Sensitive and Fast Biosensors

Abstract

Nanoscale sensors enable the detection of analytes with improved signal-to-noise ratio but suffer from mass transport limitations. Molecular shuttles, assembled from, e.g., antibody-functionalized microtubules and kinesin motor proteins, can selectively capture analytes from solution and deliver the analytes to a sensor patch. This two-stage process can accelerate mass transport to nanoscale biosensors and facilitate the rapid detection of analytes. Here, the possible increase of the signal-to-noise ratio is calculated, and the optimal layout of a system which integrates active transport is determined.

One of the applications of nanoscale transport systems, such as molecular shuttles^1,2 and nanocars,(3) is the capture and concentration of biological analytes and their subsequent deposition at a sensing element. The goal of integrating active transport into a sensor platform is enhancing performance (quantified by sensitivity AND response time) by accelerating analyte transport to the sensor, because mass transport constitutes a bottleneck in platforms based on nanoscale sensing elements.^4,5

The inspiration for this approach is of biological origin, since motor proteins have been found to fulfill diverse transport functions within cells.(6) For example, certain viruses “hijack” motor protein transporters to accelerate their travel from the periphery of the cell to the nucleus.^7,8 Furthermore, a two-stage process of capturing an analyte on a surface followed by surface diffusion to the target site has been shown to be an effective approach to accelerate the interaction of dilute analytes with small target sites in a variety of biological situations.(9)

The pursuit of such a two-stage sensor platform, where analyte capture from solution is followed by a surface transport process, is enabled by the development of nanoscale sensing elements and of molecular shuttles capable of capturing and transporting analytes.¹⁰⁻¹⁴ Here, we calculate the potential payoff of this design and the optimal layout of a platform. We find that the accumulation of analyte at the sensor can be accelerated by several orders of magnitude, which would overcome the mass transfer limitations for nanoscale sensors pointed out by Sheehan and Whitman.(4)

Our argument is organized as follows: We consider a sensor site as it would exist on a microarray chip (Figure 1) and calculate the number of analyte molecules collected at the sensor patch if the analyte molecules reach the sensor patch by three-dimensional (3D) diffusion (Figure 1A), by 3D diffusion to the surface followed by two-dimensional (2D) diffusive transport(15) to the sensor patch (Figure 1B), and finally by 3D diffusion to the surface followed by directed transport^16,17 to the sensor patch (Figure 1C). We proceed to discuss the implications for the signal-to-noise ratio of the sensor platform and apply our calculations to published experiments.

Figure 1.

A biosensor, such as a microarray, frequently employs multiplexed sensor patches arrayed on a surface. Analytes may reach the sensor patches by (A) conventional 3D diffusion to the sensor patch of radius r, or two-stage capture of analytes by surface transporters operating in a compartment with radius R and moving to the sensor via (B) diffusive motion or (C) via directed movement along defined tracks.

Since we are interested in very low analyte concentrations (less than picomolar) and fast response times (less than 30 min available for the collection of analyte), we assume that (1) detection is limited by mass transport and not by the reaction rate between analytes and sensors,(18) (2) dissociation of captured molecules can be neglected, and (3) the saturation of sensors can be neglected. Our discussion thus assumes that during the <30 min available for capture, the capture rate is determined by the steady-state flux of the analyte to the sensor surface.

Single-Stage Analyte Capture

In conventional biosensors, analytes diffuse in 3D until they encounter the sensor and are captured. Under the assumptions stated above, the number of analytes N accumulated on a disk-shaped sensor of radius r can be calculated from the diffusion-limited analyte flux J_3D-r

The steady-state flux to a disk-shaped sensor in a dilute solution of analytes is J_3D-r = 4DCr, where D is the diffusion constant and C is the concentration of the analyte.(19) The number of analytes captured by the sensor patch in time t is then given by

In current microarrays, the sensor radius varies between 10 and 200 μm and a large number of analyte molecules is rapidly accumulated.²⁰⁻²² Unfortunately, the accumulation of analyte onto nanoscale sensors is extremely slow and necessitates collection times of many hours (Figure 2).^4,23 Techniques to increase the analyte flux, e.g., stirring or flow, are effective for sensors larger than 10 μm(21) but are not very effective in increasing the analyte flux to nanoscale sensors.(4) This partially negates the advantages of nanoscale sensors in the size range of 1 μm to 10 nm: a signal enhancement due to the capture of analytes into confined sensor patches,^5,24−28 and a reduction in the background noise due to the reduced area of detection.

Figure 2.

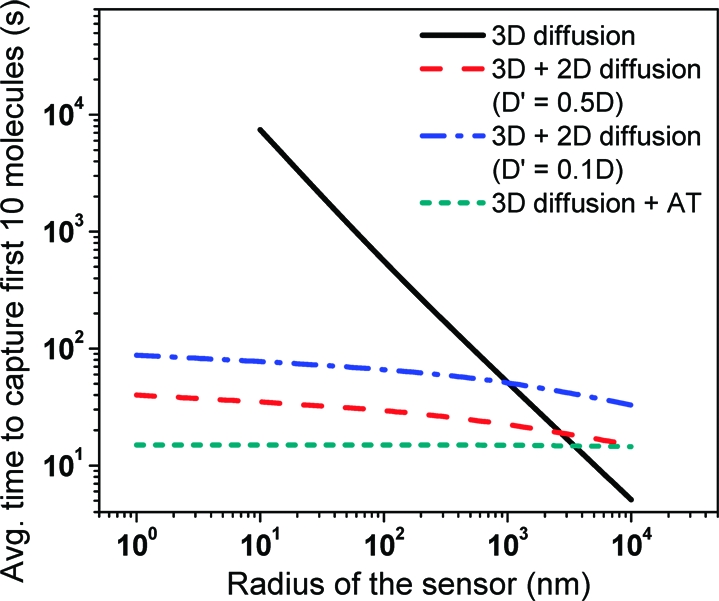
Time for capture of first 10 analyte molecules on a disk-shaped sensor of radius r by 3D diffusion, 3D + 2D diffusion and 3D diffusion followed by directed active transport of analyte. We assume a diffusion constant for 3D-diffusion of 80 μm²/s, 2D-diffusion constant is taken as one-half (∼microtubule diffusion constant on surface) or one-tenth (∼protein diffusion constant in a lipid bilayer) of the 3D-diffusion constant, an analyte concentration C of 1 pM, a compartment radius R of 100 μm, an active transport velocity of 0.5 μm/s, and a capture fraction f of 0.9.

Two-Stage Analyte Capture

Adam and Delbrück have shown that a two-stage capture process, where diffusion to a surface is followed by diffusion on the surface to a detection site, can increase the analyte flux to the sensor if the 2D surface diffusion constant is comparable to the 3D diffusion constant and the dissociation rate of analyte from the surface is small compared to the analyte capture rate.(9) In this situation, the number of analytes N at the sensor patch as a result of the surface transport can be calculated from

where N_s is the number of analytes on the surface at time t and τ_avg is the average time required for the analyte to find the sensor during the surface diffusion step.

The number of analytes at the surface N_s is determined by the 3D-diffusive flux J_3D-S of analytes to the surface of the sensor and the subsequent 2D-diffusive transport of these analytes to the sensor

A two-stage capture process can be facilitated by using molecular transporters that can capture the analytes from solution and transport them from the capture area to the sensor. Since the transporters do not cover the whole surface, the flux of analyte from solution to surface J_3D-S is a fraction f of the steady-state analyte flux to the capture area, which is assumed to be a circular surface compartment of radius R, from solution: J_3D-S = 4fDCR. The fraction f is a function of the number of transporters distributed over the compartment surface, but Berg and Purcell(29) have shown that even at low surface coverages it can be close to unity. Solving eqs 3 and 4 with initial conditions N_S = 0 at t = 0 and N = 0 at t = 0 yields the number of analytes captured at the sensor

The average duration of surface transport τ_avg depends on the geometry of the surface and sensor and the character of the transport (diffusive or directed). If the sensor patch is located in a circular compartment with radius R and the motion of the analyte transporter on the surface is diffusive, Purcell and Berg(29) have shown that τ_avg is given by

where D′ is the surface diffusion constant. If the motion of the analyte transporter is one-dimensional, i.e., directed toward the sensor, then the averaged time for analyte to reach the sensor is given by

where L_avg is the average distance traveled by a transporter to reach the sensor and v is the velocity of surface transport.

Supporting Information Available

Figures showing number of analytes collected for analyte diffusion as a function of compartment radius and optimum compartment size for a two-stage capture process. This material is available free of charge via the Internet at http://pubs.acs.org.