Dose Finding for Continuous and Ordinal Outcomes with a Monotone Objective Function: A Unified Approach

Summary

In many phase I trials, the design goal is to find the dose associated with a certain target toxicity rate. In some trials, the goal can be to find the dose with a certain weighted sum of rates of various toxicity grades. For others, the goal is to find the dose with a certain mean value of a continuous response. In this article, we describe a dose-finding design that can be used in any of the dose-finding trials described above, trials where the target dose is defined as the dose at which a certain monotone function of the dose is a prespecified value. At each step of the proposed design, the normalized difference between the current dose and the target is computed. If that difference is close to zero, the dose is repeated. Otherwise, the dose is increased or decreased, depending on the sign of the difference.

1. Introduction

Methodology for dose-finding trials in oncology is an evolving area. When cytotoxic drugs are being investigated, the primary outcome is usually toxicity, measured either as a binary or an ordinal outcome. For cytostatic drugs, the therapeutic response, measured as a continuous outcome, may be of primary interest. Cytostatic agents often target one specific process in the malignant transformation of cells and usually result in growth inhibition rather than tumor regression. Based on their specific mechanism of action, cytostatic agents are expected to have a more favorable toxicity profile (Hoekstra, Verweij, and Eskens, 2003). Because side effects are often less frequent with these agents, the dose of interest in this type of dose-finding trial may be defined by the biological activity of an agent, often measured as a continuous variable, rather than toxicity. For example, the primary endpoint in a trial of O⁶-benzylguanine for patients undergoing surgery for malignant glioma (Friedman et al., 1998) was inhibition of O⁶-alkylguanine-DNA-alkyltransferase (AGT) in brain tumors, measured as a continuous variable in fmol/mg. This inhibition was believed to decrease with dose. Several dose-finding problems where at least one of the outcomes is continuous have been previously studied in the literature (Eichhorn and Zacks, 1973; Berry et al., 2001; Bekele and Shen, 2005; Whitehead et al., 2006). Berry et al. (2001) and Bekele and Shen (2005) considered situations where the mean outcome was not necessarily a monotone function of dose. Here, we propose a design for the case where monotonicity of the outcome is assumed. Using the knowledge of monotonicity in the design of the study, and in the estimation procedure, can improve considerably the chances of selecting the correct dose at the conclusion of the study compared to situations where the assumption of monotonicity cannot be made.

The goal of most dose-finding trials for cytotoxic drugs is to find the dose that has a certain probability of dose-limiting toxicity. Sometimes the target dose is defined by using toxicity measured on an ordinal scale. Bekele and Thall (2004) presented an intuitive and flexible way to define the target dose in a trial with ordinal outcomes. The target dose was defined as the dose where a weighted sum of probabilities of the outcome categories is equal to a certain value. This effective way of aggregating different levels of toxicity is becoming popular. Ivanova (2006) described an example of a trial where an ordinal toxicity outcome was used to define the maximum tolerated dose (MTD). Bekele and Thall (2004) and Yuan, Chappell, and Bailey (2007) proposed Bayesian designs for such trials.

In this article, we will present a unified approach to dose finding in studies for which the outcome of interest is believed to be a monotone function of dose. The target dose will be defined as the dose at which the outcome of interest is equal to some prespecified value. We start in Section 2 by outlining the proposed method. In Section 3, the effect of design parameters on performance is investigated. In Sections 4, 5, and 6, we give examples of how to apply this new design to trials with continuous outcomes, ordinal toxicity outcomes, and binary outcomes. We also compare the new design with other existing methods. In Section 7, we present a discussion.

2. Notation and Methods

2.1 Defining the New Design

Let D = {d₁, …, d_K} denote the set of ordered dose levels selected for a trial. A subject's response at d_k has distribution function $F(\cdot ;{\mu }_k,{\sigma }_k^2)$, where (μ₁, …, μ_K) and $({\sigma }_1^2,\dots ,{\sigma }_K^2)$ are vectors of means and variances corresponding to D. Observations from different subjects are independent. Only one observation per subject is taken. The goal is to find dose d_m ∈ D such that μ_m = μ*. If there is no such dose, the goal is to find the dose d_m with μ_m closest to μ*. We refer to μ* as the target value and d_m as the target dose.

Subjects are assigned sequentially starting with the lowest dose. The total number of subjects is equal to M. Let n(t) = (n₁(t), …, n_K (t)) be the number of subjects at each of the K doses right after subject t, t ≤ M, has been assigned, that is, n₁(t) + ⋯ + n_K (t) = t. Let Y_ji be the observation from the ith subject assigned to dose d_j, i = 1, …, n_j (t). Let

$$\begin{array}{cc}\hfill & {\stackrel{-}{Y}}_j\left(n_j\left(t\right)\right)=\underset{i=1}{\overset{n_j\left(t\right)}{\Sigma }}{Y}_{\mathit{ji}}∕n_j\left(t\right)\text{and}\hfill \\ \hfill & s_j^2\left(n_j\left(t\right)\right)=\frac{{\displaystyle \underset{i=1}{\overset{n_j\left(t\right)}{\Sigma }}}{\{Y_{\mathit{ji}}-{\stackrel{-}{Y}}_j\left(n_j\left(t\right)\right)\}}^2}{n_j\left(t\right)-1}\hfill \end{array}$$

be the sample mean and variance computed from all available observations at d_j, n_j (t) = 2, 3 …. Define T_j(n_j(t)), n_j (t) = 2, 3 …, to be the t-statistic

$$T_j\left(n_j\left(t\right)\right)=\frac{\stackrel{-}{Y}\left(n_j\left(t\right)\right)-{\mu }^{\ast }}{s_j\left(n_j\left(t\right)\right)∕\sqrt{n_j\left(t\right)}}.$$

If s_j(n_j(t)) = 0, as it might be when F is discrete, T_j(n_j(t)) is equal to +∞ or −∞ depending on the sign of Ȳ_j(n_j(t)) − μ*. Subjects are assigned in cohorts or one at a time. Suppose the most recent subject t was assigned to dose d_j. The next subject is assigned as follows:

• (i) if T_j(n_j(t)) ≤ − Δ, the next subject is assigned to dose d_{j +1};

• (ii) if T_j(n_j(t)) ≥ Δ, the next subject is assigned to dose d_{j −1}; and

• (iii) if −Δ < T_j(n_j(t)) < Δ, the next subject is assigned to dose d_j.

Here Δ > 0 is the design parameter. The choice of the design parameter and its implications on design performance will be investigated in Section 3.

Several authors have indicated the usefulness and necessity of a start-up rule in toxicity dose-finding studies (Ivanova et al., 2003; Cheung, 2005). We recommend assigning at least two subjects to any untried dose before the dose can be escalated.

2.2 Computing the Distribution for Subject Allocation

One of the important characteristics of a dose-finding design is the allocation distribution achieved for small and moderate sample sizes. In this section, we describe how to compute the distribution of n(M), the number of subjects assigned to each dose by the time M subjects have been assigned, for a certain dose–response scenario. Without loss of generality assume that subjects are assigned in cohorts of equal size s, making the total number of cohorts equal to M/s. Denote by r_j the number of cohorts assigned to dose d_j, j = 1, …, K, at the time that all but one cohort has been assigned, r₁ + ⋯ + r_K = R = M/s − 1. Let X(r) ∈ D be the dose assigned to cohort r, r = 1, …, R+1. Let Ω_r be the outcome data accumulated after r cohorts, and let ${\Omega }_r^j$, j = 1, …, K, be the outcome data obtained at d_j after r assignments. To compute the distribution of n(M) one needs to compute the probabilities of all possible paths of the process {X(r), r = 1, …, R + 1}. In dose-finding trials X(1) is usually fixed, and therefore

$$\begin{array}{cc}\hfill \mathrm{Pr}& \{X\left(1\right)=x_1,X\left(2\right)=x_2,\dots ,X(R+1)=x_{R+1}\}\hfill \\ \hfill & =\mathrm{Pr}\{X\left(2\right)=x_2\mid X\left(1\right)=x_1,{\Omega }_1\}\hfill \\ \hfill & \times \mathrm{Pr}\{X\left(3\right)=x_3\mid X\left(2\right)=x_2,X\left(1\right)=x_1,{\Omega }_2\}\dots \hfill \\ \hfill & \times \mathrm{Pr}\{X(R+1)=x_{R+1}\mid X\left(R\right)=x_R,\dots ,X\left(1\right)=x_1,{\Omega }_R\}.\hfill \end{array}$$

The decision whether to escalate, repeat, or decrease the dose depends on the data accumulated at the current dose only, and thus

$$\begin{array}{cc}\hfill \mathrm{Pr}& \left\{X\left(1\right)=x_1,X\left(2\right)=x_2,\dots ,X(R+1)=x_{R+1}\right\}\hfill \\ \hfill & =\mathrm{Pr}\left\{X\left(2\right)=x_2\mid X\left(1\right)=x_1,{\Omega }_1^{x_1}\right\}\hfill \\ \hfill & \times \mathrm{Pr}\left\{X\left(3\right)=x_3\mid X\left(2\right)=x_2,{\Omega }_2^{x_2}\right\}\times \cdots \hfill \\ \hfill & \times \mathrm{Pr}\left\{X(R+1)=x_{R+1}\mid X\left(R\right)=x_R,{\Omega }_R^{x_R}\right\}\hfill \\ \hfill & =\prod _{r=1}^R\mathrm{Pr}\left\{X(r+1)=x_{r+1}\mid X\left(r\right)=x_r,{\Omega }_r^{x_r}\right\}.\hfill \end{array}$$ (1)

Define Υ = {1, …, R} and let S_j = {r ∈ Υ : x_r = d_j} be the set cohort numbers in Υ assigned to dose d_j, j = 1, …, K, with elements ${\alpha }_1^j<\cdots <{\alpha }_{r_j}^j$. Because Υ = S₁ υ … υ S_K, and sets S_j are disjoint, the product over assignments in (1) can be replaced by a product over S₁, …, S_K. So we have

$$\begin{array}{cc}\hfill \mathrm{Pr}& \left\{X\left(1\right)=x_1,X\left(2\right)=x_2,\dots ,X(R+1)=x_{R+1}\right\}\hfill \\ \hfill & =\prod _{j=1}^K\prod _{r\in S_j}\mathrm{Pr}\left\{X(r+1)=x_{r+1}\mid X\left(r\right)=d_j,{\Omega }_r^{d_j}\right\}.\hfill \end{array}$$ (2)

.

Define the intervals corresponding to the three possible decisions to increase, repeat, or decrease the dose as C₁ = (−∞, −Δ], C₀ = (−Δ, Δ), and C₋₁ = [Δ, +∞), so that

$$\begin{array}{cc}\hfill \mathrm{Pr}& \left\{X(r+1)-X\left(r\right)=\beta \mid {\Omega }_r^{X\left(r\right)}\right\}\hfill \\ \hfill & =\mathrm{Pr}\left\{T_{X\left(r\right)}\left(n_{X\left(r\right)}\left(\mathit{rs}\right)\right)\in C_{\beta }\mid {\Omega }_r^{X\left(r\right)}\right\}.\hfill \end{array}$$ (3)

Substituting (3) in (2), we obtain

$$\begin{array}{cc}\hfill \mathrm{Pr}& \left\{X\left(1\right)=x_1,X\left(2\right)=x_2,\dots ,X(R+1)=x_{R+1}\right\}\hfill \\ \hfill & =\prod _{j=1}^K\prod _{r\in S_j}\mathrm{Pr}\left\{T_j\left(\mathit{rs}\right)\in C_{x_{r+1}-x_r}\mid {\Omega }_r^{d_j}\right\}\hfill \\ \hfill & =\prod _{j=1}^K\prod _{j\in \{1,\dots ,K\}}\mathrm{Pr}\{T_j\left(s\right)\in C_{x_{{\alpha }_1^j+1}-x_{{\alpha }_1^j}},T_j\left(2s\right)\phantom{\}}\hfill \\ \hfill & \in C_{x_{{\alpha }_2^j+1}-x_{{\alpha }_2^j}},\dots ,T_j\left({\alpha }_{r_j}^{j}s\right)\hfill \\ \hfill & \phantom{\{}\in C_{x_{{\alpha }_{r_j}^j}-x_{{\alpha }_{r_j}^j}}\}.\hfill \end{array}$$

If F is the normal distribution function, these probabilities can be computed based on the joint distribution of sequential t-statistics, which can be obtained using the approach of Jennison and Turnbull (1991). The last step is to compute the distribution of n(M) using the probabilities of the paths {X(r), r = 1, …, R + 1}.

3. Choosing the Design Parameter

If the design parameter Δ is small, the current dose is repeated if the average response at it is very close to the target and changed otherwise. A narrow window (−Δ, Δ) results in a small probability of repeating a dose even if the true mean value of the quantity of interest at that dose is equal to μ*. In dose-finding trials it is often desirable to assign as many subjects as possible to the target dose. In this section, we will find Δ that maximizes the number of subjects assigned to the target dose and study how the choice of Δ affects design performance. The number of subjects assigned to the target dose depends on the dose–response model. We consider a set of dose–response models and compute the number of subjects assigned to the target dose averaged over the models in the set.

Consider a dose–response model where Y_j ~ N(μ_j, σ²) with μ_j = μ* + (j − k)β, j = 1, …, K, that is μ_j − μ_{j −1} = β for j = 2, …, K. When k = 1, …, K, we obtain a set of K dose–response scenarios with the target dose-taking values d₁, …, d_K. Because the operational characteristics of the design depend on β and σ only through β/σ, we set σ = 1. For each K, the number of doses, N, the total number of subjects in the trial, and β/σ, the goal is to find Δ that maximizes the number of subjects assigned to the target dose averaged over the K scenarios. The process of computing the expected number of subjects was described in Section 2.2.

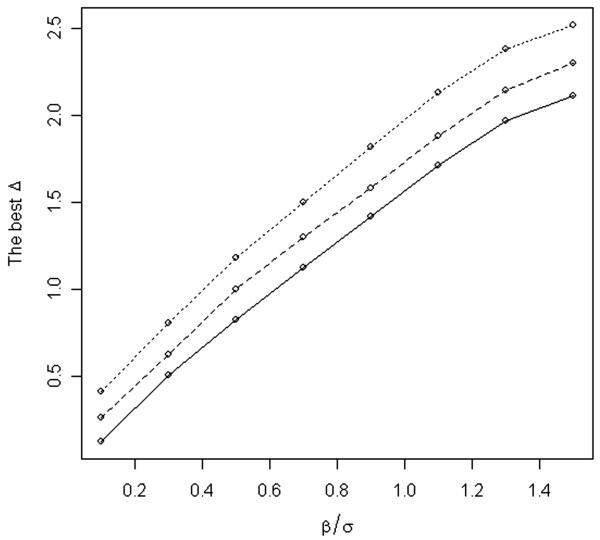
We considered scenarios with four and six doses and present the case with six doses in detail. For example, suppose we are interested in finding the best Δ to use in a trial with N = 8 cohorts of size s = 3 and β/σ = 0.3. Figure 1 presents a plot of the average number of subjects assigned to the target dose for several values of Δ. The optimal value of Δ is 0.54 yielding an average of 7.86 subjects assigned to the target dose out of the total of 24 subjects. Values of Δ in the range (0, 1) yield good averages for the number of subjects assigned to the target dose (Figure 1). Figure 2 displays the optimal values of Δ for a range of values β/σ for trials with N = 8 cohorts and s = 3 subjects per cohort (solid line). The optimal value of Δ was computed using function optim in R (R Development Core Team, 2007; http://www.R-project.org). Figure 2 also displays the optimal values of Δ for trials with N = 10 and 12. The optimal Δ increases as β/σ increases and as the number of cohorts N increases. As β/σ increases, doses become more spread out, and therefore it is beneficial to increase the window (−Δ, Δ). When the total number of “moves” N is small, it is advantageous to use a small window (−Δ, Δ) to be able to “move” faster from the lowest dose to the target dose. As N becomes larger the optimal window becomes larger. To approximate the best Δ, we fitted a linear model to the data presented in Figure 2 resulting in the formula ${\Delta }_{\mathrm{opt}}\approx -0.638+0.086N+0.854\beta \sqrt{s}∕\sigma$. Note that, for large values of $\beta \sqrt{s}∕\sigma$, Δ_opt does not increase linearly in $\beta \sqrt{s}∕\sigma$. When $\beta \sqrt{s}∕\sigma$ is large, computations similar to those described above should be repeated.

Figure 1.

The average number of subjects assigned to the target dose in a trial with eight cohorts, three subjects per cohort and β/σ = 0.3 for a range of values of the design parameter Δ. The number of subjects is maximized when Δ = 0.54.

Figure 2.

Optimal Δ for a range of β/σ. Optimal Δ was computed for trials with 8 cohorts (solid line), 10 cohorts (dashed line), and 12 cohorts (dotted line) and three subjects per cohort.

We investigated whether varying Δ in the course of a trial can lead to substantial improvements in design performance. We examined a design with two parameters Δ₁ and Δ₂. The first parameter Δ₁ was used for i = 1, …, k, whereas Δ₂ was used for i = k + 1, …, K. We maximized the number of subjects allocated to the target dose over (Δ₁, Δ₂, k). For example, for a trial with β/σ = 0.3 with eight cohorts and three patients per cohort, the optimal triple was (0.45, 1.05, 2) yielding 7.92 subjects assigned to the target dose. For comparison, a single Δ trial yielded 7.86 subjects at the target dose. In all the setups considered, the optimal pair was such that Δ₁ < Δ₂. It is logical to have Δ₁ < Δ₂, because a smaller Δ in the beginning results in a higher probability of changing the dose, thus increasing the chance of finding the target dose quickly. Because varying Δ did not lead to considerable gain, we recommend using a single Δ.

The optimal Δ depends on a dose–response scenario. We computed Δ that is optimal over a set of scenarios and is a function of β/σ. Obviously β/σ is not known before the trial to compute Δ_opt. Also the variances of Y_k can vary over doses and doses are not equally spaced. Our goal here was to give some guidelines for selecting Δ, keeping in mind that parameter values in a certain range of optimal values yield a similar average number of subjects assigned to the target dose (see, e.g., Figure 1). Suppose that we would like to compute the best Δ for a trial with binary toxicity outcomes targeting doses with toxicity rate of Γ = 0.2. The trial will accrue N = 8 cohorts with s = 3 subjects per cohort. Assume that the difference in toxicity rates between adjacent doses is 0.12, as that at the target dose $\beta ∕\sigma =0.12∕\sqrt{0.2\times 0.8}=0.3$, yielding Δ_opt = 0.54. In general, in toxicity trials with binary outcomes σ varies from 0.3 to 0.5 and the difference in toxicity rates between adjacent doses is about 0.05–0.20, yielding a range β/σ from 0.10 to 0.67. The best Δ for trials with N = 8, 10, 12 cohorts and s = 3 will be in the range of 0.20–1.40 (Figure 2). For example, a single toxicity observed in three subjects in a trial with Γ = 0.2 yields a value of the test statistic of 0.49, whereas two out of three toxicities yield 1.71; therefore a decision rule using any Δ in (0.29,1.51), will lead to repeating the dose if one out of three toxicities are observed and decreasing if two toxicities are observed. To illustrate the design performance we used Δ = 1 in the simulation study reported in Sections 5–7 with all models and outcome types. Our simulation study confirms that this is a reasonable choice of the design parameter.

We also investigated the impact of the cohort size on the average number of subjects assigned to the target dose in trials with the total sample size of 24. For β/σ = 0.3, the trial with N = 12, s = 2, and Δ_opt = 0.71 yielded 8.73 subjects assigned to the target dose; the trial with N = 8, s = 3, and Δ_opt = 0.54 yielded 7.86 assigned to the target dose; the trial with N = 6, s = 4, and Δ_opt = 0.40 yielded 7.16 subjects assigned to the target dose. Smaller cohort sizes yielded more subjects assigned to the target dose on average. This was expected, especially in this example where the number of doses is relatively large (six doses) compared to the number of cohorts (6, 8, and 12 cohorts).

4. Application to Dose Finding with Continuous Outcomes

4.1 A Numerical Example

To illustrate how to apply the new design in a trial with continuous outcomes we use data from Friedman et al. (1998). The goal of the trial was to find a dose that produces undetectable AGT activity. Friedman et al. (1998) dichotomized the continuous outcome at 10 fmol/mg for the purpose of constructing the dose-escalation rule. The trial accrued 30 patients; 3, 3, 13, and 11 patients to the doses 40, 60, 80, and 100 mg/m², respectively. As we illustrate here, it is easy to conduct the trial using a continuous outcome and therefore dichotomization is not needed. Suppose the goal is to find the dose with AGT activity equal to 5 fmol/mg protein. To construct an example of a trial with continuous outcomes, outcomes y_ij (Table 1) were selected randomly from the corresponding dose cohorts reported by Friedman et al. (1998). For example, y₃₁, y₃₂, y₃₃ were randomly selected from 13 outcomes reported at 80 mg/m². The hypothetical trial was stopped when the data at the 100 mg/m² dose-cohort were exhausted. Patients with undetectable AGT activity were assigned a value of 5 fmol/mg. Because the AGT activity was believed to be decreasing with dose, the dose was escalated for positive values of the t-statistics and deescalated for negative ones. Table 1 gives the averages of AGT activity, t-statistic, and decision for each dose cohort.

Table 1.

Example of a trial with continuous outcomes with subjects assigned in cohorts of three. The target AGT activity is 5 fmol/mg protein. Data were resampled from Friedman et al. (1998). The new design with Δ = 1 is used.

	Ȳj	t-statistic	Decision
Dose 1, 40 mg/m2
(y11, y12, y13) = (26.35, 42.00, 15.00)	27.78	2.91	Increase the dose to 60 mg/m2
Dose 2, 60 mg/m2
(y21, y22, y23) = (23.00, 13.50, 10.83)	15.78	2.92	Increase the dose to 80 mg/m2
Dose 3, 80 mg/m2
(y31, y32, y33) = (11.70, 9.03, 5.00)	8.58	1.84	Increase the dose to 100 mg/m2
Dose 4, 100 mg/m2
(y41, y42, y43) = (4.07, 5.00, 8.70)	5.92	0.65	Repeat the dose at 100 mg/m2
(y44, y45, y46) = (2.50, 4.07, 6.13)	5.08a	0.09a	Repeat the dose at 100 mg/m2
(y47, y48, y49) = (3.60, 5.00, 5.00)	4.90a	−0.18a	Repeat the dose at 100 mg/m2
(y410, y411) = (6.80, 6.60)	5.22a	0.43a	Repeat the dose at 100 mg/m2

^aCalculated based on the combined sample.

4.2 Comparison with the Feasible Sequential Procedure of Eichhorn and Zacks (1973)

For continuous outcomes, Eichhorn and Zacks (1973) proposed a feasible sequential search algorithm for finding the largest dose x such that Pr{Y (x) < μ* | x} ≥ γ, where γ is a tolerance probability. The main assumption was that response Y (x) given x is normal with mean bx and variance σ²x², where σ² is known and b > 0 is unknown. The dose x₀ = 0 was assumed to be the dose below which the response is negligible. It was also assumed that a dose $x_0^{\ast }$ such that $x_0^{\ast }$ is below the target dose is known. Eichhorn and Zacks' sequential search algorithm operates on a continuous dose space and is from a class of feasible procedures. A procedure is feasible if, for each new assignment, the probability that the dose is higher than the target does not exceed α. Eichhorn and Zacks' sequential algorithm can be briefly described as follows. If observations y₁, …, y_n at doses x₁, …, x_n have been obtained, the next dose is

$$\begin{array}{cc}\hfill x_{n+1}& =\max \left[x_0^{\ast },{\mu }^{\ast }/\left\{U_n+\sigma \left(\frac{Z_{1-\alpha }}{\sqrt{n}}+Z_{\gamma }\right)\right\}\right],\text{where}\hfill \\ \hfill U_n& =\max \left(0,\frac{1}{n}\underset{i=1}{\overset{n}{\Sigma }}\frac{Y_i}{x_i}\right),\hfill \end{array}$$

and Z_γ denotes the upper 100_γ% point of the standard normal distribution.

We compared our proposed design with the method of Eichhorn and Zacks (1973) for normally distributed outcomes. We set γ = 0.5, so that the problem considered by Eichhorn and Zacks (1973) is the same as the problem we consider (because the distribution of Y is symmetric). The value of $x_0^{\ast }$ is set to 1. The first comparison is made for a model where Y (x) given x has a normal distribution with mean 0.1x and variance 0.1²x² with dose levels from the set (1, 2, 3, 4, 5, 6) (model I in Table 2). For model I we considered six different values for the target, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, which correspond to the target dose being dose 1, 2, 3, 4, 5, and 6, respectively. The second comparison was made for a model where Y (x) given x is normal with mean 0.5 + 0.1x and variance 0.1²x² (model II in Table 2). For model II we considered six different target values, 0.6, 0.7, 0.8, 0.9, 1.0, 1.1, corresponding to the target dose being dose 1, 2, 3, 4, 5, and 6. To accommodate a discrete set of dose levels, the dose from the set 1, 2, 3, 4, 5, 6 closest to x_n+1 is chosen in Eichhorn and Zacks' procedure. When the target dose was dose 1, a sample size of 15 was used; for all other targets a sample size of 60 was used. Simulation results were obtained by simulation with 4000 replicates.

Table 2.

Proportion of times each dose is recommended as the target dose and the average number of subjects allocated to each dose for the new design with Δ = 1 (ND) and the search procedure of Eichhorn and Zacks (EZ). Subjects are assigned one at a time. The total sample size is 15 when target is at d₁, and 60 in all other cases. Results for the dose–response scenario 0.1d, where d ∊ {1, 2, 3, 4, 5, 6}, are indicated by I, and results for the dose–response scenario 0.5 + 0.1d, where d ∊ {1, 2, 3, 4, 5, 6}, are indicated by II. Results at the target dose are in bold.

	Percent recommendation						Allocation proportion
	d1	d2	d3	d4	d5	d6	d1	d2	d3	d4	d5	d6
					Target at d1
ND, I, II	0.91	0.09	0.00	0.00	0.00	0.00	11.9	2.9	0.2	0.0	0.0	0.0
EZ, α = 0.05, I	0.99	0.01	0.00	0.00	0.00	0.00	15.0	0.0	0.0	0.0	0.0	0.0
EZ, α = 0.5, I	0.89	0.10	0.01	0.00	0.00	0.00	12.1	1.8	0.4	0.1	0.1	0.6
EZ, α = 0.5, II	0.99	0.01	0.00	0.00	0.00	0.00	14.8	0.2	0.0	0.0	0.0	0.0
					Target at d2
ND, I, II	0.04	0.89	0.07	0.00	0.00	0.00	8.8	39.2	11.0	1.0	0.0	0.0
EZ, α = 0.05, I	0.08	0.90	0.02	0.00	0.00	0.00	28.6	31.2	0.2	0.0	0.0	0.0
EZ, α = 0.5, I	0.00	0.93	0.07	0.00	0.00	0.00	5.2	45.0	7.2	1.1	0.4	1.1
EZ, α = 0.5, II	0.90	0.10	0.00	0.00	0.00	0.00	0.0	54.4	5.5	0.2	0.0	0.0
					Target at d3
ND, I, II	0.01	0.12	0.73	0.13	0.01	0.00	2.4	11.6	33.0	11.2	1.6	0.2
EZ, α = 0.05, I	0.00	0.32	0.64	0.04	0.00	0.00	4.3	38.6	16.5	0.5	0.0	0.0
EZ, α = 0.5, I	0.00	0.06	0.80	0.13	0.01	0.00	1.4	9.5	35.0	9.9	2.0	2.2
EZ, α = 0.5, II	0.64	0.29	0.07	0.00	0.00	0.00	39.1	17.4	3.4	0.1	0.0	0.0
					Target at d4
ND, I, II	0.00	0.04	0.21	0.59	0.14	0.12	2.0	3.5	15.0	26.8	10.5	2.2
EZ, α = 0.05, I	0.00	0.00	0.47	0.46	0.06	0.00	1.9	9.1	37.6	10.6	0.0	0.0
EZ, α = 0.5, I	0.00	0.00	0.13	0.67	0.12	0.02	1.1	1.2	12.9	27.8	11.0	6.1
EZ, α = 0.5, II	0.08	0.32	0.52	0.09	0.00	0.00	9.0	24.7	22.9	3.2	0.1	0.0
					Target at d5
ND, I, II	0.00	0.01	0.05	0.28	0.48	0.18	2.0	2.4	5.2	17.3	22.3	10.9
EZ, α = 0.05, I	0.00	0.00	0.02	0.53	0.36	0.08	1.3	3.0	15.7	31.2	7.8	1.0
EZ, α = 0.5, I	0.00	0.00	0.00	0.19	0.57	0.25	1.1	0.3	2.2	14.4	22.9	19.1
EZ, α = 0.5, II	0.00	0.01	0.34	0.56	0.08	0.01	1.6	7.9	27.2	20.2	2.9	0.2
					Target at d6
ND, I, II	0.00	0.00	0.03	0.06	0.31	0.60	2.0	2.1	3.1	7.2	18.2	27.4
EZ, α = 0.05, I	0.00	0.00	0.00	0.08	0.52	0.40	1.1	1.4	5.4	20.7	24.1	7.3
EZ, α = 0.5, I	0.00	0.00	0.00	0.00	0.24	0.76	1.0	0.1	0.7	3.4	14.8	40.0
EZ, α = 0.5, II	0.00	0.00	0.01	0.41	0.49	0.09	1.1	3.0	10.7	26.6	15.7	2.9

Table 2 displays the proportion of runs each dose was recommended as the target dose and the dose allocation. Eichhorn and Zacks (1973) recommended using a feasibility level of α = 0.05, because the procedure was proposed for an outcome reflecting very poor toxicity. When α = 0.05, the procedure is conservative and yields low percentages of correct recommendation (lines titled EZ, α = 0.05, I) when the target is at doses 4, 5, and 6. For that reason, we also simulated Eichhorn and Zacks' procedure with α = 0.5 (lines titled EZ, α = 0.5, I). When α = 0.5 and γ = 0.5, the formula for next dose assignment simplifies to $x_{n+1}=\max (x_0^{\ast },{\mu }^{\ast }∕U_n)$, that is, no feasibility restrictions on assignments are imposed. As expected, when the true dose–response model is linear in dose the procedure of Eichhorn and Zacks performs very well (lines titled EZ, α = 0.5, I). However, for model II where the mean is 0.5 + 0.1x the procedure of Eichhorn and Zacks does not perform well (lines titled EZ, α = 0.5, II). The main conclusion from this simulation study is that in the case of linear dose response with no intercept, our new method performed reasonably well detecting the correct target dose in 9% fewer cases than the method of Eichhorn and Zacks that was specifically designed for this dose–response relationship (compare lines ND, I, II, and EZ, α = 0.5, I). The procedure of Eichhorn and Zacks performed poorly for model II. At the same time, our method is robust to the shift in the mean and performs exactly the same in models I and II.

The estimate of the target dose in our method was obtained from the isotonic estimate of the dose–response curve, whereas in Eichhorn and Zacks' procedure the estimate was obtained from fitting a linear model without an intercept to the data. In simulations with model I, if a linear model estimate was used in our method, the percentages of correct selection were nearly identical to these of Eichhorn and Zacks' procedure. The reverse was also true. This suggests that for model I both methods provide good quality data for estimation with many assignments at and around the target dose.

5. Application to Dose-Finding Trials with Ordinal Outcomes

We applied our method to a trial with ordinal toxicity outcome described in Bekele and Thall (2004). The outcome of interest is a toxicity score whose expected value is a weighted sum of rates of different toxicity grades and types. The goal was to estimate the dose with mean toxicity score 3.04. The weights and the target value were determined by physicians and we refer the reader to Bekele and Thall (2004) for the description of their Bayesian design. Thirty-six subjects were assigned in groups of four. The starting dose was d₂. We simulated the new design for all six scenarios considered in Bekele and Thall (2004) and show the results of these simulations in Table 3. Results for the new design were obtained by simulation with 4000 replicates. To estimate the target dose after the trial for the new design, we first obtained the isotonic estimate of the mean function. The dose with the estimated value of the function closest to 3.04 was declared the estimated target dose. If there were two or more such doses, the highest dose with the estimated value below 3.04 was chosen. If all the estimated values at these doses were higher than 3.04, the lowest of these doses was chosen.

Table 3.

Proportion of times each dose is recommended as the target dose and the average number of subjects allocated to each dose for the new design with Δ = 1 (ND) and the design of Bekele and Thall (BTD). Subjects are assigned in cohorts of 4. The total sample size is 36. Results for BTD are reproduced from Bekele and Thall (2004). Results at the target dose are in bold.

		d1	d2	d3	d4	d5	d6	d7	d8	d9	d10
				Scenario 1
ND	Proportion recommended	0.00	0.86	0.14	0.00	0.00	0.00	0.00	0.00	0.00	0.00
	Allocation	1.2	17.3	12.5	5.0	0.0	0.0	0.0	0.0	0.0	0.0
BTD	Proportion recommended	0.01	0.94	0.05	0.00	0.00	0.00	0.00	0.00	0.00	0.00
	Allocation	2.2	21.8	5.3	5.6	1.1	0.0	0.0	0.0	0.0	0.0
				Scenario 2
ND	Proportion recommended	0.04	0.95	0.01	0.00	0.00	0.00	0.00	0.00	0.00	0.00
	Allocation	5.7	18.0	8.0	4.3	0.0	0.0	0.0	0.0	0.0	0.0
BTD	Proportion recommended	0.04	0.92	0.04	0.00	0.00	0.00	0.00	0.00	0.00	0.00
	Allocation	4.5	22.0	4.5	4.6	0.4	0.0	0.0	0.0	0.0	0.0
				Scenario 3
ND	Proportion recommended	0.00	0.00	0.00	0.00	0.85	0.15	0.00	0.00	0.00	0.00
	Allocation	0.0	0.0	0.0	8.2	20.6	6.8	0.4	0.0	0.0	0.0
BTD	Proportion recommended	0.00	0.00	0.00	0.06	0.85	0.09	0.00	0.00	0.00	0.00
	Allocation	0.0	0.0	0.0	5.6	18.5	9.7	2.1	0.1	0.0	0.0
				Scenario 4
ND	Proportion recommended	0.00	0.00	0.00	0.03	0.94	0.03	0.00	0.00	0.00	0.00
	Allocation	0.0	0.0	0.1	11.3	20.6	4.0	0.0	0.0	0.0	0.0
BTD	Proportion recommended	0.00	0.00	0.00	0.05	0.87	0.08	0.00	0.00	0.00	0.00
	Allocation	0.0	0.0	0.1	6.6	20.6	7.7	1.0	0.0	0.0	0.0
				Scenario 5
ND	Proportion recommended	0.00	0.00	0.00	0.00	0.00	0.02	0.07	0.85	0.06	0.00
	Allocation	0.0	0.0	0.0	4.3	4.4	4.7	7.9	11.8	2.8	0.1
BTD	Proportion recommended	0.00	0.00	0.00	0.00	0.00	0.00	0.10	0.81	0.09	0.00
	Allocation	0.0	0.0	0.0	4.1	4.1	4.1	5.7	11.4	5.6	1.0
				Scenario 6
ND	Proportion recommended	0.00	0.00	0.00	0.00	0.00	0.01	0.06	0.90	0.03	0.00
	Allocation	0.0	0.0	0.0	4.1	4.1	4.4	7.9	12.9	2.6	0.0
BTD	Proportion recommended	0.00	0.00	0.00	0.00	0.00	0.00	0.14	0.80	0.06	0.00
	Allocation	0.0	0.0	0.0	4.0	4.0	4.1	5.7	11.7	5.8	0.7

The methods were compared with respect to the percentage of time the target dose was correctly selected and the proportion of subjects assigned to each dose. A comparison of the new design with Δ = 1 with the design of Bekele and Thall (2004) slightly favors the new design overall. The new design yields a higher probability of correctly selecting the target dose in four out of six scenarios. More importantly, it assigns fewer patients to doses higher than the target dose in four out of six scenarios.

Some outcomes, for example, myelosuppression, were measured on a continuous scale. If our method is used, there is no need to convert a continuous outcome to an ordinal one to score the outcome. Instead, the continuous outcome can be scored, and this and scores from ordinal and binary variables can be used to compute the average score for a patient.

6. Note on the Application to Toxicity Studies

The new design was developed for trials with ordinal or continuous outcomes. However, it can be used with binary outcomes. Numerous designs have been developed for dose-finding trials with binary outcomes (Wetherill, 1963; O'Quigley, Pepe, and Fisher, 1990; Babb, Rogatko, and Zacks, 1998). The continual reassessment method (CRM) has been shown to perform very well in dose finding (O'Quigley et al., 1990; O'Quigley and Chevret, 1991; Faries, 1994). Cheung and Chappell (2000) simulated the CRM for five scenarios from O'Quigley et al. (1990). We compared the new design with the CRM using all five scenarios. The goal was to estimate the dose with the probability of toxicity of Γ = 0.2. Subjects were assigned one at a time starting with the lowest dose. The total number of subjects was either 25 or 48. As suggested in Section 2, at least three subjects were assigned to any untried dose before it was escalated. Estimation of the target dose after the trial was carried out as described in Section 5. We simulated the new design with Δ = 1 and show the results of these simulations in Table 4. Results were obtained by simulation with 4000 replicates. As seen from Table 4, the performance of the new design is worse than that of the CRM for scenarios 1, 3, and 4; however, the new design performs substantially better in scenario 5. In scenario 5, the CRM fails to converge to the target dose (Cheung and Chappell, 2002) and therefore its performance is poor in this scenario. Allocations of subjects as far as overdosing are comparable for the new design and the CRM across all five scenarios.

Table 4.

Proportion of times each dose is recommended for the new design with Δ = 1.0 (ND) and the CRM. Subjects were assigned one at a time. The total sample size, n, is 25 and 48. Results for the CRM are reproduced from Cheung and Chappell (2000). The target is Γ = 0.2.

	Percent recommendation						Allocation
	d1	d2	d3	d4	d5	d6	d1	d2	d3	d4	d5	d6
Scenario 1	0.05	0.10	0.20	0.30	0.50	0.70
					n = 25
ND	0.06	0.20	0.45	0.26	0.03	0.00	5.1	7.4	7.8	3.8	0.9	0.1
CRM	0.01	0.20	0.49	0.29	0.02	0.00	4.0	6.4	8.6	5.2	0.7	0.0
					n = 48
ND	0.01	0.16	0.56	0.26	0.01	0.00	5.2	11.5	18.8	10.5	1.9	0.1
CRM	0.00	0.14	0.63	0.23	0.00	0.00	4.2	10.3	21.3	11.4	0.8	0.0
Scenario 2	0.30	0.40	0.52	0.61	0.76	0.87
					n = 25
ND	0.91	0.08	0.01	0.00	0.00	0.00	20.8	3.7	0.5	0.0	0.0	0.0
CRM	0.92	0.07	0.01	0.00	0.00	0.00	20.5	3.6	1.8	0.1	0.0	0.0
					n = 48
ND	0.98	0.02	0.00	0.00	0.00	0.00	42.5	4.8	0.6	0.1	0.0	0.0
CRM	0.98	0.02	0.00	0.00	0.00	0.00	42.5	4.6	0.8	0.1	0.0	0.0
Scenario 3	0.05	0.06	0.08	0.11	0.19	0.34
					n = 25
ND	0.03	0.05	0.12	0.30	0.34	0.16	4.8	5.0	5.0	4.7	3.7	1.8
CRM	0.00	0.03	0.12	0.39	0.41	0.05	3.7	4.0	5.2	6.7	4.4	1.0
					n = 48
ND	0.00	0.01	0.04	0.20	0.56	0.18	4.8	5.4	6.9	9.6	13.5	7.7
CRM	0.00	0.01	0.05	0.40	0.51	0.04	3.7	4.5	7.0	15.8	15.1	1.9
Scenario 4	0.06	0.08	0.12	0.18	0.40	0.71
					n = 25
ND	0.05	0.10	0.25	0.46	0.14	0.00	5.4	5.8	6.11	5.2	2.3	0.3
CRM	0.01	0.07	0.26	0.54	0.12	0.00	4.0	4.8	6.7	7.4	2.1	0.2
					n = 48
ND	0.00	0.04	0.19	0.64	0.12	0.00	5.7	7.3	10.5	16.2	7.7	0.7
CRM	0.00	0.03	0.22	0.68	0.07	0.00	4.1	5.9	12.0	21.7	4.1	0.2
Scenario 5	0.00	0.00	0.03	0.05	0.11	0.22
					n = 25
ND	0.00	0.00	0.01	0.10	0.34	0.56	3.0	3.1	4.0	4.5	5.3	5.1
CRM	0.00	0.00	0.00	0.10	0.61	0.29	3.0	3.0	3.2	4.9	7.5	3.4
					n = 48
ND	0.00	0.00	0.00	0.01	0.28	0.71	3.0	3.1	3.9	5.2	11.6	21.2
CRM	0.00	0.00	0.00	0.02	0.60	0.38	3.0	3.0	3.2	6.1	21.6	11.1

7. Discussion

In this article, we present a unified approach to dose-finding trials with a monotone objective function. The method is general and can be used with a variety of response types. Possible applications of our proposed methodology include trials with continuous and ordinal outcomes. Also, the design can be used in trials with bivariate outcomes, as in Ivanova (2003), as long as the function of interest is monotone in dose.

In this article, we have assumed that the mean response was monotone in dose. We used isotonic estimates of the mean responses at the end of the trial. One can compute the iso-tonic estimates of the mean responses at each step, and then use the isotonic estimate at the current dose in place of a sample mean. Using isotonic estimates improves the design performance somewhat for binary and ordinal outcomes, and more so for continuous outcomes, especially if the variability of the outcome is high. Leung and Wang (2001) used isotonic estimates of toxicity rates in their design, but proposed a different decision rule. To make an assignment, they considered the current dose, as well as the two adjacent doses, and then selected the dose with the estimated mean response closest to the target. Let us consider an example of a trial where the current dose is dose d_j and dose d_j+1 has two subjects assigned, with one of them having toxic response and the other having a nontoxic response. The probability of observing one or more toxicities out of two assignments if the true toxicity rate is 0.2 is rather high (0.36). If the target toxicity rate is 0.2, Leung and Wang's (2001) decision rule would not assign any more subjects to d_j+1 and higher dose levels. This would result in a very conservative assignment rule. Ivanova and Flournoy (2008) have compared several designs based on the isotonic estimation of dose-toxicity curve in trials with binary outcomes. Their simulation results gave strong evidence that the decision rule in an isotonic design, which uses the current dose only, is far superior to decision rules that use more doses.

On the flip side, the question of how to handle cases where the lowest dose is very safe but the next higher dose is unsafe, needs to be considered. Our proposed design would oscillate between the two doses, thereby possibly exposing subjects to a highly toxic dose. This problem is a problem of the initial incorrect choice of dose levels, and as such, it is hard to remedy with any design. For trials where there is a danger of assigning subjects to highly toxic doses, we suggest putting an additional rule in place that prevents assigning subjects to a dose if there is evidence that its mean toxicity score is higher than allowable. One can then use the sequential probability ratio test, or some other type of sequential stopping boundary. For example, Ivanova, Qaqish, and Schell (2005) described how to set up a boundary for continuous monitoring of toxicity, where the toxicity outcome was binary. Such stopping boundaries are especially useful in cases where the lowest dose appears to be highly toxic and therefore these boundaries should be used routinely in conjunction with either the CRM, or our proposed design, in oncology dose-finding trials. Another way to avoid rapid escalation when using our proposed design, which has been suggested by the associate editor, is to use an asymmetric interval in the decision rule. Here, the dose is repeated if the test statistic is in the interval (−Δ₁, Δ₂) with Δ₁ ⪢ Δ₂, and is changed if it is not.

In the examples presented in this article, the design parameter was chosen before the trial. However, and especially in the case of continuous outcomes, it might be worth tuning the design parameter during the trial as information on the spacing between doses, and the variance of the outcome, becomes available. The optimal parameter would be chosen to maximize the number of subjects assigned to the target dose. It might be even more important to maximize the proportion of trials that select the target dose correctly. Our extensive simulation study shows that the same, or nearly the same parameter Δ, maximizes the proportion of correct recommendations. (Simulation study results are available from the authors on request.) In some trials, the goal might be to estimate a dose with mean response μ*, where the estimate d* is not necessarily in D (Ivanova, Bolognese, and Perevozskaya, 2008). Because d* is estimated by interpolation, Δ = 0 would work well because it maximizes the assignments to the two doses adjacent to d*.