Abstract
Human mitoNEET is a homodimeric iron-sulfur protein located in the outer mitochondrial membrane with unknown function, but which is known to interact with thiazolidinedione diabetes drugs. Each monomer houses a [2Fe-2S] cluster with an unusual (Cys)3(His)1 ligation. The His ligand is important for enabling cluster release and for tuning the redox potential. We use multi-frequency (X-, Ka-, Q-band) and multi-technique (CW, ESEEM, ENDOR, HYSCORE) EPR spectroscopy to investigate the cluster in its paramagnetic reduced [Fe2+Fe3+] (S = 1/2) state. It has a rhombic g-tensor (2.007, 1.937, 1.897) with an average g-value of 1.947 that falls between those of Rieske-type and ferredoxin-type [2Fe-2S] clusters. Simulation and least-squares fitting of orientation-selective Ka- and Q-band ENDOR, 1D ESEEM and HYSCORE spectra of 14N and 15N-labelled mitoNEET yield the principal values and orientations of both the hyperfine tensor (14N: Aiso = −6.25 MHz, T = −0.94 MHz) and the quadrupolar tensor (e2Qq/h = −2.47 MHz, η = +0.38) of the ligating histidine nitrogen Nδ. From these, we can infer the absolute g tensor orientation with respect to the cluster: The g2 axis is close to perpendicular to the [2Fe-2S] plane, and g1 and g2 are in-plane, but skewed from the Fe-Fe and S-S axes. In X-band ENDOR and ESEEM spectra, a weakly coupled nitrogen is visible, most likely the Nε of the histidine in the protonated state. We find that the cluster is in a valence-localized state, where Fe2+ is His-bound. The field-sweep spectra show evidence of inter-cluster dipolar coupling that can be simulated using an uncoupled spin model for each cluster (SFe2+ = 2, SFe3+ = 5/2). The parameters determined in this work can function as reporters on how the cluster structure is altered upon pH changes and drug binding.
Introduction
Iron-sulfur clusters compose the redox centers of a diverse family of proteins, which abound in nature and show a broad range of biochemical activities. These functional variations are due to the fact that the iron-sulfur core can exist in an array of cluster sizes with different redox properties, e.g., [2Fe-2S], [3Fe-4S], [4Fe-4S], [8Fe-7S]. Even [2Fe-2S] cluster proteins are diverse in function, depending on the cluster’s ligand types, their orientations, and the local hydrogen bonding arrangement. Interestingly, reduction potentials vary greatly among protein bound [2Fe-2S] clusters, even among those with identical ligands and similar geometries. For example, Rieske-type [2Fe-2S] proteins have reduction potentials that range from −150 mV to +400 mV, even though they are all structurally very similar.1 [2Fe-2S] proteins participate principally as electron transport mediators, including proton-coupled electron transport. Additionally, they act as regulatory agents, sulfur donors, and participate as cellular oxygen sensors.2-6
A recently discovered [2Fe-2S] protein has received a new structural classification.7,8 Named mitoNEET, (mito) for its location in the outer mitochondrial membrane, and (NEET) for containing the amino acid sequence (Asn-Glu-Glu-Thr), this integral membrane protein incorporates a CDGSH (zinc-finger) binding domain with a redox-active [2Fe-2S] cluster. X-ray crystal structure analysis reveals that human mitoNEET is a homodimer with one [2Fe-2S] cluster per monomer.7,9,10 Ligand coordination of each Fe ion in all [2Fe-2S] clusters is essentially tetrahedral and includes, in addition to the cluster sulfide ions, two amino acid residues per iron. Previous to the discovery of mitoNEET, [2Fe-2S] clusters had been categorized as being either ferredoxin-type, where each Fe is bound to two cysteine sulfur atoms, (Cys)2FeS2Fe(Cys)2, or Rieske-type, where one Fe ion is bound to two cysteine sulfur atoms and the other Fe is bound to the Nδ atoms of two histidine ligands, (His)2FeS2Fe(Cys)2. Although other ligand arrangements are also known,11,12 mitoNEET is unusual in that it was the first reported protein with a (Cys)(His)FeS2Fe(Cys)2 configuration (Fig. 1). As in Rieske centers, the histidine binds to the cluster via the Nδ nitrogen.
Figure 1.
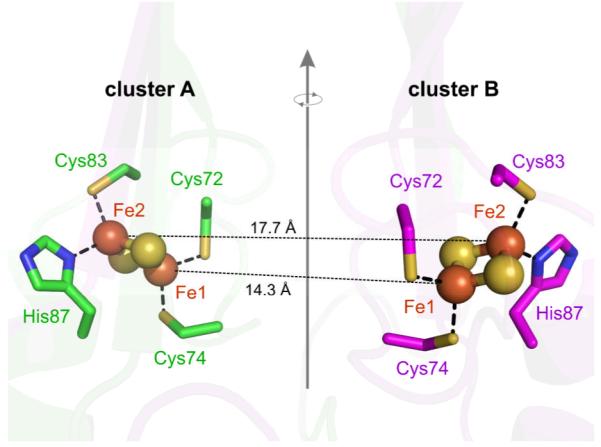
Crystal structure of the two [2Fe-2S] clusters in human mitoNEET (pdb 2QH7) and their ligand environments The two cluster sites are by a rotation around a two-fold symmetry axis.
Sharing the CDGSH domain are two human paralogs, Miner1 and Miner2. A recent X-ray structure of Miner1 shows a similar fold and a [2Fe-2S] cluster bound via the same (His)1(Cys)3 coordination as mitoNEET.13 Although the structure of Miner2 is not yet solved, it shares with the other family members similar absorbance peaks and reversible reduction with dithionite and oxygen.8 The only unrelated protein to show a (3-Cys, 1-His) ligand coordination is the D38A mutant of the iron-sulfur scaffolding protein IscU.12,13 However, in this case, it is the Nε of the histidine ligand that binds to the cluster, making the mitoNEET family and IscU proteins distinct in their ligand organization. The characteristic (3-Cys, 1-His) coordination invokes the question as to how the singly bound histidine is associated with the scaffolding role proposed for IscU and how this relates to the function of mitoNEET.
MitoNEET has other properties that support a functional role related to cluster motility. It was shown that a decrease in pH decreases the stability and increases the redox potential of the cluster in the mitoNEET protein.8,14 The cluster lability may be related to mitoNEET’s functional role in the mitochondria, perhaps as a cluster assembly, storage, or shuttling agent. The cluster is stabilized by adding the thiazolidinedione (TZD) class of insulin-sensitizing drugs, as well as by phosphate buffer.8,15,16 Additional stabilization effects have been observed for the mutant H87C where the ligating histidine in each [2Fe-2S] cluster is replaced by a cysteine.14,17
The aim of this work is to investigate the [2Fe-2S] cluster environment of mitoNEET using multi-frequency (X-,Ka,-, Q-band) electron paramagnetic resonance (EPR) spectroscopy; electron spin echo envelope modulation (ESEEM), pulsed electron-nuclear double resonance (ENDOR), and hyperfine sublevel correlation spectroscopy (HYSCORE) on native and isotopically labeled mitoNEET and the H87C mutant. We determine the g-tensor of the cluster, and the full hyperfine and nuclear quadrupolar interaction tensors of the coordinating histidine nitrogen, including all orientations. Using a single parameter set to simultaneously simulate orientation-selected multi-frequency and multi-technique datasets (continuous-wave EPR, ESEEM, ENDOR, HYSCORE) assures a high accuracy of our computational analysis. We are thus able to provide a quantitative bonding description for a model (i.e., single nitrogen) system that can serve as a benchmark for studying more complicated (e.g., Rieske) systems. The characterization of this cluster-ligand interaction provides a foundation for the investigation of the pH dependent cluster lability, mitoNEET’s potential to bind to TZD drugs, and other properties. Understanding the bonding interaction may provide clues for determining the mechanism by which the cluster uncouples from its binding pocket.
Materials and Methods
Sample preparation
Cytoplasmic domains of native and H87C mitoNEET grown in natural abundance 14N were constructed, expressed, and purified as described previously.7,8 Protein was purified to crystal quality assessed by the optical ratio A280/A458 ≤ 2.3. Stock protein solutions were stored at greater than 1 mM concentration.
15N-MitoNEET-Fusion Construct Cloning
In order to increase expression in minimal media for isotopic substitution, a fusion construct was used for 15N-mitoNEET. The portion of the CISD1 cDNA encoding the cytoplasmic part of mitoNEET (residues 33-108) was subcloned into a modified pET28-a(+) vector (Novagen) that contained the superfolder GFP cDNA.18 MitoNEET was subcloned downstream of the superfolder cDNA using the restriction site BamHI. A thrombin cleavage site and small linker were added upstream of the mitoNEET cDNA through PCR amplification of the mitoNEET cDNA using the forward primer 5′-GGCGGATCCTCTGGCCTCGTCCCTCGTGGCTCTGGCATGAGATTTTA TG- 3′ and reverse primer 5′ – GCCGCCGGATCCTTAAGTTTCTTTTTTCTTGATGTCAG - 3′. The resulting construct was confirmed by sequencing. The crystal structure of the native mitoNEET using this same fusion construct is essentially the same as that obtained in the absence of the fusion.19
Expression of the fusion protein, fusion cleavage, and mitoNEET purification
E. coli BL21-CodonPlus(DE3)-RIL cells were transformed with the sfGFP-mitoNEET cDNA construct and were grown in M9 minimal media (MM) or LB supplemented with 30 μg/mL kanamycin and 34 μg/mL chloramphenicol. For 15N material, (15NH4)2SO4 (supplied by Isotech Laboratories, Inc. Champaign, IL) was used in the M9 media. Cells were grown and induced as described previously.8 Following addition of FeCl3 and induction by IPTG, the cells were grown for 16 hours, then harvested by centrifugation and lysed by sonication. (NH4)2SO4 was added to the lysate to 60% saturation, which leads to precipitation of the mitoNEET protein that was collected as a pellet by centrifugation. The pellet was solubilized in approximately 50 – 100 mL cleavage buffer (50 mM Tris-HCl pH 8.0, 100 mM NaCl, 2 mM CaCl2), and thrombin (3 mg/mL) was added to a final concentration of 0.1 mg/mL. This solution was dialyzed at 4°C overnight against 4 L with one change of the cleavage buffer. After 24 hours, the thrombin inhibitor PPAC was added to the dialysate, which was then dialyzed against 4 L of 50 mM Tris-HCl pH 8.0 for an additional 16 hours at 4°C. To separate mitoNEET from the sfGFP and other contaminating proteins, the solution was loaded onto a 5 mL cation exchange column (S HP Hi-Trap, GE Healthcare), and mitoNEET was purified as described previously. 7 The mitoNEET fractions were further purified on a 30 × 2cm S-100 size exclusion column (GE Healthcare) equilibrated with 50 mM Tris-HCl pH 8.0 and 100 mM NaCl. The mitoNEET fractions from the size exclusion chromatography were pooled and concentrated to 10 mg/mL. Protein purity was assessed to be >99% using SDS-PAGE and an A278/A458 optical ratio of < 2.3. The protein concentrations were determined by electronic absorption spectroscopy using ε278 = 9.13 mM−1 cm−1.
Preparation of the paramagnetic spin state
Excess dithionite was added to ≈ 3 mM of the mitoNEET preparation to fully reduce the [2Fe-2S] clusters. After incubating for ≈ 30 s and observing a change in the color, the sample was then diluted to ≈ 0.5 - 0.8 mM mitoNEET in 50% glycerol and equilibrated in 100 mM Tris-HCl pH 8.0, loaded into the EPR sample tube and frozen in liquid nitrogen. Partially reduced mitoNEET was obtained similarly, by adding 3 mM of dithiothreitol to ≈ 1 mM mitoNEET preparation followed by dilution and buffer equilibration. The optical spectrum (data not shown) shows the reduction of about 50% of all clusters. All frozen solution samples were analyzed in the reduced state by EPR spectroscopy. Mastigocladus laminosus ferredoxin (Fdx) was expressed and purified as previously described,20 and the EPR sample was made as described above.
CW and Pulsed Electron Paramagnetic Resonance
All EPR data were collected at the CalEPR center at UC Davis. Continous-wave (CW) X-band (≈ 9.5 GHz) spectra were acquired in a Bruker ECS 106 spectrometer at 10 K in an Oxford ESR 900 liquid helium cryostat using an Oxford ITC503 temperature controller. X-band and Ka-band (≈ 31 GHz) ESEEM data were collected on home-built spectrometers described elsewhere.21,22 Two-pulse ESEEM experiments used the pulse sequence (π/2 – τ – π – τ – echo), incrementing the time τ between the π/2 and π pulses to produce a spin-echo, while three-pulse ESEEM used a (π/2 – τ – π/2 – T – π/2 – τ – echo) sequence to produce a stimulated spin-echo, incrementing the pulse delay time T. Two-step and four-step phase cycles were used for the 2-pulse and 3-pulse ESEEM respectively.23,24 X-band Mims ENDOR (π/2 –τ – π/2 – πRF– π/2 – echo) and Q-band (≈ 34 GHz) ESEEM, ENDOR, and HYSCORE data were performed on a Bruker E580 spectrometer. All data were acquired at 12 K.
All time domain ESEEM data were baseline corrected and scaled such that the data point with maximum intensity was set to unity. Damping effects caused by relaxation were removed by fitting 3rd order polynomials. Spectra were then windowed using Hann apodization, zero filled, and fast Fourier transformed into the frequency domain. Spectral simulations were carried out using Easyspin 3.0.25,26
Orientation selection
Typically, for transition metal complexes and clusters, the EPR line width is significantly wider than the microwave pulse excitation bandwidth. Thus, pulsed experiments performed at different magnetic fields selectively report on only the centers with certain orientations with respect to those fields. This results in distinguishable ESEEM or ENDOR patterns at different “observer” fields across the EPR envelope, making it possible to determine through numerical simulation the orientations of the hyperfine and the nuclear quadrupole tensors relative to that of the g-tensor. Each orientation is described by a set of three Euler angles (α, β, γ).27 Ka-band and Q-band orientation-selected ESEEM spectra were collected at a minimum of 10 magnetic field positions across the EPR spectrum. Orientation-selected Q-band Davies ENDOR (πinversion – πRF – π/2 – τ – π – echo) was collected at 11 magnetic field positions. Q-band HYSCORE (π/2 – τ – π/2 – t1 – π – t2 – π/2 – τ –echo) was taken at 2 field positions, nearthe low-field edge and at the spectral maximum.
EPR theory
A strong antiferromagnetic exchange coupling between the electron spins of two Fe3+ (S1 = S2 = 5/2) ions gives an “epr silent” (diamagnetic) ground state with effective spin S = 0 in the oxidized state as previously reported for native mitoNEET.8 If we assume a localized reduction of one of the iron ions from Fe3+ to Fe2+ upon reduction of the cluster (vide infra), the antiferromagnetically coupled Fe3+ (S1 = 5/2) Fe2+ (S2 = 2) cluster has an effective ground spin state of S =1/2.
In many metalloprotein systems, hyperfine interactions between the electron spins and many coupled nuclei cause an inhomogeneous broadening of the EPR spectrum. This prohibits the resolution of any distinguishable electron-nuclear coupling. Using advanced EPR methods, it is possible to resolve the coupling interactions of the electron spin with that of nearby magnetic nuclei. In this work, we are targeting the nitrogen nuclei of the [2Fe-2S] histidine ligand. The effective spin Hamiltonian used to describe an S = 1/2, I = 1 (e.g., 14N) system is
| (1) |
The first two terms describe the field-dependent energy of the electron and nuclear spins respectively in a static magnetic field, where βe, βn are the Bohr and nuclear magneton respectively, h the Planck constant, gn the nuclear g-value, and g the electron g-tensor. The last two orientation-dependent terms describe the field-independent hyperfine interaction ( Ŝ · A · Î ) and nuclear quadrupolar coupling ( Î · P · Î ). In its eigenframe, the matrix form of the P-tensor is
| (2a) |
| (2b) |
with |Px| ≤ |Py| ≤ |Pz|. As it is traceless, the P-tensor is typically expressed by two values, a coupling parameter e2Qq/h and an asymmetry parameter η, ranging from 0 to 1 (axial to rhombic). These parameters are valuable in reporting on the symmetry of the electronic environment, on the type of nitrogen, and its protonation state.
The nuclear spin transitions may be directly detectable using the complementary pulsed ENDOR and pulsed ESEEM/HYSCORE methods. All of these techniques use microwave pulse sequences to generate an electron spin-echo signal that reports on the coupled nuclei in a way specific to the applied pulsed method. ENDOR techniques directly monitor the effect radio-frequency radiation resonant with the nuclear spin has on the amplitude of electron spin echo, as the radio frequency is varied. To avoid using slow repetition rates required at low temperature due to long nuclear spin relaxation, we applied random RF sampling rather than the traditional linear RF sweep. This also reduces the effects of baseline distortions and asymmetric ENDOR intensities often encountered by sweeping the radio frequency.28,29 ESEEM methods monitor the amplitude of the electron spin echo as the time between pulses is incrementally increased. The time-domain data illustrate the change in echo amplitude (modulation) as a function of the inter-pulse delay. By transforming the time domain data into the frequency domain, it is possible to obtain direct information regarding nuclear spin transition frequencies and consequently the hyperfine interaction energies. Detailed descriptions of the theory of these techniques are accessible in several review articles.30-34
Nuclei with I = 1/2 (e.g., 15N) do not have a quadrupole moment. The spin Hamiltonian therefore reduces to the first three terms in Eq. (1). For an axially symmetric hyperfine interaction with principal values
| (3a) |
where Aiso is the isotropic component (Fermi contact term) and T is the anisotropic component (dipolar term), the nuclear spin transition frequencies for a given molecular orientation with respect to the static magnetic field are
| (3b) |
| (3c) |
| (3d) |
These transition frequencies are valid for both ENDOR and ESEEM. For ENDOR, the angular distribution of transition frequencies produces ideal powder patterns, whereby it is possible to determine the anisotropic hyperfine interaction separately from the isotropic portion. However, for the ESEEM time domain, an additional term accounts for the angular dependence of the intensity of the modulation and is reflected in the shape of the lines of ESEEM spectra. This modulation depth parameter
| (4) |
has a strong angular dependence in the non-secular (B) term, returns a modulation depth of zero for ϑ = 0 and π/2, and thus nulls the intensity at the turning points observed in the ENDOR-type powder pattern. ESEEM spectra, therefore, contain limited anisotropic information except under special matching conditions such as we report herein.
Results
X-band CW and Ka-band/Q-band Electron Spin Echo Field Swept Spectra of MitoNEET
The X-band EPR spectra of native mitoNEET fully reduced (with dithionite) and partially reduced (with dithiothreitol) are shown in Fig. 2. The spectra are characteristic of an S = 1/2 system with a rhombic g tensor. The spectrum of the fully reduced form shows a splitting on the low-field peak and a shoulder in the mid-field feature, which are due to the dipolar interaction between the two clusters separated only by about 16 Å (see Fig. 1). This splitting is not resolved at Ka band, as seen in Fig. 3, top. Simulation of the Ka-band spectrum assuming a single isolated cluster gives a rhombic g tensor with principal values g1 = 2.007, g2 = 1.937, and g3 = 1.897. The small features in Fig. 2 at low and high-field flanking the rhombic g signal are currently not understood. Their intensity varies from sample to sample and is not correlated to the degree of reduction.
Figure 2.
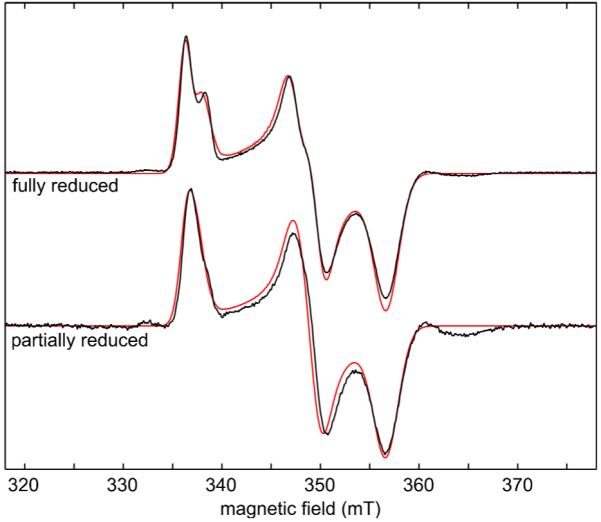
Experimental (black) and simulated (red) X-band CW EPR spectra of fully and partially reduced mitoNEET. Experimental parameters: frequency 9.475 GHz, power 10 μW, field modulation 8 G at 100 kHz, temperature 20 K. Simulation parameters: g tensor values from Ka band simulations (Fig. 3), g Euler angles in pdb frame for cluster A: (−28.3°, 33.4°, 102.7°), dipolar tensor estimated using Eq. (6).
Figure 3.
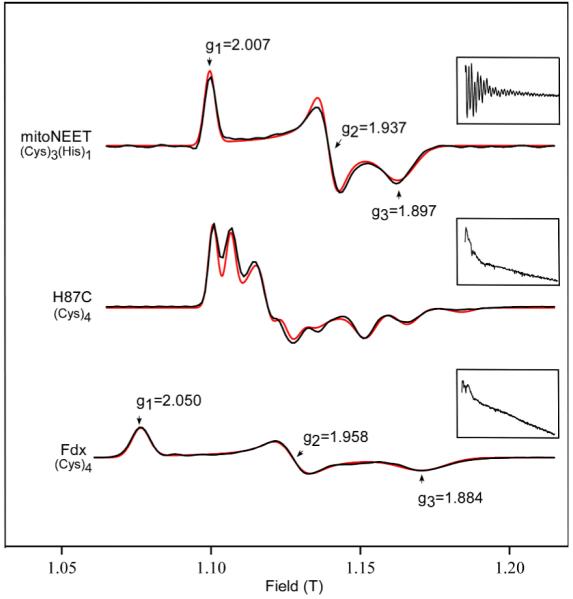
Numerical derivatives of Ka-band echo-detected field swept spectra of WT mitoNEET, H87C mitoNEET, and ferredoxin. Black: experimental data, red: simulations. Experimental conditions: frequency 30.89 GHz, π/2 width 20 ns, τ 330 ns, π width 40 ns, repetition time 5 ms, temperature 12 K. Simulation parameters for 3 contributing species of H87C: 55% g = (2.005, 1.974, 1.916). 36% g = (1.993, 1.962, 1.895), 9% g = (1.995, 1.948, 1.864). Insets: Ka-band 3-pulse ESEEM traces. Experimental conditions: frequency 30.89 GHz, π/2 width 10 ns, τ 250 ns, initial T 70 ns, T increment 20 ns, repetition time 5 ms, temperature 12 K.
The X-band spectra in Fig. 2 can only be simulated by taking both clusters, A and B, into account and by employing an uncoupled spin model35-37 to describe the dipolar interaction between them. In this model, each Fe ion is treated separately either as ferric (Fe3+, spin 5/2) or ferrous (Fe2+, spin 2), and the inter-cluster dipolar interaction tensor D for a model where the clusters are represented by SA = SB = 1/2 is given by the sum of the individual dipole tensors dij over all inter-cluster ion pairs
| (5) |
where i (j) runs over the ions in cluster A (B), rij is the corresponding inter-ion distance, nij is the unit vector along the line connecting the two ions, gAi and gBj are the intrinsic g-tensors of the individual ions, and kAi and kBj are the spin projection factors (7/3 for Fe3+ and −4/3 for Fe2+).38,39 rij and nij can be obtained from the crystal structure (pdb 2QH7), but the intrinsic g-tensors are not known. If we approximate them with the average g value gavg, we get
| (6) |
This tensor depends on how the oxidation states are assigned to the sites in each cluster. There is one Fe3+ and one Fe2+, so there are two possible assignments. Assuming first that the non-histidine coordinated inner Fe ions (see Fig. 1) are reduced, the principal values of the dipolar tensor are 2.4, 5.5, and −7.9 MHz, whereas when the histidine-coordinated outer ones are reduced, they are 34.4, 35.2 and −69.6 MHz. This stark difference in magnitude between the two assignments stems from the fact that in the first assignment, the Fe3+-Fe3+ and Fe2+-Fe2+ terms in Eq. (6) are of similar magnitude and almost cancel with the two Fe3+-Fe2+ terms that have opposite sign. In the second assignment the two ions with larger spin projection factors (Fe3+) are closer to each other, so that the Fe3+-Fe3+ term is much larger than the other three. Clearly, only the second set of values is large enough to lead to an observable splitting in the X-band spectrum. Using this dipolar tensor (including its computed orientation) and the g values from the Ka band simulations, the X-band spectra can be simulated and fitted by varying the orientations of the g tensors relative to each cluster. The same g tensor orientation relative to the cluster was used for both sites, since they are related by rotation around a two-fold symmetry axis. From our analysis, we obtained two possible g-tensor orientations for the two clusters, described relative to the pdb frame by Euler angles (−28.3°, 33.4°, 102.7°) and (151.9°, 146.7°, −116.1°). We do not have complete confidence in these fitted orientations, as they are based on an approximate estimation of the dipolar tensor D. However, one of the orientations is surprisingly consistent with what can be inferred from the analysis of the hyperfine and nuclear quadrupolar interactions, as discussed below. The best-fit simulations are shown in Fig. 2. The splitting on the low-field peak in the fully reduced sample is reproduced, including the relative intensities of the split features. To confirm that the observed splitting is due to inter-cluster dipolar coupling, we made a partially reduced sample where about half of the clusters were reduced, as evident from the optical spectrum. This should result in a 1:2:1 distribution of non-reduced, mono-reduced and direduced mitoNEET if we assume that the influence of the oxidation state of one cluster on the reduction potential of the other is negligible. The simulation of the EPR spectrum of this sample (Fig. 2, bottom) reveals a ratio of 2.3:1 between mono-reduced and direduced proteins, which is close to the expected ratio of 2:1. The partially reduced sample therefore confirms the dipolar origin of the observed splitting in the fully reduced sample. These simulations unequivocally and quantitatively show that the histidine-coordinated Fe ions are reduced. Iwasaki et al. reached a similar conclusion from a more qualitative analysis of the X-band spectra of rat mitoNEET.36
The Ka-band spectrum of the histidine mutant H87C, shown in Fig. 3, middle, which we use as a control in our ESEEM analysis, is dramatically different from the native form. It is also very rich compared to spectra from ferredoxin (Fig. 3, bottom). Even though it has the same (Cys)4 coordination. Examination of the X-band spectrum of the H87C mutant (not shown) precludes the possibility of a dipolar interaction since the size of the observed splittings scales with the magnetic field. The only way we could simulate the H87C spectrum was by assuming three different contributing species with slightly different g values. The average g value of all three component g tensors is 1.96, as for most ferredoxin clusters.
Ka-band ESEEM detects nitrogen from histidine ligand
The X-, Ka- and Q-band EPR spectra of mitoNEET are unaltered upon global 15N isotopic substitution (data not shown), indicating that the Fe—Nδ histidine hyperfine interaction is small and can possibly be targeted by ESEEM. To capture deep modulation patterns from the histidine nitrogen, the appropriate spectrometer frequency is required. This is achieved in the so-called cancellation regime where the hyperfine interaction energy is approximately equal to twice the nitrogen Larmor frequency at a resonant field position, whereby the effective field in one electron manifold is nearly cancelled (Eq. (3b)). Given that the sign of the hyperfine interaction term is yet undetermined, we arbitrarily label the transition in the cancelled manifold as να. X-band ESEEM and HYSCORE have been successfully applied to investigate the Fe—Nδ histidine interactions of Rieske centers. Reported 14N hyperfine coupling ranges for the ligating nitrogens of the two histidines are 3.4 – 4.7 MHz for N1 and 4.6 – 5.5 MHz for N230,40-53. While many of these couplings have been detected with X-band ESEEM methods, the modulation depth is attenuated for these moderately strong couplings at these relatively low microwave frequencies. We chose to collect ESEEM data on our two available mid-frequency spectrometers, operating at Ka-band (≈ 31 GHz) and Q-band (≈ 34 GHz).
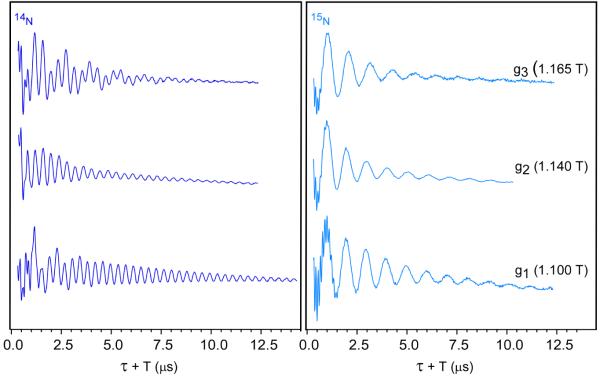
Three-pulse ESEEM experiments of the reduced mitoNEET protein taken at the canonical field positions reveal pronounced modulation patterns for both 15N labeled and natural-abundance 14N forms (Fig. 4). Verification that the ESEEM signal did indeed arise from the targeted cluster-histidine interaction came from a parallel set of Ka-band 3-pulse ESEEM experiments on native mitoNEET, H87C, and ferredoxin (Fig. 3, insets). The spectra for H87C and Fdx were measured at their spectral maxima, and the one for native mitoNEET at the same field as H87C. Deep modulation is observed for native mitoNEET, whereas modulation is essentially absent for the H87C mutant and the ferredoxin sample. This demonstrates that the modulation observed for native mitoNEET is arising from the strongly coupled nitrogen on His87.
Figure 4.
Ka-band 3-pulse ESEEM at g1, g2, and g3 field positions for 14N natural abundance mitoNEET (left) and 15N-globally labeled mitoNEET (right). Data were collected under the following conditions; π/2 width 10 ns, τ 250 ns, initial T 70 ns; T increment 20 ns, frequency 30.89 GHz, repetition time 5 ms, temperature 12 K.
Estimation of 15N Hyperfine Parameters from Ka- and Q-band ESEEM
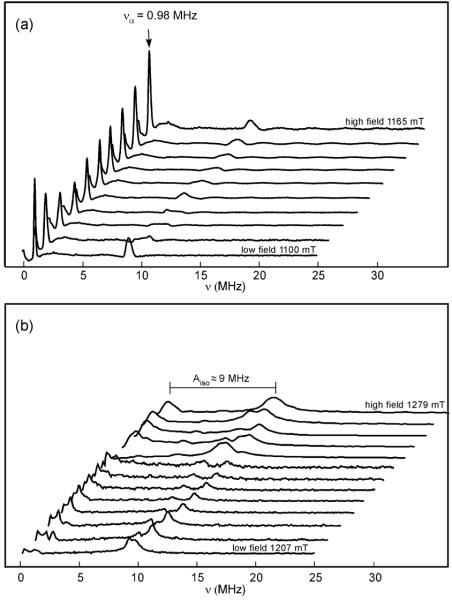
Notable modulation patterns are observed in Ka-band ESEEM spectra of global 15N substituted mitoNEET (Fig. 4). I = 1/2 nuclei, such as 15N, lack nuclear quadrupolar interactions, which can provide the off-diagonal elements in the spin Hamiltonian required to mix nuclear spin states and to drive both the allowed and semi-forbidden EPR transitions necessary to induce echo modulation. Therefore, I = 1/2 nuclei rely on the anisotropic portion of the hyperfine interaction to induce appreciable modulation. This corresponds to the non-secular term (B) of the modulation depth parameter, k (Eq. 4). Furthermore, k reaches a maximum value, thus deepest modulation, when the cancellation condition
| (7) |
is met. In this regime, the angular independent portion of the secular hyperfine term (A in Eq. (3c)) cancels the effect of the nuclear Zeeman interaction in one electron manifold (α), and produces a narrow low-frequency dispersionless peak with frequency
| (8) |
unaffected by orientation selection across the envelope.54-57 This allows for a direct estimate of the hyperfine anisotropy. Such a peak is observed in 15N 3-pulse ESEEM spectra at every field position (Fig. 5a), with a frequency of να = 0.98 MHz. From this, we estimate the 15N dipolar hyperfine coupling to be T = 1.30 MHz. Within the cancellation regime, broader weaker peaks are expected at ≈ 2νn and were observed at ≈ 9-10 MHz. Using Eq. (7) and the Larmor frequency of 4.88 MHz (1.13 T), we estimate Aiso = 9.10 MHz. Increasing the microwave frequency from 31 GHz (Ka-band) to 34 GHz (Q-band) eliminates the narrow low-frequency singularity (Fig. 5b). From the highest field position (top trace), the separation between the two peaks at 0.98 MHz and 10.00 MHz yields an estimate of Aiso = 9 MHz, similar to that predicted by Eq. (7).
Figure 5.
(a) Ka-band 3-pulse ESEEM spectra for 15N-globally labeled mitoNEET at 9 fields across the EPR field swept envelope (1100, 1110, 1112, 1130, 1140, 1145, 1150, 1155, 1160, 1165 mT). Experimental conditions: frequency 30.89 GHz, π/2 width 10 ns, τ 250 ns, initial T 70 ns, T increment 20 ns, repetition time 5 ms, temperature 12 K. (b) Q-band 3-pulse ESEEM spectra for 15N-globally labeled mitoNEET at 13 fields across the EPR field swept envelope (1207.3, 1210.9, 1218.1, 1221.7, 1225.3, 1228.9, 1232.5, 1245.5, 1251.2, 1258.1, 1265.0, 1271.9, 1278.8 mT). π/2 width 16 ns, τ 216 ns, initial T 140 ns, T increments 12 ns and 8 ns (upper 5 spectra), frequency 33.904 GHz, repetition time 5 ms; temperature 12 K.
Estimation of 15N Hyperfine Parameters from Q-band ENDOR
The hyperfine parameters can also be estimated from orientation selected Q-band Davies ENDOR of 15N-mitoNEET (Fig. 6). Single-crystal like peaks that represent a small fraction of all orientations contained in a frozen solution are observed at the highest and lowest field positions in the ENDOR spectrum. Similar to I = 1/2 ESEEM data, hyperfine values are determined by the spacing between two symmetric peaks centered at the Larmor frequency in the weak coupling (here, nearly matching) case where A/2 < νn. The low frequency partner peaks are below 1 MHz and unlike with ESEEM, are not detected with Davies ENDOR. A significant advantage of Q-band ENDOR over the more common X-band ENDOR is that 1H resonance peaks are less likely to overlap with those of low gamma nuclei (e.g. 15N), as the large magnetic moment positions the 1H Larmor frequency above 50 MHz. This allows us to characterize the mid-field ENDOR results as a somewhat distorted powder pattern contributed by a single coupled nitrogen.
Figure 6.
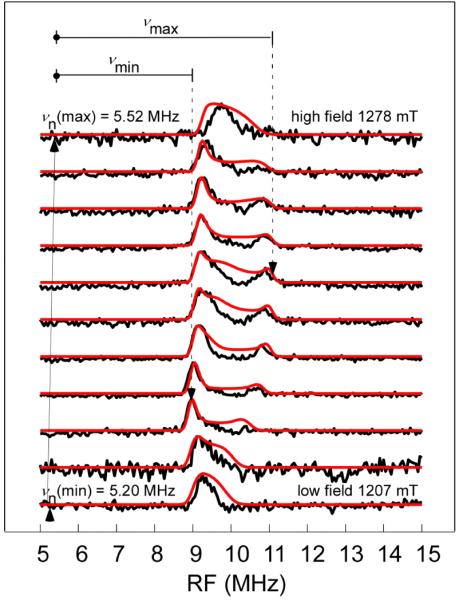
Q-band orientation-selected Davies ENDOR spectra for 15N-labeled mitoNEET taken at 11 field positions (black) with simulations (red). Experimental parameters: frequency 33.897 GHz, temperature 12 K, fields 1207.0, 1209.5, 1218.1, 1229.0, 1240.0, 1245.5, 1250.1, 1256.5, 1262.0, 1267.4, 1278.4 mT, microwave pulse widths 64 ns, 32 ns and 64 ns, RF pulse width 48 μs, τ 376 ns, RF power 250 W, repetition time 5 ms, stochastic sampling.
The maximum and minimum separation of the 15N ENDOR peaks to the corresponding Larmor frequency at each observer field are 5.75 MHz and 3.74 MHz. Setting them equal to νmax= (Aiso + 2T)/2 and νmin = (Aiso − T)/2 gives Aiso = 8.81 MHz and T = 1.34 MHz, which is very close to the estimates from Ka-band ESEEM (Aiso = 9.10 MHz, T =1.30 MHz) and Q-band ESEEM (Aiso = 9 MHz).
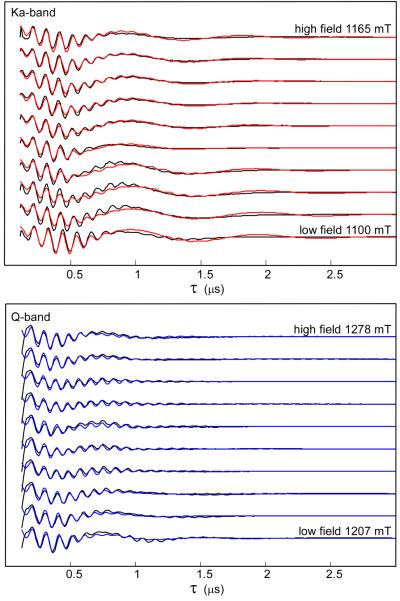
Multi-Technique, Multi-Frequency Simulations of 15N Spectra
Figures 6 and 7 show simultaneous simulations of orientation-selected Q-band 15N ENDOR (red trace) and Ka-band and Q-band 2-pulse ESEEM (red and blue traces, respectively) starting with the estimated values of the hyperfine interaction discussed above. Least-squares fitting gave the full hyperfine tensor including a complete set of Euler angles that match all 15N pulsed EPR data at the two microwave frequencies at the same time. We obtain final values of Aiso = 8.77 MHz, T = 1.32 MHz. (Table 1). These parameters also accurately describe experimental 2D-HYSCORE spectra (taken at two field positions and one τ value), as shown in Fig. 8. HYSCORE served as a third and final technique to assure an accurate hyperfine tensor for 15N-mitoNEET. It is evident in Fig. 8 that peak positions and shapes for the experimental spectra are nearly identical to those of the simulations for both the low and maximum field positions. This confirms the accuracy of both the principal values and the orientation of the hyperfine tensor. The fitted values of Aiso and T are very close to the estimates from Ka and Q-band ESEEM and ENDOR, showing that these mid-frequency techniques are ideal for this type of moderately strong coupled nitrogen.
Figure 7.
Ka-band (top) and Q-band (bottom) 2-pulse ESEEM for 15N-labeled mitoNEET across the EPR envelope, with simulations (red and blue). Ka-band conditions: frequency 30.89 GHz, fields 1100, 1110, 1120, 1130, 1140, 1145, 1150, 1155, 1160, 1165 mT, π/2 width 10 ns, π width 20 ns, initial τ 110 ns, τ increment 10 ns, repetition time 5 ms, temperature 12 K. Q-band conditions: frequency 33.904 GHz, fields 1207, 1212, 1218, 1229, 1240, 1245, 1256, 1262, 1273, 1278 mT, π/2 width 28 ns, π width 56 ns, initial τ 126 ns, τ increment 8 ns, repetition time 5 ms, temperature 12 K.
Table 1.
Experimentally determined 14N and 15N hyperfine and nuclear quadrupolar coupling parameters of the Nδ nitrogen of His87 in human mitoNEET. Euler angles describe the tensor orientations relative to the frame of the g-tensor
| 14N | 15N | |
|---|---|---|
| Aiso (MHz) | −6.25(7) | +8.77(10) |
| T (MHz) | −0.94(7) | +1.32(10) |
| Ax (MHz) | −5.28(7) | +7.4(1) |
| Ay (MHz) | −5.35(7) | +7.5(1) |
| Az (MHz) | −8.13(7) | +11.4(1) |
| α (°) | +105(180) | +105(180) |
| β (°) | +57(2) | +57(2) |
| γ (°) | +54(2) | +54(2) |
| e2Qq/h (MHz) | −2.47(4) | |
| η | +0.38(4) | |
| Px (MHz) | +0.38(2) | |
| Py (MHz) | +0.85(2) | |
| Pz (MHz) | −1.24(2) | |
| α (°) | −22(2) | |
| β (°) | +51(2) | |
| γ (°) | +66(2) | |
Figure 8.
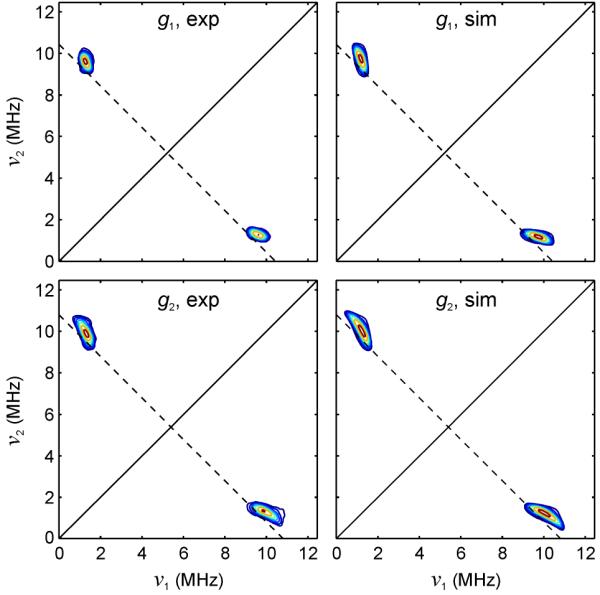
Q-band HYSCORE spectra of 15N-labeled mitoNEET (left) with corresponding simulations (right). Top: low-field position (1207.9 mT, ≈ g1), bottom: mid-field position (1251.0 mT, ≈ g2). The dashed antidiagonal lines cross the diagonals at the 15N Larmor frequency (5.40 and 5.48 MHz). Experimental conditions: frequency 33.922 GHz, temperature 10 K, π/2 pulse width 16 ns, τ 340 ns, π pulse width 32 ns, initial t1 and initial t2 100 ns, t1 and t2 increments 60 ns, 256 × 256 points.
Determination of 14N Quadrupolar Parameters from Ka-band ESEEM
Since the hyperfine parameters are fully determined from 15N-mitoNEET, 14N-mitoNEET spectra can be used to determine the parameters e2Qq/h, η, and the quadrupolar Euler angles. We start by scaling 15N to 14N values by |A(15N)/ A(14N)| = |gn(15N)/ gn(14N)| = 1.403. This provides all hyperfine values for 14N (Table 1), which remain fixed in the following 14N spectral simulations.
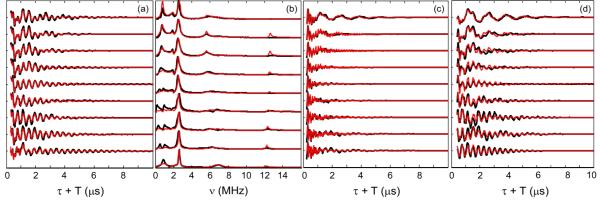
The strategy employed to determine the quadrupolar parameters was to simulate and fit 3-pulse ESEEM over 12 field orientations at three different τ values. It was not possible to directly determine the nuclear quadrupolar values from the frequency-domain spectra, despite the fact that for the cancelled manifold we observe two sharp low frequency quadrupolar peaks (ν0, ν−), which sum together to equal a third quadrupolar peak (ν+) at the extreme low and high field regions. While the practiced method for analyzing weakly coupled nitrogens at X-band is to estimate e2Qq/h and ν through e2Qq/h = 4(ν+ − ν0/2)/3 and η = 2ν0/(e2Qq/h), it fails at higher frequency for the mitoNEET system due to the intrinsic nature of the more strongly coupled nucleus. Although we are able to detect the strongly coupled nitrogens at Ka-band and Q-band, larger dipolar couplings can “taint” quadrupolar values assigned directly from ESEEM spectra.58 We therefore relied solely on simulations to provide an accurate set of parameters.
Best-fit simulations started with initial values for e2Qq/h and η taken from reported Rieske proteins, which are assumed to share the same quadrupolar interaction between the [2Fe-2S] cluster and a histidine ligand. These values for e2Qq/h range from 1.9 to 3.15 MHz for both high potential and low potential Rieske centers.48 Although estimates have been discussed for the Euler angles in the Rieske centers,50 orientation-selected simulations have not been reported. These angles are required when simulating Ka-band ESEEM spectra, as they are responsible for a variation of peak intensity across the envelope. Also, the quadrupole tensor is not expected to be collinear with either the g tensor or hyperfine tensor. To estimate the initial Euler angle values (α = −29°, β = 23°, γ = 82°) we used the coordinates from X-ray data from the [Fe3+Fe3+] form of mitoNEET and applied the same g tensor and quadrupole tensor orientations used to estimate Euler angles for the SDX and ARF Rieske proteins.50 The g1 axis was assumed along S-S, g2 perpendicular to the cluster plane and g3 along Fe-Fe. The quadrupole tensor was assumed to be aligned with the histidine with Px perpendicular to the imidazole plane, Py in-plane along Cγ and Cε and Pz along the line bisecting C-N-C. Figure 9(a), (c) and (d) show the best-fit simulations for three different τ values. The FFT spectra for the τ = 250 ns data are shown in Fig. 9(b). The Ka-band simulations along with simulations of a select subset of Q-band ESEEM data (not shown) led to a complete determination of the quadrupolar coupling parameters and quadrupolar Euler angles: |e2Qq/h| = 2.47 MHz, η = 0.38, α = −22°, β = 51°, γ = 66° (Table 1).
Figure 9.
Ka-band 3-pulse ESEEM (black) and simulations (red) of WT-mitoNEET at three different τ values. Experimental conditions: frequency 30.89 GHz;, π/2 width 10 ns, τ 250 ns (a), 160 ns (c), 330 ns (d), initial T 70 ns, T increment 20 ns, repetition time 5 ms, temperature 12 K. (b) FFT of τ = 250 ns traces.
Other Detectable Nitrogens
Although it is clear that there is only one detectable nitrogen in Ka-band and Q-band ESEEM, a second, remote, nitrogen (Nε) two bonds away from Nδ on the imidazole ring should also couple to the [2Fe-2S] cluster, but with a much weaker interaction. A preliminary X-band ESEEM investigation targeting more weakly coupled nitrogens (Fig. 10) using 15N-mitoNEET reveals two peaks split by 0.67 MHz and centered at the 15N Larmor frequency (νn = 1.49 MHz). Q-band Mims-ENDOR provides more detail about this observed splitting (Fig 10, inset) indicating either an axial powder pattern or the presence of more than one weakly coupled nitrogen. The source of additional couplings may be from peptide nitrogens hydrogen bonded to the cluster similar to those observed in some ferredoxin and Rieske centers.51,52,59-61 It may be that the weak coupling of 0.42 MHz is mostly isotropic, and that the larger 0.8 MHz coupling is due to a second nitrogen. The 0.42 MHz splitting may be assigned to the distal nitrogen of the imidazole ring, as the hyperfine interaction is approximately 1/20th of that of the bound nitrogen, a common condition seen in imidizole-bound copper and vanadium systems and in Rieske clusters.51,56,62 More than one nitrogen are also visible in the X-band ESEEM data taken on 14N-mitoNEET resulting in a very congested low frequency region where transitions would be expected to overlap (Fig. 10).
Figure 10.
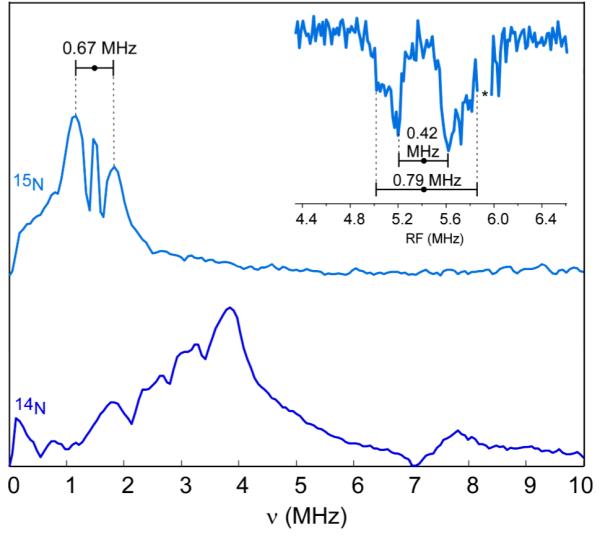
X-band 3-pulse ESEEM spectra of 15N-globally labeled mitoNEET (top) and native mitoNEET (bottom). Experimental conditions: frequency 9.32 GHz, field position 344 mT, π/2 width 16 ns, τ 192 ns, initial T 64 ns, T increment 16 ns, repetition time 5 ms, temperature 12 K. (Inset) Q-band Mims ENDOR of 15N-labeled mitoNEET. The asterisk at ~ 5.9 MHz of Mims-ENDOR spectrum indicates an RF-amplifier harmonic from 1H resonances that appeared as a spectral artifact. Experimental conditions: frequency 33.922 GHz, field position 1250.8 mT (≈ g2), π/2 width 20 ns, τ 720 ns, RF-pulse width 60 μs, RF-power 250 W, repetition time 10 ms, stochastic sampling, temperature 12 K.
Discussion
g-tensor
Human mitoNEET is characterized by an anisotropic g-tensor with principal values g1 = 2.007, g2 = 1.937, and g3 = 1.897. The average g-value gavg = 1.947 lies between those of Rieske-type centers (gavg = 1.88 to 1.92)48 and ferredoxin-type centers (gavg ≈ 1.96), consistent with expectations based on the change in the number of ligating histidines. The same average g-value of 1.947 was observed for an engineered 3-Cys, 1-His coordinated [2Fe-2S] cluster in a His/Cys mutant of a Rieske-type ferredoxin63 that features an axial spectrum with principal g-values 2.00, 1.92, and 1.92.
Theoretical models have been applied to examine the relationship between average g-values and the type and geometry of ligand coordination in [2Fe-2S] systems.64-67 Bertrand and Gayda64 have proposed that the g-value differences are attributed to differences in the ground-state orbital mixing of the Fe2+ ion. The degree of mixing directly affects the g-tensor, mostly the two smaller principal values. The g-tensor is sensitive not only to the local coordination geometry at the iron sites, but also to conformational features beyond the first ligation sphere. A recent computational study68 examined the many structural factors affecting the g-values by rigorously treating ligand type, orientation, and asymmetry at the reduced ferrous site, finding that these all influence the electronic charge and spin distribution, which in turn affects the g-values. The accurate g-tensor for mitoNEET obtained in this work should serve as a valuable addition to further developing these theoretical models.
As detailed above, from the available crystal structure we could estimate the tensor describing the dipolar coupling between the two clusters of the dimer. The dipolar splittings observable in the X-band CW spectrum led us to conclude that the valences are localized and that the histidine-coordinated iron is reduced (Fe2+). From a similar analysis, Iwasaki et al. recently identified the same valence localization in rat mitoNEET.36
Hyperfine coupling
We determined that the 14N hyperfine coupling was mostly isotropic with Aiso = −6.25 MHz and T = −0.94 MHz, corresponding to Ax = −5.28 MHz, Ay = −5.35 MHz, and Az = −8.13 MHz. The sign choice is discussed below. The isotropic part Aiso is slightly larger than that estimated for rat mitoNEET, 5.7 to 6.1 MHz, 36 but is smaller than the estimate of 8 MHz for the ligating nitrogen in the [2Fe-2S] cluster in Fra2-Grx3/4.69 However, Aiso for mitoNEET is about 1 MHz greater than the larger of the two isotropic coupling constants reported for the histidine nitrogens in Rieske clusters (N2, 4.6 – 5.5 MHz), which themselves are generally about 1 MHz larger than the smaller couplings in the same clusters (N1, 3.4 – 4.6 MHz).40,41,43-47,50 The difference between the couplings of the two nitrogen is due to the fact that the planes of the two histidines imidazole rings in Rieske-type centers are orthogonal to each other and therefore oriented differently with respect to the cluster. The mitoNEET coupling is closer to the N2 coupling than to N1, which indicates that the mitoNEET imidazole plane orientation should be similar to the corresponding one in Rieske-type centers. This is indeed the case, as can be seen from the crystal structure. Fig. 11 shows an overlay of the structures of mitoNEET and bovine bc1 Rieske protein (pdb 1RIE). The two imidazole planes almost coincide (1° difference in the Cγ-Nδ-Fe-Fe dihedral angle). Also, the N-Fe distances are very similar, (2.13 Å and 2.19 Å). From this and the closeness of the mitoNEET coupling to the N2 coupling in Rieske-type clusters we can infer that the N2 signals stem from the histidine with an imidazole plane inclination similar to His87 in mitoNEET (His141 in 1RIE, His143 in 1NYK, His45 in 1FQT).
Figure 11.
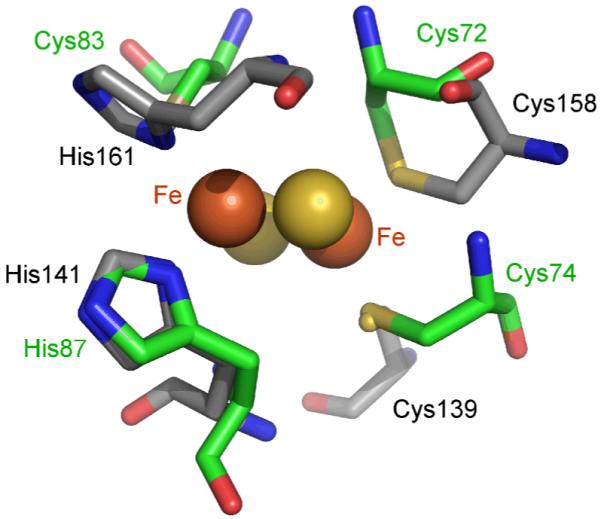
[2Fe-2S] cluster and ligands of human mitoNEET (pdb 2QH7, green) overlaid with the Rieske center from bovine heart mitochondrial cytochrome bc1 (pdb 1RIE, grey).
There is no obvious structural reason why the isotropic coupling found in mitoNEET should be higher than the one of N2 in Rieske centers. Upon closer inspection, though, the coordination geometries are slightly different. In mitoNEET, we observe a N(His)-Fe-S(Cys) angle of 99°, closer to the ideal tetrahedral angle of 109.5° than the N(His)-Fe-N(His) angle of 91° in the Rieske protein or 96° in biphenyl dioxygenase (pdb 1FQT). Otherwise, the local symmetry in mitoNEET is lower than in Rieske centers, due to the presence of two different amino acid ligands. The distance from Fe to S(Cys83) is 0.13 Å longer than the one to N(His87), which is unlike Rieske-type clusters, where the two Fe-N bond lengths are essentially equal, differing by only 0.03 Å or less. Also, the Fe2S2 plane and the N(His87)-Fe-S(Cys83) plane are not exactly orthogonal, but twisted by 14° (Rieske: 8° in 1RIE, 5° in 1FQT). Although none of these distortions are large, they could contribute to the higher isotropic coupling in mitoNEET via slightly reoriented valence orbitals on Fe and consequently better σ or π overlap with the histidine ligand.
In addition, ligand effect may contribute to the greater magnitude of the isotropic coupling compared to those reported for Rieske-type clusters. In Rieske-type clusters, the Fe ion is coordinated by two anionic sulfide ligands and two neutral histidines, whereas in mitoNEET there are three anionic sulfur ligands, which are stronger σ and π donors. Replacing one histidine with cysteinyl could increase the total charge donated to Fe and the spin density transmitted from Fe to the remaining histidine through σ or π interaction and thereby increase the isotropic hyperfine coupling either directly or through spin polarization. It might well be that the Aiso difference between mitoNEET and Rieske-type clusters arises from a simple difference in ligand spin delocalization. Histidine ligands have extended π-electron systems that can delocalize spin density away from the Fe more efficiently than a cysteinyl ligand. The two histidines in Rieske clusters can drain more spin from the central ion than the single histidine ligand in mitoNEET, allowing the histidine in the latter to receive slightly more spin. The isotropic hyperfine coupling could therefore increase compared to Rieske-type clusters. The exact mechanism of these ligand effects is not clear.
The dipolar part of the measured hyperfine tensor is small. It is the sum of several contributions
| (9) |
where TFe and TFe,dist are the dipolar coupling tensors to the proximal and distal Fe, T2p is the dipolar coupling with spin density in the lone-pair nitrogen σ donor orbital directed towards the proximal Fe, and Tπ is due to unpaired spin in the nitrogen p π orbital normal to the imidazole plane. The π contribution would cause significant rhombicity in A. As we observe an almost perfectly axial tensor, there is apparently very little spin density in that orbital, and we can neglect Tπ. Also, we neglect the coupling to the distal Fe, since it is much farther (4.34 Å) from the histidine nitrogen than the proximal Fe (2.19 Å). We also neglect contributions from small spin populations on the bridging sulfur atoms. The remaining two main contributions, TFe and T2p, are both oriented along the N-Fe bond, so that it is safe to assume that the unique axis of A, corresponding to Az, is parallel to the N-Fe bond. (Since the rhombicity is almost below experimental error, the orientations of the two other principal axes of A are essentially unknown, and the corresponding first Euler angle α in Table 1 has a very large error.) For the dipolar contribution, we can now write
| (10) |
where k is the spin projection factor for the proximal Fe, either 7/3 (Fe3+) or −4/3 (Fe2+) depending on the assigned oxidation state. Using the point-dipole approximation, the dipolar hyperfine contribution from Fe can be roughly estimated as tFe = (μ0/4πh)fFegeβegnβn / r3, where the fractional spin population on Fe, fFe, is about 0.840 based on DFT calculations,71 and r, the N-Fe bond length, is 2.19 Å from the crystal structure. The main contribution to the isotropic hyperfine coupling is from unpaired spin in the nitrogen 2s orbital,
| (11) |
From Eqs. (10) and (11), a2s and t2p can be computed. The fractional spin populations in the nitrogen 2s and the 2p σ orbital, f2s and f2p, are then given by
| (12) |
where S is the electron spin quantum number of the Fe ion (2 for Fe2+ and 5/2 for Fe3+), and the 14N hyperfine coupling constants at 100% spin population are and .72 For the ratio f2p/f2s, values of about 140 and about 2.673 have been previously reported. Assuming a negative sign for the measured 14N hyperfine tensor, the ratio is 1.9 for Fe2+ and 10 for Fe3+. With a positive sign, the values are 7.9 (Fe2+) and −0.4 (Fe3+). The ratio is therefore closest to previous reports if the measured 14N hyperfine tensor is negative and the histidine is coordinated to Fe2+. The fractional spin populations in this case are f2s = 1.0% and f2p = 1.9%. This further confirms that the histidine-coordinated Fe is reduced, consistent with the conclusion from the analysis of the inter-cluster dipolar coupling observed in the X-band CW spectrum.
Quadrupole tensor
We determined the quadrupolar coupling of the histidine Nδ nitrogen as e2Qq/h = −2.47 MHz and η = 0.38. The principal values of the corresponding quadrupole tensor are Px = +0.38 MHz, Py = +0.85 MHz, and Pz = −1.24 MHz. The sign choice is justified below. It is known from measurements on a series of Zn2+ and Cd2+ imidazole complexes that |e2Qq/h|−1 and η of imidazole nitrogens ligated to metal ions are linearly correlated.74 The correlation is shown in Fig. 12. Our data fit this relationship very well. The known quadrupole data of the two coordinating histidine nitrogens in the Rieske-type cluster of phthalate dioxygenase (PDO),40 of the nitrogen of the axially coordinating histidine in aquametmyoglobin (Mb)73 and of the histidine nitrogen coordinating the Fe2+ site of methane monooxygenase (MMO)75 also follow the relationship, though less accurately. In other studies of histidines coordinated to Rieske-type clusters where the asymmetry η of the quadrupole tensor was not reported, |e2Qq/h| values between 1.90 and 3.15 MHz were found,41-43,48 similar to ours. An important and generally applicable corollary from Fig. 12 is that if experiments allow only |e2Qq/h| to be determined, a value for η can be readily deduced. From the quadrupole data, the population of the nitrogen lone-pair orbital can be inferred, as shown in Fig. 12. This reflects the σ donor properties of the histidine ligand as well as the Lewis acid strength of the metal ion. In mitoNEET, the histidine-Fe bonding situation seems to be fairly typical.
Figure 12.
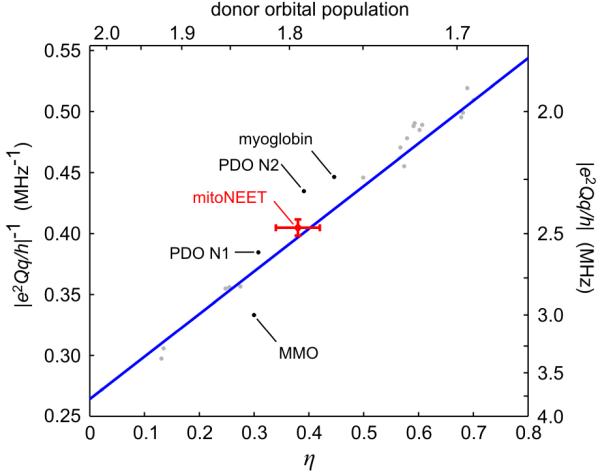
Linear correlation between |e2Qq/h|−1 and η for the nitrogens of imidazoles and histidines coordinated to divalent metal ions. Grey: data from Ashby et al. (74); red: mitoNEET data from this work; black: data from histidine-Fe coordinations in myoglobin (73), phthalate dioxygenase (PDO) (40), and methane monooxygenase (MMO) hydroxylase (75); blue: linear fit according to Ashby et al. (74).
Our negative sign choice for e2Qq/h stems from the negative sign for the ligating histidine nitrogen in Mb, which was experimentally determined through the analysis of second-order effects in single-crystal ENDOR spectra.73 The Mb quadrupole values, e2Qq/h = −2.24 MHz and η = 0.45, are very close to ours. Also, from the Mb single-crystal data it was determined that the axis corresponding to the largest-magnitude principal value Pz is directed along the line bisecting the C-N-C angle, which coincides with the N-Fe bond. This is also the case in mitoNEET, where the orientation of the Fe-N bond and the C-N-C bisector form an angle of only 14° as seen from the crystal structure. The coordinated Fe ion therefore lies approximately in the imidazole plane of the histidine. Our spectroscopic data in Table 1 give an angle of 11° between Az and Pz, which is consistent with the crystal structure and the assignment that the Pz axis is along the C-N-C bisector. Therefore, the electric field gradients at the histidine nitrogens in Mb and mitoNEET are very similar, and we confidently can assume a negative sign for e2Qq/h.
It is not clear from our data how the two quadrupole axes Px and Py are oriented in mitoNEET. The electric field gradient at the nitrogen nucleus is mostly determined by the balance of electron populations in the nitrogen valence orbitals76, and the Px and Py assignment depends on the populations in the two C-N σ bonds compared to the population of the p π orbital at the nitrogen. In PDO and Mb, the axis corresponding to the smallest-magnitude tensor value Px is perpendicular to the imidazole plane. Since the hyperfine tensors in mitoNEET, PDO and Mb are all mostly uniaxial, the π bonding interactions between the histidine and the metal ion are probably similarly small in all these centers. From this, we can assign the Px axis to be perpendicular to the imidazole plane, and Py in-plane parallel to Cγ-Cε, as in Mb and PDO.
g-tensor orientation
Using the absolute orientations of P and of the unique axis of A as determined above, we can now deduce the absolute orientation of the g-tensor from the experimentally determined orientation of P and A with respect to g. Surprisingly, it is possible to choose Euler angles for the g-tensor such that Az is exactly parallel to N-Fe and Px lies within 4° perpendicular to the imidazole plane. Then, Py is oriented within 12° along the C-C direction, and Pz is within 13° along the C-N-C bisector, consistent with the orientation discussed above. The Euler angles for the resulting g-tensor frame are (141.9°, 36.8°, −69.6°), and the g-tensor orientation is illustrated in Fig. 13. It has the g2 axis almost perpendicular to the cluster plane (13° off the plane normal), and the g1-g3 plane almost coincident with the cluster plane. Contrary to expectations, g1 and g3 are not parallel to Fe-Fe and S-S (or vice versa), but rotated by about 33°. If this g-tensor orientation is used to simulate the X-band CW spectrum of Fig. 2, the splitting at the low-field edge and the shoulder in the center of the spectrum are correctly reproduced (data not shown). The remaining discrepancies can be attributed to the fact that the inter-cluster dipolar tensor was only crudely estimated and that the relative orientation of the two clusters in the crystal was assumed to hold for the reduced state in frozen solution. The g2 orientation in Fig. 13 deviates by only 11° from the one deduced from the fit of the X-band CW spectrum with Euler angles (151.9°, 146.7°, −116.1°), so there is reasonable agreement between all our data. Still, our prediction of the g-tensor orientation is only preliminary, as the orientations of P and A might be not collinear with the histidine frame and the N-Fe direction.
Figure 13.
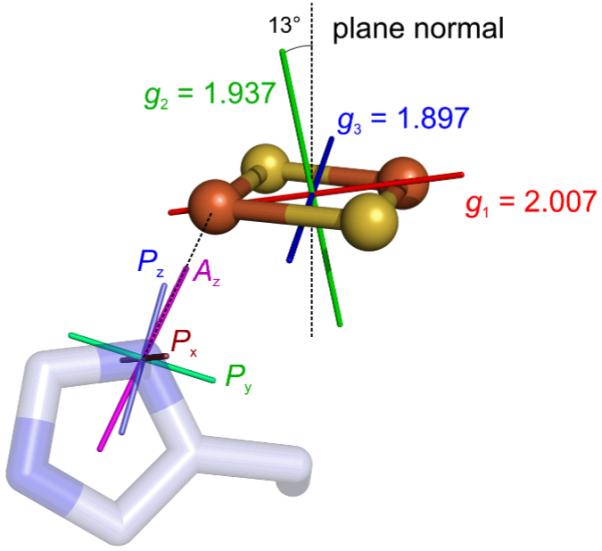
Orientation of g, hyperfine and quadrupole tensors in the mitoNEET protein (pdb 2QH7). The g tensor orientation follows from aligning Az with the N-Fe bond, and bringing Px as close as possible to the histidine plane normal. The angle between the g2 axis and the cluster plane normal is 13°, the g1 axis is 34° off the Fe-Fe direction, and g3 is 33° off the S-S direction. The Pz axis is only 4° off the histidine C-N-C bisector, and the angle between Pz and Az is 11°.
It is encouraging that the g-tensor orientation in the Rieske cluster of cytochrome bc1 determined by Bowman et al. from single-crystal EPR also features a g2 axis almost perpendicular to the cluster plane.77 This suggests that the g-tensor orientation in mitoNEET and in Rieske-type clusters might be similar, despite differences in g-values and coordination symmetry. There remain discrepancies between our deduced orientation and the ones proposed for Rieske-type clusters by Bertrand et al.,65 with g1 perpendicular to the cluster plane, and Gurbiel et al.,47 where it is g3 that is perpendicular to the cluster plane.78 Clearly, a detailed single-crystal study is needed to determine the absolute orientation more reliably.
Remote nitrogen
Resonance Raman studies on native mitoNEET in comparison with the H87C mutant show pH inducible changes in the region assigned to modes of the Fe–His87 moiety in the oxidized state of the cluster. 17 It is not clear whether a protonation event at either the Nδ or Nε in the imidizole ring is contributing to the observed Raman effects.17 However, from our data we can see that the distal nitrogen Nε is probably protonated in the reduced state of the cluster, for the following reason. Iwasaki et al.53 have shown with orientation-selected 15N HYSCORE on sulredoxin, a high-potential Rieske protein, that the hyperfine coupling of the coordinating nitrogen is sensitive to the protonation state of the distal one. At high pH, where distal nitrogens are deprotonated, the hyperfine tensors of Nδ1 and Nδ2 become significantly non-axial. The hyperfine tensor in mitoNEET is almost axial, indicating that His87 is protonated at Nε. Also, computational studies that investigated the pH dependence of redox potentials on Rieske proteins, demonstrated that when both histidines were deprotonated at the Nε sites, the histidine bound Fe was no longer more favorably reduced.79 The two iron sites become more equivalent. The pKa of Nε in Rieske centers is between 7.5 and 11.917 in the oxidized state, and it is known to increase upon reduction by about 4 units,79 so that Nε protonation at pH 8 is likely. Iwasaki et al. also conclude that Nε is protonated in the reduced state of rat mitoNEET at pH 8 by comparing the Nε quadrupole coupling constant determined from X-band HYSCORE to those from literature.36
The more weakly coupled nitrogens may be targeted directly, as we have shown in our preliminary investigation Further examination similar to Nδ analysis, including simulations, may prove useful in determining a more complete picture of detected nitrogens, as well as possibly peptide nitrogens coupled to the cluster through hydrogen bonds. It is clear from the X-band ESEEM spectrum of 15N-mitoNEET in Fig. 10 that we are only able to observe the weakly coupled nitrogens (and additional matrix nuclei which appear at the Larmor frequency).
Conclusions
Using multi-frequency, multi-technique EPR data with analytical parameter estimations, numerical simulations and least-squares fittings, the complete set of EPR parameters of the histidine nitrogen coordinating to the [2Fe-2S] cluster in human mitoNEET could be determined. Multi-frequency ESEEM was especially useful in targeting this nitrogen without interference from proton signals. Specifically, Ka- and Q-band frequencies are very well suited to access this type of nitrogen nuclei by ESEEM and to extract accurate hyperfine and quadrupole parameters.
The hyperfine tensor is almost axial, and its isotropic part is larger than that found in Rieske-type clusters, probably due to enhanced spin delocalization onto the histidine. The analysis of the quadrupole tensor shows that the histidine-Fe bond in mitoNEET is very similar to the ones in Rieske-type centers. By aligning the quadrupole tensor and the dipolar part of the hyperfine tensor with the molecular frame, the orientation of the g tensor relative to the cluster could be derived. It is reasonably consistent with the orientation derived from fitting the CW spectrum of the cluster dimer using a theoretically estimated inter-cluster dipolar tensor, but in disagreement with some previous data from Rieske-type clusters. A single-crystal EPR is needed to determine the orientations of all tensors with respect to the molecular structure and provide more detailed insight into the electronic ground state.
Quantification and understanding of the interactions of the bound nitrogen and the histidine-Fe bond provides a foundation for further investigations. In particular, pH-dependent changes to the ligation that affect the cluster lability and its proton-coupled redox potential, and changes that occur upon interaction with TDZ drugs that modify properties and changes between mitoNEET and its paralogs, Miner1 and Miner2, are targets of future studies. The details of this study may help understanding the redox chemistry of mitoNEET.
Supplementary Material
Acknowledgement
This work was supported by NIH grants GM48242 (to R.D.B.), GM41637 (to M. Okamura and M.L.P.), GM54038 and DK54441 (to P.A.J.). R. N. thanks the Zevi Hermann Shapira Foundation for supporting the collaborative USA-Israeli efforts.
References
- (1).Brown EN, Friemann R, Karlsson A, Parales JV, Couture MMJ, Eltis LD, Ramaswamy S. JBIC, J. Biol. Inorg. Chem. 2008;13:1301–1313. doi: 10.1007/s00775-008-0413-4. [DOI] [PubMed] [Google Scholar]
- (2).Unden G, Mullner M, Reinhart F, Hammel O. BIOspektrum. 2007;13:246–249. [Google Scholar]
- (3).Zheng M, Storz G. Biochem. Pharmacol. 1999;59:1–6. doi: 10.1016/s0006-2952(99)00289-0. [DOI] [PubMed] [Google Scholar]
- (4).Johnson DC, Dean DR, Smith AD, Johnson MK. Annu. Rev. Biochem. 2005;74:247–81. doi: 10.1146/annurev.biochem.74.082803.133518. [DOI] [PubMed] [Google Scholar]
- (5).Meyer J. JBIC, J. Biol. Inorg. Chem. 2008;13:157–170. doi: 10.1007/s00775-007-0318-7. [DOI] [PubMed] [Google Scholar]
- (6).Lill R. Nature. 2009;460:831–838. doi: 10.1038/nature08301. [DOI] [PubMed] [Google Scholar]
- (7).Paddock ML, Wiley SE, Axelrod HL, Cohen AE, Roy M, Abresch EC, Capraro D, Murphy AN, Nechushtai R, Dixon JE, Jennings PA. Proc. Natl. Acad. Sci. U. S. A. 2007;104:14342–14347. doi: 10.1073/pnas.0707189104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Wiley SE, Paddock ML, Abresch EC, Gross L, van der Geer P, Nechushtai R, Murphy AN, Jennings PA, Dixon JE. J. Biol. Chem. 2007;282:23745–23749. doi: 10.1074/jbc.C700107200. [DOI] [PubMed] [Google Scholar]
- (9).Hou X, Liu R, Ross S, Smart EJ, Zhu H, Gong W. J. Biol. Chem. 2007;282:33242–33246. doi: 10.1074/jbc.C700172200. [DOI] [PubMed] [Google Scholar]
- (10).Lin J, Zhou T, Ye K, Wang J. Proc. Natl. Acad. Sci. U. S. A. 2007;104:14640–14645. doi: 10.1073/pnas.0702426104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Hagen WR, Silva PJ, Amorim MA, Hagedoorn PL, Wassink H, Haaker H, Robb FT. JBIC, J. Biol. Inorg. Chem. 2000;5:527–534. doi: 10.1007/pl00021452. [DOI] [PubMed] [Google Scholar]
- (12).Shimomura Y, Wada K, Fukuyama K, Takahashi Y. J. Mol. Biol. 2008;383:133–143. doi: 10.1016/j.jmb.2008.08.015. [DOI] [PubMed] [Google Scholar]
- (13).Conlan AR, Axelrod HL, Cohen AE, Abresch EC, Zuris J, Yee D, Nechushtai R, Jennings PA, Paddock ML. J. Mol. Biol. 2009;392:143–153. doi: 10.1016/j.jmb.2009.06.079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Zuris JA, Paddock ML, Abresch EC, Conlan AR, Nechushtai R, Jennings PA. Biophys. J. 2009;96:240a. [Google Scholar]
- (15).Paddock ML, Wiley SE, Axelrod HL, Cohen AE, Roy M, Abresch EC, Capraro D, Murphy AN, Nechushtai R, Dixon JE, Jennings PA. Proc. Natl. Acad. Sci. U.S.A. 2007;104:14342–7. doi: 10.1073/pnas.0707189104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).Homer C, Yee D, Axelrod HL, Cohen AE, Abresch EC, Chang C, Nechushtai R, Jennings PA, Paddock ML. Biophys. J. 2009;96:442a. [Google Scholar]
- (17).Tirrell TF, Paddock ML, Conlan AR, Smoll EJ, Nechushtai R, Jennings PA, Kim JE. Biochemistry. 2009;48:4747–4752. doi: 10.1021/bi900028r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Pedelacq JD, Cabantous S, Tran T, Terwilliger TC, Waldo GS. Nat. Biotechnol. 2006;24:79–88. doi: 10.1038/nbt1172. [DOI] [PubMed] [Google Scholar]
- (19).Conlan AR, Paddock ML, Axelrod HL, Cohen AE, Abresch EC, Wiley SE, Roy M, Nechushtai R, Jennings PA. Acta Cryst. 2009;F65:654–659. doi: 10.1107/S1744309109019605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Fish A, Lebendiker M, Nechushtai R, Livnah O. Acta Cryst. 2003;D59:734–736. doi: 10.1107/s0907444903002245. [DOI] [PubMed] [Google Scholar]
- (21).Stich TA, Lahiri S, Yeagle G, Dicus M, Brynda M, Gunn A, Aznar C, DeRose VJ, Britt RD. Appl. Magn. Reson. 2007;31:321–341. doi: 10.1007/BF03166263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Sturgeon BE, Britt RD. Rev. Sci. Instrum. 1992;63:2187–92. [Google Scholar]
- (23).Fauth JM, Schweiger A, Braunschweiler L, Forrer J, Ernst RR. J. Magn. Reson. 1986;66:74–85. [Google Scholar]
- (24).Stoll S, Kasumaj B. Appl. Magn. Reson. 2008;35:15–32. doi: 10.1016/j.jmr.2007.11.001. [DOI] [PubMed] [Google Scholar]
- (25).Stoll S, Britt RD. Phys. Chem. Chem. Phys. 2009;11:6614–6625. doi: 10.1039/b907277b. [DOI] [PubMed] [Google Scholar]
- (26).Stoll S, Schweiger A. J. Magn. Reson. 2006;178:42–55. doi: 10.1016/j.jmr.2005.08.013. [DOI] [PubMed] [Google Scholar]
- (27).Schweiger A, Jeschke G. Principles of pulse electron paramagnetic resonance / Arthur Schweiger and Gunnar Jeschke. Oxford University Press; 2001. [Google Scholar]
- (28).Brueggemann W, Niklas JR. J. Magn. Reson., Ser. A. 1994;108:25–9. [Google Scholar]
- (29).Epel B, Arieli D, Baute D, Goldfarb D. J. Magn. Reson. 2003;164:78–83. doi: 10.1016/s1090-7807(03)00191-5. [DOI] [PubMed] [Google Scholar]
- (30).Cammack R, Gay E, Shergill JK. Coord. Chem. Rev. 1999;190-192:1003–1022. [Google Scholar]
- (31).Chasteen ND, Snetsinger PA. Physical Methods in Bioinorganic Chemistry. 2000. pp. 187–231. [Google Scholar]
- (32).Deligiannakis Y, Louloudi M, Hadjiliadis N. Coord. Chem. Rev. 2000;204:1–112. [Google Scholar]
- (33).Calle C, et al. Helv. Chim. Acta. 2006;89:2495–2521. [Google Scholar]
- (34).Van Doorslaer S, Vinck E. Phys. Chem. Chem. Phys. 2007;9:4620–4638. doi: 10.1039/b701568b. [DOI] [PubMed] [Google Scholar]
- (35).Bertrand P, More C, Guigliarelli B, Fournel A, Bennett B, Howes B. J. Am. Chem. Soc. 1994;116:3078–3086. [Google Scholar]
- (36).Iwasaki T, Samoilova RI, Kounosu A, Ohmori D, Dikanov SA. J. Am. Chem. Soc. 2009 doi: 10.1021/ja903228w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (37).More C, Asso M, Roger G, Guigliarelli B, Caldeira J, Moura J, Bertrand P. Biochemistry. 2005;44:11628–11635. doi: 10.1021/bi0510025. [DOI] [PubMed] [Google Scholar]
- (38).Gibson JF, Hall DO, Thornley JH, Whatley FR. Proc. Natl. Acad. Sci. U.S A. 1966;56:987–90. doi: 10.1073/pnas.56.3.987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Sands RH, Durham WR. Q. Rev. Biophys. 1975;7:443–504. doi: 10.1017/s0033583500001517. [DOI] [PubMed] [Google Scholar]
- (40).Gurbiel RJ, Batie CJ, Sivaraja M, True AE, Fee JA, Hoffman BM, Ballou DP. Biochemistry. 1989;28:4861–4871. doi: 10.1021/bi00437a051. [DOI] [PubMed] [Google Scholar]
- (41).Britt RD, Sauer K, Klein MP, Knaff DB, Kriauciunas A, Yu CA, Yu L, Malkin R. Biochemistry. 1991;30:1892–901. doi: 10.1021/bi00221a023. [DOI] [PubMed] [Google Scholar]
- (42).Gurbiel RJ, Ohnishi T, Robertson DE, Daldal F, Hoffman BM. Biochemistry. 1991;30:11579–84. doi: 10.1021/bi00113a013. [DOI] [PubMed] [Google Scholar]
- (43).Shergill JK, Cammack R. Biochim. Biophys. Acta, Bioenerg. 1994;1185:35–42. doi: 10.1016/0005-2728(94)90190-2. [DOI] [PubMed] [Google Scholar]
- (44).Riedel A, Fetzner S, Rampp M, Lingens F, Liebl U, Zimmermann J-L, Nitschke W. J. Biol. Chem. 1995;270:30869–73. doi: 10.1074/jbc.270.52.30869. [DOI] [PubMed] [Google Scholar]
- (45).Shergill JK, Joannou CL, Mason JR, Cammack R. Biochemistry. 1995;34:16533–42. doi: 10.1021/bi00051a001. [DOI] [PubMed] [Google Scholar]
- (46).Dikanov SA, Xun L, Karpiel AB, Tyryshkin AM, Bowman MK. J. Am. Chem. Soc. 1996;118:8408–8416. [Google Scholar]
- (47).Gurbiel RJ, Doan PE, Gassner GT, Macke TJ, Case DA, Ohnishi T, Fee JA, Ballou DP, Hoffman BM. Biochemistry. 1996;35:7834–7845. doi: 10.1021/bi960380u. [DOI] [PubMed] [Google Scholar]
- (48).Link TA. Adv. Inorg. Chem. 1999;47:83–157. [Google Scholar]
- (49).Samoilova RI, Kolling D, Uzawa T, Iwasaki T, Crofts AR, Dikanov SA. J. Biol. Chem. 2002;277:4605–4608. doi: 10.1074/jbc.C100664200. [DOI] [PubMed] [Google Scholar]
- (50).Dikanov SA, Shubin AA, Kounosu A, Iwasaki T, Samoilova RI. JBIC, J. Biol. Inorg. Chem. 2004;9:753–767. doi: 10.1007/s00775-004-0571-y. [DOI] [PubMed] [Google Scholar]
- (51).Iwasaki T, Kounosu A, Uzawa T, Samoilova RI, Dikanov SA. J. Am. Chem. Soc. 2004;126:13902–13903. doi: 10.1021/ja045898x. [DOI] [PubMed] [Google Scholar]
- (52).Dikanov SA, Kolling DRJ, Endeward B, Samoilova RI, Prisner TF, Nair SK, Crofts AR. J. Biol. Chem. 2006;281:27416–27425. doi: 10.1074/jbc.M604103200. [DOI] [PubMed] [Google Scholar]
- (53).Iwasaki T, Kounosu A, Samoilova RI, Dikanov SA. J. Am. Chem. Soc. 2006;128:2170–2171. doi: 10.1021/ja0562393. [DOI] [PubMed] [Google Scholar]
- (54).Flanagan HL, Singel DJ. J. Chem. Phys. 1987;87:5606–16. [Google Scholar]
- (55).Lai A, Flanagan HL, Singel DJ. J. Chem. Phys. 1988;89:7161–7166. [Google Scholar]
- (56).Hoff AJ, editor. Advanced EPR : applications in biology and biochemistry. Elsevier; 1989. [Google Scholar]
- (57).Gerfen GJ, Bellew BF, Singel DJ. Chem. Phys. Lett. 1991;180:490–6. [Google Scholar]
- (58).Cosgrove SA, Singel DJ. J. Phys. Chem. 1990;94:8393–6. [Google Scholar]
- (59).Cammack R, Chapman A, McCracken J, Cornelius JB, Peisach J, Weiner JH. Biochim. Biophys. Acta. 1988;956:307–12. doi: 10.1016/0167-4838(88)90148-3. [DOI] [PubMed] [Google Scholar]
- (60).Dikanov SA, Tyryshkin AM, Felli I, Reijerse EJ, Hüttermann J. J. Magn. Reson. B. 1995;108:99–102. doi: 10.1006/jmrb.1995.1110. [DOI] [PubMed] [Google Scholar]
- (61).Shergill JK, Golinelli M-P, Cammack R, Meyer J. Biochemistry. 1996;35:12842–12848. doi: 10.1021/bi961009+. [DOI] [PubMed] [Google Scholar]
- (62).Dikanov SA, Spoyalov AP, Hüttermann J. J. Chem. Phys. 1994;100:73–83. [Google Scholar]
- (63).Kounosu A, Li Z, Cosper NJ, Shokes JE, Scott RA, Imai T, Urushiyama A, Iwasaki T. J. Biol. Chem. 2004;279:12519–12528. doi: 10.1074/jbc.M305923200. [DOI] [PubMed] [Google Scholar]
- (64).Bertrand P, Gayda J-P. Biochim. Biophys. Acta. 1979;579:107–21. doi: 10.1016/0005-2795(79)90091-6. [DOI] [PubMed] [Google Scholar]
- (65).Bertrand P, Guigliarelli B, Gayda J-P, Peter B, Gibson JF. Biochimica et Biophysica Acta (BBA) - Protein Structure and Molecular Enzymology. 1985;831:261–266. [Google Scholar]
- (66).Gambarelli S, Mouesca J-M. Inorg. Chem. 2004;43:1441–1451. doi: 10.1021/ic0301167. [DOI] [PubMed] [Google Scholar]
- (67).Guigliarelli B, Bertrand P, Sykes AG. Adv. Inorg. Chem. Vol. 47. Academic Press; 1999. pp. 421–497. [Google Scholar]
- (68).Orio M, Mouesca J-M. Inorg. Chem. 2008;47:5394–5416. doi: 10.1021/ic701730h. [DOI] [PubMed] [Google Scholar]
- (69).Li HR, Mapolelo DT, Dingra NN, Naik SG, Lees NS, Hoffman BM, Riggs-Gelasco PJ, Huynh BH, Johnson MK, Outten CE. Biochemistry. 2009;48:9569–9581. doi: 10.1021/bi901182w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (70).Dudev T, Lim C. J. Am. Chem. Soc. 2002;124:6759–6766. doi: 10.1021/ja012620l. [DOI] [PubMed] [Google Scholar]
- (71).Noodleman L, Baerends EJ. J. Am. Chem. Soc. 1984;106:2316–27. [Google Scholar]
- (72).Morton JR, Preston KF. J. Magn. Reson. 1978;30:577–82. [Google Scholar]
- (73).Scholes CP, Lapidot A, Mascarenhas R, Inubushi T, Isaacson RA, Feher G. J. Am. Chem. Soc. 1982;104:2724–2735. [Google Scholar]
- (74).Ashby CIH, Cheng CP, Brown TL. J. Am. Chem. Soc. 1978;100:6057–63. [Google Scholar]
- (75).Bender CJ, Rosenzweig AC, Lippard SJ, Peisach J. J. Biol. Chem. 1994;269:15993–15998. [PubMed] [Google Scholar]
- (76).Townes CH, Dailey BP. J. Chem. Phys. 1949;17:782–96. [Google Scholar]
- (77).Bowman MK, Berry EA, Roberts AG, Kramer DM. Biochemistry. 2004;43:430–436. doi: 10.1021/bi034620z. [DOI] [PubMed] [Google Scholar]
- (78).Shubin AA, Dikanov SA. Appl. Magn. Reson. 2006;30:399–416. [Google Scholar]
- (79).Ullmann GM, Noodleman L, Case DA. JBIC, J. Biol. Inorg. Chem. 2002;7:632–639. doi: 10.1007/s00775-002-0342-6. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.