A Model of Incomplete Adaptation to a Severely Shifted Frequency-to-Electrode Mapping by Cochlear Implant Users

Abstract

In the present study, a computational model of phoneme identification was applied to data from a previous study, wherein cochlear implant (CI) users’ adaption to a severely shifted frequency allocation map was assessed regularly over 3 months of continual use. This map provided more input filters below 1 kHz, but at the expense of introducing a downwards frequency shift of up to one octave in relation to the CI subjects’ clinical maps. At the end of the 3-month study period, it was unclear whether subjects’ asymptotic speech recognition performance represented a complete or partial adaptation. To clarify the matter, the computational model was applied to the CI subjects’ vowel identification data in order to estimate the degree of adaptation, and to predict performance levels with complete adaptation to the frequency shift. Two model parameters were used to quantify this adaptation; one representing the listener’s ability to shift their internal representation of how vowels should sound, and the other representing the listener’s uncertainty in consistently recalling these representations. Two of the three CI users could shift their internal representations towards the new stimulation pattern within 1 week, whereas one could not do so completely even after 3 months. Subjects’ uncertainty for recalling these representations increased substantially with the frequency-shifted map. Although this uncertainty decreased after 3 months, it remained much larger than subjects’ uncertainty with their clinically assigned maps. This result suggests that subjects could not completely remap their phoneme labels, stored in long-term memory, towards the frequency-shifted vowels. The model also predicted that even with complete adaptation, the frequency-shifted map would not have resulted in improved speech understanding. Hence, the model presented here can be used to assess adaptation, and the anticipated gains in speech perception expected from changing a given CI device parameter.

Introduction

Cochlear implants (CIs) are prosthetic devices for people with severe to profound hearing loss. These devices represent sounds of different frequencies using electrical stimuli presented to an array of electrodes positioned along the length of the cochlea. The frequency band assigned to each electrode is determined by a programmable, tonotopically ordered frequency-to-electrode map. In postlingually deafened CI users, there is typically a mismatch between the frequency that activates a particular electrode position and the acoustic frequency that would normally stimulate the neurons at that position in the cochlea. Yet, CI users can adapt to this mismatch at least to some extent, so the question arises as to which frequency map would provide more benefit in terms of speech recognition: a more tonotopically matched map that may leave out important speech information (Fu and Shannon 1999a, b; Başkent and Shannon 2004, 2005), or a map with more speech information that may require listeners to adapt to a relatively larger frequency mismatch (Rosen et al. 1999; Faulkner et al. 2006; Reiss et al. 2007).

In the present study, the multidimensional phoneme identification (MPI) model (Svirsky 2000, 2002) was used to assess the degree of perceptual adaptation experienced by three postlingually deafened adult CI subjects tested in a previous study by Fu et al. (2002). That study was unique in that experienced CI listeners volunteered to use a severely shifted frequency map continually for 3 months, providing a relatively long-term assessment over time of CI users’ adaptation to a severe spectral shift. This map allocated more electrodes to frequency regions below 1 kHz, potentially providing better spectral resolution in a frequency range important for speech perception, but at the expense of introducing a downwards frequency shift of up to one octave in relation to the frequency allocation used in CI subjects’ clinical maps (which in themselves may have been shifted in frequency relative to subjects’ tonotopic map prior to deafness). For the most part, CI subjects’ speech recognition was poorer with the experimental (i.e. severely frequency-shifted) map than with the clinically assigned maps, even after 3 months of continual use (c.f. Fig. 1 of the present study). After subjects’ clinical maps were restored, speech recognition returned to baseline levels, suggesting that subjects were able to retain the central speech patterns developed with the clinical maps. Nonetheless, significant improvements in speech recognition were observed with the experimental map during the 3-month study period. While some adaptation occurred, the extent of adaptation was not completely clear. Do the poorer speech recognition scores with the experimental map indicate incomplete adaptation, or do they indicate that the experimental map would ultimately limit speech recognition, even if adaptation were complete? To clarify these issues, in the present study the MPI model was applied to the vowel identification data from the three subjects in Fu et al. (2002) to estimate the amount of adaptation to the experimental map. These quantitative estimates provide a window into the mechanisms underlying auditory adaptation to a frequency shift in peripheral speech input.

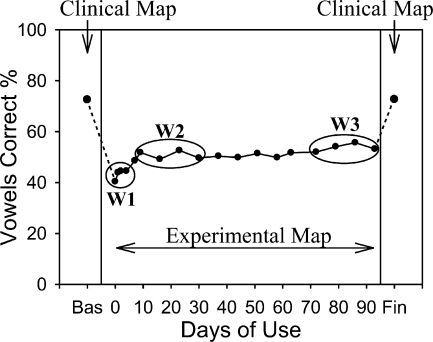
FIG. 1.

Average vowel identification percent correct scores across subjects tested by Fu et al. (2002) before, during, and immediately after the 3-month study period when subjects wore the experimental map. Clinical map conditions are baseline (=Bas) and final (=Fin). W1, W2, and W3 represent points in time in the experimental map condition over which vowel confusion matrices were compiled for the present study.

Methods

Three CI subjects (N3, N4, and N7) were tested by Fu et al. (2002); all were native speakers of American English. Subjects were postlingually deafened adult males implanted with the Nucleus-22 CI device (Cochlear Corp.) All subjects had 20 active electrodes available for use, and all used the Spectra 22 body worn speech processor programmed with the SPEAK strategy. At the time of testing, N3 was 55 years of age and had 6 years of experience with his device; N4 and N7 had 4 years of experience with their device, and were 39 and 54 years of age, respectively. All subjects had extensive experience with speech recognition experiments and were highly familiar with the speech perception tasks used for testing.

The clinical fitting software for the Spectra 22 processor provides nine possible frequency-to-electrode assignments (termed T1 through T9) when 20 active electrodes are being used. Each assignment differs in the overall frequency range mapped onto the electrode array. In Fu et al. (2002), Subject N3’s clinical map was T7 where the overall input frequency range was 120–8,658 Hz. The clinical map for subjects N4 and N7 was T9 where the overall input frequency range was 150–10,823 Hz. The severely shifted experimental map assigned to all three subjects was T1 where the overall input frequency range was 75–5,411 Hz, exactly one octave lower than T9, and ~0.625 octaves lower than T7.

In the present study, vowel identification was modeled based on the first two steady-state formant cues F1 and F2. These cues have been shown to be sufficient for normal hearing listeners to achieve high levels of vowel recognition when listening to monophthongal vowels (Peterson and Barney, 1952; Chistovich and Lublinskaya, 1979; and Hillenbrand et al. 1995). Therefore, out of the 12 vowels used by Fu et al. (2002), only the vowel identification data that included the nine nominally monophthongal vowels (in /h/-vowel-/d/ context) were used in the present study: ‘had’, ‘hawed’, ‘head’, ‘heed’, ‘hid’, ‘hod’, ‘hood’, ‘hud’, and ‘who’d’. That is, the diphthongs ‘hayed’ and ‘hoed’ were excluded because they are characterized by time-varying formant cues, and the r-colored vowel ‘heard’ was excluded because it is characterized by a low third formant. The vowel tokens used by Fu et al. (2002) were natural productions recorded from five men, five women, and five children (one production each), and were drawn from the larger corpus of speech samples collected by Hillenbrand et al. (1995).

In Fu et al. (2002), vowel confusion matrices were obtained before, during, and after the 3-month study period when CI subjects continually wore the experimental map. The vowel percent correct scores of these matrices, averaged across subjects are illustrated in Figure 1. In the present study, five confusion matrices were compiled from these data for each subject. Two matrices were the original ones obtained while listeners wore their clinical maps before (“baseline”) and after (“final”) wearing the experimental map (indicated by the downwards arrows in Fig. 1). The remaining three matrices (“W1”, “W2”, and “W3”) were subsets of the vowel matrices collected when subjects wore the experimental map (encircled in ovals in Fig. 1). Matrix W1 combined the vowel matrices obtained on days 0, 1, 2, and 4 (i.e., the first week wearing the experimental map), and represents acute speech recognition performance after subjects started using the experimental map. Matrix W2 combined the vowel matrices obtained on days 9, 16, 23, and 30 (i.e., from 1 week to 1 month after wearing the experimental map). Matrix W3 combined the vowel matrices obtained during the final 4 weeks of the 3-month study period. After being compiled, the five matrices were reduced from 12 × 12 to 9 × 9 by removing the rows and columns belonging to the three excluded vowels. These matrices (i.e., baseline, W1, W2, W3, and final) served as targets for our model, meaning that input parameters to the model were varied until they produced the best fit to the matrices obtained for each listener.

The multidimensional phoneme identification (MPI) model (Svirsky 2000, 2002) predicts phoneme confusion matrices based on a listener’s discrimination of acoustic cues along a specified set of perceptual dimensions. For example, for the steady-state first formant (F1) of a vowel, the set of all F1 values would define the perceptual dimension specific to this acoustic cue. Typically, more than one acoustic cue (and hence, more than one perceptual dimension) is required to identify a phoneme. When more than one perceptual dimension is used, each phoneme can be described as a point in a multidimensional perceptual space, where each coordinate is the value of the phoneme’s acoustic cue along its respective perceptual dimension.

The MPI model has two components: an internal noise model and a decision model. In response to repeated presentations of a token of a given phoneme, it is assumed that a listener’s percepts vary stochastically due to sensory and memory noise (Durlach and Braida 1969). The internal noise model captures this variation by adding Gaussian noise to the coordinates that define a given token, resulting in a “percept.” Along a given perceptual dimension, the standard deviation of this Gaussian distribution is defined as the listener’s just noticeable difference (JND) for the acoustic cue that defines that dimension. The decision model categorizes this percept by selecting the “response center” that is closest to the percept in the hypothesized perceptual space. The distance between the percept and each response center is scaled by the listener’s JND along each perceptual dimension, ensuring that comparisons based on distance in the perceptual space are in units of JND and independent of the physical units that define the locations of stimuli in the perceptual space.

In the decision model, the response center represents the listener’s internal representation of how a given phoneme should sound, i.e., the average location of where the listener expects a given phoneme to lie in the perceptual space. Let us define the average stimulus location of the phoneme in the perceptual space as that phoneme’s “stimulus center”. If stimulus and response centers are equal then the response center is considered unbiased. This situation would be expected to occur with normal hearing listeners, because their response centers have been formed by long-term exposure to spoken language. However, if a listener’s response center is different than its corresponding stimulus center (as might happen with a CI user, or with a frequency transposition hearing aid), then this response center is considered biased. The relationship between the location of a response center, its corresponding stimulus center and bias is defined as follows: for a given perceptual dimension, response center location  =  stimulus center location + bias. In the present study, response center locations were determined by finding the bias that best accounted for the observed data. The bias was assumed to be equal for all stimulus center locations so that stimulus centers belonging to a given frequency map were shifted as a group (thereby shifting a given polygon in Fig. 3) rather than each vowel category being shifted independently.

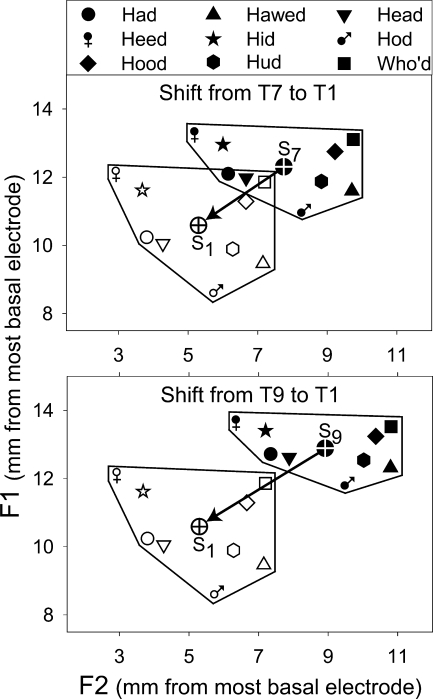
FIG. 3.

Shift in vowel stimulus center locations in the F1 vs. F2 space (in units of millimeters from the most basal electrode) after changing from the clinical map T7 or T9 (filled symbols) to the experimental map T1 (open symbols). The crossed circles show the locations of average stimulus centers S₁, S₇, and S₉, corresponding to T1, T7, and T9, respectively.

In the decision model, the listener’s ability to select a response center may be confounded by their uncertainty about that response center’s location. When this uncertainty is very small it can be said that the listener’s encoding and retrieval of response center location is highly consistent. Conversely, inconsistent retrieval of response center location suggests a large amount of response center uncertainty (RCU), or noise in the decision process. This quantity is distinct from the internal noise due to sensory and short-term memory limitations that were mentioned previously. The decision model captures the response center uncertainty by adding Gaussian noise to all response center locations, and afterwards selecting the response center closest to the percept. That is, on a given iteration of the decision model, response center locations were shifted together as a group in the F1 vs. F2 space while preserving the relative distance between individual response center locations. The amount of shift applied to the group of response center locations from one iteration to the next was sampled from the Gaussian noise. The standard deviation of this Gaussian distribution is termed the response center uncertainty, or RCU.

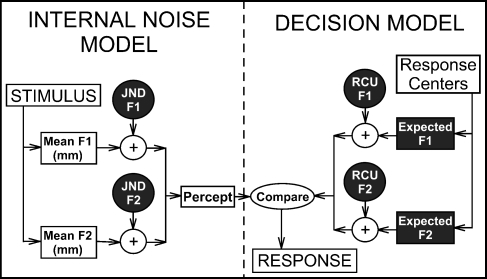
A block diagram summary of the MPI model used in the present study is presented in Figure 2 with the F1 and F2 perceptual dimensions (defined in step 1 of the next paragraph). The model generates a noisy percept from the coordinates that define the location of a given vowel stimulus (i.e., internal noise model) and then selects the response center closest to the percept after adding noise to response center locations (i.e., decision model). Using a Monte Carlo algorithm, this model of the listener’s response can be repeated many times for all vowel tokens, and the output can be tabulated in a vowel confusion matrix. This matrix is determined by the listener’s JND, their expected locations of response centers and response center uncertainty (RCU) for each perceptual dimension. In the present study, these parameters (shaded in black with white lettering in Fig. 2) were varied until a model matrix was obtained that best fit the listener’s experimentally obtained confusion matrix.

FIG. 2.

Flow chart summary of the MPI model used in the present study. The internal noise model generates a “percept” by adding JND noise to the location of a vowel stimulus in the F1 vs. F2 space. The decision model categorizes the percept by selecting the closest response center (i.e. the subject’s expected location of each vowel) after adding noise proportional to the subject’s response center uncertainty (RCU). The six model parameters optimized in the present study are highlighted in black with white lettering.

Three steps are involved in implementing the MPI model: (1) postulating a set of perceptual dimensions, (2) finding the stimulus location of each phoneme along each perceptual dimension, and (3) determining the model parameters that provide the best match between model output and experimentally obtained matrices. For the first step, two perceptual dimensions were proposed for the vowel tokens used in the present study. These dimensions were the locations of mean first and second formant energies (F1 and F2) along the implanted electrode array, measured in millimeters from the most basal electrode. That is, equal distances along the array were treated as equally discriminable. This is a reasonable first-order simplifying assumption because even though different individuals may show better discrimination at the base, the apex, or the middle of the cochlea, there are no large systematic differences in discrimination along the array that would apply to the general population of CI users (Kwon and van den Honert, 2006; Zwolan et al. 1997). Similarly, for the sake of simplicity, these perceptual dimensions are assumed to be orthogonal and equally weighted, and distances in the perceptual space are assumed to be Euclidean.

For the second step, it was not possible to measure mean formant energy locations of vowel stimuli directly from each CI subject’s implanted array. Instead, these were inferred from Hillenbrand et al.’s (1995) measures of steady-state F1 and F2 formant center frequencies. For the 135 vowel tokens used in the present study (i.e., 15 productions of nine vowels) F1 and F2 values in Hz were transformed to electrode positions using a frequency-to-place function derived from the experimental and clinical frequency allocation tables worn by the CI subjects (i.e., T1, T7, and T9). In a frequency allocation table, adjacent frequency analysis bands are mapped to adjacent electrodes, which are spaced 0.75 mm apart in the Nucleus-22 device. The frequency-to-place function was obtained by plotting the center frequency allocated to each electrode as a function of each electrode’s distance (in mm) from the most basal electrode, and then joining these points with straight lines. In this way, measurements of mean formant energy locations along the implanted array were obtained for F1 and F2 for each vowel token, with T1, T7, and T9. Figure 3 shows the shift in locations of stimulus centers for each vowel from the clinical maps (filled symbols: T7 in top panel, T9 in bottom panel) to the experimental map (T1, unfilled symbols in both panels). Also shown are the average stimulus centers for all the vowels in a given frequency allocation table (crossed circle in polygon; S₁ from T1, S₇ from T7, and S₉ from T9).

For the third step, model confusion matrices were fit to experimentally obtained matrices using six parameters: two for the JND parameters (representing the F1 and F2 perceptual dimensions), two for the bias parameters (representing the F1 and F2 perceptual dimensions), and two for the RCU parameters (representing the F1 and F2 perceptual dimensions). Allowing all parameters to vary simultaneously would have been too time-consuming. Instead, these parameters were fit to the data in the following stages. For the baseline clinical map condition, model matrices were fit to observed matrices by allowing the JND and bias parameters to vary while assuming RCU = 0. As a starting point, this assumption is supported by the fact that listeners had been using their clinical maps (T7 or T9) for 4 to 6 years so it is reasonable to expect that their response centers had already settled to well-known locations (i.e., RCU near zero), even if those locations do not coincide exactly with the locations of stimulus centers (i.e., bias may be nonzero). Nevertheless, the JND and bias parameters thus obtained were then used to fit model matrices again to the observed matrices in this condition while allowing RCU to vary, in order to assess the possibility of a nonzero RCU in the baseline condition. For all other conditions (i.e. W1, W2, W3, and final) model matrices were fit to the experimentally obtained matrices by allowing the bias and RCU parameters to vary, while JND parameters were set to the optimal values obtained in the baseline condition. That is, it was assumed that the JNDs of the internal noise model remained constant between the clinical and experimental map conditions. This is also a reasonable assumption, because sensory noise should not be affected by how frequency ranges are allocated to specific electrodes.

For these simulations, JND parameters ranged from 0.03 mm to 5 mm, bias parameters ranged from −3 to 3 mm, and RCU parameters ranged from 0 to 4 mm, in all cases using a step size of 0.01 mm. Confusion matrices were obtained using the Monte Carlo algorithm described above with 300 iterations per vowel token. This number of iterations ensured that the same input parameters would produce a model matrix with cell entries that did not differ from their steady-state value by more than 1% (when matrix rows are expressed as percentages). Optimized parameters were obtained by minimizing the root-mean-square (i.e. rms) difference between elements of the matrices predicted by the model and elements of the experimentally obtained matrices (i.e., baseline, W1, W2, W3, and final). Note that according to the MPI model, changes in the optimized bias parameters reflect changes in the location of subjects’ response centers relative to average stimulus centers (S₁, S₇, and S₉ in Fig. 3) in the F1 vs. F2 perceptual space, and changes in the RCU parameters reflect changes in subjects’ uncertainty about the location of response centers. In the present study, the optimized bias and RCU parameters were used to assess the amount of adaptation experienced by CI subjects with the clinical and experimental maps before, during, and after the 3-month study period.

Results

Table 1 summarizes the optimal MPI model parameters that provided a best fit to the observed matrices (i.e., baseline, W1, W2, W3, and final) for CI subjects N3, N4, and N7. Regarding the fit of the MPI model to the observed matrices, the minimized rms difference between best-fit model matrices and observed matrices ranged from 8.3% and 13.4% with an average rms difference of 11.2% (see fourth row). The coefficient of determination R², obtained from an element-wise correlation between best-fit model and observed matrices, ranged from 0.44 to 0.91 with an average R² of 0.73 (see fifth row). Additionally, percent correct scores of best-fit model matrices (see tenth row) and observed matrices (see 11th row) differed by no more than 9 percentage points with an average difference of 4 percentage points. Percent correct scores for model and observed matrices were also comparable in that baseline and final scores were better than those with the experimental map (W1, W2, and W3). The JNDs that produced best-fit model matrices to the observed matrices in the baseline condition, and subsequently used for all other conditions (see Methods) appear in the second row of Table 1.

TABLE 1.

MPI model input parameters obtained by minimizing the percent rms differences between model matrices and observed matrices (baseline, W1, W2, W3, and final)

Subject	N3					N4					N7
JND (mm)	jF1 = 0.1 jF2 = 0.33					jF1 = 0.06 jF2 = 0.19					jF1 = 0.1 jF2 = 0.34
Condition	Bas	W1	W2	W3	Fin	Bas	W1	W2	W3	Fin	Bas	W1	W2	W3	Fin
rms	11.6	13.2	12.5	13.4	9.5	8.3	11.3	11.1	11.0	8.3	11.1	13.4	12.6	11.1	9.6
R2	0.79	0.58	0.64	0.63	0.83	0.91	0.71	0.74	0.75	0.91	0.79	0.44	0.67	0.75	0.86
RCU1	0.06	0.17	0.10	0.13	0.14	0.06	0.26	0.14	0.12	0	0.03	0.50	0.20	0.12	0.03
RCU2	0.06	1.38	1.32	0.90	0.18	0.07	1.48	1.16	1.22	0.02	0.17	1.34	0.93	0.54	0.10
b1	0.07	−0.04	−0.06	−0.04	0.01	−0.03	−0.06	−0.10	−0.14	−0.06	−0.05	−0.09	−0.15	−0.09	−0.02
b2	0.21	0.58	0.58	0.63	0.15	−0.07	−0.44	−0.24	−0.39	−0.08	−0.03	−0.62	−0.48	−0.09	−0.10
Model %	72.9	55.4	56.5	60.0	69.6	77.9	53.4	59.5	58.4	77.7	72.5	47.2	59.1	65.5	74.0
Actual %	70.7	50.9	53.8	56.0	67.8	86.6	60.4	64.9	64.7	86.6	68.9	44.3	61.9	65.2	75.6

Just noticeable difference, response center uncertainty and bias parameters are jF1, RCU1, and b1 for F1 and jF2, RCU2, and b2 for F2, expressed in millimeters along the implanted electrode array. The last two rows show predicted and observed vowel identification percent correct scores

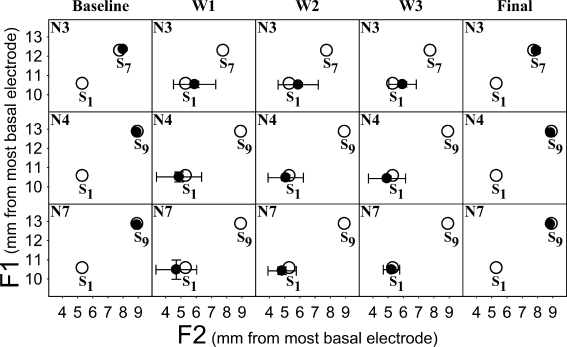
The focus of the present study is the response center uncertainty (RCU) and bias parameters in Table 1 (rows 6 through 9) because they provide insights about the degree and nature of the adaptation experienced by CI users with the severely shifted experimental map during the 3-month study period. That is, the bias parameters provide the locations of response centers relative to stimulus centers, and the RCU parameters provide the error with which those response centers are recalled by subjects. In Table 1, RCU1 = response center uncertainty for the F1 perceptual dimension, RCU2 = response center uncertainty for the F2 perceptual dimension, b1 = bias for the F1 perceptual dimension, and b2 = bias for the F2 perceptual dimension. The manner in which these parameters indicate the degree of adaptation is illustrated in Figure 4, where average response centers (filled circles) are plotted for each subject at each condition (i.e., baseline, W1, W2, W3, and final) relative to the average stimulus centers of Fig. 3 (i.e., S₁, S₇, and S₉; plotted as unfilled circles in Fig. 4). The response centers were obtained by adding the bias parameter values to the corresponding stimulus centers along each perceptual dimension. That is, the response centers in the baseline and final conditions were obtained by adding the bias parameter values to the stimulus centers corresponding to each subject’s clinical map (i.e., S₇ for Subject N3, and S₉ for subjects N4 and N7), and the response centers in the experimental conditions (W1, W2, and W3) were obtained by adding the bias parameter values to the stimulus center corresponding to the experimental map (i.e. S₁ for all subjects). Superimposed over each response center are bi-directional bars which represent ±1 RCU (in mm) along each formant dimension.

FIG. 4.

Average response centers (filled black circles) ±1 RCU (in millimeters) along each dimension (F1 and F2) for CI subjects N3, N4, and N7, in relation to average stimulus centers (unfilled circles) at different points in time during the 3-month study period: baseline (with the clinical map), W₁ = after 1 week with the experimental map, W₂ = after 1 month with the experimental map, W₃ = after 3 months with the experimental map, and final (after restoring the clinical map). S₁, S₇, and S₉ are the average stimulus centers corresponding to frequency maps T1, T7, and T9, respectively.

Let us first consider the response center locations and RCU bi-directional bars in the baseline and final conditions (i.e., first and last columns in Fig. 4, respectively). For subjects N4 and N7 (second and third rows in Fig. 4), locations of average response centers at baseline were extremely close to the S₉ average stimulus center, within 0.1 mm. Furthermore, consistent with our starting point assumption for fitting the baseline condition, these subjects’ RCUs were relatively small at baseline (i.e., hardly discernible in Fig. 4). Taken together, these results suggest that subjects N4 and N7 had fully adapted to their clinical map before wearing the experimental map. In other words, these subjects’ percent correct scores with their clinical map were limited only by their JND. In the case of Subject N3 (first row in Fig. 4), although RCUs were near zero (consistent with our starting point assumption for fitting this condition), a small positive bias was found in the F2 dimension (about 0.2 mm to the right of the S₇ average stimulus center). This bias may indicate that this listener experienced an incomplete adaptation to the basalward shift imposed by his clinical map in comparison to the tonotopic map stored in long-term memory, prior to onset of deafness. After the 3-month study period, when CI subjects’ clinical maps were restored, response center locations and RCUs in the final condition returned to their baseline positions (although with a slight increase in RCU for Subject N3), reinforcing the notion that these listeners were able to retain the internal representations of these vowels developed with their clinical maps. This result is even more compelling when one takes into account the fact that speech recognition levels in the final condition were measured acutely after restoring the clinical map, with no adjustment period.

For the experimental map conditions (W1, W2, and W3), the MPI model can be used to estimate the degree of adaptation. If adaptation were complete, one would expect that the average response centers would be extremely close to the S₁ average stimulus center. As shown in Figure 3, the locations of vowel stimulus centers shifted as a result of changing from the clinical maps to the experimental map. For Subject N3, the average stimulus center for the experimental map (S₁) was shifted away from the average stimulus center of the clinically assigned map (S₇) towards the base by 1.7 mm in the F1 dimension and 2.5 mm in the F2 dimension. For subjects N4 and N7, S₁ was shifted away from the average stimulus center of the clinically assigned map (S₉) towards the base by 2.3 mm in the F1 dimension and 3.6 mm in the F2 dimension. As shown in Figure 4, during the first week of wearing the experimental map (W1), the average response centers for subjects N4 and N7 overcame the shift imposed by the experimental map (although with some overshoot in the F2 dimension). Whereas the average response center for Subject N3 overcame the shift in the F1 dimension, the average response center in the F2 dimension fell short of S₁ by almost 1 mm, even after wearing the experimental map for 3 months (W3). That is, it appears that Subject N3 experienced much less adaptation to the basalward shift (in terms of the F2 dimension) with the experimental map, in comparison to the clinical map.

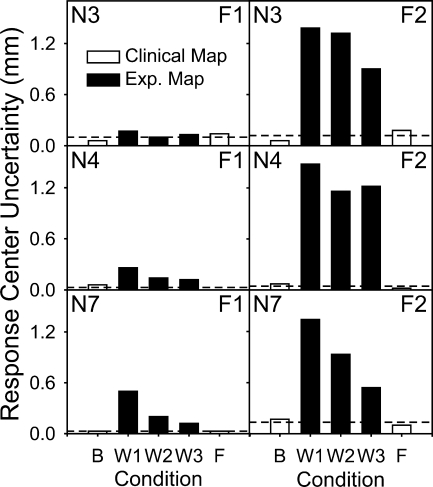
If adaptation were complete we would also expect that the RCU bi-directional bars with the experimental map would be as small as those with the clinical map. However, as shown in Table 1 and Figure 4, there was a systematic increase in the RCU for all subjects when they changed from the clinical map to the experimental map. Figure 5 shows RCU values for each subject (rows) for the F1 and F2 dimensions (columns). The RCUs are shown for the clinical map (white bars) and the experimental map (black bars) at different points during the 3-month study period. With the experimental map, RCU tended to decrease by the end of the 3-month study period (except for Subject N4 in the F2 dimension), but remained much larger than the RCUs for the clinical map (except for Subject N3 in the F1 dimension).

FIG. 5.

Response center uncertainty (RCU) for locations of mean formant energies F1 and F2 along the implanted electrode array, as a function of different points in time during the 3-month study period; RCUs are expressed in millimeters. Values of RCU tended to be larger with the frequency-shifted map conditions (W1, W 2, and W3) than with the clinical map conditions (Bas = baseline and Fin = final), for all subjects (N3, N4, and N7). Horizontal dashed line shows the average of baseline and final RCUs with the clinical map.

Taken together, the locations of response centers relative to stimulus centers and the response center uncertainties obtained with the MPI model indicate the extent of adaptation to the experimental map experienced by the three CI subjects. The locations of response centers represent the listener’s ability to adjust their expectations of how vowels should sound; when locations of stimulus and response centers are equal, the listener’s expectations of how vowels should sound are consistent with the physical characteristics of the vowels being presented. The RCU parameters estimate the listener’s uncertainty about the location of response centers in the F1 vs. F2 perceptual space, and reflects the listener’s ability to consistently categorize each vowel token into its appropriate vowel category. If complete adaptation to the experimental map is defined as having response centers equal to stimulus centers and RCUs equal, or nearly equal, to zero, then none of the three subjects experienced complete adaptation. The decrease in RCUs over the 3-month period indicates that some adaptation occurred, and Subject N7 appeared to achieve nearly complete adaptation by the end of the 3-month study period. Hence, the MPI model not only addresses whether adaptation was complete, but also quantifies the deficit in adaptation.

Discussion

For the three subjects of Fu et al. (2002), the present study indicates that incomplete adaptation to the experimental map was primarily driven by subjects’ response center uncertainty. Whereas subjects could adjust the average locations of their response centers towards the new vowel locations within the first week of wearing the experimental map, their response center uncertainties remained substantially larger than with their clinical maps even after 3 months of continual use, particularly along the F2 dimension (c.f. Fig. 5). This result suggests that even if subjects’ expectations of vowel sounds are, on average, exactly matched to the acoustic properties of the shifted vowels, their vowel scores could still be adversely affected by an inability to consistently recall those expectations.

One explanation for why subjects’ response center uncertainty increased with the experimental map may be that subjects were required to remap their phoneme labels stored in long-term memory. That is, in addition to adjusting their expectations of how vowels should sound, adapting to frequency-shifted speech also requires subjects to assign lexically meaningful labels to those sounds, especially when the frequency-shift is large (Li and Fu 2007). In the framework of the MPI model, a phoneme label stored in a listener’s long-term memory would reduce the listener’s response center uncertainty and ‘anchor’ the response center for a given phoneme in the perceptual space, reducing the listener’s errors in classifying a given speech token. When there is a large amount of learning and deeply ingrained phoneme labels, these phoneme labels help improve classification performance. In contrast, with poor phoneme labels (or no labels at all), the response center uncertainty will be higher and will contribute to greater errors in classifying speech tokens.

As observed in Table 1 and Figure 5 of the present study, CI subjects’ overall response center uncertainty was relatively small in the baseline condition, suggesting that these listeners were able to develop phoneme labels with long-term use of their clinical maps. Furthermore, in the final condition, when CI subjects were switched back to their clinical maps at the end of the 3-month study period, their response centers and RCUs returned to baseline levels, exemplifying the extent to which these phoneme labels were ingrained in long-term memory. As a side note, this result is consistent with the study of Hofman et al. (1998), wherein normal hearing listeners wore ear molds for a 6-week period and were required to learn new cues to localize sound. After the ear molds were removed, these listeners could immediately recall the central representations developed with the original (undistorted) cues. With the experimental map, CI users’ RCUs increased substantially. Presumably, they were uncertain about the phoneme labels associated with the unfamiliar vowel stimulation patterns. By the end of the 3-month study period with the experimental map, RCUs tended to decrease, suggesting that listeners could improve their labeling of vowels, but could not do so to the same extent as with the clinical map.

It is important to note that the incomplete adaptation observed in Fu et al. (2002) occurred with passive learning, i.e., via everyday exposure to the experimental map without active training. For vowel identification in particular, adapting to spectral mismatch requires a process of central remapping in which vowel categories are adjusted to the new stimulation patterns, i.e., remapping response centers to new stimulus centers and reducing RCUs to baseline levels. When a spectral shift is sufficiently severe, lexically meaningful feedback and/or active training may be required for adaptation (Li and Fu 2007). Whereas the subjects in Fu et al. (2002) may have received lexically meaningful feedback, there was no active training, and the passive exposure was not sufficient for complete adaptation. It is possible that an active training regimen with lexically meaningful feedback and/or introducing the spectral mismatch in gradual stages (as opposed to abruptly) would have allowed subjects to completely adapt to the experimental map (Svirsky et al. 2004; Fu and Galvin 2007).

Up to this point, it has been demonstrated how the MPI model can be used to measure the adaptation, or lack thereof, experienced by the CI subjects in Fu et al. (2002). This was necessary particularly because vowel identification scores alone do not reflect the degree of adaptation. Because different frequency allocation tables result in different stimulation patterns, the maximum percent correct score that can be achieved with a given JND (assuming zero bias) will depend on the specific boundaries of each frequency allocation table. For illustration purposes consider a frequency allocation map whose total range spans 1,000 to 6,000 Hz. Even in the case of complete adaptation (i.e., zero bias and RCU) such a map would result in much lower percent correct scores than T1, T7, or T9, due to the absence of F1 information. Thus, complete adaptation to a given frequency map does not necessarily result in achieving the same fixed percent correct for all maps. Instead, it results in achieving a “maximum” percent correct that is limited by the listener’s JND and the specific characteristics of the frequency allocation map. In this regard, the MPI model can be used to estimate vowel identification performance with complete adaptation to the experimental map (T1). That is, using CI subjects’ JNDs in Table 1 and assuming complete adaptation to T1 (i.e., setting RCU = 0 and bias = 0), the MPI model would predict T1 to produce vowel identification scores of 67.1% correct for N3, 69.1% correct for N4, and 66.6% correct for N7. At baseline, the MPI model predicted T7 to produce a score of 72.9% correct for N3, and T9 to produce scores of 77.9% and 72.5% correct for N4 and N7, respectively (see Table 1). Hence, the MPI model predicts that relative to their clinical maps, T1 would have resulted in poorer vowel identification in these subjects, even with complete adaptation.

Offhand, this result may be surprising. If adaptation were complete, why should T1 produce lower vowel scores than the baseline conditions with the clinical maps? After all, was not T1 supposed to increase resolution below 1 kHz? Indeed, as shown in Figure 3, shifting from the clinical map to the experimental map provided twice as much space for vowel stimulus centers in the F1 dimension (though no extra space along F2). However, not shown in Figure 3 are the stimulus locations of the individual vowel tokens that were obtained from adult males and females, and children (i.e., the variability in locations of vowel tokens inherent in productions from different groups of speakers). Although T1 increased the relative spacing of stimulus centers along F1, it also caused the individual tokens to spread out along this dimension. In a case of complete adaptation, the stimulus centers would act as response centers, and the spreading out of the individual tokens along one dimension altered the relative locations between vowel tokens and stimulus centers in the F1 vs. F2 space, thus altering the rates with which vowel tokens were misclassified. Factoring in each subject’s JNDs, the MPI model predicted that these altered relative locations decreased overall percent correct. That is, the MPI model predicted that T1 would ultimately result in poorer vowel identification than the subjects’ clinical maps, even with complete adaptation to T1. If the frequency allocation of the experimental map had been arranged so that F2 was afforded more resolution, and if we maintained the hypothesis of complete adaptation, we speculate that the MPI model would have predicted better vowel identification scores with this experimental map than with the subjects’ clinical maps. Indeed, one could carry on this exercise for any number of possible frequency allocation assignments.

In summary, the MPI model used in the present study provides important new insights into the unique adaptation data collected by Fu et al. (2002). The model explains possible mechanisms that underlie CI users’ adaptation to spectrally shifted speech by providing quantitative estimates of CI users' ability to adjust their response center locations and response center uncertainty, i.e., their expectations of how speech should sound relative to the acoustic properties of shifted speech, as well as their uncertainty associating new phoneme labels to the shifted speech tokens. In particular, the model can be used to estimate gains in speech perception with changes in CI fitting parameters (e.g., the frequency-to-electrode assignment), estimate the amount of adaptation required to achieve this benefit, and to determine whether adaptation to a CI parameter change was complete or incomplete.