The imprinted DLK1-MEG3 gene region on chromosome 14q32.2 alters susceptibility to type 1 diabetes

Abstract

Genomewide association studies to map common disease susceptibility loci have been hugely successful with over 300 reproducibly associated loci reported to date,¹ but, perhaps surprisingly, have not yet provided convincing evidence for any susceptibility locus subject to parent of origin effects. We used imputation to extend existing genomewide association datasets^{2, 3, 4} and here report robust evidence, at rs941576, for paternally inherited risk of type 1 diabetes (T1D, ratio of allelic effects for paternal vs maternal transmissions = 0.75, 95%CI=0.71–0.79), in the imprinted region of chromosome 14q32.2, which contains a functional candidate gene, DLK1. Our meta-analysis also provided support at genomewide significance for a T1D locus at chromosome 19p13.2, with the highest association at marker rs2304256 (OR=0.86, 95%CI=0.82–0.90) in the TYK2 gene, which has previously associated with systemic lupus erythematosus.⁵

We used imputation to assess association with T1D across 2.6 million polymorphic SNPs from the International HapMap Project in a total of 7514 cases and 9405 controls of European ancestry from three existing genomewide association studies: WTCCC (UK)², GAIN/NIMH (USA)³, T1DGC (UK)⁴ (supplementary table 1). The R package snpMatrix⁶ was used to conduct the imputation and calculate single SNP association score tests for each HapMap SNP. The score tests are based on the Cochran-Armitage test, with a Mantel extension to allow combination over different strata (UK region in the case of the WTCCC and T1DGC samples, and an estimated ancestry score derived from principal components in the case of the GoKinD/NIMH samples³). For imputed SNPs, the score statistics are calculated using the expected value of the imputed SNP, given observed SNPs, with the expectation calculated under the null hypothesis.

Overall, there was some over-dispersion of test statistics (λ = 1.14 and λ = 1.09 for 1 degree of freedom (df) and 2df tests respectively). This is consistent with the large sample size (almost 17,000 samples) and the over-dispersion observed in earlier analysis of these data without HapMap imputation⁴. Barrett et al argue that the greater contributor to over-dispersion in these data is bias (eg differential genotyping error) rather than population structure,⁴ and therefore cluster plots for all SNPs used to impute associated SNPs were examined carefully. Three loci showed suggestive evidence for association (p < 10⁻⁷) in regions not previously associated with T1D (supplementary figure 1​;​ supplementary table 2). One SNP, rs229484, is proximal (30kb) to a nearby known T1D locus (rs229541³), also at 22q13.1, but is separated by two moderate recombination hotspots and there is low LD between the two markers (r²=0.1, D′=0.4).

In order to replicate these potential effects, we carried out direct genotyping of the three SNPs using TaqMan in a subset of the GWA samples, additional case-control and family samples and obtained evidence for association in two of the three loci (table 1, supplementary table 3). In these two loci, the overall levels of significance were < 10⁻⁸: rs2304256 p = 4.13 × 10⁻⁹, rs941576 p = 1.62 × 10⁻¹⁰.

Table 1.

Association testing of two SNPs using direct genotyping in case-control and family samples

a. rs2304256 C>A on chromosome 19p13.2
Cohort	N	Fq (A)	Odds ratio (A:C)	(95% CI)	p value
WTCCC	1766/1384	0.299	0.84	(0.75–0.94)	2.68 × 10−3
T1DGC	3838/3883	0.294	0.85	(0.80–0.92)	1.45 × 10−5
Additional	2686/4794	0.290	0.87	(0.81–0.94)	6.02 × 10−4
Families	3099	0.266	0.96	(0.90–1.03)	0.290
Case-control combined	8290/10061	0.293	0.86	(0.82–0.90)	1.43 × 10−10
Families & case-control	(see above)	-	-	-	4.13 × 10−9

b. rs941576 A>G on chromosome 14q32.2
Cohort	N	Fq (G)	Odds ratio G:A	(95% CI)	p value
WTCCC	1798/1406	0.43	0.90	(0.81–1.00)	0.049
T1DGC	3754/3736	0.43	0.88	(0.82–0.94)	9.3 × 10−5
Additional	2670/4840	0.43	0.92	(0.86–0.99)	0.030
Families	4057	0.45	0.87	(0.82–0.93)	1.8 × 10−5
Case-control combined	8222/9982	0.43	0.90	(0.86–0.94)	9.8 × 10−7
Families & case-control	(see above)	-	-	-	1.62 × 10−10

Association testing using observed (not imputed) genotypes in a subset of GWA samples, additional case control samples and family samples. SNP names are followed by alleles, ordered as major>minor. N is number of cases/controls, or number of informative transmissions. Fq is the frequency of the minor allele in controls or parents.

rs2304256 C>A (OR for A vs C = 0.86) is located within the TYK2 gene at chromosome 19p13.2, which is implicated in IFN-α, IL-6, IL-10 and IL-12 signalling. This is a region of wide LD containing several functional candidate genes (supplementary figure 2). rs2304256 is one of six SNPs in 1000 Genomes (pilot 1, April 2009) in mutual tight LD (r² > 0.9); two are located within TYK2 (rs34725611 and rs11085725 in introns 6 and 23 respectively) and the remaining three (not yet in dbSNP) are downstream of TYK2 and upstream of ICAM3. No other SNPs had r² > 0.62 with any of these six. rs2304256 itself is a non-synonymous SNP (Val362Phe) which has also been associated with systemic lupus erythematosus (SLE)⁵; in both T1D and SLE the minor (and inferred non-ancestral⁷) allele (A/Phe) appears protective⁵.

Most interestingly, the newly identified locus with the strongest association with T1D susceptibility occured in a well established imprinted region on chromosome 14q32.2⁸ marked by SNP rs941576 A>G (OR for G vs A = 0.9). Beyond the insulin T1D susceptibility locus, marked by rs7111341 in Barrett et al,⁴ we do not know of any other T1D SNPs in established imprinted genes. Within this imprinted region of just over 1Mb, a mixture of paternally derived (DLK1, RTL1, DIO3) and maternally derived (MEG3, MEG8) genes are expressed⁸ (figure 1). Therefore, we tested for a parent of origin effect, expecting to see excess transmissions of the risk allele from either fathers or mothers (but not both) if the SNP was acting to influence one of these imprinted genes. A simple way to do this is to consider separately the paternal and maternal transmissions in a transmission disequilibrium testing (TDT) framework, and this showed strong evidence for reduced paternal transmission of the protective G allele (p=6.3 × 10⁻⁸). Although the maternal transmissions are distorted in the same direction and a small effect of the maternal copy cannot be discounted, there is no significant evidence for such an effect (p = 0.11; table 2). However, effects due to the action of maternal genotype in utero are confounded with imprinting effects⁹, so we fitted a model allowing for both maternal genotype and imprinting effects. This has been approached in case-parent trio data by log-linear modelling of counts of trios by parental and affected offspring genotype. We extended this method to allow for the fact that many of our families had multiple affected offspring (see supplementary methods) and found that the imprinting-only model was preferred (supplementary table 4); under that model, the imprinting effect was highly significant (p = 1.85 × 10⁻⁸) with the ratio of allelic effects for paternally to maternally inherited alleles equal to 0.75. This test gains power by using information on parental asymmetry induced by parent-of-origin effects. Asymmetry was clearly exhibited in our data: the protective allele (G) is less common amongst fathers of affected offspring than mothers (0.43 vs 0.47, p = 6.53 × 10⁻⁷). To reassure ourselves against a false positive result, driven by unusual patterns in a subset of the data, we reanalysed the families subdivided by broad geographical region, and found consistent effect estimates across all regions (table 3).

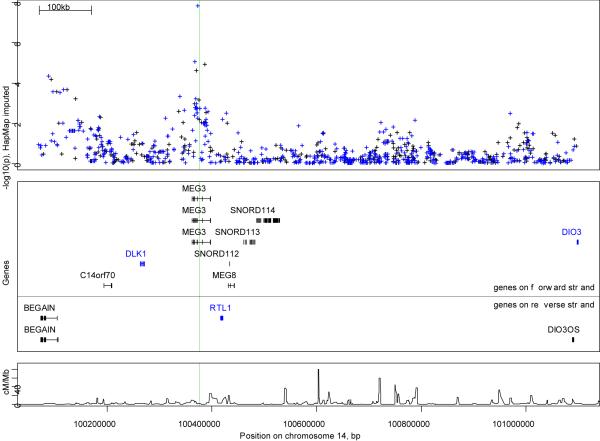
Figure 1.

The imprinted region on chromosome 14q32.2. The region shown is delimited by the most distant genes known to be imprinted 8 with positions according to Hs_NCBI36. The top panel shows -log 10(p) from 1 degree of freedom tests of association with SNPs across the region. SNPs which were directly genotyped are in black, SNPs imputed from HapMap in blue. The second panel shows the location and orientation of genes in the region. Paternally expressed genes are shown in blue, maternally expressed genes in black. The third panel shows recombination rates (cm/Mb) from HapMap. A solid green line shows the location of rs941576 in all panels for reference.

Table 2.

Transmission Disequilibrium Tests of rs941576 A>G

Transmissions from	Fq	G Untransmitted	G Transmitted	p value
All parents	0.45	2166	1891	1.6 × 10−5
Fathers	0.43	869	657	6.3 × 10−8
Mothers	0.47	793	730	0.11

Parental frequency (Fq) and transmissions of the rs941576 protective G allele, overall and separated by parent of origin. Frequencies are calculated using all parents. Note that because only transmissions from heterozygous (informative) parents are shown, transmission of a G allele implies non-transmission of A (and vice versa). The sum of maternal and paternal transmissions is less than the number of transmissions from all parents because it is not always possible to identify which parent transmitted which allele.

Table 3.

Imprinting analysis of rs941576 A>G

Region	N	exp(-θ̂)	95% CI	p
UK	361	0.792	0.724 – 0.866	9.40 × 10−3
Asia-Pacific	32	0.88	0.656 – 1.18	0.662
Other Europe	257	0.725	0.644 – 0.815	6.08 × 10−3
USA	184	0.764	0.676 – 0.863	0.028
Finland	397	0.697	0.632 – 0.769	2.25 × 10−4
Overall	1231	0.749	0.712 – 0.789	1.85 × 10−8

Imprinting analysis using family data divided by broad geographical region. N is the number of informative families (which is less than the total number of families available, as only transmissions from asymmetric parents are informative). exp(-θ̂) is the ratio of the allelic effect for a paternally inherited risk allele compared to a maternally inherited allele.

The SNP rs941576 lies within intron 6 of the maternally expressed non-coding RNA gene, MEG3. However, our observation that only transmissions from fathers alter T1D risk suggest the causal variant influences one of the paternally expressed imprinted genes in its neighbourhood: DLK1, RTL1 or DIO3. rs941576 is between and downstream of both DLK1 and RTL1 and upstream of DIO3, at distances of 105kb, 41kb and 721kb respectively. Unusually for a locus identified from GWA data, the signal is restricted to rs941576 and there are no SNPs in HapMap or the current pre-release of 1000 Genomes Project (pilot 1, April 2009) which are in strong or moderate LD with rs941576 (all r² < 0.5, data not shown). Although that does not preclude the existence of an as yet unknown variant (SNP or structural variant) in tighter LD, rs941576 lies within a region conserved across mammalian species, including opossum. This is interesting because the region is not imprinted in the opossum, there is no sequence homology to MEG3 and, while there is some sequence homology to mouse and human RTL1 gene, it appears to be extensively degraded in opossum¹⁰. Thus, if the region is conserved because it contains regulatory elements of nearby genes, these must regulate one of the genes common to all mammals, ie DLK1 or DIO3.

Although rs941576 lies some distance from the paternally expressed genes in the region, regulatory regions can lie >100kb from their target genes, particularly in imprinted regions¹¹. This region is already subject to long-range cis-acting regulation from the intergenic differentially methylated region (DMR) located 12.5kb upstream of MEG3.¹² Insertion of a transgene in the mouse downstream of this DMR causes loss of imprinting on the paternal chromosome, biallelic expression of the mouse homologue of MEG3, Gtl2 and reduced expression of Dlk1​¹³. Thus, it is plausible that this SNP (or another unknown variant nearby) could alter the regulation of the paternally expressed DLK1 or RTL1 genes.

Of the paternally expressed genes, only DLK1 has a strong functional candidacy. It is most strongly expressed in human heart, pancreatic islet cells, pituitary tissue, ovaries, placenta and testes (T1DBase, BioGPS), is related to members of the Notch-Delta family of signalling molecules and encodes a membrane bound protein, which can be cleaved to form fetal antigen 1 (FA1).¹⁴ FA1 is involved in differentiation of many cell types¹⁵ including pancreatic beta cells where FA1 immunoreactivity has been localised to glucagon-negative cells in the mature pancreas.¹⁶ FA1 is also involved in hematopoiesis including differentiation and function of B lymphocytes^17,18 and has been shown to increase expression of pro-inflammatory cytokines in human bone marrow mesenchymal stem cells and promote B cell proliferation in human peripheral blood.¹⁹ Thus there are a number of ways in which variation in the expression of DLK1 could alter susceptibility to T1D, which is caused by autoimmune destruction of insulin-producing beta cells in the pancreas.

The mechanisms underlying imprinting are not yet fully understood, but are known to involve epigenetic processes including DNA methylation and histone acetylation. The causal variant underlying this association could be acting directly to alter the expression of the paternally inherited copy of a nearby gene (DLK1 appears to be the strongest candidate), or it could act by interfering subtly with the imprinting mechanism and in turn alter expression of either the paternally or maternally inherited copies of a target gene. Although rs941576 may be tagging an unknown causal variant, there is support for the hypothesis that this SNP is itself the causal variant, given its isolation from other SNPs in terms of linkage disequilibrium, and its location in a conserved and, presumably, regulatory region.

Rare disorders related to imprinting defects are known (eg Prader-Willi syndrome, OMIM 176270). For common complex diseases, over 300 reproducibly associated¹ loci have been reported, but we are not aware of any convincing evidence for another susceptibility locus subject to parent of origin effects. At least one common disease locus overlaps a known imprinted region: the T1D associated region of chromosome 11p15 contains the insulin and IGF2 genes, but a previous report by our group of potential parent of origin effects at this locus in T1D²⁰ has not yet been substantiated. We are aware of only one other report of a parent of origin effect, in basal cell carcinoma,²¹ although this was only demonstrated in a single population and at a relatively modest level of statistical significance (p ≈ 0.01).

Appendix

Online Methods

Sample selection and genotyping

A total of 7514 cases and 9045 controls samples were included, from three GWA studies: WTCCC (UK), T1DGC (UK) GAIN/NIMH (USA); the samples, and their genotyping have been described previously.²,³,⁴ Numbers of samples from each study, and genotyping platform are given in supplementary table 1. SNP and sample exclusion criteria were as applied previously.⁴ Briefly, all subjects were of White European ancestry, and samples were excluded if they showed evidence of non-European ancestry, or of being duplicates of or closely related to another sample in the study. SNPs were excluded if the minor allele frequency (MAF) fell below 1% in cases or controls, if they deviated from Hardy-Weinberg equilibrium (p < 5.7 × 10⁻⁷), if the call rate fell below 95% (WTCCC and T1DGC) or if a genotype-calling metric indicated insufficient separation of the signal clouds (GoKinD/NIMH).²²

SNPs showing suggestive association in the imputed analysis were genotyped directly using TaqMan (Applied Biosystems) on a subset of the GWA samples (the T1DGC, all WTCCC cases and about half the WTCCC controls were unavailable to us), additional case-control samples, and a set of family samples with T1D affected offspring (supplementary table 1). The additional case and control samples have also been described previously.⁴ The family samples were drawn from across Europe and America, and are predominantly of White European origin; we did not exclude subjects who self-reported a non-White European origin as testing for transmissions within families is equivalent to a pseudo case control approach, with ethnically matched controls. All Taqman genotyping data were scored twice to minimize error; the second operator was unaware of case-control status and family structure.

Imputation

For each of the three studies considered, we divided SNPs from HapMap version 2 (release 24) into two sets - those which were genotyped and passed quality control (QC) thresholds in the study (X) and those which were not genotyped or failed QC (Y). The R package snpMatrix​⁶ from the Bioconductor project²³ was to used calculate imputation “rules” for prediction of each SNP in Y from nearby SNPs in X using HapMap genotypes and to carry out association tests for the imputed SNPs. The algorithms used in snpMatrix, together with the parameter settings we used, are described below.

In regions of high LD, the genotype of one SNP can be related to the genotypes of others by a linear regression²⁴,²⁵,²⁶. The first step in calculating an imputation rule is to select a set of “tag” SNPs by forward stepwise regression of the the Y SNP on the nearest 50 X SNPs (subject to a maximum missing data requirement). New SNPs are added to the regression until either (a) R² > 0.95, (b) the change in R² is < 0.05, or (c) the number of tag SNPs reaches four. Regression calculations are carried out at the genotype level, with each SNP genotype coded 0, 1, or 2. If a prediction R² ≥ 0.95 cannot be achieved using this stepwise regression approach, then an alternative imputation rule is attempted using the set of tag SNPs selected by the forward stepwise procedure. Using the conventional EM algorithm, frequencies are estimated for the haplotypes of the Y SNP plus the selected tags. Conditional probabilites of the Y allele given the tag SNP haplotype are calculated and provide the imputation rule. This rule is used in preference to the regression rule if the improvement in R² exceeds 0.1.

These imputation rules are then applied to the main study dataset to calculate the expectation of each Y SNP conditional on typed SNPs. Note that this expectation is not generally an integer and the Cochran-Armitage test then becomes a t-test comparing the mean imputation score in cases with that in controls. Extension to allow for stratified comparisons and to combine information from different studies is straightforward: differences between mean scores are simply averaged over strata (and studies), with weights inversely proportional to their variances. These procedures are all implemented in snpMatrix.

This imputation method is computationally faster than those based on hidden Markov models²⁷ or on variable length Markov chains.²⁸ For a subset of our data we compared our imputation results with those from IMPUTE²⁷ and found them to be very similar. It has an additional advantage over such methods in that, since each imputation is based on a small number of tag SNPs, it is easier to differentiate between genuine associations and those caused by poor clustering and differential measurement error; for each putative association, allele signal plots for all tags were visually inspected.

Association analysis

Single SNP association score tests were performed for each HapMap SNP within each cohort using direct genotypes if available, or imputed genotypes if not. The score is

$$\sum _i(Y_i-\stackrel{‒}{Y})(X_i-\stackrel{‒}{X})$$

where Y _i and X_i are the phenotypic (case/control) and genotype data respectively for subject i. When a SNP is not directly observed, X_i is replaced by its expected value calculated under the null hypothesis as described above. When it is poorly imputed, this expected value is shrunk towards X̅ and contributes little to the test statistic. The permutation variance (the variance under random permutation of Y ) is used to calculate the χ² test. The score statistics were combined first across strata within cohorts and finally across cohorts using the method proposed by Mantel.²⁹ The scores (U_i where i denotes cohort or stratum) and the variances (V _i) are summed to form an overall test of association, (Σ U_i)^T (Σ V _i)>⁻¹ (Σ U_i). Strata were defined by UK region in the case of the WTCCC and T1DGC samples, and an estimated ancestry score derived from principal components in the case of the GoKinD/NIMH samples.³ Testing for association with SNPs on the X chromosome was carried out using the method proposed by Clayton.³⁰ Over-dispersion of the test statistics was calculated after removal of known T1D loci⁴ and these parameters used to calculate adjusted p values given in table 2.

SNPs showing overall association (p < 1 × 10⁻⁷) in regions not previously reported⁴ were subject to further screening. Cluster plots of each SNP used for imputation were examined manually, and the result discarded unless all cluster plots for all cohorts were considered clearly separated. One of the cohorts studied (USA) was not designed as a T1D case-control study, and was serendipitously assembled after cases and controls were genotyped on different versions of the Affymetrix 500K chip and to different protocols. This cohort was subject to greater differential bias than the other cohorts. As a result, many SNPs were found which showed (often extreme) association in the USA samples (p < 1 × 10⁻⁷) but no association in the T1DGC and WTCCC samples combined (p < 1 × 10⁻³); for these SNPs, only the data from T1DGC and WTCCC were combined.

Family data were analysed by transmission disequilibrium test, splitting mulitplex families into parent offspring trios and using a pseudo-case control framework to estimate allelic effects. A score statistic was also generated, and a score test for association in case-controls and families combined conducted by summing the scores and variances as described above.

Imprinting test

We use a logistic regression approach to test for imprinting/and or maternal genotype effects on risk in offspring. This approach was originally proposed by Weinberg⁹,³¹ for data consisting of trios of an affected case and both his or her parents, but required extension to deal with our data which included families with multiple affected offspring. Weinberg’s approach is to analyse counts of case-parent trios classified by genotype of mother, M, father, P, and the affected offspring, O, in a 3 × 3 × 3 table. Of the 15 cells in this table consistent with Mendelian transmission, five concern families in which the genotypes of the two parents are concordant; these are not informative in the analysis. The remaining ten cells can be organized by mating type and offspring genotype into five pairs in which the maternal and paternal genotypes are considered interchangable (Supplementary Table 5). In the absence of maternal genotype and imprinting effects, and assuming that, in the population from which families are drawn, the two possible parental genotype combinations within each mating type are equally frequent, then their frequencies in case-parent trios will also not differ systematically. However maternal genotype and imprinting effects will distort these ratios. In supplementary table 5, pairs of genotype configurations are set out with the configuration in which the mother carries more copies of the “2” allele than the father appearing first. The table also sets out the predictions of a multiplicative model for relative risk conditional upon genotype and upon parents; the genotype relative risk for the offspring (γ_1/1, γ_1/2, and γ_2/2), are modified by multiplicative effects of the maternal genotype (φ_1/2 and φ_1/2, φ_1/1 being taken as 1) and by a factor λ if a “2” allele was received from the mother rather than from the father. The ratio of these two risks for each mating type gives the ratio of expected frequencies in case-parent trios. This model can be fitted to the observed pairs of case-parent trio frequencies using any standard logistic regression program, thus allowing estimation and testing of maternal genotype and imprinting effects.

Extension of this method to deal with families in which there may be several affected offspring is relatively straightforward. Again we tabulate counts of families by genotype of mothers, father, and offspring, but there are now more possible cells in the tabulation. For example, with two affected offspring there are seven informative pairs of genotype configurations (Supplementary Table 6). Under the assumption that the SNP under observation is the sole causal variant or has r² = 1 with a sole causal variant, disease occurrences in the offspring are conditionally independent given their genotypes and their parents, and the ratio of expected frequencies is given by the ratio of products of predicted relative risks for the two offspring. Extension to the case of more than two affected offspring follows similar principles. For families with three affected offspring there are nine informative pairs of genotype configuration, for four affected offspring, eleven, and so on. Logistic regression can then be used to estimate and test for effects of maternal genotype and imprinting in the general case where, as in our study, the data consist of families with varying numbers of affected offspring.

In the case where the SNP tested is not the sole causal variant (or in perfect LD with it), disease occurrences in offspring are not conditionally independent and there may be some bias. We would expect this to be small when the SNP has high r² with the causal variant. We also note that type 1 error rate will be unaffected by departure from conditional independence when testing the hypothesis of no imprinting and no maternal genotype effect against presence of either (or both) effects, although the method may then not be fully efficient.