Factors determining antibody distribution in tumors

Abstract

The development of antibody therapies for cancer is increasing rapidly, primarily owing to their specificity. Antibody distribution in tumors is often extremely uneven, however, leading to some malignant cells being exposed to saturating concentrations of antibody, whereas others are completely untargeted. This is detrimental because large regions of cells escape therapy, whereas other regions might be exposed to suboptimal concentrations that promote a selection of resistant mutants. The distribution of antibody depends on a variety of factors, including dose, affinity, antigens per cell and molecular size. Because these parameters are often known or easily estimated, a quick calculation based on simple modeling considerations can predict the uniformity of targeting within a tumor. Such analyses should enable experimental researchers to identify in a straightforward way the limitations in achieving evenly distributed antibody, and design and test improved antibody therapeutics more rationally.

Introduction

Traditional small molecule cancer therapeutics are often marginally selective between tumor cells and healthy tissue, leading to side effects and poor therapeutic indices. Antibodies provide a promising solution with their ability to bind specifically to surface antigens on cancer cells and selectively target the disease. Bound antibodies, in turn, can destroy tumor cells by recruiting immune effectors, blocking proliferative signaling or delivering toxic pay-loads such as small molecule drugs, biological toxins and radioisotopes [1,2]. For most of these mechanisms, cytotoxicity is limited to the cells that are bound by antibody, such that all of the cells in the tumor must be targeted to achieve a complete therapeutic response (exceptions include long-range radioisotope emissions and other bystander effects.) However, incomplete drug penetration into tumors has long been noted for antibodies [3-5], and also for chemotherapeutics [6] (Figure 1). This heterogeneous distribution can significantly reduce therapeutic efficacy by leaving a fraction of cells untargeted and viable. A qualitative understanding of the causes of incomplete antibody penetration into tumors is necessary to craft improved targeting molecules and better dosing strategies rationally [7].

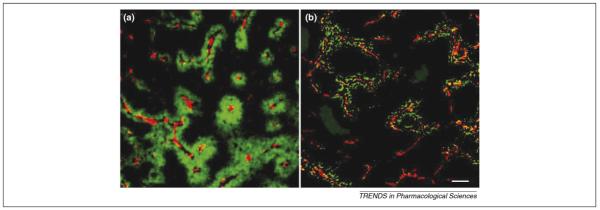
Figure 1.

Poor penetration of trastuzumab (a) and doxorubicin (b) into tumor tissue in xenograft tumor samples. Capillaries are labeled red and the drugs are labeled green. Large zones are essentially free of drug. The scale bar represents 100 μm. Modified, with permission, from Refs. [4] and [6].

Antibody targeting of tumors is a complex process involving extravasation across tumor capillaries, diffusion and binding within the tumor interstitium, plasma clearance, and internalization and catabolism in tumor cells (Figure 2). Furthermore, the clinical presentation of cancer often involves both vascularized solid tumors and prevascular micrometastases embedded in normal tissue, each of which have particular targeting properties and challenges. In particular, solid tumors have heterogeneous vasculature and high interstitial fluid pressure that limit convective flow and antibody extravasation, in addition to large regions of necrosis and hypoxia [8]. Due to the complex nature of tumor targeting, it is difficult to understand or predict antibody distribution without the aid of computational modeling.

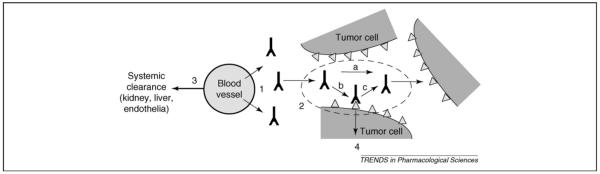
Figure 2.

Processes of antibody distribution in tumor tissue. (1) Extravasation of antibody across the tumor blood vessel walls is a function of the vessel permeability and occurs slowly. (2) Once in the tumor tissue, the antibodies diffuse freely in the extracellular matrix (a), with their motion retarded by formation of immobile complexes owing to binding (b) and dissociation (c), which are functions of affinity. (3) Antibody administered in the plasma, which supplies free antibody to the tumor, is cleared through several mechanisms, depending on its size, charge and Fc receptor binding. (4) While bound to surface antigens, local clearance of antibodies occurs owing to internalization and degradation at a rate determined by the target antigen.

Static images of tumors taken after systemic delivery of antibodies reveal regions of high concentration adjacent to areas that have no detectable antibody, a phenomenon often referred to as a ‘binding site barrier’ [9]. Despite the crisp outline of drug penetration shown in Figure 1, this does not result from a discrete morphological or physical barrier. Rather, it is a dynamic, potentially moving front resulting from a balance of opposing rates. The key rates that determine where this boundary is located are shown in schematic and tabular form in Figure 2 and Table 1. In broad terms, antibody penetration from capillary extravasation and diffusion is limited by systemic clearance from the plasma and antibody degradation in the tumor tissue. Here, we consider each of these processes in turn, focusing in particular on parameter values appropriate for antibodies and antibody fragments. We then illustrate how these processes can be reduced to simple ratios of critical rates that can be used to predict antibody penetration in tumors and aid in therapeutic development and testing.

Table 1.

Characteristic penetration and consumption terms for antibody distribution

	Process	Rate	Typical characteristic times (1/rate)
1	Capillary extravasation	$\frac{2{\mathsf{PR}}_{\text{capillary}}}{{\mathsf{R}}^2}$	Hours to days (from tumor vasculature)
2	Diffusion with bindinga	$\frac{\mathsf{D}({\left[\mathsf{Ab}\right]}_{\mathrm{surf}}+{\mathsf{K}}_{\mathsf{d}})}{{\mathsf{R}}^2\left[\mathsf{Ag}\right]∕\epsilon }$	Minutes to days
3	Systemic clearance	$\frac{1}{\frac{\mathsf{A}}{\alpha }+\frac{\mathsf{B}}{\beta }}$	Minutes: scFv and peptides Hours: Fab Days: IgG
4	Internalization	ke	Minutes: receptors (ErbB) Hours: constitutive surface (CEA, mucins) Days: tight junction, extracellular (A33, EDB)
a	Free diffusion	D/R2	Minutes (R = 100 μm)
b	Association	kon[Ag]/ε	Seconds
c	Dissociation	koff	Minutes to days

Abbreviations: A33, antigen bound by monoclonal antibody A33; CEA, carcinoembryonic antigen; EDB, extra domain B fibronectin antigen.

Parameters: capillary extravasation is given by $\mathrm{P}\frac{\mathrm{S}}{\mathrm{V}}({\left[\mathrm{Ab}\right]}_{\text{plasma}}-{\left[\mathrm{Ab}\right]}_{\text{surf}})$ where P ≡ permeability coefficient; $\frac{\mathrm{S}}{\mathrm{V}}\approx \frac{2{\mathrm{R}}_{\text{capillary}}}{{\mathrm{R}}^2}$ ≡ capillary surface area per tumor volume;

[Ab]_surf ≡ antibody concentration at capillary surface;

R_capillary ≡ capillary radius, R ≡ half-maximum inter-capillary distance;

D ≡ effective drug diffusivity in tumor tissue;

[Ag] ≡ antigen concentration per tumor volume;

ε ≡ drug-accessible tumor volume fraction;

${\mathrm{K}}_{\mathrm{d}}=\frac{{\mathrm{k}}_{\mathrm{off}}}{{\mathrm{k}}_{\mathrm{on}}}$ ≡ equilibrium, dissociation and association constants;

systemic clearance is described by a biexponential form, [Ab]_plasma = [Ab]_plasma,o(Ae^-αt + Be^-βt);

k_e ≡ net endocytic uptake rate constant.

^aThis equation is only valid for cases in which the antibody concentration and affinity are lower than the antigen concentration ([Ab]_surf < < [Ag]/ε, K_d < < [Ag]/ε), both requirements that are satisfied for most targeting experiments. For all other situations, binding is insignificant and the diffusion rate reverts to D/R².

Antibody penetration rate processes

Capillary extravasation

In healthy vasculature, macromolecules move into tissues by convection, transcytosis and diffusion across the capillary wall [8]. However, tumors largely lack draining lymphatics [10] and, consequently, build up interstitial hydrostatic pressure, severely restricting convection [11]. As a result, exit of antibodies from the capillary occurs primarily by diffusion across pores. This causes few problems for small molecules with rapid diffusion rates but puts a significant restriction on the extravasation of macromolecules. Poor extravasation across tumor blood vessels results in tumors being exposed to antibody concentrations that can be several orders of magnitude below the concentration in the plasma. By contrast, avascular metastases embedded in healthy tissue are exposed to levels close to that in the plasma owing to normal draining convective fluid flow. This difference produces qualitatively worse penetration into bulk tumors. The rate of macromolecular extravasation depends on the capillary surface area-to-tumor volume ratio and the macromolecular permeability coefficient P (Table 1, point 1), values of which have been measured for proteins [12] and dextrans [13] of various sizes.

Diffusion with binding

This process is less well described in the literature and consists of the progressive movement of antibody through the tumor interstitium by random Brownian motion, retarded by formation of immobile antibody-antigen complexes [14] (Table 1, point 2). An analogous situation occurs with many small molecule chemotherapeutics that bind to DNA, such as doxorubicin [6]. Diffusion of antibodies is quantified by the coefficient D, which has been measured in tumor xenografts and biopsies previously [15,16]. Antigen-antibody complex formation can be considered to reach equilibrium rapidly when binding (Figure 2, point b) is faster than free diffusion (Figure 2, point a), and also more rapid than endocytic uptake (Figure 2, point 4), conditions often met in practice. In this situation, unbound antibody is rapidly depleted to ‘fill up’ available antigen-binding sites, and the zone containing free antibody moves into the tumor volume only as quickly as those sites can be fully occupied. This process has been described previously for antibodies with high affinity [14,17], and here it is generalized to the case of weaker binders. The required distance R for penetration to target all cells in a tumor is determined by the maximum intercapillary distance, and is ∼100 μm for viable cells in most tumor types [18]. Longer distances can also be used for more conservative estimates.

Clearance rate processes

Systemic clearance

The concentration gradient driving penetration into the tumor is only maintained until the drug has cleared from circulation to a concentration below that present in the tumor. The organ of clearance is a function of the size of the molecule and its interaction with receptors such as the asialoglycoprotein receptor in the liver or neonatal Fc receptor (FcRn) disseminated throughout the endothelial vascular surface area. Whereas small molecule drugs can be heavily influenced by their physiochemical properties (e.g. lipophilicity), antibodies and fragments are hydrophilic and primarily remain in the plasma and extracellular (interstitial) space before clearance. Most current antibody therapeutics (e.g. rituximab, trastuzumab and cetuximab) are whole IgGs (immunoglobulin G molecules), which persist in the plasma for several weeks owing to their large size and salvage from endothelial pinocytosis by the FcRn. Antibody fragments smaller than ∼50 kDa [e.g. single-chain variable fragments (scFv), variable fragments (Fabs)] are rapidly cleared through renal filtration. Systemic clearance is generally well described by a biexponential decay of the plasma concentration with rate terms A, B, α and β (Table 1, point 3).

Endocytic metabolism

All antigens on the cell surface are turned over at a nonzero constitutive rate, ranging from minutes to days [19-21] (Table 1, point 4). After binding, antibodies are internalized at a similar rate as the antigen and eventually trafficked to the lysosome for degradation. Newly synthesized antigen molecules refill the surface pool, binding and internalizing additional antibody molecules to produce a constitutive route of antibody clearance. Rapid antibody uptake can be reduced by efficient recycling of the antibody-antigen complex to the cell surface following endocytosis, a process observed for trastuzumab, an FDA-approved antibody for breast cancer that targets ErbB2 (erythroblastic leukemia viral oncogene homolog 2) [20,22]. Internalization rates are often confounded in biodistribution experiments owing to retention of labeled byproducts (e.g. with radiometals) or loss of degraded label (e.g. radioiodine) [23].

Scaling analyses of antibody penetration versus endocytic and systemic clearance

Although each of the rates described in Table 1 are individually important for describing antibody distribution in tumors, it is the relative values of these rates that ultimately determine the extent of antibody penetration. A simple and qualitative approach to considering which processes dominate and which are limiting in a particular situation is to define dimensionless ratios of the rates [24] (Table 2). Three such dimensionless numbers are useful in understanding the tumor penetration problem - two analogous to previously defined terms (the Thiele modulus and the Biot number) and one unique to pharmacokinetic modeling (the clearance modulus) [17].

Table 2.

Dimensionless numbers predicting antibody penetration into tumors^a

Dimensionless ratios	Definition	Notes
Biot number (Bi)
$\frac{\text{Capillary extravasation}(\text{Table 1},\text{point 1})}{\text{Free diffusion rate}(\text{Table 1},\text{point a})}$	$\mathsf{Bi}=\frac{2{\mathsf{PR}}_{\text{capillary}}}{\mathsf{D}}$	<<1 for both IgG and scFv giving [Ab]surf ≈ Bi [Ab]plasma for solid tumors
Clearance modulus (Γ)
$\frac{\text{Systemic clearance rate}(\text{Table 1},\text{point 3})}{\text{Diffusion with binding rate}(\text{Table 1},\text{point 2})}$	$\Gamma =\frac{1}{\frac{\mathsf{A}}{\alpha }+\frac{\mathsf{B}}{\beta }}\frac{{\mathsf{R}}^2\left[\mathsf{Ag}\right]∕\epsilon }{\mathsf{D}({\left[\mathsf{Ab}\right]}_{\text{surf}}+{\mathsf{K}}_{\mathsf{d}})}$	$\text{Alternative form}(\Gamma =1)\mathsf{R}\approx \sqrt{\frac{\mathsf{D}({\left[\mathsf{Ab}\right]}_{\text{surf}}+{\mathsf{K}}_{\mathsf{d}})}{(\left[\mathsf{Ag}\right]∕\epsilon )}\left(\frac{\mathsf{A}}{\alpha }+\frac{\mathsf{B}}{\beta }\right)}$
Thiele modulus (φ2)
$\frac{\text{Internalization rate}(\text{Table 1},\text{point 4})}{\text{Diffusion with binding rate}(\text{Table 1},\text{point 2})}$	${\varphi }^2=\frac{{\mathsf{k}}_{\mathsf{e}}{\mathsf{R}}^2\left[\mathsf{Ag}\right]∕\epsilon }{\mathsf{D}({\left[\mathsf{Ab}\right]}_{\text{surf}}+{\mathsf{K}}_{\mathsf{d}})}$	$\text{Alternative form}({\varphi }^2=1)\mathsf{R}\approx \sqrt{\frac{\mathsf{D}({\left[\mathsf{Ab}\right]}_{\text{surf}}+{\mathsf{K}}_{\mathsf{d}})}{{\mathsf{k}}_{\mathsf{e}}(\left[\mathsf{Ag}\right]∕\epsilon )}}$

^aThe units must cancel for each of these numbers to give the correct value, hence the name ‘dimensionless ratio’.

The Biot number is a ratio between the rates of antibody extravasation from the capillary versus diffusion through the tumor tissue. For typical parameter values, the Biot number is small (Bi << 1), indicating that extravasation is a more significant barrier to targeting than subsequent diffusion. When the Biot number is small, the antibody concentration at the surface of the tumor [Ab]_surf can be approximated as Bi [Ab]_plasma. With typical Biot numbers for antibodies of the order of 0.001, a plasma concentration of 1 μM is reduced to only 1 nM at the capillary surface in contact with the tumor tissue. The low Biot number highlights the essential difficulty in antibody delivery to vascularized tumors in contrast to micrometastases.

The Thiele and clearance moduli compare the rates of passive antibody transport due to capillary extravasation and diffusion to the rates of antibody loss due to cellular catabolism or plasma clearance, respectively. Both values can be calculated for specific cases and used to predict whether antibody will reach the target distance R. If both the Thiele and clearance moduli are <1, penetration will be faster than clearance and the antibody will reach the target distance [17]. If either modulus is >1, clearance will be faster than penetration and the moving antibody front will stop before reaching the target distance. IgGs generally satisfy the clearance modulus criterion (Γ < 1) owing to their long serum half-lifes; however, antibody fragments (scFvs and Fabs) often fail this test because they are rapidly cleared through the kidney. Both IgG and fragments can exhibit internalization-mediated limitations to penetration by the Thiele modulus criterion.

The Thiele and clearance moduli can also be used to predict the approximate penetration depth for an antibody by finding the distance R for which the Thiele or clearance modulus is ∼1 (Table 2). Because penetration depth is predicted by this analysis to be proportional to the square root of antibody concentration [Ab]_surf, this relationship predicts a requirement for excessive dosages to obtain antibody penetration to a depth of 100 μm for many antibodies. These predictions are consistent with early observations using radiolabeled antibody, where doses of 800 μg to 1 mg per mouse were required to achieve relatively homogeneous targeting of xenografts [25,26]. In a similar manner, the dose necessary to achieve saturation can be determined by setting the Thiele and clearance numbers to 1 and solving for [Ab]_plasma.

In the cited theoretical analyses [14,17], high-affinity antibodies were considered. The more general moduli defined here include the possibility of lower affinity interactions (i.e. K_d ≥ [Ab]_surf). Such antibodies are typically able to penetrate farther into the tumor tissue owing to their ability to dissociate from antigen following binding and continue diffusing through the interstitial space. It is crucial, however, to distinguish penetration from saturation - in the high-affinity limit, all antigen sites are saturated, layer after layer, as antibody penetrates into the tissue. In the low-affinity case, antibody penetrates farther but targets a smaller fraction of antigen on the cell surface owing to its weaker interaction strength. In general, with a sustained plasma concentration the fractional antigen saturation of targeted cells will be approximately:

$$\frac{{\left[\mathrm{Ab}\right]}_{\text{surf}}}{\frac{{\mathrm{k}}_{\mathrm{off}}+{\mathrm{k}}_{\mathrm{e}}}{{\mathrm{k}}_{\mathrm{on}}}+{\left[\mathrm{Ab}\right]}_{\text{surf}}}$$

Conclusions

Mathematical modeling of antibody penetration into tumors will be most useful if it can lead to qualitative insights that are incorporated into improved therapeutic design and experimentation. We suggest that calculation of the dimensionless numbers in Table 2 is a straightforward and accessible approach to gain useful perspectives on the dominant rate processes inherent to any tumor-targeting strategy without the need for complex computational tools. Parameter values for the terms present in these dimensionless groups have been measured and tabulated for many antibody formats and tumor types [14,17,27,28]. Additionally, parameters that are antibody- or target dependent, such as antibody affinity, antigen density and net internalization rate, can be measured in vitro by antibody titrations, surface quenching uptake assays and other experimental approaches [20,29]. For cases in which parameter values are less well known, conservative estimates can be made to ensure saturation if the criteria are achieved.

The three dimensionless numbers in Table 2 provide guidance on how variation of the particular parameters could be expected to affect antibody penetration into tumors. For example, if φ² > 1, then endocytic consumption is limiting and saturation cannot be obtained simply by extending the lifetime of the antibody in circulation. As another example, doubling the penetration depth of antibody is expected to require at least a quadrupling of the antibody dose, regardless of whether systemic or endocytic clearance is the limiting factor. Such insights should help experimental researchers to interpret biodistribution results, predict targeting outcomes and engineer improved targeting agents or dosing strategies.